Screening Constant per Unit Nuclear Charge Studies of Rydberg Resonances Due to the 4p → nd and ns Transitions in Se⁺ Ions

Abstract

Calculations of high-lying energy resonances of 12 Rydberg series due to the 4p → nd and 4p → ns transitions from the 4s²4p^3 3S°_3/2 ground-state and the 4s²4p^3 2P°_3/2,1/2 and 4s²4p^3 2D°_5/2,3/2 metastable states of the Se⁺ ion are reported. The calculations believed to be the first theoretical ones are performed using the Screening Constant per Unit Nuclear Charge (SCUNC) method up to n = 40. Analysis of the present results is achieved in the framework of the standard quantum-defect theory and of the SCUNC-procedure by calculating the effective nuclear charge. For many resonances, the SCUNC-method reproduces the ALS measurements excellently [Esteves et al., Phys. Rev. A, 84 013406 (2011)] up to n = 25. However, for some resonances belonging to the 4s²4p² (¹D₂)nd (²D) and 4s²4p² (¹D₂)ns (²D) and to the 4s²4p² (¹D₂)nd (²S) and 4s²4p² (¹D₂)nd (²P_1/2) Rydberg series, the ALS data overlap at high n values. In addition, negative quantum-defect values were determined where positive values are allowable. In the present work, positive quantum defect values almost constants are obtained along all the series investigated up to n = 40, and the narrow resonances are clearly separated. Overall, the present theoretical study provides confidence in the ALS data on Se⁺ ions for astrophysical interest as far as the understanding of the chemical evolution of Se in the universe is concerned.

1. Introduction

It is well-known that visible matter in the universe is almost in the plasma state, and most observational data about the distant universe are conveyed through interstellar space by photons. Some of these photons are sufficiently energetic to induce the photoionization of atoms and ions according to the process:

γ + A^q+ → A^(q+m)+ + me⁻

Photoionization of atoms and ions is then a fundamental process of importance in many astrophysical systems such as stars and nebulae. Of the greatly important ions, interesting to investigate are those of the elements in connection with their abundances in photoionized astrophysical nebulae. For Z > 30, neutron (n)-capture elements (e.g., Se, Kr, Br, Xe, Rb, Ba and Pb) produced by slow or rapid n-capture nucleosynthesis have been detected in a large number of ionized nebulae [1,2,3,4]. As stated by Covington et al. [5], quantitative measurements of photoionization of ions provide precision data on ionic structure and guidance to the development of theoretical models of multielectron interactions. In the particular case of the Se element, absolute single photoionization cross-section measurements for Se⁺ ions were performed at the Advanced Light Source (ALS) at Lawrence Berkeley National Laboratory using the photo-ion merged-beams technique [6]. The measurements were made at a photon energy resolution of 5.5 meV from 17.75 to 21.85 eV spanning the 4s²4p^{3 3}S°_3/2 ground-state ionization threshold and the 4s²4p^{3 2}P°_3/2,1/2 and 4s²4p^{3 2}D°_5/2,3/2 metastable states. Analysis of the autoionizing resonance features produced detailed identifications of numerous Rydberg series of resonances where as many as 19 members of a series due to the 4p → nd and 4p → ns transitions in the Se⁺ ions were identified. The Rydberg resonance series identifications included comparative analysis of the quantum defect parameter. Using the Breit-Pauli and Dirac-Coulomb R-matrix approximations, McLaughlin and Ballance [7] reported the first theoretical calculations of the resonance positions and quantum defects of the 4s²4p² (¹D₂)nd and 4s²4p² (¹S₀)nd Rydberg series of Se⁺. It should be underlined that, in the earlier experiments on Se⁺ [6,8], the measurements were motivated by the detection of Se emission lines in a large number of ionized astrophysical nebulae [6]. In these works, the photon energy studied in the experiments ranged from 18.0 to 31.0 eV and was scanned with a nominal spectral resolution of 28 meV. After the publication of the results in Ref. [8], the possibility of errors in absolute measurements due to higher-order radiation in the photon beam at these very low beamline energies was a concern [6]. To augment the resonance analysis in Ref. [8], higher photon energy resolution of 5.5 meV from 17.75 to 21.85 eV have been used to correct all the experimental energy positions and quantum defects measured previously [8]. Subsequently, the accurate results and the reach structures in the photoionization process of Se⁺ ions are those reported in Esteves et al. [6]. In connection with the importance of neutron (n)-capture elements produced by slow or rapid n-capture nucleosynthesis, various methods have been applied recently to study photoionization of Br³⁺ [9,10] and Rb²⁺ [11,12]. In these studies, the Screening Constant per Unit Nuclear Charge (SCUNC) method has been used to report accurate results [10,12]. In addition, in the recent past [13], the SCUNC-method has been used to excellently reproduce the ALS data [6] up to n = 25 as far as the 4s²4p² (¹D₂)nd and 4s²4p² (¹S₀)nd Rydberg series of Se⁺ are concerned. In general, the SCUNC formalism is known to be a powerful semi-empirical method very suitable to the study of photoionization of atomic species, as demonstrated in various recent papers [14,15,16,17,18,19]. The motivation of the present work is to complete our previous study [13]. We report high-lying energy resonances of 12 Rydberg series due to the 4p → nd and 4p → ns transitions from 4s²4p^{3 3}S°_3/2 ground-state ionization threshold and the 4s²4p^{3 2}P°_3/2,1/2 and 4s²4p^{3 2}D°_5/2,3/2 metastable states of the Se⁺ ion. Comparison is performed with the ALS measurements [6]. Analysis of the present results is achieved in the framework of the standard quantum-defect theory and of the SCUNC-procedure by calculating the effective charge. The present paper is organized as follows. Section 2 presents a brief outline of the theoretical part of the work. In Section 3, we present and discuss our results compared with the available ALS experimental data [6]. We summarize our study and draw conclusions in Section 4.

2. Theory

2.1. Brief Description of the SCUNC Formalism

In the framework of the Screening Constant per Unit Nuclear Charge formalism, the total energy of the (Nl, nl′; ^2S+1L^π) excited states is expressed in the form (in Rydberg) [8,9]:

$$E\left(Nl,n{l}^{\prime } ; {}^{2S+1}L^{\pi }\right) = - Z^2 \left(\frac{1}{N^2} + \frac{1}{n^2} {\left[ 1 - \beta \left(Nl,n{l}^{\prime } ; {}^{2S+1}L^{\pi }; Z\right) \right] }^2\right)$$

(1)

In this equation, the principal quantum numbers N and n are, respectively, for the inner and the outer electron of the helium-isoelectronic series. The β-parameters are screening constants per unit nuclear charge expanded in inverse powers of the nuclear charge Z and given by:

$$\beta \left(Nl n{l}^{\prime }; {}^{2S+1}L^{\pi };Z\right) = {\displaystyle \sum _{k = 1}^q{f}_k{\left(\frac{1}{Z}\right)}^k}$$

(2)

where $f_k = f_k\left(Nl n{l}^{\prime }; {}^{2S+1}L^{\pi }\right)$ are screening constants to be evaluated empirically.

For a given Rydberg series originating from a-^2S+1L_J state, we obtain:

$$E_n=E_{\infty }-\frac{Z^2}{n^2}{\left[1-\beta (nl;s,\mu ,\nu {,}^{2S+1}{L}^{\pi }.Z)\right]}^{{}^2}$$

(3)

In Equation (1), ν and μ (μ > ν) denote the principal quantum numbers of the (^2S+1L_J) nl Rydberg series used in the empirical determination of the f_i screening constants, s represents the spin of the nl-electron (s = ½), E_∞ is the energy value of the series limit, E_n denotes the resonance energy and Z₀ stands for the atomic number. The β-parameters are screening constants per unit nuclear charge expanded in inverse powers of Z₀ and given by:

$$\beta (Z,{}^{2S+1}L_J,n,s,\mu ,\nu ) = {\displaystyle \sum _{k = 1}^q{f}_k{\left(\frac{1}{Z}\right)}^k}$$

(4)

where $f_k = f_k({}^{2S+1}L_J,n,s,\mu ,\nu )$ are screening constants to be evaluated empirically.

$$E_n=E_{\infty }-\frac{Z^2}{n^2}\{1-\frac{f_1({}^{2S+1}L_J^{\pi })}{Z(n-1)}-\frac{f_2({}^{2S+1}L_J^{\pi })}{Z}{\pm {\displaystyle \sum _{k=1}^q{\displaystyle \sum _{k^{\prime }=1}^{q^{\prime }}{f}_1^{k^{\prime }}F(n,\mu ,\nu ,s)\times {\left(\frac{1}{Z}\right)}^k}}\}}^2$$

(5)

In Equation (5), $\pm {\displaystyle \sum _{k=1}^q{\displaystyle \sum _{k^{\prime }=1}^{q^{\prime }}{f}_1^{k^{\prime }}F(n,\mu ,\nu ,s)\times {\left(\frac{1}{Z}\right)}^k}}$ is a corrective term introduced to stabilize the resonance energies by increasing the principal quantum number n.

Equation (3) can be rewritten in terms of the effective nuclear charge Z* as follows [19].

$$E_n=E_{\infty }-\frac{Z{*}^2}{n^2}$$

(6)

In the framework of the SCUNC formalism, the relationship between the nuclear effective charge Z* and the quantum defect δ is in the form [18,19]:

$$Z^{*}=\frac{Z_{core}}{\left(1-\delta /n\right)}$$

(7)

According to this equation, each Rydberg series must satisfy the following conditions:

$$\{\begin{array}{ll}{Z}^{*}\ge Z_{core}\hspace{1em}& if\hspace{1em}\delta \ge 0\\ Z^{*}\le Z_{core}\hspace{1em}& if\hspace{1em}\delta \le 0\\ \lim Z{*}_{n\to \infty }& =Z_{core}\end{array}$$

(8)

Additionally, the f₂-parameter in Equation (3) is theoretically given by the equation [18,19]:

f₂ = Z − Z_core

(9)

2.2. Energy Resonances of the Rydberg Series Due to the 4p → nd and 4p → ns Transitions

As stated by Esteves et al. [6], the NIST source data from Moore [20] reports the energies of the ³P₁ and ³P₂ levels of Se²⁺ to be, respectively, 0.216 and 0.488 eV above the ground-state, while the online version of the Cowan atomic code available from Los Alamos National Laboratory [21] quoted these energies to be 0.194 and 0.448 eV, respectively. However, the ALS studies [6] determined the ³P₂ fine-structure energy level at 0.493 ± 0.010 eV above the ground-state, and no series were found to converge to the ³P₁ state. As a result, the ³P₁ level is not considered in this work. Hence, the present calculations are focused on the Rydberg series of resonances due to the 4p→ nd and 4p → ns transitions in Se⁺ converging to the ¹D₂ and ³P₂ series limits in the Se²⁺ residual ion.

For a photoionization process from an atomic X^p+, we get:

X^p+ + hν → X^(p+1)+ + e⁻.

(10)

For the Se⁺ ions considered in this work, Equation (7) gives:

Se⁺ + hν → Se²⁺ + e⁻.

(11)

Thus, for the Se⁺ ions, Z_core = 2 and f₂ = (34 − 2) = 32.0.

Using Equation (5), we find the semi-empirical formulas used in the present work.

• For the Rydberg series starting from the lowest resonance n = ν = 6:

$$E_n=E_{\infty }-\frac{Z^2}{n^2}\{1-\frac{f_1({}^{2S+1}L_J^{\pi })}{Z(n-1)}-\frac{32}{Z}{-\frac{f_1({}^{2S+1}L_J^{\pi })\times (n-6)}{Z^2{(n-5)}^2}-\frac{f_1({}^{2S+1}L_J^{\pi })\times {(n-6)}^2}{Z^3{(n-5)}^2}\}}^2$$

(12)

• For the Rydberg series starting from the lowest resonance n = ν = 7:

$$E_n=E_{\infty }-\frac{Z^2}{n^2}\{1-\frac{f_1({}^{2S+1}L_J^{\pi })}{Z(n-1)}-\frac{32}{Z}{-\frac{f_1({}^{2S+1}L_J^{\pi })\times (n-7)}{Z^2{(n+2)}^2}-\frac{f_1({}^{2S+1}L_J^{\pi })\times {(n-7)}^2}{Z^3{(n-6)}^2}\}}^2$$

(13)

• For the Rydberg series starting from the lowest resonance n = ν = 11:

$$E_n=E_{\infty }-\frac{Z^2}{n^2}\{1-\frac{f_1({}^{2S+1}L_J^{\pi })}{Z(n-1)}-\frac{32}{Z}{-\frac{f_1({}^{2S+1}L_J^{\pi })\times (n-11)}{Z^2{(n-7)}^2}-\frac{f_1({}^{2S+1}L_J^{\pi })\times {(n-11)}^2}{Z^3{(n-9)}^2}\}}^2$$

(14)

The remaining f₁ parameters in Equations (12)–(14) are to be evaluated empirically using the ALS data [6] for ν = 6, 7 or 11 according to the Rydberg series considered. The values obtained are presented in the last line of each table.

3. Results and Discussion

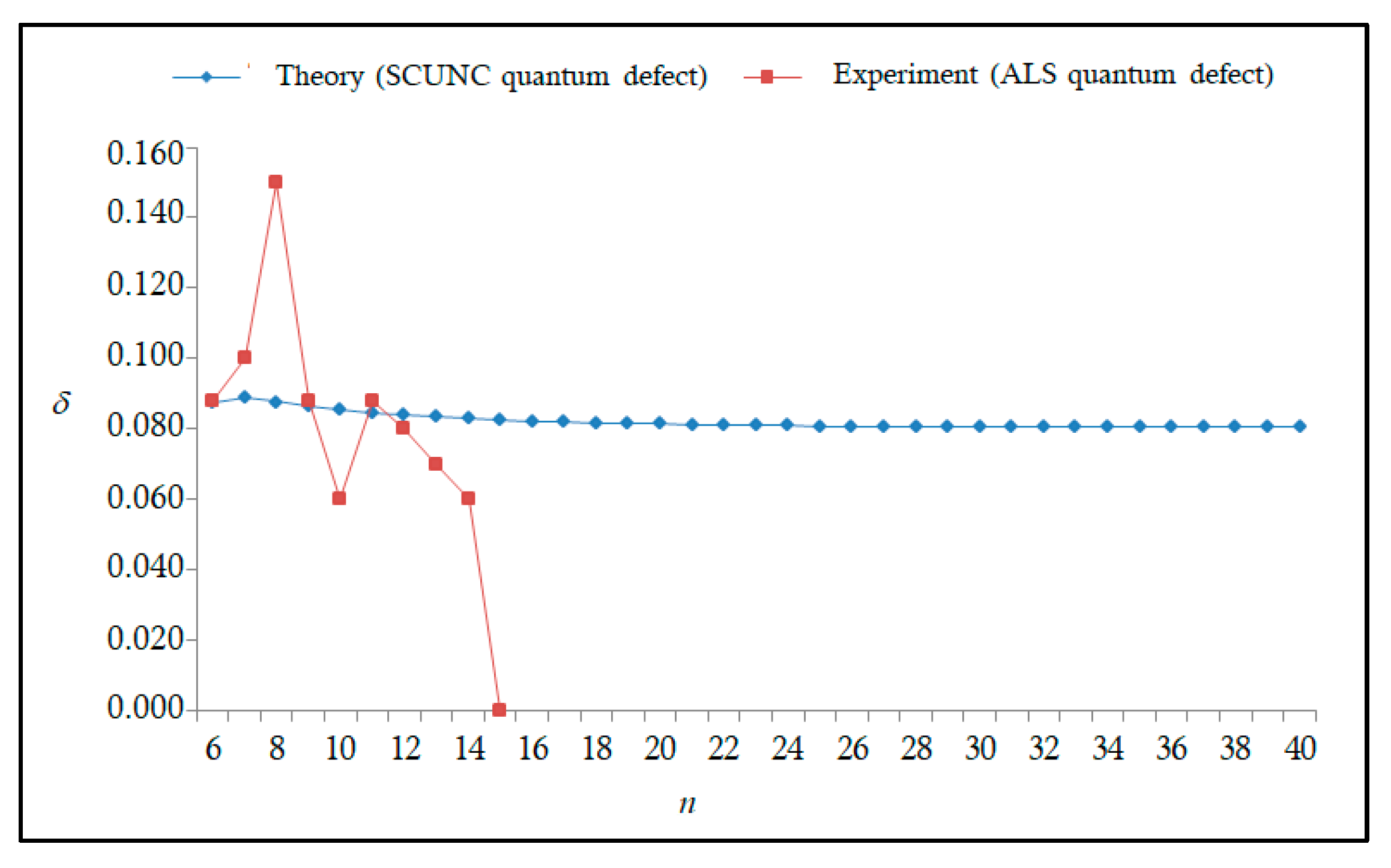
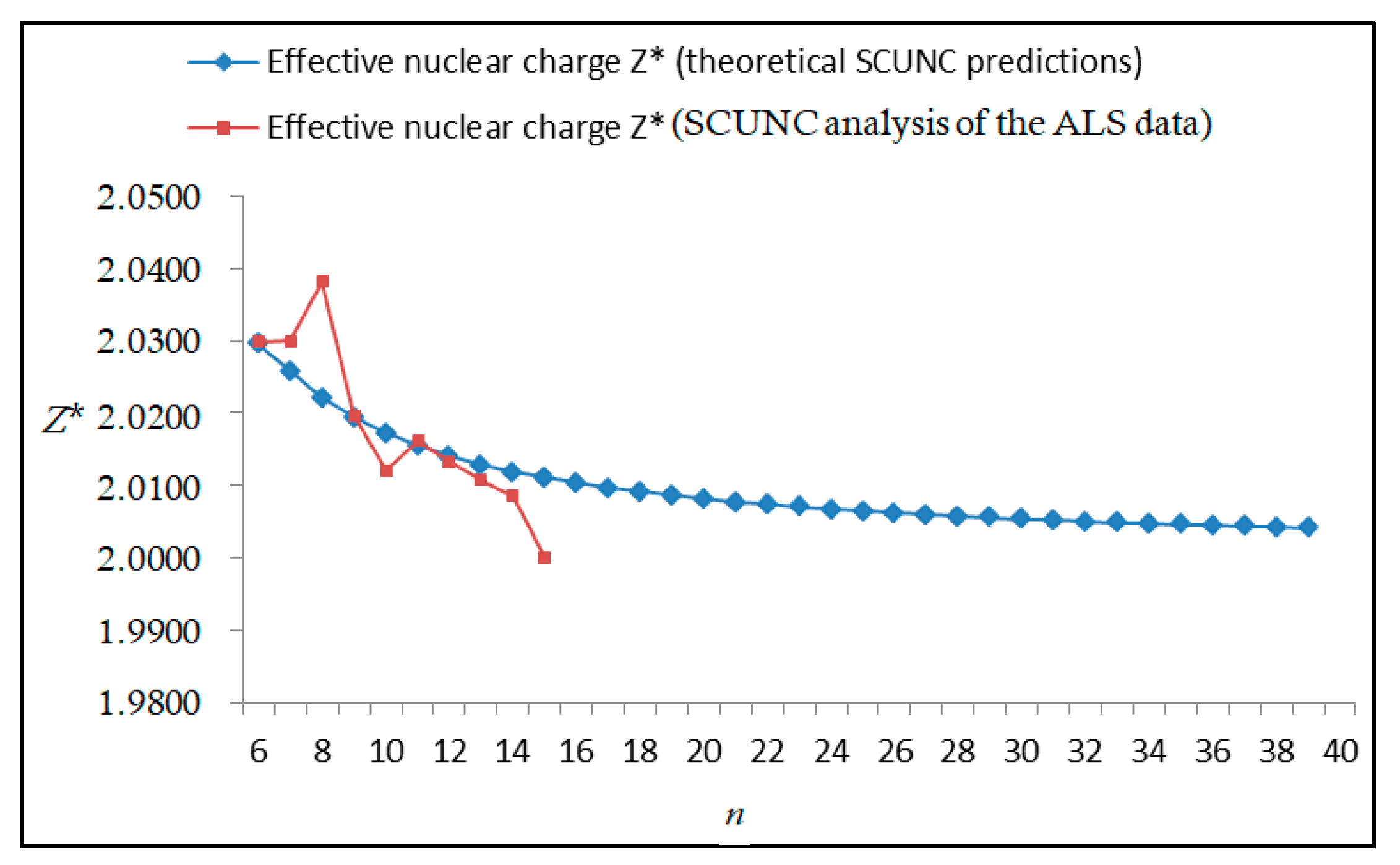
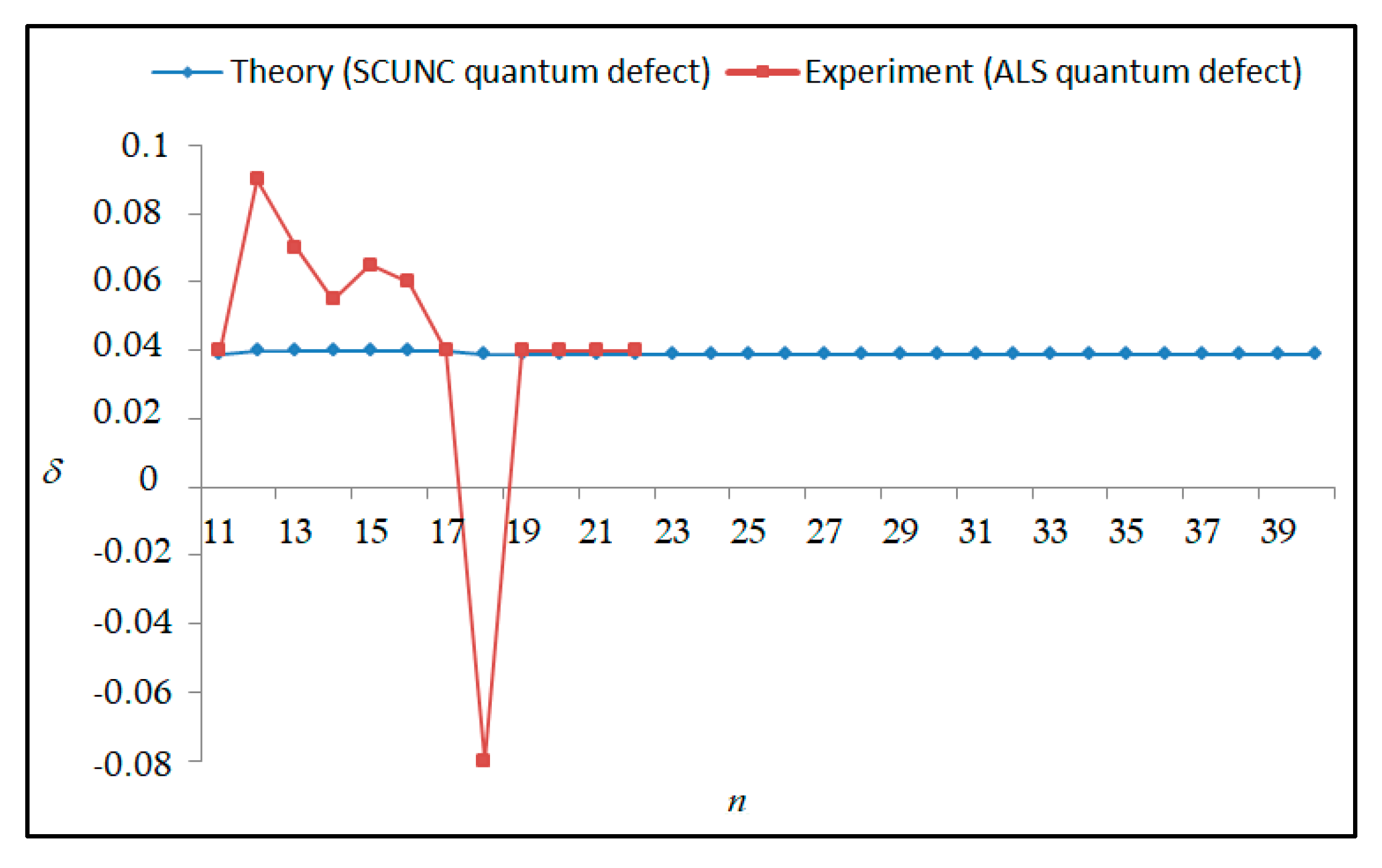
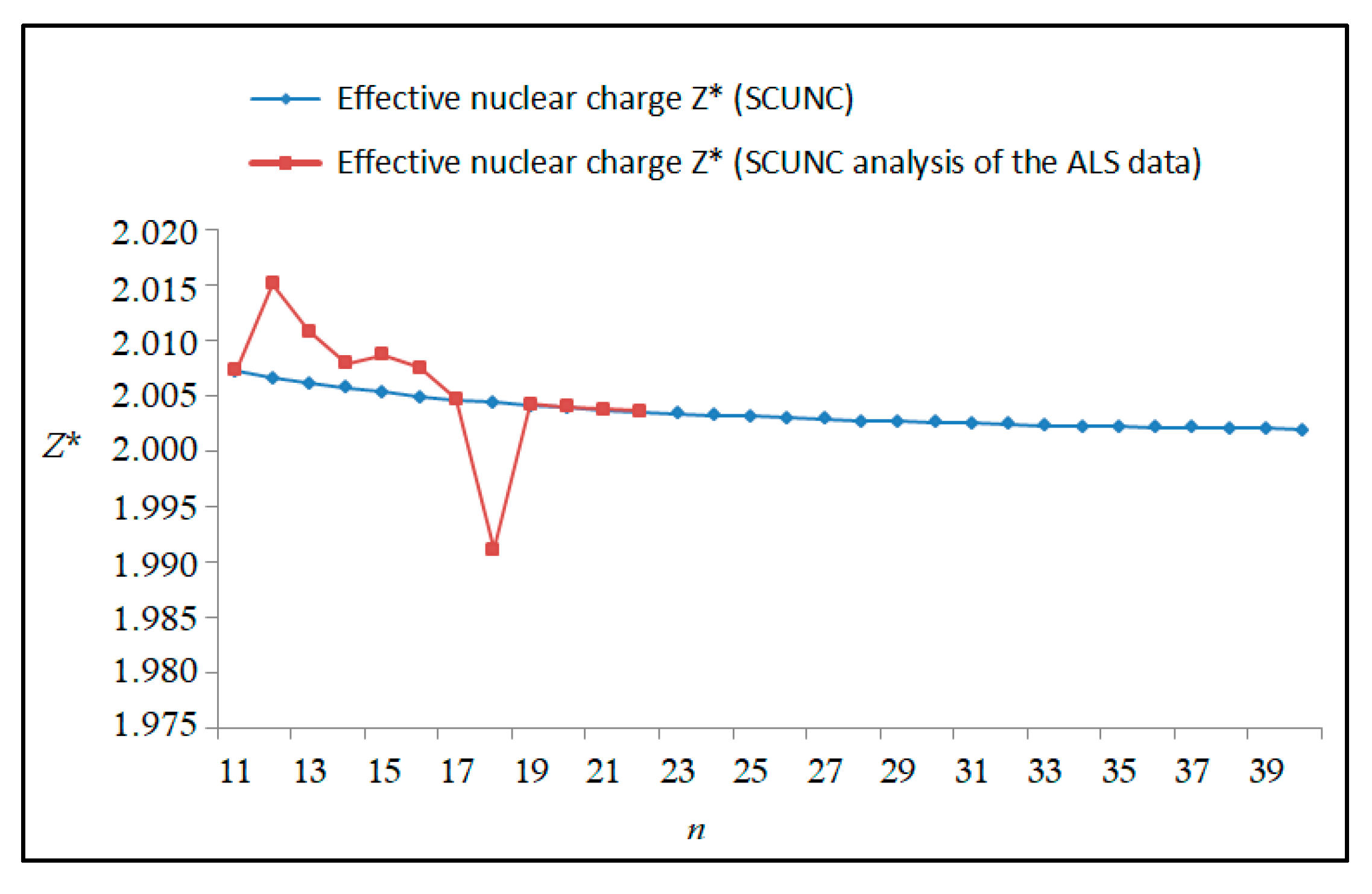
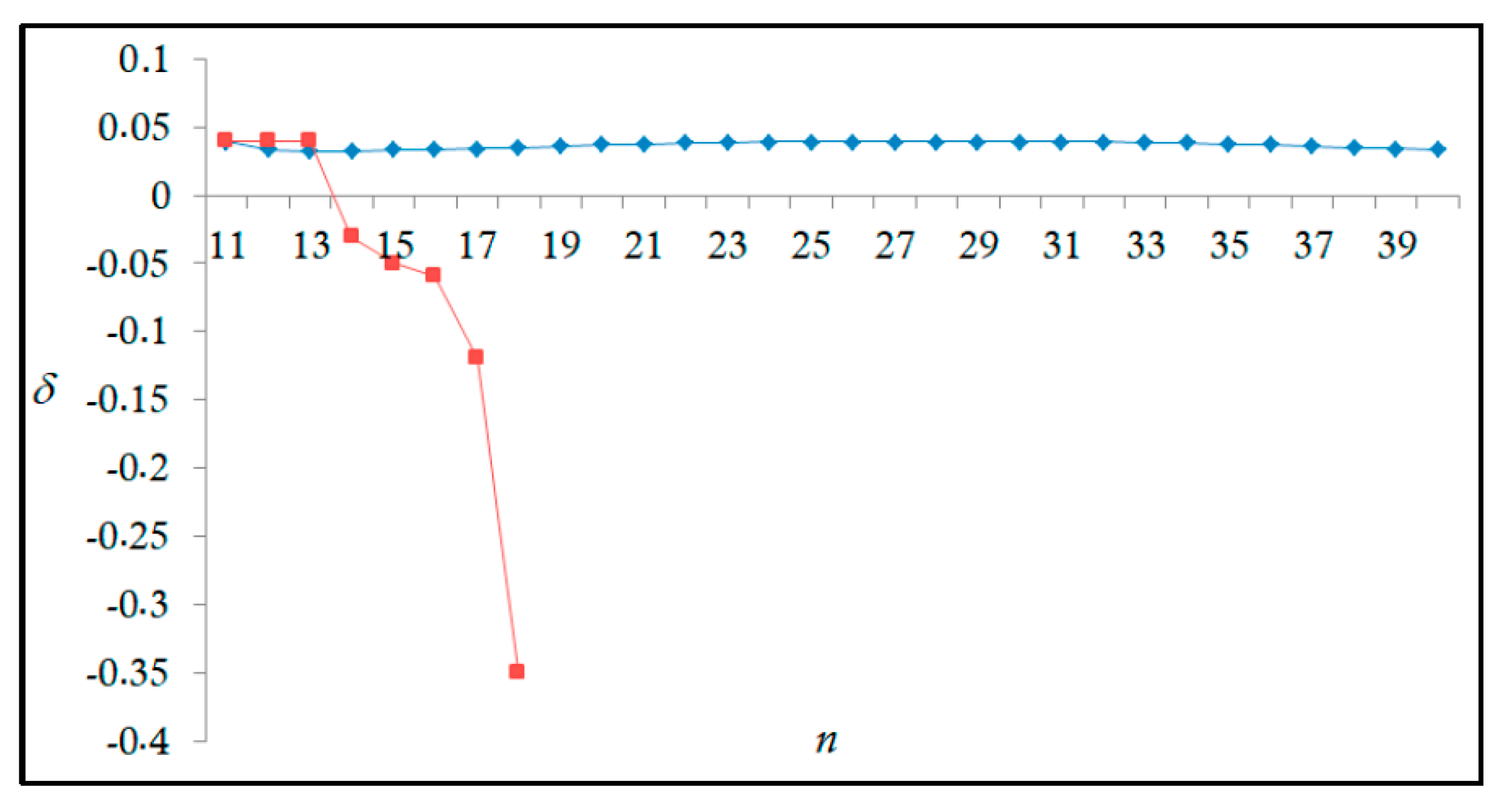
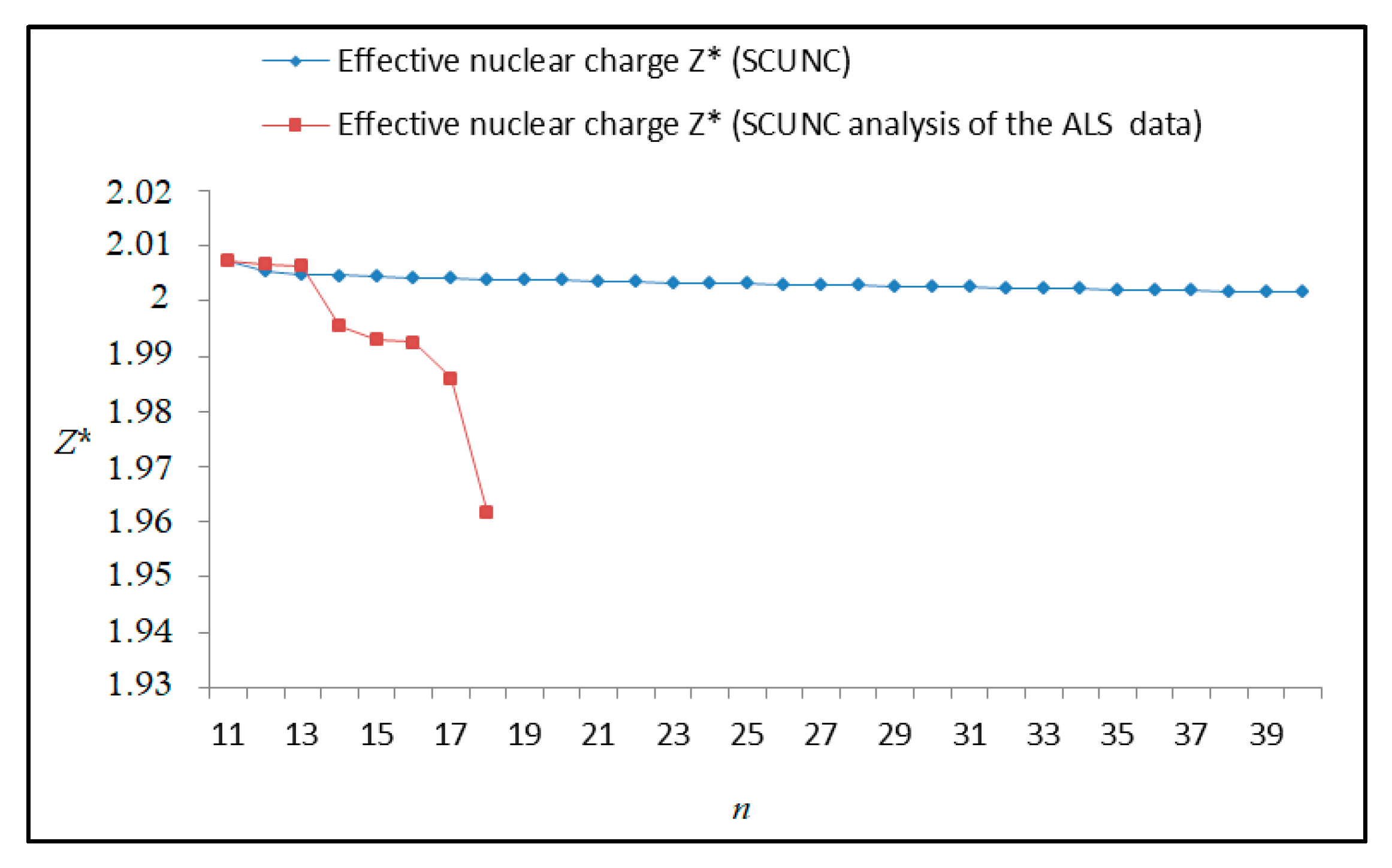
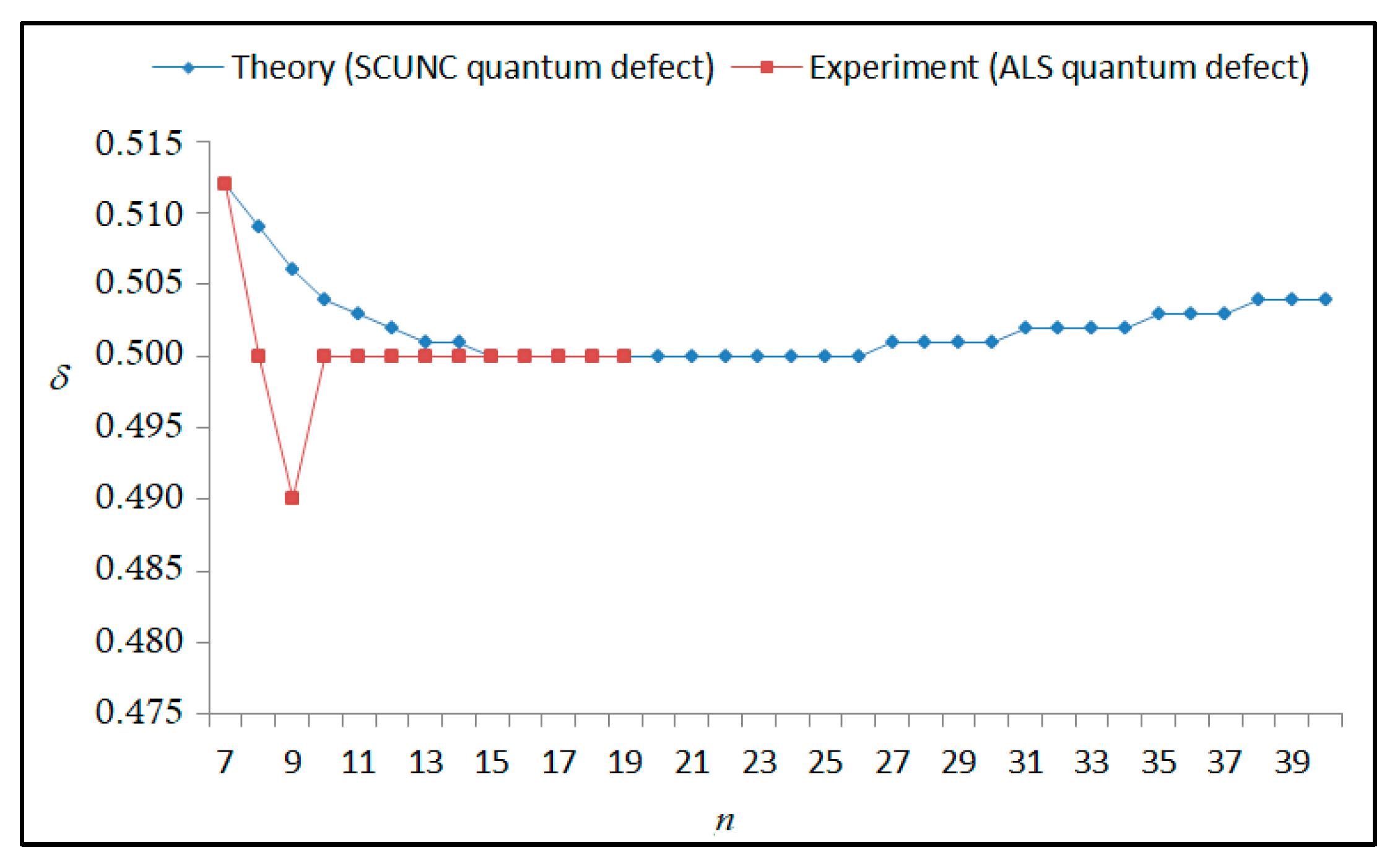
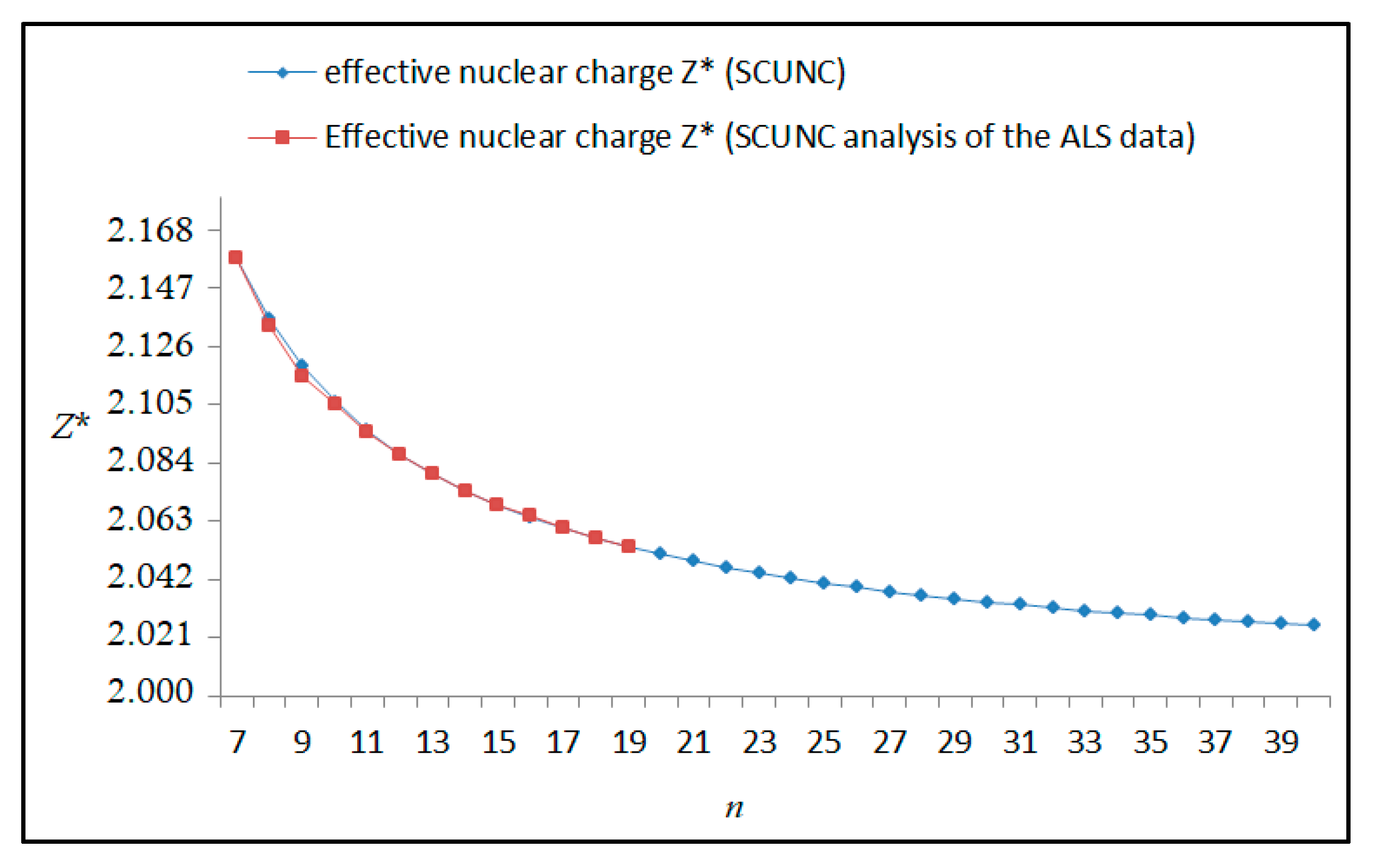
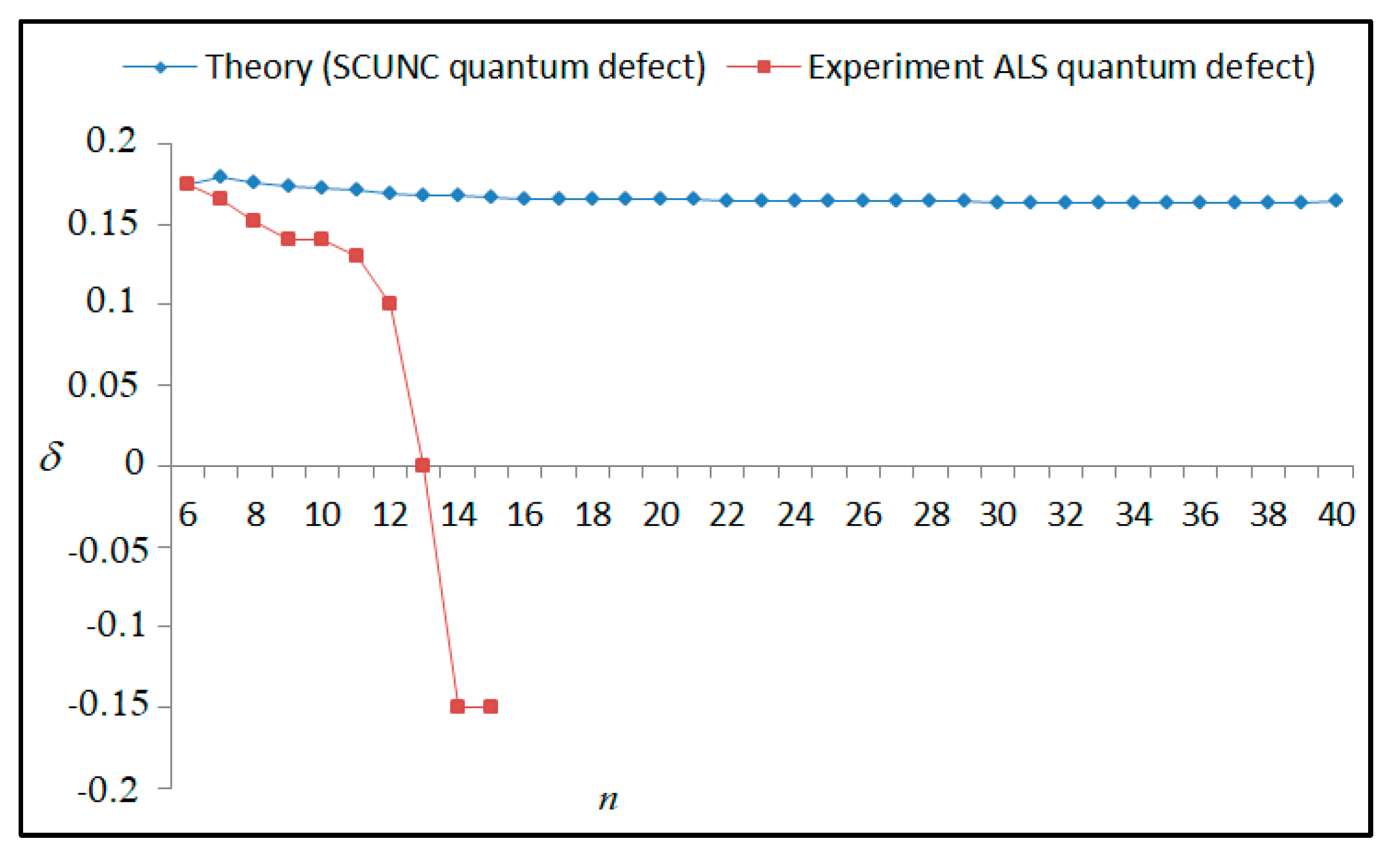
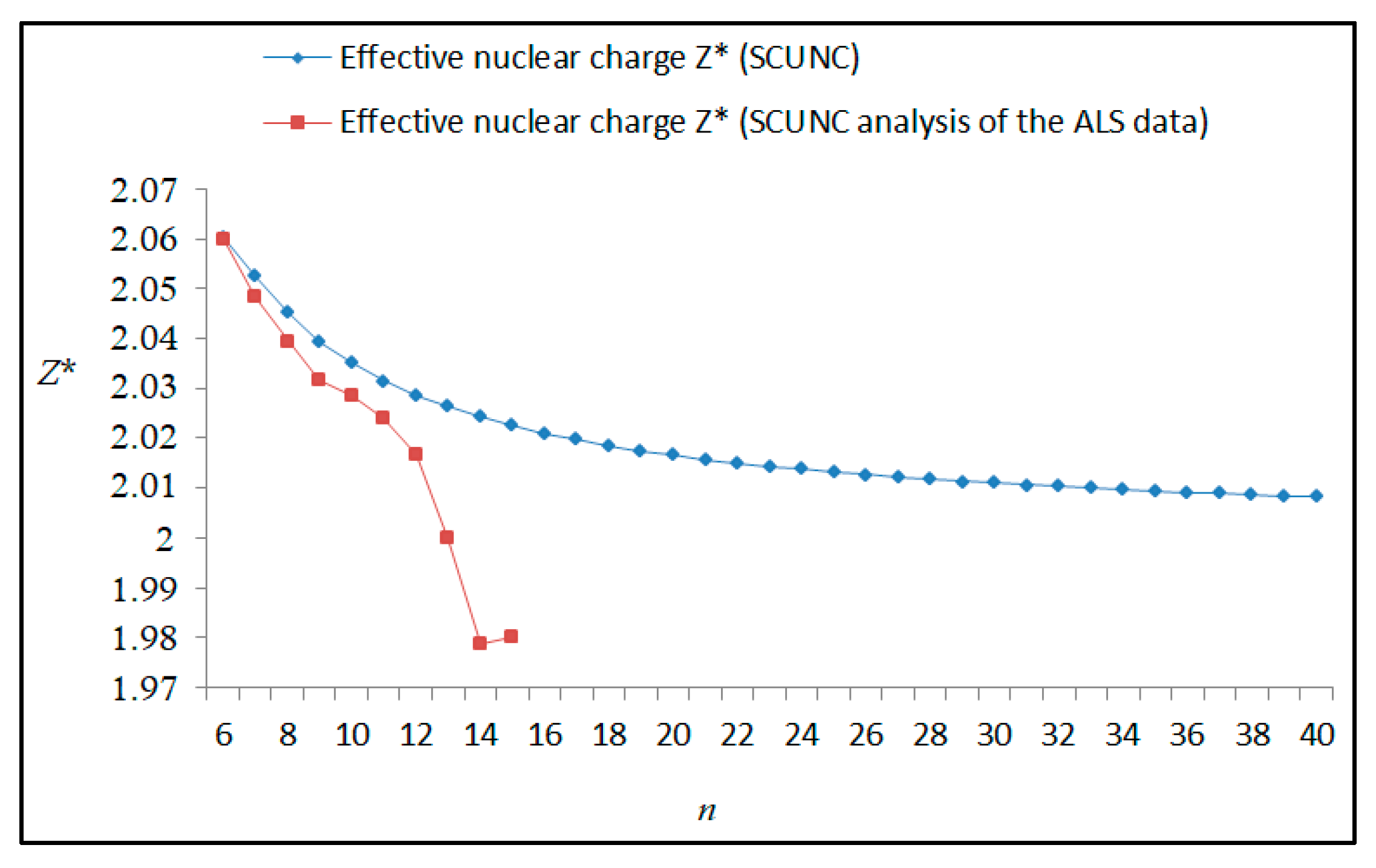
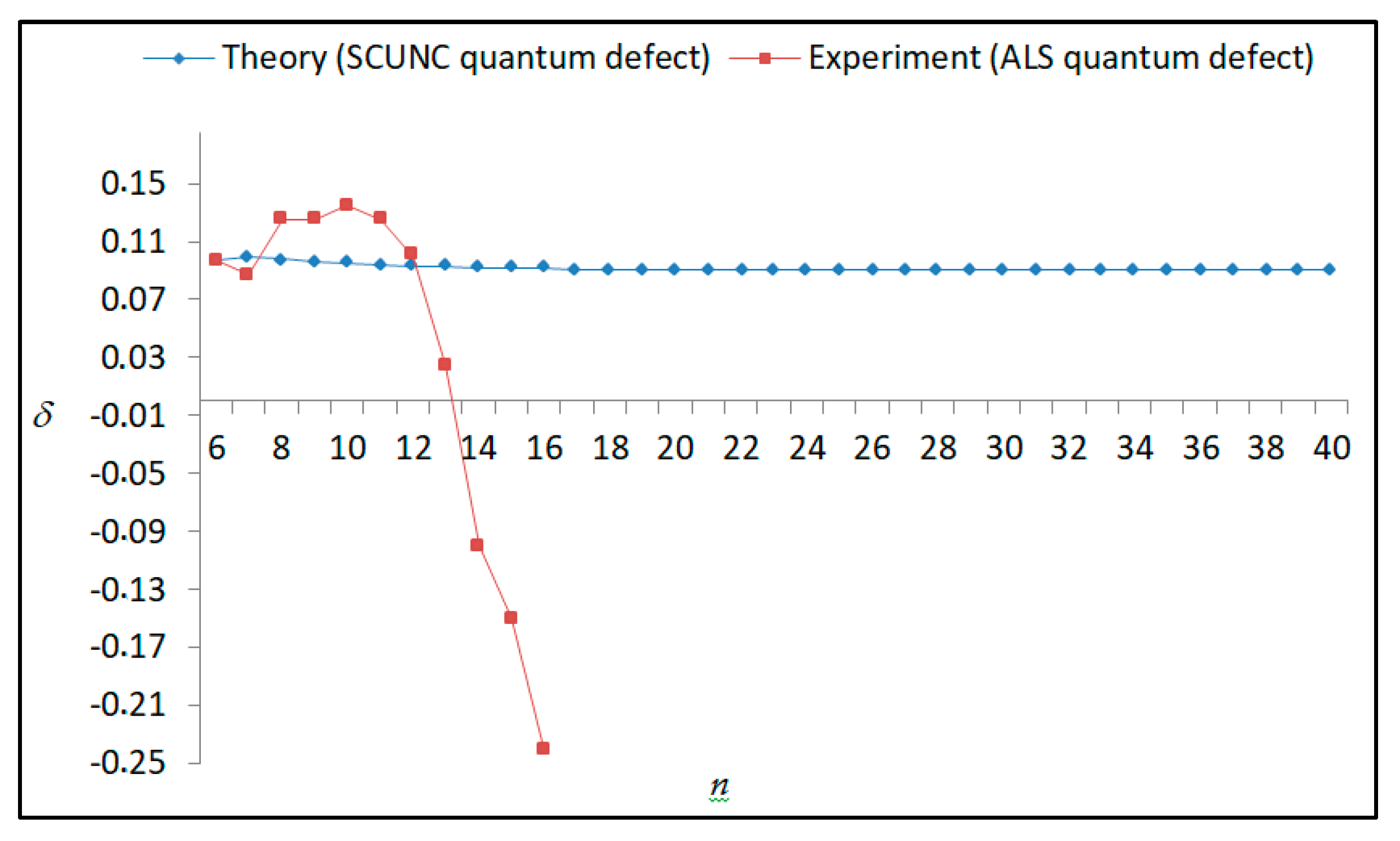
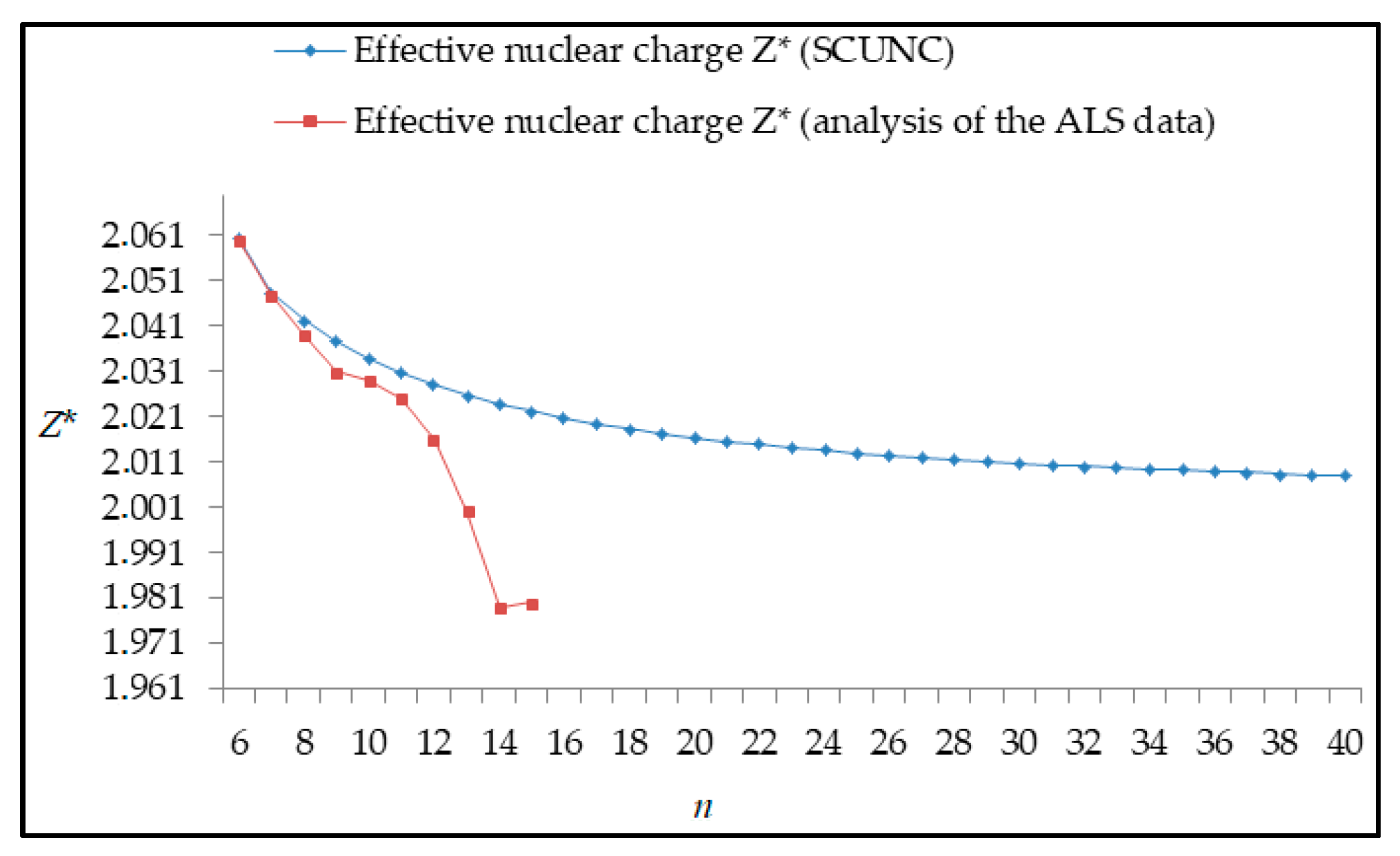
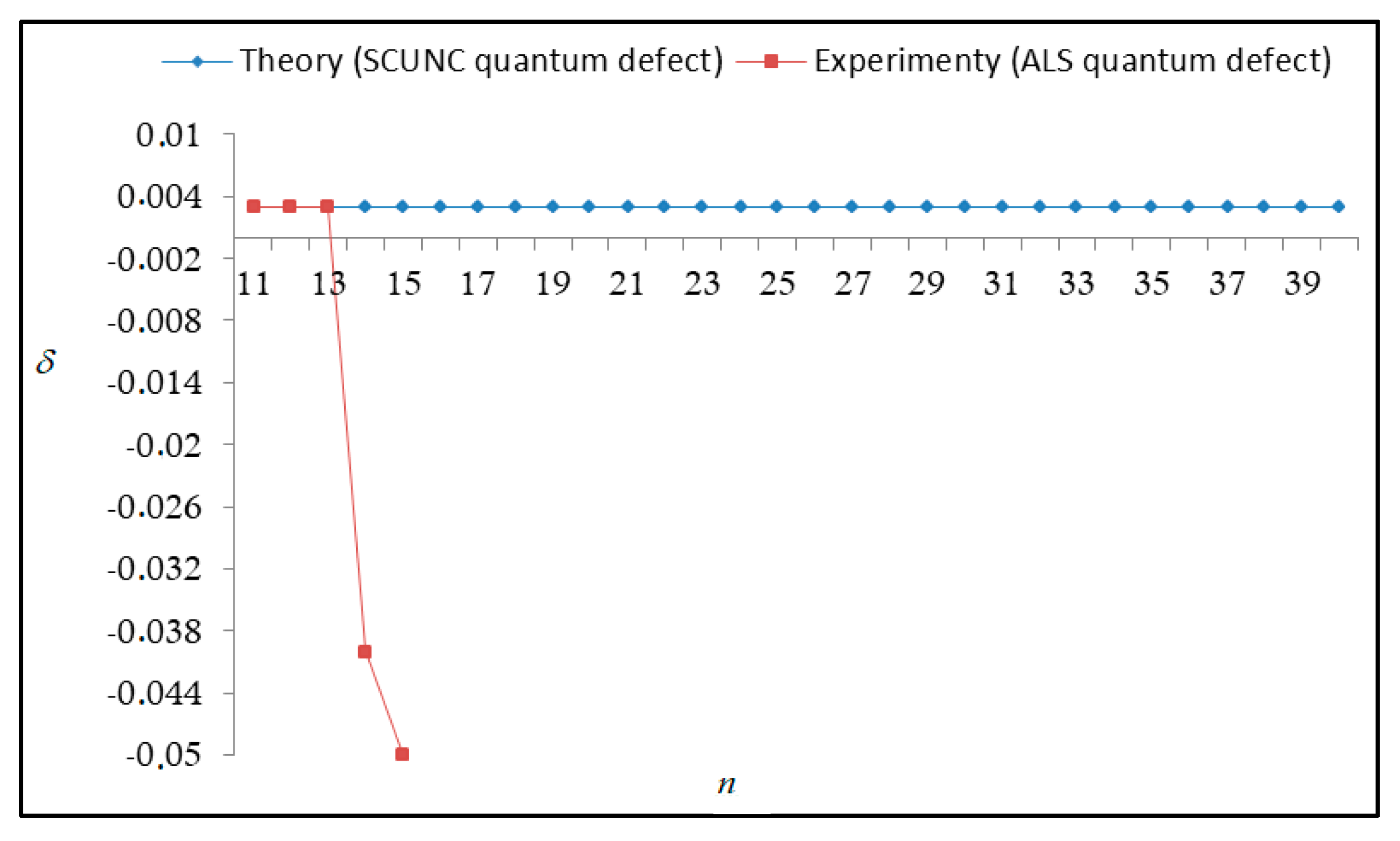
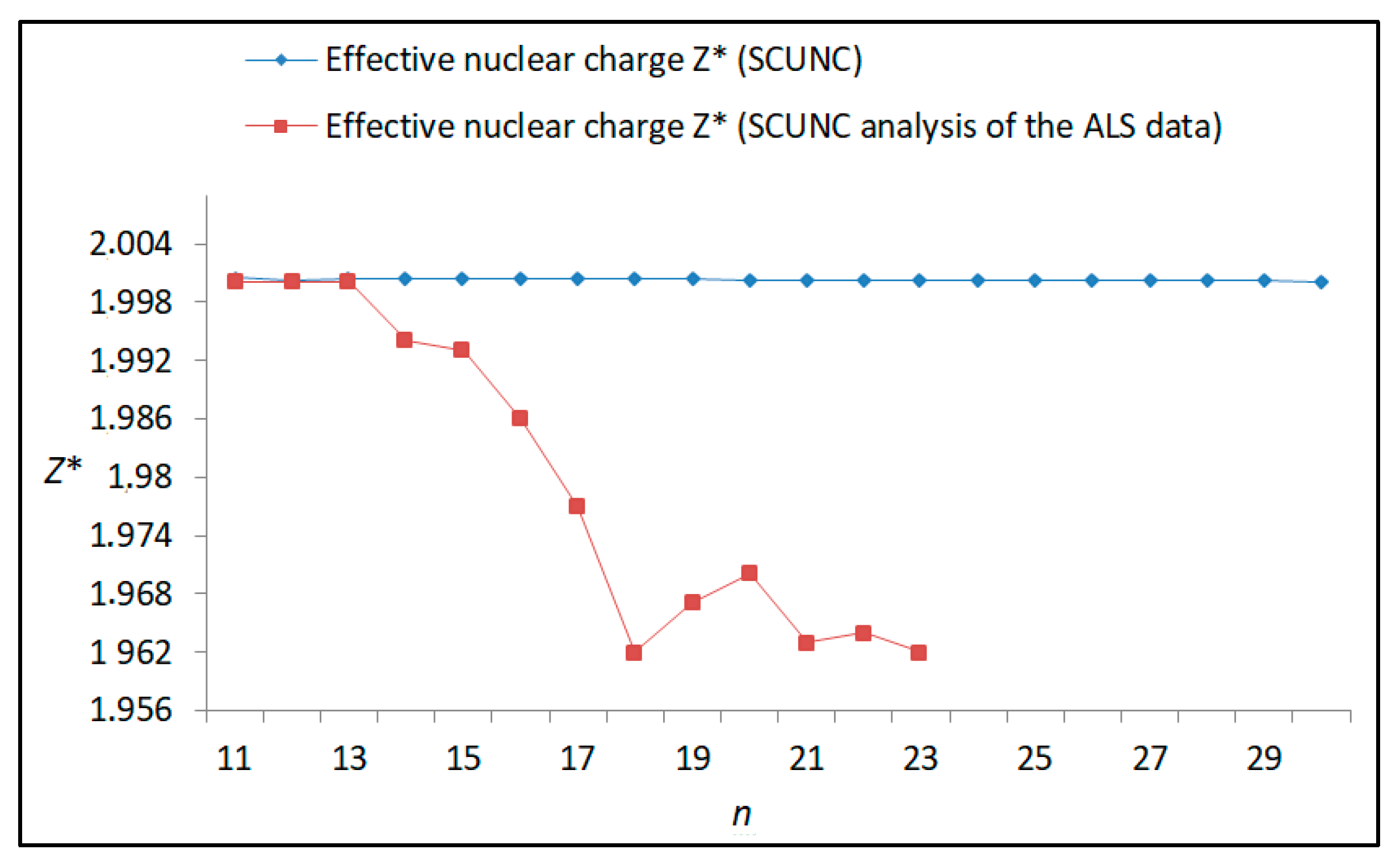
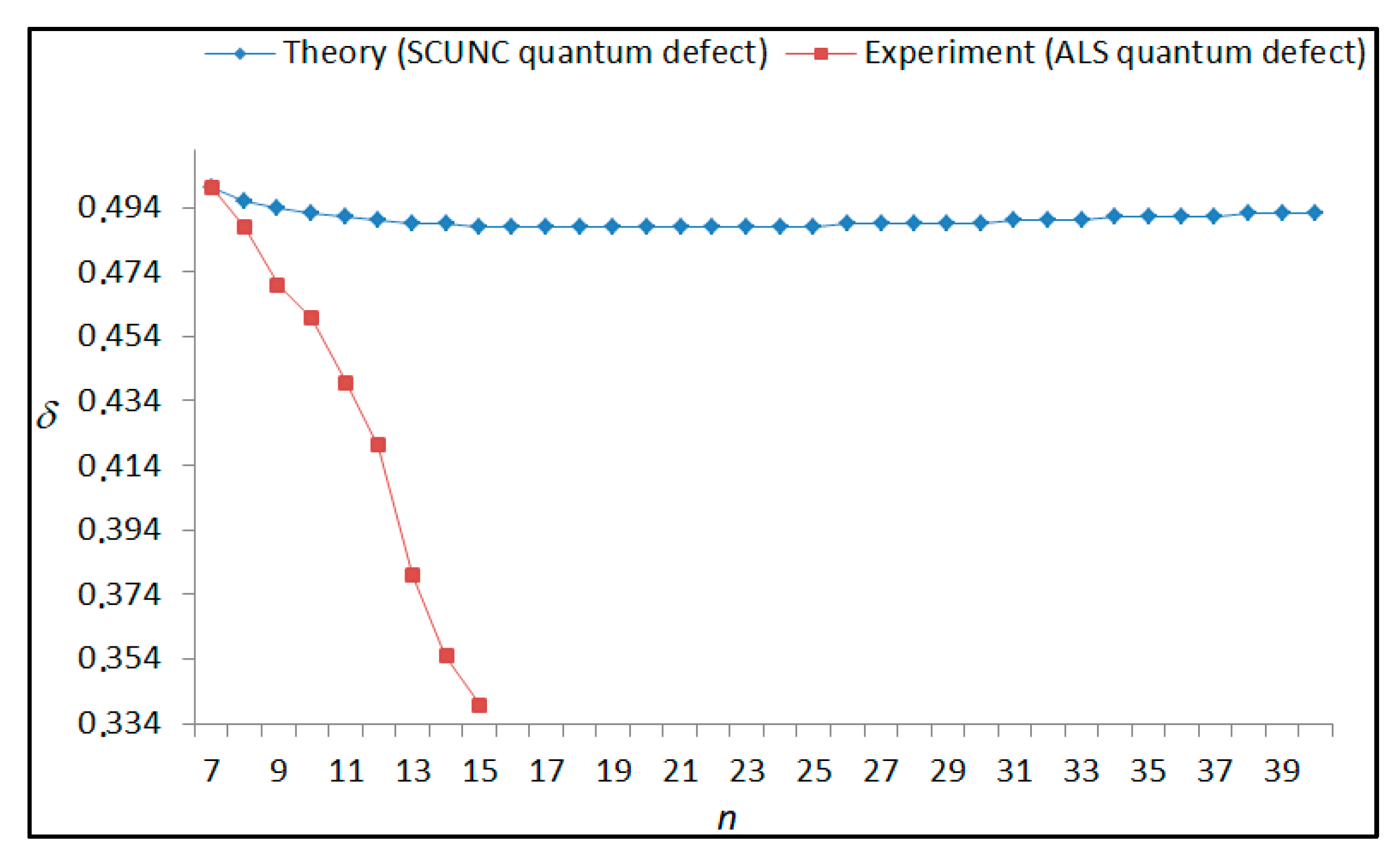
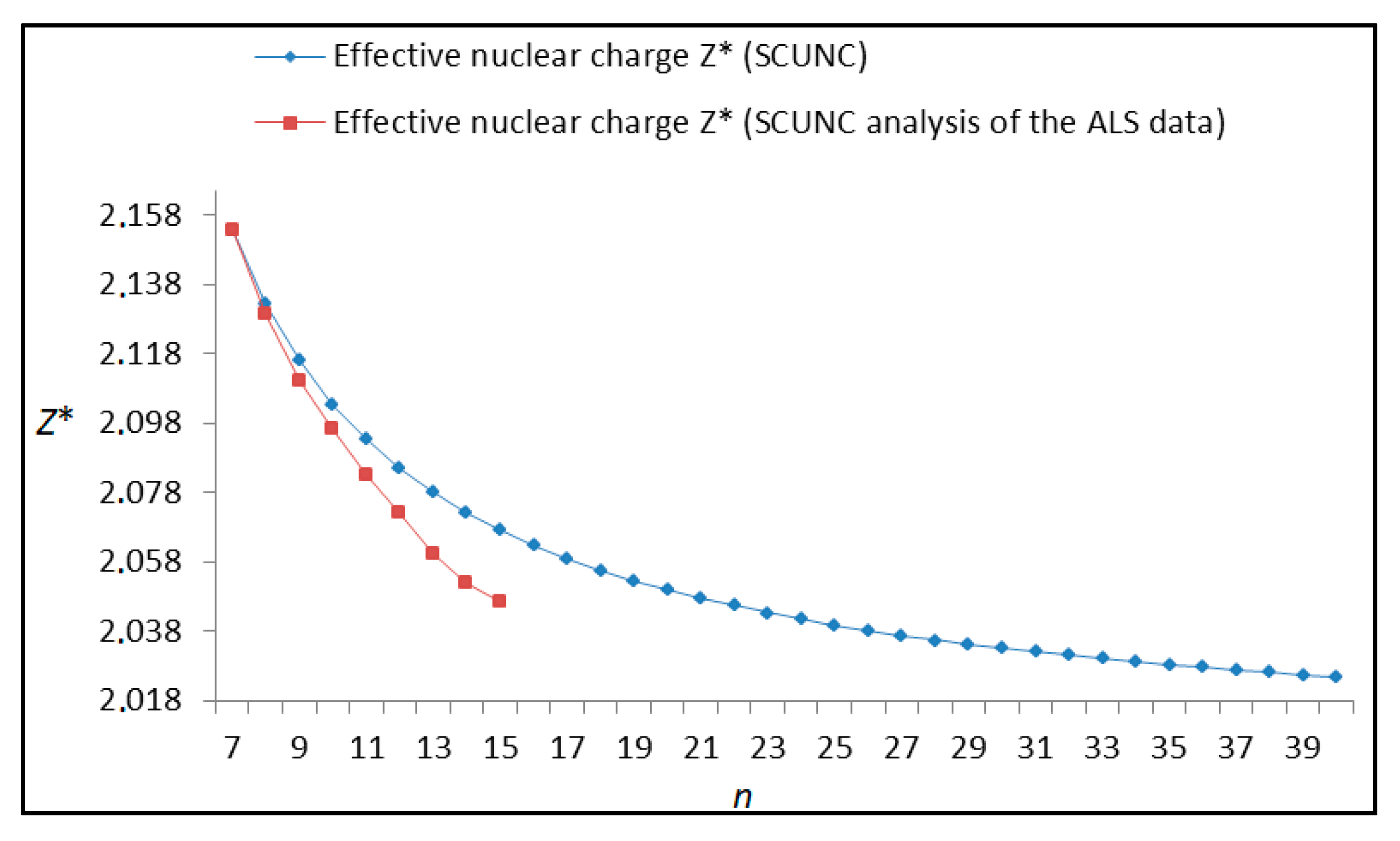
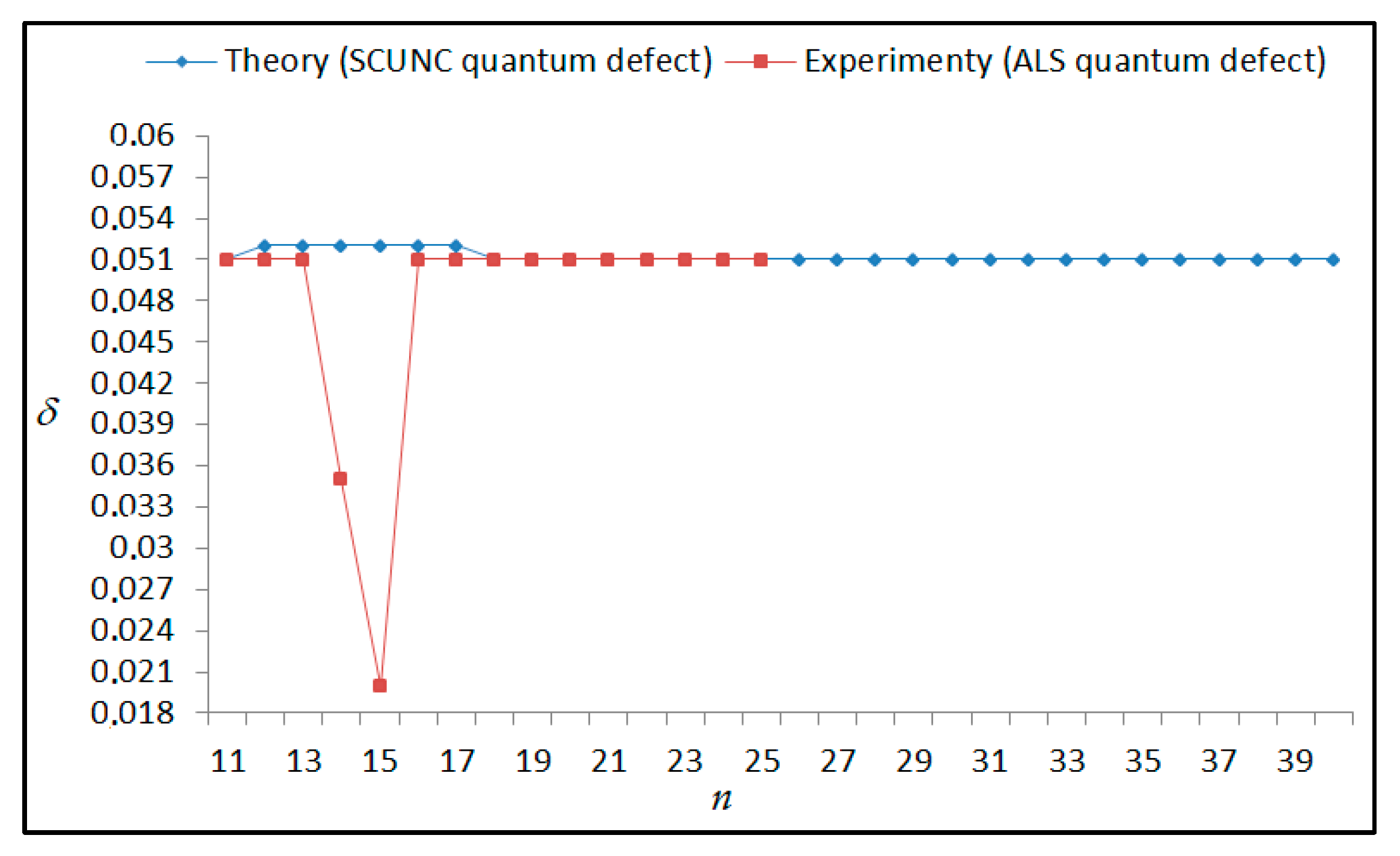
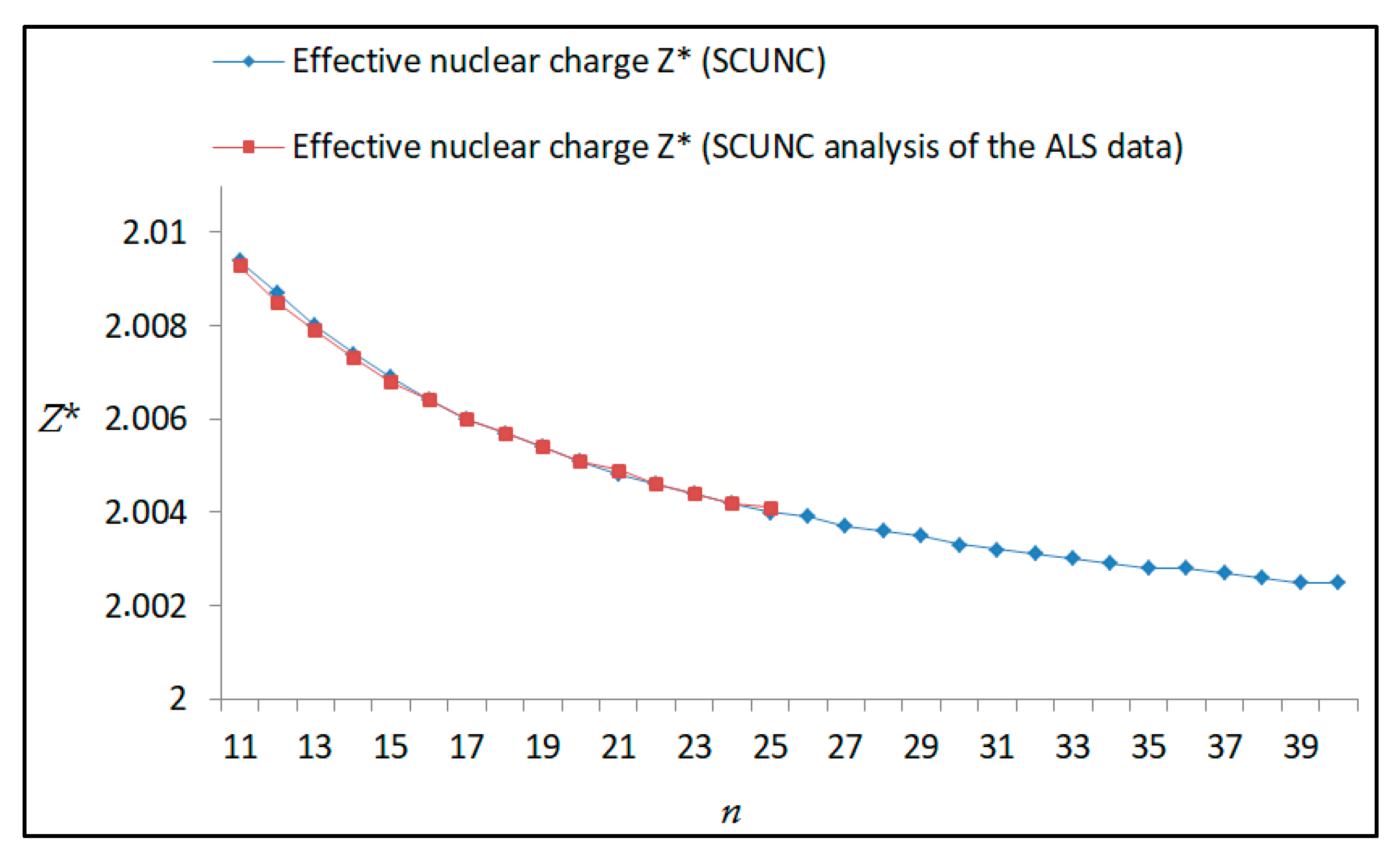
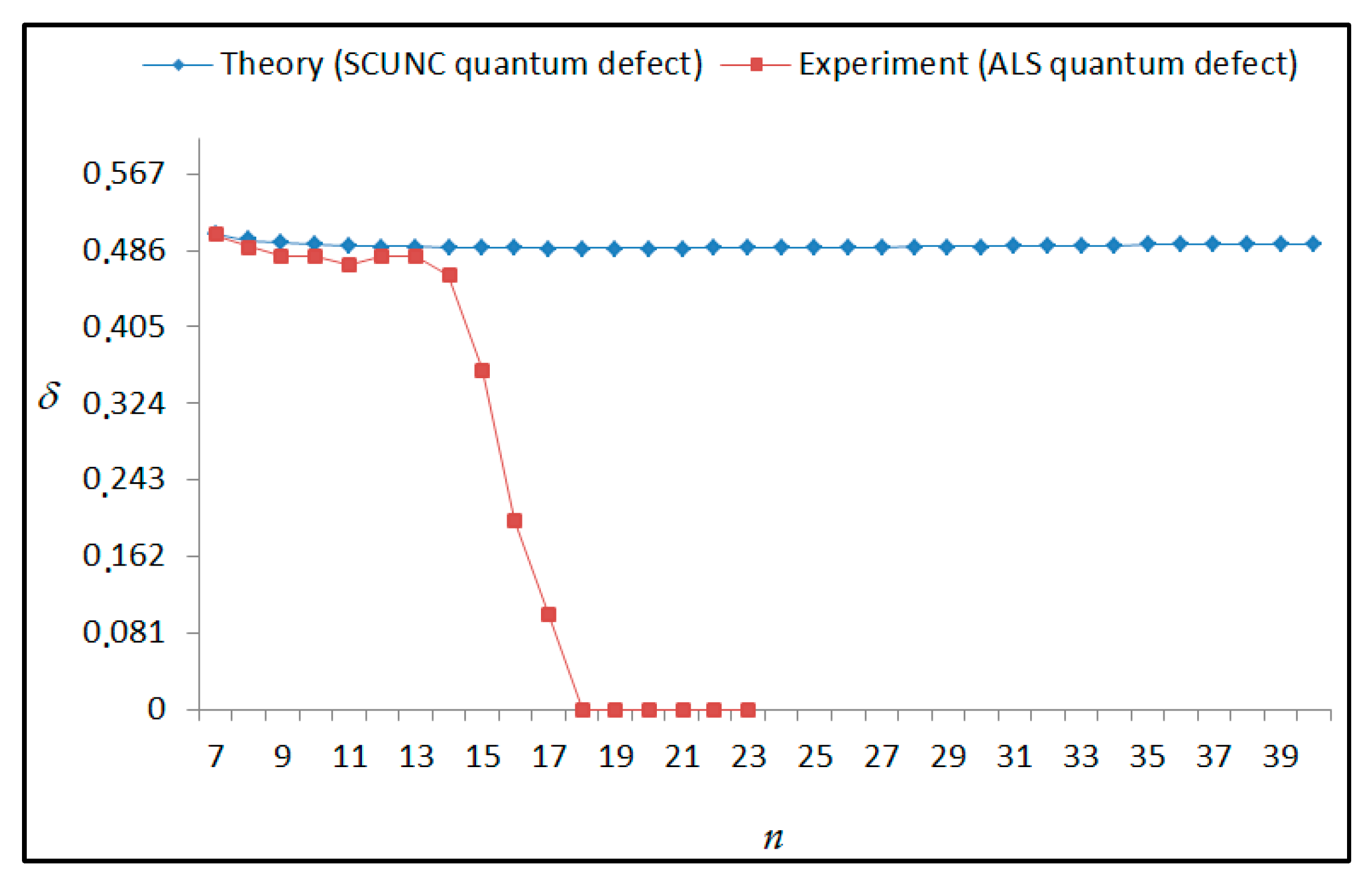
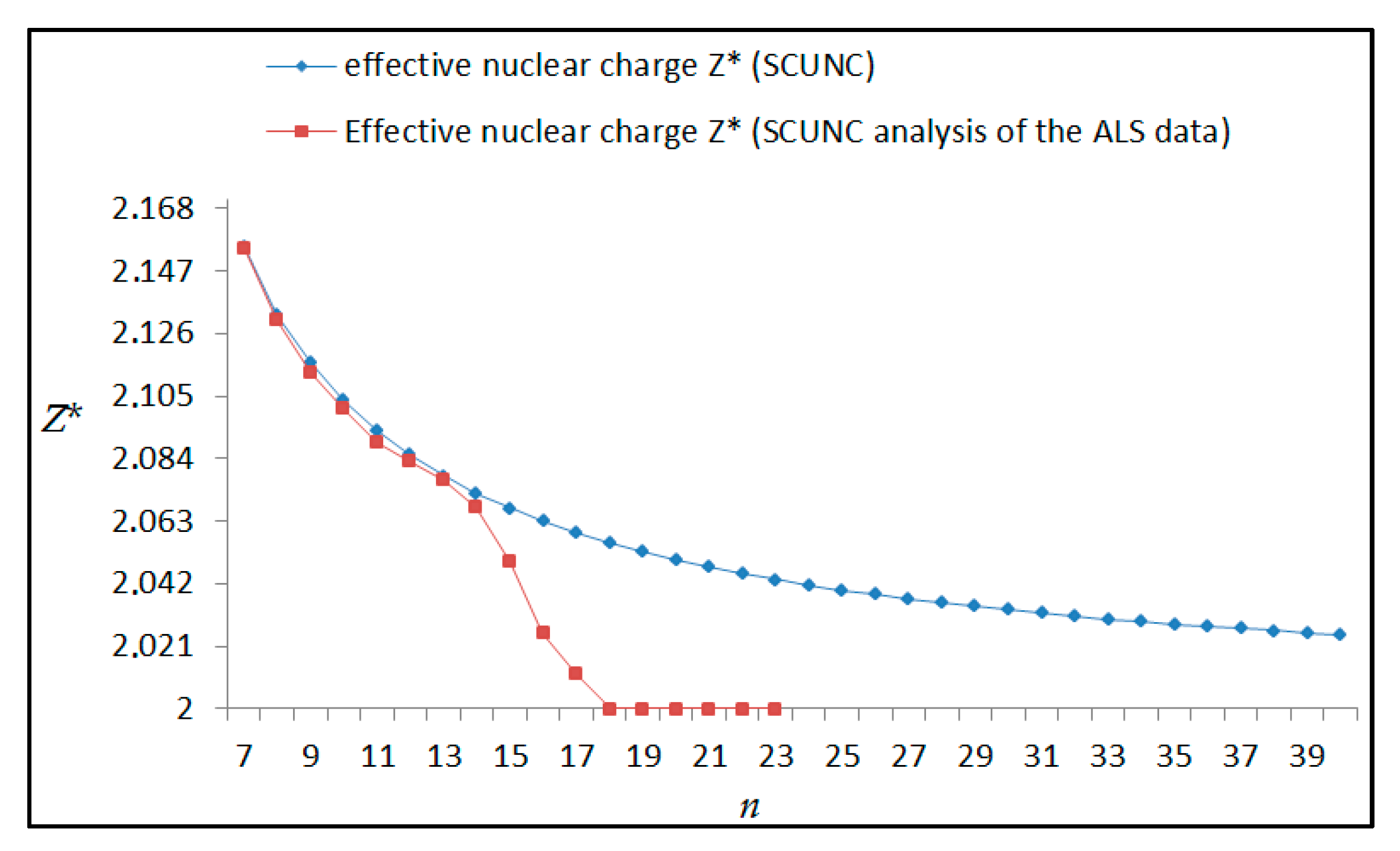
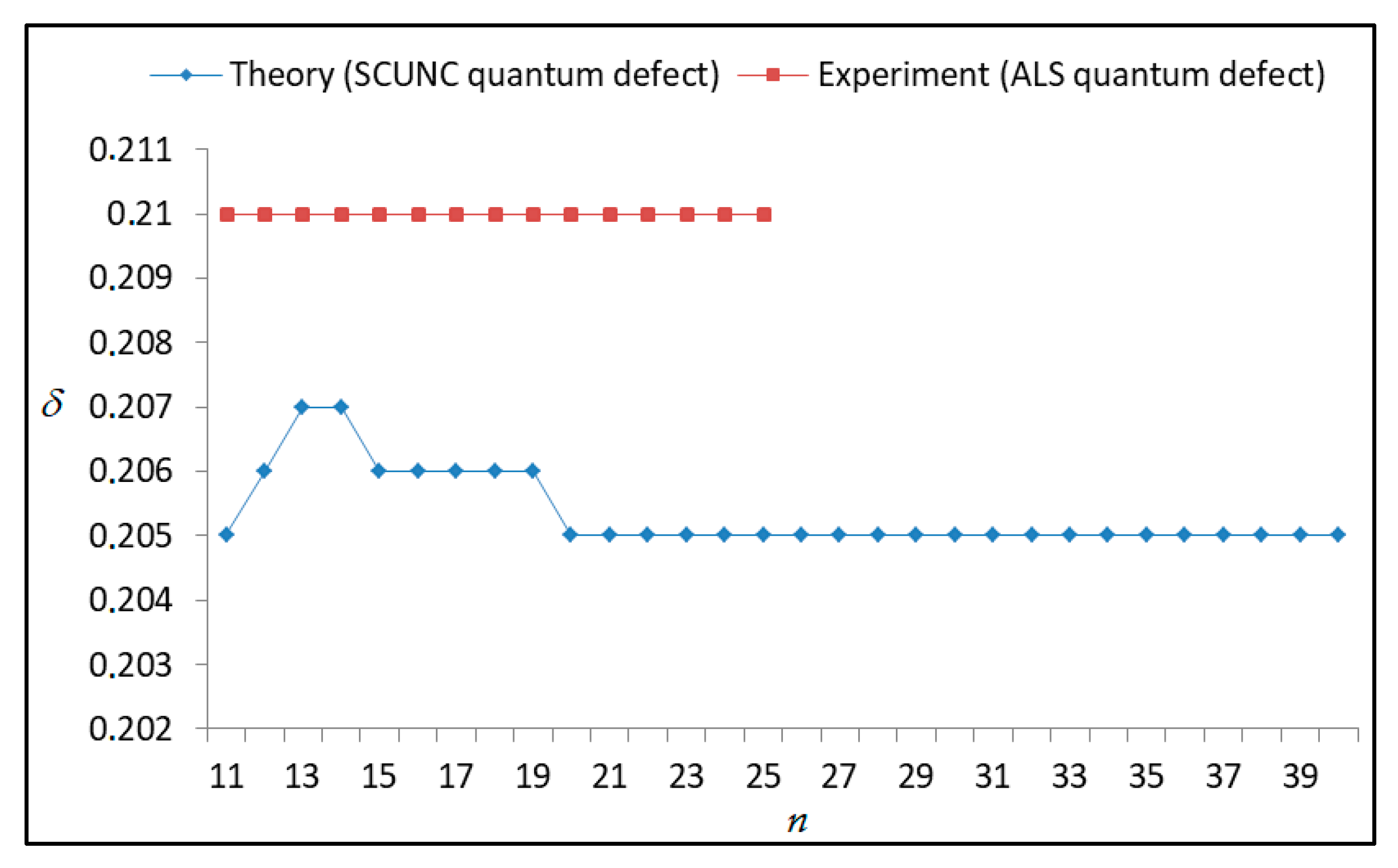
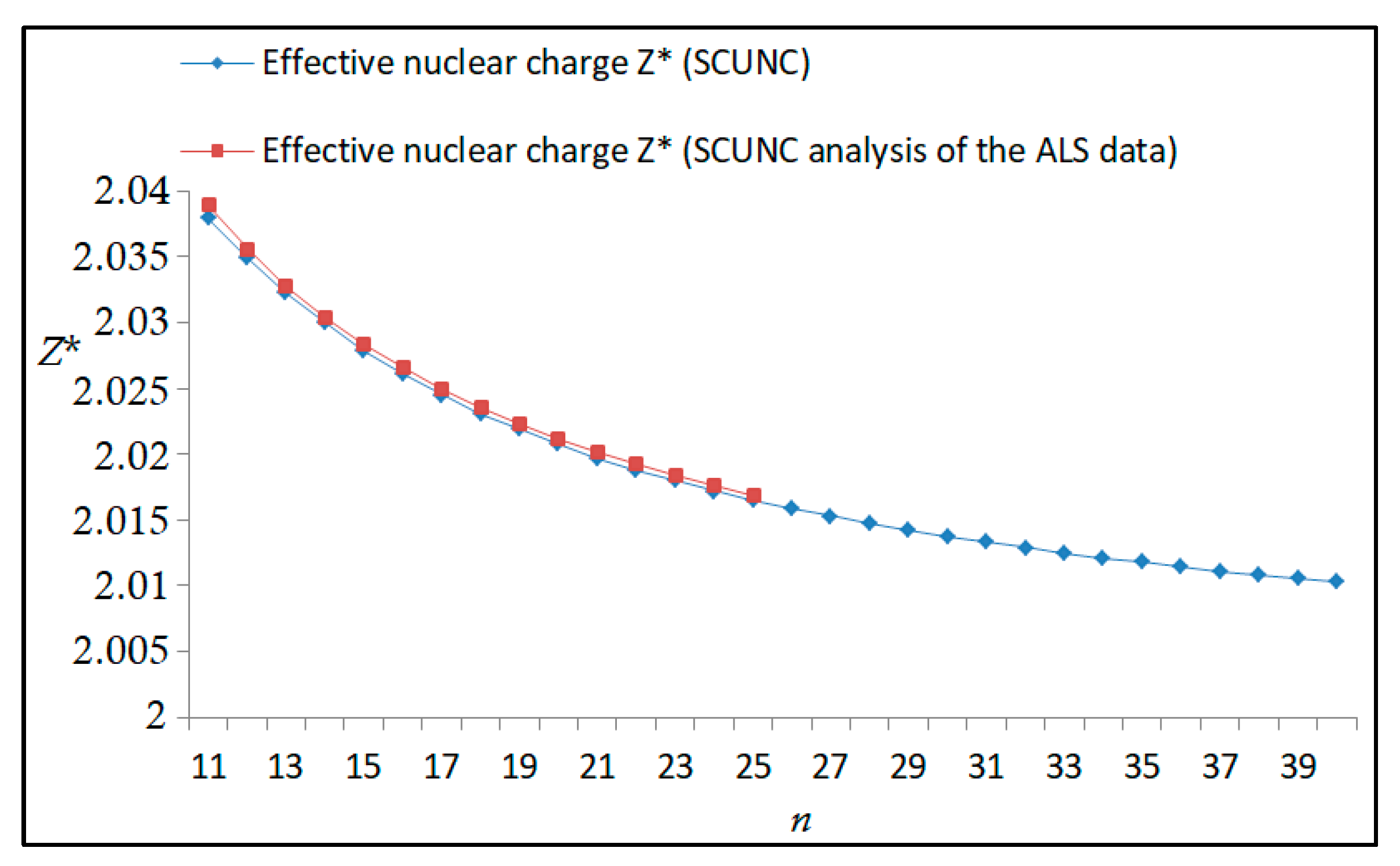
The results obtained in this work are listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 and compared to the ALS measurements [6]. For all the Rydberg series investigated, the effective nuclear charge Z* related to the ALS data are evaluated from Equation (7) using the experimental ALS quantum defect. Table 1 lists the energy resonances, quantum defect and effective charge of the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. Comparison indicates excellent agreements between the SCUNC energy resonances and the ALS measurements [6] up to n = 15. For these lines, the shift in energy is less than 0.007 eV. However, the same is not true for quantum defect. The SCUNC data are almost constant up to n = 40, in contrast with the ALS measurements where the quantum defect is equal to zero for n = 15. This is not allowed, as zero quantum defect is obtained in the case of a pure hydrogenic atomic system. As is well-known, the quantum defect is a quantification of the deviation of the true energy of an excited electron in a Rydberg atom from the hydrogenic model [6]. In Figure 1 and Figure 2, the SCUNC and ALS quantum defects and effective nuclear charges are, respectively, plotted versus the principal quantum number n. Correct behaviors of the SCUNC quantum defect and nuclear effective charge are obtained. Table 2 presents the resonances’ parameters evaluated for the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺. Here again, the SCUNC and ALS data for energy resonances agree very well. It should be mentioned that the SCUNC formula excellently reproduces the ALS data for n = 16–22, except for n = 18, where negative ALS quantum defect equal to –0.080 is obtained. Subsequently, the SCUNC energy at 18.557 eV corresponding to quantum defect equal to 0.039 is preferable to the ALS data equal to 18.560 eV. The details on the behaviors of the SCUNC and ALS quantum defects and effective nuclear charges with increasing the principal quantum number n are presented in Figure 3 and Figure 4, respectively. Table 3 shows a comparison of the results obtained for the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺. Here, the SCUNC formula again excellently reproduces the ALS data for n = 11–13. For n = 14–18, negative ALS quantum defects are obtained where positive values are allowed, which was also mentioned by Esteves et al. [6]. Figure 5 and Figure 6 show the good behaviors of both the quantum defect and effective nuclear charge up to n = 40. For n = 14–18, the SCUNC data may be considered as very accurate. Table 4 shows an excellent agreement between theory and experiment for energy resonances, quantum defect and effective charge of the 4s²4p² (¹D₂)ns Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The details of these agreements are presented in Figure 7 and Figure 8. It should be indicated that analysis of the data with respect to the effective nuclear charge give a best way of evaluating the agreement between theory and experiment, as shown in Figure 8. Table 5 indicates a comparison for the SCUNC and ALS energy resonances, quantum defect and effective charge of the 4s²4p² (¹D₂)nd(²P_1/2) Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. For n = 6-12, the SCUNC energy deviations with respect to the ALS data are less than 0.007 eV. For n = 13–15, the ALS quantum defect is equal to zero and becomes negative from n = 14, as shown in Figure 9. However, for all the series, the SCUNC quantum defect is almost constant up to n = 40 (see Figure 9). The SCUNC effective nuclear charge also decreases correctly toward Z_core = 2.0000 when n tends toward infinity, as indicated in Figure 10. It should be underlined that this value is achieved by the ALS measurement for n = 13. Comparison of the results obtained for the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limit in Se²⁺ is performed in Table 6. Here again, the SCUNC quantum defect is practically constant up to n = 40, while the ALS quantum defects decrease and become negative for n = 14–16. Overall, the shift in energy is less than 0.007 eV for the positive ALS quantum defect. For the resonances n = 14, 15 and 16, the SCUNC energy are, respectively, at 19.674 eV, 19.710 eV and 19.740 eV, and the associated quantum defect is constant and equal to 0.92, which is in contrast with the ALS quantum defects at −0.100, −0.150 and −0.240, respectively. The details regarding the evolution of the quantum defect and the effective nuclear charge are presented in Figure 11 and Figure 12, respectively. Table 7 also indicates negative ALS quantum defects for n = 14–23 as far as the 4s²4p² (³P₂)nd Rydberg series are concerned. For these series, the SCUNC quantum defect is constant and equal to 0.003 up to n = 40, as revealed in Figure 13 and Figure 14. The SCUNC energy resonances for n = 14–23 may be very good data references. Table 8 and Table 9 list the results obtained, respectively, for the 4s²4p² (¹D₂)ns Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺ and for the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}D°_3/2 metastable state of Se⁺ converging to the ³P₂ series limit in Se²⁺. For Table 8, the energy deviation with respect to the ALS data is less than 0.007 eV, attesting to the very good agreement between theory and experiment. Table 9 shows an excellent agreement between the SCUNC data and the ALS measurements, where the SCUNC reproduces the ALS data, except for n = 14 and 15, with a shift in energy at 0.001 and 0.002 eV, respectively. The details regarding the behaviors of both quantum defects and effective nuclear charges for the 4s²4p² (¹D₂)ns and 4s²4p² (³P₂)nd Rydberg series are presented in Figure 15 and Figure 16 for the 4s²4p² (¹D₂)ns states and in Figure 17 and Figure 18 for the 4s²4p² (³P₂)nd states. Table 10 and Table 11 present the results obtained, respectively, for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the 4s²4p^{3 2}D°_5/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺ and the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the 4s²4p^{3 2}D°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. For these data, it is seen that the SCUNC quantum defects are almost constant up to n = 40, which is in contrast with the ALS quantum defects becoming equal to zero for n = 18–23, corresponding to an effective nuclear charge at 2.0000 as shown, respectively, in Figure 19 and Figure 20. For these resonances, constant SCUNC quantum defects are obtained and equal to 0.490 (Table 10) and to 0.481 (Table 11). For the accurate ALS quantum defect more than 0.450, the energy deviations are less than 0.005 eV for the data quoted in both Table 10 and Table 11. The details in the accuracy of both quantum defect and effective nuclear charge for the data quoted in Table 11 are presented in Figure 21 and Figure 22. Finally, Table 12 lists the energy resonances, quantum defect and effective charge of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 4}S°_3/2 ground state of Se⁺ converging to the ³P₂ series limit in Se²⁺. Here, the SCUNC formula excellently reproduces the ALS energy resonances except for n = 12, where the ALS data is at 21.219 eV compared to the accurate SCUNC prediction at 21.291 eV. Using the ALS effective nuclear charge Z* = 2.0356 from the SCUNC analysis and E_∞ = 21.682 eV, Equation (4) gives the corrected ALS data E₁₂ = 21,290 eV for the (³P₂)12d. Subsequently, the ALS data at 21.219 may probably be an error occurring during the typewriting step (it seems that the positions of 1 and 9 have been inverted). As far as quantum defect and effective nuclear charge are concerned, the good agreement between theory and experiment is shown in Figure 23 and Figure 24. On the other hand, it should be mentioned that for the 4s²4p² (¹D₂)nd (²D) and 4s²4p² (¹D₂)ns (²D) and of the 4s²4p² (¹D₂)nd (²S) and 4s²4p² (¹D₂)nd (²P_1/2) Rydberg series, the ALS data overlap. As shown in Table 5 and Table 6, the ALS data for the two levels 4s²4p² (¹D₂)12d(²P_1/2) and 4s²4p² (¹D₂)12d (²S) are equal to 19.571 eV, with a quantum defect at 0.100. In the same way, the levels 4s²4p² (¹D₂)18d(²P_1/2) and 4s²4p² (¹D₂)18d (²S) are equal to 19.718 eV, with a negative quantum defect at −0.150. For these overlap lines, the SCUNC predicts separate levels associated with the energies 19.556 eV and 19.571 eV, respectively, for the 4s²4p² (¹D₂)12d(²P_1/2) and 4s²4p² (¹D₂)12d (²S) levels. The corresponding quantum defects are at 0.169 and 0.093, respectively. As a result, the 19.571 eV ALS data may be for the 4s²4p² (¹D₂)12d (²S) level and not for 4s²4p² (¹D₂)12d(²P_1/2). In addition, the SCUNC predictions for the 4s²4p² (¹D₂)18d(²P_1/2) and 4s²4p² (¹D₂)18d (²S) levels are at 19.708 eV and 19.710 eV, respectively. The ALS data at 19.718 eV associated with a negative quantum defect at –0.150 may be uncertain. As explained by Esteves et al. [6], some resonances in the ALS analysis have not been resolved, either due to interference from other series or to limitations in photon energy resolution at high n values. In addition, McLaughlin and Balance [7] have shown in their works how the presence of interloping resonances disrupt the regular Rydberg pattern of the resonances. Probable strong coupling series occur in the photoionization processes of the Se⁺ ions. Anyway, the overlapping ALS lines and the negative quantum defects measured may be explained by the interference from other series, causing strong interseries coupling and/or limitations in photon energy resolution at high n values. In the SCUNC predictions, these narrow lines are clearly identified. The constant behavior of δ along all the series may indicate that the probable strong interseries perturbations due to interference between series has no effect on the fitting parameters f₁ and f₂. This may demonstrate the stability of Equations (12)–(14) and, subsequently, the utility of the SCUNC formalism to separately identify high-lying narrow interfering series. On the other hand, before closing the discussion section, it is interesting to remind one what the main advantages of using the SCUNC method are. For the various techniques of calculations applied in atomic physics, the R-matrix approach is seen to be the most sophisticated and widely used method [22]. As pointed out by McLaughlin and Ballance [7], in R-matrix theory, all photoionization (PI) cross-section calculations require the generation of atomic orbitals based primarily on the atomic structure of the residual ion. In their works, the PI of the Se⁺ ions employs relativistic atomic orbitals generated for the residual Se²⁺ ions which were calculated using the extended-optimal-level (EOL) procedure within the GRASP structure code. In addition, to calculate the direct photoionization cross-sections in these experiments, Bizau et al. [23] performed the multiconfiguration Dirac-Fock (MCDF) calculations using the code developed by Bruneau [24]. These particular examples indicate that calculations or experiments based on PI cross-section studies require at least:

Table 1. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV. The value of Z_core = 2.0000 is indicated in the last line of the table, f₁ (¹D₂; ²P°_3/2) = −0.148 ± 0.033 with ν = 6.

Initial State 4s24p3 2P°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
6	18.296	0.088	2.0296	18.296	0.088	2.0298	0.000
7	18.714	0.089	2.0258	18.710	0.100	2.0300	0.004
8	18.984	0.088	2.0222	18.990	0.150	2.0382	0.006
9	19.168	0.086	2.0194	19.169	0.088	2.0197	0.001
10	19.299	0.085	2.0172	19.302	0.060	2.0121	0.003
11	19.396	0.085	2.0155	19.396	0.088	2.0161	0.000
12	19.470	0.084	2.0141	19.470	0.080	2.0134	0.000
13	19.527	0.083	2.0129	19.528	0.070	2.0108	0.001
14	19.572	0.083	2.0119	19.574	0.060	2.0086	0.002
15	19.608	0.083	2.0111	19.613	0	2.0000	0.003
16	19.638	0.082	2.0103
17	19.663	0.082	2.0097
18	19.683	0.082	2.0091
19	19.701	0.082	2.0086
20	19.716	0.081	2.0082
21	19.729	0.081	2.0078
22	19.740	0.081	2.0074
23	19.749	0.081	2.0071
24	19.758	0.081	2.0068
25	19.765	0.081	2.0065
26	19.772	0.081	2.0062
27	19.778	0.081	2.0060
28	19.783	0.081	2.0058
29	19.788	0.081	2.0056
30	19.792	0.081	2.0054
31	19.796	0.081	2.0052
32	19.800	0.081	2.0050
33	19.803	0.081	2.0049
34	19.806	0.081	2.0047
35	19.808	0.081	2.0046
36	19.811	0.081	2.0045
37	19.813	0.081	2.0044
38	19.815	0.081	2.0042
39	19.817	0.081	2.0041
40	19.819	0.081	2.0040
…	…	…	…	…	…	…	…
∞	19.853		2.0000	19.853		2.0000

** Energy differences relative to the ALS experimental data.

Table 2. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (³P₂; ²P°_3/2) = −0.072 ± 0.042 with ν = 11.

Initial Se+ State: 4s24p3 2P°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
11	18.273	0.039	2.0072	18.273	0.040	2.0073	0.000
12	18.346	0.040	2.0066	18.342	0.090	2.0151	0.004
13	18.402	0.040	2.0061	18.401	0.070	2.0108	0.001
14	18.447	0.040	2.0057	18.446	0.055	2.0079	0.001
15	18.483	0.040	2.0053	18.482	0.065	2.0087	0.001
16	18.512	0.040	2.0049	18.512	0.060	2.0075	0.000
17	18.537	0.040	2.0046	18.537	0.040	2.0047	0.000
18	18.557	0.039	2.0044	18.560	−0.080	1.9911	0.003
19	18.575	0.039	2.0041	18.575	0.040	2.0042	0.000
20	18.589	0.039	2.0039	18.589	0.040	2.0040	0.000
21	18.602	0.039	2.0037	18.602	0.040	2.0038	0.000
22	18.613	0.039	2.0035	18.613	0.040	2.0036	0.000
23	18.623	0.039	2.0034
24	18.631	0.039	2.0032
25	18.639	0.039	2.0031
26	18.645	0.039	2.0030
27	18.651	0.039	2.0029
28	18.656	0.039	2.0027
29	18.661	0.039	2.0027
30	18.665	0.039	2.0026
31	18.669	0.039	2.0025
32	18.673	0.039	2.0024
33	18.676	0.039	2.0023
34	18.679	0.039	2.0022
35	18.681	0.039	2.0022
36	18.684	0.039	2.0021
37	18.686	0.039	2.0021
38	18.688	0.039	2.0020
39	18.690	0.039	2.0020
40	18.692	0.039	2.0019
…	…	…	…	…	…	…	…
∞	18.726		2.0000	18.726		2.0000

** Energy differences relative to the ALS experimental data.

Table 3. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (³P₂; ²P°_1/2) = −0.072 ± 0.042 with ν = 11.

Initial Se+ State: 4s24p3 3P°1/2
	SCUNC			ALS
n	E (eV)	Δ	Z*	E (eV)	δ	Z*	|ΔE| **
11	18.375	0.039	2.0072	18.375	0.040	2.0073	0.000
12	18.448	0.040	2.0055	18.448	0.040	2.0067	0.000
13	18.504	0.040	2.0049	18.504	0.040	2.0062	0.000
14	18.549	0.040	2.0046	18.552	−0.030	1.9954	0.003
15	18.585	0.040	2.0044	18.588	−0.050	1.9929	0.003
16	18.614	0.040	2.0042	18.617	−0.060	1.9925	0.003
17	18.639	0.040	2.0040	18.642	−0.120	1.9860	0.003
18	18.659	0.039	2.0039	18.666	−0.350	1.9618	0.007
19	18.677	0.039	2.0038
20	18.691	0.039	2.0037
21	18.704	0.039	2.0035
22	18.715	0.039	2.0034
23	18.725	0.039	2.0033
24	18.733	0.039	2.0032
25	18.741	0.039	2.0031
26	18.747	0.039	2.0030
27	18.753	0.039	2.0029
28	18.758	0.039	2.0028
29	18.763	0.039	2.0027
30	18.767	0.039	2.0026
31	18.771	0.039	2.0025
32	18.775	0.039	2.0024
33	18.778	0.039	2.0023
34	18.781	0.039	2.0022
35	18.783	0.039	2.0021
36	18.786	0.039	2.0020
37	18.788	0.039	2.0019
38	18.790	0.039	2.0018
39	18.792	0.039	2.0017
40	18.794	0.039	2.0016
…	…	…	…	…	…	…	…
∞	18.828		2.0000	18.828		2.0000

** Energy differences relative to the ALS experimental data.

Table 4. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)ns Rydberg series originating from the 4s²4p^{3 2}P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (¹D₂; ²P°_3/2) = −0.947 ± 0.050 with ν = 7.

Initial State 4s24p3 2P°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
7	18.560	0.512	2.1578	18.560	0.512	2.1578	0.000
8	18.883	0.509	2.1358	18.886	0.500	2.1333	0.003
9	19.099	0.506	2.1192	19.102	0.490	2.1152	0.003
10	19.249	0.504	2.1062	19.250	0.500	2.1052	0.001
11	19.359	0.503	2.0959	19.359	0.500	2.0952	0.000
12	19.441	0.502	2.0873	19.442	0.500	2.0870	0.001
13	19.505	0.501	2.0802	19.505	0.500	2.0800	0.000
14	19.554	0.501	2.0742	19.554	0.500	2.0741	0.000
15	19.594	0.500	2.0690	19.594	0.500	2.0690	0.001
16	19.626	0.500	2.0645	19.627	0.500	2.0652	0.001
17	19.653	0.500	2.0606	19.653	0.500	2.0610	0.000
18	19.675	0.500	2.0571	19.675	0.500	2.0571	0.000
19	19.694	0.500	2.0540	19.694	0.500	2.0541	0.000
20	19.710	0.500	2.0513
21	19.724	0.500	2.0488
22	19.735	0.500	2.0465
23	19.745	0.500	2.0444
24	19.754	0.500	2.0426
25	19.762	0.500	2.0408
26	19.769	0.500	2.0393
27	19.775	0.501	2.0378
28	19.781	0.501	2.0364
29	19.786	0.501	2.0352
30	19.790	0.501	2.0340
31	19.794	0.502	2.0329
32	19.798	0.502	2.0319
33	19.801	0.502	2.0309
34	19.804	0.502	2.0300
35	19.807	0.503	2.0291
36	19.810	0.503	2.0283
37	19.812	0.503	2.0276
38	19.814	0.504	2.0269
39	19.816	0.504	2.0262
40	19.818	0.504	2.0255
…	…	…	…	…	…	…	…
∞	19.853		2.0000	19.853		2.0000

** Energy differences relative to the ALS experimental data.

Table 5. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)nd(²P_1/2) Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (¹D₂; ²P_1/2; ²P°_1/2) = −0.301 ± 0.032 with ν = 6.

Initial Se+ State: 4s24p3 2P°1/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
6	18.351	0.175	2.0602	18.351	0.175	2.0600	0.000
7	18.785	0.179	2.0524	18.790	0.165	2.0483	0.005
8	19.066	0.176	2.0451	19.071	0.152	2.0395	0.005
9	19.256	0.174	2.0394	19.262	0.140	2.0316	0.006
10	19.392	0.172	2.0350	19.395	0.140	2.0284	0.003
11	19.491	0.171	2.0315	19.494	0.130	2.0239	0.003
12	19.566	0.169	2.0286	19.571	0.100	2.0168	0.005
13	19.624	0.168	2.0263	19.633	0	2.000	0.009
14	19.671	0.168	2.0242	19.683	−0.150	1.9788	0.012
15	19.708	0.167	2.0225	19.718	−0.150	1.9802	0.010
16	19.738	0.166	2.0210
17	19.763	0.166	2.0197
18	19.784	0.165	2.0186
19	19.802	0.165	2.0175
20	19.817	0.165	2.0166
21	19.830	0.165	2.0158
22	19.841	0.164	2.0151
23	19.851	0.164	2.0144
24	19.859	0.164	2.0138
25	19.867	0.164	2.0132
26	19.873	0.164	2.0127
27	19.879	0.164	2.0122
28	19.885	0.164	2.0118
29	19.890	0.164	2.0113
30	19.894	0.163	2.0110
31	19.898	0.163	2.0106
32	19.901	0.163	2.0103
33	19.905	0.163	2.0100
34	19.907	0.163	2.0097
35	19.910	0.163	2.0094
36	19.913	0.163	2.0091
37	19.915	0.163	2.0089
38	19.917	0.163	2.0086
39	19.919	0.163	2.0084
40	19.921	0.164	2.0082
…	…	…	…	…	…	…	…
∞	19.955		2.0000	19.955		2.0000

** Energy differences relative to the ALS experimental data.

Table 6. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (¹D₂; ²S; ²P°_1/2) = −0.165 ± 0.033 with ν = 6.

Initial Se+ State: 4s24p3 2P°1/2
	SCUNC			ALS
n	E (eV)	δ	Z *	E (eV)	δ	Z*	|ΔE| **
6	18.393	0.097	2.0330	18.393	0.097	2.0329	0.000
7	18.812	0.099	2.0287	18.816	0.087	2.0252	0.004
8	19.083	0.098	2.0247	19.077	0.125	2.0317	0.006
9	19.269	0.096	2.0216	19.264	0.125	2.0282	0.005
10	19.400	0.095	2.0192	19.396	0.135	2.0274	0.004
11	19.497	0.094	2.0173	19.495	0.125	2.0230	0.002
12	19.571	0.093	2.0157	19.571	0.100	2.0168	0.000
13	19.628	0.093	2.0144	19.632	0.025	2.0038	0.004
14	19.674	0.092	2.0133	19.681	−0.100	1.9858	0.007
15	19.710	0.092	2.0123	19.718	−0.150	1.9802	0.008
16	19.740	0.092	2.0115	19.749	−0.240	1.9704	0.009
17	19.765	0.091	2.0108
18	19.785	0.091	2.0102
19	19.803	0.091	2.0096
20	19.818	0.091	2.0091
21	19.831	0.091	2.0087
22	19.842	0.090	2.0083
23	19.851	0.090	2.0079
24	19.860	0.090	2.0075
25	19.867	0.090	2.0072
26	19.874	0.090	2.0069
27	19.880	0.090	2.0067
28	19.885	0.090	2.0064
29	19.890	0.090	2.0062
30	19.894	0.090	2.0060
31	19.898	0.090	2.0058
32	19.902	0.090	2.0056
33	19.905	0.090	2.0055
34	19.908	0.090	2.0053
35	19.910	0.090	2.0051
36	19.913	0.090	2.0050
37	19.915	0.090	2.0049
38	19.917	0.090	2.0047
39	19.919	0.090	2.0046
40	19.921	0.090	2.0045
…	…	…	…	…	…	…	…
∞	19.955		2.0000	19.955		2.000

** Energy differences relative to the ALS experimental data.

Table 7. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}D°_5/2 metastable state of Se⁺ converging to the ³P₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (³P₂; ²D°_5/2) = −0.005 ± 0.001 with ν = 11.

Initial Se+ State: 4s24p3 2D°5/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
11	19.523	0.003	2.0005	19.523	0.003	2.0005	0.0000
12	19.595	0.003	2.0005	19.595	0.003	2.0005	0.0000
13	19.651	0.003	2.0004	19.651	0.003	2.0005	0.0002
14	19.695	0.003	2.0004	19.697	−0.040	1.9943	0.0018
15	19.731	0.003	2.0004	19.733	−0.050	1.9933	0.0020
16	19.760	0.003	2.0003	19.764	−0.110	1.9863	0.0037
17	19.785	0.003	2.0003	19.789	−0.200	1.9767	0.0044
18	19.805	0.003	2.0003	19.811	−0.350	1.9618	0.0060
19	19.822	0.003	2.0003	19.827	−0.320	1.9669	0.0048
20	19.837	0.003	2.0003	19.842	−0.300	1.9704	0.0051
21	19.850	0.003	2.0003	19.855	−0.400	1.9626	0.0054
22	19.861	0.003	2.0002	19.865	−0.400	1.9643	0.0045
23	19.870	0.003	2.0002	19.874	−0.450	1.9616	0.0039
24	19.878	0.003	2.0002
25	19.886	0.003	2.0002
26	19.892	0.003	2.0002
27	19.898	0.003	2.0002
28	19.904	0.003	2.0002
29	19.908	0.003	2.0002
30	19.913	0.003	2.0002
31	19.916	0.003	2.0002
32	19.920	0.003	2.0002
33	19.923	0.003	2.0002
34	19.926	0.003	2.0002
35	19.929	0.003	2.0002
36	19.931	0.003	2.0001
37	19.933	0.003	2.0001
38	19.935	0.003	2.0001
39	19.937	0.003	2.0001
40	19.939	0.003	2.0001
…	…	…	…	…	…	…	…
∞	19.973		2.0000	19.973		2.0000

** Energy differences relative to the ALS experimental data.

Table 8. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)ns Rydberg series originating from the 4s²4p^{3 2}P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (¹D₂; ²P°_1/2) = −0.923 ± 0.050 with ν = 7.

Initial State 4s24p3 2P°1/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
7	18.667	0.500	2.1538	18.667	0.500	2.1538	0.000
8	18.988	0.496	2.1323	18.991	0.488	2.1294	0.003
9	19.203	0.494	2.1162	19.207	0.470	2.1102	0.004
10	19.353	0.492	2.1036	19.357	0.460	2.0964	0.004
11	19.462	0.491	2.0935	19.467	0.440	2.0833	0.005
12	19.544	0.490	2.0852	19.549	0.420	2.0725	0.005
13	19.607	0.489	2.0782	19.613	0.380	2.0602	0.006
14	19.657	0.489	2.0724	19.663	0.355	2.0520	0.006
15	19.697	0.488	2.0673	19.702	0.340	2.0464	0.005
16	19.729	0.488	2.0629
17	19.755	0.488	2.0591
18	19.778	0.488	2.0557
19	19.796	0.488	2.0527
20	19.812	0.488	2.0500
21	19.826	0.488	2.0476
22	19.837	0.488	2.0454
23	19.848	0.488	2.0434
24	19.857	0.488	2.0415
25	19.864	0.488	2.0398
26	19.871	0.489	2.0383
27	19.878	0.489	2.0369
28	19.883	0.489	2.0355
29	19.888	0.489	2.0343
30	19.893	0.489	2.0332
31	19.897	0.490	2.0321
32	19.900	0.490	2.0311
33	19.904	0.490	2.0302
34	19.907	0.491	2.0293
35	19.909	0.491	2.0284
36	19.912	0.491	2.0277
37	19.914	0.491	2.0269
38	19.916	0.492	2.0262
39	19.918	0.492	2.0256
40	19.920	0.492	2.0249
…	…	…	…	…	…	…	…
∞	19.955		2.0000	19.955		2.0000

** Energy differences relative to the ALS experimental data.

Table 9. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 2}D°_3/2 metastable state of Se⁺ converging to the ³P₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (³P₂; ²D°_3/2) = −0.094 ± 0.042 with ν = 11.

Initial Se+ State: 4s24p3 2D°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
11	19.595	0.051	2.0094	19.595	0.051	2.0093	0.000
12	19.668	0.052	2.0087	19.668	0.051	2.0085	0.000
13	19.724	0.052	2.0080	19.724	0.051	2.0079	0.000
14	19.769	0.052	2.0074	19.770	0.035	2.0073	0.001
15	19.805	0.052	2.0069	19.807	0.020	2.0068	0.002
16	19.835	0.052	2.0064	19.835	0.051	2.0064	0.000
17	19.860	0.052	2.0060	19.860	0.051	2.0060	0.000
18	19.880	0.051	2.0057	19.880	0.051	2.0057	0.000
19	19.897	0.051	2.0054	19.897	0.051	2.0054	0.000
20	19.912	0.051	2.0051	19.912	0.051	2.0051	0.000
21	19.925	0.051	2.0048	19.925	0.051	2.0049	0.000
22	19.936	0.051	2.0046	19.936	0.051	2.0046	0.000
23	19.946	0.051	2.0044	19.946	0.051	2.0044	0.000
24	19.954	0.051	2.0042	19.954	0.051	2.0042	0.000
25	19.962	0.051	2.0040	19.962	0.051	2.0041	0.000
26	19.968	0.051	2.0039
27	19.974	0.051	2.0037
28	19.979	0.051	2.0036
29	19.984	0.051	2.0035
30	19.988	0.051	2.0033
31	19.992	0.051	2.0032
32	19.996	0.051	2.0031
33	19.999	0.051	2.0030
34	20.002	0.051	2.0029
35	20.004	0.051	2.0028
36	20.007	0.051	2.0028
37	20.009	0.051	2.0027
38	20.011	0.051	2.0026
39	20.013	0.051	2.0025
40	20.015	0.051	2.0025
…	…	…	…	…	…	…	…
∞	20.049		2.0000	20.049		2.0000

** Energy differences relative to the ALS experimental data.

Table 10. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the 4s²4p^{3 2}D°_5/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. The uncertainties in the experimental energies are stated to be ±0.010 eV, f₁ (¹D₂; ²D°_5/2) = −0.927 ± 0.050 with ν = 7.

Initial Se+ State: 4s24p3 2D°5/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE|**
7	19.811	0.503	2.1550	19.811	0.502	2.1545	0.000
8	20.133	0.497	2.1324	20.135	0.490	2.1305	0.002
9	20.348	0.494	2.1162	20.350	0.480	2.1127	0.002
10	20.498	0.492	2.1036	20.501	0.480	2.1008	0.003
11	20.607	0.491	2.0935	20.610	0.470	2.0893	0.003
12	20.689	0.490	2.0852	20.690	0.480	2.0833	0.001
13	20.752	0.490	2.0783	20.753	0.480	2.0767	0.001
14	20.802	0.489	2.0724	20.803	0.460	2.0679	0.001
15	20.842	0.489	2.0674	20.846	0.360	2.0492	0.004
16	20.874	0.489	2.0630	20.882	0.200	2.0253	0.008
17	20.900	0.488	2.0592	20.909	0.100	2.0118	0.009
18	20.923	0.488	2.0558	20.932	0	2.0000	0.009
19	20.941	0.488	2.0528	20.949	0	2.0000	0.008
20	20.957	0.488	2.0501	20.964	0	2.0000	0.007
21	20.971	0.488	2.0476	20.977	0	2.0000	0.006
22	20.982	0.489	2.0454	20.988	0	2.0000	0.006
23	20.993	0.489	2.0434	20.997	0	2.0000	0.004
24	21.002	0.489	2.0416
25	21.009	0.489	2.0399
26	21.016	0.489	2.0384
27	21.023	0.489	2.0369
28	21.028	0.490	2.0356
29	21.033	0.490	2.0344
30	21.038	0.490	2.0332
31	21.042	0.491	2.0322
32	21.045	0.491	2.0312
33	21.049	0.491	2.0302
34	21.052	0.491	2.0293
35	21.054	0.492	2.0285
36	21.057	0.492	2.0277
37	21.059	0.492	2.0270
38	21.061	0.493	2.0263
39	21.063	0.493	2.0256
40	21.065	0.493	2.0250
…	…	…	…	…	…	…	…
∞	21.100		2.0000	21.100		2.0000

** Energy differences relative to the ALS experimental data.

Table 11. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the 4s²4p^{3 2}D°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. f₁ (¹D₂; ²D°_3/2) = −0.912 ± 0.050 with ν = 7.

Initial Se+ State: 4s24p3 2D°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE|**
7	19.890	0.496	2.1525	19.890	0.495	2.1522	0.000
8	20.211	0.489	2.1303	20.214	0.480	2.1276	0.003
9	20.425	0.487	2.1143	20.428	0.470	2.1102	0.003
10	20.575	0.485	2.1019	20.576	0.480	2.1008	0.001
11	20.684	0.484	2.0920	20.685	0.470	2.0893	0.001
12	20.766	0.483	2.0838	20.770	0.420	2.0725	0.004
13	20.829	0.482	2.0770	20.830	0.460	2.0734	0.001
14	20.878	0.481	2.0712	20.883	0.380	2.0558	0.005
15	20.918	0.481	2.0663	20.922	0.360	2.0492	0.004
16	20.950	0.481	2.0620	20.955	0.300	2.0382	0.005
17	20.977	0.481	2.0582	20.985	0.100	2.0118	0.008
18	20.999	0.481	2.0549	21.008	0	2.0000	0.009
19	21.017	0.481	2.0519	21.025	0	2.0000	0.008
20	21.033	0.481	2.0492	21.040	0	2.0000	0.007
21	21.047	0.481	2.0469	21.053	0	2.0000	0.006
22	21.058	0.481	2.0447	21.064	0	2.0000	0.006
23	21.069	0.481	2.0427	21.073	0	2.0000	0.004
24	21.078	0.481	2.0409
25	21.085	0.481	2.0393
26	21.092	0.481	2.0377
27	21.099	0.482	2.0363
28	21.104	0.482	2.0350
29	21.109	0.482	2.0338
30	21.114	0.482	2.0327
31	21.118	0.483	2.0316
32	21.121	0.483	2.0306
33	21.125	0.483	2.0297
34	21.128	0.484	2.0289
35	21.130	0.484	2.0280
36	21.133	0.484	2.0273
37	21.135	0.484	2.0265
38	21.137	0.485	2.0258
39	21.139	0.485	2.0252
40	21.141	0.485	2.0246
…	…	…	…	…	…	…	…
∞	21.176		2.0000	21.176		2.0000

** Energy differences relative to the ALS experimental data.

Table 12. Energy resonances (E), quantum defect (δ) and effective charge (Z*) of the 4s²4p² (³P₂)nd Rydberg series originating from the 4s²4p^{3 4}S°_3/2 ground state of Se⁺ converging to the ³P₂ series limit in Se²⁺. The present results (SCUNC) are compared with the experimental data from ALS measurements [6]. f₁ (³P₂; ⁴S°_3/2) = −0.379 ± 0.042 with ν = 11.

Initial Se+ State: 4s24p3 4S°3/2
	SCUNC			ALS
n	E (eV)	δ	Z*	E (eV)	δ	Z*	|ΔE| **
11	21.215	0.205	2.0379	21.215	0.210	2.0389	0.000
12	21.291	0.206	2.0349	21.219	0.210	2.0356	0.072
13	21.349	0.207	2.0323	21.349	0.210	2.0328	0.000
14	21.396	0.207	2.0300	21.396	0.210	2.0304	0.000
15	21.433	0.206	2.0279	21.433	0.210	2.0284	0.000
16	21.464	0.206	2.0261	21.464	0.210	2.0266	0.000
17	21.489	0.206	2.0245	21.489	0.210	2.0250	0.000
18	21.510	0.206	2.0231	21.510	0.210	2.0236	0.000
19	21.528	0.206	2.0219	21.528	0.210	2.0223	0.000
20	21.543	0.205	2.0208	21.543	0.210	2.0212	0.000
21	21.556	0.205	2.0197	21.556	0.210	2.0202	0.000
22	21.567	0.205	2.0188	21.567	0.210	2.0193	0.000
23	21.577	0.205	2.0180	21.577	0.210	2.0184	0.000
24	21.586	0.205	2.0172	21.586	0.210	2.0176	0.000
25	21.593	0.205	2.0165	21.593	0.210	2.0169	0.000
26	21.600	0.205	2.0159
27	21.606	0.205	2.0153
28	21.612	0.205	2.0147
29	21.616	0.205	2.0142
30	21.621	0.205	2.0137
31	21.625	0.205	2.0133
32	21.628	0.205	2.0129
33	21.631	0.205	2.0125
34	21.634	0.205	2.0121
35	21.637	0.205	2.0118
36	21.640	0.205	2.0114
37	21.642	0.205	2.0111
38	21.644	0.205	2.0108
39	21.646	0.205	2.0106
40	21.648	0.205	2.0103
…	…	…	…	…	…	…	…
∞	21.682		2.0000	21.682		2.0000

** Energy differences relative to the ALS experimental data.

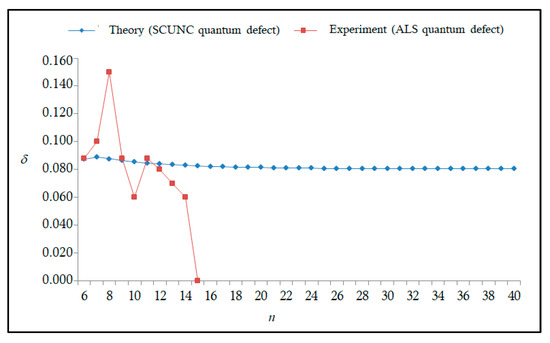
Figure 1. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺.

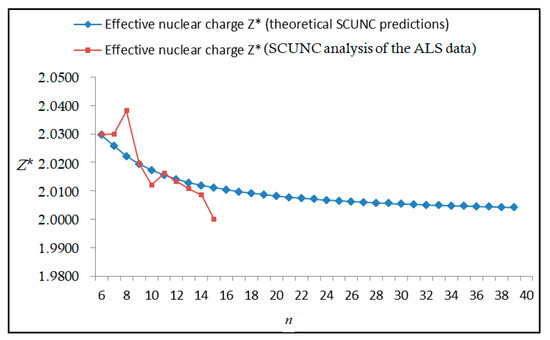
Figure 2. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limit in Se²⁺.

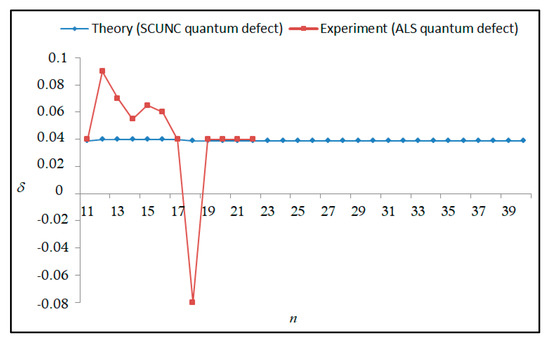
Figure 3. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

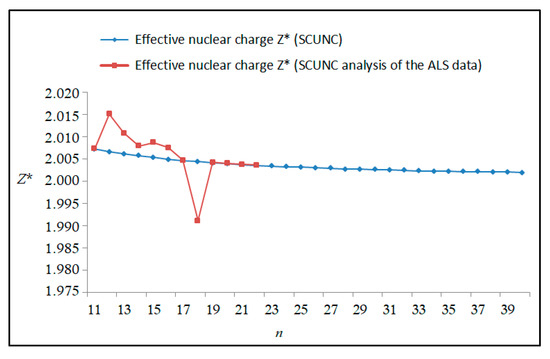
Figure 4. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

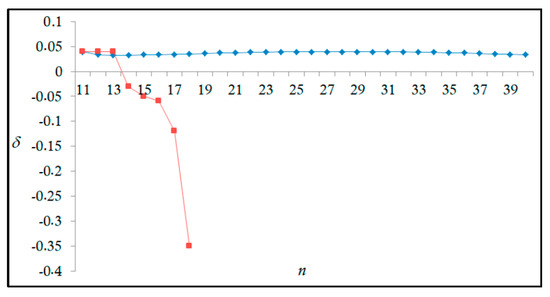
Figure 5. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺⁺.

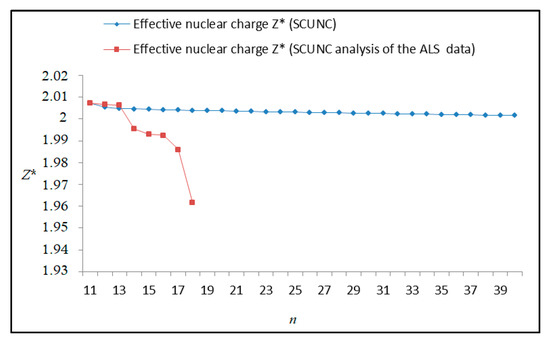
Figure 6. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

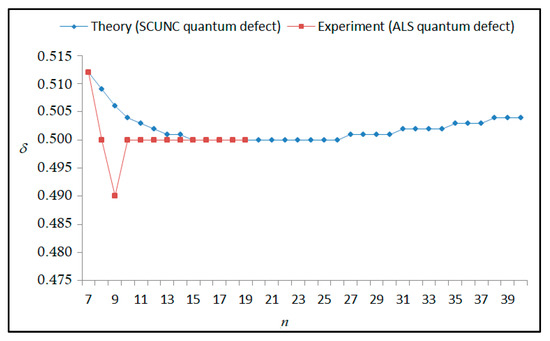
Figure 7. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)ns Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

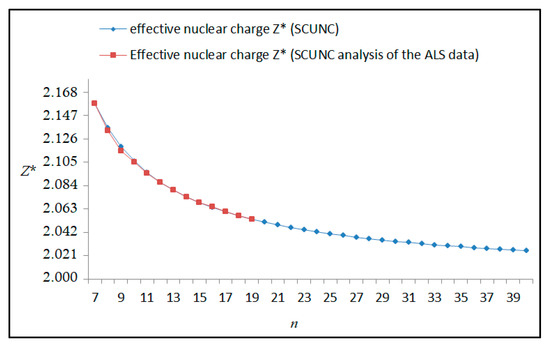
Figure 8. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²P°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

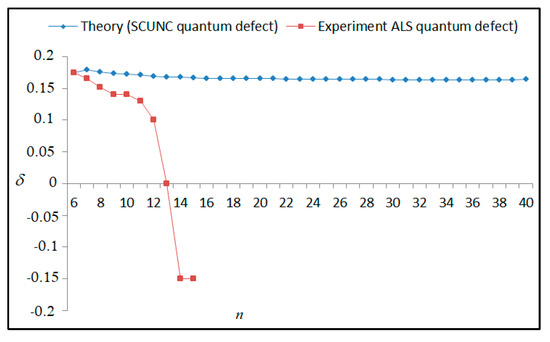
Figure 9. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)nd(²P_1/2) Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ²D₁ series limits in Se²⁺.

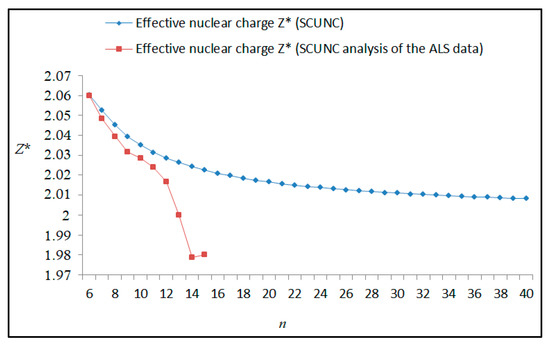
Figure 10. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)nd(²P_1/2) Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ²D₁ series limits in Se²⁺.

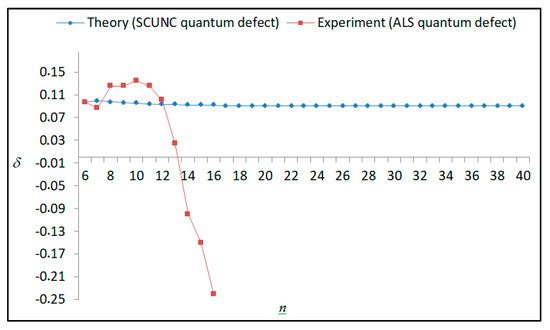
Figure 11. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

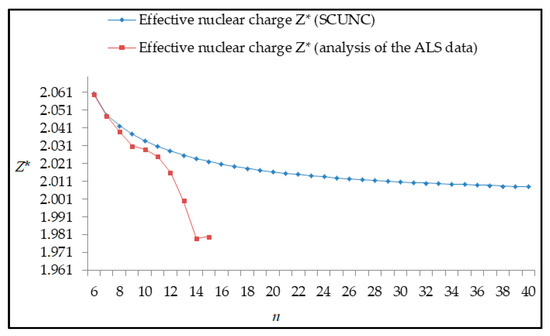
Figure 12. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)nd (²S) Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

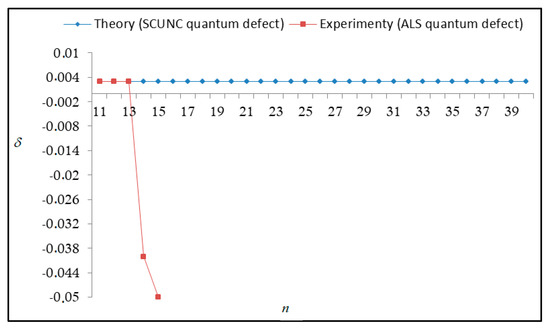
Figure 13. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²D°_5/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

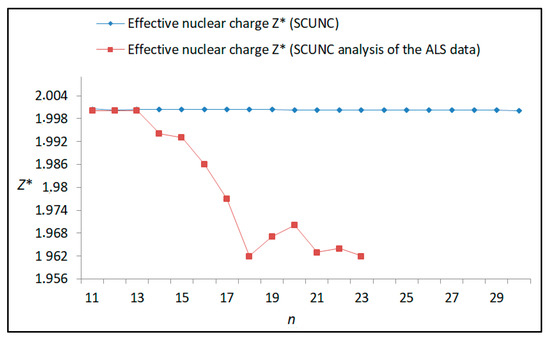
Figure 14. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ²D°_5/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

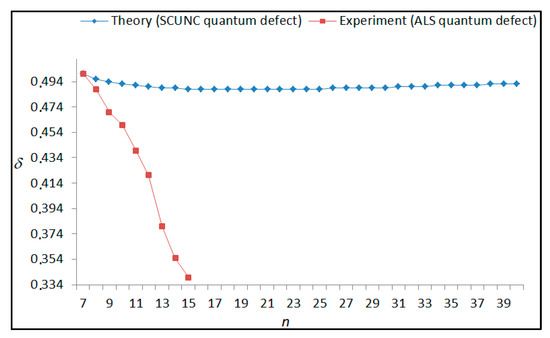
Figure 15. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)ns Rydberg series originating from the ²P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

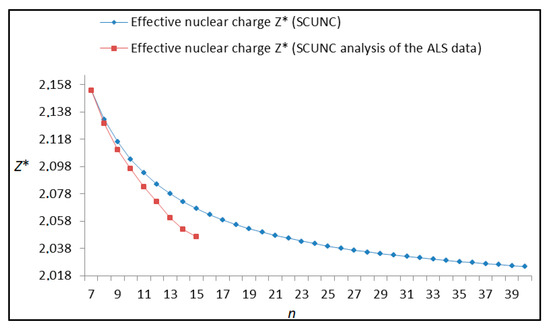
Figure 16. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)ns Rydberg series originating from ²P°_1/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

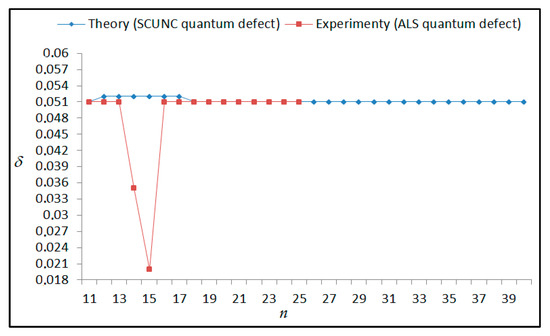
Figure 17. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)ns Rydberg series originating from the ²D°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

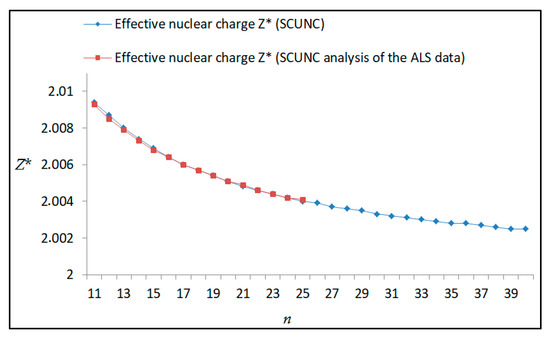
Figure 18. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)ns Rydberg series originating from ²D°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

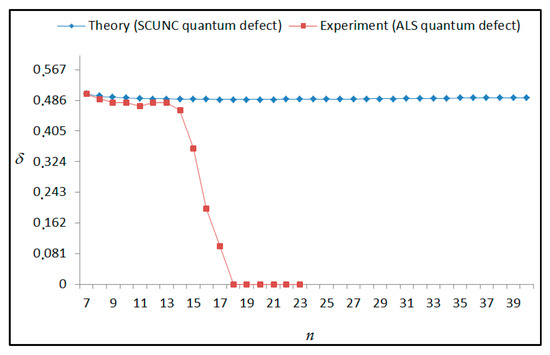
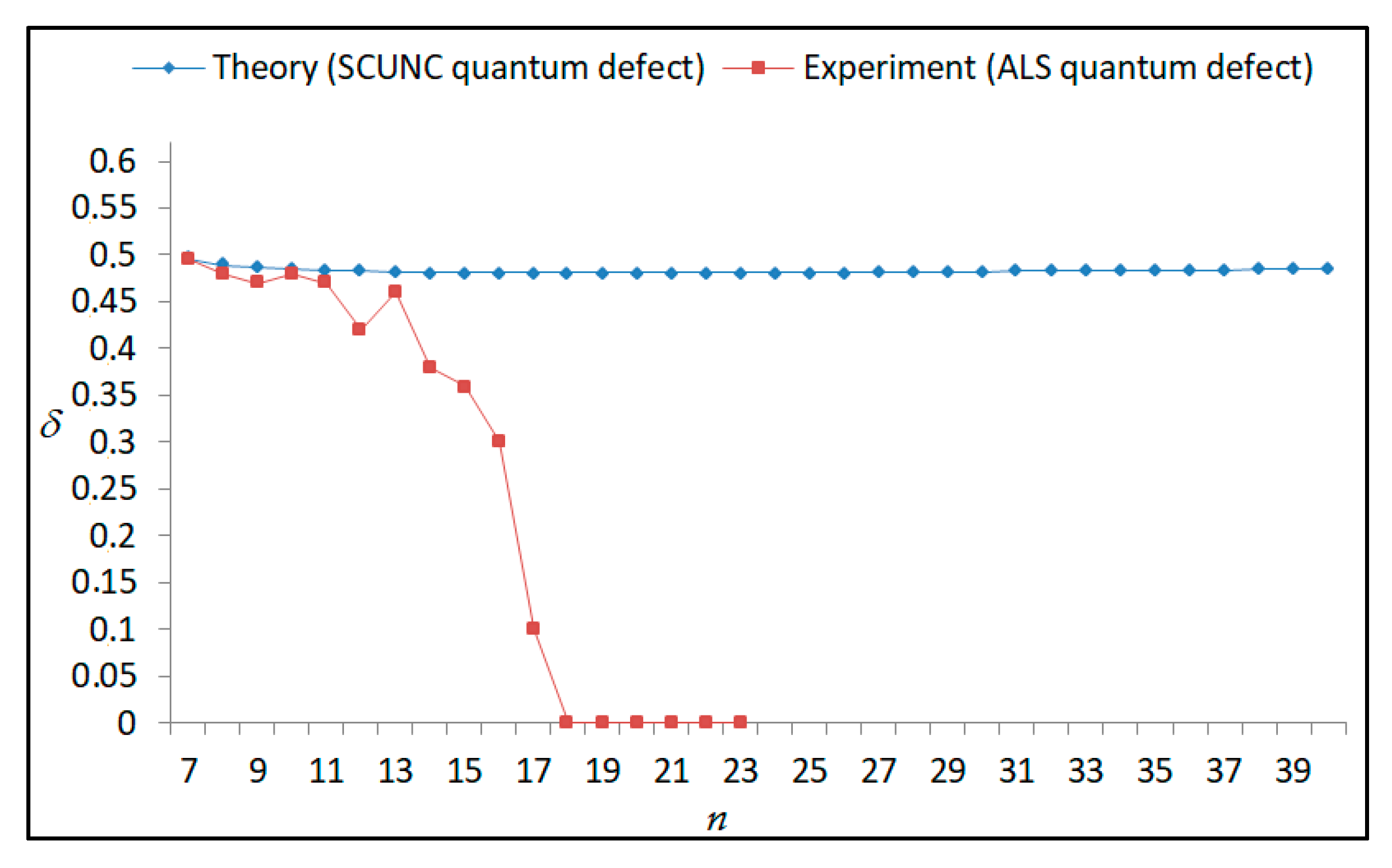
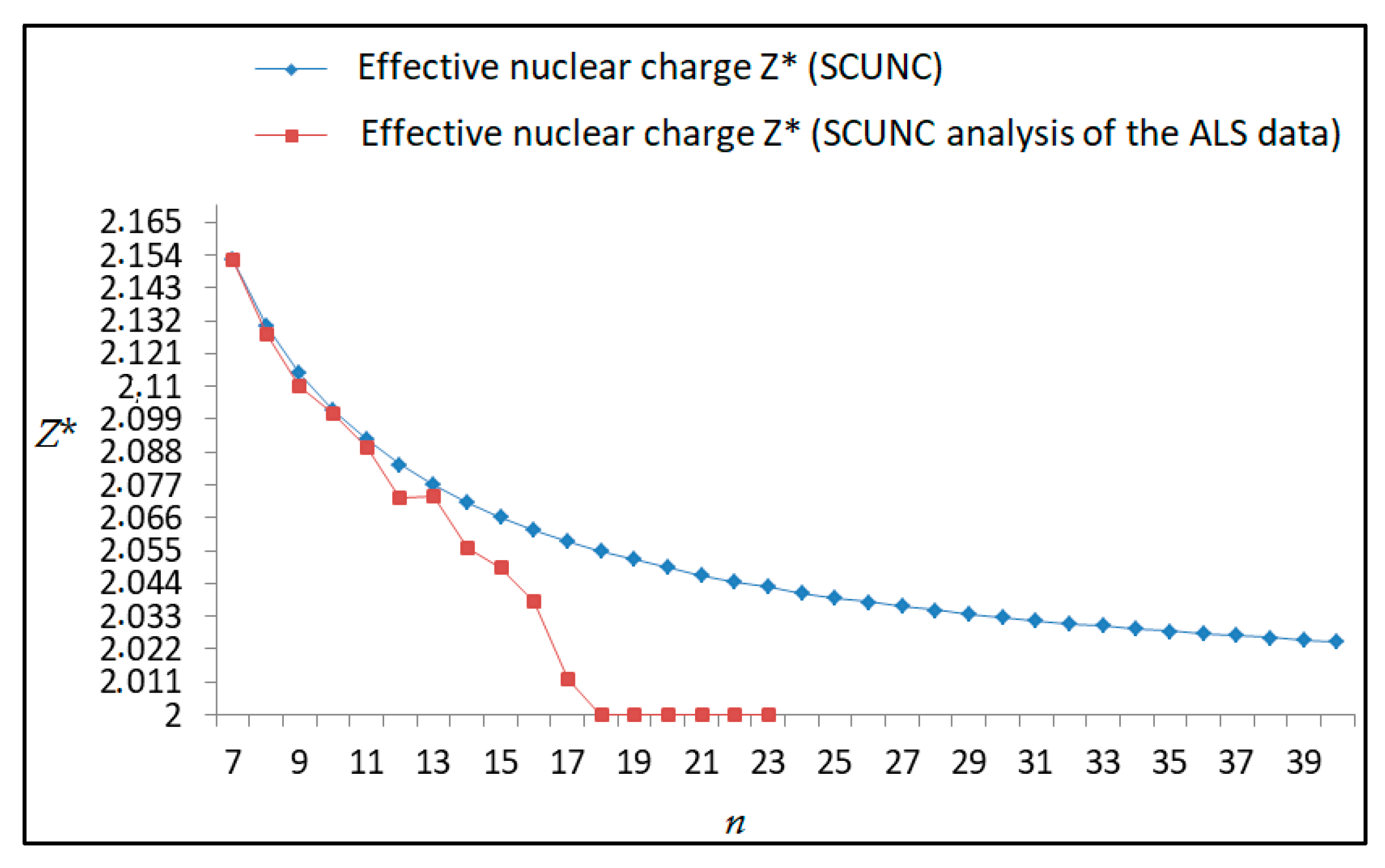
Figure 19. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the ²D°_5/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

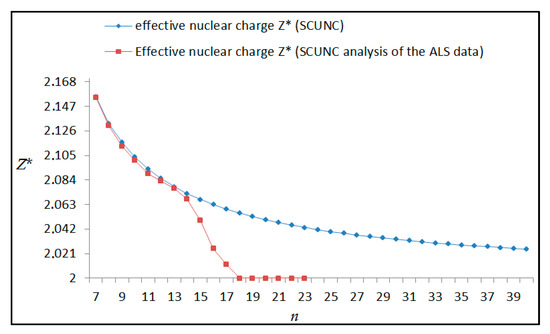
Figure 20. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from ²D°_5/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

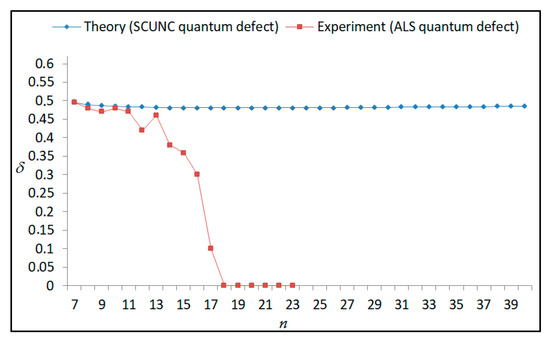
Figure 21. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from the ²D°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

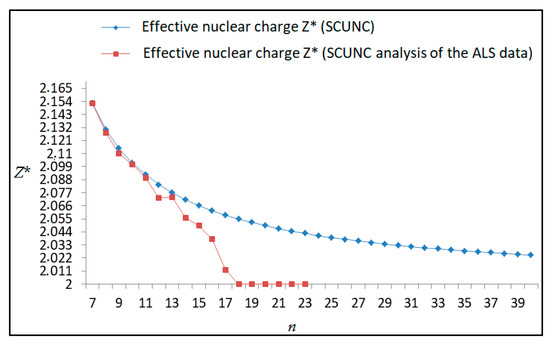
Figure 22. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from ²D°_3/2 metastable state of Se⁺ converging to the ¹D₂ series limits in Se²⁺.

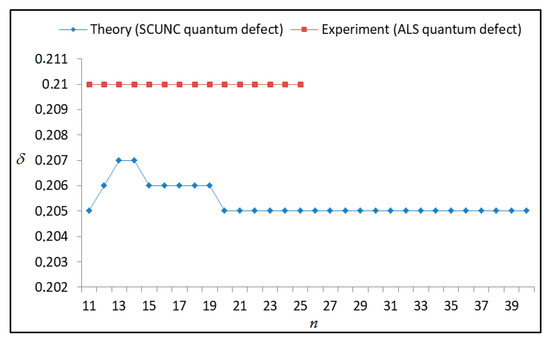
Figure 23. Variations of the quantum defect (δ) with the principal quantum number n for the 4s²4p² (³P₂)nd Rydberg series originating from the ⁴S°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

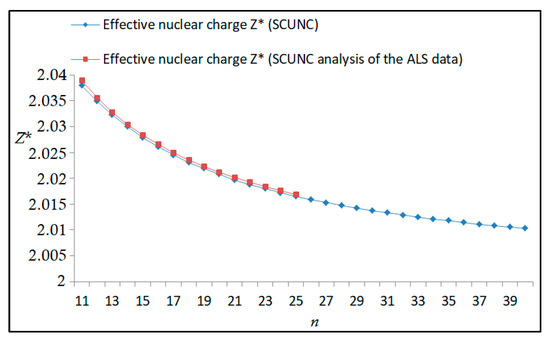
Figure 24. Variations of the effective nuclear charge Z* with the principal quantum number n for the 4s²4p² (¹D₂)ns (²D) Rydberg series originating from ²S°_3/2 metastable state of Se⁺ converging to the ³P₂ series limits in Se²⁺.

• The generation of atomic orbitals based primarily on the atomic structure of the residual ion;
• The use of specific codes in the investigations (and then inevitably a fastidious computer program);
• Mathematical complexity in the formalism.

The merit of the SCUNC formalism is due to the fact that accurate energy positions can be obtained within a simple analytical formula for whole members of the Rydberg series by only varying the n-principal quantum number without needing to generate atomic orbitals, to use specific codes or to invoke mathematical complexity in the formalism. Another important point that deserves to be underlined is linked to the limitation of the PI cross-section for high-lying states even when investigations are performed with high photon resolution. In fact, when the n-principal quantum number increases, the peaks of the cross-section become more and more narrow and overlap for high n-values or for high photon energy. As a result, unresolved lines appear necessary, and the corresponding energy positions cannot be determined theoretically or experimentally. The SCUNC method does not face such problems, as accurate energy positions can be obtained up to very high-n, as demonstrated in our recent papers [14,15,16,17,18,19].

4. Summary and Conclusions

The SCUNC method is used to investigate as many as 12 Rydberg series due to the 4p → nd and 4p → ns transitions from the ⁴S°_3/2 ground-state and the ²P°_3/2,1/2 and ²D°_5/2,3/2 metastable states of the Se⁺ ions in the energy region (17.75–21.85 eV). Over the entire Rydberg series, positive δ values are obtained, and it is shown that the SCUNC method excellently reproduces the experimental energy resonances from ALS measurements [6] for various resonances. The strength of the present work is that the SCUNC formalism has permitted us to provide confidence in the experimental data on Se⁺ ions for numerous Rydberg series. In addition, the ALS work is part of a broader investigation of absolute photoionization cross-section measurements of Se⁺ through Se⁵⁺ [6]. The excellent agreements between the ALS measurements [6] and the present calculations and that performed previously [13] on Se⁺ ions point out the prominent role that the SCUNC formalism can play in the investigations of high-lying energy resonances of Rydberg series of the Se²⁺, Se³⁺, Se⁴⁺ and Se⁵⁺ ions in connections with the understanding of the chemical evolution of Se in the universe.