Differential Description of Multiple Ionization of Uracil by 3.5 MeV/u C6+ Impact
Abstract
:1. Introduction
2. Theoretical Method
Ad-CTMC Method
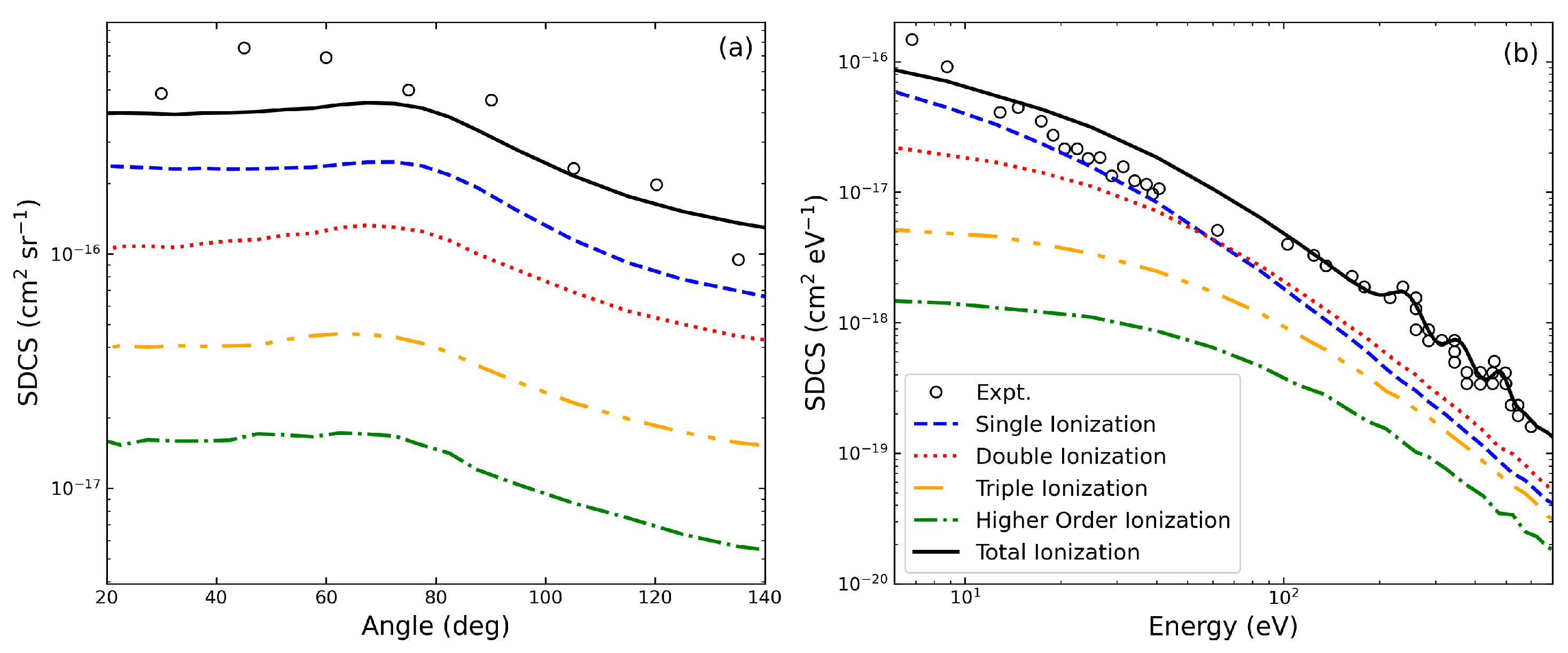
3. Results and Discussion
3.1. Double Ionization
3.2. Triple Ionization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lisse, C.M.; Dennerl, K.; Englhauser, J.; Harden, M.; Marshall, F.E.; Mumma, M.J.; Petre, R.; Pye, J.P.; Ricketts, M.J.; Schmitt, J.; et al. Discovery of X-ray and Extreme Ultraviolet Emission from Comet C/Hyakutake 1996 B2. Science 1996, 274, 205–209. [Google Scholar] [CrossRef]
- Otranto, S.; Olson, R.E.; Beiersdorfer, P. X-ray emission cross sections following charge exchange by multiply charged ions of astrophysical interest. Phys. Rev. A 2006, 73, 022723. [Google Scholar] [CrossRef]
- Otranto, S.; Olson, R.E.; Beiersdorfer, P. Cometary X-rays: Line emission cross sections for multiply charged solar wind ion charge exchange. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1755–1766. [Google Scholar] [CrossRef]
- Isler, R.C. An overview of charge-exchange spectroscopy as a plasma diagnostic. Plasma Phys. Controlled Fusion 1994, 36, 171–208. [Google Scholar] [CrossRef]
- Otranto, S.; Olson, R.E. Charge exchange and X-ray emission cross sections for multiply charged ions colliding with H2O. Phys. Rev. A 2008, 77, 022709. [Google Scholar] [CrossRef]
- Illescas, C.; Errea, L.F.; Méndez, L.; Pons, B.; Rabadán, I.; Riera, A. Classical treatment of ion-H2O collisions with a three-center model potential. Phys. Rev. A 2011, 83, 052704. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Nikjoo, H. Cross sections for bare and dressed carbon ions in water and neon. Phys. Med. Biol. 2013, 58, 641–672. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Nikjoo, H. A Monte Carlo track structure simulation code for the full-slowing-down carbon projectiles of energies 1 keV u-1-10 MeV u-1 in water. Phys. Med. Biol. 2013, 58, 673–701. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Biswas, S.; Monti, J.M.; Rivarola, R.D.; Tribedi, L.C. Double-differential cross section for ionization of H2O molecules by 4-MeV/u C6+ and Si13+ ions. Phys. Rev. A 2017, 96, 052707. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Bagdia, C.; Chowdhury, M.R.; Monti, J.M.; Rivarola, R.D.; Tribedi, L.C. Energy and angular distribution of electrons ejected from water by the impact of fast O8+ ion beams. Eur. Phys. J. D 2018, 72, 15. [Google Scholar] [CrossRef]
- Otranto, S.; Bachi, N.; Olson, R.E. Cross section scaling for H2O ionization by highly-charged ion impact. Eur. Phys. J. D 2019, 73, 41. [Google Scholar] [CrossRef]
- Bachi, N.; Otranto, S.; Otero, G.S.; Olson, R.E. The role of multiple ionization of H2O in heavy ion collisions. Phys. Med. Biol. 2019, 64, 205020. [Google Scholar] [CrossRef] [PubMed]
- Bachi, N.; Otero, G.S.; Otranto, S.; Olson, R.E. The role of multiple electron processes for fast ion H2O collisions. AIP Conf. Proc. 2019, 2160, 070006. [Google Scholar]
- Jorge, A.; Horbatsch, M.; Illescas, C.; Kirchner, T. Classical-trajectory Monte Carlo calculations of differential electron-emission cross sections in fast heavy-ion collisions with water molecules. Phys. Rev. A 2019, 99, 062701. [Google Scholar] [CrossRef]
- Jorge, A.; Horbatsch, M.; Kirchner, T. Multicharged-ion–water-molecule collisions in a classical-trajectory time-dependent mean-field theory. Phys. Rev. A 2020, 102, 012808. [Google Scholar] [CrossRef]
- Lüdde, H.J.; Kalkbrenner, T.; Horbatsch, M.; Kirchner, T. Nonperturbative scaling behavior for net ionization of biologically relevant molecules by multiply charged heavy-ion impact. Phys. Rev. A 2020, 101, 062709. [Google Scholar] [CrossRef]
- Moretto-Capelle, P.; Le Padellec, A. Electron spectroscopy in proton collisions with dry gas-phase uracil base. Phys. Rev. A 2006, 74, 062705. [Google Scholar] [CrossRef]
- Galassi, M.E.; Champion, C.; Weck, P.F.; Rivarola, R.D.; Fojón, O.; Hanssen, J. Quantum-mechanical predictions of DNA and RNA ionization by energetic proton beams. Phys. Med. Biol. 2012, 57, 2081. [Google Scholar] [CrossRef]
- Itoh, A.; Iriki, Y.; Imai, M.; Champion, C.; Rivarola, R.D. Cross sections for ionization of uracil by MeV-energy-proton impact. Phys. Rev. A 2013, 88, 052711. [Google Scholar] [CrossRef]
- Sarkadi, L. Classical treatment of the electron emission from collisions of uracil molecules with fast protons. Phys. Rev. A 2015, 92, 062704. [Google Scholar] [CrossRef]
- Agnihotri, A.N.; Nandi, S.; Kasthurirangan, S.; Kumar, A.; Galassi, M.E.; Rivarola, R.D.; Champion, C.; Tribedi, L.C. Doubly differential distribution of electron emission in ionization of uracil in collisions with 3.5-MeV/u bare C ions. Phys. Rev. A 2013, 87, 032716. [Google Scholar] [CrossRef]
- Agnihotri, A.N.; Kasthurirangan, S.; Nandi, S.; Kumar, A.; Champion, C.; Lekadir, H.; Hanssen, J.; Weck, P.F.; Galassi, M.E.; Rivarola, R.D.; et al. Absolute total ionization cross sections of uracil (C4H4N2O2) in collisions with MeV energy highly charged carbon, oxygen and fluorine ions. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 185201. [Google Scholar] [CrossRef]
- Sarkadi, L. Classical trajectory Monte Carlo model calculations for ionization of the uracil molecule by impact of heavy ions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 185203. [Google Scholar] [CrossRef]
- Lüdde, H.J.; Horbatsch, M.; Kirchner, T. Proton-impact-induced electron emission from biologically relevant molecules studied with a screened independent atom model. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 195203. [Google Scholar] [CrossRef]
- Abbas, I.; Champion, C.; Zarour, B.; Lasri, B.; Hanssen, J. Single and multiple cross sections for ionizing processes of biological molecules by protons and α-particle impact: A classical Monte Carlo approach. Phys. Med. Biol. 2008, 53, N41. [Google Scholar] [CrossRef] [PubMed]
- Olson, R.E.; Ullrich, J.; Schmidt-Bocking, H. Dynamics of multiply charged ion-atom collisions: U32+ + Ne. J. Phys. B Atom. Mol. Phys. 1987, 20, L809. [Google Scholar] [CrossRef]
- Cariatore, N.D.; Bachi, N.; Otranto, S. C6+-impact ionization of uracil at MeV/u impact energies: The role of the multiple-ionization channel. Phys. Rev. A 2022, 106, 012808. [Google Scholar] [CrossRef]
- Abrines, R.; Percival, I.C. A generalized correspondence principle and proton-hydrogen collisions. Proc. Phys. Soc. 1966, 88, 873–883. [Google Scholar] [CrossRef]
- Olson, R.E.; Salop, A. Charge-transfer and impact-ionization cross sections for fully and partially stripped positive ions colliding with atomic hydrogen. Phys. Rev. A 1977, 16, 531–541. [Google Scholar] [CrossRef]
- Reinhold, C.O.; Falcón, C.A. Classical ionization and charge-transfer cross sections for H+ + He and H+ + Li+ collisions with consideration of model interactions. Phys. Rev. A 1986, 33, 3859–3866. [Google Scholar] [CrossRef]
- Garvey, R.H.; Jackman, C.H.; Green, A.E.S. Independent-particle-model potentials for atoms and ions with 36<Z≤54 and a modified Thomas–Fermi atomic energy formula. Phys. Rev. A 1975, 12, 1144. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cariatore, N.D.; Bachi, N.; Otranto, S. Differential Description of Multiple Ionization of Uracil by 3.5 MeV/u C6+ Impact. Atoms 2023, 11, 38. https://doi.org/10.3390/atoms11020038
Cariatore ND, Bachi N, Otranto S. Differential Description of Multiple Ionization of Uracil by 3.5 MeV/u C6+ Impact. Atoms. 2023; 11(2):38. https://doi.org/10.3390/atoms11020038
Chicago/Turabian StyleCariatore, N. D., N. Bachi, and S. Otranto. 2023. "Differential Description of Multiple Ionization of Uracil by 3.5 MeV/u C6+ Impact" Atoms 11, no. 2: 38. https://doi.org/10.3390/atoms11020038
APA StyleCariatore, N. D., Bachi, N., & Otranto, S. (2023). Differential Description of Multiple Ionization of Uracil by 3.5 MeV/u C6+ Impact. Atoms, 11(2), 38. https://doi.org/10.3390/atoms11020038





