Positron Scattering from Pyrimidine
Abstract
:1. Introduction
2. The Single-Centre Expansion Method and the Binary-Encounter-Bethe Model
2.1. Elastic Cross-Sections
2.2. Direct Ionisation Cross-Sections
3. Computational Details
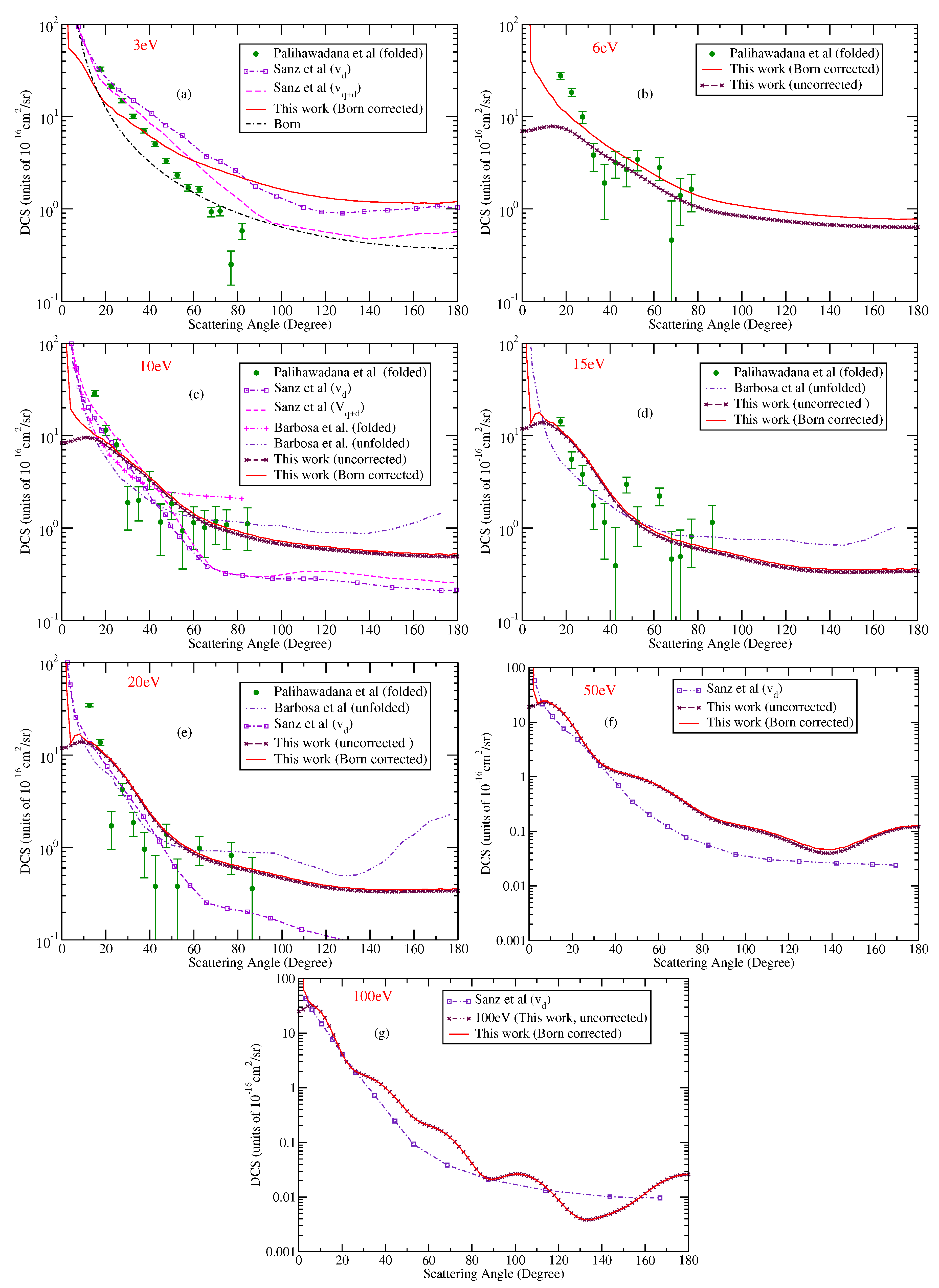
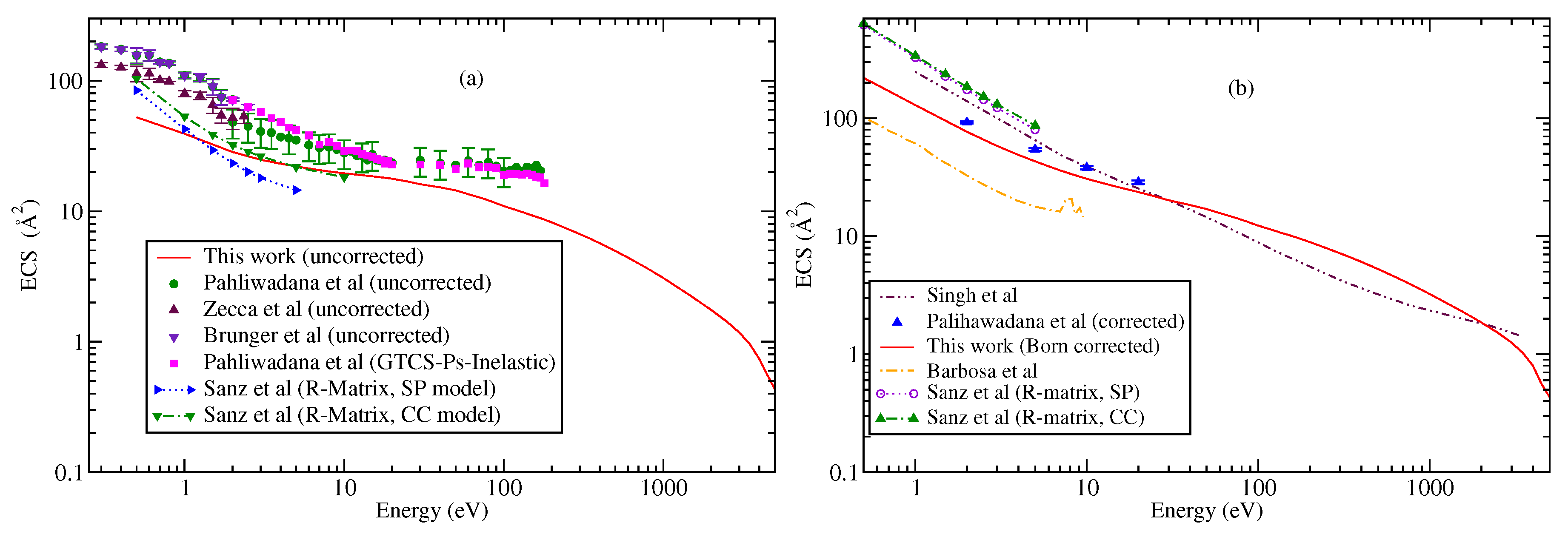
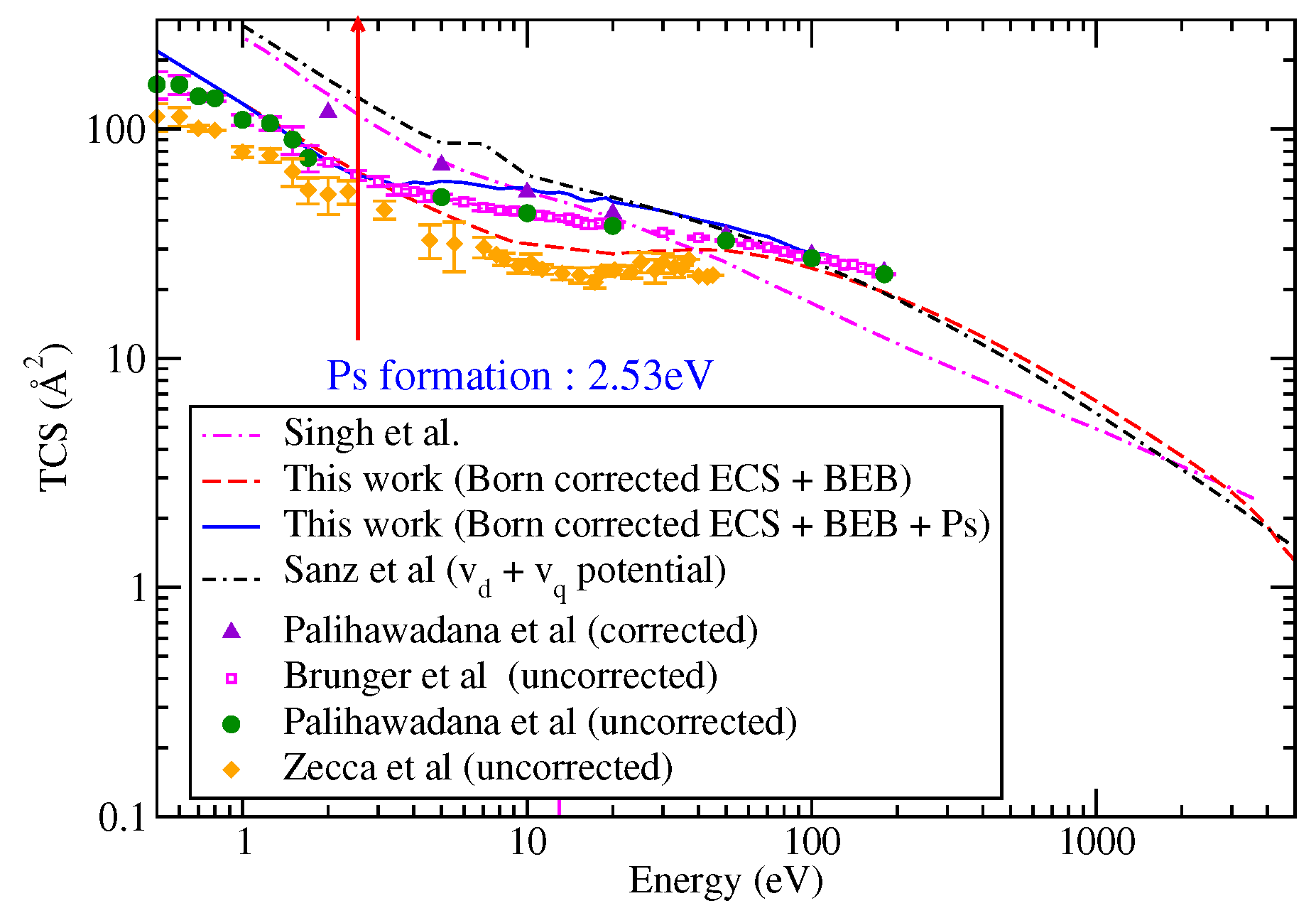
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCE | Single-Centre Expansion |
| ECS | Elastic Cross-Sections |
| DCS | Differential Cross-Sections |
| TCS | Total Cross-Sections |
| TICS | Total Ionisation Cross-Sections |
| IE | Ionisation Energy |
| BEB | Binary–Encounter–Bethe |
| HF | Hartree–Fock |
| DFT | Density Functional Theory |
| IE | Ionisation Energy |
| CC | Close-Coupling |
| eV | Electron Volt |
| au | Atomic Unit |
| IAM | Independent Atom Approximation |
References
- Cherry, S.R.; Sorenson, J.A.; Phelps, M.E. Physics in Nuclear Medicine, 4th ed.; Elsevier: Philadelphia, PA, USA, 2012. [Google Scholar]
- Jaini, S.; Dadachova, E. FDG for Therapy of Metabolically Active Tumors. Nucl. Med. 2012, 42, 185. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; Taleei, R.; Liamsuwan, T.; Liljequist, D.; Emfietzoglou, D. Perspectives in radiation biophysics: From radiation track structure simulation to mechanistic models of DNA damage and repair. Radiat. Phys. Chem. 2016, 128, 3–10. [Google Scholar] [CrossRef]
- Tejedor Gomez, G.G.; Fuss, M.C. Radiation Damage in Biomolecular Systems; Springer: Berlin, Germany, 2012. [Google Scholar]
- Surko, C.M.; Gianturco, F.A. (Eds.) New Directions in Antimatter Chemistry and Physics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Wahl, R.L.; Buchanan, J.W. Principles and Practice of Positron Emission Tomography; Lippincott, Williams and Wilkins: Philadelphia, PA, USA, 2002. [Google Scholar]
- Bailey, D.; Townsend, W.; Valk, P.; Maisey, M. Positron Emission Tomography; Springer: London, UK, 2005. [Google Scholar]
- Müller, H.; Enghardt, W. In-beam PET at high-energy photon beams: A feasibility study. Phys. Med. Biol. 2006, 51, 1779. [Google Scholar] [CrossRef] [PubMed]
- Pshenichnov, I.; Mishustin, I.; Greiner, W. Distributions of positron-emitting nuclei in proton and carbon-ion therapy studied with GEANT4. Phys. Med. Biol. 2006, 51, 6099. [Google Scholar] [CrossRef]
- Moadel, R.M.; Weldon, R.H.; Katz, E.B.; Lu, P.; Mani, J.; Stahl, M.; Blaufox, M.D.; Pestell, R.G.; Charron, M.J.; Dadachova, E. Positherapy: Targeted Nuclear Therapy of Breast Cancer with 18F-2-Deoxy-2-Fluoro-D-Glucose. Can. Res. 2005, 65, 698–702. [Google Scholar] [CrossRef]
- Dijkers, E.C.; Oude Munnink, T.H.; Kosterink, J.G.; Brouwers, A.H.; Jager, P.L.; de Jong, J.R.; van Dongen, G.A.; Schröder, C.P.; Lub-de Hooge, M.N.; de Vries, E.G. Biodistribution of 89Zr-trastuzumab and PET Imaging of HER2-Positive Lesions in Patients with Metastatic Breast Cancer. Clin. Pharmacol. Ther. 2010, 87, 586–592. [Google Scholar] [CrossRef]
- Barbosa, S.A.; Pastega, D.F.; Bettegaa, H.F.M. Low-energy positron scattering by pyrimidine. J. Chem. Phys. 2015, 143, 244316. [Google Scholar] [CrossRef]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant Formation of DNA Strand Breaks by Low-Energy (3 to 20 eV) Electrons. Science 2000, 287, 1658–1660. [Google Scholar] [CrossRef]
- Sanche, L. Nanoscopic aspects of radiobiological damage: Fragmentation induced by secondary low-energy electrons, Mass Spectrom. Mass Spectr. Rev. 2002, 21, 349–369. [Google Scholar] [CrossRef]
- Turi, L.; Rossly, P.J. Theoretical studies of spectroscopy and dynamics of hydrated electrons. Chem. Rev. 2012, 112, 5641–5674. [Google Scholar] [CrossRef] [Green Version]
- von Sonntag, C. Free-Radical-Induced DNA Damage and Its Repair; Springer: New York, NY, USA, 2005; pp. 357–482. [Google Scholar]
- Sanche, L. Beyond radical thinking. Nature 2009, 461, 358–359. [Google Scholar] [CrossRef] [PubMed]
- De Sarkar, A.; Biswas, S.; Gupta, N. Positron excess from cosmic ray interactions in galactic molecular clouds. J. High Energy Astrophys. 2021, 29, 1–18. [Google Scholar] [CrossRef]
- Guessoum, N. Positron astrophysics and areas of relation to low-energy positron physics. Euro. Phys. J. D 2014, 68, 137. [Google Scholar] [CrossRef]
- Hulett, L.D., Jr.; Donohue, D.L.; Xu, J.; Lewis, T.A.; McLuckey, S.A.; Glish, G.L. Mass spectrometry studies of the ionization of organic molecules by low-energy positrons. Chem. Phys. Lett. 1993, 216, 236–240. [Google Scholar] [CrossRef]
- Schultz, P.J.; Lynn, K.G. Interaction of positron beams with surfaces, thin films, and interfaces. Rev. Mod. Phys. 1988, 60, 701. [Google Scholar] [CrossRef]
- Sarri, G.; Poder, K.; Cole, J.M.; Schumaker, W.; Di Piazza, A.; Reville, B.; Zepf, M.; Mangles, S.P.D.; Najmudin, Z.; Shukla, N.; et al. Generation of neutral and high-density electron–positron pair plasmas in the laboratory. Nat. Commun. 2015, 6, 6747. [Google Scholar] [CrossRef] [Green Version]
- Sanz, A.G.; Fuss, M.C.; Muñoz, A.; Blanco, F.; Limão-Vieira, P.; Brunger, M.J.; Buckman, S.J.; García, G. Modelling low energy electron and positron tracks for biomedical applications. Int. J. Radiat. Biol. 2012, 88, 71. [Google Scholar] [CrossRef] [Green Version]
- Blanco, F.; Roldán, A.M.; Krupa, K.; McEachran, R.P.; White, R.D.; Marjanović, S.; García, G. Scattering data for modelling positron tracks in gaseous and liquid water. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 145001. [Google Scholar] [CrossRef]
- Blanco, F.; Muñoz, A.; Almeida, D.; Silva, F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron–and positron–molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Tennyson, J. Electron–molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Stryer, L. Biochemistry; W. H. Freeman: New York, NY, USA, 1995. [Google Scholar]
- Sanz, A.G.; Fuss, M.C.; Blanco, F.; Mašin, Z.; Gorfinkiel, J.D.; McEachran, R.P.; Brunger, M.J.; García, G. Cross-section calculations for positron scattering from pyrimidine over an energy range from 0.1 to 10000 eV. Phys. Rev. A 2013, 88, 062704. [Google Scholar] [CrossRef] [Green Version]
- Sinha, N.; Sahoo, A.K.; Antony, B. Positron scattering from pyridine and pyrimidine. J. Phys. Chem. A 2020, 124, 5147–5156. [Google Scholar] [CrossRef] [PubMed]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. Interference effects in the electron and positron scattering from molecules at intermediate and high energies. Chem. Phys. Lett. 2015, 635, 321–327. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Blanco, F.; García, G. Screening corrections for calculation of electron scattering from polyatomic molecules. Phys. Lett. A 2003, 317, 458–462. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. Screening corrections for calculation of electron scattering differential cross sections from polyatomic molecules. Phys. Lett. A 2004, 330, 230–237. [Google Scholar] [CrossRef]
- Franz, J.; Gianturco, F.A. Low-energy positron scattering from gas-phase pyrimidine: A quantum treatment of the dynamics and a comparison with experiments. Phys. Rev. A 2013, 88, 042711. [Google Scholar] [CrossRef] [Green Version]
- Fabrikant, I.I. Long-range effects in electron scattering by polar molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222005. [Google Scholar] [CrossRef]
- Itikawa, Y. The Born closure approximation for the scattering amplitude of an electron-molecule collision. Theor. Chem. Acc. 2000, 105, 123. [Google Scholar] [CrossRef]
- Bederson, B.; Kieffer, L.J. Total Electron—Atom Collision Cross Sections at Low Energies—A Critical Review. Rev. Mod. Phys. 1971, 43, 601. [Google Scholar] [CrossRef]
- Gilbert, S.J.; Kurz, C.; Greaves, R.G.; Surko, C.M. Creation of a monoenergetic pulsed positron beam. Appl. Phys. Lett. 1997, 70, 1944. [Google Scholar] [CrossRef]
- Sullivan, J.P.; Jones, A.; Caradonna, P.; Makochekanwa, C.; Buckman, S.J. A positron trap and beam apparatus for atomic and molecular scattering experiments. Rev. Sci. Instrum. 2008, 79, 113105. [Google Scholar] [CrossRef]
- Sullivan, J.P.; Makochekanwa, C.; Jones, A.; Caradonna, P.; Slaughter, D.S.; Machacek, J.; McEachran, R.P.; Mueller, D.W.; Buckman, S.J. Forward angle scattering effects in the measurement of total cross sections for positron scattering. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 035201. [Google Scholar] [CrossRef]
- Zecca, A.; Chiari, L.; García, G.; Blanco, F.; Trainotti, E.; Brunger, M.J. Total cross sections for positron and electron scattering from pyrimidine. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 215204. [Google Scholar] [CrossRef]
- Palihawadana, P.; Boadle, R.; Chiari, L.; Anderson, E.K.; Machacek, J.R.; Brunger, M.J.; Buckman, S.J.; Sullivan, J.P. Positron scattering from pyrimidine. Phys. Rev. A 2013, 88, 01271. [Google Scholar] [CrossRef] [Green Version]
- Brunger, M.J.; Buckman, S.J.; Ratnavelu, K. Positron scattering from molecules: An experimental cross section compilation for positron transport studies and benchmarking theory. J. Phys. Chem. Ref. Data 2017, 46, 023102. [Google Scholar] [CrossRef]
- Sahgal, V.; Bharadvaja, A.; Baluja, K.L. Positron-induced scattering of acetone from 0.1 eV to 5 keV. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 075202. [Google Scholar] [CrossRef]
- Sahgal, V.; Bharadvaja, A.; Baluja, K.L.; Arora, A.K.; Gupta, K.K. Positron-induced scattering from pentane isomers beyond ionization threshold. Eur. Phys. J. D 2021, 75, 259. [Google Scholar]
- Arora, A.K.; Sahgal, V.; Bharadvaja, A.; Baluja, K.L. Positron-impact scattering off 1-1 C2H2F2 from 0.1 eV to 4 keV. Phys. Rev. A 2021, 104, 022816. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G.P. Binary-encounter dipole Model for positron-impact direct ionization. Phys. Rev. A 2019, 100, 062702. [Google Scholar] [CrossRef]
- Kim, Y.-K. Scaled Born cross sections for excitations of H2 by electron impact. J. Chem. Phys. 2007, 126, 064305. [Google Scholar] [CrossRef] [PubMed]
- Gianturco, F.A.; Lucchese, R.R.; Sanna, N.; Talamo, A. A generalized single centre approach for treating electron scattering from polyatomic molecules. In Electron Collisions with Molecules, Clusters, and Surfaces; Springer: Boston, MA, USA, 1994; pp. 71–86. [Google Scholar]
- Gianturco, F.A.; Sanna, N. SCELIB: A parallel computational library of molecular properties in the single-center expansion approach. Comput. Phys. Commun. 2000, 128, 139. [Google Scholar]
- Zhang, R.; Faure, A.; Tennyson, J. Electron and positron collisions with polar molecules: Studies with the benchmark water molecule. Phys. Scr. 2009, 80, 015301. [Google Scholar] [CrossRef] [Green Version]
- Faisal, F.H.M. Electron-molecule interactions. I. Single-centre wave functions and potentials. J. Phys. B At. Mol. Opt. Phys. 1970, 3, 636. [Google Scholar] [CrossRef]
- Burke, P.G.; Sinfailam, A.L. Electron-molecule interactions. II. Scattering by closed-shell diatomic molecules. J. Phys. B At. Mol. Opt. Phys. 1970, 3, 641. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef] [Green Version]
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347–425. [Google Scholar] [CrossRef]
- Chang, E.S.; Fano, U. Theory of Electron-Molecule Collisions by Frame Transformations. Phys. Rev. A 1972, 6, 173. [Google Scholar] [CrossRef]
- Bray, I.; Abdurakhmanov, I.B.; Bailey, J.J.; Bray, A.W.; Fursa, D.V.; Kadyrov, A.S.; Rawlins, C.M.; Savage, J.S.; Stelbovics, A.T.; Zammit, M.C. Convergent close-coupling approach to light and heavy projectile scattering on atomic and molecular hydrogen. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 202001. [Google Scholar] [CrossRef]
- Kadyrov, A.S.; Bray, I. Recent progress in the description of positron scattering from atoms using the convergent close-coupling theory. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222002. [Google Scholar] [CrossRef] [Green Version]
- Utamuratov, R.; Kadyrov, A.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Two-center close-coupling calculations of positron–molecular-hydrogen scattering. Phys. Rev. A 2015, 92, 032707. [Google Scholar] [CrossRef] [Green Version]
- Klar, H. Threshold ionisation of atoms by positrons. J. Phys. B At. Mol. Opt. Phys. 1981, 14, 4165–4170. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.D., III (Ed.) Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 21, August 2020. Available online: http://cccbdb.nist.gov/ (accessed on 20 December 2022).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. GAUSSIAN 03; Gaussian, Inc.: Wallingford, UK, 2003. [Google Scholar]
- Sanna, N.; Baccarelli, I.; Morelli, G. SCELib3.0: The new revision of SCELib, the parallel computational library of molecular properties in the Single Center Approach. Comput. Phys. Commun. 2009, 180, 2544–2549. [Google Scholar] [CrossRef]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Jones, D.B.; Bellm, S.M.; Blanco, F.; Fuss, M.; García, G.; Limão-Vieira, P.; Brunger, M.J. Differential cross sections for the electron impact excitation of pyrimidine. J. Chem. Phys. 2012, 137, 074304. [Google Scholar] [CrossRef] [Green Version]
- Fischer, G.; Cai, Z.-L.; Reimers, J.R.; Wormell, P. Singlet and Triplet Valence Excited States of Pyrimidine. Phys. Chem. A 2003, 107. [Google Scholar] [CrossRef]
- Bassi, M.; Bharadvaja, A.; Baluja, K.L. A study of electron scattering from 1-1 C2H2F2 from 0.1 eV to 5 keV. Eur. Phys. D. 2019, 74, 232. [Google Scholar] [CrossRef]
- Luthra, M.; Garkoti, P.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. Electron impact cross-sections of tetraethyl silicate. Plasma Sources Sci. Technol. 2022, 31, 095013. [Google Scholar] [CrossRef]
- Kaur, S.; Bharadvaja, A.; Baluja, K.L. Electron interactions with AlF. Eur. Phys. J. D 2022, 76, 176. [Google Scholar] [CrossRef]
- Meltzer, T.; Tennyson, J.; Mašin, Z.; Zammit, M.C.; Scarlett, L.H.; Fursa, D.V.; Bray, I. Benchmark calculations of electron impact electronic excitation of the hydrogen molecule. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 145204. [Google Scholar] [CrossRef] [Green Version]
- Machacek, J.R.; McEachran, R.P. Partial wave analysis for folded differential cross sections. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 065007. [Google Scholar] [CrossRef]
- Dickinson, A.J. Differential cross sections for electron scattering by strongly polar molecules. J. Phys. B 1977, 10, 967. [Google Scholar] [CrossRef]
- Bug, M.U.; Woon, Y.B.; Rabus, H.; Villagrasa, C.; Meylan, S.; Rosenfeld, A.B. An electron-impact cross section data set (10 eV–1 keV) of DNA constituents based on consistent experimental data: A requisite for Monte Carlo simulations. Radiat. Phys. Chem. 2017, 130, 459–479. [Google Scholar] [CrossRef]
- Linert, I.; Dampc, M.; Mielewska, B.; Zubek, M. Cross sections for ionization and ionic fragmentation of pyrimidine molecules by electron collisions. Eur. Phys. J. D 2012, 66, 20. [Google Scholar] [CrossRef]
- Champion, C.; Quinto, M.A.; Weck, P.F. Electron- and proton-induced ionization of pyrimidine. Eur. Phys. J. D 2015, 69, 127. [Google Scholar] [CrossRef]
- Garkoti, P.; Luthra, M.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization. Atoms 2022, 10, 60. [Google Scholar] [CrossRef]
- Charlton, M.; Humberston, J.W. Positron Physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Chiari, L.; Zecca, A.; Girardi, S.; Trainotti, E.; García, G.; Blanco, F.; McEachran, R.P.; Brunger, M.J. Positron scattering from O2. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215206. [Google Scholar] [CrossRef]
- Luthra, M.; Goswami, K.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV. Atoms 2022, 10, 74. [Google Scholar] [CrossRef]
- Goswami, K.; Luthra, M.; Bharadvaja, A.; Baluja, K.L. Partial Ionization Cross Sections of Tungsten Hexafluoride Due to Electron Impact. Atoms 2022, 10, 101. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prashant, A.; Luthra, M.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. Positron Scattering from Pyrimidine. Atoms 2023, 11, 55. https://doi.org/10.3390/atoms11030055
Prashant A, Luthra M, Goswami K, Bharadvaja A, Baluja KL. Positron Scattering from Pyrimidine. Atoms. 2023; 11(3):55. https://doi.org/10.3390/atoms11030055
Chicago/Turabian StylePrashant, Abhishek, Meetu Luthra, Kanupriya Goswami, Anand Bharadvaja, and Kasturi Lal Baluja. 2023. "Positron Scattering from Pyrimidine" Atoms 11, no. 3: 55. https://doi.org/10.3390/atoms11030055







