Attosecond Time Delay Trends across the Isoelectronic Noble Gas Sequence
Abstract
:1. Introduction
2. Theoretical Overview of the Relativistic Random-Phase Approximation (RRPA)
3. Results and Discussion
3.1. Dirac–Hartree–Fock (DHF) Orbital Subshell Ionization Calculations
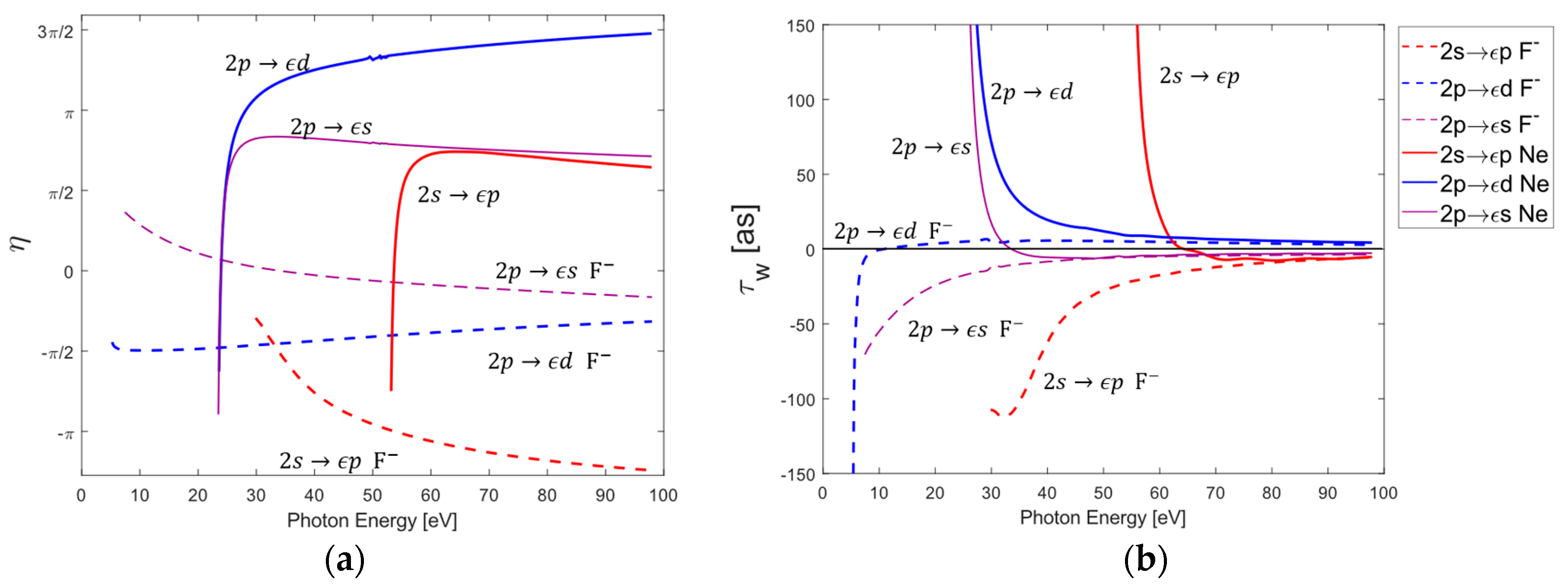
3.2. Individual Photoionization Channel Phases and Wigner Time Delays of Neon and
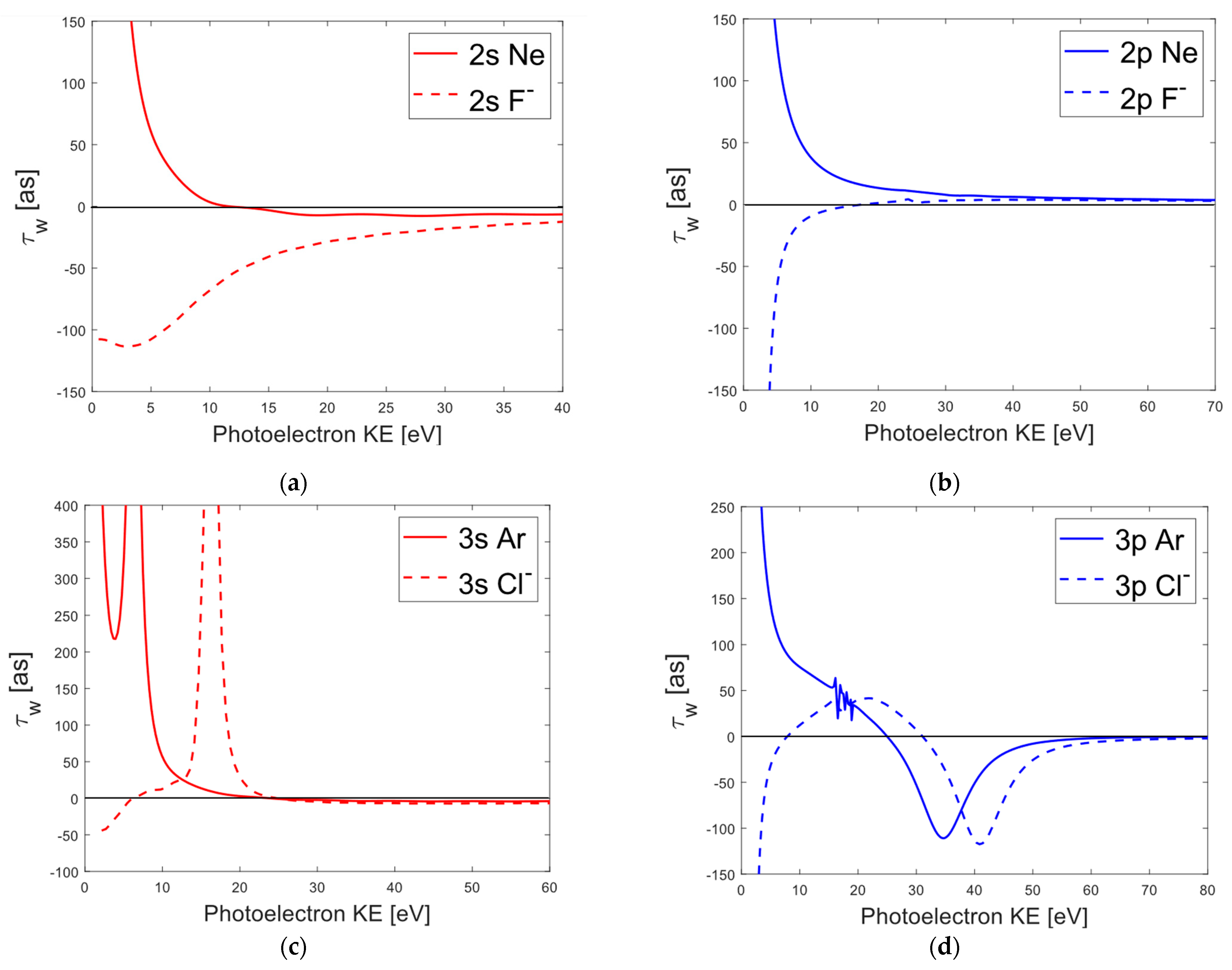
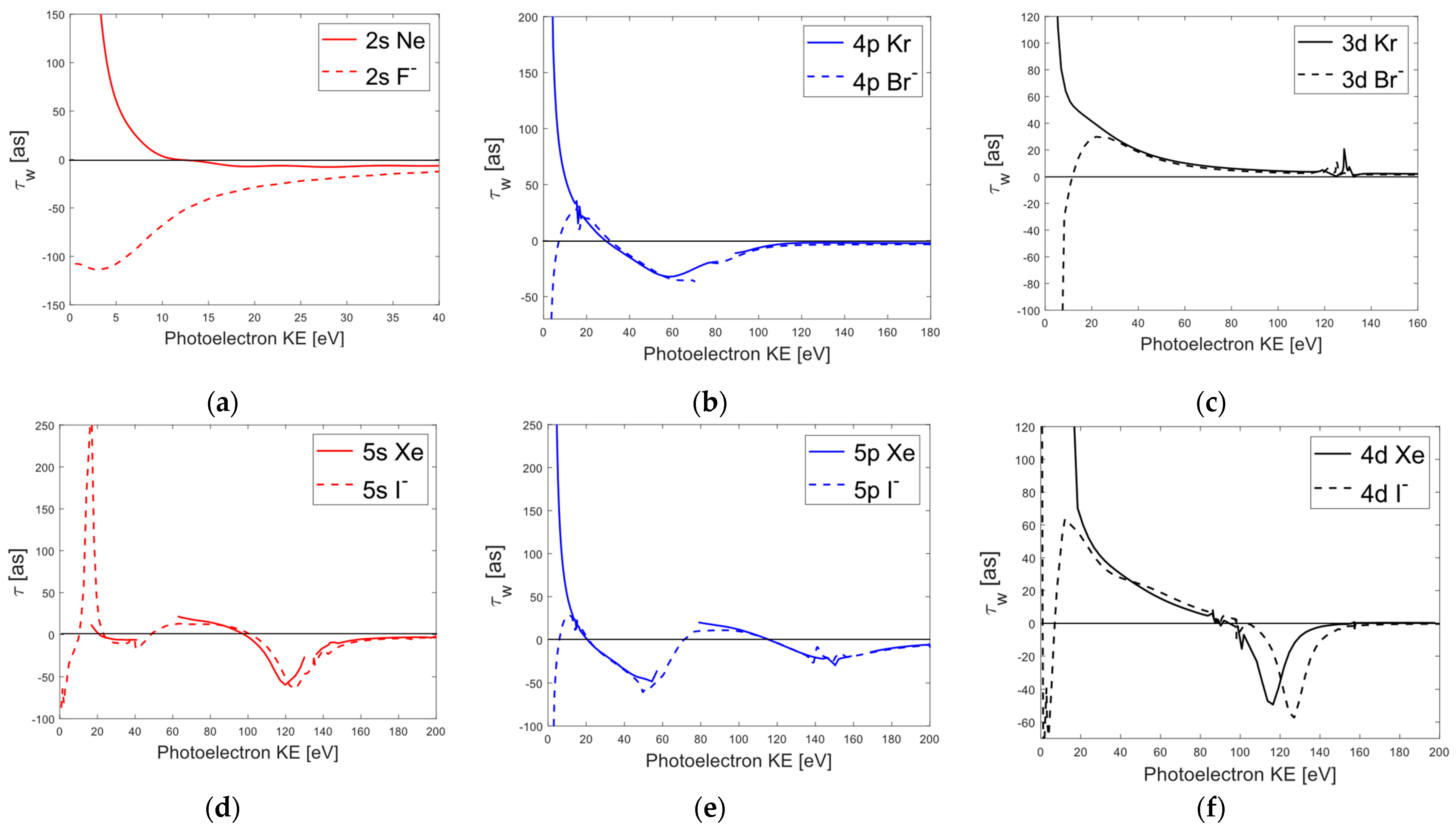
3.3. Comparison of Average Wigner Delays for Halogen Ions and Noble Gases
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determining
References
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond Metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Krausz, F. From Femtochemistry to Attophysics. Phys. World 2001, 14, 41. [Google Scholar] [CrossRef]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-Ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923–1927. [Google Scholar] [CrossRef] [PubMed]
- Varjú, K.; Johnsson, P.; Mauritsson, J.; L’Huillier, A.; López-Martens, R. Physics of Attosecond Pulses Produced via High Harmonic Generation. Am. J. Phys. 2009, 77, 389–395. [Google Scholar] [CrossRef]
- Orfanos, I.; Makos, I.; Liontos, I.; Skantzakis, E.; Förg, B.; Charalambidis, D.; Tzallas, P. Attosecond Pulse Metrology. APL Photonics 2019, 4, 080901. [Google Scholar] [CrossRef]
- Frank, F.; Arrell, C.; Witting, T.; Okell, W.A.; McKenna, J.; Robinson, J.S.; Haworth, C.A.; Austin, D.; Teng, H.; Walmsley, I.A.; et al. Invited Review Article: Technology for Attosecond Science. Rev. Sci. Instrum. 2012, 83, 071101. [Google Scholar] [CrossRef]
- Itatani, J.; Quéré, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond Streak Camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef]
- Zaïr, A.; Mével, E.; Cormier, E.; Constant, E. Ultrastable Collinear Delay Control Setup for Attosecond IR-XUV Pump–Probe Experiment. J. Opt. Soc. Am. B JOSAB 2018, 35, A110–A115. [Google Scholar] [CrossRef]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing Single-Photon Ionization on the Attosecond Time Scale. Phys. Rev. Lett. 2011, 106, 143002. [Google Scholar] [CrossRef]
- Vos, J.; Cattaneo, L.; Patchkovskii, S.; Zimmermann, T.; Cirelli, C.; Lucchini, M.; Kheifets, A.; Landsman, A.S.; Keller, U. Orientation-Dependent Stereo Wigner Time Delay and Electron Localization in a Small Molecule. Science 2018, 360, 1326–1330. [Google Scholar] [CrossRef]
- Kheifets, A.S. Wigner Time Delay in Atomic Photoionization. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 022001. [Google Scholar] [CrossRef]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in Photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Palatchi, C.; Dahlström, J.M.; Kheifets, A.S.; Ivanov, I.A.; Canaday, D.M.; Agostini, P.; DiMauro, L.F. Atomic Delay in Helium, Neon, Argon and Krypton*. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 245003. [Google Scholar] [CrossRef]
- Guénot, D.; Klünder, K.; Arnold, C.L.; Kroon, D.; Dahlström, J.M.; Miranda, M.; Fordell, T.; Gisselbrecht, M.; Johnsson, P.; Mauritsson, J.; et al. Photoemission-Time-Delay Measurements and Calculations Close to the 3s-Ionization-Cross-Section Minimum in Ar. Phys. Rev. A 2012, 85, 053424. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Ivanov, I.A. Delay in Atomic Photoionization. Phys. Rev. Lett. 2010, 105, 233002. [Google Scholar] [CrossRef]
- Huppert, M.; Jordan, I.; Baykusheva, D.; von Conta, A.; Wörner, H.J. Attosecond Delays in Molecular Photoionization. Phys. Rev. Lett. 2016, 117, 093001. [Google Scholar] [CrossRef]
- Caillat, J.; Maquet, A.; Haessler, S.; Fabre, B.; Ruchon, T.; Salières, P.; Mairesse, Y.; Taïeb, R. Attosecond Resolved Electron Release in Two-Color Near-Threshold Photoionization of N2. Phys. Rev. Lett. 2011, 106, 093002. [Google Scholar] [CrossRef]
- Serov, V.V.; Kheifets, A.S. Time Delay in XUV/IR Photoionization of H2O. J. Chem. Phys. 2017, 147, 204303. [Google Scholar] [CrossRef]
- Baykusheva, D.; Wörner, H.J. Theory of Attosecond Delays in Molecular Photoionization. J. Chem. Phys. 2017, 146, 124306. [Google Scholar] [CrossRef]
- Haessler, S.; Fabre, B.; Higuet, J.; Caillat, J.; Ruchon, T.; Breger, P.; Carré, B.; Constant, E.; Maquet, A.; Mével, E.; et al. Phase-Resolved Attosecond near-Threshold Photoionization of Molecular Nitrogen. Phys. Rev. A 2009, 80, 011404. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Thumm, U. Streaking and Wigner Time Delays in Photoemission from Atoms and Surfaces. Phys. Rev. A 2011, 84, 033401. [Google Scholar] [CrossRef]
- Borrego-Varillas, R.; Lucchini, M.; Nisoli, M. Attosecond Spectroscopy for the Investigation of Ultrafast Dynamics in Atomic, Molecular and Solid-State Physics. Rep. Prog. Phys. 2022, 85, 066401. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.; Chen, C.; Szilvási, T.; Keller, M.; Mavrikakis, M.; Kapteyn, H.; Murnane, M. Direct Time-Domain Observation of Attosecond Final-State Lifetimes in Photoemission from Solids. Science 2016, 353, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E.P. Lower Limit for the Energy Derivative of the Scattering Phase Shift. Phys. Rev. 1955, 98, 145–147. [Google Scholar] [CrossRef]
- Smith, F.T. Lifetime Matrix in Collision Theory. Phys. Rev. 1960, 118, 349–356. [Google Scholar] [CrossRef]
- Dahlström, J.M.; Guénot, D.; Klünder, K.; Gisselbrecht, M.; Mauritsson, J.; L’Huillier, A.; Maquet, A.; Taïeb, R. Theory of Attosecond Delays in Laser-Assisted Photoionization. Chem. Phys. 2013, 414, 53–64. [Google Scholar] [CrossRef]
- Dahlström, J.M.; Carette, T.; Lindroth, E. Diagrammatic Approach to Attosecond Delays in Photoionization. Phys. Rev. A 2012, 86, 061402. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Time-Resolved Photoemission on the Attosecond Scale: Opportunities and Challenges. Faraday Discuss. 2013, 163, 353–376. [Google Scholar] [CrossRef]
- Wätzel, J.; Moskalenko, A.S.; Pavlyukh, Y.; Berakdar, J. Angular Resolved Time Delay in Photoemission. J. Phys. B At. Mol. Opt. Phys. 2014, 48, 025602. [Google Scholar] [CrossRef]
- Heuser, S.; Galán, Á.J.; Cirelli, C.; Marante, C.; Sabbar, M.; Boge, R.; Lucchini, M.; Gallmann, L.; Ivanov, I.; Kheifets, A.S.; et al. Angular Dependence of Photoemission Time Delay in Helium. Phys. Rev. A 2016, 94, 063409. [Google Scholar] [CrossRef]
- Cirelli, C.; Marante, C.; Heuser, S.; Petersson, C.L.M.; Galán, Á.J.; Argenti, L.; Zhong, S.; Busto, D.; Isinger, M.; Nandi, S.; et al. Anisotropic Photoemission Time Delays Close to a Fano Resonance. Nat. Commun. 2018, 9, 955. [Google Scholar] [CrossRef]
- Ivanov, I.A.; Kheifets, A.S. Angle-Dependent Time Delay in Two-Color XUV+IR Photoemission of He and Ne. Phys. Rev. A 2017, 96, 013408. [Google Scholar] [CrossRef]
- George, J.; Pradhan, G.B.; Rundhe, M.; Jose, J.; Aravind, G.; Deshmukh, P.C. Autoionization Resonances in the Argon Iso-Electronic Sequence. Can. J. Phys. 2012, 90, 547–555. [Google Scholar] [CrossRef]
- Magrakvelidze, M.; Madjet, M.E.-A.; Chakraborty, H.S. Attosecond Delay of Xenon 4d Photoionization at the Giant Resonance and Cooper Minimum. Phys. Rev. A 2016, 94, 013429. [Google Scholar] [CrossRef]
- Magrakvelidze, M.; Madjet, M.E.-A.; Dixit, G.; Ivanov, M.; Chakraborty, H.S. Attosecond Time Delay in Valence Photoionization and Photorecombination of Argon: A Time-Dependent Local-Density-Approximation Study. Phys. Rev. A 2015, 91, 063415. [Google Scholar] [CrossRef]
- Jordan, I.; Huppert, M.; Pabst, S.; Kheifets, A.S.; Baykusheva, D.; Wörner, H.J. Spin-Orbit Delays in Photoemission. Phys. Rev. A 2017, 95, 013404. [Google Scholar] [CrossRef]
- Keating, D.A.; Manson, S.T.; Dolmatov, V.K.; Mandal, A.; Deshmukh, P.C.; Naseem, F.; Kheifets, A.S. Intershell-Correlation-Induced Time Delay in Atomic Photoionization. Phys. Rev. A 2018, 98, 013420. [Google Scholar] [CrossRef]
- Saha, S.; Mandal, A.; Jose, J.; Varma, H.R.; Deshmukh, P.C.; Kheifets, A.S.; Dolmatov, V.K.; Manson, S.T. Relativistic Effects in Photoionization Time Delay near the Cooper Minimum of Noble-Gas Atoms. Phys. Rev. A 2014, 90, 053406. [Google Scholar] [CrossRef]
- Lindroth, E.; Dahlström, J.M. Attosecond Delays in Laser-Assisted Photodetachment from Closed-Shell Negative Ions. Phys. Rev. A 2017, 96, 013420. [Google Scholar] [CrossRef]
- Pi, L.-W.; Landsman, A.S. Attosecond Time Delay in Photoionization of Noble-Gas and Halogen Atoms. Appl. Sci. 2018, 8, 322. [Google Scholar] [CrossRef]
- Saha, S.; Jose, J.; Deshmukh, P.C.; Aravind, G.; Dolmatov, V.K.; Kheifets, A.S.; Manson, S.T. Wigner Time Delay in Photodetachment. Phys. Rev. A 2019, 99, 043407. [Google Scholar] [CrossRef]
- Saha, S.; Deshmukh, P.C.; Kheifets, A.S.; Manson, S.T. Dominance of Correlation and Relativistic Effects on Photodetachment Time Delay Well above Threshold. Phys. Rev. A 2019, 99, 063413. [Google Scholar] [CrossRef]
- Banerjee, S.; Deshmukh, P.C.; Kheifets, A.S.; Manson, S.T. Effects of Spin-Orbit-Interaction-Activated Interchannel Coupling on Photoemission Time Delay. Phys. Rev. A 2020, 101, 043411. [Google Scholar] [CrossRef]
- Saha, S.; Jose, J.; Deshmukh, P.C.; Kheifets, A.S.; Dolmatov, V.K.; Manson, S.T. Effects of Relativistic Interactions in Photodetachment Time Delay of Br−. J. Phys. Conf. Ser. 2020, 1412, 092013. [Google Scholar] [CrossRef]
- Banerjee, S.; Aarthi, G.; Saha, S.; Aravind, G.; Deshmukh, P.C. Time Delay in Negative Ion Photodetachment. Phys. Scr. 2021, 96, 114005. [Google Scholar] [CrossRef]
- Lindle, D.W.; Kobrin, P.H.; Truesdale, C.M.; Ferrett, T.A.; Heimann, P.A.; Kerkhoff, H.G.; Becker, U.; Shirley, D.A. Inner-Shell Photoemission from the Iodine Atom in CH3I. Phys. Rev. A 1984, 30, 239–244. [Google Scholar] [CrossRef]
- Magrakvelidze, M.; Chakraborty, H. Attosecond Time Delays in the Valence Photoionization of Xenon and Iodine at Energies Degenerate with Core Emissions. J. Phys. Conf. Ser. 2017, 875, 022015. [Google Scholar] [CrossRef]
- Biswas, S.; Förg, B.; Ortmann, L.; Schötz, J.; Schweinberger, W.; Zimmermann, T.; Pi, L.; Baykusheva, D.; Masood, H.A.; Liontos, I.; et al. Probing Molecular Environment through Photoemission Delays. Nat. Phys. 2020, 16, 778–783. [Google Scholar] [CrossRef]
- Johnson, W.R.; Lin, C.D. Multichannel Relativistic Random-Phase Approximation for the Photoionization of Atoms. Phys. Rev. A 1979, 20, 964–977. [Google Scholar] [CrossRef]
- Kheifets, A.; Mandal, A.; Deshmukh, P.C.; Dolmatov, V.K.; Keating, D.A.; Manson, S.T. Relativistic Calculations of Angle-Dependent Photoemission Time Delay. Phys. Rev. A 2016, 94, 013423. [Google Scholar] [CrossRef]
- Mandal, A.; Deshmukh, P.C.; Kheifets, A.S.; Dolmatov, V.K.; Manson, S.T. Angle-Resolved Wigner Time Delay in Atomic Photoionization: The 4d Subshell of Free and Confined Xe. Phys. Rev. A 2017, 96, 053407. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.10), National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: https://physics.nist.gov/asd(accessed on 22 February 2023).
- NIST: Atomic Spectra Database—Energy Levels Form. Available online: https://physics.nist.gov/PhysRefData/ASD/levels_form.html (accessed on 22 February 2023).
- CCCBDB Electron Affinities. Available online: https://cccbdb.nist.gov/elecaff1x.asp (accessed on 22 February 2023).
- King, G.C.; Tronc, M.; Read, F.H.; Bradford, R.C. An Investigation of the Structure near the L2,3 Edges of Argon, the M4,5 Edges of Krypton and the N4,5 Edges of Xenon, Using Electron Impact with High Resolution. J. Phys. B At. Mol. Phys. 1977, 10, 2479. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Ivanov, V.K.; Cherepkov, N.A.; Chernysheva, L.V. Interference Effects in Photoionization of Noble Gas Atoms Outer S-Subshells. Phys. Lett. A 1972, 40, 361–362. [Google Scholar] [CrossRef]
- Hammerland, D.; Zhang, P.; Bray, A.; Perry, C.F.; Kuehn, S.; Jojart, P.; Seres, I.; Zuba, V.; Varallyay, Z.; Osvay, K.; et al. Effect of Electron Correlations on Attosecond Photoionization Delays in the Vicinity of the Cooper Minima of Argon. arXiv 2019. Available online: https://arxiv.org/pdf/1907.01219 (accessed on 27 February 2023).
- Fano, U.; Cooper, J.W. Spectral Distribution of Atomic Oscillator Strengths. Rev. Mod. Phys. 1968, 40, 441–507. [Google Scholar] [CrossRef]
- Ganesan, A.; Banerjee, S.; Deshmukh, P.C.; Manson, S.T. Photoionization of Xe 5s: Angular Distribution and Wigner Time Delay in the Vicinity of the Second Cooper Minimum. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 225206. [Google Scholar] [CrossRef]
- Aarthi, G.; Jose, J.; Deshmukh, S.; Radojevic, V.; Deshmukh, P.C.; Manson, S.T. Photoionization Study of Xe 5s: Ionization Cross Sections and Photoelectron Angular Distributions. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 025004. [Google Scholar] [CrossRef]
- Berzinsh, U.; Gustafsson, M.; Hanstorp, D.; Klinkmüller, A.; Ljungblad, U.; Mårtensson-Pendrill, A.-M. Isotope Shift in the Electron Affinity of Chlorine. Phys. Rev. A 1995, 51, 231–238. [Google Scholar] [CrossRef]
- Jose, J.; Pradhan, G.B.; Radojević, V.; Manson, S.T.; Deshmukh, P.C. Electron Correlation Effects near the Photoionization Threshold: The Ar Isoelectronic Sequence. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 195008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grafstrom, B.; Landsman, A.S. Attosecond Time Delay Trends across the Isoelectronic Noble Gas Sequence. Atoms 2023, 11, 84. https://doi.org/10.3390/atoms11050084
Grafstrom B, Landsman AS. Attosecond Time Delay Trends across the Isoelectronic Noble Gas Sequence. Atoms. 2023; 11(5):84. https://doi.org/10.3390/atoms11050084
Chicago/Turabian StyleGrafstrom, Brock, and Alexandra S. Landsman. 2023. "Attosecond Time Delay Trends across the Isoelectronic Noble Gas Sequence" Atoms 11, no. 5: 84. https://doi.org/10.3390/atoms11050084
APA StyleGrafstrom, B., & Landsman, A. S. (2023). Attosecond Time Delay Trends across the Isoelectronic Noble Gas Sequence. Atoms, 11(5), 84. https://doi.org/10.3390/atoms11050084







