Atomic Lifetimes of Astrophysical Interest in Ions of Fe

Träbert, Elmar

doi:10.3390/atoms11050085

Open AccessReview

Atomic Lifetimes of Astrophysical Interest in Ions of Fe

by

Elmar Träbert

AIRUB, Faculty of Physics and Astronomy, Ruhr-University Bochum, 44780 Bochum, Germany

Atoms 2023, 11(5), 85; https://doi.org/10.3390/atoms11050085

Submission received: 31 March 2023 / Revised: 8 May 2023 / Accepted: 15 May 2023 / Published: 22 May 2023

(This article belongs to the Special Issue Atomic and Molecular Data in Astronomy and Astrophysics)

Download

Browse Figure

Versions Notes

Abstract

:

Multiply charged ions of iron dominate the EUV spectrum of the solar corona. For the interpretation of such spectra, data on both the atomic structure and the transition rate are essential, most of which are provided by theory and computation. The wavelengths of observed spectra are used to test the predicted energy level structure, while the line intensities depend on level lifetimes and branch fractions. A number of electric dipole and higher-order transition rates have been measured over the years in the laboratory, mostly by beam-foil spectroscopy, at heavy-ion storage rings, and at various ion traps. In this paper, the state of the knowledge base on level lifetimes in all ions of Fe is assessed, and the problems of further progress are outlined.

Keywords:

atomic physics; atomic level lifetimes; transition rates

1. Introduction

Iron (

Z = 26

) is near the peak of the curve that describes the binding energy per nucleon of the elements. Thus, it marks the end of stellar processes that form heavier elements by nuclear fusion. Consequently, Fe is rather abundant in stars that have evolved or been formed from material that has previously been processed by other stars. What we can see of elements depends on their electron shells and the environmental conditions. In our immediate environment, Fe appears gray to black when reflecting ambient light or orange to red in the form of rust (Fe

_{2}

O

_{3}

). When heated (as a typical material used for stoves), Fe emits a glow that is typical of any blackbody radiator, not of the element. The Sun has a surface temperature of about 5600 K which at face value does not suffice to excite Fe atoms. However, the solar spectrum shows absorption lines of Fe.

In the middle of the 19th century, a solar corona far above the solar “surface” was detected during solar eclipses, that is, visible light emission of a kind that for more than a century could not be reproduced on Earth. The emitter, a hypothetical element “coronium”, was retired in the early 1940s after Grotrian [1] noted that Edlén’s X-ray spectra of highly ionized Ca and Fe showed energy differences between certain lines that came close to the energies of the visible light seen in the corona, and after Edlén in response had refined his X-ray and extreme ultraviolet (EUV) measurements to reduce the uncertainties even further until the energy coincidences left the range of mere chance [2]. This success indirectly proved the presence of highly charged ions above the solar surface and issued a long-lasting challenge to astrophysics, having to explain the production of such ions, which require much higher temperatures (MK) above a much less hot (kK) photosphere.

Direct observations had to wait for another two decades, until the late 1960s, when rocket-borne X-ray and EUV spectrographs were carried above Earth’s atmosphere and recorded spectra of the Sun. These contained line emissions from all abundant elements and of ions in all charge states. These findings coincided with a new era in fusion plasma research [3,4,5,6], whose protagonists recognised the similarities of their terrestrial spectra with the new solar EUV spectra. Doschek provided an early overview of the solar X-ray spectrum [7] based largely on Western satellite data; soon, additional X-ray spectra were provided by Soviet spacecraft that included lines of the Fe XXV spectrum and its satellites (here, using the other indication of the word satellite, i.e., “companion”) [8]). These latter satellite lines provided a useful tool for plasma diagnostics (density and temperature) both on Earth and in space. Such high charge states of Fe require multi-keV collisions beyond the energies available in the quiet corona, which limits these observations to solar flares.

Many journal volumes have been dedicated to describing and investigating phenomena in the solar corona; however, this is not the place to provide yet another digest of that complex endeavour. In addition, there have been many reports on computing the energy levels, transition energies, oscillator strengths, and/or transition rates of various single spectra or of several ions in sections of isoelectronic sequences. There are many more such works than a single review could do justice to. Moreover, the results of such theoretical efforts scatter, in cases quite badly, which would merit yet another discussion (or several). The present text merely discusses one detail in atomic physics, namely, the lifetime (inverse of the sum of all decay rates of a given level) of sample levels of the ions of Fe, all of which play a (significant or minor) role in astrophysics. The discussion considers the context, data range, typical measurements, and evaluation techniques, and asks whether experiment or theory has yielded more reliable atomic lifetime results to date. In certain cases only theoretical results are provided, allowing the reader to easily recognise why there has been no measurement. The material is grouped by increasing number of electrons, from the spectrum of Fe XXVI (ion Fe

^{25 +}

) to Fe II (Fe

^{+}

).

2. Lifetime Data and Results

The simplest atom is the hydrogen atom, and its ground state is 1s

^{2}

S

_{1 / 2}

. However, the proton makes for an odd nucleus, with a nuclear spin different from zero, and as such there is a hyperfine splitting of the ground level. In our environment, the particle density is so high that free hydrogen atoms easily find another atom to form a molecule. In outer space, the density is so low that neutral hydrogen atoms survive for extended periods, and occasionally an atom in the upper hyperfine level of the ground state (nuclear and electron spin aligned) may flip to the lower one (spins antiparallel) while emitting a 21-cm wavelength photon. The rate of this electric-dipole (

E 1

-) forbidden transition is low; it has been calculated to correspond to a lifetime on the order of 10 million years. However, there is so much hydrogen in outer space that a viable signal nevertheless emerges that permits the study of the structure of our galaxy (and of many others). The astrophysically important 21-cm line is emitted only if the atom remains unperturbed until such times, which translates to environmental densities on the order of single atoms per cm

^{3}

. If we replace the proton with an iron nucleus of charge

Z = 26

, the hyperfine splitting is larger by a factor

Z^{3}

, and the corresponding wavelength shrinks to about 11.9

μ

m in the infrared (IR). However, no such radiation from highly charged Fe ions has been detected from the cool realms of outer space. The dominant isotopes of Fe have even-even nuclei, and consequently they carry no nuclear spin and do not suffer hyperfine splitting. Odd isotopes of Fe exist (for example, in natural iron there is

^{57}

Fe at about 2.2% relative abundance). The (unstable) isotope

^{55}

Fe can be produced technically, though not in quantities that matter in the universe. First, highly charged Fe ions would capture electrons and recombine; thus, any highly charged Fe observed in quantity must be freshly produced, and likely at a relatively high density and temperature. This speaks against any astrophysical relevance of Fe

^{25 +}

ions. However, whatever an astrophysicist can think of may well exist somewhere in the universe. For example, among the very highest-energy cosmic rays reaching Earth, it is assumed that there are a few bare Fe nuclei at relativistic velocities (which are hardly distinguishable from protons at such extreme energies). The rate of detection when combining all detectors on Earth is on the order of (possibly) one or a few particles per year. In summarising this paragraph, it is apparent that almost everything about Fe ions may be of interest to astrophysicists (and neutral Fe to astro-seismologists, etc.); out of this vast field, I pick only a few items that are compatible with laboratory astrophysics and down-to-earth atomic physics. Among these, my interest in the present review is on atomic lifetimes (transition rates, branch fractions, and so on).

Before delving into details, I explain why certain well-established databases are not simply referred to in the text. The Astrophysical Plasma Emission Database (APED), which is based on the Astrophysical Plasma Emission Code (APEC) [9], explicitly mentions H- and He-like ions in astrophysics and offers web-based access to their spectrum simulations. The APEC project advertises continuing improvements. However, this does not guarantee that specific datasets are up to date. An example is discussed below and in [10]. A range of publications exist on the excitation of medium to highly charged Fe ions, with extensive tables on collision strengths, for example by Bhatia (Goddard Space Flight Center), Kastner (US Naval Research Laboratory (NRL)), and colleagues. While such work has its specific merit, I have noted that some of their transition rates between certain low-lying levels are far from the results of more dedicated computations or from those of experiment (see the discussion in [11]). The TOPbase database lists transition rates in the framework of an opacity project, but these are averaged over terms, that is, they are not level-specific. In contrast, the CHIANTI project [12,13,14] addresses mostly solar spectra, and for many spectra of Fe the CHIANTI project has produced extensive analyses (by Del Zanna, Dere, Storey, Mason, Young and others) that can serve both as benchmarks [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31], and as spectrum simulations. The trailblazing work of Czyzak et al. [32,33] on

E 1

-forbidden transitions does not reach up to Fe. The compilation of forbidden transitions by Kaufman and Sugar [34] does include elements as heavy as Fe and beyond; it is based on simple computations and deserves to be consulted. However, it does not comprise the low charge states of Fe. The holdings of the NIST data group have at various occasions been presented in tables of transition arrays including the transition rates (see [35,36] for Fe). The NIST ASD online database [37] lists transition rates (usually computed) of many spectral lines, however, these entries are not sufficient to yield level lifetimes as long as not all decays of a level are represented. In these tables, the transition rates are often stated with an assumed uncertainty class, which reflects a certain healthy skepticism. This is well justified, as most atomic structure computations, especially those of transition rates, do not include intrinsic assurances of quality.

However, my concern here is mostly with measured level lifetimes, which are obtained in the laboratory and then made available for the interpretation of astrophysical data. Of course, this is not the first discussion of atomic level lifetimes in the astrophysical context, Bowen [38,39] recognised the importance of electric-dipole forbidden transitions for the understanding of emissions from planetary nebulae and other low-density plasmas. As an example, I have dealt with many other elements elsewhere [40], whereas the present text concentrates only on Fe.

2.1. Ions with an $n = 1$ Ground Configuration

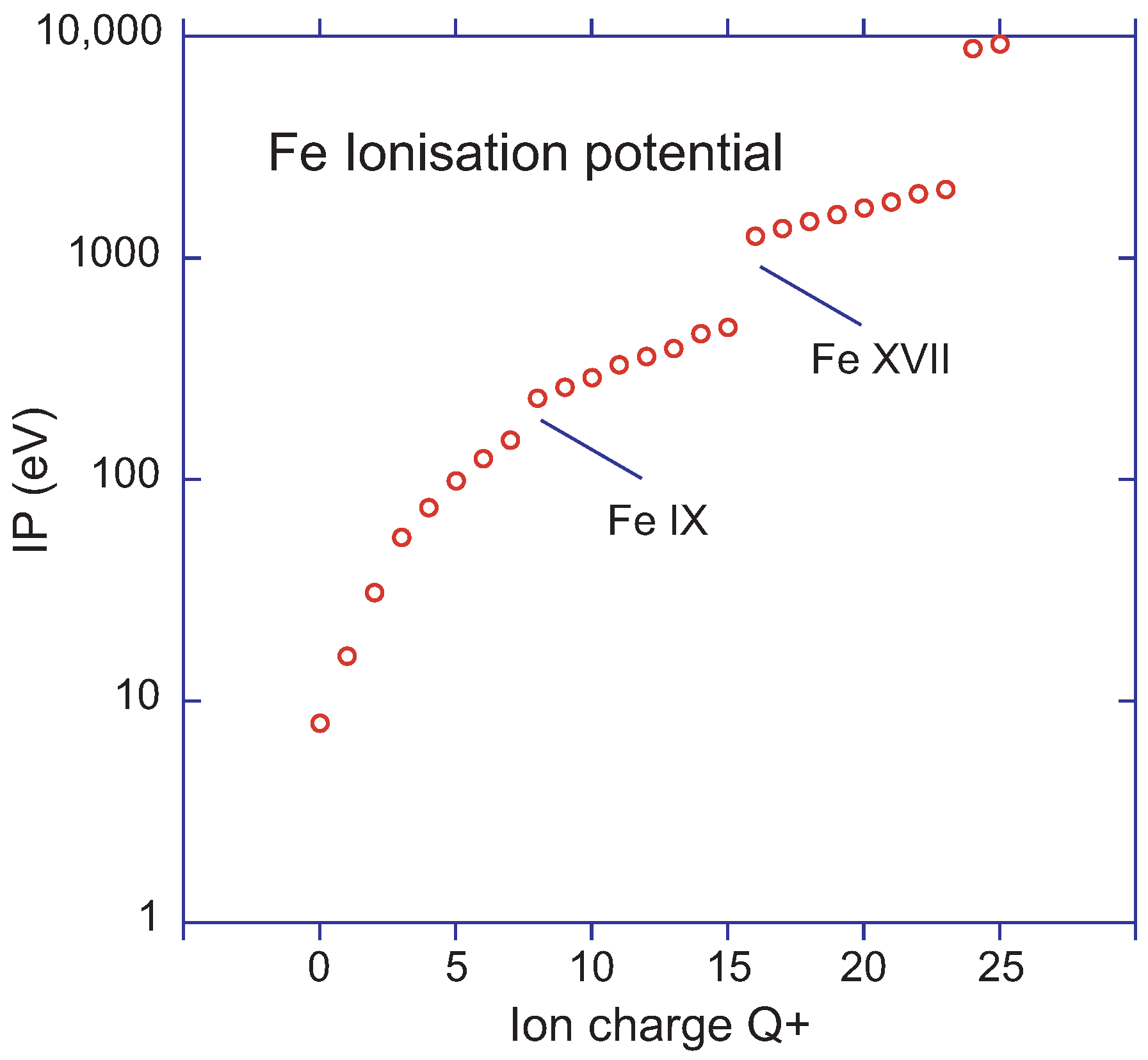
Figure 1 shows the ionisation potentials of the ions of Fe. Ions with an open K shell have a first excitation energy in the multi-keV range; the high temperatures of solar flares are necessary to produce such ions. A second structural property is linked to the first, in that the one-electron and two-electron ions of Fe have principal transitions in the X-ray range, the Fe ions with an open

n = 2

valence shell have prominent transitions in the EUV range, and Fe ions with an open

n = 3

valence shell radiate most strongly in the EUV and VUV ranges. At the same time, there are

E 1

-forbidden transitions in the ground configurations of ions with five or more electrons, which in Fe ions fall into the UV and visible spectral ranges.

The level structure of the H-like spectrum, Fe XXVI, is practically the same as that of H I, though at level energies that are a factor of

Z^{2}

higher, with certain quantum electrodynamical (QED) corrections that can be neglected in astrophysics. Other atomic properties, such as many of the level lifetimes in Fe XXVI, may seem unimportant for astrophysics; however, they are nevertheless illustrative of the role of decay modes in highly charged ions (HCI); see Table 1 and the subsequent tables for displays of the examples discussed in the text. For a general overview of the systematics of multi-polar transition probabilities in H-like ions, consult [41].

In H I, the three low-lying excited terms 2p

^{2}

P

^{o}

, 3d

^{2}

D, and 3s

^{2}

S feature level lifetimes of about 1.6 ns, 16 ns, and 160 ns, respectively (approximate ratios of 1:10:100); the 2s level lifetime of about 0.125 s exceeds that of the2p levels by about eight orders of magnitude, and the principal decay mode of the2s level is the

2 E 1

decay. The

E 1

transition rate scales with

Z^{4}

, meaning that the lifetime of the Fe XXVI 2p levels amounts to only 3.5 fs (3s and 3d follow in the same ratios as stated above). The 2s level lifetime, however, is predicted as 345 ps, “only” five orders of magnitude longer than the 2p level lifetime; in Fe XXVI, the

M 1

transition rate catches up somewhat, such that the

2 E 1

decay rate of the 2s level dominates by only a single order of magnitude. At a somewhat higher Z, the

M 1

decay branch begins to dominate, as has been demonstrated in X-ray spectra of foil-excited fast ion beams. In Fe XXVI, all of these lifetimes are too short for present precise measurements, and researchers using transition rates for spectrum simulations or similar investigations would be better advised to use results that that can be more reliably predicted (i.e., to better than ±1%) by quantum mechanics.

He-like ions (spectrum Fe XXV) offer a higher complexity than H-like ions, and as such they feature additional physics angles worth disentangling. The six

n = 2

levels have long drawn theoretical attention [42,43,51]. There are two measurements [44,45] that address Fe XXV

n = 2

levels by the beam-foil technique [52], which involves sending a fast ion beam through a thin foil; the ions in the beam find a new charge balance and are excited by the interaction with a solid-state density electron gas, and then they travel on (in high vacuum) with almost the same speed as before and largely on the same trajectory. Following the light emission as a function of distance from the exciter foil translates into decay curves as a function of time after excitation. This works well in time ranges near a nanosecond, with an uncertainty of roughly 10% (see Table 1). A third experimental approach attempts to exploit the line broadening that is associated with short atomic lifetimes (the natural line width) [53]. Using this approach, an ion cloud stored in an electron beam ion trap was cooled until the Doppler width detected on two somewhat more long-lived level decays (Fe XXVI 1s2s

^{3}

S

_{1}

, 1s2p

^{3}

P

_{1}^{o}

) appeared to become as small as the instrumental line width of the spectrometer (or even smaller). This combined line width was then subtracted (in quadrature) from the clearly larger line width of the 1s2p

^{1}

P

_{1}^{o}

level decay. However, as the obtained result did not agree with the theoretical prediction, the tentative experimental result was considered to be not yet reliable. Further analysis (not yet finished) seems to indicate that a specific problem lies in the positional scattering of the individual data files versus the line width of an averaged dataset [54]. Thus, while a much-sought experimental data point using a very different technique (i.e., different from the beam-foil technique) appears to lie in reach, the final accuracy may turn out to not be higher than for the other lifetime measurements of He-like ions. For the time being, the calculated transition rates for the He-like ion of Fe should be considered better than the measured rates (to date, ±10%). For example, considering the

M 1

decay of the 1s2s

^{3}

S

_{1}

level, the isoelectronic trend (over fifteen orders of magnitude, from He I to Xe LIII) is tightly constrained by measurements of low-Z ions in an electron beam ion trap and at a heavy-ion storage ring (see [55]) and found to agree with theory [51], meaning that even for an ion of higher Z, such as Fe, the

M 1

transition rate can safely be assumed as being known to better than 1%.

2.2. Ions with an $n = 2$ Ground Configuration: Li- and Be-like Ions

Most of the high-lying levels of Li-like ions can be computed accurately in a hydrogenic approximation. The transition rates of

Δ n > 0

transitions should be rather reliably computable by the numerical Coulomb approximation (established more than 70 years ago) and its more modern offspring. However, of greater practical appeal are the

Δ n = 0

transitions 2s–2p, which are prominent in many plasmas, because they are easily excited and their transition energies (wavelengths Fe XXIV

λ

19.201 nm, 25.509 nm) have been well measured and computed [56]. For the transition rates in the

n = 2

shell of Li through F-like ions, Cheng, Kim, and Desclaux [49] have early on provided results of their fully relativistic computations.

Lifetime measurements of the 2p levels of Fe

^{23 +}

have been undertaken by the beam-foil technique [45,46], with results (see Table 1) of merely 4 to 8% uncertainty. To me, it appears telling that the later experiment is stated with a larger uncertainty than the earlier one, as the early excitement investigating experimental achievements of the beam-foil technique was later moderated based on the recognition that the apparent simplicity of the data may have been deceptive. Such measurements have been performed on many elements, well into the region of medium-high Z, where the fine structure interval of the 2p

^{2}

P

^{o}

term increases notably and relativistic effects distinguish the 2p

_{3 / 2}

wave function from the 2p

_{1 / 2}

one. The decay curves of both levels appear deceptively straight on a logarithmic plot, and it is necessary to measure quite far out in order to see the (power-law) cascade tail diverge from this trend. Practically all measurements agree with the expected trends (see [57]), although this does not represent a validity test of the error estimate. In my interpretation, though the individual measurements may not all merit their stated uncertainties, the combination of all measurements nevertheless corroborates the theoretical prediction [49] to better than about 3%.

The cascade problem is particularly notable in beam-foil spectroscopy, as the interaction of fast ions with a solid-state density electron gas excites atomic levels very efficiently, including those of multiple excitation character as well as high-lying ones. An exemplary situation is encountered in Be-like (or in the rather similar Mg-like) ions. The upper level of the resonance line, 2s2p

^{1}

P

_{1}^{o}

, is repopulated from two displaced levels in the same atomic shell, 2p

^{2}

^{1}

S

_{0}

and 2p

^{2}

^{1}

D

_{2}

. The first of these levels has a lifetime not very different from that of the resonance level, though shorter, which causes a growing-in cascade that is difficult to analyse reliably. The second of these cascade levels is substantially longer-lived than the resonance level, which should be easily disentangled in a multi-exponential fit procedure. However, this level is the spout of a funnel of cascades along the yrast line (levels of maximum angular momentum ℓ for a given principal quantum number n). Such a cascade needs to be measured quite far out in order to reach and establish the background level. Of course, there are more cascade paths than these two dominant ones, and a sensible analysis might use a level population (and cascade) model or correlate the major direct cascades with the decay curve of the resonance line. This problem has been discussed and treated repeatedly. Nevertheless, even after the problem had been explained and its attempted solution published, studies continued to be presented that neglected the complexity of such a decay scheme and arrived at results up to 50% different from those of better work. Such a wide data scatter has surely contributed to giving beam-foil spectroscopy a poor reputation in the eyes of certain researchers, although if used with appropriate care the capabilities of the technique are much better, indeed, and often better than the alternatives.

In the given case, the evident complexity of the decay scheme has often been mentioned as an excuse for a conservative error estimate of beam-foil results for the 2s2p

^{1}

P

_{1}^{o}

level lifetime. Excessively conservative estimates, however, limit the actual value of such data. As a way to constrain the uncertainty, Reistad and Martinson [58] employed a combination of results for several elements based on the expected isoelectronic trend of the line strength stated by Edlén in his Handbook article [59]. Träbert [60] extended this approach through a critical review of the data sources. The complete set of data from the literature show a significant scatter (reduced

χ^{2}

); removing the data that appear to have been incompletely analysed yields a recommended dataset without such outliers and with a reduced

χ^{2}

value, representing an improvement by considerably more than an order of magnitude. From such a critically evaluated dataset, beam-foil experiments would test theory with an uncertainty of about 3% (see [57]), a quite respectable figure of merit.

The other key 2s2p level in Be-like ions, 2s2p

^{3}

P

_{1}^{o}

, poses very different problems. There are cascades from displaced terms in the same shell and yrast cascades; however, practically all cascade levels of significance are much shorter lived than the level of interest. Though the repopulation boosts the intensity of the 2s2p

^{3}

P

_{1}^{o}

level decay, this simply requires measuring far enough out to let the cascade distortion of the decay curve become negligible. Unfortunately, this represents a technical problem of its own; thus, the Berkeley accelerator fast-ion beam measurement on Fe [46] carries an uncertainty of about 30%, while a similar measurement in Japan reaches ±8% [47]. This line of experimentation has been extended upwards to higher Z [61] as well as downwards, the latter using heavy-ion storage rings that permit storage of low-Z ions for notable time intervals to avoid geometry problems associated with mechanical motion. A key experiment on Be-like C III [62] reached an uncertainty for the lifetime measurement of well below 1%. In a systematic synopsis of all data for the isoelectronic sequence, the same regularisation that worked well for the singlet level displayed a marked offset between measurement and theory for the triplet level lifetime (see [57]). However, several computational approaches have since converged with the accurate experimental findings at low Z [48], and at present the theoretical expectation for Fe XXIII can be ascribed a percent uncertainty in the single digits.

2.3. Ions with an $n = 2$ Ground Configuration: B- to F-like Ions

There are two excitations in B- to F-like ions that dominate the contributions to EUV and VUV spectra: first, displaced terms (single and double 2s-2p excitations) in the same shell as the ground term, with mostly

E 1

decays; and second, fine structure levels within the ground term. The latter share the same parity, and consequently most transitions are of the

M 1

and

E 2

types. The level structure in the

n = 2

shell has long since been studied and consolidated by Edlén ([63,64] and associated further papers).

In principle, the rates of the

E 1

-forbidden transitions between the fine structure levels of a given term are “simply” calculated from the transition energy (to third (for

M 1

transitions) or fifth (for

E 2

transitions) power) and a factor from Racah algebra. While using a precise transition energy from experiment helps for a so-called “semi-empirical adjustment”, the seemingly “simple” Racah factor relates to a single-configuration picture that is valid only to a certain degree. The fine structure splitting is a relativistic effect (the splitting is generally proportional to

Z^{4}

), and in combination with the steep energy dependences of

M 1

,

E 2

, and corresponding transition rates, the wavelengths of

E 1

-forbidden transitions change drastically from element to element in an isoelectronic sequence. The actual rates change even more, which may render a given measurement technique applicable or inapplicable. Owing to (time-resolving multi-channel) detector challenges in the EUV and the lifetime range to be addressed (see the theory results in Table 1), there has been little work on the level lifetimes in the ground configurations of B- to F-like Fe, and more work on the corresponding levels in the

n = 3

levels in Al- through Cl-like Fe ions (see below). In lower-Z elements of the B- to F-like isoelectronic sequences, the lifetimes of interest fall into the millisecond range, which has been studied at the Heidelberg heavy-ion storage ring TSR [55,65]. A reasonable agreement between lifetime predictions and measurements has been found.

Another group of transitions with upper levels in a possibly interesting lifetime range are intercombination transitions, for example, the 2s

^{2}

2p

^{2}

P

_{J}^{o}

–2s2p

^{2}

^{4}

P

_{J}

lines in B-like ions. In the low-Z ions C

^{+}

and N

^{2 +}

, the wavelengths lie in the UV/vacuum UV and the level lifetimes in the millisecond range. In these atomic systems, ion trap and ion storage ring experiments have to exploit good signal statistics in order to analyse decay curves that represent three superimposed decay components (with a lifetime spread by one order of magnitude). Under these conditions, the longest lifetime was obtained with the smallest uncertainty. For the much higher-Z Fe

^{21 +}

ion, the fine structure is so much larger that the five intercombination lines of this multiplet feature well-separated EUV wavelengths. The pattern of lifetimes is the same as at low Z, with the

J = 3 / 2

level being much longer lived than the

J = 1 / 2, 5 / 2

levels (see Table 1). The strongest signal is expected for the one unbranched decay, that is, of the

J = 5 / 2

level, which was indeed studied [47], finding a lifetime in agreement with expectation and with an uncertainty estimate of about 7%.

Not many measurements have been conducted for the lifetimes of displaced levels in B- to F-like Fe ions. One exception is the work by the Buchet group at Lyon with data for Fe XIX and Fe XVIII [50]. Their data analysis includes population models; thus, I expect their results to be accurate as specified at 7 to 8%. The scatter of the theory results they quote is somewhat larger. My home group at Bochum could not reach these charge states of Fe; our corresponding lifetime measurements on ions of Mg through P usually agreed with the predictions by Fawcett [66], who fitted parameters in the Cowan code to reproduce the measured wavelengths, then used the same wave functions for the determination of oscillator strengths. For more recent ab initio calculations (which, while not necessarily more accurate, are not biased by observation), see for example the studies by the Lithuanian group of Gaigalas, Merkelis, Vilkas, Kisielius, and their colleagues [67,68,69,70,71,72].

E 1

-forbidden decay rates in lighter C-, N-, and O-like ions have been measured precisely at a heavy-ion storage ring [65], finding good agreement with predictions.

Thus far, measurement and computation of the atomic lifetimes of B- to F-like Fe ions largely seem to agree. However, it may be advisable to note that all is not necessarily well. An astrophysics study has claimed that the XUV spectrum of the (double) star Capella shows a higher flux than is compatible with the EUV flux from the same object. This claim has been investigated in a set of measurements of XUV versus EUV line ratios in Fe XVIII and Fe XIX with an electron beam ion trap [10]. The laboratory measurement concluded that the reason for the (quite substantial) discrepancy lies not in nature, but in the computation of atomic structure and spectrum simulation. In this case, a reviewer at the time suggested that the development of databases such as APEC [9] had surely improved the spectrum models over the decades, meaning that the discrepancy must have gone away in the interim; alas, while other parts of APEC have been worked on, the basic atomic parameters used in the model have remained unchanged. Thus, the web-access “self-service” spectral model has maintained the same line intensities. The experiment did not determine the underlying reason for the apparent discrepancy between various computational models and the EBIT spectra (which in certain properties agreed with astrophysical observations). Various “minor” patches of the observed data (obtained mostly by the Chandra spacecraft) or laboratory measurements have been suggested to bridge this discrepancy with the results of computation. However, rather than modifying nature to match computation, it seems advisable to instead try to work on a complete interpretation of the observations and on the production of better spectrum models.

The experiment in question actually did not employ any time resolution; however, this does not guarantee that transition rates are not part of the problem. Moreover, consistent with earlier measurements [73], a line that has been ascribed to a two-electron decay of the Fe XVIII 2s

^{2}

2p

^{4}

3p

^{2}

P

_{3 / 2}^{o}

level appears much more prominently than predicted by various atomic structure models. It is an open question whether this intensity peculiarity is a direct consequence of a transition rate or an indirect one via a level population. No lifetime measurements have been attempted on this line yet. Interestingly, the aforementioned level supposedly decays to a displaced level, namely, 2s2p

^{6}

^{2}

S

_{1 / 2}

. The corresponding 3s3p

^{6}

^{2}

S

_{1 / 2}

level in the Cl-like spectrum Fe X is discussed below, as predictions for its lifetime scatter by a factor of two, and the same level lifetime has been checked by beam-foil spectroscopic measurements.

2.4. Ions with an Open $n = 3$ Valence Shell

These ions contribute the bulk of the many prominent Fe lines in the solar XUV and EUV spectrum. The CHIANTI solar spectrum synthesis corroborates this observation. The variety of atomic systems, wavelengths, level lifetimes, and peculiarities necessitates a discussion of the individual charge states and spectra. On the theory side, Ne- to Ar-like levels and lifetimes have been repeatedly tackled, with a consistent dataset on levels and their decays in Na- to Ar-like ions has been published by Froese Fischer and her group [74].

2.4.1. Ne-like Fe XVII

The ground state of rare-gas configuration ions is simple, with all shells closed; however, when this symmetry is broken by the excitation of even only one electron, there are many levels (in Ne-like ions, there are 36 excited levels with a single electron promoted from the

n = 2

shell to the

n = 3

shell), with many peculiarities to consider because of symmetries and selection rules. The Lyon beam-foil group has tried to establish all these levels, and has been successful with most of them [75]. Such experiments are necessary in order to check the results of many theoretical attempts, while the computations are helpful in guiding future experiments and checking the data for completeness. While the present review targets measured lifetimes (see Table 2), I want to cite at least one computational study that includes levels and transition rates [76].

The Fe XVII XUV and EUV spectrum has been simulated for typical low-density conditions in an electron beam ion trap [77,78,79] using the Flexible Atomic code (FAC) [80]. The strongest line is not one of the basic resonance lines, but rather the decay from the (2s

^{2}

2p

^{5}

3d

_{3 / 2}

)

_{J = 1}

level. Actually, the resonance/intercombination line pair 2s

^{2}

2p

^{6}

^{1}

S

_{0}

–2s

^{2}

2p

^{5}

3d

_{3 / 2}

^{1}

P

_{1}^{o}

and 2s

^{2}

2p

^{6}

^{1}

S

_{0}

–2s

^{2}

2p

^{5}

3d

_{5 / 2}

^{3}

D

_{1}^{o}

(known as lines 3C and 3D) has a story of astrophysical observations and interpretations of its own. The line pair is prominent in astrophysical and laboratory plasmas [81]; however, the line ratio appeared differently in theory, astrophysical data, and laboratory measurements. Effects were hypothesised that should modify the (theoretical) emission pattern to allow the observed pattern to emerge. Experiments were then conducted that agreed with pure theory, invalidating the purported effects of the environment, while other experiments differed. An experiment that was thought to be particularly clean, in an EBIT at the LCLS X-ray light source, did not cut through the fog either [82], and the astrophysical interpretative struggle continued [83]. An attempt at measuring the two level lifetimes expected from theory (44 fs and 166 fs, respectively) unfortunately failed [84]. Further attempts continued to find the reasons for the line ratio being different from the theory for Ne-like ions, assuming, for example, non-linear excitation dynamics or population transfers from adjacent charge state ions [85] (for further references, see [86]). A full decade after the EBIT experiment at LCLS, after various technical insights and improvements, such as employing even higher spectral resolving power and reaching a much better signal-to-background ratio with a much-improved detector, a new measurement [86] resolved the conflict with theory. In this experiment, the oscillator strengths of the lines of interest (2.32 ± 0.17/0.60 ± 0.08) were obtained from the line widths. These values correspond to level lifetimes of 44 fs and 175 fs, respectively, not that far from the older NIST listings. This experimental achievement implies the insight that astrophysics needs much better spectral resolution in the EUV/XUV range in order to obtain data that can be evaluated with less uncertainty and bias.

The lifetimes of the 2s

^{2}

2p

^{5}

3s

^{3}

P

_{0, 2}^{o}

levels have been measured at the Livermore electron beam ion traps [87,88]. Of these, the 2s

^{2}

2p

^{5}

3s

^{3}

P

_{0}^{o}

level is of particular astrophysical interest. Its signal is expected to be density-sensitive [79], though at densities in the upper range of coronal events. Moreover, the level lifetime is shortened by external magnetic fields [88,89], which opens a

J = 0 - 0

decay channel to ground. Thus, the relative intensity of the intra-shell

M 1

transition to the 3s

^{3}

P

_{1}^{o}

level would be reduced, and might serve as a magnetic field diagnostic. It is, however, difficult to measure the intensity of the

M 1

transition in the VUV (near 110 nm) and compare it sensibly with the XUV ground state transitions (at wavelengths on the short side of 2 nm). A practical problem with the lifetime measurement is that while crystal spectrometers are able to separate the major XUV transitions, they are too inefficient to serve time-resolving photon detectors. Thus, timing detectors of lower spectral resolution have to be used, and the resulting analysis faces superpositions of several decay curves. However, it is possible to use the option of modulating the electron beam energy in EBIT, which permits temporal decoupling of the product of a certain maximum ion charge state caused by exciting the ions produced and trapped earlier. The same technique has already served to identify a blend with a nearby lower charge state line in the aforementioned experiments on the 3C/3D line ratio.

Table 2. Fe XVII-Fe XIII level lifetimes and dominant decay modes (

E 1, M 1, E 2

), MIT magnetically induced transition, IC intercombination transition; ANDC arbitrarily normalized direct cascade evaluation, cascmod evaluation using a cascade model.

Table 2. Fe XVII-Fe XIII level lifetimes and dominant decay modes (

E 1, M 1, E 2

), MIT magnetically induced transition, IC intercombination transition; ANDC arbitrarily normalized direct cascade evaluation, cascmod evaluation using a cascade model.

Spectrum	Sequence	Level	Decay	Lifetime	Expt/Theory
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3s $^{1}$ P $_{1}^{o}$	E1 $Δ n = 1$	1.20 ps	T [37]
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3s $^{3}$ P $_{2}^{o}$	M2 $Δ n = 1$	4.90 + 0.23−0.07 $μ$ s	E [87]
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3s $^{3}$ P $_{1}^{o}$	E1 $Δ n = 1$ IC	1.08 ps	T [37]
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3s $^{3}$ P $_{0}^{o}$	M1 $Δ n = 0$ ,	62.5 ms	T [79]
			MIT $Δ n = 1$	69 ± 7 ms	E [88]
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3d $_{3 / 2}$ $^{1}$ P $_{1}^{o}$	E1	44 fs	T [37]
XVII	Ne			43.7 ± 3 fs	E [86]
XVII	Ne	2s $^{2}$ 2p $^{5}$ 3d $_{5 / 2}$ $^{3}$ D $_{1}^{o}$	E1 IC	166 fs	T [37]
XVII	Ne			175 fs	T [86]
XVI	Na	3p $^{2}$ P $_{3 / 2}^{o}$	E1 $Δ n = 0$	125 ± 10 ps	E [50] cascmod
				138 ± 9 ps	E [90] ANDC
XVI	Na	3p $^{2}$ P $_{1 / 2}^{o}$	E1 $Δ n = 0$	155 ± 10 ps	E [50] cascmod
				167 ± 11 ps	E [90] ANDC
XVI	Na	3d $^{2}$ P $_{3 / 2}$	E1 $Δ n = 0$	55 ± 4 ps	E [50]
				51 ± 11 ps	E [90]
XVI	Na	3d $^{2}$ P $_{5 / 2}$	E1 $Δ n = 0$	62 ± 5 ps	E [50]
				69 ± 10 ps	E [90]
XV	Mg	3s3p $^{1}$ P $_{1}^{o}$	E1 $Δ n = 0$	47 ± 5 ps	E [91] cascmod
				42 ± 3 ps	E [90] ANDC
XV	Mg	3s3p $^{3}$ P $_{1}^{o}$	E1 $Δ n = 0$ IC	28 ± 4 ns	E [92,93]
XV	Mg	3p $^{2}$ $^{1}$ S $_{0}$	E1 $Δ n = 0$	63 ± 5 ps	E [90]
XV	Mg	3p $^{2}$ $^{1}$ D $_{2}$	E1 $Δ n = 0$	160 ± 20 ps	E [91] cascmod
			E1 $Δ n = 0$	190 ± 20 ps	E [90]
XV	Mg	3s3d $^{1}$ D $_{2}$	E1 $Δ n = 0$	36 ± 4 ps	E [90]
XV	Mg	3p $^{2}$ $^{3}$ P $_{1}$	E1 $Δ n = 0$	70 ± 10 ps	E [91]
XV	Mg	3p $^{2}$ $^{3}$ P $_{2}$	E1 $Δ n = 0$	80 ± 10 ps	E [91]
XIV	Al	3s $^{2}$ 3p $^{2}$ P $_{3 / 2}^{o}$	M1	17.52 ± 0.29 ms	E [94]
				18.0 ± 1.2 ms	E [95]
				16.74 ± 0.12 ms	E [96]
				17.0 ± 0.2 ms	E [97]
				16.726+0.020-0.010 ms	E [98]
XIV	Al	3s3p $^{2}$ $^{2}$ P $_{1 / 2}^{o}$	E1	80 ± 10 ps	E [91]
XIV	Al	3p $^{3}$ $^{4}$ S $_{3 / 2}^{o}$	E1	70 ± 15 ps	E [91]
XIV	Al	3s3p $^{2}$ $^{4}$ P $_{1 / 2}$	E1 $Δ n = 0$ IC	29 ± 3 ns	E [99]
XIV	Al	3s3p $^{2}$ $^{4}$ P $_{3 / 2}$	E1 $Δ n = 0$ IC	160 ± 20 ns	T see [99]
XIV	Al	3s3p $^{2}$ $^{4}$ P $_{5 / 2}$	E1 $Δ n = 0$ IC	35 ± 4 ns	E [99]
XIII	Si	3s3p $^{3}$ $^{3}$ S $_{1}^{o}$	E1 $Δ n = 0$	21 ± 4 ps	E [91]
XIII	Si	3s3p $^{3}$ $^{5}$ S $_{2}^{o}$	E1 $Δ n = 0$ IC	≈82 ns	T [100]
XIII	Si	3s $^{2}$ 3p3d $^{3}$ F $_{4}^{o}$	M2	9.9 ± 0.4 ms	[101]
XIII	Si	3s $^{2}$ 3p $^{2}$ $^{1}$ D $_{2}$	M1	6.93 ± 0.18 ms	E [94]
				8.0 ± 0.1 ms	E [95]
				8.1 ± 0.2 ms	E [101,102]

2.4.2. Na-like Fe XVI

Ions with an open

n = 3

valence shell have been addressed many times from the theoretical side. There are few studies, however, that cover different atomic systems using the same computational approach, such as was done in [74] for Na- through Ar-like ions. This wide-ranging setup is convenient for reference and intercomparison, while individual atomic systems may be described in a wider extent or in more detail elsewhere.

In Fe XVII, the spectrum arises from at least one electron excited from a closed shell, that is, from a valence electron interacting with an open electron core. In Fe XVI and the subsequent spectra, the valence electron ground state is in an open shell outside of a closed-shell core. Thus, the theoretical description (to a high degree) is much simpler, as are the spectra, with lines in the EUV (most lines at wavelengths longer than 10 nm), not the XUV. Such alkali-like ions have been studied with high accuracy (aiming at the 100 ppm range) for both their computed and measured level structures. At the same time, fast-beam lifetime experiments of laser-excited neutral alkalis claim lifetime uncertainties of a fraction of one percent, though not all wholly agree with theory. This possible inconsistency (since removed) has raised interest in measuring the corresponding lifetimes in alkali-like ions. However, as no selective excitation by laser was available in the above case, the practical uncertainties remain somewhat above 7%.

The 3s–3p resonance transitions in the alkali-like ions stand out brightly in many spectra, especially after foil-excitation of fast ion beams. Obviously, the 3p–3d transitions feed the resonance levels, as do the levels along the yrast chain. Thus, the 3s–3p decay curves show strong distortions from the fast cascades as well as a slow tail. In their early data, the Lyon group [50] applied fits with three exponential components and alternatively with a population simulation. The later Bochum work employed the same techniques and added fits correlated using the ANDC scheme (arbitrarily normalised direct cascades) where feasible (here, with the same 3p–3d cascades through which the yrast cascade is funneled). The results of the different fitting techniques differ somewhat, as is to be expected, with the better results agreeing among the laboratories. In Table 2, only one result from each laboratory is quoted for a given level lifetime. Apparently, the Lyon lifetime results are rather shorter than those from Bochum, and those for the 3d levels are stated to be more accurate. The ion beam energy was more suited to the production of the Fe ion charge state at Lyon than at the lower-energy accelerator at Bochum; however, it remains unknown whether this is of any importance here. Similarly, Bochum data on the 3p levels in Na-like Ca ions (without known data from other laboratories) show a slightly longer lifetime result than that expected from theory. This has incited specialists to use various evaluation techniques in order to demonstrate that their method can solve this (small) riddle, alas, no solution has yet been forthcoming. It is possible that there is an as-yet not understood complexity in the level population after foil excitation that may depend on the ion beam energy. Decay curves recorded at a wider range of ion beam energies might elucidate this case; however, a sufficiently powerful and flexible heavy ion accelerator is not yet available. For astrophysics this problem is not important, as the level population of high-n and high-ℓ levels should be very low at the typically low density of astrophysical plasmas from which we see radiation of Fe XVI, and the cascade problem is largely absent.

2.4.3. Mg-like Fe XV

Mg-like ions resemble Be-like ions, though the former are produced at much lower temperatures in the solar corona than the latter. In beam-foil light sources, where it is possible to measure the significant level lifetimes of the 3s3p

^{1}

P

_{1}^{o}

resonance level and 3s3p

^{3}

P

_{1}^{o}

level (at the upper end of the intercombination transition), the measurements are both boosted and complicated by cascade replenishment. In low-density environments, for which it is desirable to know the transition rates, these complications are largely absent; however, the available light sources and required detectors are unsuitable. In Fe XV, these lifetimes fall into the range from roughly a twentieth of a nanosecond (resonance line) to twenties of nanoseconds (intercombination line). Beam-foil lifetime measurements have addressed the low-lying

n = 3

levels in Fe XV [90,91,92] (see Table 2).

For the Fe XV 3s

^{2}

–3s3p resonance line, which is fed by cascades from displaced levels (3p

^{2}

), intra-shell cascades (3s3d), and the yrast chain of levels 3s

n ℓ

and 3p

n ℓ

, simple multi-exponential fits are not satisfactory. Fits with population models, though crude and not verifiable in detail (with dozens or more levels representing the many more levels in nature), usually yield shorter primary lifetime values than the exponential fits, and in many cases the shorter lifetime fit results are believed to be more accurate. It helps that models can be run with many assumptions and tested to determine how well the fit procedure manages to retrieve the input values. In addition, it is helpful to make measurements on many elements in an isoelectronic sequence, as the geometric properties of the detection system do not follow the variation of the parameters of the atomic system. For the Fe XV 3s3p singlet level lifetimes, the data quoted in Table 2 are compatible with the isoelectronic trend. For the triplet level the measured value is on the slow side, though not far away from the trend [92]. The rather sizeable uncertainty of 15% results from the fact that the length of travel between exciter foil and detector position was restricted by the Bochum vacuum chamber to about 17 cm. This is less than the decay length (lifetime × velocity) of the ion under study, meaning that only a fraction of one decay length could be measured, which affects the error of the lifetime result.

The 3p

^{2}

^{1}

D

_{2}

level is longer-lived than the 3s3p

^{1}

P

_{1}^{o}

level from which it feeds, though much less long-lived than the aforementioned 3s3p

^{3}

P

_{1}^{o}

level, which is difficult to measure. Early non-relativistic theory results for the level lifetime were largely in agreement, with experiment yielding a lifetime shorter than that of the theoretical number set by about a quarter, which is quite significant for a level lifetime that can fairly easily be measured without major evaluational corrections. A relativistic computation provided results much closer to experiment, however, the improvement was not caused by the relativistic wave functions, but was rather a result of a different mind-set; with increasing atomic number Z, there emerges an intercombination decay branch of the 3p

^{2}

^{1}

D

_{2}

level to the 3s3p

^{3}

P

_{1}^{o}

level, which was overlooked in the earlier work and was automatically included in the relativistic approach, as it does not distinguish between singlet and triplet levels. An iso-electronic exposition is shown in [103], though the reader should be warned of a repeated mix-up of the 3s3d and 3p

^{2}

^{1}

D

_{2}

level labels that occurred between manuscript and publication.

The 3p

^{2}

^{3}

P

_{J}

displaced level lifetimes measured at Brookhaven [91] exceed the theoretical predictions by 40% and more (the same pertains to many

E 1

decays in Fe XIV and Fe XIII discussed below). This is likely the result of multiple cascade feeding (including the yrast cascade). In a hydrogenic approximation, it can easily be see that the sequence of cascade levels begins with short lifetimes and then incrementally grows in lifetime in steps that are too small and too numerous to disentangle by multi-exponential fits. In addition, the population models suggest that the populations of the levels of interest are not significantly different from the cascading levels, which is much more difficult to analyse than the case of resonance line with their much higher upper-level populations. Nevertheless, these two fit results from Brookhaven, the data analysis of which probably falls systematically short, reflect the expected level lifetime difference among the fine structure levels.

2.4.4. Al-like Fe XIV

With this spectrum, we enter the realm of the visible corona lines first observed in the middle of the 19th century. Because they could not be identified with (low charge states of) terrestrial elements, the speculative element “coronium” was suggested. No sooner than the 1940s, Edlén was able to prove that the 530-nm line seen in the corona corresponded to the fine structure interval of Fe XIV 3s

^{2}

3p

^{2}

P

_{1 / 2, 3 / 2}^{o}

. This wavelength has subsequently been measured with very high precision at the Heidelberg EBIT [104] as 530.28113(13) nm. The transition is a magnetic dipole (

M 1

) one with a small

E 2

admixture. Early in the present century, several experiments investigated the measurement of the transition rate, specifically the

J = 3 / 2

level lifetime, which had been predicted near 16.7 ms. At the beginning of these experiments, the intention was a straightforward test of the predictions using newly developed techniques for storing highly charged ions in ion traps. Four measurements, all from different laboratories, were published in two-year intervals [94,96,97,98] (see Table 2).

The first and third of these measurements used an electrostatic (Kingdon) ion trap, whereas the other two used electron beam ion traps. A learning curve might be expected; indeed, for each technique the later results carried smaller uncertainty. However, the Kingdon trap results both remained (slightly) on the longer side of the bulk of the lifetime predictions, while the more precise EBIT results (see Table 2) agreed both with each other and with most of the predictions. Because the transition rate can be predicted from a combination of the fine structure interval (possibly taken from spectroscopy) and a tabulated Racah coefficient, it may not be surprising for most predictions to be close to each other (within about 1%). Amusingly, there are three predictions that result from more tortuous ab initio computations and that scatter in a 25% wide interval. While one of the three agrees with the bulk of the predictions that agree with experiment, it is nevertheless not reliable; the same computation deviates markedly from experiment on a similar transition in Fe X (see graphics in [11]). The differences between the laboratory results most probably do not relate to the nature of the ion traps (i.e., Kingdon trap, heavy-ion storage ring, and EBIT), and are likely rather due to differences in ambient pressure. While all of these measurements used a very high vacuum when preparing the ions before trapping, only in EBIT did the vacuum remain ultrahigh throughout; this issue has been discussed in [55,101]. There is one long-lived level, 3s3p3d

^{4}

F

_{9 / 2}^{o}

, which can only decay by an

M 1

transition of low energy to the 3s3p3d

^{4}

F

_{7 / 2}^{o}

level (from where the further decays are fast). Incidentally, the lifetime of this level is close to that of the upper fine structure level of the ground term. It is likely that this slow cascade does affect lifetime measurements of the corona transition, but only when the density is not as low as in the solar corona. The long-lived

J = 9 / 2

level has been neglected in several computations; the earliest computation of which I am aware that includes is one by Froese Fischer and Liu [105]. However, their transition rate prediction for the fine structure transition in the ground term differs from almost all other predictions and from measurement by some 15%. Owing to two measurements obtained using electron beam ion traps, the key coronal

M 1 / E 2

transition rate in the ground configuration has since been measured to better than 1% (see Table 2). This is a rare achievement in the context of lifetime measurements of highly charged ions.

The Brookhaven measurement of lifetimes of the Fe XIV 3s3p

^{2}

^{2}

P

_{1 / 2}

and 3p

^{3}

^{4}

S

_{3 / 2}^{o}

levels (all

E 1

decays) yielded values about three times the predictions (at the time informally provided by B.C. Fawcett, today roughly similarly measurements are available in [37]). The reason for these discrepancies is not actually known, however, it can be plausibly assumed to be related to the complexity of the decay scheme, rather than to an individual level lifetime; see the discussion below. The Brookhaven dataset of decay curves of nine levels was simultaneously measured by a multichannel position-sensitive detector (very newly introduced at the time). Electronic faults should have affected several decay curves at the same time, however, there is no sign of such an effect. The beam-foil light source is mono-isotopic, which avoids the occurrence of blends with other elements but does not remove the chance of unrecognised blends with other lines of the same or nearby charge states of Fe. More experiments with higher spectral resolution might resolve the discrepancy. It is not likely that atomic structure computation would be so wrong; in this case, I see it as much more likely that the data contain more decay contributions than have been recognised to date. For ordinary

E 1

transition rates, atomic structure computations should be sufficiently accurate for most practical purposes, but should not be expected to be more reliable than 10%; however, many digits are listed from the computations. Of course, this expectation is not the same as an experimental test.

Of course, experiment involves more than data taking; there is also the problem of data analysis. Pinnington et al. [106] recorded beam-foil decay curves of many resonance lines of Fe XIV (from the five displaced levels 3s3p

^{2}

^{2}

S

_{1 / 2}

,

^{2}

P

_{1 / 2, 3 / 2}

,

^{2}

D

_{3 / 2, 5 / 2}

, and the 3s

^{2}

3d

^{2}

D

_{3 / 2, 5 / 2}

levels) and applied four different techniques of decay curve analysis (free multi-exponential fit, constrained multi-exponential fit, Pinnington’s own VNET code that addressed the vignetting problem of the exciter foil moving through the observation window and thereby having a particular effect on short-lived contributions, and correlated analysis including arbitrarily normalised direct cascades (ANDC)). The displaced levels experience repopulation from the doubly displaced 3p

^{3}

^{2}

P

_{1 / 2, 3 / 2}^{o}

and

^{2}

D

_{3 / 2, 5 / 2}^{o}

levels and from many 3s3p

n ℓ

levels. Thus, there are plenty of cascades with lifetimes close to those of the levels of interest (for which, meanwhile, Fawcett had published predictions [107]). There are several points that induce me to not include all of the fit results in Table 2. First, the multi-exponential fit results and VNET yielded statistical error estimates on the order of 5%, while the results were systematically some 30% or more above theory, which seems implausible except in a cascade situation that overburdens the evaluation technique. The ANDC results in most cases are closer to theory here; however, while they carry intrinsic error estimates on the order of 20%, which seems more realistic than the simple statistical errors of the multi-exponential fits, the numbers are systematically inconsistent (outside of the 1-

σ

range) with theory. The only exceptions are the rather long-lived 3s3p

^{2}

^{2}

D

_{3 / 2, 5 / 2}

levels, which show lifetimes on the order of 500 ps, in contrast to the other levels with their lifetimes of a few dozen picoseconds. Considering these findings, my recommendation would be to use the Fawcett or NIST [37,107]

E 1

transition rates in the doublet term system of Fe XIV and an uncertainty guesstimate of no better than 20%. The beam-foil technique, which in principle should be applicable, has not been able to deliver reliable answers in this case, because data analysis has been unable to cope with the complexity of the cascade problem. A more recent ab initio computation of Al-like ions [108] addresses the structural aspect more than the lifetime.

The five intercombination lines 3s

^{2}

3p

^{2}

P

_{1 / 2, 3 / 2}^{o}

–3s3p

^{2}

^{4}

P

_{1 / 2, 3 / 2, 5 / 2}

are prominent in the EUV spectrum of the solar corona. These lines were seen by [109], though not yet identified, more than a decade before a beam-foil measurement performed in the basement (away from sunlight) tagged them thanks to their delayed emission [93,99]. Though the multi-nanosecond lifetimes of the

J = 1 / 2, 5 / 2

levels exceeded the time-of-flight of the excited ions inside the measurement chamber, the observations nevertheless yielded lifetime results with about 10% uncertainty. In this type of level multiplet, the

J = 3 / 2

level is about another factor of five more long-lived than the other two quartet levels, which proved too long for a meaningful lifetime estimate based on a decay curve. Interestingly, various theoretical predictions of this lifetime scatter by some ±10% as well.

2.4.5. Si-like Fe XIII

In the spectral section seen by the multichannel EUV detector in the Brookhaven beam-foil experiment of 1979, only a single

E 1

transition of Fe XIII was covered, namely, one of the decay branches of the 3s3p

^{3}

^{3}

S

_{1}^{o}

level. The measured lifetime of about 21 ps was compatible with the 17 ps prediction. For computed lifetime predictions in Fe XIII, see [100,110,111,112], for further measurements by beam-foil spectroscopy or at a heavy-ion storage ring, as well as for more references, see [95,102,113]. This Brookhaven lifetime result is close to the practical (geometrical) time resolution of the particular experimental setup. The same would have been a limitation for most other lifetime studies of “ordinary”

E 1

decays in Fe XIII or other Fe ions with an open

n = 3

shell. In beam-foil spectroscopy, the charge state distribution would not have favoured Fe

^{12 +}

over, say, Fe

^{15 +}

, because there are more

n = 3

valence shell levels. Consequently, each of the levels would have received a smaller share of the total level population, making it twice as difficult to measure statistically significant data. At the same time, the many levels in the same atomic shell provide multiple cascade repopulation, with many levels not differing drastically in lifetime, which renders multi-exponential analysis unreliable. Therefore, beam-foil lifetime measurements targeting “any level” have largely ended. The research interest has instead turned to the lowest excited levels of parity opposite the ground configuration, as the spin change in the intercombination transition to ground would imply a more comfortably measurable longer level lifetime [99] (what matters is mostly the lifetime contrast compared to other decay contributions, see the discussion section), and to the levels of the ground configuration which cannot decay by

E 1

transitions and are longer-lived yet again [94,95], and which are rather few (examples are included in Table 2).

The specific value of a level lifetime is not always important, though it may be interesting to know for comparisons between theory and measurement. For example, the Fe XIII 3s

^{2}

3p3d

^{3}

F

_{3}^{o}

level has a low decay rate because the

J = 2

target levels that can be reached by an

E 1

transition are 3s

^{2}

3p

^{2}

^{1}

D

_{2}

and 3s

^{2}

3p

^{2}

^{3}

P

_{2}

, which differ from the initial level by spin or angular momentum quantum number. In the Bochum beam-foil spectra, the latter line was not seen near its predicted wavelength [114]; in any event, a single line offers hardly any clues to its identity. However, the results of calculations of the

^{3}

F

_{2}^{o}

level [114] indicated a certain offset from the measured values, suggesting a corresponding correction for the

J = 3

level prediction. The long lifetime of that level reduced the number of candidate lines to those that might appear in significantly delayed beam-foil spectra. While these spectra usually are not very accurately calibrated for a lack of suitable reference lines, in this instance a precise wavelength of an otherwise unclassified line in the solar EUV spectrum clinched the case [115]. Although the

M 1

transition of the (long-lived)

J = 4

level to the

J = 3

level of the same

^{3}

F

^{o}

term has been searched for in the EUV spectrum of the solar corona, the hunt has not yet been concluded [25,116].

Lifetime measurements on Fe XIV to Fe X have been discussed in [117]. Another set of discussion and graphical presentations on

E 1

-forbidden decays in Si- to S-like ions of iron group elements can be found in [118]. Although measurements of Fe ions are not available in all cases, the isoelectronic trends of theory and experiment are telling. In certain cases, experiment has barely managed to measure a lifetime at an ion trap, a heavy-ion storage ring, or an EBIT, and the error bars are large (10% and more), while in others there are plenty of measurements with individual uncertainties of 8% or significantly less which nevertheless scatter considerably from one element to the next. Clearly, it would be good if more laboratories had attempted and improved on parts of the technique; however, it is not only the scatter of the experimental results that is striking—in several cases, the scatter of the theoretical predictions exceeds that of the measurements by a factor of two to three. Moreover, the intercomparison of computational predictions for many elements reveals likely clerical errors in the reference literature. In any case, it is good if a given set of atomic structure computations (for example, [119,120]) covers several elements, as this means that experiment has a better basis with which to test the systematics.

2.4.6. P-like Fe XII

Among comprehensive computations of P-like ions that include the elements of the iron group, Fritzsche et al. [121] have covered

E 1

transitions only, while Wang et al. [122] have covered

E 1

-forbidden transitions as well. Concerning the ordinary

E 1

transitions in the valence shell, I have not found any experimental level lifetime data for Fe XII. P-like ions, however, have five levels in the 3p

^{3}

ground configuration, and consequently a fair number of

M 1

transitions occur within this configuration. The low-Z ions of the isoelectronic sequence are of astrophysical interest. The results of lifetime measurements of six long-lived levels in Fe XII [95,123] are provided in Table 3. Of these levels, four are the excited levels in the ground configuration; the two other similarly long-lived levels are

J = 9 / 2

levels in the 3s

^{2}

3d configuration. These have no

E 1

decays, only

M 1

,

E 2

, and

M 2

decay channels to

J = 5 / 2

and

J = 7 / 2

levels of the three lowest configurations, where they show up as slow cascades in the decay curves of levels that themselves are shorter-lived.

The 3s

^{2}

3p

^{3}

^{4}

S

_{3 / 2}^{o}

–3s

^{2}

3p

^{3}

^{2}

D

_{3 / 2, 5 / 2}^{o}

transitions in P-like ions are of particular interest, though not in Fe XII. The line pair in S II is prominent in astrophysical spectra, and the line ratio is considered an excellent probe of very low electron densities, such as exist in planetary nebulae (for references, see [124,125]). Unfortunately, the upper level lifetimes (on the order of half an hour and one hour, respectively) are beyond present measurement capabilities. One might be tempted to measure the lifetimes of the same levels in heavier ions (where possible) and extrapolate to low Z. However, while there are data for Fe XII with few-percent uncertainties, various computational results differ by up to 30% from each other, and the scatter of the predictions increases for lower-Z elements [118].

Table 3. Fe ion (Fe XII-X) level lifetimes and dominant decay modes (

E 1, M 1, E 2

).

Table 3. Fe ion (Fe XII-X) level lifetimes and dominant decay modes (

E 1, M 1, E 2

).

Spectrum	Sequence	Level	Decay	Lifetime	Expt/Theory
XII	P	3s $^{2}$ 3p $^{3}$ $^{2}$ D $_{5 / 2}^{o}$	M1	306 ± 10 ms	E [95]
XII	P	3s $^{2}$ 3p $^{3}$ $^{2}$ D $_{3 / 2}^{o}$	M1	20.35 ± 1.24 ms	E [94]
				18.0 ± 0.1 ms	E [95]
XII	P	3s $^{2}$ 3p $^{3}$ $^{2}$ P $_{3 / 2}^{o}$	M1	1.85 ± 0.24 ms	E [94]
				1.70 ± 0.08 ms	E [95]
XII	P	3s $^{2}$ 3p $^{3}$ $^{2}$ P $_{1 / 2}^{o}$	M1	4.38 ± 0.42 ms	E [94]
				4.1 ± 0.12 ms	E [95]
XII	P	3s $^{2}$ 3p $^{2}$ 3d $^{4}$ F $_{9 / 2}$	E2,M2	11 ± 1 ms	E [123]
XII	P	3s $^{2}$ 3p $^{2}$ 3d $^{2}$ G $_{9 / 2}$	M1,E2,M2	4 ± 1 ms	E [123]
XI	S	3s $^{2}$ 3p $^{4}$ $^{3}$ P $_{1}$	M1	23 ms	T [126]
XI	S	3s $^{2}$ 3p $^{4}$ $^{3}$ P $_{0}$	M1	3.8 s	T [126]
XI	S	3s $^{2}$ 3p $^{4}$ $^{1}$ D $_{2}$	M1	9.86 ± 0.22 ms	E [94]
			M1	11.05 ± 0.5 ms	E [95,101]
			M1	9.91 ± 0.1 ms	E [97]
			M1	9.9 ms	T [126]
XI	S	3s $^{2}$ 3p $^{4}$ $^{1}$ S $_{0}$	M1	1.0 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{4}$ S) 3d $^{5}$ D $_{0}^{o}$	E1 $Δ n = 0$ IC	9.0 ns	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{4}$ S) 3d $^{5}$ D $_{1}^{o}$	E1 $Δ n = 0$ IC	9.5 ns	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{4}$ S) 3d $^{5}$ D $_{2}^{o}$	E1 $Δ n = 0$ IC	14.7 ns	T [126]
				13 ± 2 ns	E [127]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{4}$ S) 3d $^{5}$ D $_{3}^{o}$	E1 $Δ n = 0$ IC	40 ns	T [126]
				60–70 ns	E [127]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{4}$ S) 3d $^{5}$ D $_{4}^{o}$	M1	28 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ D) 3d $^{3}$ D $_{3}^{o}$	E1 $Δ n = 0$	460 ns	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ D) 3d $^{3}$ F $_{4}^{o}$	M1	8.2 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ D) 3d $^{3}$ G $_{4}^{o}$	M1	68 ± 4 ms	E [95]
				45 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ D) 3d $^{3}$ G $_{5}^{o}$	M1	94 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ D) 3d $^{1}$ G $_{4}^{o}$	M1	16 ms	T [126]
XI	S	3s $^{2}$ 3p $^{3}$ ( $^{2}$ P) 3d $^{3}$ F $_{4}^{o}$	M1	1.5 ms	T [126]
X	Cl	3s $^{2}$ 3p $^{5}$ $^{2}$ P $_{1 / 2}^{o}$	M1	13.64 ± 0.25 ms	E [94]
				14.40 ± 0.14 ms	E [11]
				14.2 ± 0.2 ms	E [128]
				14.37 ms	T [129]
X	Cl	3s3p $^{6}$ $^{2}$ S $_{1 / 2}$	E1	167–380 ps	T (see [130])
				270 ± 20 ps	E [130]
				241 ps	T [129]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{3}$ P) 3d $^{4}$ D $_{7 / 2}$	M2	17.3 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{3}$ P) 3d $^{4}$ F $_{9 / 2}$	M1	85.7 ± 9.2 ms	E [132]
				110 ± 5 ms	E [102]
				108 ms	T [129]
				90 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{3}$ P) 3d $^{4}$ F $_{7 / 2}$	M2	93 ± 30 ms	E [132]
				58 ± 10 ms	E [95]
				66.5 ms	T [129]
				70.0 ± 0.8 ms	E [97]
				59 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{3}$ P)3d $^{2}$ F $_{7 / 2}$	M2	16.0 ± 1.6 ms	E [95]
				14.8 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{1}$ D)3d $^{2}$ G $_{9 / 2}$	M1	17.8 ± 3.1 ms	E [132]
				15.3 ms	T [129]
				13.6 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{1}$ D)3d $^{2}$ G $_{7 / 2}$	M2	14.0 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{4}$ ( $^{1}$ D)3d $^{2}$ F $_{7 / 2}$	M1	4.6 ± 0.4 ms	E [95]
			M1	5 ms	T [131]
X	Cl	3s $^{2}$ 3p $^{3}$ 3d $^{2}$ $^{4}$ H $_{13 / 2}^{o}$	M1	31.5 ms	T [131]

2.4.7. S-like Fe XI

Corresponding to the ground configuration of Fe XIV, the levels 3s

^{2}

3p

^{4}

^{3}

P

_{1}

,

^{1}

D

_{2}

, and

^{1}

S

_{0}

seem most promising for measuring the

E 1

-forbidden decay rates. Lifetime measurements on P-like Fe ions have apparently only been done for the

^{1}

D

_{2}

level [118]. The uncertainty of a heavy-ion storage ring lifetime result amounts to about 1% (see Table 3). A result from a Kingdon ion trap [94] differs by 10% from the other measurement but agrees with later theory, albeit at a somewhat larger uncertainty. There are several predictions that scatter by only a few percent, while others deviate by more than 20% (see [118]). An interesting point is the appearance of strong cascades in the decay curve of the heavy-ion storage ring experiment. These are ascribed to long-lived 3s

^{2}

3p

^{3}

3d levels, one of which, with

J = 4

, is provided in Table 3. The longevity of this level arises from the limitation of its decay options to only a low-energy

M 1 / E 2

transition. Hence, this level does not directly decay to the 3s

^{2}

3p

^{4}

^{1}

D

_{2}

level in the decay curve, with a slow component noted in the experiment. At least one

E 1

(spin- and parity-changing) intercombination transition is also needed. This observed slow cascade is evidence for levels of high J values that have at long last been included in recent atomic structure computations [126], after early experimental and theoretical work apparently preferentially considered those levels that combine by

E 1

transitions with the ground configuration [133]. The ensuing under-recognition of the role of high-J levels has been discussed in [134], and the particular interest in high-J levels in [135].

The five levels of the ground configuration, 3s

^{2}

3p

^{4}

^{3}

P

_{2, 1, 0}

,

^{1}

D

_{2}

, and

^{1}

S

_{0}

, combine easily with the four displaced levels, 3s3p

^{5}

^{3, 1}

P

_{J}^{o}

, and with the lower-J singlet and triplet levels of the 3s

^{2}

3p

^{3}

3d configuration. However, this is not the full picture, as

E 1

intercombination transitions connect the triplet levels of the ground configuration with the quintet 3s

^{2}

3p

^{3}

3d

^{5}

D

^{o}

levels. Moreover,

E 1

-forbidden transitions, as within the ground configuration, matter here among the high-J levels of the 3s

^{2}

3p

^{3}

3d configuration. This is visualised in the level diagrams of [133]; however, the long-lived levels are most easily identified in the tables provided by Wang et al. [126], because there the level lifetimes are stated as well. This is a significant convenience for an exploratory experimenter. It immediately becomes clear that there is not just one level with a millisecond lifetime, but six. A few levels with lifetimes of many nanoseconds stand out from the majority of levels which feature lifetimes near a few nanoseconds. An experiment at a heavy-ion storage ring [95] has reported a very strong slow cascade to the decay of an already long-lived 3s

^{2}

3p

^{4}

^{1}

D

_{2}

level in the ground configuration. In multi-exponential data analysis this cascade was described by a single exponential, because fits with several (few) cascade components were not stable. The identity of the cascade level was taken from computation; however, there was insufficient theoretical information on whether a single cascade or the superposition of several slow cascades was to be expected. The computational results subsequently provided by Wang et al. [126] indicate that several levels out of a pool of long-lived high-J levels may have possibly contributed. Thus, on statistical grounds, the reported cascade lifetime with a 6% error bar [95] represents a superposition of several contributions, and should not be associated with a single level. This physico-mathematical detail may or may not be of any interest to astrophysics. Level populations depend on electron density, with different results for low density and high density. The transition between the two regimes is defined by the ratio of collision rates and radiative decay rates; within this transition range, certain line ratios have plasma diagnostic potential. For levels with millisecond lifetimes, the density range of interest would be that of the solar corona. Whether the 3s

^{2}

3p

^{3}

3d high-J levels may be of practical interest for diagnostics will have to be explored by spectrum simulations, which could additionally provide hints as to which spectral lines should be observed.

The 3s

^{2}

3p

^{3}

3d

^{5}

D

^{o}

term is an illustrative example. The four lower-J fine structure levels decay by

E 1

intercombination transition to the various triplet levels of the ground configuration. A superposition of the four level lifetimes can be recognised in the multi-exponential decay curves of a beam-foil spectroscopic lifetime measurement [127], in the analysis of which they were approximated by just two decay components. In a multi-exponential fit, the time constants of the components need to be at least a factor of three apart in order for an analysis to have an expectation of meaningfulness. In the Fe XI 3d

^{5}

D decay multiplet, theory [126] predicts components of 9 ns, 9.5 ns, and 14.7 ns, which are too closely spaced to be resolved in the analysis. Positioning the detector at different wavelengths inside the line blend may modify the individual contribution to the observed signal; however, this does not resolve the mathematical superposition problem of exponentials being too close to each other in the lifetime, a problem that persists even with data of high statistical reliability. In this experiment, the spectral lines were only partly resolved and were recorded with rather limited statistical significance. However, the identification of these lines in delayed beam-foil spectra with quintet level intercombination decays has been corroborated by finding matching lines in the EUV spectrum of the solar corona [115]. It would be interesting to find the

M 1

decay of the fifth quintet level,

^{5}

D

_{4}^{o}

, to the

J = 3

level of the same term, either as a long-wavelength (actually infrared, as a wavelength of λ ≈ 12

μ

m can be calculated from [126]) spectral line or by way of a decay curve measurement on one of the subsequent levels of the decay chain. The predicted lifetime of that level, 27.9 ms [126], is far too long to be observed in a beam-foil geometry, though it would be measurable in an ion trap. The same problems pertain to measuring the lifetimes of the other 3s

^{2}

3p

^{4}

3d levels; if the levels decay to the ground configuration, the level lifetimes will be on the order of nanoseconds, while for those levels of high J that cannot decay to the ground configuration, the level lifetimes are in the millisecond range. However, the wavelength predictions for the

M 1

and

E 2

decays are for much longer wavelengths, and they are much more uncertain.

2.4.8. Cl-like Fe X

In the Cl-like ion Fe

^{9 +}

(spectrum Fe X), we find the same groups of levels of distinct lifetime ranges as in Fe XI. There is a fine structure transition in the ground term,

E 1

transitions to the ground term from levels with lifetimes shorter than a nanosecond, intercombination transitions from levels with lifetimes of many nanoseconds, and high-J levels with millisecond lifetimes. The

M 1

transition in the 3s

^{2}

3p

^{5}

^{2}

P

^{o}

ground term gives rise to a prominent red solar corona line. Measurements using electrostatic ion traps or electron beam ion traps have established a level lifetime [11,94,128,132] (see Table 3) close to the dominant majority of theoretical predictions, with a few exceptions (see [11]) that grossly deviate from what basic considerations permit us to estimate. The lifetime measurement may safely be considered as accurate, as the vast majority of cascades are much shorter-lived, allowing the measured decay curve to be well approximated by a single exponential.

The first excited level, 3s3p

^{6}

^{2}

S

_{1 / 2}

, appears to pose a minor problem for theory. There are only two

E 1

decay branches to the ground term, and the branching ratio ought to be well calculable from the statistical weights (2

J + 1

) of the final levels with a correction for the wavelength ratio. The two EUV lines are easily excited (the lowest excitations in Fe X beyond the ground term fine structure), and as such are good indicators of the presence of this ionisation stage in an astrophysical plasma. Nevertheless, the theoretical predictions of the line ratio span a band of about 10% width. A beam-foil measurement [130] has found agreement with prediction based on the

ν^{3}

law and assuming pure

L S

coupling. The beam-foil lifetime measurement [130] (with an uncertainty of about 7%) happens to coincide with the centre of the distribution of predictions, which remarkably span a bandwidth of a factor of two (for theoretical approaches and further references, see [136,137]). The beam-foil decay curves reveal that the displaced term is less affected than regular levels by cascade repopulation from other regular levels; thus, the cascade problem is considered a minor nuisance here. While the averaging of various lifetime predictions may yield a more valid predictive pointer than the individual results, that does not have the same merit as an intrinsic quality assessment of atomic structure such as computations might offer.

There are many 3s

^{2}

3p

^{4}

3d levels with

E 1

decays to the ground term. I am not aware of any systematic attempt at measuring the upper level lifetimes of the short-lived levels of Fe X. However, there are many long-lived levels, especially (

^{3}

P)

^{4}

D

_{1 / 2, 3 / 2, 5 / 2}

, with calculated lifetimes in the range of 100 to 612 ns [138]. While these particular lifetimes are too long for practical beam-foil measurements, there should be many level lifetimes in the accessible range as well. An experiment [127] was undertaken as a first step to check on these. However, the spectra of Fe X of Fe XI (and other Fe spectra) in the EUV wavelength range of interest were (and still are) not well known, and must suffer from many line blends, in particular because of the relatively wide spectrometer slits that are needed in order to collect a sufficient signal in delayed beam-foil spectra. The aforementioned experiment returned a dozen lifetime values, a number of which were close to expectations for specific levels, though most of them cannot be considered as actually measuring specific level lifetimes as long as the spectroscopic analysis has not sufficiently progressed. For this reason, only a few of these results are included in Table 3. In general, the beam-foil experiment confirms a number of assumptions, although the details remain incomplete. This corresponds to atomic structure (and lifetime) computations that have improved over the decades [129,131,138,139], but at a present energy reliability (on the order of 1%, and in certain cases 0.1%) they offer wavelength windows that usually coincide with a fair number of observed lines (with wavelengths not yet calibrated accurately) that remain to be identified.

As in the case of Fe XI discussed above, Fe X features a number of 3d levels of high total angular momentum quantum number J that cannot decay to the ground term by

E 1

transition, and as such have millisecond lifetimes rather than the nanosecond lifetimes of levels with

E 1

decay channels. The computations by Ishikawa et al. [129] consider decay multipole orders up to

M 2

and

E 3

. Both these tabulations and those by Wang et al. [131] helpfully provide listings with lifetimes. In Fe XI, the 3d levels increase in energy with increasing J, whereas in Fe X the sequence is inverted. This means that in Fe XI the highest-J level can decay by

M 1

transition to the next-lowest J level (and eventually to a level with an

E 1

intercombination decay channel), whereas in Fe X the lowest fine structure levels of a term are those of highest J value, and as such cannot decay by

M 1

transition (in the IR spectral range) to a level with lower J. The usual selection rules suggest

M 2

intercombination transitions (in the EUV) to the ground term instead. Incidentally, the computed level lifetimes [131] fall into the same multi-millisecond time range in both cases. Out of seven such long-lived Fe X 3d levels, lifetime values have been obtained experimentally (at a Kingdon trap and at a heavy-ion storage ring) for five, in most cases with moderately good agreement with theory [131]. A peculiar case emerges from the calculations of a 3d

^{2}

^{4}

H

^{o}

level with a very high total angular momentum,

J = 13 / 2

. This level has not yet been studied by experiments.

Atomic structure computations of highly charged ions usually assume that the ion resides in a field-free environment. Thus, the central Coulomb field would be spherically symmetric. This spatial symmetry is essential, and selection rules such as “

J = 0 - 0

is strictly forbidden” arise. However, external magnetic fields can spoil such symmetries; see the Livermore EBIT lifetime measurements on Fe XVII discussed above. A collaboration of researchers from Lund and Shanghai has searched for more such cases of magnetically-induced transitions (MITs) of possible interest in astrophysics and has recently reported success, finding a line ratio in Fe X (3d

^{4}

D

_{7 / 2, 5 / 2}

decays) that is susceptible to magnetic fields as strong as those that occur in the solar corona [140].

2.4.9. Ar-like Fe IX

The Ar-like spectrum Fe IX has long found considerable interest in astrophysics due to the occurrence of long level lifetimes [141,142]. Storey and Zeippen [143] claimed a high value of certain Fe IX lines in density diagnostics. A very recent study has marked a significant stepping stone in the process [144] towards calibrating this tool. Yet, while on the one hand the spectrum is fairly well known, on the other it has not yet been completely established [145].

The theoretical lifetime entries for Fe IX in Table 4 may lie systematically on the high side, as Del Zanna et al. [18] provide transition rates for only a selection of the brightest lines, where a meaningful lifetime prediction would require a complete set of all decay channels. This example underlines why a lifetime table extracted at source (i.e., from such a computation) would be rather helpful. Nevertheless, there is useful material to discuss.

In most spectra,

E 1

transitions to the ground state dominate; in Ar-like ions there are three such

E 1

resonance transitions, corresponding to the decays of the 3s

^{2}

3p

^{5}

3d

^{1}

P

_{1}^{o}

,

^{3}

D

_{1}^{o}

, and

^{3}

P

_{1}^{o}

levels to the 3p

^{6}

^{1}

S

_{0}

ground level. In Fe IX, the three levels have predicted lifetimes [18] of about 4 ps, 4 ns, and 70 ns, respectively. Two of these lines have been seen in the Bochum beam-foil spectra [130], but not the third. This non-observation is likely due to the long level lifetime. I have not found any beam-foil lifetime measurement on these lines, although the 4-ns lifetime should have been practically measurable. All three lines have been seen in the solar corona, and the longest-lived level of these three is of interest as the short-lived level in the level pair useful for electron density diagnostics at coronal (low) density. The 3s

^{2}

3p

^{5}

3d

^{3}

P

_{1}^{o}

level belongs to the

^{3}

P

^{o}

term, which also comprises a

J = 0

level (strictly forbidden to decay by one-photon transition to the

J = 0

ground state) and a

J = 2

level. The latter can (dominantly) decay by

M 2

transition to the ground state (and by a minor

M 1

branch to the

J = 1

level); the predicted level lifetime is about 11 ms [18]. The ratio of the two transition rates of lines 0–1 and 0–2 is roughly six million, yet the astrophysically observed line ratio is on the order of 1 to 10. This gross deviation from what would be expected under conventional laboratory conditions is explained by the roles of collisional excitation rate and radiative decay rate in the level population. Only at a very low density does the

J = 2

level have a chance to decay radiatively instead of being quenched by collisions, while the high radiative decay rate of the

J = 1

level cannot produce a brighter line than the occasional collisional excitation of the same level provides in terms of population. This line pair was observed in the solar corona decades ago; however, observation in a laboratory requires the excellent vacuum of an electron beam ion trap, and such an experiment succeeded only very recently [144]. The lines of interest have appeared in the spectra obtained at another electron beam ion trap [140], but were not discussed.

In the multitude of Fe IX 3d levels, there are several more

J = 2

levels that may decay by

M 2

transition to the ground state as well as levels of higher J that decay to other 3d levels by

M 1

transition. Several of these transitions have wavelengths in the visible spectral range, and are accessible to measurements by the heavy-ion storage ring TSR [102]. Meanwhile, theory [18] provides a few results for the lifetimes studied. Table 4 shows that theory and measurement agree within a factor of two or better, which is much poorer than the experimental uncertainty. However, more experiments are needed to ascertain whether only the envisaged transitions have contributed to the observed decay curves. For the planning and interpretation of such experiments, it would be helpful to have a more complete set of theoretical predictions on transition rates and level lifetimes. Because a complete set of transition rates may be cumbersome to tabulate and handle, a set of level lifetimes might at least help to estimate the branch fraction of the decay for which the rate is given.

2.4.10. K-like Fe VIII

Various Li- and Na-like ions have been studied computationally and experimentally for the rates of the resonance and other important transitions. The coverage is poorer for the heavier alkali-like ions such as the K-like ion sequence. A venerable Coulomb approximation computation [152] ends short of reaching Fe VIII. However, this tabulation addresses only hydrogenic levels from the 4s level and upwards. Astrophysically more interesting are the

n = 3

valence shell excitations. These can be found, for example, in the NIST ASD online database [37], which offers one search form for levels and and another for lines; the latter includes transition rates for some of the transitions, from which it is possible to assemble decay patterns and possibly a total decay rate, which is the inverse of the level lifetime. In addition, there are links to the underlying publications (51 publications on transition rates in K-like Fe VIII according to a recent search, including impressive compilations such as [35,36]). The interesting point for present purposes is that all of the publications in this case appear to be based on theory/computation, and none on lifetime measurements. Moreover, the compilations are based on individual studies by various authors, comparing

L S

-coupling (non-relativistic) computations with others in intermediate coupling (introducing relativistic effects) and finding partial agreement and partial serious disagreement. Such computations of the 1960s to 1980s are not wrong or outdated, per se, but the reader has to be aware that while “theory” has not fundamentally changed in the interim, certain atomic systems are deserving of a relativistic treatment. The computing effort required by relativistic wave functions is much larger than in most non-relativistic approaches, and unfortunately the accuracy of the results is not guaranteed by either.

Biémont and Hansen [146] have studied ions with a K-like 3p

^{6}

3d ground configuration theoretically, revealing that there is an

E 1

-forbidden

M 1 / E 2

transition in the 3d

^{2}

D ground term and that this transition lies in the infrared. As such, it is beyond the scope of such helpful reference tabulations as Kaufman and Sugar [34] have provided on forbidden lines, and has a level lifetime of many seconds. This combination of a multi-second lifetime (requiring an ion trap for measurement) and an infrared transition wavelength (thus far out of experimental reach for single-photon low-noise detectors) explains why there is no experimental lifetime result. There are, of course, many

E 1

-allowed transitions in Fe VIII; however, their typical lifetimes are in the sub-nanosecond range. While this should be accessible by beam-foil spectroscopy in the EUV, at the time when beam-foil spectroscopy was being used to address Fe ions in low- to medium-charge states (in the late 1970s/early 1980s), multi-channel photo-electric EUV detectors were rare, and the many multiplets that would have to be spectrally resolved were too challenging. Consequently, the Fe VIII spectrum has apparently not been studied in time-resolving experiments. Thus, Table 4 is meagre as far as this spectrum is concerned.

2.4.11. Ca-like Fe VII, Sc-like Fe VI, Ti-like Fe V, V-like Fe IV, and Cr-like Fe III

The Fe VII 3d

^{2}

^{1}

S

_{0}

level decays by

M 1

or

E 2

transition to the

^{1}

D

_{2}

,

^{3}

P

_{1, 2}

and

^{3}

F

_{2}

levels of the same configuration. The transition wavelengths lie in the UV/VUV; thus, a decay curve of this level could be obtained using a photomultiplier at a heavy-ion storage ring [102]. The single experimental lifetime result with its 6% uncertainty agrees reasonably well with theory as cited in [36]. This measurement marks the lower end of the medium-charge state Fe ion range studied for atomic lifetimes that are dominated by

E 1

-forbidden decays in experiments that used conventional ion traps, a heavy-ion storage ring, or an electron beam ion trap. While there is no technical limit that determines this range, the impracticality of such experiments means that forbidden lines with IR wavelengths must wait for suitable detectors, while ion traps suitable for second-range lifetime measurements need to obtain an extremely high vacuum. Cryogenic heavy-ion storage rings, such as operated at Stockholm (DESIREE) and Heidelberg (CSR), may eventually offer suitable venues.

Much more practical in these relatively low-charge Fe ions are measurements on

E 1

transitions, which in these spectra are mostly 3d-4p transitions. Dumont et al. [148] have measured lifetimes in Fe V and Fe VI using the beam-foil technique, and Jacques et al. [147] have done the same for levels in Fe IV to Fe VII. The obtained lifetimes are in the range from 150 ps to 1.5 ns. While the latter work [147] quotes lower uncertainties (5 to 30%) than the former [148], there is general agreement between the results of both studies. However, there are various unresolved line multiplets (unsurprising with the VUV and EUV spectroscopic equipment of the time), and at least one case of conflict. One Fe V lifetime measurement of a threefold blend (in the same transition array) is reported with about 7% uncertainty, yet the results differ between the laboratories by a factor of 1.7; moreover, Dumont et al. refer to theory work by Abbott [153], who used the well-established (which is not the same as “proven to yield accurate results”) Superstructure code. Their experimental lifetime results exceed the computational prediction by factors from 1.4 to 2. This ties in with the systematic deviation noted above for ions with more than two electrons in the

n = 3

shell, which may relate to the complexity of the atomic structure, with its many cascade contributions of a rather similar lifetime feeding the levels of interest and thereby overburdening multi-exponential decay curve analysis.

For these reasons, I have elected to list only a few examples of levels and lifetimes in these Fe spectra in Table 4. Experimental data are available from laboratories on two continents (Liège and Québec), largely corroborating each other, with valuable statistical significance; however, I find it likely that the measurement situation, that is, excitation in a high-density environment, cannot be appropriately resolved by the analysis technique. Astrophysical light sources are usually of much lower electron density, and feature a very different excitation environment. Hence, theory might be a better guide in the case of these Fe ions than beam-foil experiments. However, intrinsic quality assurance of transition rate computations is very rare, and the results from theory are known to sometimes scatter greatly.

Fe III and Fe II are of high interest in astrophysics (see below), as has very recently been discussed by expert practitioners of spectral modeling and emission line analysis [154]. I agree with the uncertainty assessment of transition rate and level lifetime prediction, which is discussed there with many more examples than would be appropriate in the present text. Fe III has several thousand line entries in the NIST ASD database, yet there are very few results for atomic lifetime measurements. A second look at the database suggests why the richness in lines has not initiated a similar number of decay rate measurements. There are many

M 1

transitions in the 3d

^{6}

ground configuration, with wavelengths from 205 nm to at least 7.8

μ

m. The transition rates [36] seem to be below 1 s

^{- 1}

, and consequently the associated level lifetimes mostly lie well above 1 s. Ion traps are advisable for lifetime measurements on these levels; however, I have not yet found any on Fe III. In addition, there are 3d

^{5}

4s levels, which need

E 2

transitions in order to decay to the ground configuration. Such

E 2

transitions 3d

^{6}

–3d

^{5}

4s, with wavelengths from 87 nm up to 250 nm, are listed in the NIST ASD database [37]; again, however, the typical level lifetimes should be in the range of many seconds. The lowest levels with much shorter lifetimes are 3d

^{5}

4p levels, which decay to 3d

^{5}

4s levels. These are ordinary

E 1

transitions, and their level lifetimes are expected to be in the range of a few nanoseconds [36]. Dolby et al. [149] have produced Fe II and Fe III spectra in beam-foil geometry, reporting a single lifetime of 2.26 ± 0.5 ns that supposedly belongs to an unresolved level multiplet.

2.4.12. Mn-like Fe II

The same experiment by Dolby et al. [149] reported three lifetimes of spectral features in Fe II, with stated uncertainties of 4%, 9%, and about 20%, respectively. The authors mention their poor spectral resolution in a crowded spectrum as well as a statistically poor signal. Considering the complexity of the Fe II spectrum this experiment represents a daring attempt, and the results are not suitable for use as benchmarks. Thus, the calculations of

E 1

transition rates in Fe

^{+}

ions (see [35,36,155] and references therein) have been tested on only a very few examples, and without much discrimination. Singly charged ions are abundant in many astrophysical plasmas, and it would be unfortunate if these few measurements were all that could be obtained on Fe II. Indeed, the excitation of levels that can decay by

E 1

transition requires higher energies than those of the many ground configuration levels. Outside of stars, the typical temperatures of the interstellar medium are low, and the ground configuration levels may be all that can be notably excited. Because transitions within a given electron configuration are

E 1

-forbidden, the levels are called metastable and require specific techniques to measure their many-second lifetimes [156]. As Sveneric Johansson and his group at Lund have spent decades on analysing the Fe II spectrum, it is fitting that another Swedish group, that around Henrik Hartman at Stockholm, has tended to the measurement of long level lifetimes in singly charged ions, including Fe II [150,151] (see Table 4).

The fact that the metastable levels of interest (with

M 1

and

E 2

decay channels) are much longer lived than the regular levels (with

E 1

decay channels) after whatever excitation is promising in terms of decay curve systematics (as cascades will die out sooner than the principal level), though it carries its own problems. For example, the excited ions have to be stored in order to monitor their decay behaviour, while the collisional losses (recombination of ions) occur on time scales commensurate with the radiative decay. Moreover, it is problematic to achieve selective population of the level of interest; if laser excitation were to be used, the laser(s) would have to match mostly UV/VUV transitions, which is challenging. The Stockholm group has found a specific approach that economises on the laser through a scheme that, rather than addressing the ground level and excitation, starts with the smaller energy step from an excited metastable level in the ground configuration to a low-lying level, which then decays rapidly by UV/VUV photon emission. To make this scheme practical, a number of steps have to be taken. The ions are produced and excited collisionally in a gas discharge, extracted as a beam of about 40 keV kinetic energy, mass-separated in a magnetic field (to ensure that a specific isotope survives), and fed into an ion storage ring of about 50 m circumference (in this case, the Cryring cryogenic storage ring). While the spontaneous radiative decay of any stored ion may happen anywhere along the circumference, the aperture of a typical photodetector makes up only about 1/1000th of the circumference. In order to boost the signal-to-noise ratio, the ions have to be “convinced” to radiate only in front of the detector. This can be effected by superimposing the beam of the (collinear) probing laser and the circulating ion beam at the location of the detector. When the laser is on resonance, the ions in the stored beam all pass within a fraction of a millisecond through the probing zone and cause a signal burst. Then, the ion beam is dumped and the storage ring is refilled. The signal observed is proportional to the number of ions in the original metastable level until the time of the laser pulse. With many such laser probing exercises, the level population can be monitored as a function of time after excitation and a decay curve can be constructed on a point by point basis.

The Stockholm authors note that their lifetime results largely agree with theoretical predictions, but that for weak decay branches there are significant deviations among predictions. In addition, there are just four lifetime results for many dozens of levels in the ground configuration alone. Many of these levels are mixed with others, which causes uncertainties in the theoretical description. This is important for the prediction of branching fractions, which are of interest in astrophysical studies. The Stockholm Fe II lifetimes are quoted with uncertainties from 3% to about 14%, which is the same order of magnitude as the assessed prediction uncertainty in the study by Mendoza et al. [154] mentioned above. A major uncertainty, in particular for very long lifetimes, is the correction for ion loss during storage in the ring. Their group has measured atomic lifetimes up to about 30 s on other atomic systems. It would be interesting to reach even farther, which would require further improvements to an already highly developed vacuum system. However, the Stockholm heavy-ion storage ring has been dismantled and moved to GSI Darmstadt (Germany) for a second operational life under the name of CRYRING@ESR [157]. Whether this will include astrophysical activities on Fe ions, and on which charge state ions, remains to be seen.

3. Discussion

Atomic level lifetimes play a secondary role in astrophysical observations, as most macroscopic matter time scales are very long compared to most atomic processes. One might expect some influence of atomic lifetimes on the details of transient events, such as the aftermath of supernovae. The actual importance lies much less in the transient time scale than in the steady-state balances, which depend more on atomic lifetimes (in comparison to competing reaction rates, which generally depend on density). Thus, astrophysical observations usually do not pertain to atomic processes in real time, but instead to the situation reached after complex interactions between many processes have taken place. Clearly, then, the description of the resulting situation is not a function of a single parameter, and needs to be understood via simulations that incorporate many parameters, including atomic decay rates. Such simulation is a theoretical enterprise, and for most atomic parameters only theory (i.e., computation) can provide sufficient data. The purpose of atomic lifetime measurements is to check theory wherever basic assumptions and atomic data can be checked. A very limited (but interesting) example is a spectral XUV line of Fe (

λ

1.762 nm) that appears surprisingly bright in solar spectra. In order to explain this observation, the spectrum has been modelled [73] in terms of the decay modes (possibly involving two electrons), affecting the effective level lifetime, which relates to the level population. While no lifetime measurement has been performed in this case yet, it should be interesting if it ever becomes feasible.

Concerning atomic lifetimes in Fe ions, the task of experimental work ranges from femtoseconds to many seconds. In principle, the goal is “simply” to selectively excite a specific atomic level and then monitor its natural decay. However, there is no single technique to provide a single ion of each charge state in isolation without any detrimental interaction, no single method to selectively excite the ion, nor any single detection and time measurement technique. Lasers may selectively excite levels in an atom, but the photon energy and small bandwidth needed to reach an arbitrary level in an ion are rarely available, and this is even less for a multiply charged one. A combination of several techniques is usually required, and the excitation is not selective. If several levels are excited simultaneously, problems arise with level mixing and multi-exponential decay curves. While the true number of exponential decay components may be high, analyses are practical for only a few components at a time, and each may represent several decay components of the true sample.

In addition, the quality of data analysis suffers from detector noise and signal background. It is usually instructive when authors show sample decay curves, as these allow the reader to form ideas about the limiting contributions. Sadly, I have seen decay curves presented in papers in prominent research journals without any indication of the background level, for which the atomic lifetime results were stated with few-percent error margins and “in agreement with theory”—a comforting but fallacious argument. On purpose, I have not marked such work (which is included, for example, in Table 2), because other data and analysis may similarly be less accurate than presently thought, possibly for less obvious reasons. For example, I have discussed decay curves (from beam-foil or heavy-ion storage ring experiments) that could be practically described by two exponentials, with later progress in theory/computation suggesting that groups of decay components with rather similar lifetimes must have been present (more than a multi-exponential analysis could have separated reliably). Thus, while the published error bars were statistically justified, they should be seen only as results of an approximation of a considerably more complex situation. This general problem has been discussed for decades, at least since Bennett and Kindlmann [158] recognised that near-threshold excitation may be a way towards selective excitation (at the cost of poor signal but with the benefit of cleaner data). In addition to the reviews and data mentioned above, discussions of ion lifetime data and their accuracies may be found, for example, in [159,160,161,162,163].

The decay curves most easily evaluated seem to be single-exponential. If not truly the result of selective excitation of a single level, the curves may appear to be if they result from a long-lived level, such as the 2p level in a Li-like ion. After the interaction of a fast ion beam with a foil target, that level may possibly be fed by a number of more short-lived cascades, mainly from yrast levels (of maximum quantum number ℓ for a given principal quantum number n), which leads to a flattening of the principal decay curve as long as the cascades matter. For low values of n the yrast levels are short-lived, however, for high n, their lifetimes progress towards long values. Thus, at late times a weak slow cascade may bend the primary decay curve slightly upwards while remaining in decrease overall. Nonetheless, a single exponential may represent a suitable approximation without a significant systematic error of the extracted 2p level lifetime result. It pays to follow a decay over as many level lifetimes as possible until the background level is reached. A heavy-ion storage ring measurement on C III [62] has reached an uncertainty of better than 0.2% simply by recording decay curves over a dynamic range of larger than three orders of magnitude, or about six lifetimes, before the decay curve reached the (very low) detector noise level. In this case, the principal level had a level lifetime near 10 ms, while cascades would show lifetime components on the order of nanoseconds, which would have been exhausted long before the actual measurement zone was reached. Under such conditions, theory can truly be tested by measurement. It is no chance coincidence that the most accurate lifetime measurements on Fe ions, those on the

M 1

transition in the ground term of Fe XIV, deal with a similar level lifetime, which falls into the optimum range for such work [55]. In these latter experiments, cascades were largely avoided, because the experiments [96,98] employed an electron beam ion trap with its very low electron density (

n_{e} \approx 10^{11}

cm

^{- 3}

). Under such conditions, most of the level population is in the ground state. However, it may be instructive to vary the density in the device in a study of systematic error sources.

Decades ago, an eminent theorist (after a talk of mine) derided beam-foil spectroscopy as a wasted effort because of its limited success at reaching high precision in lifetime measurements. While his idea of pursuing only the path towards the most significant results is certainly sensible, a key point was missed: experiment deals with atomic systems as found; thus, the same basic techniques have struggled in many measurement situations while succeeding in others. The most precise and possibly most accurate lifetime measurements discussed here did not result from a unique technical development; instead, what was decisive were circumstances having to do with natural atomic structure that permitted such excellent data to be obtained. There is a corresponding story for atomic structure theory. Almost 50 years ago, Harry Nussbaumer regularly produced calculation results that have usually withstood the test of time, although his computational resources were rather limited. Colleagues admired him for “picking the right wave functions”.

Is there a foreseeable chance of future improvements of lifetime determinations by theory or experiment on Fe ions? Concerning computations, a problem lies in the radial wave functions that govern the transition moments, which are not orthogonal and seem to not obey known optimisation rules. Thus, while improvement may eventually be achievable by obtaining even more computing power, or by new conceptual approaches, the essential first step should be an intrinsic quality assessment of the atomic structure computations in order to ensure that any improvement is quantifiable. On the experimental side, the problem is quite different. Atomic lifetime measurements depend on clocks, which can be highly accurate and can determine practically any time interval extremely well. The pervasive problem is that exponential functions are so similar to each other in shape that even with extremely good counting statistics one cannot state with certainty whether a single or a sum of many exponentials is best for interpreting a data sample. Corollary information on the level excitation is essential, and in most cases will discourage the pursuit of higher accuracy. Selective excitation is key, whether by (laser) photons or by patience (letting all shorter-lived levels die out). Thus far, laser excitation from the ground or metastable levels has been limited to a few levels in neutral atoms or singly charged ions. Patience translates into ion trap measurements for some higher charge states and for extremely long-lived levels in low-charge ions, which is clearly a task for laboratory astrophysics.

4. Conclusions

The Fe ion level lifetime data reviewed here have been gathered over more than four decades. The experimental techniques and tools used comprise beam-foil spectroscopy for lifetimes shorter than about 100 ns and electrostatic ion traps, electron beam ion traps, and heavy-ion storage rings for lifetimes in the range from (roughly) milliseconds to seconds. For multiply charged ions, there are no tools available yet that might effect selective excitation of a level of interest, a process that is essential for achieving highly accurate lifetime measurements. In the absence of such achievement, the few cases in which the relatively long lifetime of a level of interest (compared to other levels that might feed this level via cascades) stands out by orders of magnitude come closest to the wished-for situation, and permit lifetime measurements to better than 1%. One might be tempted to say that in these cases theory can be tested once and for all by comparison with the outcome of measurements. Indeed, most calculations are corroborated at this level; however, “theory” does not always yield reliable ab initio calculations, and surprisingly large deviations among the lifetime predictions can occur. While the deviations are usually much smaller among computations that are scaled to other experimental data, such fudging produces results that, while potentially useful, do not have the real predictive power often claimed for theory.

A major problem in atomic lifetime measurements is the occurrence of cascade re-population, which distorts the decay curves of the levels of interest away from a single exponential to a superposition of components. While the complexity of such decay curves is easily modelled, the process cannot be reliably inverted and the component of interest cannot be extracted from the fray. In rare cases, the (statistical and analytical) uncertainty of the lifetime result may be as small as a few percent. This mostly applies to a few low-lying levels in few-electron ions (He-, Li-, Be-, Na-, and Mg-like); it helps that such systems are often studied in several ions along an isoelectronic sequence, meaning that the extended sample permits systematic studies of the data evaluation procedure. I see it more as a matter of longevity (low decay rate), rather than multipole order, that

M 1

decays in He-, B-, and Al-like ions in various ions have been measured with high accuracy (among the Fe ions, only Al-like Fe XIV has been measured with notable precision). Although such

E 1

-forbidden decays may be seen as rather easily calculated, certain computations have nevertheless deviated grossly both from the majority of others and from experiment. This experience reminds us of the need for skepticism even when encountering results from well-reputed theory/theorists.

For probably the majority of atomic systems with more than two electrons in the valence shell, the decay pattern usually so is complex that lifetime values extracted by multi-exponential analysis may exceed the true values by 30 to 200%. In most of these cases, the shape of the measured decay curves can easily be reproduced by simulated decay curves. Unfortunately, such an exercise demonstrates just as easily that even with near-perfect data statistics the level lifetime of interest cannot always be recovered from either the simulated curve or from the real data. Of course, as astrophysics mostly deals with low-density environments, the cascade situation is expected to matter much less in this context, although this implies that there is hardly any way to perform lifetime measurements in situ. The analysis of astrophysical plasmas relies on modelling and simulation using a wealth of atomic data, including level lifetimes, and some of these assumptions can and should be be tested in the laboratory.

Funding

This research received no external funding.

Data Availability Statement

All the data presented are from the open literature cited.

Acknowledgments

Decades ago, Indrek Martinson (Lund) linked the Bochum beam-foil data to solar corona spectra, and Christer Jupén (Lund) has been very helpful in the exploration of intercombination transitions in S- and Cl-like ions by running Cowan code computations. In hindsight, these were keys to much of my later beam-foil work.

Conflicts of Interest

The author declares no conflict of interest.

References

Grotrian, W. Zur Frage der Deutung der Linien im Spektrum der Sonnenkorona. Naturwissenschaften 1939, 27, 214. [Google Scholar] [CrossRef]
Edlén, B. Die Deutung der Emissionslinien im Spektrum der Sonnenkorona. Z. Astrophys. 1943, 22, 30–64. [Google Scholar]
Fawcett, B.C.; Gabriel, A.H.; Griffin, W.G.; Jones, B.B.; Wilson, R. Observations of the Zeta spectrum in the wave-length range 16 Å–400 Å. Nature 1963, 200, 1303–1304. [Google Scholar] [CrossRef]
Fawcett, B.C.; Gabriel, A.H. New spectra of the iron transition elements of astrophysical interest. Astrophys. J. 1965, 141, 343–355. [Google Scholar] [CrossRef]
Gabriel, A.H.; Fawcett, B.C.; Jordan, C. Classification of iron lines in the spectrum of the Sun and Zeta in the range 167 Å to 220 Å. Nature 1965, 206, 390–392. [Google Scholar] [CrossRef]
Gabriel, A.H.; Fawcett, B.C. Identification of the solar spectrum in the region 60-170 Å. Nature 1965, 206, 808–809. [Google Scholar] [CrossRef]
Doschek, G.A. The solar flare plasma: Observation and interpretation. Space Sci. Rev. 1972, 13, 765–821. [Google Scholar] [CrossRef]
Edlén, B.; Tyrén, F. Atomic energy states of an unusual type. Nature 1939, 143, 940–941. [Google Scholar] [CrossRef]
Smith, R.K.; Brickhouse, N.S.; Liedahl, D.A.; Raymond, J.C. Collisional plasma models with APEC/APED: Emission-line diagnostics of hydrogen-like and helium-like ions. Astrophys. J. Lett. 2001, 556, L91. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Beiersdorfer, P. Laboratory data on the EUV/soft-X-ray flux problem of Fe XVIII and Fe XIX. Astrophys. J. 2021, 913, 20. [Google Scholar] [CrossRef]
Träbert, E. On the transition rates of the Fe X and Fe XIV coronal lines. Astron Astrophys. 2004, 415, L39–L42. [Google Scholar] [CrossRef]
Dere, K.P.; Landi, E.; Mason, H.E.; Monsignori Fossi, B.C.; Young, P.R. CHIANTI—An atomic database for emission lines. Astrophys. J. 1997, 125, 149–173. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E.; Mason, H.E. CHIANTI—An atomic database for emission lines. Version 8. Astron. Astrophys. 2015, 582, 56. [Google Scholar] [CrossRef]
Del Zanna, G.; Young, P.R. Atomic data for plasma spectroscopy: The CHIANTI database, improvements and challenges. Atoms 2020, 8, 46. [Google Scholar] [CrossRef]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe VII and other cool lines observed by Hinode EIS. Astron. Astrophys. 2009, 508, 501–511. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Mason, H.E.; Storey, P.J.; Young, P.R. Benchmarking atomic data for astrophysics: Fe VIII. Astron. Astrophys. 2009, 508, 501–511. [Google Scholar] [CrossRef] [Green Version]
O’Dwyer, B.; Del Zanna, G.; Badnell, N.R.; Mason, H.E.; Storey, P.J. Atomic data for the X-ray lines of Fe VIII and Fe IX. Astron. Astrophys. 2012, 537, 22. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Storey, P.J.; Badnell, N.R.; Mason, H.E. Atomic data for astrophysics: Fe IX. Astron. Astrophys. 2014, 565, A77. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Berrington, K.A.; Mason, H.E. Benchmarking atomic data for astrophysics: Fe X. Astron. Astrophys. 2004, 422, 731–749. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Storey, P.J.; Badnell, N.R.; Mason, H.E. Atomic data for astrophysics: Fe X soft X-ray lines. Astron. Astrophys. 2012, 541, 90. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XI. Astron. Astrophys. 2010, 514, 41. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Storey, P.J. Atomic data for astrophysics: Fe XI soft X-ray lines. Astron. Astrophys. 2013, 549, 42. [Google Scholar] [CrossRef]
Del Zanna, G.; Mason, H.E. Benchmarking atomic data for astrophysics: Fe XII. Astron. Astrophys. 2005, 433, 731–744. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Storey, P.J.; Badnell, N.R.; Mason, H.E. Atomic data for astrophysics: Fe XII soft X-ray lines. Astron. Astrophys. 2012, 533, 139. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XIII EUV lines. Astron. Astrophys. 2011, 533, 12. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Storey, P.J. Atomic data for astrophysics: Fe XIII soft X-ray lines. Astron. Astrophys. 2012, 543, 144. [Google Scholar] [CrossRef] [Green Version]
Storey, P.J.; Mason, H.E.; Young, P.R. Atomic data from the IRON project XL. Electron impact excitation of the Fe XIV EUV transitions. Astron. Astrophys. Suppl. Ser. 2000, 141, 283–296. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XVII X-ray lines. Astron. Astrophys. 2011, 536, 59. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XVIII. Astron. Astrophys. 2006, 459, 307–316. [Google Scholar] [CrossRef] [Green Version]
Del Zanna, G.; Chidichimo, M.C.; Mason, H.E. Benchmarking atomic data for astrophysics: Fe XXIII. Astron. Astrophys. 2005, 432, 1137–1150. [Google Scholar] [CrossRef]
Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XXIV. Astron. Astrophys. 2006, 447, 761–768. [Google Scholar] [CrossRef] [Green Version]
Czyzak, S.J.; Krueger, T.K. Forbidden transition probabilities for some P, S, Cl, and A ions. Mon. Not. R. Astron. Soc. 1963, 126, 177–194. [Google Scholar] [CrossRef] [Green Version]
Czyzak, S.J.; Keyes, C.D.; Aller, L.H. Atomic structure calculations and nebular diagnostics. Astroph. J. Suppl. 1986, 61, 159–175. [Google Scholar] [CrossRef]
Kaufman, V.; Sugar, J. Forbidden lines in ns²np^k ground configurations and nsnp excited configurations of beryllium through molybdenum atoms and ions. J. Phys. Chem. Ref. Data 1986, 15, 321–426. [Google Scholar] [CrossRef]
Fuhr, J.R.; Martin, G.A.; Wiese, W.L.; Younger, S.M. Atomic transition probabilities for iron, cobalt, and nickel (A critical data compilation of allowed lines). J. Phys. Chem. Ref. Data 1981, 10, 305–565. [Google Scholar] [CrossRef]
Fuhr, J.R.; Martin, G.A.; Wiese, W.L. Atomic transition probabilities. Iron through nickel. J. Phys. Chem. Ref. Data 1988, 17 (Suppl. 4), 1–499. [Google Scholar]
Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.7.1). 2019. Available online: Https://physics.nist.gov/asd (accessed on 31 March 2023).
Bowen, I.S. The origin of the chief nebular lines. Proc. Astron. Soc. Pac. 1927, 39, 295B. [Google Scholar] [CrossRef]
Bowen, I.S. The origin of the nebular lines and the structure of the planetary nebulae. Astroph. J. 1928, 67, 1B–15B. [Google Scholar] [CrossRef]
Träbert, E. E1-forbidden transition rates in ions of astrophysical interest. Phys. Scr. 2014, 89, 114003. [Google Scholar] [CrossRef]
Jitrik, O.; Bunge, C.F. Salient features of electric and magnetic multipole transition probabilities of hydrogen-like systems. Phys. Scr. 2004, 69, 196–202. [Google Scholar] [CrossRef]
Drake, G.W.F. Spontaneous two-photon decay rates in hydrogenlike and heliumlike ions. Phys. Rev. A 1986, 34, 2871–2880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Lin, C.D.; Johnson, W.R.; Dalgarno, A. Radiative decays of the n=2 states of He-like ions. Phys. Rev. A 1977, 15, 154–161. [Google Scholar] [CrossRef]
Gould, H.; Marrus, R.; Mohr, P.J. Radiative decay of the 2 ³S₁ and 2 ³P₂ states of heliumlike vanadium (Z=23) and iron (Z=26). Phys. Rev. Lett. 1974, 33, 676–680. [Google Scholar] [CrossRef]
Buchet, J.P.; Buchet-Poulizac, M.C.; Denis, A.; Désesquelles, J.; Druetta, M.; Grandin, J.P.; Huet, M.; Husson, X.; Lecler, D. Radiative lifetimes and oscillator strengths for 2s–2p transitions in He-, Li-, and Be-like iron. Phys. Rev. A 1984, 30, 309–315. [Google Scholar] [CrossRef]
Dietrich, D.D.; Leavitt, J.A.; Bashkin, S.; Conway, J.G.; Gould, H.; MacDonald, D.; Marrus, R.; Johnson, B.M.; Pegg, D.J. Oscillator strengths of the 2s ²S_1/2-2p ² $P_{1 / 2, 3 / 2}^{o}$ transitions in Fe XXIV and the 2s²¹S₀-2s2p ³ $P_{1}^{o}$ transition in Fe XXIII. Phys. Rev. A 1978, 18, 208–211. [Google Scholar] [CrossRef]
Hutton, R.; Martinson, I.; Nyström, B.; Ando, K.; Awaya, Y.; Bengtsson, P.; Kambara, T.; Kanai, Y.; Kojima, T.M.; Nakai, Y.; et al. Intercombination transitions in beryllium-like and boron-like iron. Phys. Scr. 1997, 55, 431–433. [Google Scholar] [CrossRef]
Jönsson, P.; Froese Fischer, C.; Träbert, E. On the status and perspectives of MCDF calculations and measurements of transition data in the Be isoelectronic sequence. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 3497–3511. [Google Scholar] [CrossRef]
Cheng, K.T.; Kim, Y.-K.; Desclaux, J.P. Electric dipole, quadrupole, and magnetic dipole transition probabilities of ions isoelectronic to the first-row atoms, Li through F. At. Data Nucl. Data Tables 1979, 24, 111–189. [Google Scholar] [CrossRef]
Buchet, J.P.; Buchet-Poulizac, M.C.; Denis, A.; Désesquelles, J.; Druetta, M. Measurement of radiative lifetimes of low-lying excited states in sodiumlike, fluorinelike, and oxygenlike iron. Phys. Rev. A 1980, 22, 2061–2068. [Google Scholar] [CrossRef]
Johnson, W.R.; Plante, D.R.; Sapirstein, J. Relativistic calculations of transition amplitudes in the helium isoelectronic sequence. In Advances of Atomic, Molecular and Optical Physics; Bederson, B., Walther, H., Eds.; Academic Press: San Diego, CA, USA, 1995; Volume 35, pp. 255–329. [Google Scholar]
Träbert, E. Radiative-lifetime measurements on highly-charged ions. In Accelerator-Based Atomic Physics Techniques and Applications; Shafroth, S.M., Austin, J.C., Eds.; American Institute of Physics: Washington, DC, USA, 1997; pp. 567–607. [Google Scholar]
Graf, A.; Beiersdorfer, P.; Harris, C.L.; Hwang, D.Q.; Neill, P.A. Lifetime of the 1s2p ¹P₁ excited level in Fe²⁴⁺. In AIP Conference Proceedings; Back, C.A., Ed.; American Institute of Physics: Washington, DC, USA, 2002; Volume 645, pp. 74–78. [Google Scholar]
Beiersdorfer, P. (Lawrence Livermore National Laboratory, Livermore, CA, USA). Personal communication, 2015.
Träbert, E. In pursuit of highly accurate atomic lifetime measurements of multiply charged ions. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074034. [Google Scholar] [CrossRef] [Green Version]
Kim, Y.-K.; Baik, D.H.; Indelicato, P.; Desclaux, J.P. Resonance transition energies of Li-, Na-, and Cu-like ions. Phys. Rev. A 1991, 44, 148–166. [Google Scholar] [CrossRef] [PubMed]
Träbert, E.; Curtis, L.J. Isoelectronic trends of line strength data in the Li and Be isoelectronic sequences. Phys. Scr. 2006, 74, C46–C54. [Google Scholar] [CrossRef]
Reistad, N.; Martinson, I. Accurate transition probabilities in ions obtained by isoelectronic smoothing of line strengths. Phys. Rev. A 1986, 34, 2632–2637. [Google Scholar] [CrossRef] [PubMed]
Edlén, B. Atomic Spectra. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin, Germany, 1964; Volume 27, pp. 80–220. [Google Scholar]
Träbert, E. Isoelectronic smoothing of oscillator strengths in the beryllium sequence. Z. Phys. D At. Mol. Clust. 1988, 9, 143–145. [Google Scholar] [CrossRef]
Träbert, E.; Doerfert, J.; Granzow, J.; Büttner, R.; Brauckhoff, J.; Nicolai, M.; Schartner, K.-H.; Folkmann, F.; Mokler, P.H. Lifetimes of n = 2 levels in foil-excited Kr³²⁺ and Kr³³⁺ ions. Phys. Lett. A 1995, 202, 91–98. [Google Scholar] [CrossRef]
Doerfert, J.; Träbert, E.; Wolf, A.; Schwalm, D.; Uwira, O. Precision measurement of the electric dipole intercombination rate in C²⁺. Phys. Rev. Lett. 1997, 78, 4355–4358. [Google Scholar] [CrossRef]
Edlén, B. Accurate values of the energy intervals in the configurations 1s²2s²2p^k (k = 1–5). Phys. Scr. 1982, 26, 71–83. [Google Scholar] [CrossRef]
Edlén, B. Comparison of theoretical and experimental level values of the k=2 configurations in the boron isoelectronic sequence. Phys. Scr. 1983, 28, 483–495. [Google Scholar] [CrossRef]
Träbert, E.; Grieser, M.; Hoffmann, J.; Krantz, C.; Repnow, R.; Wolf, A. Heavy-ion storage-ring-lifetime measurement of metastable levels in the C-, N-, and O-like ions of Si, P, and S. Phys. Rev. A 2012, 85, 042508. [Google Scholar] [CrossRef]
Fawcett, B.C. Theoretical oscillator strengths for 2s²2pⁿ – 2s2pⁿ⁺¹ and 2s2pⁿ⁺¹ – 2pⁿ⁺² transitions and for 2s²2pⁿ “forbidden” transitions Be I, B I, C I, N I, O I series, Z ≤ 26. At. Data Nucl. Data Tables 1978, 22, 473–489. [Google Scholar] [CrossRef]
Merkelis, G.; Vilkas, M.J.; Gaigalas, G.; Kisielius, R. MBPT calculation of energy spectra and E1 transition probabilities for boron isoelectronic sequence. Phys. Scr. 1995, 51, 233–251. [Google Scholar] [CrossRef]
Galavís, M.E.; Mendoza, C.; Zeippen, C.J. Atomic data from the IRON project: XXII. Radiative rates for forbidden transitions within the ground configuration of ions in the carbon and oxygen isoelectronic sequences. Astron. Astrophys. Suppl. Ser. 1997, 123, 159–171. [Google Scholar] [CrossRef] [Green Version]
Merkelis, G.; Vilkas, M.J.; Kisielius, R.; Gaigalas, G. Electric dipole transitions in ions of the N I isoelectronic sequence. Phys. Scr. 1997, 56, 41–55. [Google Scholar] [CrossRef]
Gaigalas, G.; Kaniauskas, J.; Kisielius, R.; Merkelis, G.; Vilkas, M.J. Second-order MBPT results for the oxygen isoelectronic sequence. Phys. Scr. 1994, 49, 135–147. [Google Scholar] [CrossRef]
Vilkas, M.J.; Ishikawa, Y.; Koc, K. Relativistic multireference many-body perturbation theory for quasidegenerate systems: Energy levels of ions of the oxygen isoelectronic sequence. Phys. Rev. A 1999, 60, 2808–2821. [Google Scholar] [CrossRef]
Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, and M2 transition rates for states of the 2s²2p⁴, 2s2p⁵, and 2p⁶ configurations in oxygen-like ions between F II and Kr XXIX. Astron. Astrophys. 2013, 557, A136. [Google Scholar] [CrossRef] [Green Version]
Drake, J.J.; Swartz, D.A.; Beiersdorfer, P.; Brown, G.V.; Kahn, S.M. On photospheric fluorescence and the nature of the 17.62 Åfeature in solar X-ray spectra. Astrophys. J. 1999, 521, 839–843. [Google Scholar] [CrossRef]
Froese Fischer, C.; Tachiev, G.; Irimia, A. Relativistic energy levels, lifetimes, and transition probabilities for the sodium-like to argon-like sequences. At. Data Nucl. Data Tab. 2006, 92, 607–812. [Google Scholar] [CrossRef]
Buchet, J.P.; Buchet-Poulizac, M.C.; Denis, A.; Désesquelles, J.; Druetta, M.; Martin, S.; Grandin, J.P.; Husson, X.; Lesteven, I. Beam-foil study of the 2s²2p⁵3ℓ and 2s2p⁶3ℓ configurations of Fe XVll. Phys. Scr. 1985, 31, 364–368. [Google Scholar] [CrossRef]
Hibbert, A.; Le Dourneuf, M.; Mohan, M. Energies, oscillator strengths, and lifetimes for neon-like ions up to Kr XXVII. At. Data Nucl. Data Tables 1993, 53, 23–112. [Google Scholar] [CrossRef]
Beiersdorfer, P. A “brief” history of spectroscopy on EBIT. Can. J. Phys. 2008, 86, 1–10. [Google Scholar] [CrossRef]
Beiersdorfer, P. Spectroscopy with trapped highly charged ions. Phys. Scr. 2008, 134, 014010. [Google Scholar] [CrossRef]
Beiersdorfer, P.; Obst, M.; Safronova, U.I. Radiative decay probabilities of the (2s²2p⁵ 3s_1/2)_J=0 level in neonlike ions. Phys. Rev. A 2011, 83, 012514. [Google Scholar] [CrossRef] [Green Version]
Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
Bhatia, A.K.; Kastner, S.O. Expected intensities of solar neon-like ions. Sol. Phys. 1985, 96, 11–26. [Google Scholar] [CrossRef]
Bernitt, S.; Brown, G.V.; Rudolph, J.K.; Steinbrügge, R.; Graf, A.; Leutenegger, M.; Epp, S.W.; Eberle, S.; Kubiček, K.; Mäckel, V.; et al. An unexpectedly low oscillator strength as the origin of the Fe XVII emission problem. Nature 2012, 492, 225–228. [Google Scholar] [CrossRef] [Green Version]
Oreshkina, N.S.; Cavaletto, S.M.; Keitel, C.H.; Harman, Z. Astrophysical line diagnosis requires nonlinear dynamical atomic modeling. Phys. Rev. Lett. 2014, 113, 143001. [Google Scholar] [CrossRef] [Green Version]
Träbert, E. Measurement of femtosecond atomic lifetimes using ion traps. Appl. Phys. B 2014, 114, 167–172. [Google Scholar] [CrossRef]
Wu, C.; Gao, X. Change of the relative line strengths due to the resonance induced population transfer between Fe XVII and Fe XVI ions. Sci. Rep. 2019, 9, 7463. [Google Scholar] [CrossRef] [Green Version]
Kühn, S.; Cheung, C.; Oreshkina, N.S.; Steinbrügge, R.; Togawa, M.; Bernitt, S.; Berger, L.; Buck, J.; Hoesch, M.; Seltmann, J.; et al. New measurement resolves key astrophysical Fe XVII oscillator strength problem. Phys. Rev. Lett. 2022, 129, 245001. [Google Scholar] [CrossRef]
Crespo López-Urrutia, J.R.; Beiersdorfer, P. Measurement of the radiative decay rate of the metastable (2s²2 $p_{3 / 2}^{5}$ 3s_1/2)_(J=2) level in Fe XVII. Astrophys. J. 2010, 721, 576–581. [Google Scholar] [CrossRef] [Green Version]
Beiersdorfer, P.; Crespo López-Urrutia, J.R.; Träbert, E. Measurement of the radiative decay rate and energy of the metastable (2s²2 $p_{1 / 2}^{5}$ 3s_1/2)_(J=0) level in Fe XVII. Astrophys. J. 2016, 817, 67. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Beiersdorfer, P.; Crespo López-Urrutia, J.R. Atomic lifetime measurements of Ne-like Fe ions in a magnetic field. Nucl. Instrum. Meth. Phys. Res. B 2017, 408, 107–109. [Google Scholar] [CrossRef]
Hutton, R.; Engström, L.; Träbert, E. Experimental oscillator strengths for the resonance lines in Na- and Mg-like iron. Nucl. Instr. Meth. Phys. Res. B 1988, 31, 294–299. [Google Scholar] [CrossRef]
Träbert, E.; Jones, K.W.; Johnson, B.M.; Gregory, D.C.; Kruse, T.H. Beam-foil lifetimes of n=3 levels in Fe XIII to Fe XVI II. Analysis of decay curves. Phys. Lett. 1982, 87A, 336–340. [Google Scholar] [CrossRef]
Träbert, E.; Hutton, R.; Martinson, I. Intercombination lines of Mg I-, Al I- and Si I-like ions in the beam foil spectra of Ti, Fe, Ni and Cu. Z. Phys. D At. Mol. Clusters. 1987, 5, 27–31. [Google Scholar] [CrossRef]
Träbert, E.; Heckmann, P.H.; Hutton, R.; Martinson, I. Intercombination lines in delayed beam-foil spectra. J. Opt. Soc. Am. B 1988, 5, 2173–2182. [Google Scholar] [CrossRef]
Moehs, D.P.; Bhatti, M.I.; Church, D.A. Measurements and calculations of metastable level lifetimes in Fe X, Fe XI, Fe XII, Fe XIII, and Fe XIV. Phys. Rev. A 2001, 63, 032515. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Gwinner, G.; Wolf, A.; Knystautas, E.J.; Garnir, H.-P.; Tordoir, X. M1/E2 transition rates in Fe X through Fe XIII measured at a heavy-ion storage ring. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 671–689. [Google Scholar] [CrossRef] [Green Version]
Beiersdorfer, P.; Träbert, E.; Pinnington, E.H. Experimental transition rate of the green coronal line of Fe XIV. Astrophys. J. 2003, 587, 836–840. [Google Scholar] [CrossRef]
Smith, S.J.; Chutjian, A.; Lozano, J.A. Measurement of metastable lifetimes for transitions in Fe⁹⁺, Fe¹⁰⁺, and Fe¹³⁺. Phys. Rev. A 2005, 72, 062504. [Google Scholar] [CrossRef]
Brenner, G.; Crespo López-Urrutia, J.R.; Harman, Z.; Mokler, P.H.; Ullrich, J. Lifetime determination of the Fe XIV 3s²3p ²P^o metastable level. Phys. Rev. A 2007, 75, 032504. [Google Scholar] [CrossRef]
Träbert, E.; Hutton, R.; Martinson, I. Identification of intercombination transitions in Fe XIV and Fe XIII in the spectra of foil-excited ions and solar flares. Mon. Not. R. Astron. Soc. 1987, 227, 27P–31P. [Google Scholar] [CrossRef] [Green Version]
Huang, K.-N. Energy-level scheme and transition probabilities of Si-like ions. At. Data Nucl. Data Tables 1985, 32, 503–566. [Google Scholar] [CrossRef]
Träbert, E.; Hoffmann, J.; Krantz, C.; Wolf, A.; Ishikawa, Y.; Santana, J.A. Atomic lifetime measurements on forbidden transitions of Al-, Si-, P- and S-like ions at a heavy-ion storage ring. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 025002. [Google Scholar] [CrossRef]
Träbert, E.; Calamai, A.G.; Gwinner, G.; Knystautas, E.J.; Pinnington, E.H.; Wolf, A. M1/E2/M2 decay rates in Fe VII, Fe IX, Fe X and Fe XIII measured using a heavy-ion storage ring. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 1129–1141. [Google Scholar] [CrossRef]
Träbert, E.; Pinnington, E.H.; Kernahan, J.A.; Doerfert, J.; Granzow, J.; Heckmann, P.H.; Hutton, R. Beam–foil study of the lifetimes of n = 3 levels in Na-like Ca X, Mg-like Ca IX and Si-like Ca VII. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 2647–2659. [Google Scholar] [CrossRef]
Bekker, H.; Hensel, C.; Daniel, A.; Windberger, A.; Pfeifer, T.; Crespo López-Urrutia, J.R. Laboratory precision measurements of optical emissions from coronal iron. Phys. Rev. A 2018, 98, 062514. [Google Scholar] [CrossRef]
Froese Fischer, C.; Liu, B. Energy levels, lifetimes, wavelengths, and transition probabilities of Fe XIV. At. Data Nucl. Data Tables 1986, 34, 261–277. [Google Scholar] [CrossRef]
Pinnington, E.H.; Ansbacher, W.; Tauheed, A.; Träbert, E.; Heckmann, P.H.; Möller, G.; Blanke, J.H. Beam-foil lifetime study of Al-ike titanium, iron and nickel. Z. Phys. D At. Mol. Clust. 1990, 17, 5–9. [Google Scholar] [CrossRef]
Fawcett, B.C. Calculated oscillator strengths and wavelengths for allowed transitions within the third shell for ions in the Al-like isoelectronic sequence between Cl V and Ni XVI. At. Data Nul. Data Tab. 1983, 28, 557–578. [Google Scholar] [CrossRef]
Santana, J.A.; Ishikawa, Y.; Träbert, E. Relativistic multireference Møller-Plesset perturbation theory results on levels and transition rates in Al-like ions of iron group elements. Phys. Scr. 2009, 79, 065301. [Google Scholar] [CrossRef]
Behring, W.E.; Cohen, L.; Feldman, U.; Doschek, G.A. The solar spectrum: Wavelengths and identifications from 160 to 770 Angstroms. Astrophys. J. 1976, 203, 521–527. [Google Scholar] [CrossRef]
Jönsson, P.; Radžiūtė, L.; Gaigalas, G.; Godefroid, M.; Marques, J.P.; Brage, T.; Froese Fischer, C.; Grant, I. Accurate multiconfiguration calculations of energy levels, lifetimes, and transition rates for the silicon isoelectronic sequence Ti IX–Ge XIX, Sr XXV, Zr XXVII, Mo XXIX. Astron. Astrophys. 2016, 585, A26. [Google Scholar] [CrossRef] [Green Version]
Vilkas, M.J.; Ishikawa, Y. Relativistic multireference many-body perturbation theory calculations for siliconlike argon, iron and krypton ions. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 4641–4650. [Google Scholar] [CrossRef]
Vilkas, M.J.; Ishikawa, Y. High-accuracy calculations of term energies and lifetimes of silicon-like ions with nuclear charges Z = 24–30. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 1803–1816. [Google Scholar] [CrossRef]
Träbert, E. EUV Beam-Foil Spectra of Titanium, Iron, Nickel, and Copper. Atoms 2021, 9, 45. [Google Scholar] [CrossRef]
Biémont, E. Energy-level scheme and oscillator strengths for the 3s-3p and 3p-3d transitions in silicon sequence for elements vanadium through nickel. Phys. Scr. 1986, 33, 324–335. [Google Scholar] [CrossRef]
Träbert, E. Solar EUV line identifications from delayed beam-foil spectra. Mon. Not. R. Astron. Soc. 1998, 297, 399–404. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Ishikawa, Y.; Santana, J.A.; Del Zanna, G. The 3s²3p3d ³F^o term in the Si-like spectrum of Fe (Fe XIII). Can. J. Phys. 2011, 89, 403–412. [Google Scholar] [CrossRef]
Träbert, E. EUV line identifications and lifetime measurements in highly charged iron ions. Phys. Scr. 2005, T120, 56–61. [Google Scholar] [CrossRef]
Träbert, E.; Grieser, M.; Krantz, C.; Repnow, R.; Wolf, A.; Diaz, F.J.; Ishikawa, Y.; Santana, J.A. Isoelectronic trends of the E1-forbidden decay rates of Al-, Si-, P-, and S-like ions of Cl, Ti, Mn, Cu, and Ge. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215003. [Google Scholar] [CrossRef]
Jönsson, P.; Gaigalas, G.; Rynkun, P.; Radžiūtė, L.; Ekman, J.; Gustafsson, S.; Hartman, H.; Wang, K.; Godefroid, M.; Froese Fischer, C.; et al. Multiconfiguration Dirac-Hartree-Fock calculations with spectroscopic accuracy: Applications to astrophysics. Atoms 2017, 5, 16. [Google Scholar] [CrossRef]
Froese Fischer, C. Towards accurate transition data for 3p², 3p³, 3p⁴ levels of Fe, Co and Ni ions. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074020. [Google Scholar] [CrossRef]
Fritzsche, S.; Froese Fischer, C.; Fricke, B. Calculated level energies, transition probabilities, and lifetimes for phosphorus-like ions of the iron group in the 3s3p⁴ and 3s²3p23d configurations. At. Data Nucl. Data Tables 1998, 68, 149–179. [Google Scholar] [CrossRef] [Green Version]
Wang, K.; Jönsson, P.; Gaigalas, G.; Radžiūtė, L.; Rynkun, P.; Del Zanna, G.; Chen, C.Y. Energy levels, lifetimes, and transition rates for P-like ions from Cr X to Zn XVI from large-scale relativistic multiconfiguration calculations. Astrophys. J. Suppl. Ser. 2018, 235, 27. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Hoffmann, J.; Reinhardt, S.; Wolf, A.; Del Zanna, G. Measurement of electric-dipole forbidden 3p and 3d level decay rates in Fe XII. J. Phys. Conf. Ser. 2008, 130, 012018. [Google Scholar] [CrossRef]
Träbert, E. A laboratory astrophysics problem: The lifetime of very long-lived levels in low-charge ions. Atoms 2020, 8, 21. [Google Scholar] [CrossRef]
Morisset, C.; Luridiana, V.; García-Roja, J.; Gómez-Llanos, V.; Bautista, M.; Mendoza, C. Atomic data assessment with PyNeb. Atoms 2020, 8, 66. [Google Scholar] [CrossRef]
Wang, K.; Song, C.X.; Jönsson, P.; Del Zanna, G.; Schiffmann, S.; Godefroid, M.; Gaigalas, G.; Zhao, X.H.; Si, R.; Chen, C.Y.; et al. Benchmarking atomic data from large-scale multiconfiguration Dirac-Hartree-Fock calculations for astrophysics: S-like Ions from Cr IX to Cu XIV. Astrophys. J. Suppl. Ser. 2018, 239, 30. [Google Scholar] [CrossRef]
Träbert, E.; Brandt, M.; Doerfert, J.; Granzow, J.; Heckmann, P.H.; Meurisch, J.; Martinson, I.; Hutton, R.; Myrnäs, R. Beam-foil measurements on intercombination transitions in Cl-like ions of elements Mn through Zn. Phys. Scr. 1993, 48, 580–585. [Google Scholar] [CrossRef]
Brenner, G.; Crespo López-Urrutia, J.R.; Bernitt, S.; Fischer, D.; Ginzel, R.; Kubiček, K.; Mäckel, V.; Mokler, P.H.; Simon, M.C.; Ullrich, J. On the transition rate of the Fe X red coronal line. Astrophys. J. 2009, 703, 68–73. [Google Scholar] [CrossRef]
Ishikawa, Y.; Santana, J.A.; Träbert, E. Relativistic multireference many-body perturbation theory for open-shell ions with multiple valence shell electrons: The transition rates and lifetimes of the excited levels in chlorinelike Fe X. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 074022. [Google Scholar] [CrossRef]
Träbert, E. Experimental checks on calculations for Cl-, S- and P-like ions of the iron group elements. J. Phys. B At. Mol. Opt. Phys. 1996, 29, L217–L224. [Google Scholar] [CrossRef]
Wang, K.; Jönsson, P.; Del Zanna, G.; Godefroid, M.; Chen, Z.B.; Chen, C.Y.; Yan, J. Large-scale multiconfiguration Dirac-Hartree-Fock calculations for astrophysics: Cl-like Ions from Cr VIII to Zn XIV. Astrophys. J. Suppl. Ser. 2020, 246, 1. [Google Scholar] [CrossRef] [Green Version]
Moehs, D.P.; Church, D.A.; Bhatti, M.I.; Perger, W. Excited-configuration metastable level lifetimes of Cl-like Mn IX and Fe X. Phys. Rev. Lett. A 2000, 85, 38–41. [Google Scholar] [CrossRef]
Chou, H.-S.; Chang, J.-Y.; Chang, Y.-H.; Huang, K.-N. Energy-level scheme and transition probabilities of S-like ions. At. Data Nucl. Data Tables 1996, 62, 77–145. [Google Scholar] [CrossRef]
Träbert, E. EUV beam-foil spectra of germanium and a blind-spot problem in spectroscopy. Atoms 2023, 11, 45. [Google Scholar] [CrossRef]
Träbert, E. The allure of high total angular momentum levels in multiply-excited ions. Atoms 2019, 7, 103. [Google Scholar] [CrossRef] [Green Version]
Berrington, K.A.; Pelan, J.C.; Waldock, J.A. Oscillator strength for 3s²3p⁵ – 3s3p⁶ in Cl-like ions. J. Phys. B At. Mol. Opt. Phys. 1996, 29, L217–L224. [Google Scholar]
Biémont, E.; Träbert, E. Transition rates of the resonance line doublet in the Cl I sequence, Ar II – Ge XVI. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 2939–2946. [Google Scholar] [CrossRef]
Huang, K.-N.; Kim, Y.-K.; Cheng, K.T.; Desclaux, J.P. Energy-level scheme and transition probabilities of Cl-like ions. At. Data Nucl. Data Tables 1983, 28, 355–377. [Google Scholar] [CrossRef]
Fritzsche, S.; Finkbeiner, M.; Fricke, B.; Sepp, W.-D. Level energies and lifetimes in the 3p⁴3d configuration of chlorine-like ions. Phys. Scr. 1995, 52, 258–266. [Google Scholar] [CrossRef]
Xu, G.; Yan, C.; Lu, Q.; Tang, Z.; Yang, Y.; Li, W.; Ma, S.; Zhao, Z.; Huang, S.; Song, L.; et al. First laboratory measurement of magnetic-field-induced transition effect in Fe X at different magnetic fields. Astrophys. J. 2022, 937, 48. [Google Scholar] [CrossRef]
Wagner, W.J.; House, L.L. Hartree-Fock calculations of coronal forbidden lines in the argon I isoelectronic sequence. Astrophys. J. 1969, 155, 677–686. [Google Scholar] [CrossRef]
Wagner, W.J.; House, L.L. Empirically corrected calculations of coronal visible lines from the 3p⁵3d configuration. Astrophys. J. 1971, 166, 683–698. [Google Scholar] [CrossRef]
Storey, P.J.; Zeippen, C.J. Coronal Fe IX line intensities and electron density diagnostics. Mon. Not. R. Astron. Soc. 2001, 324, L7–L10. [Google Scholar] [CrossRef] [Green Version]
Träbert, E.; Beiersdorfer, P.; Brown, G.V.; Hell, N.; Lepson, J.K.; Fairchild, A.J.; Hahn, M.; Savin, D.W. Laboratory search for Fe IX solar diagnostic lines using an electron beam ion trap. Atoms 2022, 10, 115. [Google Scholar] [CrossRef]
Beiersdorfer, P.; Lepson, J.K.; Brown, G.V.; Hell, N.; Träbert, E.; Hahn, M.; Savin, D.W. High-resolution laboratory measurements and identification of Fe IX Lines near 171 Å. Atoms 2022, 10, 148. [Google Scholar] [CrossRef]
Biémont, E.; Hansen, J.E. Energy levels and transition probabilities in 3d and 3d⁹ configurations. Phys. Scr. 1989, 39, 308–313. [Google Scholar] [CrossRef]
Jacques, C.; Moreau, J.-P.; Knystautas, E.J. Etude de fer, du cobalt et du nickel par la spectroscopie d’ions rapides. J. Phys. 1984, 45, 1607–1613. [Google Scholar] [CrossRef]
Dumont, P.D.; Baudinet-Robinet, Y.; Garnir, H.P.; Biemont, E.; Grevesse, N. Beam-foil lifetime measurements in Fe V and Fe VI. Phys. Rev. A 1979, 20, 1347–1351. [Google Scholar] [CrossRef]
Dolby, J.S.; McWhirter, R.W.P.; Sofield, C.J. The measurement of Fe II and Fe III lifetimes by beam-foil spectroscopy in the vacuum ultraviolet. J. Phys. B At. Mol. Phys. 1979, 12, 187–201. [Google Scholar] [CrossRef]
Rostohar, D.; Derkatch, A.; Hartman, H.; Johansson, S.; Lundberg, H.; Mannervik, S.; Norlin, L.-O.; Royen, P.; Schmitt, A. Lifetime measurements of metastable states in Fe⁺. Phys. Rev. Lett. 2001, 86, 1466–1469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Hartman, H.; Derkatch, A.; Donnelly, M.P.; Gull, T.; Hibbert, A.; Johansson, S.; Lundberg, H.; Mannervik, S.; Norlin, L.-O.; Rostohar, D.; et al. The FERRUM project: Experimental transition probabilities of [Fe II] and astrophysical applications. Astron. Astrophys. 2003, 398, 1143–1149. [Google Scholar] [CrossRef] [Green Version]
Lindgård, A.; Nielsen, S.E. Transition probabilities for the alkali isoelectronic sequences Li I, Na I, K I, Rb I, Cs I, Fr I. At. Data Nucl. Data Tables 1977, 19, 533–633. [Google Scholar] [CrossRef]
Abbott, D.C. The structure and transition probabilities of ionised Cr, Mn, Fe and Ni. J. Phys. B At. Mol. Phys. 1978, 11, 3479–3497. [Google Scholar] [CrossRef]
Mendoza, C.; Méndez-Delgado, J.E.; Bautista, M.; García-Rojas, J.; Morisset, C. Atomic data assessment with PyNeb: Radiative and electron impact excitation rates for [Fe II] and [Fe III]. Atoms 2023, 11, 63. [Google Scholar] [CrossRef]
Fuhr, J.R.; Wiese, W.L. A critical compilation of atomic transition probabilities for neutral and singly ionized iron. J. Phys. Chem. Ref. Data 2006, 35, 1669–1809. [Google Scholar] [CrossRef] [Green Version]
Mannervik, S. Experimental lifetime studies of metastable levels. Phys. Scr. 2003, 2003, 67–75. [Google Scholar] [CrossRef]
Lestinsky, M.; Andrianov, V.; Aurand, B.; Bagnoud, V.; Bernhardt, D.; Beyer, H.; Bishop, S.; Blaum, K.; Bleile, A.; Borovik, A.; et al. Physics book: CRYRING@ESR. Eur. Phys. J. Spec. Top. 2016, 225, 797–882. [Google Scholar] [CrossRef] [Green Version]
Bennett, W.R.; Kindlmann, P.J. Radiative and collision-induced relaxation of atomic states in the 2p⁵3p configuration of neon. Phys. Rev. 1966, 149, 38–51. [Google Scholar] [CrossRef]
Träbert, E. Atomic lifetime measurements with ion traps of many sizes. Phys. Scr. 2000, 61, 257–286. [Google Scholar] [CrossRef]
Träbert, E. Precise measurements of long atomic lifetimes using stored ion beams and ion traps. Can. J. Phys. 2002, 80, 1481–1503. [Google Scholar] [CrossRef]
Träbert, E. Atomic lifetime measurements using electron beam ion traps. Can. J. Phys. 2008, 86, 73–97. [Google Scholar] [CrossRef]
Träbert, E. Problems with accurate atomic lifetime measurements of multiply charged ions. Phys. Scr. 2009, 79, 068101. [Google Scholar] [CrossRef]
Träbert, E. Critical assessment of theoretical calculations of atomic structure and transition probabilities: An experimenter’s view. Atoms 2014, 2, 15–85. [Google Scholar] [CrossRef] [Green Version]

Figure 1. Ionisation potentials of Fe atoms and ions. The ions with rare-gas-like electron shells (Ne-like Fe XVII and Ar-like Fe IX) are marked.

Table 1. Levels of Fe ions (Fe XXVI-XVIII) with their lifetimes and dominant decay modes (

E 1, M 1, E 2

). IC intercombination transition.

Table 1. Levels of Fe ions (Fe XXVI-XVIII) with their lifetimes and dominant decay modes (

E 1, M 1, E 2

). IC intercombination transition.

Spectrum	Sequence	Level	Decay	Lifetime	Expt/Theory
XXVI	H	2p $^{2}$ P $_{1 / 2, 3 / 2}^{o}$	E1 $Δ n = 1$	3.5 10 $^{- 15}$ s	T
XXVI	H	2s $^{2}$ S $_{1 / 2}$	M1, 2E1	3.45 10 $^{- 10}$ s	T
XXVI	H	3d $^{2}$ D $_{3 / 2, 5 / 2}^{o}$	E1 $Δ n = 1$	3.5 10 $^{- 14}$ s	T
XXV	He	1s2s $^{1}$ S $_{0}$	2E1	243 ps	T [42]
XXV	He	1s2s $^{3}$ S $_{1}$	M1	4.80 ns	T [43]
				4.8 ± 0.6 ns	E [44]
XXV	He	1s2p $^{1}$ P $_{1}^{o}$	E1 $Δ n = 1$	2.18 fs	T [43]
XXV	He	1s2p $^{3}$ P $_{0}^{o}$	E1 $Δ n = 0$	2.62 ns	T [43]
XXV	He	1s2p $^{3}$ P $_{1}^{o}$	E1 IC	23.5 fs	T [43]
XXV	He	1s2p $^{3}$ P $_{2}^{o}$	M2, E1 $Δ n = 0, 1$	125 ps	T [43]
				110 ± 20 ps	E [44]
				121 ± 15 ps	E [45]
XXIV	Li	2p $^{2}$ P $_{1 / 2}^{o}$	E1 $Δ n = 0$	550 ± 20 ps	E [46]
				555 ± 30 ps	E [45]
XXIV	Li	2p $^{2}$ P $_{3 / 2}^{o}$	E1 $Δ n = 0$	235 ± 10 ps	E [46]
				242 ± 20 ps	E [45]
XXIII	Be	2s2p $^{3}$ P $_{1}^{o}$	E1 $Δ n = 0$ IC	13 ± 4 ns	E [46]
				17.5 ± 1.5 ns	E [47]
				19.7 ± 0.2 ns	T [48]
XXIII	Be	2s2p $^{1}$ P $_{1}^{o}$	E1 $Δ n = 0$	51 ± 5 ns	E [45]
XXIII	Be	2p $^{2}$ $^{1}$ S $_{0}$	E1 $Δ n = 0$	34 ± 5 ps	E [45]
XXIII	Be	2p $^{2}$ $^{1}$ D $_{2}$	E1 $Δ n = 0$	100 ± 8 ps	E [45]
XXIII	Be	2p $^{2}$ $^{3}$ P $_{2}$	E1 $Δ n = 0$	79 ± 8 ps	E [45]
XXII	B	2s $^{2}$ 2p $^{2}$ P $_{3 / 2}^{o}$	M1,E2	673 $μ$ s	T [49]
XXII	B	2s2p $^{2}$ $^{4}$ P $_{5 / 2}$	E1 IC $Δ n = 0$	14.8 ns	T [49]
				14.8 ± 1.0 ns	E [47]
		2s2p $^{2}$ $^{4}$ P $_{3 / 2}$	E1 IC $Δ n = 0$	102 ns	T [49]
		2s2p $^{2}$ $^{4}$ P $_{1 / 2}$	E1 IC $Δ n = 0$	10.3 ns	T [49]
XXI	C	2s $^{2}$ 2p $^{2}$ $^{3}$ P $_{1}$	M1	153 $μ$ s	T [49]
XXI	C	2s $^{2}$ 2p $^{2}$ $^{3}$ P $_{2}$	M1, E2	1.13 ms	T [49]
XXI	C	2s $^{2}$ 2p $^{2}$ $^{1}$ D $_{2}$	M1, E2	31 $μ$ s	T [49]
XXI	C	2s $^{2}$ 2p $^{2}$ $^{1}$ S $_{0}$	M1	7 $μ$ s	T [49]
XX	N	2s $^{2}$ 2p $^{3}$ $^{2}$ P $_{1 / 2, 3 / 2}^{o}$	M1	26 $μ$ s, 12 $μ$ s	T [49]
XX	N	2s $^{2}$ 2p $^{3}$ $^{2}$ D $_{3 / 2, 5 / 2}^{o}$	M1	57 $μ$ s, 580 $μ$ s	T [49]
XIX	O	2s $^{2}$ 2p $^{4}$ $^{3}$ P $_{1}$	M1	70 $μ$ s	T [49]
XIX	O	2s $^{2}$ 2p $^{4}$ $^{3}$ P $_{0}$	M1, E2	32 ms	T [49]
XIX	O	2s $^{2}$ 2p $^{4}$ $^{1}$ D $_{2}$	M1	54 $μ$ s	T [49]
XIX	O	2s $^{2}$ 2p $^{4}$ $^{1}$ S $_{0}$	M1	6.8 $μ$ s	T [49]
XIX	O	2s2p $^{5}$ $^{3}$ P $_{2}^{o}$	E1	23.5 ± 2.0 ps	E [50]
XVIII	F	2s $^{2}$ 2p $^{5}$ $^{2}$ P $_{1 / 2}^{o}$	M1	521 $μ$ s	T [49]
XVIII	F	2s2p $^{6}$ $^{2}$ P $_{1 / 2}$	E1	12.2 ± 0.8 ps	E [50]

Table 4. Fe ion (Fe IX-II) level lifetimes and dominant decay modes (

E 1, M 1, E 2

).

Table 4. Fe ion (Fe IX-II) level lifetimes and dominant decay modes (

E 1, M 1, E 2

).

Spectrum	Sequence	Level	Decay	Lifetime	Expt/Theory
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{1}$ P $_{1}^{o}$	E1 $Δ n = 0$	4.3 ps	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ P $_{1}^{o}$	E1 $Δ n = 0$ IC	83 ns	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ P $_{2}^{o}$	M2 $Δ n = 0$ IC	11.5 ms	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ D $_{1}^{o}$	E1 $Δ n = 0$ IC	4.2 ns	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ F $_{2}^{o}$	M1,M2	204 ms	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{1}$ D $_{2}^{o}$	M1	13.2 ms	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ D $_{3}^{o}$	M1	29 ± 3 ms	E [102]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{3}$ D $_{2}^{o}$	M1,M2	10.5 ± 1 ms	E [102]
				15.7 ms	T [18]
IX	Ar	3s $^{2}$ 3p $^{5}$ 3d $^{1}$ F $_{3}^{o}$	M1	6.9 ± 0.3 ms	E [102]
				11.9 ms	T [18]
VIII	K	3p $^{6}$ 3d $^{2}$ D $_{5 / 2}$	M1	14 s	T [146]
VII	Ca	3p $^{6}$ 3d $^{2}$ $^{1}$ S $_{0}$	M1,E2	29.6 ± 1.8 ms	E [102]
		3p $^{6}$ 3d4p $^{1}$ D $_{2}^{o}$	E1	920 ± 70 ps	E [147]
VI	Sc	3p $^{6}$ 3d $^{2}$ 4p $^{4}$ G $_{11 / 2}^{o}$	E1	810 ± 60 ps	E [148]
				880 ± 80 ps	E [147]
V	Ti	3p $^{6}$ 3d $^{3}$ 4p $^{5}$ D $_{J}^{o}$	E1	300 ± 20 ps	E [148]
V				530 ± 40 ps	E [147]
IV	V	3p $^{6}$ 3d $^{4}$ 4p $^{4}$ D $_{J}^{o}$	E1	620 ± 30 ps	E [147]
III	Cr	3p $^{6}$ 3d $^{5}$ 4p $^{5}$ G $_{J}^{o}$	E1	2.26 ± 0.5 ns	E [149]
II	Mn	3p $^{6}$ 3d $^{5}$ 4s4p	E1	0.88 ± 0.04 ns	E [149]
II	Mn	3p $^{6}$ 3d $^{6}$ 4p	E1	1.39 ± 0.30 ns	E [149]
II	Mn	3p $^{6}$ 3d $^{5}$ 4s4p	E1	1.89 ± 0.17 ns	E [149]
II	Mn	a $^{6}$ S $_{5 / 2}$	E2	230 ± 30 ms	E [150]
II	Mn	b $^{4}$ D $_{7 / 2}$	M1,E2	530 ± 30 ms	E [150]
II	Mn	a $^{4}$ G $_{9 / 2}$	M1,E2	650 ± 20 ms	E [151]
II	Mn	b $^{2}$ H $_{11 / 2}$	M1,E2	3.8 ± 0.3 s	E [151]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Träbert, E. Atomic Lifetimes of Astrophysical Interest in Ions of Fe. Atoms 2023, 11, 85. https://doi.org/10.3390/atoms11050085

AMA Style

Träbert E. Atomic Lifetimes of Astrophysical Interest in Ions of Fe. Atoms. 2023; 11(5):85. https://doi.org/10.3390/atoms11050085

Chicago/Turabian Style

Träbert, Elmar. 2023. "Atomic Lifetimes of Astrophysical Interest in Ions of Fe" Atoms 11, no. 5: 85. https://doi.org/10.3390/atoms11050085

APA Style

Träbert, E. (2023). Atomic Lifetimes of Astrophysical Interest in Ions of Fe. Atoms, 11(5), 85. https://doi.org/10.3390/atoms11050085

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Atomic Lifetimes of Astrophysical Interest in Ions of Fe

Abstract

1. Introduction

2. Lifetime Data and Results

2.1. Ions with an $n = 1$ Ground Configuration

2.2. Ions with an $n = 2$ Ground Configuration: Li- and Be-like Ions

2.3. Ions with an $n = 2$ Ground Configuration: B- to F-like Ions

2.4. Ions with an Open $n = 3$ Valence Shell

2.4.1. Ne-like Fe XVII

2.4.2. Na-like Fe XVI

2.4.3. Mg-like Fe XV

2.4.4. Al-like Fe XIV

2.4.5. Si-like Fe XIII

2.4.6. P-like Fe XII

2.4.7. S-like Fe XI

2.4.8. Cl-like Fe X

2.4.9. Ar-like Fe IX

2.4.10. K-like Fe VIII

2.4.11. Ca-like Fe VII, Sc-like Fe VI, Ti-like Fe V, V-like Fe IV, and Cr-like Fe III

2.4.12. Mn-like Fe II

3. Discussion

4. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI

Article Menu

Atomic Lifetimes of Astrophysical Interest in Ions of Fe

Abstract

1. Introduction

2. Lifetime Data and Results

2.1. Ions with an n = 1 Ground Configuration

2.2. Ions with an n = 2 Ground Configuration: Li- and Be-like Ions

2.3. Ions with an n = 2 Ground Configuration: B- to F-like Ions

2.4. Ions with an Open n = 3 Valence Shell

2.4.1. Ne-like Fe XVII

2.4.2. Na-like Fe XVI

2.4.3. Mg-like Fe XV

2.4.4. Al-like Fe XIV

2.4.5. Si-like Fe XIII

2.4.6. P-like Fe XII

2.4.7. S-like Fe XI

2.4.8. Cl-like Fe X

2.4.9. Ar-like Fe IX

2.4.10. K-like Fe VIII

2.4.11. Ca-like Fe VII, Sc-like Fe VI, Ti-like Fe V, V-like Fe IV, and Cr-like Fe III

2.4.12. Mn-like Fe II

3. Discussion

4. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI

2.1. Ions with an $n = 1$ Ground Configuration

2.2. Ions with an $n = 2$ Ground Configuration: Li- and Be-like Ions

2.3. Ions with an $n = 2$ Ground Configuration: B- to F-like Ions

2.4. Ions with an Open $n = 3$ Valence Shell