Mean-Field Description of Cooperative Scattering by Atomic Clouds
Abstract
:1. Introduction
2. General Equations
3. Average Quantities
4. Specific Radial Distribution
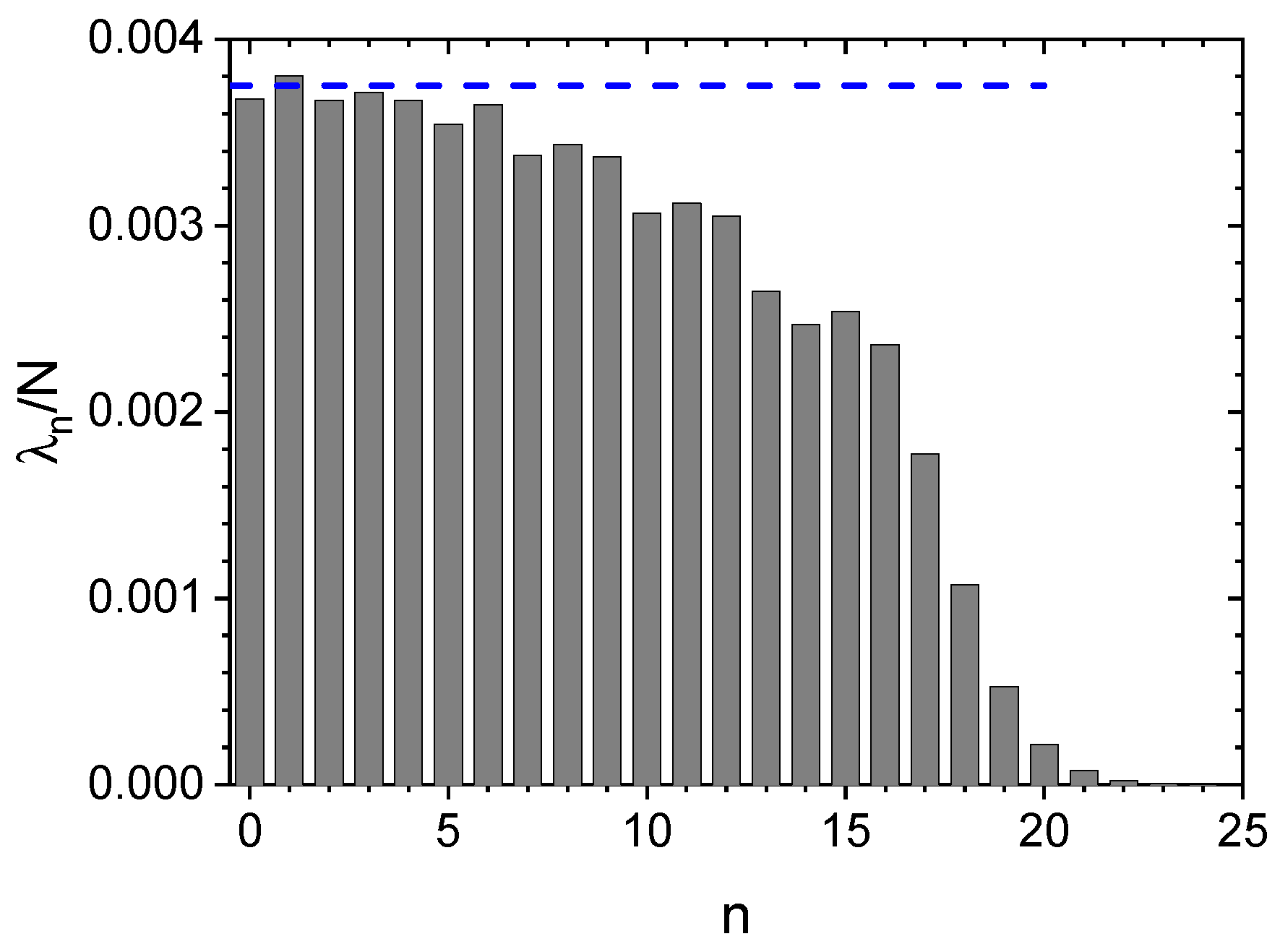
4.1. Uniform Sphere [10,11]
4.2. Parabolic Profile
4.3. Gaussian Profile
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–100. [Google Scholar] [CrossRef] [Green Version]
- Hayden, P.M.; Inamori, H.; John, S.; Stamper-Kurn, D.M.; Bernard, J.C.; Müeller, C.A.; Zhu, X.; Paz, J.P.; TC, H.; Ekert, A.K.; et al. Coherent Atomic Matter Waves; EDP Sciences; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Cherroret, N.; Delande, D.; van Tiggelen, B.A. Induced dipole-dipole interactions in light diffusion from point dipoles. Phys. Rev. A 2016, 94, 012702. [Google Scholar] [CrossRef] [Green Version]
- Kwong, C.C.; Wilkowski, D.; Delande, D.; Pierrat, R. Coherent light propagation through cold atomic clouds beyond the independent scattering approximation. Phys. Rev. A 2019, 99, 043806. [Google Scholar] [CrossRef] [Green Version]
- Saint-Jalm, R.; Aidelsburger, M.; Ville, J.L.; Corman, L.; Hadzibabic, Z.; Delande, D.; Nascimbene, S.; Cherroret, N.; Dalibard, J.; Beugnon, J. Resonant-light diffusion in a disordered atomic layer. Phys. Rev. A 2018, 97, 061801. [Google Scholar] [CrossRef] [Green Version]
- Jennewein, S.; Besbes, M.; Schilder, N.J.; Jenkins, S.D.; Sauvan, C.; Ruostekoski, J.; Greffet, J.J.; Sortais, Y.R.P.; Browaeys, A. Coherent Scattering of Near-Resonant Light by a Dense Microscopic Cold Atomic Cloud. Phys. Rev. Lett. 2016, 116, 233601. [Google Scholar] [CrossRef] [Green Version]
- Labeyrie, G.; Vaujour, E.; Mueller, C.A.; Delande, D.; Miniatura, C.; Wilkowski, D.; Kaiser, R. Slow diffusion of light in a cold atomic cloud. Phys. Rev. Lett. 2003, 91, 223904. [Google Scholar] [CrossRef] [Green Version]
- Guerin, W.; Rouabah, M.; Kaiser, R. Light interacting with atomic ensembles: Collective, cooperative and mesoscopic effects. J. Mod. Opt. 2017, 64, 895–907. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.; Fry, E.; Ooi, C.; Wodkiewicz, K. Directed Spontaneous Emission from an Extended Ensemble of N Atoms: Timing Is Everything. Phys. Rev. Lett. 2006, 96, 010501. [Google Scholar] [CrossRef] [Green Version]
- Svidzinsky, A.A.; Chang, J.T.; Scully, M.O. Dynamical Evolution of Correlated Spontaneous Emission of a Single Photon from a Uniformly Excited Cloud of N Atoms. Phys. Rev. Lett. 2008, 100, 160504. [Google Scholar] [CrossRef] [Green Version]
- Svidzinsky, A.A.; Chang, J.T.; Scully, M.O. Cooperative spontaneous emission of N atoms: Many-body eigenstates, the effect of virtual Lamb shift processes, and analogy with radiation of N classical oscillators. Phys. Rev. A 2010, 81, 053821. [Google Scholar] [CrossRef]
- Lehmberg, R.H. Radiation from an N-Atom System. I. General Formalism. Phys. Rev. A 1970, 2, 883–888. [Google Scholar] [CrossRef]
- Courteille, P.W.; Bux, S.; Lucioni, E.; Lauber, K.; Bienaimé, T.; Kaiser, R.; Piovella, N. Modification of radiation pressure due to cooperative scattering of light. Eur. Phys. J. D 2010, 58, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Bienaimé, T.; Bux, S.; Lucioni, E.; Courteille, P.; Piovella, N.; Kaiser, R. Observation of a Cooperative Radiation Force in the Presence of Disorder. Phys. Rev. Lett. 2010, 104, 183602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bienaimé, T.; Bachelard, R.; Piovella, N.; Kaiser, R. Cooperativity in light scattering by cold atoms. Fortschritte Der Phys. 2013, 61, 377–392. [Google Scholar] [CrossRef] [Green Version]
- Chabé, J.; Rouabah, M.T.; Bellando, L.; Bienaimé, T.; Piovella, N.; Bachelard, R.; Kaiser, R. Coherent and incoherent multiple scattering. Phys. Rev. A 2014, 89, 043833. [Google Scholar] [CrossRef] [Green Version]
- Bachelard, R.; Piovella, N.; Guerin, W.; Kaiser, R. Collective effects in the radiation pressure force. Phys. Rev. A 2016, 94, 033836. [Google Scholar] [CrossRef] [Green Version]
- Bienaimé, T.; Piovella, N.; Kaiser, R. Controlled Dicke Subradiance from a Large Cloud of Two-Level Systems. Phys. Rev. Lett. 2012, 108, 123602. [Google Scholar] [CrossRef] [Green Version]
- Guerin, W.; Araújo, M.O.; Kaiser, R. Subradiance in a Large Cloud of Cold Atoms. Phys. Rev. Lett. 2016, 116, 083601. [Google Scholar] [CrossRef] [Green Version]
- Bellando, L.; Gero, A.; Akkermans, E.; Kaiser, R. Cooperative effects and disorder: A scaling analysis of the spectrum of the effective atomic Hamiltonian. Phys. Rev. A 2014, 90, 063822. [Google Scholar] [CrossRef] [Green Version]
- Guerin, W.; Kaiser, R. Population of collective modes in light scattering by many atoms. Phys. Rev. A 2017, 95, 053865. [Google Scholar] [CrossRef] [Green Version]
- Cottier, F.; Kaiser, R.; Bachelard, R. Role of disorder in super- and subradiance of cold atomic clouds. Phys. Rev. A 2018, 98, 013622. [Google Scholar] [CrossRef] [Green Version]
- Bachelard, R.; Piovella, N.; Courteille, P.W. Cooperative scattering and radiation pressure force in dense atomic clouds. Phys. Rev. A 2011, 84, 013821. [Google Scholar] [CrossRef] [Green Version]
- Bachelard, R.; Courteille, P.; Kaiser, R.; Piovella, N. Resonances in Mie scattering by an inhomogeneous atomic cloud. Europhys. Lett. 2012, 97, 14004. [Google Scholar] [CrossRef] [Green Version]
- Bienaimé, T.; Petruzzo, M.; Bigerni, D.; Piovella, N.; Kaiser, R. Atom and photon measurement in cooperative scattering by cold atoms. J. Mod. Opt. 2011, 58, 1942–1950. [Google Scholar] [CrossRef]
- Scully, M.O. Collective Lamb Shift in Single Photon Dicke Superradiance. Phys. Rev. Lett. 2009, 102, 143601. [Google Scholar] [CrossRef]
- Araújo, M.O.; Krešić, I.; Kaiser, R.; Guerin, W. Superradiance in a Large and Dilute Cloud of Cold Atoms in the Linear-Optics Regime. Phys. Rev. Lett. 2016, 117, 073002. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.O. Single photon subradiance: Quantum control of spontaneous emission and ultrafast readout. Phys. Rev. Lett. 2015, 115, 243602. [Google Scholar] [CrossRef] [Green Version]
- Manassah, J.T. Comparison of the cooperative emission profile from a spherical distribution of two-level atoms resulting from the choice of the interaction kernel. Phys. Rev. A 2012, 85, 015801. [Google Scholar] [CrossRef]
- Manassah, J.T. Cooperative radiation from atoms in different geometries: Decay rate and frequency shift. Adv. Opt. Photonics 2012, 4, 108–156. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piovella, N. Mean-Field Description of Cooperative Scattering by Atomic Clouds. Atoms 2023, 11, 101. https://doi.org/10.3390/atoms11070101
Piovella N. Mean-Field Description of Cooperative Scattering by Atomic Clouds. Atoms. 2023; 11(7):101. https://doi.org/10.3390/atoms11070101
Chicago/Turabian StylePiovella, Nicola. 2023. "Mean-Field Description of Cooperative Scattering by Atomic Clouds" Atoms 11, no. 7: 101. https://doi.org/10.3390/atoms11070101





