Energetic and Spectroscopic Properties of the Low-Lying Isomers of C5H: A High-Level Ab Initio Study
Abstract
1. Introduction
2. Computational Methodology
3. Results and Discussion
3.1. Energetics
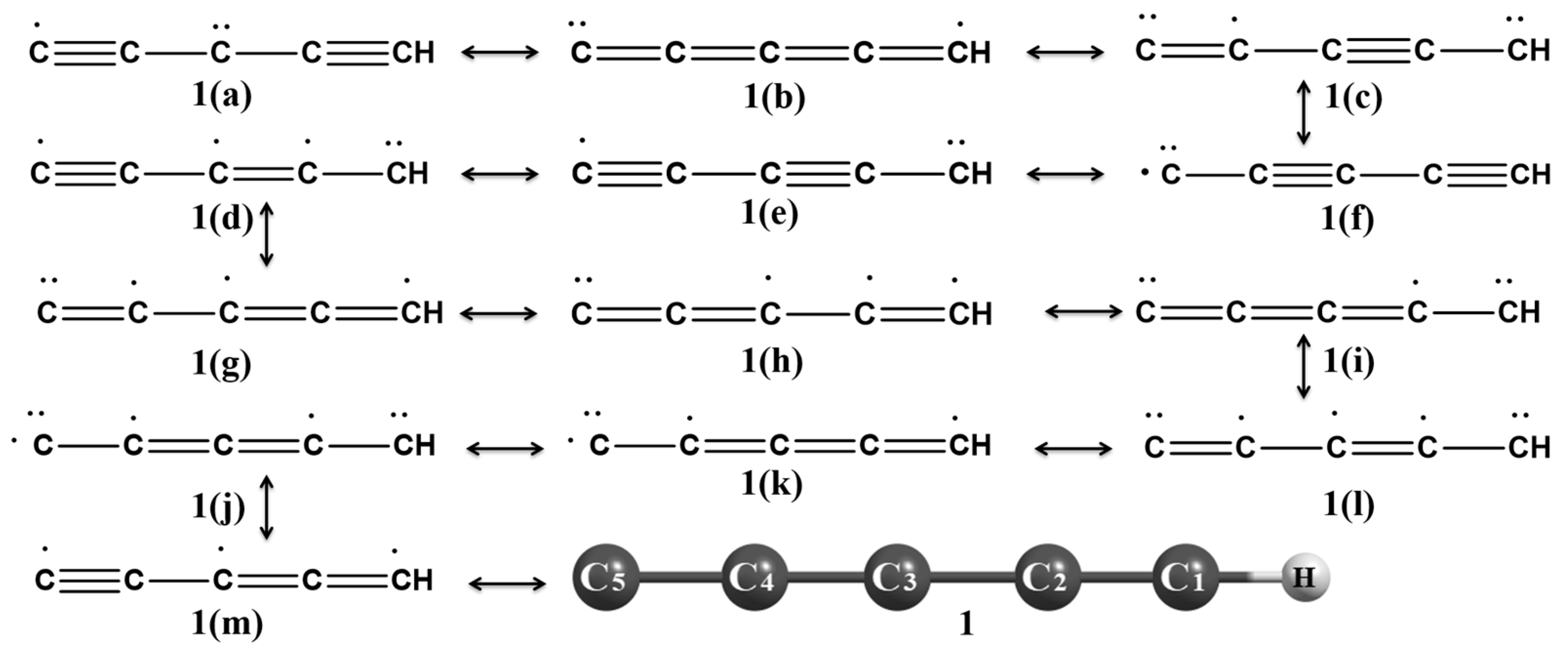
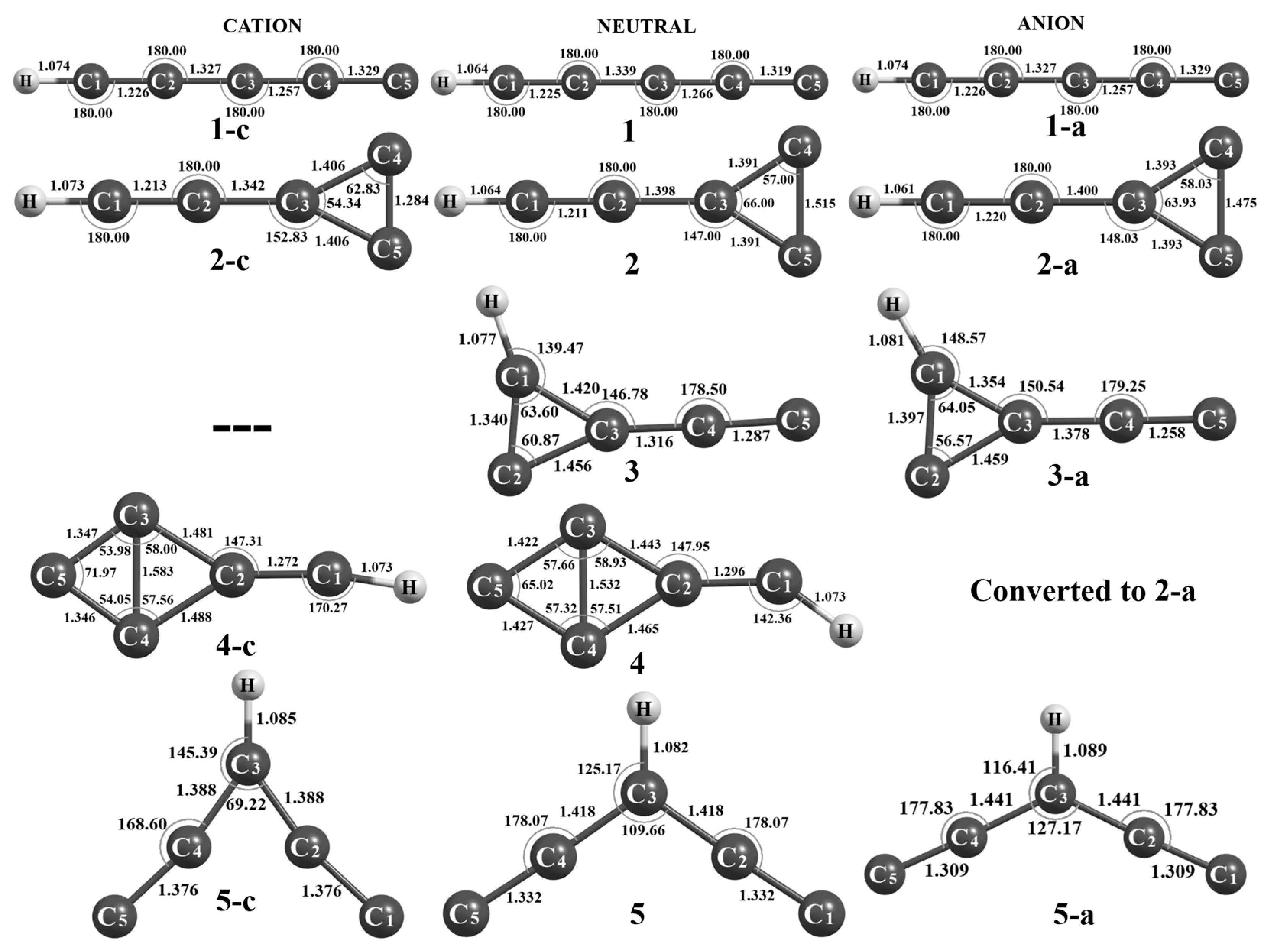
3.1.1. C5H Global Minima [Pent-1,3-diyn-5-yliden-1-yl (1)]
3.1.2. 1-Ethynylcycloprop-1-en-2-yl-3-ylidene (2) and (2λ3-Cycloprop-2-en-1-ylidene)ethenylidene (3)
3.1.3. (2λ3-Meth-1-ylidene)bicyclo[1.1.0]- But-1(3)-en-4-ylidene (4)
3.1.4. Pent-1,4-diyn-1,3,5-triyl(5)
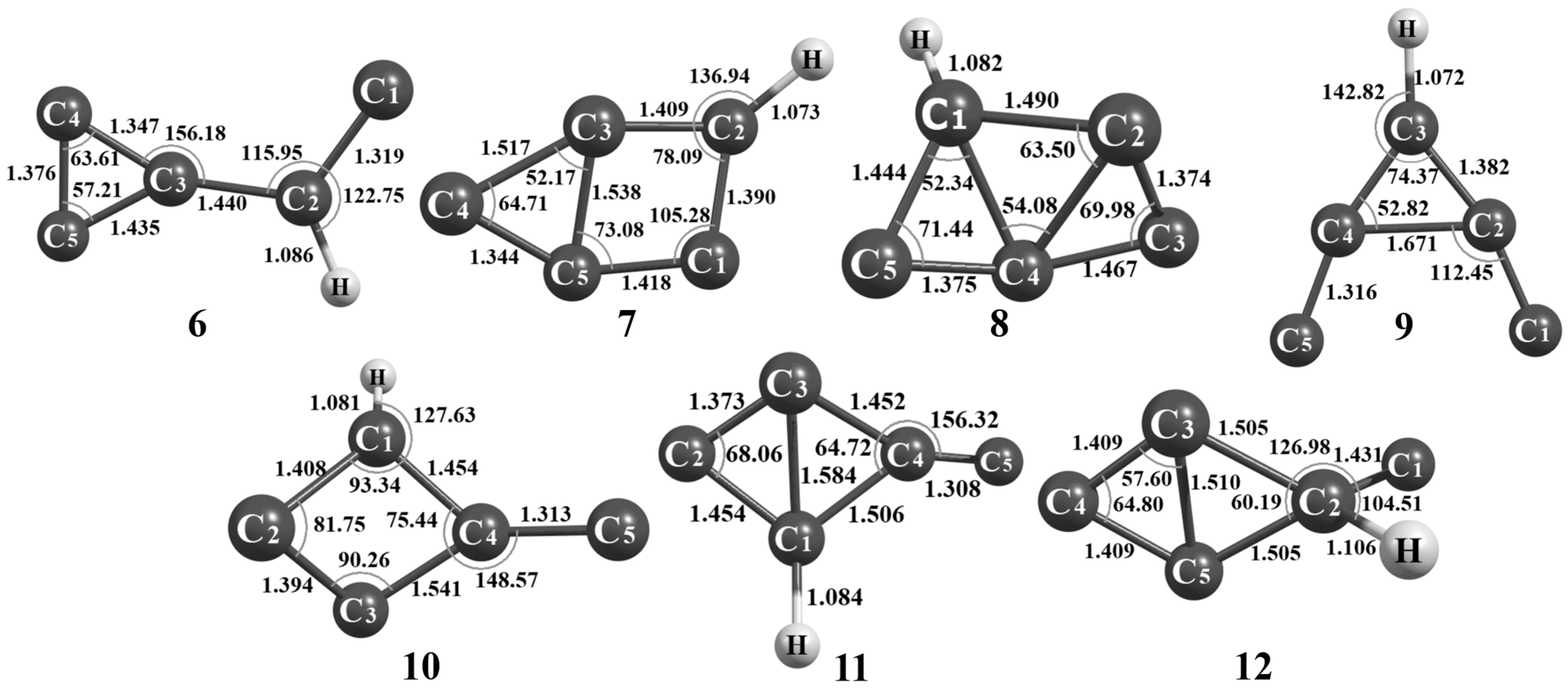
3.1.5. Other Isomers: C5H (6) to C5H (14)
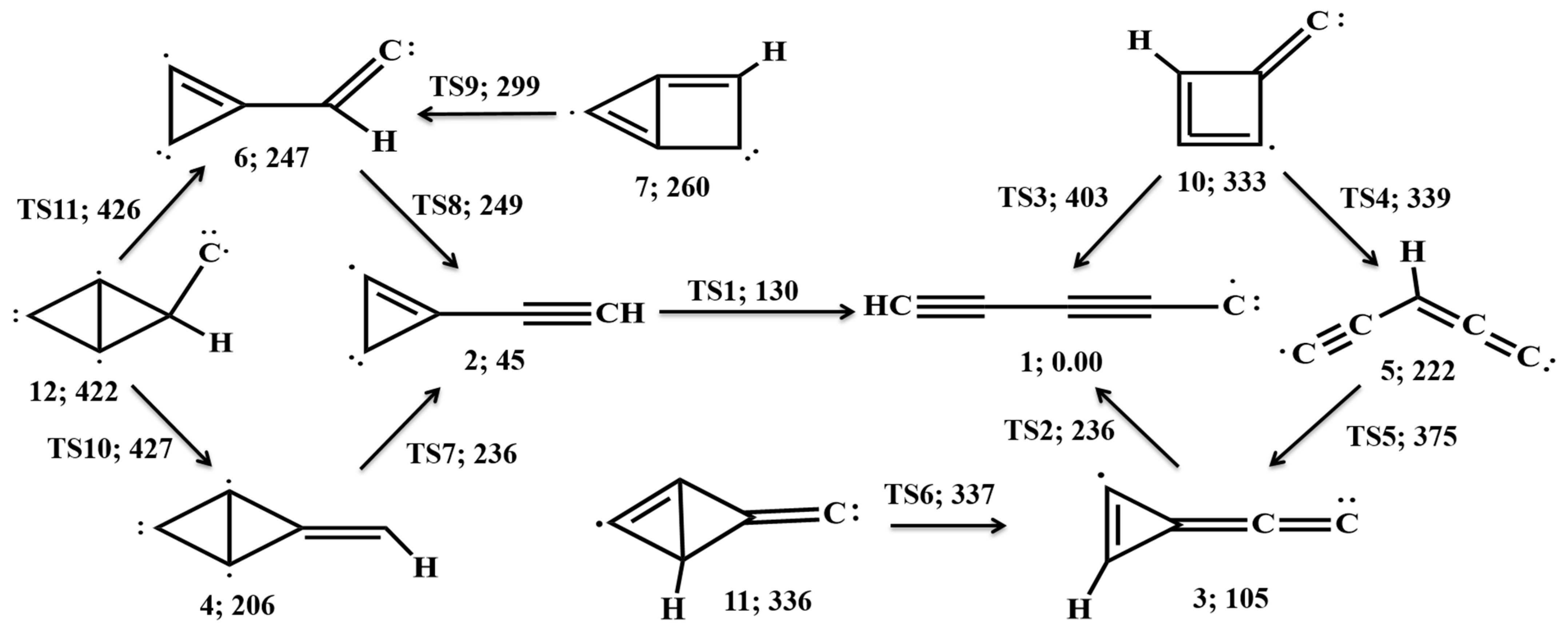
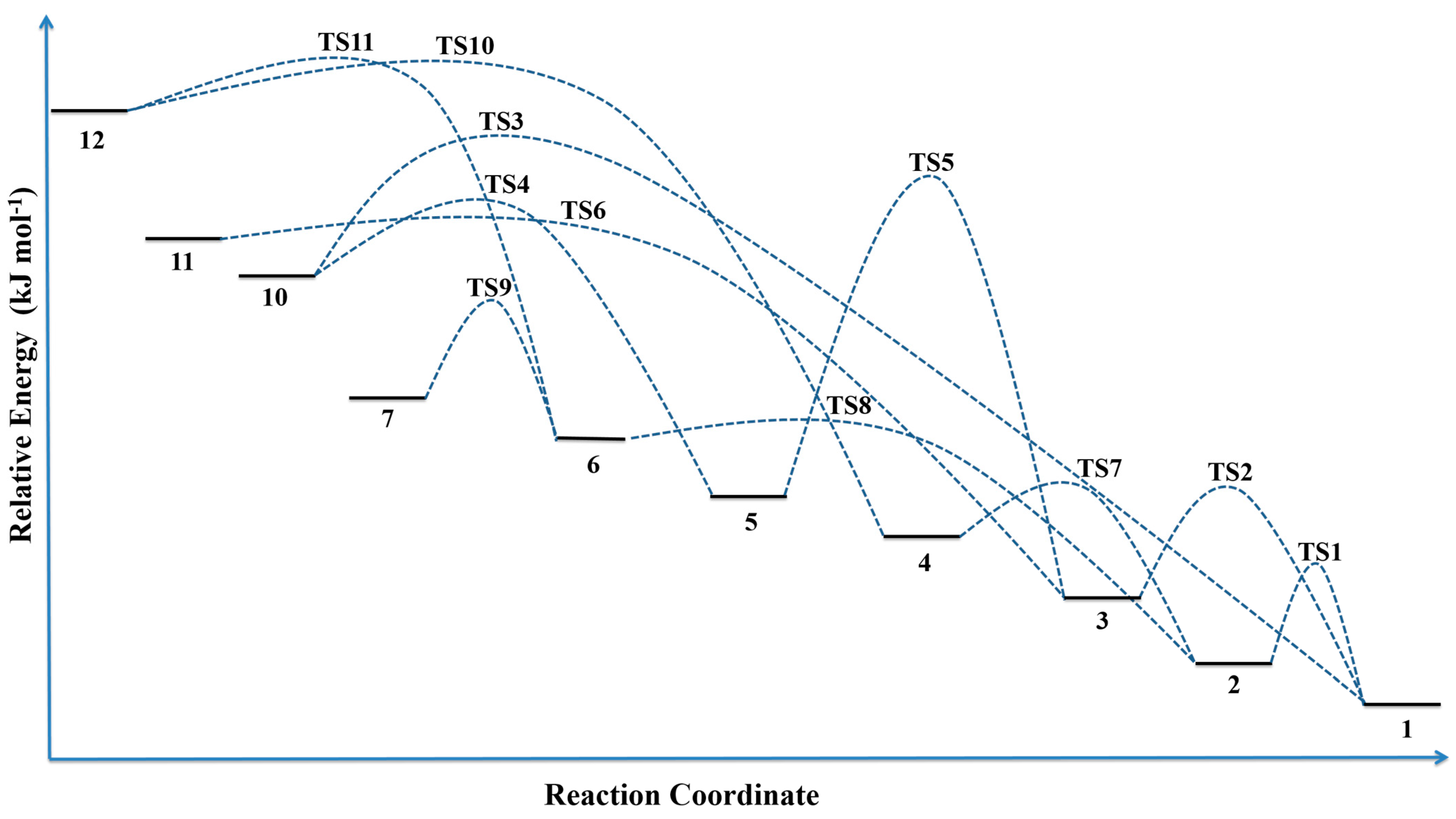
3.2. Rearrangement Scheme
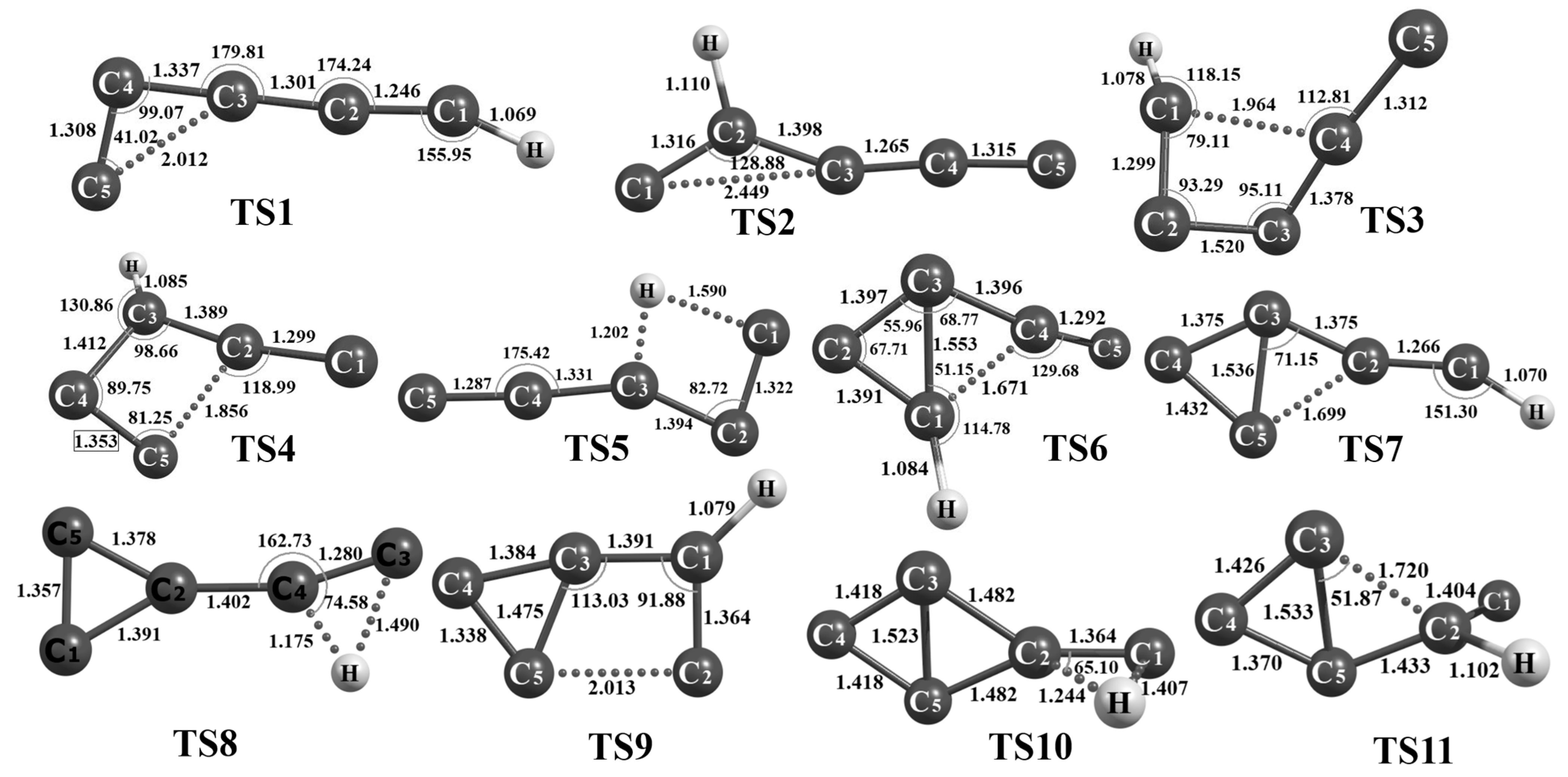
3.3. Spectroscopic Data
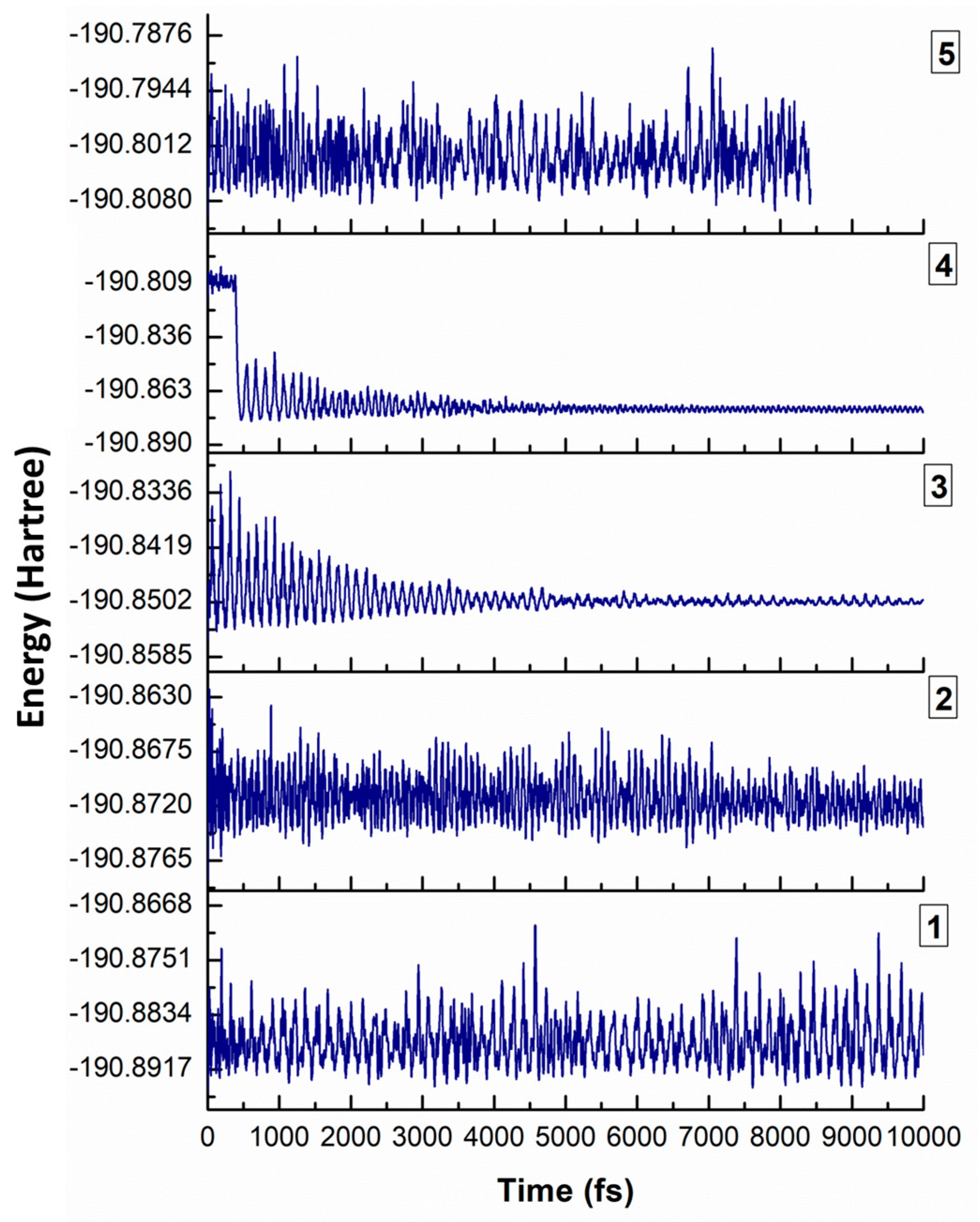
3.4. Ab Initio Molecular Dynamics Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adams, W.S. Some Results with the COUDÉ Spectrograph of the Mount Wilson Observatory. Astrophys. J. 1941, 93, 11. [Google Scholar] [CrossRef]
- Dunham, T., Jr. Interstellar neutral potassium and neutral calcium. Publ. Astron. Soc. Pac. 1937, 49, 26–28. [Google Scholar] [CrossRef]
- McKellar, A. Evidence for the Molecular Origin of Some Hitherto Unidentified Interstellar Lines. Publ. Astron. Soc. Pac. 1940, 52, 187–192. [Google Scholar] [CrossRef]
- Swings, P.; Rosenfeld, L. Considerations regarding interstellar molecules. Astrophys. J. 1937, 86, 483–486. [Google Scholar] [CrossRef]
- Endres, C.P.; Schlemmer, S.; Schilke, P.; Stutzki, J.; Müller, H.S. The cologne database for molecular spectroscopy, CDMS, in the virtual atomic and molecular data centre, VAMDC. J. Mol. Spectrosc. 2016, 327, 95–104. [Google Scholar] [CrossRef]
- Müller, H.S.; Schlöder, F.; Stutzki, J.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS: A useful tool for astronomers and spectroscopists. J. Mol. Struct. 2005, 742, 215–227. [Google Scholar] [CrossRef]
- Müller, H.S.; Thorwirth, S.; Roth, D.; Winnewisser, G. The Cologne database for molecular spectroscopy, CDMS. Astron. Astrophys. 2001, 370, L49–L52. [Google Scholar] [CrossRef]
- McGuire, B.A. 2021 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2022, 259, 30. [Google Scholar] [CrossRef]
- Mebel, A.M.; Kim, G.-S.; Kislov, V.V.; Kaiser, R.I. The reaction of tricarbon with acetylene: An ab initio/RRKM study of the potential energy surface and product branching ratios. J. Phys. Chem. A 2007, 111, 6704–6712. [Google Scholar] [CrossRef]
- Roy, T.; Ghosal, S.; Thimmakondu, V.S. Six Low-Lying Isomers of C11H8 Are Unidentified in the Laboratory–A Theoretical Study. J. Phys. Chem. A 2021, 125, 4352–4364. [Google Scholar] [CrossRef]
- Roy, T.; Satpati, S.; Thimmakondu, V.S.; Ghosal, S. Theoretical Investigation on C11H8 Bicyclic Carbene and Allene Isomers. Front. Phys. 2022, 10, 907466. [Google Scholar] [CrossRef]
- Roy, T.; Thimmakondu, V.S.; Ghosal, S. New Carbenes and Cyclic Allenes Energetically Comparable to Experimentally Known 1-Azulenylcarbene. ACS Omega 2022, 7, 30149–30160. [Google Scholar] [CrossRef]
- Schmidt, T.; Boguslavskiy, A.; Pino, T.; Ding, H.; Maier, J. Optical detection of C9H3, C11H3, and C13H3 from a hydrocarbon discharge source. Int. J. Mass Spectrom. 2003, 228, 647–654. [Google Scholar] [CrossRef]
- McGuire, B.A. 2018 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2018, 239, 17. [Google Scholar] [CrossRef]
- Woon, D.E. A correlated ab initio study of linear carbon-chain radicals CnH (n = 2−7). Chem. Phys. Lett. 1995, 244, 45–52. [Google Scholar] [CrossRef]
- Irvine, W.; Hoglund, B.; Friberg, P.; Askne, J.; Ellder, J. The increasing chemical complexity of the Taurus dark clouds-Detection of CH3CCH and C4H. Astrophys. J. 1981, 248, L113–L117. [Google Scholar] [CrossRef]
- Nyman, L.-A. Detection of CS and C2H in absorption. Astron. Astrophys. 1984, 141, 323–327. [Google Scholar]
- Pardo, J.R.; Cernicharo, J. Molecular Abundances in CRL 618. Astrophys. J. 2007, 654, 978–987. [Google Scholar] [CrossRef]
- Teyssier, D.; Fossé, D.; Gerin, M.; Pety, J.; Abergel, A.; Roueff, E. Carbon budget and carbon chemistry in Photon Dominated Regions. Astron. Astrophys. 2004, 417, 135–149. [Google Scholar] [CrossRef]
- Thaddeus, P.; Gottlieb, C.; Hjalmarson, A.; Johansson, L.; Irvine, W.; Friberg, P.; Linke, R. Astronomical identification of the C3H radical. Astrophys. J. 1985, 294, L49–L53. [Google Scholar] [CrossRef]
- Tucker, K.; Kutner, M.; Thaddeus, P. The ethynyl radical C2H-A new interstellar molecule. Astrophys. J. 1974, 193, L115–L119. [Google Scholar] [CrossRef]
- Turner, B.E.; Herbst, E.; Terzieva, R. The Physics and Chemistry of Small Translucent Molecular Clouds. XIII. The Basic Hydrocarbon Chemistry. Astrophys. J. Suppl. Ser. 2000, 126, 427–460. [Google Scholar] [CrossRef]
- Bell, M.; Feldman, P.; Watson, J.; McCarthy, M.; Travers, M.; Gottlieb, C.; Thaddeus, P. Observations of long CnH molecules in the dust cloud TMC-1. Astrophys. J. 1999, 518, 740. [Google Scholar] [CrossRef]
- Cernicharo, J.; Guélin, M.; Walmsley, C. Detection of the hyperfine structure of the C5H radical. Astron. Astrophys. 1987, 172, L5. [Google Scholar]
- Cernicharo, J.; Kahane, C.; Gomez-Gonzalez, J.; Guelin, M. Tentative detection of the C5H radical. Astron. Astrophys. 1986, 164, L1–L4. [Google Scholar]
- Cernicharo, J.; Kahane, C.; Gomez-Gonzalez, J.; Guélin, M. Detection of the 2Pi3/2 state of C5H. Astron. Astrophys. 1986, 167, L5–L7. [Google Scholar]
- Guélin, M.; Cernicharo, J.; Travers, M.; McCarthy, M.; Gottlieb, C.; Thaddeus, P.; Ohishi, M.; Saito, S.; Yamamoto, S. Detection of a new linear carbon chain radical: C7H. Astron. Astrophys. 1997, 317, L1–L4. [Google Scholar]
- Saito, S.; Kawaguchi, K.; Suzuki, H.; Ohishi, M.; Kaifu, N.; Ishikawa, S.-I. Detection of C6H in the 2Pi1/2 state toward IRC+ 10216. Publ. Astron. Soc. Jpn. 1987, 39, 193–199. [Google Scholar]
- Suzuki, H.; Ohishi, M.; Kaifu, N.; Ishikawa, S.-I.; Kasuga, T. Detection of the interstellar C6H radical. Publ. Astron. Soc. Jpn. 1986, 38, 911–917. [Google Scholar]
- Blanksby, S.J.; Dua, S.; Bowie, J.H. Generation of Two Isomers of C5H from the Corresponding Anions. A Theoretically Motivated Mass Spectrometric Study. J. Phys. Chem. A 1999, 103, 5161–5170. [Google Scholar] [CrossRef]
- Fossé, D.; Cernicharo, J.; Gerin, M.; Cox, P. Molecular carbon chains and rings in TMC-1. Astrophys. J. 2001, 552, 168. [Google Scholar] [CrossRef]
- Gottlieb, C.A.; Vrtilek, J.; Gottlieb, E.; Thaddeus, P.; Hjalmarson, A. Laboratory detection of the C3H radical. Astrophys. J. 1985, 294, L55–L58. [Google Scholar] [CrossRef]
- Liszt, H.; Pety, J.; Gerin, M.; Lucas, R. HCO, c-C3H and CF+: Three new molecules in diffuse, translucent and “spiral-arm” clouds. Astron. Astrophys. 2014, 564, A64. [Google Scholar] [CrossRef]
- McGuire, B.A.; Carroll, P.B.; Loomis, R.A.; Blake, G.A.; Hollis, J.M.; Lovas, F.J.; Jewell, P.R.; Remijan, A.J. A Search for l-C3H+ and l-C3H in Sgr B2 (N), Sgr B2 (OH), and the Dark Cloud TMC-1. Astrophys. J. 2013, 774, 56. [Google Scholar] [CrossRef]
- Yamamoto, S.; Saito, S.; Ohishi, M.; Suzuki, H.; Ishikawa, S.-I.; Kaifu, N.; Murakami, A. Laboratory and Astronomical Detection of the Cyclic H3H Radical. Astrophys. J. 1987, 322, L55. [Google Scholar] [CrossRef]
- Gottlieb, C.; Gottlieb, E.W.; Thaddeus, P. Laboratory detection of the C5H radical. Astron. Astrophys. 1986, 164, L5. [Google Scholar]
- McCarthy, M.; Chen, W.; Apponi, A.; Gottlieb, C.; Thaddeus, P. Hyperfine Structure of the C5H, C6H, and C8H Radicals. Astrophys. J. 1999, 520, 158. [Google Scholar] [CrossRef]
- Apponi, A.; Sanz, M.; Gottlieb, C.; McCarthy, M.; Thaddeus, P. The cyclic C5H radical. Astrophys. J. 2001, 547, L65. [Google Scholar] [CrossRef]
- Crawford, T.D.; Stanton, J.F.; Saeh, J.C.; Schaefer, H.F. Structure and energetics of isomers of the interstellar molecule C5H. J. Am. Chem. Soc. 1999, 121, 1902–1911. [Google Scholar] [CrossRef]
- Cabezas, C.; Agúndez, M.; Fuentetaja, R.; Endo, Y.; Marcelino, N.; Tercero, B.; Pardo, J.R.; de Vicente, P.; Cernicharo, J. Discovery of the cyclic C5H radical in TMC-1. Astron. Astrophys. 2022, 663, L2. [Google Scholar] [CrossRef]
- Cernicharo, J.; Agúndez, M.; Cabezas, C.; Fuentetaja, R.; Tercero, B.; Marcelino, N.; Endo, Y.; Pardo, J.; de Vicente, P. Discovery of C5H+ and detection of C3H+ in TMC-1 with the QUIJOTE line survey. Astron. Astrophys. 2022, 657, L16. [Google Scholar] [CrossRef]
- Cernicharo, J.; Gottlieb, C.; Guélin, M.; Killian, T.; Paubert, G.; Thaddeus, P.; Vrtilek, J. Astronomical detection of H2CCC. Astrophys. J. 1991, 368, L39–L41. [Google Scholar] [CrossRef]
- Cernicharo, J.; Gottlieb, C.; Guélin, M.; Killian, T.; Thaddeus, P.; Vrtilek, J. Astronomical detection of H2CCCC. Astrophys. J. 1991, 368, L43–L45. [Google Scholar] [CrossRef]
- Cabezas, C.; Tercero, B.; Agúndez, M.; Marcelino, N.; Pardo, J.; de Vicente, P.; Cernicharo, J. Cumulene carbenes in TMC-1: Astronomical discovery of l-H2C5. Astron. Astrophys. 2021, 650, L9. [Google Scholar] [CrossRef]
- McCarthy, M.; Travers, M.; Kovács, A.; Chen, W.; Novick, S.E.; Gottlieb, C.; Thaddeus, P. Detection and characterization of the cumulene carbenes H2C5 and H2C6. Science 1997, 275, 518–520. [Google Scholar] [CrossRef] [PubMed]
- Steglich, M.; Fulara, J.; Maity, S.; Nagy, A.; Maier, J.P. Electronic spectra of linear HC5H and cumulene carbene H2C5. J. Chem. Phys. 2015, 142, 244311. [Google Scholar] [CrossRef]
- Blanksby, S.J.; Dua, S.; Bowie, J.H.; Schröder, D.; Schwarz, H. Gas-phase syntheses of three isomeric C5H2 radical anions and their elusive neutrals. a joint experimental and theoretical study. J. Phys. Chem. A 1998, 102, 9949–9956. [Google Scholar] [CrossRef]
- Langer, W.; Velusamy, T.; Kuiper, T.; Peng, R.; McCarthy, M.; Travers, M.; Kovacs, A.; Gottlieb, C.; Thaddeus, P. First astronomical detection of the cumulene carbon chain molecule H2C6 in TMC-1. Astrophys. J. 1997, 480, L63. [Google Scholar] [CrossRef]
- McCarthy, M.C.; Thaddeus, P. Laboratory Detection of a Bent-Chain Carbene Isomer of C6H2. Astrophys. J. 2002, 569, L55. [Google Scholar] [CrossRef]
- Sattelmeyer, K.W.; Stanton, J.F. Computational studies of C6H2 isomers. J. Am. Chem. Soc. 2000, 122, 8220–8227. [Google Scholar] [CrossRef]
- Nandi, S.; McAnanama-Brereton, S.R.; Waller, M.P.; Anoop, A. A tabu-search based strategy for modeling molecular aggregates and binary reactions. Comput. Theor. Chem. 2017, 1111, 69–81. [Google Scholar] [CrossRef]
- Khatun, M.; Majumdar, R.S.; Anoop, A. A Global Optimizer for Nanoclusters. Front. Chem. 2019, 7, 644. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+ G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D. Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
- Pople, J.; Krishnan, R.; Schlegel, H.; Binkley, J. Electron correlation theories and their application to the study of simple reaction potential surfaces. Int. J. Quantum Chem. 1978, 14, 545–560. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Peterson, K.A.; Dunning, T.H., Jr. Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited. J. Chem. Phys. 2002, 117, 10548–10560. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Matthews, D.A.; Cheng, L.; Harding, M.E.; Lipparini, F.; Stopkowicz, S.; Jagau, T.-C.; Szalay, P.G.; Gauss, J.; Stanton, J.F. Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys. 2020, 152, 214108. [Google Scholar] [CrossRef]
- Thimmakondu, V.S.; Karton, A. The quest for the carbene bent-pentadiynylidene isomer of C5H2. Chem. Phys. 2018, 515, 411–417. [Google Scholar] [CrossRef]
- Thimmakondu, V.S.; Ulusoy, I.; Wilson, A.K.; Karton, A. Theoretical studies of two key low-lying carbenes of C5H2 missing in the laboratory. J. Phys. Chem. A 2019, 123, 6618–6627. [Google Scholar] [CrossRef]
- Karton, A.; Thimmakondu, V.S. From molecules with a planar tetracoordinate carbon to an astronomically known C5H2 carbene. J. Phys. Chem. A 2022, 126, 2561–2568. [Google Scholar] [CrossRef]
- Seburg, R.A.; McMahon, R.J.; Stanton, J.F.; Gauss, J. Structures and stabilities of C5H2 isomers: Quantum chemical studies. J. Am. Chem. Soc. 1997, 119, 10838–10845. [Google Scholar] [CrossRef]
- Watts, J.D.; Gauss, J.; Stanton, J.F.; Bartlett, R.J. Linear and cyclic isomers of C4. A theoretical study with coupled-cluster methods and large basis sets. J. Chem. Phys. 1992, 97, 8372–8381. [Google Scholar] [CrossRef]
- Botschwina, P. A binitio calculations on HC+5, a cation of interest to astrochemistry. J. Chem. Phys. 1991, 95, 4360–4365. [Google Scholar] [CrossRef]
- Aoki, K. Rotational constants of linear and/or bent Cn+1H+ and CnN+ (n = 1–6): A DFT study. Adv. Space Res. 2014, 54, 1651–1658. [Google Scholar] [CrossRef]
- Bennedjai, S.; Hammoutène, D.; Senent, M.L. Theoretical Characterization of C3H and C5H and Their Anions. Astrophys. J. 2019, 871, 255. [Google Scholar] [CrossRef]
| Energy Parameter | Level of Theory | Isomer-1 | Isomer-2 | Isomer-3 | Isomer-4 | Isomer-5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-c | 1 | 1-a | 2-c | 2 | 2-a | 3-c | 3 | 3-a | 4-c | 4 | 4-a | 5-c | 5 | 5-a | ||
| ∆E0 | UCCSD(T)/cc-pCVTZ | 0 | 0 | 0 | 105 | 34 | −51 | --- | 105 | −76 | --- | 160 | --- | 369 | 167 | 188 |
| UB3LYP/6-311+G(d,p) | 0 | 0 | 0 | 116 | 45 | −13 | --- | 105 | −40 | --- | 209 | −13 | 377 | 222 | −46 | |
| UB3LYP-D3/6-311+G(d,p) | 0 | 0 | 0 | 114 | 45 | −12 | --- | 104 | −41 | --- | 207 | −13 | 375 | 220 | −44 | |
| UωB97XD/6-311+G(d,p) | 0 | 0 | 0 | 96 | 17 | −45 | −1 | 87 | −74 | --- | 169 | --- | 353 | 194 | −58 | |
| ∆G298.15 | UCCSD(T)/cc-pCVTZ | 0 | 0 | 0 | 102 | 26 | −48 | 90 | −70 | 168 | 359 | 203 | 138 | |||
| UB3LYP/6-311+G(d,p) | 0 | 0 | 0 | 109 | 32 | −16 | --- | 92 | −41 | --- | 192 | −18 | 365 | 203 | −48 | |
| UωB97XD/6-311+G(d,p) | 0 | 0 | 0 | 90 | 13 | −46 | 3 | 83 | −75 | --- | 165 | --- | 340 | 204 | −60 | |
| ∆ES-T | UCCSD(T)/cc-pCVTZ | 262 | --- | −80 | 164 | --- | 132 | --- | --- | 199 | --- | --- | --- | 129 | --- | 188 |
| UB3LYP/6-311+G(d,p) | 136 | --- | −76 | 157 | --- | 108 | --- | --- | 188 | --- | --- | --- | −1 | --- | 158 | |
| UωB97XD/6-311+G(d,p) | 121 | --- | −84 | 143 | --- | 117 | 175 | --- | 203 | --- | --- | --- | 1 | --- | 162 | |
| T1 Diagnostic | UCCSD/6-311+G(d,p)// UB3LYP/6-311+G(d,p) | 0.022 | 0.040 | 0.024 | 0.027 | 0.024 | 0.027 | 0.051 | 0.049 | 0.018 | --- | 0.05 | 0.020 | 0.085 | 0.066 | 0.022 |
| IP | UCCSD(T)/cc-pCVTZ | 8.36 | --- | --- | 9.11 | --- | --- | --- | --- | --- | --- | --- | --- | 10.45 | --- | --- |
| EA | UCCSD(T)/cc-pCVTZ | --- | --- | 1.42 | --- | --- | 2.30 | --- | --- | 3.30 | --- | --- | --- | --- | --- | 3.63 |
| <S2> | UCCSD(T)/cc-pCVTZ | 0.749 | 0.749 | 0.747 | 0.750 | 0.749 | ||||||||||
| Energy Parameter | Level of Theory | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|
| ∆E0 | UCCSD(T)/cc-pCVTZ | 224 | 262 | 271 | 294 | 301 | 302 | 312 | --- |
| UB3LYP/6-311+G(d,p) | 249 | 260 | 318 | 320 | 333 | 336 | 422 | 428 | |
| UB3LYP-D3/6-311+G(d,p) | 248 | 261 | 319 | 318 | 332 | 335 | 422 | 429 | |
| UωB97XD/6-311+G(d,p) | 214 | 247 | 277 | --- | 299 | 300 | 380 | 386 | |
| ∆G298.15 | UCCSD(T)/cc-pCVTZ | 222 | 246 | 268 | 286 | 294 | 296 | 310 | --- |
| UB3LYP/6-311+G(d,p) | 228 | 248 | 304 | 296 | 318 | 320 | 405 | 413 | |
| UωB97XD/6-311+G(d,p) | 203 | 215 | 267 | --- | 293 | 294 | 373 | 376 | |
| T1 Diagnostic | UCCSD/6-311+G(d,p)// UB3LYP/6-311+G(d,p) | 0.034 | 0.050 | 0.046 | 0.034 | 0.054 | 0.044 | 0.040 | 0.058 |
| <S2> | UCCSD(T)/cc-pCVTZ | 0.749 | 0.750 | 0.747 | 0.749 | 0.751 | 0.750 | 0.750 | --- |
| Isomer | μa | μb | μc | |μ| | DJ | DK | DJK | d1 | d2 | Ae | Be | Ce | Experiment | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ae | Be | Ce | |||||||||||||
| 1-c-s | 3.47 | --- | --- | 3.47 | 1.02 × 10−4 | 1.02 × 10−4 | −2.05 × 10−4 | 0.00 | 0.00 | 2389.14 | --- | --- | --- | 2404.2 | --- |
| 1-c-t | 4.97 | --- | --- | 4.97 | 1.01 × 10−4 | 1.01 × 10−4 | −2.03 × 10−4 | 0.00 | 0.00 | 2331.84 | --- | --- | --- | --- | --- |
| 1 | 4.81 | --- | --- | 4.81 | 1.05 × 10−4 | 1.05 × 10−4 | −2.10 × 10−4 | 0.00 | 0.00 | 2375.44 | --- | --- | --- | 2395.127 | --- |
| 1-a-s | 2.98 | --- | --- | 2.98 | 1.01 × 10−4 | 1.01 × 10−4 | −2.03 × 10−4 | 0.00 | 0.00 | 2354.84 | --- | --- | --- | --- | --- |
| 1-a-t | 1.96 | --- | --- | 1.96 | 1.02 × 10−4 | 1.02 × 10−4 | −2.05 × 10−4 | 0.00 | 0.00 | 2352.48 | --- | --- | --- | --- | --- |
| 2-c-s | 2.52 | --- | --- | 2.51 | 2.53 × 10−4 | 2.21 × 10−1 | 3.22 × 10−2 | −3.01 × 10−5 | −1.82 × 10−5 | 51,117.71 | 3511.56 | 3285.84 | --- | --- | --- |
| 2-c-t | 0.83 | --- | --- | 0.83 | 2.87 × 10−4 | 2.28 × 10−1 | 3.20 × 10−2 | −3.17 × 10−5 | −1.89 × 10−5 | 46,241.09 | 3523.06 | 3273.65 | --- | --- | --- |
| 2 | 3.26 | --- | --- | 3.26 | 2.88 × 10−4 | 2.29 × 10−1 | 3.32 × 10−2 | −3.19 × 10−5 | −1.95 × 10−5 | 36,681.22 | 3555.18 | 3241.05 | 45,018.00 | 3504.06 | 3246.94 |
| 2-a-s | 6.11 | --- | --- | 6.11 | 2.83 × 10−4 | 2.26 × 10−1 | 3.29 × 10−2 | −3.11 × 10−5 | −1.88 × 10−5 | 38,715.32 | 3510.89 | 3218.98 | --- | --- | --- |
| 2-a-t | 3.59 | --- | --- | 3.59 | 2.69 × 10−4 | 1.82 × 10−1 | 2.90 × 10−2 | −2.91 × 10−5 | −1.84 × 10−5 | 48,223.49 | 3324.13 | 3109.77 | --- | --- | --- |
| 3-c-s | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 3-c-t | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 3 | 4.19 | 2.2 | 4.73 | 3.24 × 10−4 | 1.27 × 10−1 | 3.55 × 10−2 | −4.31 × 10−5 | −2.47 × 10−5 | 37,025.81 | 3624.13 | 3301.02 | --- | --- | --- | |
| 3-a-s | 5.15 | 2.75 | 5.85 | 2.96 × 10−4 | 1.09 × 10−1 | 2.70 × 10−2 | −3.51 × 10−5 | −1.96 × 10−5 | 35,410.60 | 3605.51 | 3272.32 | --- | --- | --- | |
| 3-a-t | 5.33 | 2.10 | 5.73 | 2.87 × 10−4 | 1.08 × 10−1 | 2.52 × 10−1 | −3.49 × 10−5 | −1.82 × 10−5 | 36,284.2 | 3516.49 | 3205.8 | --- | --- | --- | |
| 4-c-s | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 4-c-t | 5.62 | 0.21 | 5.62 | 5.22 × 10−4 | 1.79 × 10−1 | 9.56 × 10−3 | −8.06 × 10−5 | −1.71 × 10−5 | 33,563.59 | 4970.89 | 4329.65 | --- | --- | --- | |
| 4 | 3.78 | 0.45 | --- | 3.81 | 5.42 × 10−4 | 1.82 × 10−1 | 9.71 × 10−3 | −8.15 × 10−5 | −1.77 × 10−5 | 34,960.74 | 4813.53 | 4230.99 | --- | --- | --- |
| 4-a-s | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 4-a-s | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 5-c-s | 3.48 | --- | --- | 3.48 | 5.70 × 10−3 | 9.47 × 10−2 | −3.78 × 10−2 | −2.49 × 10−3 | −8.40 × 10−5 | 12,099.53 | 5565.98 | 3812.27 | --- | --- | --- |
| 5-c-t | 2.95 | --- | --- | 2.95 | 5.68 × 10−3 | 2.17 × 10−1 | −5.41 × 10−2 | −1.88 × 10−3 | 1.49 × 10−4 | 14,503.32 | 4145.05 | 3223.71 | --- | --- | --- |
| 5 | 3.14 | --- | --- | 3.14 | 5.73 × 10−3 | 2.23 × 10−1 | −5.46 × 10−2 | −1.91 × 10−3 | 1.51 × 10−4 | 21,155.74 | 3233.26 | 2804.62 | --- | --- | --- |
| 5-a-s | 3.5 | --- | --- | 3.5 | 4.48 × 10−4 | 1.41 × 100 | −2.96 × 10−2 | −7.57 × 10−5 | −1.74 × 10−6 | 34,412.33 | 2686.25 | 2491.74 | --- | --- | --- |
| 5-a-t | 3.26 | --- | --- | 3.26 | 4.25 × 10−4 | 1.38 × 100 | −2.83 × 10−2 | −7.48 × 10−5 | −1.68 × 10−6 | 37,841.38 | 2599.35 | 2432.27 | --- | --- | --- |
| Isomer | μa | μb | μc | |μ| | DJ | DK | DJK | d1 | d2 | Ae | Be | Ce |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 1.86 | 1.22 | --- | 2.22 | 7.58 × 10−3 | 8.80 × 10−1 | −1.43 × 10−1 | −1.86 × 10−3 | −7.05 × 10−5 | 26,343.64 | 4293.87 | 3692.08 |
| 7 | 3.05 | 0.07 | 0.08 | 3.05 | 2.22 × 10−3 | 4.22 × 10−2 | 9.70 × 10−3 | −8.71 × 10−4 | −2.32 × 10−4 | 20,151.76 | 7724.96 | 5656.38 |
| 8 | 1.07 | 1.95 | 1.01 | 2.44 | 1.62 × 10−3 | 3.61 × 10−3 | 2.30 × 10−2 | −6.21 × 10−4 | −3.61 × 10−4 | 17,421.72 | 8205.63 | 6000.80 |
| 9 | 4.88 | --- | --- | 4.88 | 5.72 × 10−2 | 9.52 × 10−2 | −1.28 × 10−1 | −2.86 × 10−2 | −2.37 × 10−3 | 9773.01 | 8461.83 | 4535.14 |
| 10 | 1.58 | 2.05 | 0.55 | 2.65 | 2.07 × 10−3 | 4.49 × 10−2 | 4.51 × 10−2 | −2.30 × 10−4 | −2.30 × 10−4 | 18,175.52 | 6034.16 | 4959.54 |
| 11 | 0.33 | 0.99 | 1.22 | 1.61 | 1.51 × 10−3 | 1.28 × 10−1 | 1.75 × 10−2 | −1.27 × 10−4 | −5.92 × 10−5 | 24,227.66 | 5367.71 | 4624.20 |
| 12 | 2.11 | 0.00 | 2.01 | 2.92 | 1.49 × 10−3 | 1.36 × 10−1 | 1.87 × 10−2 | −1.22 × 10−4 | −5.36 × 10−5 | 24,897.01 | 5066.38 | 4732.01 |
| 13 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satpati, S.; Roy, T.; Anoop, A.; Thimmakondu, V.S.; Ghosal, S. Energetic and Spectroscopic Properties of the Low-Lying Isomers of C5H: A High-Level Ab Initio Study. Atoms 2023, 11, 115. https://doi.org/10.3390/atoms11090115
Satpati S, Roy T, Anoop A, Thimmakondu VS, Ghosal S. Energetic and Spectroscopic Properties of the Low-Lying Isomers of C5H: A High-Level Ab Initio Study. Atoms. 2023; 11(9):115. https://doi.org/10.3390/atoms11090115
Chicago/Turabian StyleSatpati, Sayon, Tarun Roy, Anakuthil Anoop, Venkatesan S. Thimmakondu, and Subhas Ghosal. 2023. "Energetic and Spectroscopic Properties of the Low-Lying Isomers of C5H: A High-Level Ab Initio Study" Atoms 11, no. 9: 115. https://doi.org/10.3390/atoms11090115
APA StyleSatpati, S., Roy, T., Anoop, A., Thimmakondu, V. S., & Ghosal, S. (2023). Energetic and Spectroscopic Properties of the Low-Lying Isomers of C5H: A High-Level Ab Initio Study. Atoms, 11(9), 115. https://doi.org/10.3390/atoms11090115









