EWS Time Delay in Low Energy e−C60 Elastic Scattering
Abstract
:1. Introduction
2. Theoretical Details
3. Results and Discussion
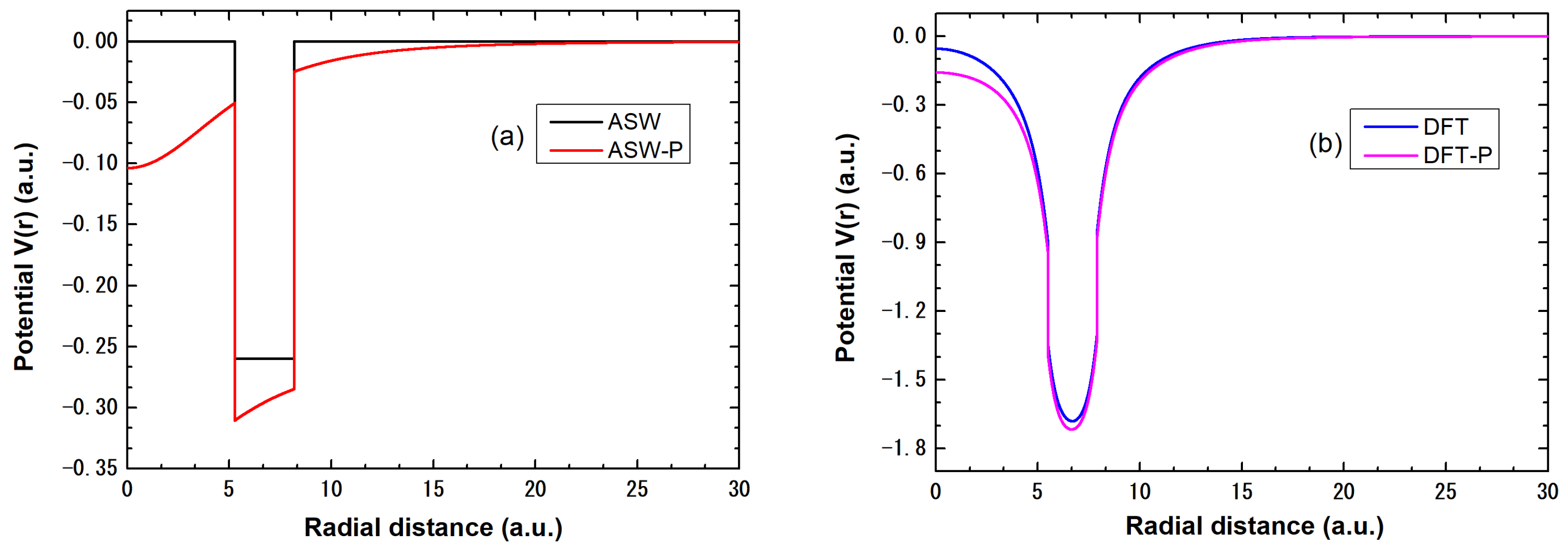
3.1. TCS and Near-Threshold Behavior of Phase Shift and Time Delay
3.2. Fano Parameterization of Resonances
3.3. Resonant Phase Shift and Time Delay
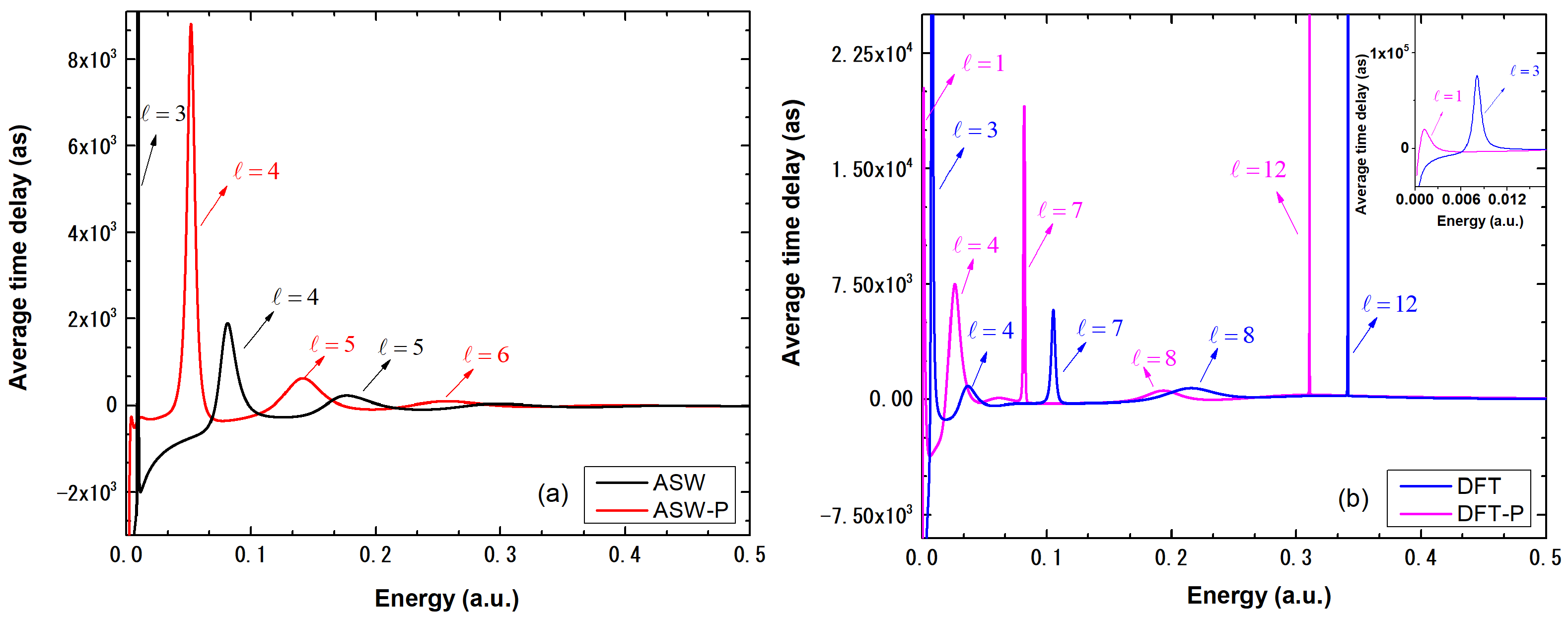
3.4. Average Time Delay
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A. Time delay in electron-C60 elastic scattering in a dirac bubble potential model. J. Phys. B At. Mol. Opt. Phys. 2018, 52, 015101. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S.; Woiciechowski, I. Partial time delays in elastic electron scattering by rectangular potential well with arising discrete levels. Eur. Phys. J. D 2019, 73, 265. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A. Time delay of slow electrons-endohedral elastic scattering. Fullerenes Nanotub. Carbon Nanostruct. 2020, 28, 10–13. [Google Scholar] [CrossRef]
- Eisenbud, L. The Formal Properties of Nuclear Collisions; Princeton University: Princeton, NJ, USA, 1948. [Google Scholar]
- Wigner, E.P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 1955, 98, 145. [Google Scholar] [CrossRef]
- Smith, F.T. Lifetime matrix in collision theory. Phys. Rev. 1960, 118, 349. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.; Woiciechowski, I. Wigner time delay of particles elastically scattered by a cluster of zero-range potentials. Phys. Rev. A 2022, 105, 012807. [Google Scholar] [CrossRef]
- Aiswarya, R.; Jose, J. An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering. Atoms 2022, 10, 77. [Google Scholar]
- Deshmukh, P.; Banerjee, S. Time delay in atomic and molecular collisions and photoionisation/photodetachment. Int. Rev. Phys. Chem. 2021, 40, 127–153. [Google Scholar] [CrossRef]
- Guenot, D.; Klünder, K.; Arnold, C.; Kroon, D.; Dahlström, J.M.; Miranda, M.; Fordell, T.; Gisselbrecht, M.; Johnsson, P.; Mauritsson, J.; et al. Photoemission-time-delay measurements and calculations close to the 3 s-ionization-cross-section minimum in ar. Phys. Rev. A 2012, 85, 053424. [Google Scholar] [CrossRef]
- Wang, H.; Chini, M.; Chen, S.; Zhang, C.H.; He, F.; Cheng, Y.; Wu, Y.; Thumm, U.; Chang, Z. Attosecond time-resolved autoionization of argon. Phys. Rev. Lett. 2010, 105, 143002. [Google Scholar] [CrossRef]
- Bain, R.; Bardsley, J. Shape resonances in atom-atom collisions. I. Radiative association. J. Phys. B At. Mol. Phys. 1972, 5, 277. [Google Scholar] [CrossRef]
- Yao, X.C.; Qi, R.; Liu, X.P.; Wang, X.Q.; Wang, Y.X.; Wu, Y.P.; Chen, H.Z.; Zhang, P.; Zhai, H.; Chen, Y.A.; et al. Degenerate Bose gases near ad-wave shape resonance. Nat. Phys. 2019, 15, 570–576. [Google Scholar] [CrossRef]
- Bianconi, A.; Congiu-Castellano, A.; Durham, P.; Hasnain, S.; Phillips, S. The CO bond angle of carboxymyoglobin determined by angular-resolved XANES spectroscopy. Nature 1985, 318, 685–687. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Petersen, H.; Brown, F.C.; Bachrach, R. K-shell photoabsorption spectra of N2 and N2O using synchrotron radiation. Phys. Rev. A 1978, 17, 1907. [Google Scholar] [CrossRef]
- Bianconi, A. On the possibility of new high Tc superconductors by producing metal heterostructures as in the cuprate perovskites. Solid State Commun. 1994, 89, 933–936. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257. [Google Scholar] [CrossRef]
- Chai, Y.; Guo, T.; Jin, C.; Haufler, R.E.; Chibante, L.F.; Fure, J.; Wang, L.; Alford, J.M.; Smalley, R.E. Fullerenes with metals inside. J. Phys. Chem. 1991, 95, 7564–7568. [Google Scholar] [CrossRef]
- Deshmukh, P.; Jose, J.; Varma, H.; Manson, S. Electronic structure and dynamics of confined atoms. Eur. Phys. J. D 2021, 75, 166. [Google Scholar] [CrossRef]
- Hartman, K.B.; Wilson, L.J.; Rosenblum, M.G. Detecting and treating cancer with nanotechnology. Mol. Diagn. Ther. 2008, 12, 1–14. [Google Scholar] [CrossRef]
- Shu, C.Y.; Ma, X.Y.; Zhang, J.F.; Corwin, F.D.; Sim, J.H.; Zhang, E.Y.; Dorn, H.C.; Gibson, H.W.; Fatouros, P.P.; Wang, C.R.; et al. Conjugation of a water-soluble gadolinium endohedral fulleride with an antibody as a magnetic resonance imaging contrast agent. Bioconj. Chem. 2008, 19, 651–655. [Google Scholar] [CrossRef] [PubMed]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.O.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; Van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 2009, 8, 208–212. [Google Scholar] [CrossRef]
- Hedley, G.J.; Ward, A.J.; Alekseev, A.; Howells, C.T.; Martins, E.R.; Serrano, L.A.; Cooke, G.; Ruseckas, A.; Samuel, I.D. Determining the optimum morphology in high-performance polymer-fullerene organic photovoltaic cells. Nat. Commun. 2013, 4, 2867. [Google Scholar] [CrossRef] [PubMed]
- Harneit, W.; Boehme, C.; Schaefer, S.; Huebener, K.; Fostiropoulos, K.; Lips, K. Room temperature electrical detection of spin coherence in C60. Phys. Rev. Lett. 2007, 98, 216601. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Kim, Y.H.; Dillon, A.; Heben, M.; Zhang, S. Hydrogen storage in novel organometallic buckyballs. Phys. Rev. Lett. 2005, 94, 155504. [Google Scholar] [CrossRef] [PubMed]
- Zadik, R.H.; Takabayashi, Y.; Klupp, G.; Colman, R.H.; Ganin, A.Y.; Potočnik, A.; Jeglič, P.; Arčon, D.; Matus, P.; Kamarás, K.; et al. Optimized unconventional superconductivity in a molecular Jahn-Teller metal. Sci. Adv. 2015, 1, e1500059. [Google Scholar] [CrossRef] [PubMed]
- Campbell, E.K.; Holz, M.; Gerlich, D.; Maier, J.P. Laboratory confirmation of as the carrier of two diffuse interstellar bands. Nature 2015, 523, 322–323. [Google Scholar] [CrossRef] [PubMed]
- Cami, J.; Bernard-Salas, J.; Peeters, E.; Malek, S.E. Detection of C60 and C70 in a young planetary nebula. Science 2010, 329, 1180–1182. [Google Scholar] [CrossRef]
- Cordiner, M.; Linnartz, H.; Cox, N.; Cami, J.; Najarro, F.; Proffitt, C.; Lallement, R.; Ehrenfreund, P.; Foing, B.; Gull, T.; et al. Confirming interstellar using the hubble space telescope. Astrophys. J. Lett. 2019, 875, L28. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765. [Google Scholar] [CrossRef]
- Magrakvelidze, M.; Anstine, D.M.; Dixit, G.; Madjet, M.E.A.; Chakraborty, H.S. Attosecond structures from the molecular cavity in fullerene photoemission time delay. Phys. Rev. A 2015, 91, 053407. [Google Scholar] [CrossRef]
- Biswas, S.; Trabattoni, A.; Rupp, P.; Magrakvelidze, M.; Madjet, M.E.A.; De Giovannini, U.; Castrovilli, M.C.; Galli, M.; Liu, Q.; Månsson, E.P.; et al. Attosecond correlated electron dynamics at C60 giant plasmon resonance. arXiv 2021, arXiv:2111.14464. [Google Scholar]
- Amusia, M.Y.; Chernysheva, L.V. Time delay of photoionization by Endohedrals. JETP Lett. 2020, 112, 219–224. [Google Scholar] [CrossRef]
- Dixit, G.; Chakraborty, H.S.; Madjet, M.E.A. Time delay in the recoiling valence photoemission of ar endohedrally confined in C60. Phys. Rev. Lett. 2013, 111, 203003. [Google Scholar] [CrossRef] [PubMed]
- Thuppilakkadan, A.; Banerjee, S.; Varma, H.R. Modifications in the angular photoemission time delay in Ar@ : Coulomb confinement resonance as an amplifier of the spin-orbit-interaction-activated interchannel coupling effect. Phys. Rev. A 2023, 107, 052804. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V. Elastic electron scattering by fullerene C60. Phys. Rev. A 2006, 73, 012711. [Google Scholar] [CrossRef]
- Hargreaves, L.; Lohmann, B.; Winstead, C.; McKoy, V. Elastic scattering of intermediate-energy electrons from C60 molecules. Phys. Rev. A 2010, 82, 062716. [Google Scholar] [CrossRef]
- Gianturco, F.; Lucchese, R.; Sanna, N. Computed elastic cross sections and angular distributions of low-energy electron scattering from gas phase C60 fullerene. J. Phys. At. Mol. Opt. Phys. 1999, 32, 2181. [Google Scholar] [CrossRef]
- Tanaka, H.; Boesten, L.; Onda, K.; Ohashi, O. Crossed-beam experiment for the scattering of low energy electrons from gas phase C60. J. Phys. Soc. Jpn. 1994, 63, 485–492. [Google Scholar] [CrossRef]
- Tanaka, H.; Hoshino, M.; Brunger, M. Elastic and inelastic scattering of low-energy electrons from gas-phase C60: Elastic scattering angular distributions and coexisting solid-state features revisited. Eur. Phys. J. D 2021, 75, 293. [Google Scholar] [CrossRef]
- Madjet, M.E.; Chakraborty, H.S.; Rost, J.M.; Manson, S.T. Photoionization of C60: A model study. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 105101. [Google Scholar] [CrossRef]
- Choi, J.; Chang, E.; Anstine, D.M.; Madjet, M.E.A.; Chakraborty, H.S. Effects of exchange-correlation potentials on the density-functional description of C60 versus C240 photoionization. Phys. Rev. A 2017, 95, 023404. [Google Scholar] [CrossRef]
- Dolmatov, V.; Cooper, M.; Hunter, M. Electron elastic scattering off endohedral fullerenes A@ C60: The initial insight. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 115002. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.; Dolmatov, V. Angle-differential elastic-electron scattering off C60: A simple semi-empirical theory versus experiment. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 085201. [Google Scholar] [CrossRef]
- Baltenkov, A.; Manson, S.; Msezane, A. Jellium model potentials for the C60 molecule and the photoionization of endohedral atoms, A@C60. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 185103. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Dolmatov, V.; Amusia, M.Y.; Chernysheva, L. Effects of target polarization in electron elastic scattering off endohedral A@C60. Phys. Rev. A 2017, 95, 012709. [Google Scholar] [CrossRef]
- Aiswarya, R.; Shaik, R.; Jose, J.; Varma, H.R.; Chakraborty, H.S. Simultaneous real and momentum space electron diffraction from a fullerene molecule. arXiv 2024, arXiv:2402.08103. [Google Scholar]
- Rüdel, A.; Hentges, R.; Becker, U.; Chakraborty, H.S.; Madjet, M.E.; Rost, J.M. Imaging delocalized electron clouds: Photoionization of C60 in fourier reciprocal space. Phys. Rev. Lett. 2002, 89, 125503. [Google Scholar] [CrossRef]
- Thijssen, J.M. Computational Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Joachain, C.J. Quantum Collision Theory; North Holland Publishing Company: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Zhang, S.; Jin, J. Computation of Special Functions; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Scully, S.; Emmons, E.; Gharaibeh, M.; Phaneuf, R.; Kilcoyne, A.; Schlachter, A.; Schippers, S.; Müller, A.; Chakraborty, H.; Madjet, M.; et al. Photoexcitation of a volume plasmon in C60 ions. Phys. Rev. Lett. 2005, 94, 065503. [Google Scholar] [CrossRef] [PubMed]
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866. [Google Scholar] [CrossRef]
- Sarswat, S.; Aiswarya, R.; Jose, J. Shannon entropy of resonant scattered state in the e-C60 elastic collision. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 055003. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.; Krakov, B. Photodetachment of negative ions. Phys. Lett. A 1998, 243, 99–105. [Google Scholar] [CrossRef]
- Wigner, E.P. On the behavior of cross sections near thresholds. Phys. Rev. 1948, 73, 1002. [Google Scholar] [CrossRef]
- Baral, S.; Jose, J.; Deshmukh, P.; Manson, S. 6p Cooper minima in the photoionization in high-Z atoms. In Proceedings of the APS Division of Atomic, Molecular and Optical Physics Meeting Abstracts, Orlando, FL, USA, 30 May–3 June 2022. [Google Scholar]
- Deshmukh, P.; Mandal, A.; Saha, S.; Kheifets, A.; Dolmatov, V.; Manson, S. Attosecond time delay in the photoionization of endohedral atoms A@C60: A probe of confinement resonances. Phys. Rev. A 2014, 89, 053424. [Google Scholar] [CrossRef]



| DFT-P | ASW-P | ASW | GASW | Lorentzian | Shell | |
|---|---|---|---|---|---|---|
| [44] | [57] | [57] | [58] | |||
| Resonance 1 | 0.0013 () | 0.0524 () | 0.0107 () | 0.0691 () | 0.0908 () | 0.0364 () |
| Resonance 2 | 0.0258 () | 0.1380 () | 0.0815 () | 0.1628 () | 0.1988 () | 0.1301 () |
| Resonance 3 | 0.0818 () | 0.2350 () | 0.1835 () | 0.3359 () | 0.2738 () | |
| Resonance 4 | 0.1920 () | |||||
| Resonance 5 | 0.3109 () |
| Fano Parameters | |||||
|---|---|---|---|---|---|
| Model Potential | ℓ | q | |||
| a.u. | a.u. | ||||
| ASW | 3 | 0.0092 | 28.00 | 0.08 | 8.00 |
| 4 | 0.0795 | 2.69 | 10.40 | 82.00 | |
| 5 | 0.1620 | 1.19 | 31.00 | 148.00 | |
| ASW-P | 4 | 0.0524 | −419.30 | 4.40 | 2.90 |
| 5 | 0.1380 | 3.90 | 26.00 | 29.00 | |
| 6 | 0.2350 | 1.69 | 60.00 | 76.00 | |
| Fano Parameters | |||||
|---|---|---|---|---|---|
| Model Potential | ℓ | q | |||
| a.u. | a.u. | ||||
| DFT | 3 | 0.0080 | 6.23 | 0.60 | 135.00 |
| 4 | 0.0340 | 1.65 | 11.40 | 359.00 | |
| 7 | 0.1050 | −21.20 | 2.50 | 2.00 | |
| 8 | 0.2120 | 12.45 | 28.20 | 3.20 | |
| 12 | 0.3414 | −5.60 | 0.09 | 12.00 | |
| DFT-P | 1 | 0.0013 | 2.48 | 1.35 | 920.00 |
| 4 | 0.0258 | 2.79 | 5.50 | 228.00 | |
| 7 | 0.0818 | −9.30 | 0.75 | 13.10 | |
| 8 | 0.1920 | −15.25 | 20.60 | 2.40 | |
| 12 | 0.3109 | −4.53 | 0.50 | 16.70 | |
| Resonant Partial Wave | ASW | ASW-P | ||
|---|---|---|---|---|
| ℓ | Energy (a.u.) | Time Delay (fs) | Energy (a.u.) | Time Delay (fs) |
| 3 | 0.0092 | 410.45 | – | – |
| 4 | 0.0795 | 4.73 | 0.0524 | 11.09 |
| 5 | 0.1620 | 1.32 | 0.1380 | 1.89 |
| 6 | – | – | 0.2350 | 0.75 |
| Resonant Partial Wave | DFT | DFT-P | ||
|---|---|---|---|---|
| ℓ | Energy (a.u.) | Time Delay (fs) | Energy (a.u.) | Time Delay (fs) |
| 1 | – | – | 0.0013 | 29.68 |
| 3 | 0.0080 | 81.60 | – | – |
| 4 | 0.0340 | 4.12 | 0.0258 | 8.49 |
| 7 | 0.1050 | 18.79 | 0.0818 | 65.48 |
| 8 | 0.2120 | 1.63 | 0.1920 | 2.26 |
| 12 | 0.3414 | 227.29 | 0.3109 | 237.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
R., A.; Shaik, R.; Jose, J.; Varma, H.R.; Chakraborty, H.S. EWS Time Delay in Low Energy e−C60 Elastic Scattering. Atoms 2024, 12, 18. https://doi.org/10.3390/atoms12030018
R. A, Shaik R, Jose J, Varma HR, Chakraborty HS. EWS Time Delay in Low Energy e−C60 Elastic Scattering. Atoms. 2024; 12(3):18. https://doi.org/10.3390/atoms12030018
Chicago/Turabian StyleR., Aiswarya, Rasheed Shaik, Jobin Jose, Hari R. Varma, and Himadri S. Chakraborty. 2024. "EWS Time Delay in Low Energy e−C60 Elastic Scattering" Atoms 12, no. 3: 18. https://doi.org/10.3390/atoms12030018
APA StyleR., A., Shaik, R., Jose, J., Varma, H. R., & Chakraborty, H. S. (2024). EWS Time Delay in Low Energy e−C60 Elastic Scattering. Atoms, 12(3), 18. https://doi.org/10.3390/atoms12030018








