A Collisional-Radiative Model for Kr III Ions
Abstract
:1. Intoduction
2. Theoretical Approach
2.1. MCDHF
2.2. RDW Approximation
3. Results and Discussion
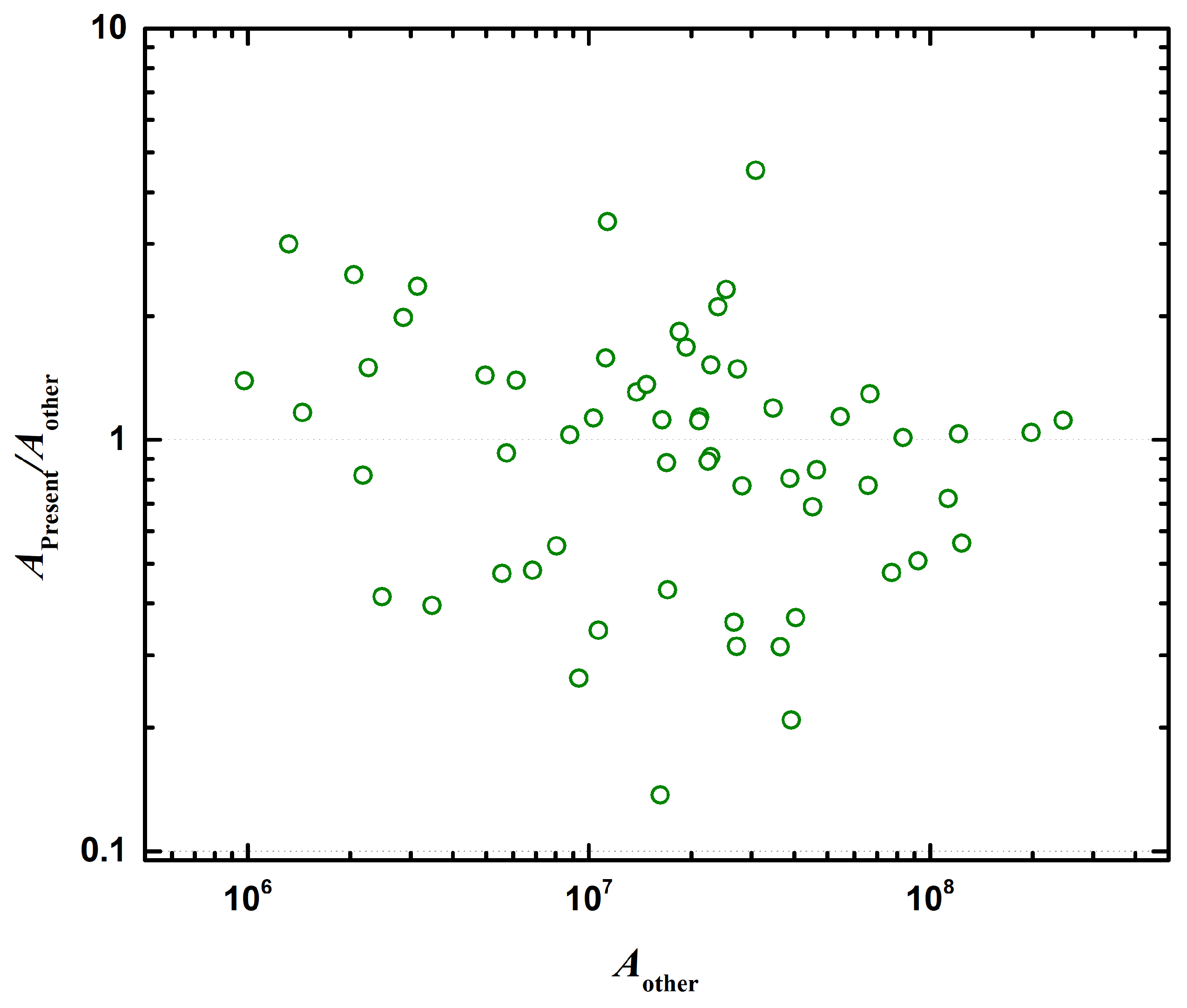
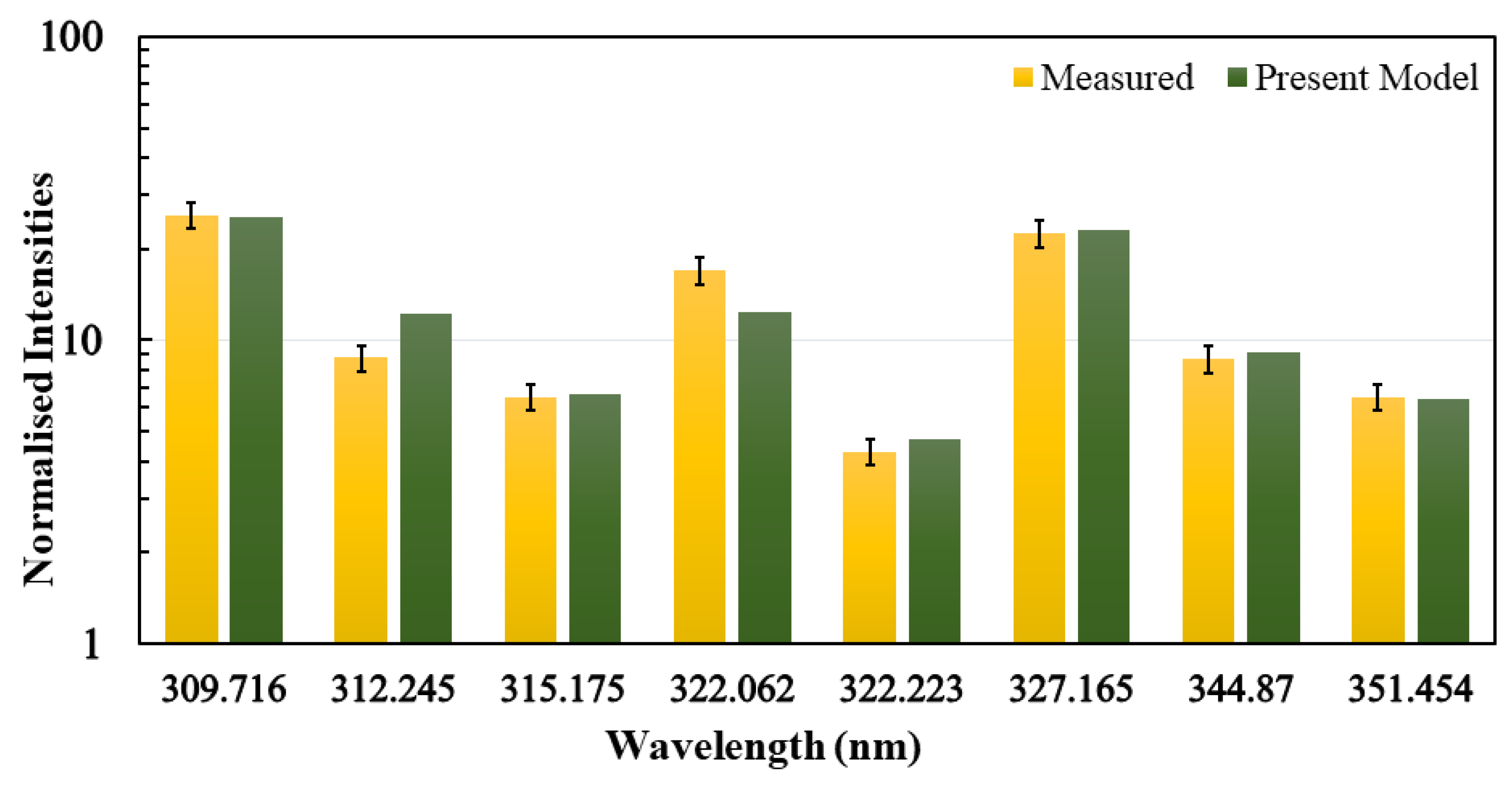
3.1. Energies and Transition Rates
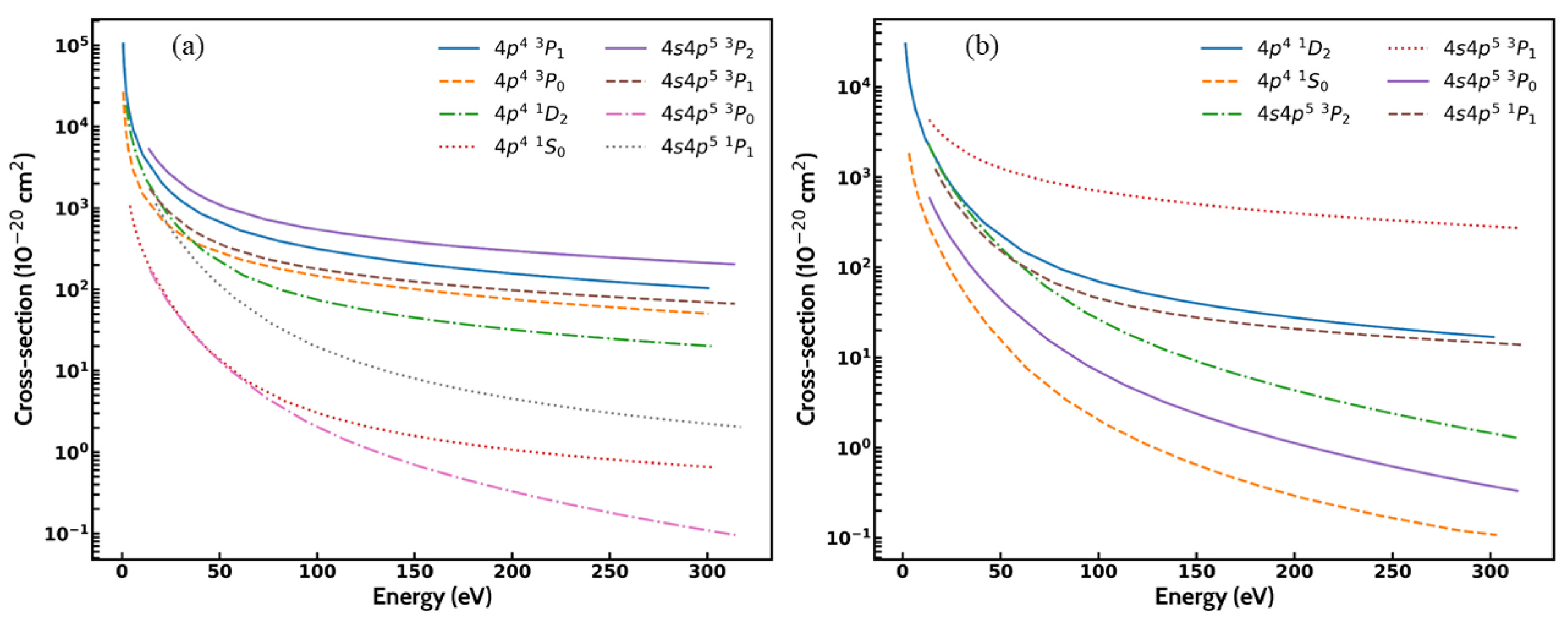
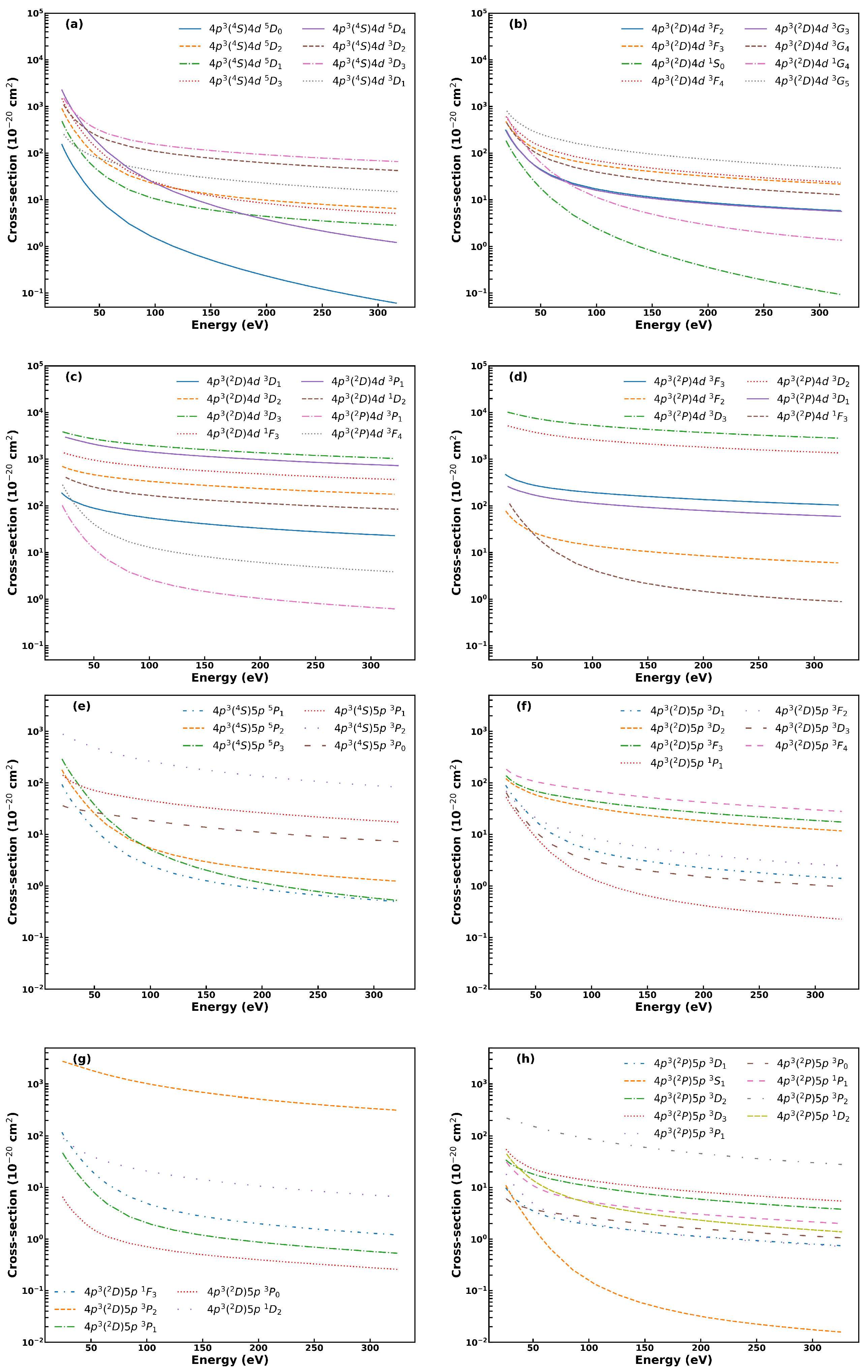
3.2. EIE Cross-Sections
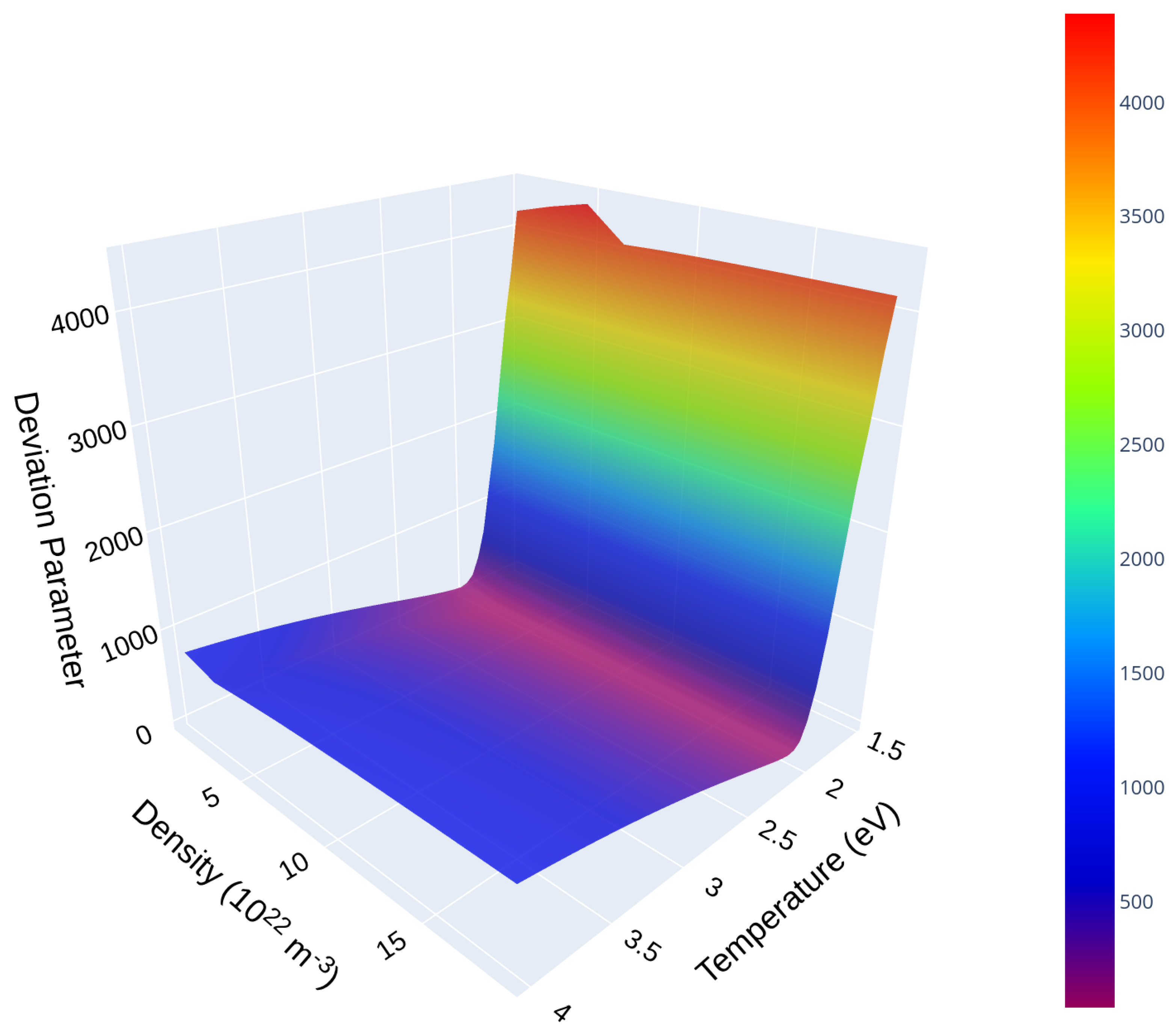
3.3. CR Model for Kr III
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sterling, N. Atomic data for neutron-capture elements-II. Photoionization and recombination properties of low-charge krypton ions. Astron. Astrophys. 2011, 533, A62. [Google Scholar] [CrossRef]
- Cardelli, J.A.; Meyer, D.M. The abundance of interstellar krypton. Astrophys. J. 1997, 477, L57. [Google Scholar] [CrossRef]
- Morton, D.C. Atomic data for resonance absorption lines. II. Wavelengths longward of the Lyman limit for heavy elements. Astrophys. J. Suppl. Ser. 2000, 130, 403. [Google Scholar] [CrossRef]
- Gupta, S.; Oishi, T.; Murakami, I. Study of Electron Impact Excitation of Na-like Kr Ion for Impurity Seeding Experiment in Large Helical Device. Atoms 2023, 11, 142. [Google Scholar] [CrossRef]
- Priti; Gangwar, R.K.; Srivastava, R. Collisional-radiative model of xenon plasma with calculated electron-impact fine-structure excitation cross-sections. Plasma Sources Sci. Technol. 2019, 28, 025003. [Google Scholar] [CrossRef]
- Hill, C. Summary Report of a Consultancy Meeting in Preparation of a Coordinated Research Project on Atomic Data for Injected Impurities in Fusion Plasmas; International Atomic Energy Agency: Vienna, Austria, 2022. Available online: https://www-nds.iaea.org/publications/indc/indc-nds-0854 (accessed on 30 June 2024).
- Beiersdorfer, P. Highly charged ions in magnetic fusion plasmas: Research opportunities and diagnostic necessities. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 144017. [Google Scholar] [CrossRef]
- Belmonte, M.T.; Gavanski, L.; Djurović, S.; Mar, S.; Aparicio, J.A. Experimental transition probabilities and oscillator strengths of doubly ionised krypton in the ultraviolet region. J. Quant. Spectrosc. Radiat. Transf. 2021, 271, 107703. [Google Scholar] [CrossRef]
- Rathi, S.; Sharma, L. Extended calculations of atomic structure parameters for Na-like Ar, Kr and Xe ions using relativistic MCDHF and MBPT methods. Atoms 2022, 10, 131. [Google Scholar] [CrossRef]
- Srivastava, R.; Stauffer, A.; Sharma, L. Excitation of the metastable states of the noble gases. Phys. Rev. A 2006, 74, 012715. [Google Scholar] [CrossRef]
- Li, W.; Jönsson, P.; Amarsi, A.M.; Li, M.C.; Grumer, J. Extended atomic data for oxygen abundance analyses. Astron. Astrophys. 2023, 674, A54. [Google Scholar] [CrossRef]
- Linnell, J.A.; Gallimore, A.D. Efficiency analysis of a Hall thruster operating with krypton and xenon. J. Propuls. Power 2006, 22, 1402–1418. [Google Scholar] [CrossRef]
- Prince, B.D.; Bemish, R.J.; Chiu, Y.H. Emission-excitation cross sections relevant to krypton-propelled electric thrusters. J. Propuls. Power 2015, 31, 725–736. [Google Scholar] [CrossRef]
- Zhu, X.; Pu, Y. Determination of non-Maxwellian electron energy distributions in low-pressure plasmas by using the optical emission spectroscopy and a collisional-radiative model. Plasma Sci. Technol. 2011, 13, 267. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Srivastava, R.; Stafford, L. Spectroscopic diagnostics of low-pressure inductively coupled Kr plasma using a collisional—Radiative model with fully relativistic cross sections. Plasma Sources Sci. Technol. 2016, 25, 035025. [Google Scholar] [CrossRef]
- Agrawal, A.; Gupta, S.; Sharma, L.; Srivastava, R. Spectroscopic study of Kr+ plasma through a detailed collisional radiative plasma model with extended ground, metastable and quasi-metastable electron impact excitation cross-section calculations. Spectrochim. Acta Part B At. Spectrosc. 2024, 217, 106953. [Google Scholar] [CrossRef]
- Kaur, S.; Srivastava, R.; McEachran, R.; Stauffer, A. Electron impact excitation of the states of Ar, Kr and Xe atoms. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 4833. [Google Scholar] [CrossRef]
- Grant, I. Relativistic calculation of atomic structures. Adv. Phys. 1970, 19, 747–811. [Google Scholar] [CrossRef]
- Sharma, L.; Surzhykov, A.; Srivastava, R.; Fritzsche, S. Electron-impact excitation of singly charged metal ions. Phys. Review. A 2011, 83, 062701. [Google Scholar] [CrossRef]
- Fischer, C.F.; Godefroid, M.; Brage, T.; Jönsson, P.; Gaigalas, G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 182004. [Google Scholar] [CrossRef]
- Fischer, C.F.; Gaigalas, G.; Jönsson, P.; Bieroń, J. GRASP2018—A Fortran 95 version of the general relativistic atomic structure package. Comput. Phys. Commun. 2019, 237, 184–187. [Google Scholar] [CrossRef]
- Rathi, S.; Sharma, L. Benchmarking calculations of level energies, transition parameters and electron impact excitation cross sections of S-like Xe38+. Spectrochim. Acta Part B At. Spectrosc. 2024, 214, 106897. [Google Scholar] [CrossRef]
- Malker, P.; Sharma, L. Electron impact excitation of Ge-like Te20+–Cd16+ ions. Atoms 2022, 10. [Google Scholar] [CrossRef]
- Bharti, S.; Sharma, L.; Srivastava, R. Electron impact excitation of Ge-like to Cu-like xenon ions in the extreme ultraviolet. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 165001. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.11); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: https://physics.nist.gov/asd (accessed on 16 November 2023).
- Saloman, E.B. Energy levels and observed spectral lines of krypton, Kr I through Kr XXXVI. J. Phys. Chem. Ref. Data 2007, 36, 215–386. [Google Scholar] [CrossRef]
- Bredice, F.; Almandos, J.R.; Gallardo, M.; Di Rocco, H.; Trigueiros, A. Revised and extended analysis of the low configurations in Kr III. JOSA B 1988, 5, 222–235. [Google Scholar] [CrossRef]
- Almandos, J.R.; Bredice, F.; Raineri, M.; Gallardo, M.; Trigueiros, A. New energy levels of the Kr III spectrum. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 5643. [Google Scholar] [CrossRef]
- Raineri, M.; Almandos, J.R.; Bredice, F.; Gallardo, M.; Trigueiros, A.; Pettersson, S. Weighted oscillator strengths for Kr III spectrum. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 25–42. [Google Scholar] [CrossRef]
- Gu, M.F. Flexible Atomic Code (v.1.1.5). Online. 2017. Available online: https://www.amdis.iaea.org/FAC/ (accessed on 10 October 2022).
| Level | Energies (eV) | Level | Energies (eV) | ||
|---|---|---|---|---|---|
| NIST | Present | NIST | Present | ||
| 0 | 0 | 24.03125 | 23.6193 | ||
| 0.56393 | 0.5428 | 24.035001 | 23.4991 | ||
| 0.65872 | 0.6369 | 24.067844 | 23.6501 | ||
| 1.81566 | 1.9110 | 24.172308 | 23.8821 | ||
| 4.10135 | 3.9061 | 24.236183 | 23.7685 | ||
| 14.373603 | 13.7131 | 24.260546 | 23.8377 | ||
| 14.801262 | 14.1146 | 24.336391 | 25.0925 | ||
| 15.069406 | 14.3671 | 24.562234 | 24.4161 | ||
| 17.165202 | 16.3392 | 24.646677 | 24.4735 | ||
| 17.168212 | 16.3402 | 24.651078 | 24.4653 | ||
| 17.169406 | 16.3398 | 25.15589 | 25.0686 | ||
| 17.170888 | 16.3434 | 25.695354 | 25.5247 | ||
| 17.190304 | 16.3586 | 25.851944 | 25.661 | ||
| 17.590402 | 17.1945 | 25.864287 | 25.6377 | ||
| 18.066837 | 17.3267 | 25.94796 | 25.8534 | ||
| 18.325429 | 17.9033 | 26.010191 | 25.9622 | ||
| 18.440829 | 17.9794 | 26.020381 | 25.8194 | ||
| 18.482554 | 18.0286 | 26.299951 | 26.3276 | ||
| 18.793548 | 18.3347 | 26.31735 | 26.1997 | ||
| 19.03941 | 18.6926 | 26.415767 | 26.295 | ||
| 19.143124 | 18.9904 | 26.72122 | 25.758 | ||
| 19.180338 | 18.8405 | 26.842635 | 25.9435 | ||
| 19.351697 | 18.9913 | 26.844388 | 25.944 | ||
| 19.837029 | 19.5961 | 26.846142 | 25.9445 | ||
| 19.888908 | 19.6399 | 26.848131 | 25.945 | ||
| 19.974922 | 19.6921 | 26.855511 | 25.949 | ||
| 20.189717 | 20.0581 | 26.951175 | 26.0715 | ||
| 20.242766 | 20.0101 | 27.448687 | 26.8588 | ||
| 20.288258 | 20.0529 | 27.495681 | 26.881 | ||
| 20.46402 | 20.1883 | 27.49775 | 26.9104 | ||
| 20.514847 | 20.2645 | 28.902074 | 28.8061 | ||
| 21.102396 | 21.1161 | 28.905521 | 28.5747 | ||
| 21.188768 | 21.2353 | 28.91979 | 28.606 | ||
| 21.32477 | 21.304 | 28.931251 | 28.3947 | ||
| 21.382994 | 21.3741 | 29.014873 | 28.7654 | ||
| 21.447172 | 21.458 | 29.059434 | 28.8263 | ||
| 21.629161 | 21.6529 | 29.082588 | 28.5158 | ||
| 21.676239 | 21.6721 | 29.158831 | 28.636 | ||
| 21.702564 | 21.6694 | 29.180492 | 28.6806 | ||
| 21.723415 | 21.7447 | 29.18709 | 29.3112 | ||
| 21.76466 | 20.9086 | 29.262809 | 28.7683 | ||
| 21.793774 | 20.9397 | 29.282912 | 29.3084 | ||
| 21.885693 | 21.0073 | 29.321552 | 29.3128 | ||
| 21.919259 | 21.8438 | 29.40363 | 29.361 | ||
| 22.09938 | 22.1812 | 29.411375 | 29.5393 | ||
| 22.1013 | 22.2034 | 29.430526 | 29.3017 | ||
| 22.271137 | 21.627 | 29.504579 | 29.1699 | ||
| 22.32744 | 21.672 | 29.583614 | 29.4387 | ||
| 22.346555 | 21.6797 | 29.759332 | 29.8347 | ||
| 22.347791 | 22.4825 | 30.646034 | 30.5037 | ||
| 22.473805 | 22.771 | 30.648076 | 30.5708 | ||
| 22.597971 | 22.6612 | 30.862835 | 32.1173 | ||
| 22.684996 | 22.938 | 30.892804 | 30.3303 | ||
| 22.923664 | 23.2994 | 30.91693 | 30.5728 | ||
| 23.022456 | 23.5221 | 30.926328 | 30.9189 | ||
| 23.337946 | 23.7662 | 30.974683 | 30.681 | ||
| 23.379594 | 24.1609 | 31.071757 | 30.9028 | ||
| 23.585044 | 24.4554 | 31.10901 | 31.0026 | ||
| 23.64671 | 23.2735 | 31.24481 | 31.1903 | ||
| 23.891984 | 23.6566 | 31.971241 | 32.1922 | ||
| 24.009753 | 24.5708 | ||||
| Line Index | Wavelength (nm) | Level | Energies (eV) (NIST) | |||
|---|---|---|---|---|---|---|
| NIST | Present | Upper | Lower | Upper Level | Lower Level | |
| L1 | 309.716 | 328.984 | 22.32744 | 18.325429 | ||
| L2 | 312.246 | 333.544 | 26.31735 | 22.347791 | ||
| L3 | 315.175 | 324.804 | 25.851944 | 21.919259 | ||
| L4 | 322.062 | 337.629 | 25.94796 | 22.09938 | ||
| L5 | 322.224 | 339.683 | 25.94796 | 22.1013 | ||
| L6 | 327.165 | 344.554 | 22.271137 | 18.482554 | ||
| L7 | 344.871 | 373.300 | 25.695354 | 22.1013 | ||
| L8 | 351.455 | 362.983 | 25.15589 | 21.629161 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathi, S.; Sharma, L. A Collisional-Radiative Model for Kr III Ions. Atoms 2024, 12, 39. https://doi.org/10.3390/atoms12080039
Rathi S, Sharma L. A Collisional-Radiative Model for Kr III Ions. Atoms. 2024; 12(8):39. https://doi.org/10.3390/atoms12080039
Chicago/Turabian StyleRathi, Shikha, and Lalita Sharma. 2024. "A Collisional-Radiative Model for Kr III Ions" Atoms 12, no. 8: 39. https://doi.org/10.3390/atoms12080039
APA StyleRathi, S., & Sharma, L. (2024). A Collisional-Radiative Model for Kr III Ions. Atoms, 12(8), 39. https://doi.org/10.3390/atoms12080039






