Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra
Abstract
:1. Introduction
2. Results
2.1. Laboratory Experiments
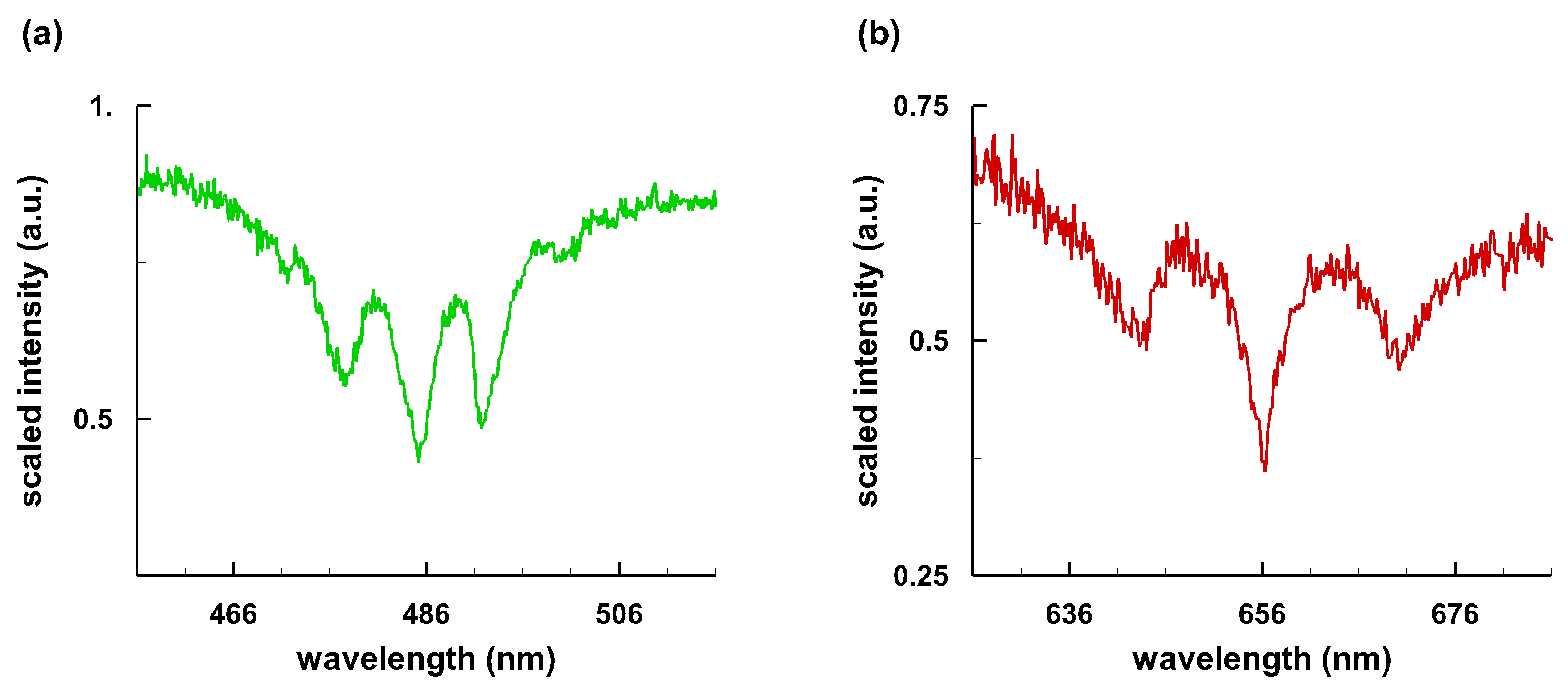
2.2. Astrophysical White Dwarf Spectra
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| c | speed of light |
| CMa | Canis Majoris—big dog |
| CMi | Canis Minoris—little dog |
| hydrogen alpha FWHM | |
| hydrogen alpha redshift | |
| hydrogen beta FWHM | |
| hydrogen beta peak separation | |
| hydrogen beta central dip-shift | |
| DA | dwarf A—hydrogen lines are present |
| DAH | dwarf A with magnetic field |
| DQZ | dwarf Q and Z—carbon and metal rich atmosphere |
| FWHM | full width at half maximum |
| G | gravitational constant |
| H | hydrogen beta line |
| H | hydrogen alpha line |
| HIRES | high resolution spectrometer |
| ICCD | intensified charge coupled device |
| JA | Jarrel-Ash |
| JY | Jobin Yvon |
| KOA | Keck observatory archive |
| wavelength of H | |
| wavelength of H | |
| M | WD mass |
| M⊙ | WD mass in solar units |
| N | electron interstellar density of the hydrogen column |
| N | electron density |
| R | WD radius |
| R⊙ | WD radius in solar units |
| blue- and red-peak Zeeman separation for H | |
| blue- and red-peak Zeeman separation for H | |
| SDSS | Sloan digital sky survey |
| time delay from optical breakdown | |
| v | gravitational redshift |
| WD | white dwarf |
| integral describing predominant Holtsmark contribution | |
| integral describing predominant Lorentz contribution | |
| integral describing predominant Doppler contribution | |
| ration of electric and normal field strength | |
| F | electric field strength |
| F | normal field strength |
| CGP | Christian Gerhard Parigger |
| CMH | Christopher Matthew Helstern |
| KAD | Kyle Anthony Drake |
| GG | Ghaneshwar Gautam |
Appendix A. Formulae for Determination of Electron Density from Hβ and Hα Profiles
| Time Delay (ns) | H Dip-Shift (nm) | H Width (nm) | N from Dip-Shift (10 cm) | N from Width (10 cm) |
|---|---|---|---|---|
| 25 | 1.02 ± 0.15 | - | 20 (15–24) | - (H: 17) |
| 50 | 0.83 ± 0.15 | - | 14 (11–19) | - (H: 14) |
| 75 | 0.77 ± 0.1 | ∼25 | 13 (10–15) | ∼11 |
| 100 | 0.65 ± 0.1 | ∼23 ± 4 | 10 (7.7–12) | ∼10 |
| 125 | 0.58 ± 0.1 | ∼21 ± 4 | 8.4 (6.3–11) | ∼8.8 |
| 150 | 0.50 ± 0.1 | ∼15 ± 3 | 6.7 (4.8–8.9) | ∼5.5 |
| 175 | 0.42 ± 0.1 | 11 ± 2 | 5.2 (3.5–7.2) | 3.5 |
| 200 | 0.37 ± 0.1 | 9 ± 1 | 4.3 (2.7–6.1) | 2.7 |
| 225 | 0.32 ± 0.1 | 8 ± 0.5 | 3.5 (2.0–5.2) | 2.3 |
| 250 | 0.26 ± 0.05 | 7.5 ± 0.5 | 2.5 (1.8–3.3) | 2.1 |
| 275 | 0.24 ± 0.05 | 7.0 ± 0.5 | 2.2 (1.6–3.0) | 1.9 |
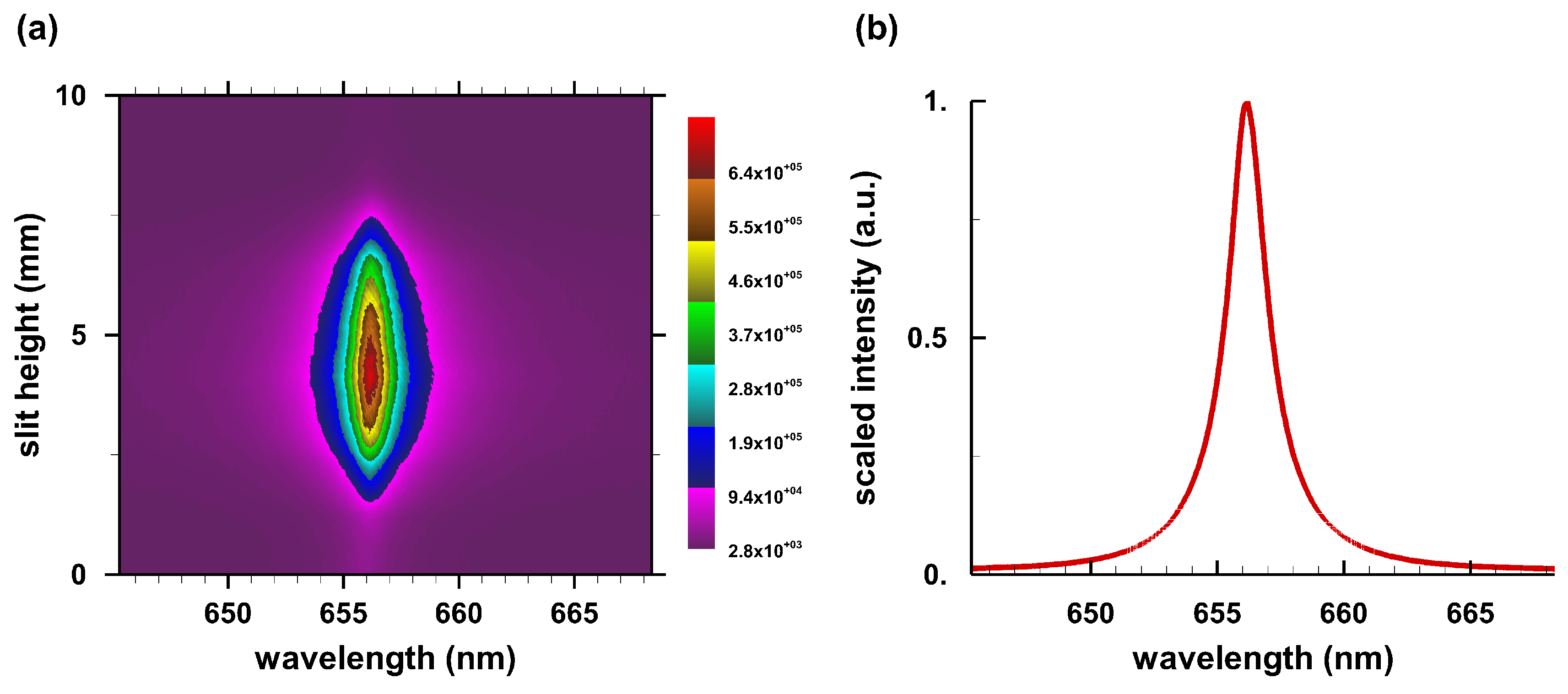
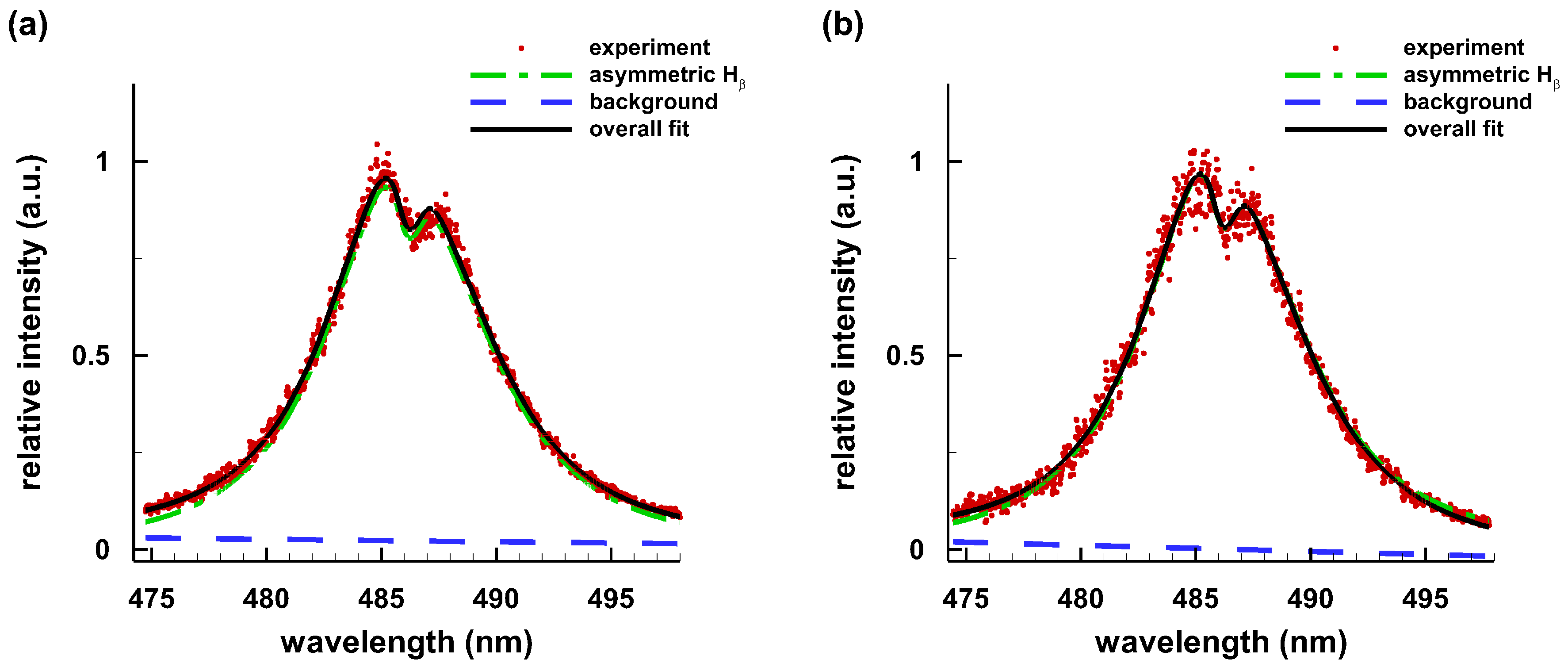
Appendix B. Typical Laboratory Spectra of Hβ and Hα

Appendix C. Line Shapes
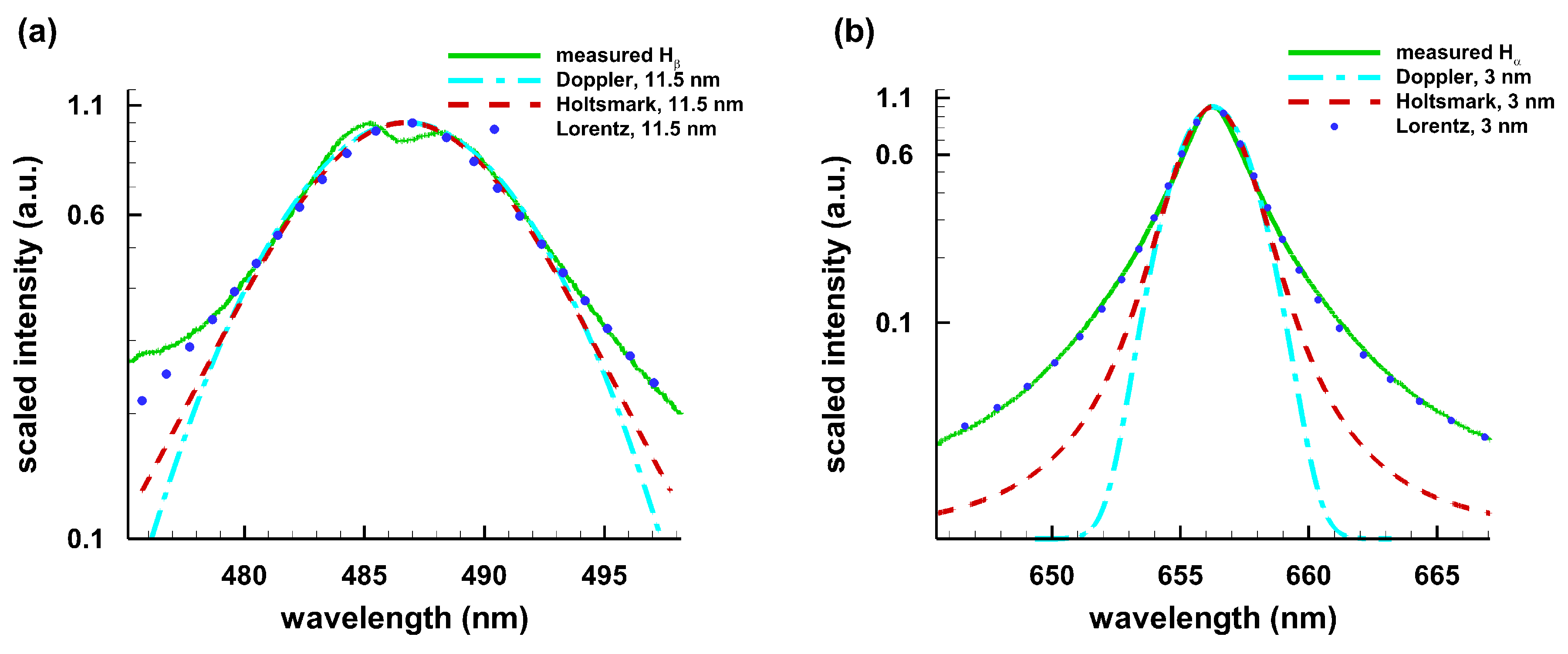
| Holtsmark | Lorentz | Doppler |
|---|---|---|
References
- Rowland, H.A. Preliminary Table of the Solar Spectruim Wave-Lengths VI. Astrophys. J. 1895, 2, 45–54. [Google Scholar] [CrossRef]
- Rowland, H.A. Preliminary Table of the Solar Spectruim Wave-Lengths XIII. Astrophys. J. 1895, 3, 356–360. [Google Scholar] [CrossRef]
- Moore, C.E.; Minnaert, M.G.J.; Houtgast, J. The Solar Spectrum 2935 Å to 8770 Å; National Burea of Standards Monograph 61; United Styates Department of Commerce: Washington, DC, USA, 1966; pp. 197–283.
- Barstow, M.A.; Bond, H.E.; Holberg, J.B.; Burleigh, M.R.; Hubeny, I.; Koester, D. Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B. Mon. Not. R. Astron. Soc. 2005, 362, 1134–1142. [Google Scholar] [CrossRef]
- Dufour, P.; Blouin, S.; Coutu, S.; Fortin-Archambault, M.; Thibeault, C.; Bergeron, P.; Fontaine, G. The Montreal White Dwarf Database: A Tool for the Community. In Astronomical Society of the Pacific (ASP) Conference Series 509, Proceedings of the 20th European White Dwarf workshop, Warwick, UK, 25–29 July 2016; Tremblay, P.-E., Gaensicke, B., Marsh, T., Eds.; Utah Valley University: Orem, UT, USA, 2017; pp. 3–8. ISBN 978-1-58381-903-6. Available online: http://dev.montrealwhitedwarfdatabase.org (accessed on 11 May 2018).
- Kodaira, K. A Spectrum of Sirius B. Astron. Soc. J. 1967, 19, 172–179. [Google Scholar]
- Wiese, W.L.; Kelleher, D.E. On the Cause of the Redshifts in White-Dwarf Spectra. Astrophys. J. 1971, 166, L59–L63. [Google Scholar] [CrossRef]
- Wiese, W.L.; Kelleher, D.E.; Paquette, D.R. Detailed Study of Stark Broadening of Balmer Lines in High-Density Plasma. Phys. Rev. A 1972, 6, 1132–1153. [Google Scholar] [CrossRef]
- Greenstein, J.L.; Oke, J.B.; Shipman, H.L. Effective temperature, radius, and gravitational redshift of Sirius B. Astrophys. J. 1971, 169, 563–566. [Google Scholar] [CrossRef]
- Holberg, J.B. Sirius B and the Measurement of the Gravitational Redshift. J. His. Astron. 2010, 41, 41–64. [Google Scholar] [CrossRef]
- Grabowski, B.; Halenka, J. On red shifts and asymmetries of hydrogen spectral lines. Astron. Astrophys. 1975, 45, 159–166. [Google Scholar]
- Shipman, H.L.; Mehan, R.G. The unimportance of pressure shifts in the measurement of gravitational redshifts in white dwarfs. Astrophys. J. 1976, 209, 205–207. [Google Scholar] [CrossRef]
- Halenka, J.; Olchawa, W.; Madej, J.; Grabowski, B. Pressure shift and gravitational redshift of Balmer lines in white dwarfs: Rediscussion. Astrophys. J. 2015, 808, 131–140. [Google Scholar] [CrossRef]
- Cremers, D.A.; Radziemski, L.J. Handbook of Laser-Induced Breakdown Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 1–97. ISBN 978-0-470-09299-6. [Google Scholar]
- Hahn, D.W.; Omenetto, N. Laser-Induced Breakdown Spectroscopy (LIBS), Part II: Review of Instrumental and Methodological Approaches to Material Analysis and Applications to Different Fields. Appl. Spectrosc. 2012, 66, 47–419. [Google Scholar] [CrossRef] [PubMed]
- Ispolatov, Y.; Oks, E. A convergent theory of Stark broadening of hydrogen lines in dense plasmas. J. Quant. Spectrosc. Rad. Trans. 1994, 51, 129–138. [Google Scholar] [CrossRef]
- Parigger, C.G.; Plemmons, D.H.; Oks, E. Balmer series Hβ measurements in a laser-induced hydrogen plasma. Appl. Opt. 2003, 42, 5992–6000. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Fisher, D.V.; Maron, Y.; Griem, H.R.; Alexiou, S. Correlation effects and their influence on line broadening in plasmas. High Energy Density Phys. 2007, 3, 272–277. [Google Scholar] [CrossRef]
- Gomes, T.A.; Nagayama, T.; Kilcrease, D.P.; Montgomery, M.H.; Winget, D.E. Effect of higher-order multipole moments on the Stark line shape. Phys. Rev. A 2016, 94, 022501. [Google Scholar] [CrossRef]
- Demura, A.V. Beyond the Linear Stark Effect: A Retrorespective. Atoms 2018, 6, 33. [Google Scholar] [CrossRef]
- Gigosos, M.A.; González, M.Á.; Cardeñoso, V. Computer simulated Balmer-alpha, -beta and -gamma Stark line profiles for non-equilibrium plasmas diagnostics. Spectrochim. Acta B At. Spectrosc. 2003, 58, 1489–1504. [Google Scholar] [CrossRef]
- Parigger, C.G.; Helstern, C.M.; Drake, K.A.; Gautam, G. Balmer-series hydrogen-beta line dip-shifts for electron density measurements. Int. Rev. At. Mol. Phys. 2017, 8, 53–61. [Google Scholar]
- Parigger, C.G.; Gautam, G.; Surmick, D.M. Radial electron density measurements in laser-induced plasma from Abel inverted hydrogen Balmer beta line profiles. Int. Rev. At. Mol. Phys. 2015, 6, 43–55. [Google Scholar]
- Konjević, N.; Ivković, M.; Sakan, N. Hydrogen Balmer lines for low electron number density plasma diagnostics. Spectrochim. Acta B At. Spectrosc. 2012, 76, 16–26. [Google Scholar] [CrossRef]
- Ivković, M.; Konjević, N.; Pavlović, Z. Hydrogen Balmer beta: The separation between line peaks for plasma electron density diagnostics and self-absorption test. J. Quant. Spectrosc. Radiat. Trans. 2015, 154, 1–8. [Google Scholar] [CrossRef]
- Leonard, S.L. Basic Macroscopic Measurements. In Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965; pp. 7–67. [Google Scholar]
- Griem, H.R. Plasma Spectroscopy; McGraw-Hill Book Company: New York, NY, USA, 1964. [Google Scholar]
- Griem, H.R. Spectral Line Boradening by Plasmas; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer: New York, NY, USA, 2009; ISBN 978-3-642-02232-6. [Google Scholar]
- Wiese, W.L. Line Broadening. In Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965; pp. 265–317. [Google Scholar]
- McWhirter, R.W.P. Spectral Intensities. In Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965; pp. 201–264. [Google Scholar]
- Sobel’man, I.I.; Vainshtein, L.A.; Yukov, E.A. Ecitation of Atoms and Broadening of Spectral Lines, 2nd ed.; Springer: New York, NY, USA, 1995; ISBN 978-3-540-58686-9. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Clarendon Press: Oxford, UK, 2004; pp. 213–235. ISBN 9780198530282. [Google Scholar]
- Djurović, S.; Ćirišan, M.; Demura, A.V.; Demchenko, G.V.; Nikolić, D.; Gigosos, M.A.; Gonzáles, M.Á. Measurements of Hβ central asymmetry and its analysis through standard theory and computer simulations. Phys. Rev. E 2009, 79, 046402. [Google Scholar] [CrossRef] [PubMed]
- Stambulchick, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Oks, E. Stark Broadening of Hydrogen and Hydrogenlike Spectral Lines in Plasmas: The Physical Insight; Alpha Science International: Oxford, UK, 2006; pp. 1–118. ISBN 1-84265-252-4. [Google Scholar]
- Oks, E. Diagnostics of Laboratory and Astrophysical Plasmas Using Spectral Lineshapes of One-, Two-, and Three-Electron Systems; World Scientific: Singapore, 2017; pp. 1–47. ISBN 9789814699075. [Google Scholar]
- Tremblay, P.-E.; Bergeron, P. Spectroscopic Analysis of DA White dwarfs: Stark broadening of hydrogen lines including nonideal effects. Astrophys. J. 2009, 696, 1755–1770. [Google Scholar] [CrossRef]
- Gianninas, A.; Bergeron, P.; Dupuis, J.; Ruiz, M.T. Spectroscopic analysis of hot, hydrogen-rich white dwarf: The presence of metals and the Balmer-line problem. Astrophys. J. 2010, 720, 581–602. [Google Scholar] [CrossRef]
- Tremblay, P.-E. Analyse Spectroscopique D’étoiles Naines Blanches Riches en Hydrogène (DA): Vers des Modèles D’atmosphère Améliorés Sans Paramètres Libres. Ph.D. Thesis, Université de Montéal, Montréal, QC, Canada, 2011. [Google Scholar]
- Falcon, R.E.; Winget, D.E.; Montgomery, M.H.; Williams, K.A. A gravitational redshift determination of the mean mass of white dwarf DA stars. Astrophys. J. 2010, 712, 585–595. [Google Scholar] [CrossRef]
- Koester, D. White dwarf spectra and atmosphere models. Mem. Soc. Astronom. Ital. 2010, 81, 921–931. [Google Scholar]
- Falcon, R.E. Creating and Measuring White Dwarf Photospheres in a Terrestrial Laboratory. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2014. [Google Scholar]
- Falcon, R.E.; Rochau, G.A.; Bailey, J.E.; Gomez, T.A.; Montgomery, M.H.; Winget, D.E.; Nagayama, T. Laboratory measurements of white dwarf photospheric spectral lines: Hβ. Astrophys. J. 2015, 806, 214–224. [Google Scholar] [CrossRef]
- Holberg, J.B.; Barstow, M.A.; Bruhweiler, F.C.; Cruise, A.M.; Penny, A.J. Sirius B: A new, more accurate view. Astrophys. J. 1998, 497, 935–942. [Google Scholar] [CrossRef]
- Provencal, J.L.; Shipman, H.L.; Høg, E.; Thejll, P. Testing the white dwarf mass-radius relation with Hipparcos. Astrophys. J. 1998, 494, 759–767. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- King, A.R. Accretion and evolution in close binaries. In Astrophysical and Laboratory Plasmas—A Festschrift for Professor Robert Wilson; Willis, A.J., Hartquist, T.W., Eds.; Springer: Dordrecht, NL, USA, 1996; pp. 169–186. ISBN 978-90-481-4729-8. [Google Scholar]
- Halenka, J.; Vujićić, B.; Djurović, S. Shift of the peaks of the Hβ spectral line. J. Quant. Spectrosc. Radiat. Trans. 1989, 42, 571–573. [Google Scholar] [CrossRef]
- Mijatović, Z.; Pavlov, M.; Djurović, S. Shift of the Hβ line in dense hydrogen plasmas. Phys. Rev. A 1991, 43, 6095–6097. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 385, 437–490. [Google Scholar] [CrossRef]
- Holtsmark, J. Über die Verbreiterung von Spectrallinien. Ann. Phys. 1919, 58, 577–630. [Google Scholar] [CrossRef]
- Van Regenmorter, H. Spectral line broadening. Ann. Rev. Astron. Astrophys. 1965, 3, 71–92. [Google Scholar] [CrossRef]
- Limoǵe, M.-M.; Bergeron, P.; Lépine, S. Physical properties of the current census of northern white dwarfs within 40 pc of the sun. Astrophys. J. 2011, 219, 19–53. [Google Scholar] [CrossRef]
- Gianninas, A.; Bergeron, P.; Ruiz, M.T. A spectroscopic survey and analysis of bright, hydrogen-rich white dwarfs. Astrophys. J. 2011, 743, 138–164. [Google Scholar] [CrossRef]
- Koester, D.; Voss, B.; Napiwotzki, R.; Christlieb, N.; Homeier, D.; Lisker, T.; Reimers, D.; Heber, U. High-resolution UVES/VLT spectra of white dwarfs observed for the ESO SN Ia Progenitor Survey III. DA white dwarfs. Astron. Astrophys. 2009, 505, 441–462. [Google Scholar] [CrossRef]
- Narayan, G.; Axelrod, T.; Holberg, J.B.; Matheson, T.; Saha, A.; Olszewski, E.; Claver, J.; Stubbs, C.W.; Bohlin, R.C.; Deustua, S.; Rest, A. Toward a network of faint DA white dwarfs as high-precision spectrophotometric standards. Astrophys. J. 2016, 822, 67–80. [Google Scholar] [CrossRef]
- Kleinman, S.J.; Harris, H.C.; Eisenstein, D.J.; James Liebert, J.; Nitta, A.; Jurek Krzesiński, J.; Munn, J.A.; Dahn, C.C.; Hawley, S.L.; Pier, J.R.; et al. A catalog of spectroscopically confirmed white dwarfs oin the first data realease of the Sloan digital sky survey. Astrophys. J. 2004, 607, 426–444. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Liebert, J.; Harris, H.C.; Kleinman, S.J.; Nitta, A.; Nicole Silvestri, N.; Anderson, S.A.; Barentine, J.C.; Brewington, H.J.; Brinkmann, J.; et al. A catalog of spectroscopically confirmed white dwarfs from the Sloan digital sky survey data release 4. Astrophys. J. Suppl. Ser. 2006, 167, 40–58. [Google Scholar] [CrossRef]
- Tremblay, P.-E.; Bergeron, P.; Gianninas, A. An improved spectroscopic analysis of DA white dwarfs from the Sloan digital survey data release 4. Astrophys. J. Suppl. Ser. 2011, 730, 128–150. [Google Scholar] [CrossRef]
- Rosato, J.; Kieu, N.; Hannachi, I.; Koubiti, M.; Marandet, Y.; Stamm, R.; Dimitrijevicć, M.S.; Simić, Z. Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge Plasmas: Common Challenges. Atoms 2017, 5, 36. [Google Scholar] [CrossRef]
- Kieu, N.; Rosato, J.; Stamm, R.; Kovačević-Dojicinović, J.; Dimitrijević, M.S.; Popović, L.Č.; Simić, Z. A New Analysis of Stark and Zeeman Effects on Hydrogen Lnes in Magnetized DA White Dwarfs. Atoms 2017, 5, 44. [Google Scholar] [CrossRef]
- Vogt, S.S.; Penrod, D.G. HIRES: A High Resolution Echelle Spectrometer for the Keck 10-Meter Telescope. In Instrumentation for Ground-Based Optical Astronomy—Santa Cruz Summer Workshops in Astronomy and Astrophysics; Robinson, L.B., Ed.; Springer: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- W.M. Keck Observatory Archive (KOA). Extracted HIRES Spectra for the White Dwarf HG7-85, KOA-ID: HI.20121028.35667. Available online: https://koa.ipac.caltech.edu (accessed on 5 May 2018).
- Zuckerman, B.; Xu, S.; Klein, B.; Jura, A. Thy Hyades cluster: Identification of a planetary system and ascaping white dwarfs. Astrophys. J. 2013, 770, 140–141. [Google Scholar] [CrossRef]
- Keller, J. Nonlinear Fitting n-Dimensional Data with Arbitrary Functions; Mathworks File Exchange: Natick, MA, USA, 2008; Available online: https://www.mathworks.com/matlabcentral/fileexchange/20540-nonlinear-fitting-n-dimensional-data-with-arbitrary-functions (accessed on 14 February 2018).
- Parigger, C.G.; Woods, A.C.; Witte, M.J.; Swafford, L.D.; Surmick, D.M. Measurement and Analysis of Atomic Hydrogen and Diatomic Molecular AlO, C2, CN, and TiO Spectra Following Laser-induced Optical Breakdown. J. Vis. Exp. 2014, 84, e51250. [Google Scholar] [CrossRef]
- Parigger, C.G.; Woods, A.C.; Surmick, D.M.; Gautam, G.; Witte, M.J.; Hornkohl, J.O. Computation of diatomic molecular spectra for selected transitions of aluminum monoxide, cyanide, diatomic carbon, and titanium monoxide. Spectrochim. Acta B At. Spectrosc. 2015, 107, 132–138. [Google Scholar] [CrossRef]
- Surmick, D.M.; Parigger, C.G. Empirical Formulae for Electron Density Diagnostics from Hα and Hβ Line Profiles. Int. Rev. At. Mol. Phys. 2014, 5, 73–81. [Google Scholar]
- Büscher, S.; Wrubel, T.; Ferri, S.; Kunze, H.-J. The Stark width and shift of the hydrogen Hα line. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 2889–2897. [Google Scholar] [CrossRef]
- Kask, N.E.; Michurin, S.V. Broadening of the spectral lines of a buffer gas and target substance. Quant. Electron. 2012, 42, 1002–1007. [Google Scholar] [CrossRef]
- Kask, N.E.; Lexsina, E.G.; Michurin, S.V.; Fedorov, G.M.; Chopornyak, D.B. Broadening and shift of the spectral lines of hydrogen atoms and silicon ions in laser plasma. Quant. Electron. 2015, 45, 527–532. [Google Scholar] [CrossRef]
- Witkovsky, V. CharFunTool: The Characteristic Functions Toolbox. Matlab® File Exchange: Script cfX_PDF.m for Exponential Distributions in the CF_Repository. Available online: https://www.mathworks.com/matlabcentral/fileexchange/64400-charfuntool–the-characteristic-functions-toolbox (accessed on 19 March 2018).
- Demura, A.V. Physical Models of Plasma Microfield. Int. J. Spectrosc. 2010, 2010, 671073. [Google Scholar] [CrossRef]
- Griem, H.R. Stark Broadening of Higher Hydrogen and Hydrogen-like lines by electrons and ions. Astrophys. J. 1960, 132, 883–893. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark Profile Calculations for the Hβ Line of Hydrogen. Astrophys. J. 1962, 135, 272–276. [Google Scholar] [CrossRef]
- Sapar, A.; Poolamäe, R.; Sapar, L. High-precision approximation expressions for line profiules of hydrogenic particles. Baltic Astron. 2006, 15, 435–447. [Google Scholar]
- Sapar, A.; Poolamäe, R. Revised line profile function for hydrogenic species. Open Astron. 2012, 21, 243–254. [Google Scholar] [CrossRef]

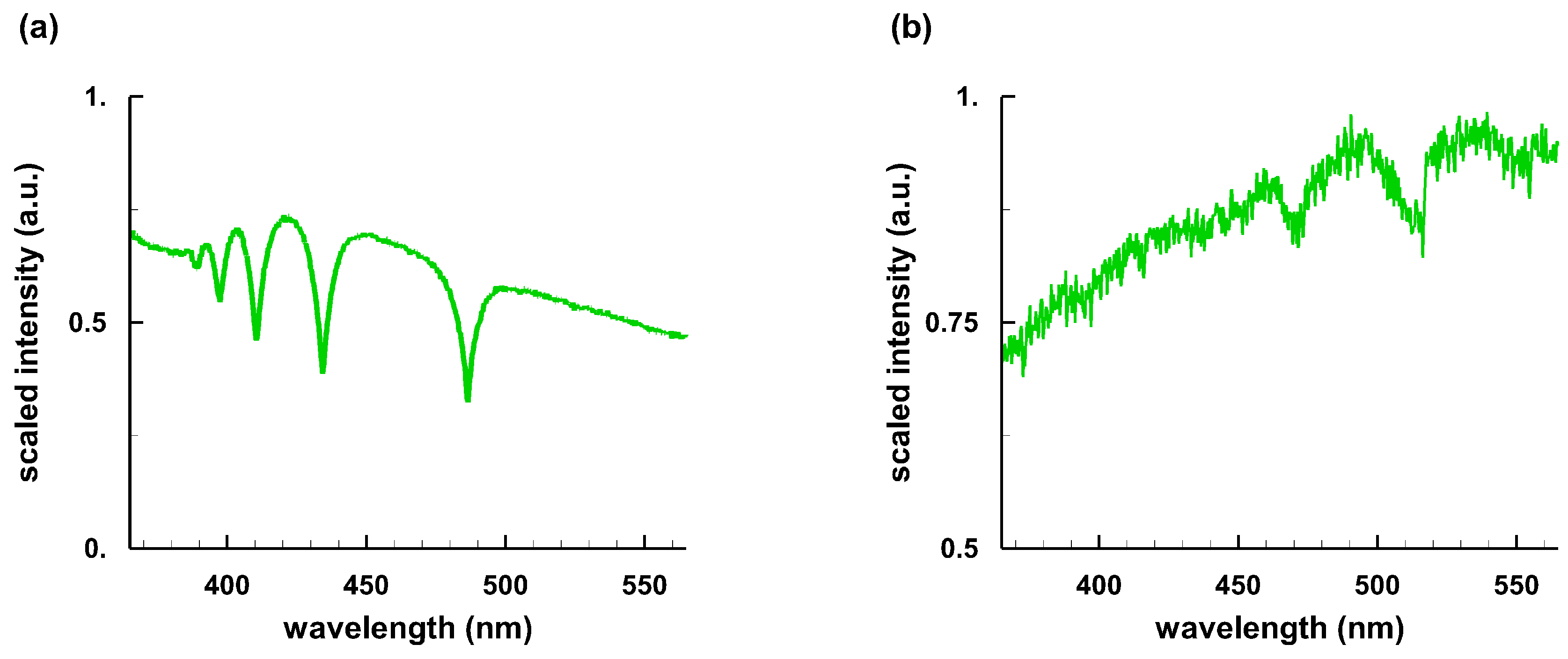



| Temperature [K] | Gravity [cm/s] | Mass/Mass | Radius/Radius |
|---|---|---|---|
| 24,790 ± 100 | 0.984 ± 0.074 | 0.0084 ± 0.00025 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parigger, C.G.; Drake, K.A.; Helstern, C.M.; Gautam, G. Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra. Atoms 2018, 6, 36. https://doi.org/10.3390/atoms6030036
Parigger CG, Drake KA, Helstern CM, Gautam G. Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra. Atoms. 2018; 6(3):36. https://doi.org/10.3390/atoms6030036
Chicago/Turabian StyleParigger, Christian G., Kyle A. Drake, Christopher M. Helstern, and Ghaneshwar Gautam. 2018. "Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra" Atoms 6, no. 3: 36. https://doi.org/10.3390/atoms6030036
APA StyleParigger, C. G., Drake, K. A., Helstern, C. M., & Gautam, G. (2018). Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra. Atoms, 6(3), 36. https://doi.org/10.3390/atoms6030036






