Empirical Line Lists in the ExoMol Database
Abstract
:1. Introduction
2. Method
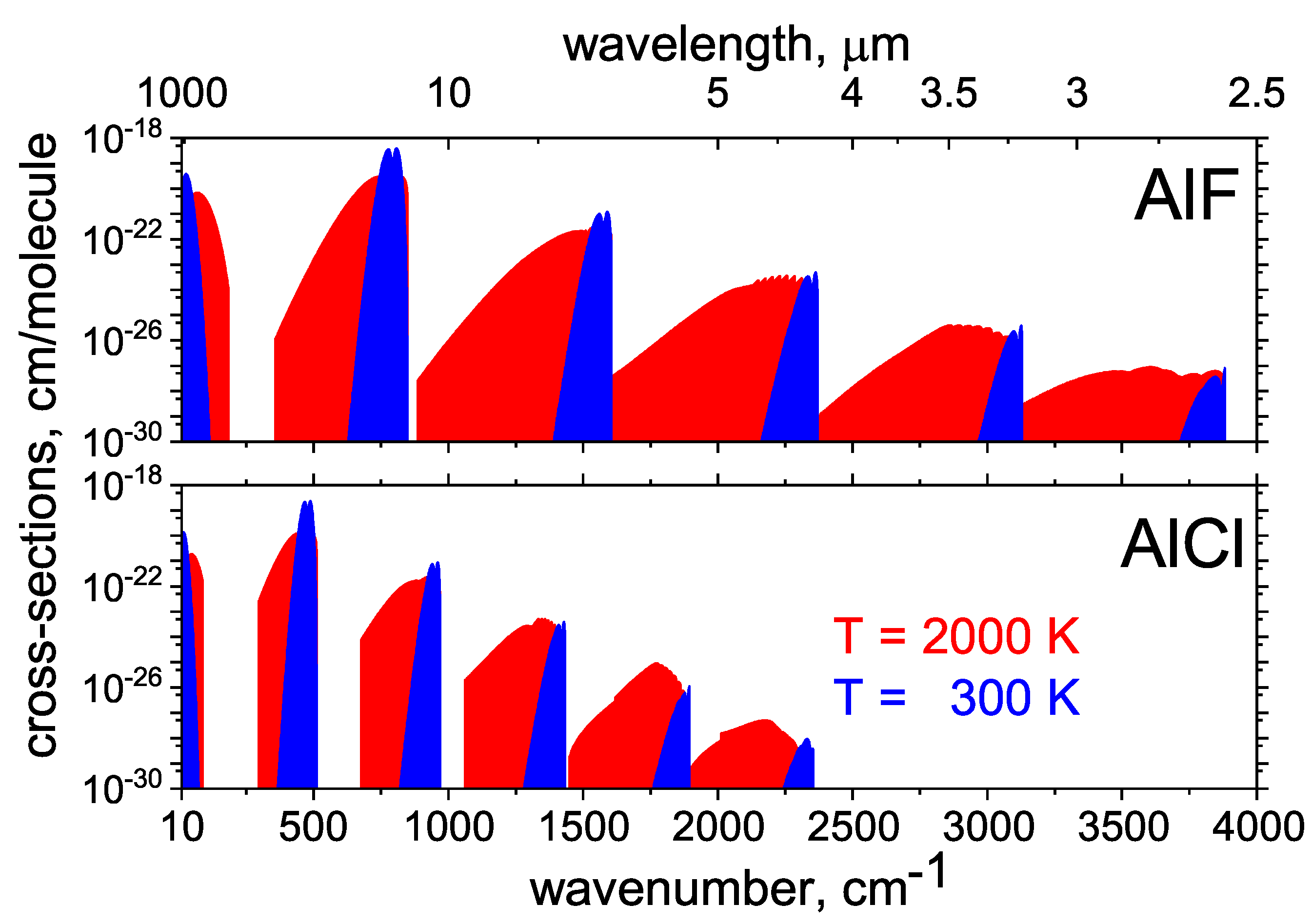
2.1. AlCl and AlF
2.2. CH
2.3. NH
2.4. OH
2.5. OH
2.6. CaF
2.7. KF and NaF
2.8. MgF
2.9. LiCl and LiF
2.10. MgH
2.11. TiH
2.12. CrH
2.13. FeH
2.14. C
2.15. CP
2.16. CN
2.17. CaH
2.18. N
2.19. Lifetimes
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tennyson, J.; Yurchenko, S.N. ExoMol: Molecular line lists for exoplanet and other atmospheres. Mon. Not. R. Astron. Soc. 2012, 425, 21–33. [Google Scholar] [CrossRef] [Green Version]
- Lodi, L.; Tennyson, J. Theoretical methods for small-molecule ro-vibrational spectroscopy. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 133001. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N. The ExoMol project: Software for computing molecular line lists. Intern. J. Quantum Chem. 2017, 117, 92–103. [Google Scholar] [CrossRef] [Green Version]
- McKemmish, L.K.; Yurchenko, S.N.; Tennyson, J. Ab initio calculations to support accurate modelling of the rovibronic spectroscopy calculations of vanadium monoxide (VO). Mol. Phys. 2016, 114, 3232–3248. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J. Accurate variational calculations for line lists to model the vibration rotation spectra of hot astrophysical atmospheres. WIREs Comput. Mol. Sci. 2012, 2, 698–715. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N. Laboratory spectra of hot molecules: Data needs for hot super-Earth exoplanets. Mol. Astrophys. 2017, 8, 1–18. [Google Scholar] [CrossRef]
- Tennyson, J. Vibration-rotation transition dipoles from first principles. J. Mol. Spectrosc. 2014, 298, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Zak, E.J.; Tennyson, J.; Polyansky, O.L.; Lodi, L.; Tashkun, S.A.; Perevalov, V.I. A room temperature CO2 line list with Ab Initio Comput. Intensities. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Yurchenko, S.N.; Barber, R.J.; Tennyson, J.; Thiel, W.; Jensen, P. Towards efficient refinement of molecular potential energy surfaces: Ammonia as a case study. J. Mol. Spectrosc. 2011, 268, 123–129. [Google Scholar] [CrossRef]
- Tennyson, J.; Lodi, L.; McKemmish, L.K.; Yurchenko, S.N. The ab initio calculation of spectra of open shell diatomic molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 102001. [Google Scholar] [CrossRef] [Green Version]
- Yurchenko, S.N.; Lodi, L.; Tennyson, J.; Stolyarov, A.V. Duo: A general program for calculating spectra of diatomic molecules. Comput. Phys. Commun. 2016, 202, 262–275. [Google Scholar] [CrossRef] [Green Version]
- Barber, R.J.; Strange, J.K.; Hill, C.; Polyansky, O.L.; Mellau, G.C.; Yurchenko, S.N.; Tennyson, J. ExoMol line lists—III. An improved hot rotation-vibration line list for HCN and HNC. Mon. Not. R. Astron. Soc. 2014, 437, 1828–1835. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J.; Yurchenko, S.N.; Al-Refaie, A.F.; Barton, E.J.; Chubb, K.L.; Coles, P.A.; Diamantopoulou, S.; Gorman, M.N.; Hill, C.; Lam, A.Z.; et al. The ExoMol database: Molecular line lists for exoplanet and other hot atmospheres. J. Mol. Spectrosc. 2016, 327, 73–94. [Google Scholar] [CrossRef] [Green Version]
- Bernath, P.F. Molecular astronomy of cool stars and sub-stellar objects. Int. Rev. Phys. Chem. 2009, 28, 681–709. [Google Scholar] [CrossRef] [Green Version]
- Yurchenko, S.N.; Barber, R.J.; Tennyson, J. A variationally computed hot line list for NH3. Mon. Not. R. Astron. Soc. 2011, 413, 1828–1834. [Google Scholar] [CrossRef] [Green Version]
- Western, C.M. PGOPHER: A program for simulating rotational, vibrational and electronic spectra. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 221–242. [Google Scholar] [CrossRef] [Green Version]
- Le Roy, R.J. LEVEL: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 167–178. [Google Scholar] [CrossRef]
- Bernath, P.F. MoLLIST: Molecular Line Lists, Intensities and Spectra. J. Quant. Spectrosc. Radiat. Transf. 2020, 240, 106687. [Google Scholar] [CrossRef]
- Semenov, M.; Yurchenko, S.N.; Tennyson, J. Predicted Landé g-factors for open shell diatomic molecules. J. Mol. Spectrosc. 2017, 330, 57–62. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J.; Yurchenko, S.N. The 2020 release of the ExoMol database: Molecular line lists for exoplanet and other hot atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2020. in preparation. [Google Scholar]
- Western, C.M.; Carter-Blatchford, L.; Crozet, P.; Ross, A.J.; Morville, J.; Tokaryk, D.W. The spectrum of N2 from 4,500 to 15,700 cm−1 revisited with PGOPHER. J. Quant. Spectrosc. Radiat. Transf. 2018, 219, 127–141. [Google Scholar] [CrossRef] [Green Version]
- Villanueva, G.L.; Smith, M.D.; Protopapa, S.; Faggi, S.; Mandell, A.M. Planetary Spectrum Generator: An accurate online radiative transfer suite for atmospheres, comets, small bodies and exoplanets. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 86–104. [Google Scholar] [CrossRef] [Green Version]
- Sauval, A.J.; Tatum, J.B. A set of partition functions and equilibrium constants for 300 diatomic molecules of astrophysical interest. Astrophys. J. Suppl. 1984, 56, 193–209. [Google Scholar] [CrossRef]
- Barklem, P.S.; Collet, R. Partition functions and equilibrium constants for diatomic molecules and atoms of astrophysical interest. Astron. Astrophys. 2016, 588, A96. [Google Scholar] [CrossRef]
- Pavlenko, Y.V.; Yurchenko, S.N.; Tennyson, J. Analysis of first overtone bands of isotopologues of CO and SiO in stellar spectr. Astron. Astrophys. 2020, 633, A52. [Google Scholar] [CrossRef]
- Gamache, R.R.; Roller, C.; Lopes, E.; Gordon, I.E.; Rothman, L.S.; Polyansky, O.L.; Zobov, N.F.; Kyuberis, A.A.; Tennyson, J.; Yurchenko, S.N.; et al. Total Internal Partition Sums for 167 isotopologues of 53 molecules important in planetary atmospheres: Application to HITRAN2016 and beyond. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 70–87. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J.; Hulme, K.; Naim, O.K.; Yurchenko, S.N. Radiative lifetimes and cooling functions for astrophysically important molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 044002. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, M.; Bernath, P.F. Line Lists for AlF and AlCl in the X1Σ+ Ground State. Astrophys. J. Suppl. 2018, 237, 8. [Google Scholar] [CrossRef] [Green Version]
- Masseron, T.; Plez, B.; Van Eck, S.; Colin, R.; Daoutidis, I.; Godefroid, M.; Coheur, P.F.; Bernath, P.; Jorissen, A.; Christlieb, N. CH in stellar atmospheres: An extensive linelist. Astron. Astrophys. 2014, 571, A47. [Google Scholar] [CrossRef] [Green Version]
- Brooke, J.S.A.; Bernath, P.F.; Western, C.M.; van Hemert, M.C.; Groenenboom, G.C. Line strengths of rovibrational and rotational transitions within the X 3Σ− ground state of NH. J. Chem. Phys. 2014, 141, 054310. [Google Scholar] [CrossRef] [Green Version]
- Brooke, J.S.A.; Bernath, P.F.; Western, C.M. Note: Improved line strengths of rovibrational and rotational transitions within the X 3Σ− ground state of NH. J. Chem. Phys. 2015, 143, 026101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernando, A.M.; Bernath, P.F.; Hodges, J.N.; Masseron, T. A new linelist for the A3Π – X 3Σ− transition of the NH free radical. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 29–34. [Google Scholar] [CrossRef]
- Brooke, J.S.A.; Bernath, P.F.; Western, C.M.; Sneden, C.; AfÅŸar, M.; Li, G.; Gordon, I.E. Line strengths of rovibrational and rotational transitions in the X2Π ground state of OH. J. Quant. Spectrosc. Radiat. Transf. 2016, 138, 142–157. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, M.; Bernath, P.F.; Hodges, J.; Masseron, T. A new line list for the A2Σ+ − X2Π electronic transition of OH. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 416–424. [Google Scholar] [CrossRef]
- Hodges, J.N.; Bernath, P.F. Fourier Transform Spectroscopy of the A3Π − X3Σ− Transition of OH+. Astrophys. J. 2017, 840, 81. [Google Scholar] [CrossRef]
- Hodges, J.N.; Bittner, D.M.; Bernath, P.F. Improved Ultraviolet and Infrared Oscillator Strengths for OH+. Astrophys. J. 2018, 855. [Google Scholar] [CrossRef] [Green Version]
- Hou, S.; Bernath, P.F. Line list for the ground state of CaF. J. Quant. Spectrosc. Radiat. Transf. 2018, 210, 44–51. [Google Scholar] [CrossRef]
- Frohman, D.J.; Bernath, P.F.; Brooke, J.S.A. Molecular line lists: The ro-vibrational spectra of NaF and KF. J. Quant. Spectrosc. Radiat. Transf. 2016, 169, 104–110. [Google Scholar] [CrossRef]
- Hou, S.; Bernath, P.F. Line list for the MgF ground state. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 511–516. [Google Scholar] [CrossRef]
- Bittner, D.M.; Bernath, P.F. Line Lists for LiF and LiCl in the X 1Σ+ Ground State. Astrophys. J. Suppl. 2018, 235, 8. [Google Scholar] [CrossRef]
- GharibNezhad, E.; Shayesteh, A.; Bernath, P.F. Einstein A coefficients for rovibronic lines of the A2Π→X2Σ+ and B′2Σ+→X2Σ+ transitions of MgH. Mon. Not. R. Astron. Soc. 2013, 432, 2043–2047. [Google Scholar] [CrossRef] [Green Version]
- Burrows, A.; Dulick, M.; Bauschlicher, C.W.; Bernath, P.F.; Ram, R.S.; Sharp, C.M.; Milsom, J.A. Spectroscopic constants, abundances, and opacities of the TiH molecule. Astrophys. J. 2005, 624, 988–1002. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, P.K.; Merer, A.J.; Rixon, S.J.; Bernath, P.F.; Ram, R.S. Low-N lines of the A6Σ+ − X 6Σ+ (1,0) band of CrH. PCCP 2006, 8, 822–826. [Google Scholar] [CrossRef] [PubMed]
- Wende, S.; Reiners, A.; Seifahrt, A.; Bernath, P.F. CRIRES spectroscopy and empirical line-by-line identification of FeH molecular absorption in an M dwarf. Astron. Astrophys. 2010, 523, A58. [Google Scholar] [CrossRef] [Green Version]
- Brooke, J.S.A.; Bernath, P.F.; Schmidt, T.W.; Bacskay, G.B. Line strengths and updated molecular constants for the C2 Swan system. J. Quant. Spectrosc. Radiat. Transf. 2013, 124, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Ram, R.S.; Brooke, J.S.A.; Western, C.M.; Bernath, P.F. Einstein A-values and oscillator strengths of the A2Π − X 2Σ+ system of CP. J. Quant. Spectrosc. Radiat. Transf. 2014, 138, 107–115. [Google Scholar] [CrossRef]
- Brooke, J.S.A.; Ram, R.S.; Western, C.M.; Li, G.; Schwenke, D.W.; Bernath, P.F. Einstein A coefficients and oscillator strengths for the A 2Π − X 2Σ+ (red) and B 2Σ+ − X 2Σ+ violet systems and rovibrational transitions in the X 2Σ+ state of CN. Astrophys. J. Suppl. 2014, 210, 23. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Harrison, J.J.; Ram, R.S.; Western, C.M.; Bernath, P.F. Einstein A coefficients and absolute line intensities for the E 2Π − X 2Σ+ transition of CaH. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 67–74. [Google Scholar] [CrossRef]
- Shayesteh, A.; Ram, R.S.; Bernath, P.F. Fourier transform emission spectra of the A2Π→X2Σ+ and B2Σ+→X2Σ+ band systems of CaH. J. Mol. Spectrosc. 2013, 288, 46–51. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, B.; Braun, V.; Dulick, M.; Bernath, P. Infrared emission spectroscopy of BF and AlF. J. Mol. Spectrosc. 1995, 170, 82–93. [Google Scholar] [CrossRef]
- Hedderich, H.; Dulick, M.; Bernath, P. High resolution emission spectroscopy of AlCl at 20 μ. J. Chem. Phys. 1993, 99, 8363–8370. [Google Scholar] [CrossRef]
- Yurchenko, S.N.; Al-Refaie, A.F.; Tennyson, J. ExoCross: A general program for generating spectra from molecular line lists. Astron. Astrophys. 2018, 614, A131. [Google Scholar] [CrossRef] [Green Version]
- Colin, R.; Bernath, P.F. Revised molecular constants and term values for the X2Π state of CH. J. Mol. Spectrosc. 2010, 263, 120–122. [Google Scholar] [CrossRef]
- Bernath, P.F.; McElroy, C.T.; Abrams, M.; Boone, C.D.; Butler, M.; Camy-Peyret, C.; Carleer, M.; Clerbaux, C.; Coheur, P.F.; Colin, R.; et al. Atmospheric chemistry experiment (ACE): Mission overview. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Bernath, P.; Brazier, C.; Olsen, T.; Hailey, R.; Fernando, W.; Woods, C.; Hardwick, J. Spectroscopy of the CH free radical. J. Mol. Spectrosc. 1991, 147, 16–26. [Google Scholar] [CrossRef]
- Zachwieja, M. New Investigations of the A2Δ − X2Π Band System in the CH Radical and a New Reduction of the Vibration-Rotation Spectrum of CH from the ATMOS Spectra. J. Mol. Spectrosc. 1995, 170, 285–309. [Google Scholar] [CrossRef]
- Kepa, R.; Para, A.; Rytel, M.; Zachwieja, M. New Spectroscopic Analysis of the B2Σ− − X2Π Band System of the CH Molecule. J. Mol. Spectrosc. 1996, 178, 189–193. [Google Scholar] [CrossRef]
- Kumar, A.; Hsiao, C.C.; Hung, W.C.; Lee, Y.P. Highly predissociative levels of CH B2Σ− state detected with two-color resonant four-wave mixing spectroscopy. J. Chem. Phys. 1998, 109, 3824–3830. [Google Scholar] [CrossRef]
- Bembenek, Z.; Ke, R.; Rytel, M. Analysis of the 0–0 Band of the C2Σ+ − X2Π Band System in the 12CH and 13CH Isotopic Radicals. J. Mol. Spectrosc. 1997, 183, 1–5. [Google Scholar] [CrossRef]
- Ubachs, W.; Meyer, G.; Ter Meulen, J.; Dymanus, A. Hyperfine structure and lifetime of the C2Σ+, v=0 state of CH. J. Chem. Phys. 1986, 84, 3032–3041. [Google Scholar] [CrossRef] [Green Version]
- Heimer, T. Untersuchung über die Kohlenwasserstoffbande λ 3143. Z. Für Phys. 1932, 78, 771–780. [Google Scholar] [CrossRef]
- Li, X.; Kumar, A.; Hsiao, C.C.; Lee, Y.P. Two-Color Resonant Four-Wave Mixing Spectra of the C2Σ+ − X2Π (1 - 1) Band of CH in a Flame. J. Phys. Chem. A 1999, 103, 6162–6166. [Google Scholar] [CrossRef]
- Herzberg, G.; Johns, J. New spectra of the CH molecule. Astrophys. J. 1969, 158, 399–418. [Google Scholar] [CrossRef]
- Le Roy, R.J. RKR1: A computer program implementing the first-order RKR method for determining diatomic molecule potential energy functions. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 158–166. [Google Scholar] [CrossRef]
- Ram, R.; Bernath, P. Revised molecular constants and term values for the X3Σ- and A3Π states of NH. J. Mol. Spectrosc. 2010, 260, 115–119. [Google Scholar] [CrossRef]
- Brazier, C.; Ram, R.; Bernath, P. Fourier transform spectroscopy of the A3Π − X3Σ− transition of NH. J. Mol. Spectrosc. 1986, 120, 381–402. [Google Scholar] [CrossRef]
- Ram, R.; Bernath, P.; Hinkle, K. Infrared emission spectroscopy of NH: Comparison of a cryogenic echelle spectrograph with a Fourier transform spectrometer. J. Chem. Phys. 1999, 110, 5557–5563. [Google Scholar] [CrossRef] [Green Version]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Bernath, P.F.; Colin, R. Revised molecular constants and term values for the X2Π and B2Σ+ states of OH. J. Mol. Spectrosc. 2009, 257, 20–23. [Google Scholar] [CrossRef]
- Martin-Drumel, M.; Pirali, O.; Balcon, D.; Brechignac, P.; Roy, P.; Vervloet, M. High resolution far-infrared Fourier transform spectroscopy of radicals at the AILES beamline of SOLEIL synchrotron facility. Rev. Sci. Instrum. 2011, 82, 113106. [Google Scholar] [CrossRef]
- Stark, G.; Brault, J.W.; Abrams, M.C. Fourier-transform spectra of the A2Σ+ − X2ΠΔv=0 bands of OH and OD. JOSA B 1994, 11, 3–32. [Google Scholar] [CrossRef]
- Coxon, J. Optimum molecular constants and term values for the X2Π (v≤ 5) and A2Σ+ (v≤3) states of OH. Can. J. Phys. 1980, 58, 933–949. [Google Scholar] [CrossRef]
- Coxon, J.A.; Sappey, A.D.; Copeland, R.A. Molecular constants and term values for the hydroxyl radical, OH: The X2Π (v = 8, 12), A2Σ+(v = 4–9), B2Σ+(v = 0, 1), and C2Σ+(v = 0, 1) states. J. Mol. Spectrosc. 1991, 145, 41–55. [Google Scholar] [CrossRef]
- Derro, E.L.; Pollack, I.B.; Dempsey, L.P.; Greenslade, M.E.; Lei, Y.; Radenović, D.Č.; Lester, M.I. Fluorescence-dip infrared spectroscopy and predissociation dynamics of OH A2Σ+ (v= 4) radicals. J. Chem. Phys. 2005, 122, 244313. [Google Scholar] [CrossRef] [PubMed]
- Yarkony, D.R. A theoretical treatment of the predissociation of the individual rovibronic levels of OH/OD (A2Σ+). J. Chem. Phys. 1992, 97, 1838–1849. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN 2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Rothman, L.; Gordon, I.; Barber, R.; Dothe, H.; Gamache, R.; Goldman, A.; Perevalov, V.; Tashkun, S.; Tennyson, J. HITEMP, the high-temperature molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2139–2150. [Google Scholar] [CrossRef]
- Goldman, A.; Schoenfeld, W.G.; Goorvitch, D.; Chackerian, C.; Dothe, H.; Melen, F.; Abrams, M.C.; Selby, J.E.A. Updated line parameters for OH X2Π − X2Π(ν″,ν′) transitions. J. Quant. Spectrosc. Radiat. Transf. 1998, 59, 453–469. [Google Scholar] [CrossRef]
- Bekooy, J.P.; Verhoeve, P.; Meerts, W.L.; Dymanus, A. Submillimeter spectroscopy on OH+: The rotational transition at 1 THz. JCP 1985, 82, 3868–3869. [Google Scholar] [CrossRef]
- Liu, D.J.; Ho, W.C.; Oka, T. Rotational spectroscopy of molecular ions using diode lasers. J. Chem. Phys. 1987, 87, 2442–2446. [Google Scholar] [CrossRef]
- Rehfuss, B.D.; Jagod, M.F.; Xu, L.W.; Oka, T. Infrared spectroscopy of highly excited vibrational levels of the hydroxyl ion, OH+. J. Mol. Spectrosc. 1992, 151, 59–70. [Google Scholar] [CrossRef]
- Markus, C.R.; Hodges, J.N.; Perry, A.J.; Kocheril, G.S.; Müller, H.S.; McCall, B.J. High precision rovibrational spectroscopy of OH+. Astrophys. J. 2016, 817, 138. [Google Scholar] [CrossRef] [Green Version]
- Pickett, H.M. The fitting and prediction of vibration-rotation spectra with spin interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
- Endres, C.P.; Schlemmer, S.; Schilke, P.; Stutzki, J.; Müller, H.S.P. The cologne database for molecular spectroscopy, CDMS, in the virtual atomic and molecular data centre, VAMDC. J. Mol. Spectrosc. 2016, 327, 95–104. [Google Scholar] [CrossRef] [Green Version]
- Rodgers, D.J.; Batey, A.; Sarre, P.J. High-resolution laser spectroscopy and photodissociation dynamics of OH+. Mol. Phys. 2007, 105, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Charron, F.; Guo, B.; Zhang, K.; Morbi, Z.; Bernath, P. High-resolution infrared emission spectrum of CaF. J. Mol. Spectrosc. 1995, 171, 160–168. [Google Scholar] [CrossRef]
- Liu, M.C.; Muntianu, A.; Zhang, K.Q.; Colarusso, P.; Bernath, P. Infrared emission spectrum of KF. J. Mol. Spectrosc. 1996, 180, 188–192. [Google Scholar] [CrossRef]
- Muntianu, A.; Guo, B.; Bernath, P.F. High-resolution infrared emission spectrum of NaF. J. Mol. Spectrosc. 1996, 176, 274–279. [Google Scholar] [CrossRef]
- Bauer, R.K.; Lew, H. Rotational constants and electric dipole moment of NaF. Can. J. Phys. 1963, 41, 1461–1469. [Google Scholar] [CrossRef]
- Veazey, S.E.; Gordy, W. Millimeter-wave molecular-beam spectroscopy: Alkali fluorides. Phys. Rev. 1965, 138, A1303. [Google Scholar] [CrossRef]
- Green, G.W.; Lew, H. Rotational spectrum of 39KF by the molecular beam electric resonance method. Can. J. Phys. 1960, 38, 482–494. [Google Scholar] [CrossRef]
- Dijkerman, H.; Flegel, W.; Gräff, G.; Mönter, B. Beiträge zum Stark-Effekt der Moleküle 205Tl19F und 39K19F/Contributions to the Stark-Effect of the Molecules 205Tl19F and 39K19F. Z. Für Naturforschung A 1972, 27, 100–110. [Google Scholar] [CrossRef]
- Barber, B.; Zhang, K.; Guo, B.; Bernath, P. Vibration-rotation emission spectrum of MgF. J. Mol. Spectrosc. 1995, 169, 583–589. [Google Scholar] [CrossRef]
- Le Roy, R.J. dPotFit: A computer program to fit diatomic molecule spectral data to potential energy functions. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 179–196. [Google Scholar] [CrossRef]
- Shayesteh, A.; Bernath, P.F. Rotational analysis and deperturbation of the A2Π→X2Σ+ and B′2Σ+→X2Σ+ emission spectra of MgH. J. Chem. Phys. 2011, 135, 094308. [Google Scholar] [CrossRef] [Green Version]
- Mostafanejad, M.; Shayesteh, A. Ab initio potential energy curves and transition dipole moments for the X2Σ+, A2Π and B2Σ+ states of MgH. Chem. Phys. Lett. 2012, 551, 13–18. [Google Scholar] [CrossRef]
- Shayesteh, A.; Henderson, R.D.E.; Le Roy, R.J.; Bernath, P.F. Ground state potential energy curve and dissociation energy of MgH. J. Phys. Chem. A 2007, 111, 12495–12505. [Google Scholar] [CrossRef]
- Yadin, B.; Vaness, T.; Conti, P.; Hill, C.; Yurchenko, S.N.; Tennyson, J. ExoMol Molecular linelists: I The rovibrational spectrum of BeH, MgH and CaH the X2Σ+ state. Mon. Not. R. Astron. Soc. 2012, 425, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Steimle, T.C.; Shirley, J.E.; Simard, B.; Vasseur, M.; Hackett, P. A laser spectroscopic study of gas-phase TiH. J. Chem. Phys. 1991, 95, 7179–7182. [Google Scholar] [CrossRef]
- Launila, O.; Lindgren, B. Spectroscopy of TiH: Rotational analysis of the 4Γ→X4Φ (0,0) band at 530 nm. J. Chem. Phys. 1996, 104, 6418–6422. [Google Scholar] [CrossRef]
- Andersson, N.; Balfour, W.J.; Bernath, P.F.; Lindgren, B.; Ram, R.S. Emission spectra of TiH and TiD near 938 nm. J. Chem. Phys. 2003, 118, 3543–3548. [Google Scholar] [CrossRef] [Green Version]
- Andersson, N.; Balfour, W.J.; Lindgren, B. Rotational analysis of the 4Γ − 4Φ spectrum of TiD. J. Mol. Spectrosc. 2003, 217, 298–299. [Google Scholar] [CrossRef]
- Bauschlicher, C.W.; Ram, R.S.; Bernath, P.F.; Parsons, C.G.; Galehouse, D. The A6Σ+ − X6Σ+ transition of CrH, Einstein coefficients, and an improved description of the A state. J. Chem. Phys. 2001, 115, 1312–1318. [Google Scholar] [CrossRef] [Green Version]
- Dulick, M.; Bauschlicher, C.W.; Burrows, A.; Sharp, C.M.; Ram, R.S.; Bernath, P. Line intensities and molecular opacities of the FeH F 4Δ – X 4Δ transition. Astrophys. J. 2003, 594, 651–663. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.G.; Davis, S.P.; Lindgren, B.; Balfour, W.J. The Near-Infrared Spectrum Of The FeH Molecule. Astrophys. J. Suppl. 1987, 65, 721–778. [Google Scholar] [CrossRef]
- Curtis, M.C.; Sarre, P.J. High-resolution laser spectroscopy of the Swan system (d3Πg − a3Πu) of C2 in an organic halide-alkali metal flame. J. Mol. Spectrosc. 1985, 114, 427–435. [Google Scholar] [CrossRef]
- Suzuki, T.; Saito, S.; Hirota, E. Doppler-limited dye-laser excitation spectrum of the C2 Swan band (NU′-NU″=1-0). J. Mol. Spectrosc. 1985, 113, 399–409. [Google Scholar] [CrossRef]
- Prasad, C.V.V.; Bernath, P.F. Fourier transform spectroscopy of the Swan (d3Πg − a3Πu) system of the jet-cooled C2 molecule. Astrophys. J. 1994, 426, 812–821. [Google Scholar] [CrossRef]
- Tanabashi, A.; Amano, T. New identification of the visible bands of the C2 Swan system. J. Mol. Spectrosc. 2002, 215, 285. [Google Scholar] [CrossRef]
- Tanabashi, A.; Hirao, T.; Amano, T.; Bernath, P.F. The Swan system of C2: A global analysis of Fourier transform emission spectra. Astrophys. J. Suppl. 2007, 169, 472–484, Erratum: 2007 ApJS 170 261. [Google Scholar] [CrossRef] [Green Version]
- Yurchenko, S.N.; Szabo, I.; Pyatenko, E.; Tennyson, J. ExoMol Molecular line lists XXXI: The spectrum of C2. Mon. Not. R. Astron. Soc. 2018, 480, 3397–3411. [Google Scholar] [CrossRef]
- Furtenbacher, T.; Szabó, I.; Császár, A.G.; Bernath, P.F.; Yurchenko, S.N.; Tennyson, J. Experimental Energy Levels and Partition Function of the 12C2 Molecule. Astrophys. J. Suppl. 2016, 224, 44. [Google Scholar] [CrossRef] [Green Version]
- Ram, R.S.; Bernath, P.F. Fourier transform spectroscopy of the A2Πi − X2Σ+ system of CP. J. Mol. Spectrosc. 1987, 122, 282–292. [Google Scholar] [CrossRef]
- Ram, R.S.; Tam, S.; Bernath, P.F. The A2Πi − X2Σ+ system of CP: Observation of new bands. J. Mol. Spectrosc. 1992, 152, 89–100. [Google Scholar] [CrossRef]
- Saito, S.; Yamamoto, S.; Kawaguchi, K.; Ohishi, M.; Suzuki, H.; Ishikawa, S.I.; Kaifu, N. The microwave spectrum of the CP radical and related astronomical search. Astrophys. J. 1989, 341, 1114–1119. [Google Scholar] [CrossRef]
- Klein, H.; Klisch, E.; Winnewisser, G.; Königshofen, A.; Hahn, J. CP’s triple-bond strength experienced in its THz spectrum. Z. Für Naturforschung A 1999, 54, 187–190. [Google Scholar] [CrossRef]
- de Brouckère, G.; Feller, D. Configuration interaction calculations on the state of CP and the-transition bands. Miscellaneous properties. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 5053. [Google Scholar] [CrossRef]
- Ram, R.S.; Wallace, L.; Bernath, P.F. High resolution emission spectroscopy of the A2Π − X2Σ+ (red) system of 12C14N. J. Mol. Spectrosc. 2010, 263, 82–88. [Google Scholar] [CrossRef]
- Ram, R.S.; Davis, S.P.; Wallace, L.; Engleman, R.; Appadoo, D.R.T.; Bernath, P.F. Fourier transform emission spectroscopy of the B2Σ+ − X2Σ+ system of CN. J. Mol. Spectrosc. 2006, 237, 225–231. [Google Scholar] [CrossRef]
- Davis, S.P.; Abrams, M.C.; Rao, M.L.P.; Brault, J.W. CN Vibration-Rotation Spectrum. J. Opt. Soc. Am. B 1991, 8, 198–200. [Google Scholar] [CrossRef]
- Horka, V.; Civis, S.; Spirko, V.; Kawaguchi, K. The infrared spectrum of CN in its ground electronic state. Collect. Czech. Chem. Commun. 2004, 69, 73–89. [Google Scholar] [CrossRef]
- Ram, R.S.; Tereszchuk, K.; Gordon, I.E.; Walker, K.A.; Bernath, P.F. Fourier transform emission spectroscopy of the E2Π − X2Σ+ transition of CaH and CaD. J. Mol. Spectrosc. 2011, 266, 86–91. [Google Scholar] [CrossRef]
- Weck, P.F.; Stancil, P.C.; Kirby, K. Theoretical study of the rovibrationally resolved transitions of CaH. J. Chem. Phys. 2003, 118, 9997–10005. [Google Scholar] [CrossRef]
- Furtenbacher, T.; Császár, A.G.; Tennyson, J. MARVEL: Measured active rotational-vibrational energy levels. J. Mol. Spectrosc. 2007, 245, 115–125. [Google Scholar] [CrossRef] [Green Version]
- Alavi, S.F.; Shayesteh, A. Einstein A coefficients for rovibronic lines of the A2Π − X2Σ+ and B2Σ+ − X2Σ+ transitions of CaH and CaD. Mon. Not. R. Astron. Soc. 2017, 474, 2–11. [Google Scholar] [CrossRef]
- Boesch, A.; Reiners, A. Spectral line lists of a nitrogen gas discharge for wavelength calibration in the range 4500–11 000 cm−1. Astron. Astrophys. 2015, 582, A43. [Google Scholar] [CrossRef] [Green Version]







| i | Energy (cm) | J | v | ||
|---|---|---|---|---|---|
| 1 | 0.000000 | 16 | 0 | −1.0000E+00 | 0 |
| 2 | 1.405000 | 48 | 1 | 6.4935E+04 | 0 |
| 3 | 4.215000 | 80 | 2 | 6.8027E+03 | 0 |
| 4 | 8.430000 | 112 | 3 | 1.8762E+03 | 0 |
| 5 | 14.049000 | 144 | 4 | 7.6336E+02 | 0 |
| 6 | 21.072000 | 176 | 5 | 3.8168E+02 | 0 |
| 7 | 29.499000 | 208 | 6 | 2.1786E+02 | 0 |
| 8 | 39.331000 | 240 | 7 | 1.3569E+02 | 0 |
| 9 | 50.564000 | 272 | 8 | 9.0090E+01 | 0 |
| 10 | 63.200000 | 304 | 9 | 6.2893E+01 | 0 |
| 11 | 77.237000 | 336 | 10 | 4.5662E+01 | 0 |
| 12 | 92.674000 | 368 | 11 | 3.4130E+01 | 0 |
| 13 | 109.511000 | 400 | 12 | 2.6247E+01 | 0 |
| 14 | 127.747000 | 432 | 13 | 2.0576E+01 | 0 |
| 15 | 147.380000 | 464 | 14 | 1.6447E+01 | 0 |
| f | i | (s) | |
|---|---|---|---|
| 492 | 475 | 1.1900E+01 | 110.073000 |
| 1381 | 1370 | 1.5400E+01 | 110.207000 |
| 951 | 939 | 1.3300E+01 | 110.289000 |
| 1190 | 1178 | 1.4400E+01 | 110.386000 |
| 859 | 840 | 1.3100E+01 | 110.544000 |
| 1323 | 1313 | 1.5200E+01 | 110.605000 |
| 1122 | 1110 | 1.4200E+01 | 110.716000 |
| 738 | 721 | 1.2800E+01 | 110.780000 |
| 1264 | 1252 | 1.5000E+01 | 110.988000 |
| 624 | 606 | 1.2600E+01 | 110.997000 |
| 1049 | 1035 | 1.3900E+01 | 111.028000 |
| 1390 | 1381 | 1.5900E+01 | 111.110000 |
| 513 | 492 | 1.2300E+01 | 111.193000 |
| Molecule | El. States | Lines | N States | Ref. | ||
|---|---|---|---|---|---|---|
| AlCl | X | 11 | 200 | 20245 | 2423 | Yousefi and Bernath [28] |
| AlCl | X | 11 | 200 | 20245 | 2423 | Yousefi and Bernath [28] |
| AlF | X | 11 | 200 | 40490 | 2423 | Yousefi and Bernath [28] |
| CH | X , A , B , C | 6 | 49.5 | 53,079 | 2526 | Masseron et al. [29] |
| CH | X , A , B , C | 6 | 49.5 | 51,349 | 2428 | Masseron et al. [29] |
| NH | X , A | 6 | 45 | 22,545 | 1285 | Brooke et al. [30], Brooke et al. [31], Fernando et al. [32] |
| OH | X , A | 13 | 58.5 | 54,276 | 1878 | Brooke et al. [33], Yousefi et al. [34] |
| OH | X , A | 4 | 30 | 12,044 | 823 | Hodges and Bernath [35], Hodges et al. [36] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| CaF | X | 10 | 123 | 14,817 | 1363 | Hou and Bernath [37] |
| KF | X | 10 | 110 | 10,572 | 1065 | Frohman et al. [38] |
| KF | X | 10 | 109 | 10,379 | 1047 | Frohman et al. [38] |
| NaF | X | 10 | 90 | 7884 | 839 | Frohman et al. [38] |
| MgF | X | 8 | 101 | 8136 | 917 | Hou and Bernath [39] |
| MgF | X | 8 | 101 | 8136 | 917 | Hou and Bernath [39] |
| MgF | X | 8 | 101 | 8136 | 917 | Hou and Bernath [39] |
| LiCl | X | 11 | 201 | 26,260 | 2423 | Bittner and Bernath [40] |
| LiCl | X | 11 | 201 | 26,260 | 2423 | Bittner and Bernath [40] |
| LiCl | X | 11 | 201 | 26,260 | 2423 | Bittner and Bernath [40] |
| LiCl | X | 11 | 201 | 26,260 | 2423 | Bittner and Bernath [40] |
| LiF | X | 11 | 201 | 10,621 | 2423 | Bittner and Bernath [40] |
| LiF | X | 11 | 201 | 10,621 | 2423 | Bittner and Bernath [40] |
| MgH | X, A, , | 11 | 50.5 | 30896 | 1935 | GharibNezhad et al. [41] |
| TiH | X, A, B | 5 | 50.5 | 199,072 | 5788 | Burrows et al. [42] |
| CrH | X, A | 3 | 39.5 | 13,824 | 1646 | Chowdhury et al. [43] |
| FeH | X, F | 4 | 50.5 | 93,040 | 3564 | Wende et al. [44] |
| C | a, d | 3 | 97 | 155,110 | 4653 | Brooke et al. [45] |
| CP | X, A | 8 | 55.5 | 28,752 | 2114 | Ram et al. [46] |
| CN | X, A, B | 22 | 115.5 | 195,120 | 7703 | Brooke et al. [47] |
| CaH | X, A, B, E | 4 | 50.5 | 19,095 | 1771 | Li et al. [48], Shayesteh et al. [49] |
| N | A, B, , | 29 | 75 | 7,182,000 | 40,380 | Western et al. [21] |
| Molecule | Molecule | ||
|---|---|---|---|
| AlCl | 24 | MgF | 2 |
| AlCl | 24 | MgF | 12 |
| AlF | 12 | MgF | 2 |
| CaF | 2 | NaF | 8 |
| CaF | 2 | NH | 6 |
| CaF | 16 | OH | 2 |
| CaF | 2 | OH+ | 2 |
| CaF | 2 | CH | 2 |
| CaF | 2 | MgH | 2 |
| KF | 8 | TiH | 2 |
| KF | 8 | CrH | 2 |
| LiCl | 12 | FeH | 2 |
| LiCl | 12 | C | 1 |
| LiCl | 16 | CP | 2 |
| LiCl | 16 | CN | 3 |
| LiF | 6 | CaH | 2 |
| LiF | 8 | N | 3 & 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tennyson, J.; Yurchenko, S.N. Empirical Line Lists in the ExoMol Database. Atoms 2020, 8, 7. https://doi.org/10.3390/atoms8010007
Wang Y, Tennyson J, Yurchenko SN. Empirical Line Lists in the ExoMol Database. Atoms. 2020; 8(1):7. https://doi.org/10.3390/atoms8010007
Chicago/Turabian StyleWang, Yixin, Jonathan Tennyson, and Sergei N. Yurchenko. 2020. "Empirical Line Lists in the ExoMol Database" Atoms 8, no. 1: 7. https://doi.org/10.3390/atoms8010007
APA StyleWang, Y., Tennyson, J., & Yurchenko, S. N. (2020). Empirical Line Lists in the ExoMol Database. Atoms, 8(1), 7. https://doi.org/10.3390/atoms8010007








