Excitation of the 6d ²D → 6p ²P^o Radiative Transitions in the Pb⁺ Ion by Electron Impact ^†

Abstract

Results of experimental and theoretical investigation of electron-impact excitation of the $6s^{2}6d\hspace{0.17em}{}^{2}D\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}^{\mathrm{o}}$ spectral transitions from the ground $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ level in the Pb⁺ ion are presented. The experimental excitation functions for the transitions, measured by a VUV spectroscopy method, using the crossed electron and ion beams technique, reveal a rather distinct resonance structure resulting mainly from the electron decay of both atomic and ionic autoionizing states. The absolute values of the emission cross-sections, obtained by normalizing the experimental data at the incident electron energy 100 eV by those calculated using the Flexible Atomic Code software package, were found to be (0.35 ± 0.17) × 10^–16 cm² for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ → $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transition and (0.19 ± 0.09) × 10^–16 cm² for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ → $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) transition.

1. Introduction

The process of electron-impact excitation of positive ions plays a significant role in various types of laboratory and astrophysical plasma. Therefore, knowledge of the mechanisms and fundamental characteristics of this process (oscillator strengths, effective cross-sections of radiative transitions, and their energy dependences, etc.) is of great interest for solving a number of fundamental problems of modern plasma physics and plasma technologies [1,2]. Cross-sections of excitation of the heavy metal ions by the slow electrons are important in astrophysics for determination of the chemical composition of astrophysical objects, for development of models of the atmospheres and interiors of stars, as well as for testing theories of nucleosynthesis.

At present, the process of electron excitation of single charged metal ions of group II is thoroughly studied both experimentally and theoretically (see, for example, [3,4,5,6,7,8]). For the ions of group III, there are experimental investigations of the electron excitation of the Ga⁺ [9], In⁺ [10,11], and Tl⁺ [12] ions as well as theoretical calculations of the excitation cross-sections for the Al⁺ [13] and In⁺ [14] ions. As for the data on electron-impact excitation of the metal ions of group IV, they are very poor, and are presented, to our knowledge, with only one experimental [15] and one theoretical [16] study for the electron-impact excitation of singly charged lead. The radiation constants for this ion are of great interest in recent years since spectral lines of the Pb⁺ ion have been detected in several stars, including Ap and Am stars, as well as in the interstellar medium [17,18]. Radiative transitions in the Pb⁺ ion are also of great importance in astrophysics from the viewpoint of fundamental understanding of the processes assisted by this ion, occurring in astrophysical plasma, as well as determination of the elemental abundance, which is the highest among the elements heavier than barium, on the basis of the observed optical signal.

In this paper, we present the results of experimental and theoretical investigation for electron-impact excitation of the Pb⁺ ionn corresponding to the $6s^{2}6d\hspace{0.17em}{}^{2}D\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}^{\mathrm{o}}$ radiative transitions, as follows:

$$\begin{array}{ll}e+{\mathrm{Pb}}^{+}(6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}})& \to {\mathrm{Pb}}^{+\ast }(6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2})+e^{\prime }\\ & \downarrow \\ & {\mathrm{Pb}}^{+}(6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}})+h\nu (\lambda 143.4\hspace{0.17em}\mathrm{nm}),\end{array}$$

(1)

$$\begin{array}{ll}e+{\mathrm{Pb}}^{+}(6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}})\to & {\mathrm{Pb}}^{+\ast }(6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2})+e^{\prime }\\ & \downarrow \\ & {\mathrm{Pb}}^{+}(6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}})+h\nu (\lambda 182.2\hspace{0.17em}\mathrm{nm}).\end{array}$$

(2)

Both radiative transitions were excited from the same $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ ground level. Since, to our knowledge, there are no theoretical calculations of excitation cross-section for the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ transition available in the literature, we performed our own calculation of the excitation cross-section for this transition as well as for the ${}^{2}P{}_{1/2}^{\mathrm{o}}\to {}^{2}D{}_{3/2}$ transition using Flexible Atomic Code package (FAC) [19]. So far, FAC is the convenient tool for constructing high-quality wave functions of electron scattering on atoms and ions and has proven to be good for the analysis of energy levels, Auger cascades, electron-impact excitation, and ionization cross-sections [20,21,22]. Likewise, in the GRASP2k package used in the calculation [16], FAC also incorporates a core–valence correlation, configuration mixing, and relativistic effects, which are very important to account for in the case of such a heavy ion as singly charged lead.

2. Experiment

The experiment was performed using the apparatus described in detail in our previous work [23]. Briefly, in the equipotential interaction region under the vacuum of 7 × 10⁻⁶ Pa a beam of monoenergetic electrons (FWHM ≈ 0.6 eV) crossed a beam of Pb⁺ ions in the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ ground state, which was provided by the use of an ion source with thermal ionization. The electron beam current was (50–300) × 10⁻⁶ A within the electron energy range of 5–100 eV. The ion beam current was (0.5–1.0) × 10⁻⁶ A at the ion energy of 800 eV. The electron energy scale was calibrated using the excitation threshold of the λ121.6 nm line of atomic hydrogen by electron impact.

Emission from the interaction region resulting from the radiative $6s^{2}6d\hspace{0.17em}{}^{2}D\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}^{\mathrm{o}}$ transitions was separated by a 70° VUV monochromator, based on the Seya–Namioka scheme with the reciprocal linear dispersion of 1/7 nm/mm and detected by a solar-blind FEU-142 photomultiplier. The spectral sensitivity of the detection system was determined on the basis of measuring the emission intensities of the VUV spectral lines of atomic nitrogen resulting from the electron impact of N₂ molecules at the electron energy of 100 eV. The calibration uncertainty of the spectral sensitivity of the detection system was 16%.

Since the signal, due to the process under investigation, was observed against a large background, resulting from the interaction of both beams with the residual gas, modulation of electron and ion beams with rectangular pulses shifted with respect to each other by a quarter of a period, was used. This, in combination with a four-way chopping registration scheme, allows one to extract the desired signal of (0.2–0.5) counts s⁻¹ at the signal-to-background ratio of 0.05–0.1. All the signals were accumulated for 1000–2000 s with typically 5–10 times per each data point and transferred into a PC for further processing. The uncertainty of the relative measurement did not exceed 15%, while that of the absolute emission cross-section determination was about ±50%.

3. Theoretical Method

Energy levels, radiative and Auger transition probabilities, as well as electron-impact excitation cross-sections, are studied using FAC [19], which implements the Dirac–Fock–Slater (DFS) approximation. The electron-impact excitation cross-sections are calculated in the distorted wave approximation. The influence of correlation effects on excitation cross-sections is investigated using configuration interaction method.

The ${\mathrm{Pb}}^{+}$ $6d{ }^2{D}_{3/2}$ and $6d{ }^2{D}_{5/2}$ levels are populated by three processes: direct excitation from the ground level, excitation to the higher levels with subsequent radiative cascade, and dielectronic capture to the states of the $\mathrm{Pb}$ atom with subsequent radiative and Auger decay.

Excitations to the higher levels from the ground level can be described by

$$5d^{10}6s^{2}6p{ }^2{P}_{1/2}+e^{-} \to \left\{\begin{array}{l}5d^{10}6s^{2}nl\hfill \\ 5d^{10}6s 6p nl\hfill \end{array}\right.+e^{-},$$

(3)

where $6\le n\le 10$, $l<5$. The radiative and Auger cascade from the produced states is investigated. The Auger transitions are included in the study since some states are above the single ionization threshold and, therefore, part of population, can be transferred to the next ionization stage.

Dielectronic capture produces states of the $\mathrm{Pb}$ atom, as follows:

$$5d^{10}6s^{2}6p+e^{-} \to \left\{\begin{array}{l}5d^{10}6s^{2}nl n\prime l\prime \hfill \\ 5d^{10}6s 6p nl n\prime l\prime \hfill \\ 5d^{9}6s^{2}6p nl n\prime l\prime \hfill \end{array}\right..$$

(4)

Here, $n\le 7$, $n\prime \le 10$, and $l,l^{\prime }<5$. The obtained autoionizing states of the Pb atom can decay further to the ${\mathrm{Pb}}^{+}$ $6d_{3/2}$ and $6d_{5/2}$ levels. The study of DC to other configurations of the $\mathrm{Pb}$ atom would be less important compared with the ones provided in Equation (4).

The bases of interacting configurations for $6s^{2}6p$ and $6s^{2}6d$ configurations are built using the configuration interaction strength [24,25,26]:

$$T\left(K,K^{\prime }\right)=\frac{{\sum }_{\gamma \gamma \prime }{〈\mathsf{\Phi }\left(K\gamma \right)\left|H\right|\mathsf{\Phi }\left(K^{\prime }\gamma \prime \right)〉}^2}{\overline{E}{\left(K,K\prime \right)}^2}$$

(5)

Here, $\overline{E}\left(K,K\prime \right)$ is the average energy distance between the energy levels of the configurations $K$ and $K\prime$, as follows:

$$\begin{gathered} \overline{E}\left(K,K^{\prime }\right)=\frac{{\sum }_{\gamma {\gamma }^{\prime }}\left[〈\mathsf{\Phi }\left(K\gamma \right)\left|H\right|\mathsf{\Phi }\left(K\gamma \right)〉-〈\mathsf{\Phi }\left(K^{\prime }{\gamma }^{\prime }\right)\left|H\right|\mathsf{\Phi }\left(K^{\prime }{\gamma }^{\prime }\right)〉\right]}{{\sum }_{\gamma {\gamma }^{\prime }}{〈\mathsf{\Phi }\left(K\gamma \right)\left|H\right|\mathsf{\Phi }\left(K^{\prime }{\gamma }^{\prime }\right)〉}^2} \\ \times {〈\mathsf{\Phi }\left(K\gamma \right)\left|H\right|\mathsf{\Phi }\left(K^{\prime }{\gamma }^{\prime }\right)〉}^2 \end{gathered}$$

(6)

The summation is performed over all states $\gamma$ and $\gamma \prime$ of the configurations $K$ and $K\prime$, respectively. The term $〈\mathsf{\Phi },\left(K\gamma \right),\left|H\right|,\mathsf{\Phi },\left(K\gamma \right)〉$ is the interconfiguration matrix element of the pseudo-relativistic Hartree–Fock Hamiltonian $H$ [25].

Single and double excitations from the $6s^{2}6p$ and $6s^{2}6d$ configurations are considered to build the list of admixed configurations. The single excitations from $4f$, $5s$, $5p$, $5d$, $5f$, $6s$, $6p$, and $6d$ subshells up to subshells with the principal quantum number $n=8$ and orbital quantum number $l=4$ ($l<n$) are investigated. Promotion of electrons up to subshells with $n=6$ is considered for double excitations. The study included 71 even and 50 odd configurations, having the highest values of configuration interaction strengths. This approach was previously successfully used to analyze energy levels, Auger cascades, electron-impact excitation, and ionization cross-sections [20,21,22].

4. Results and Discussion

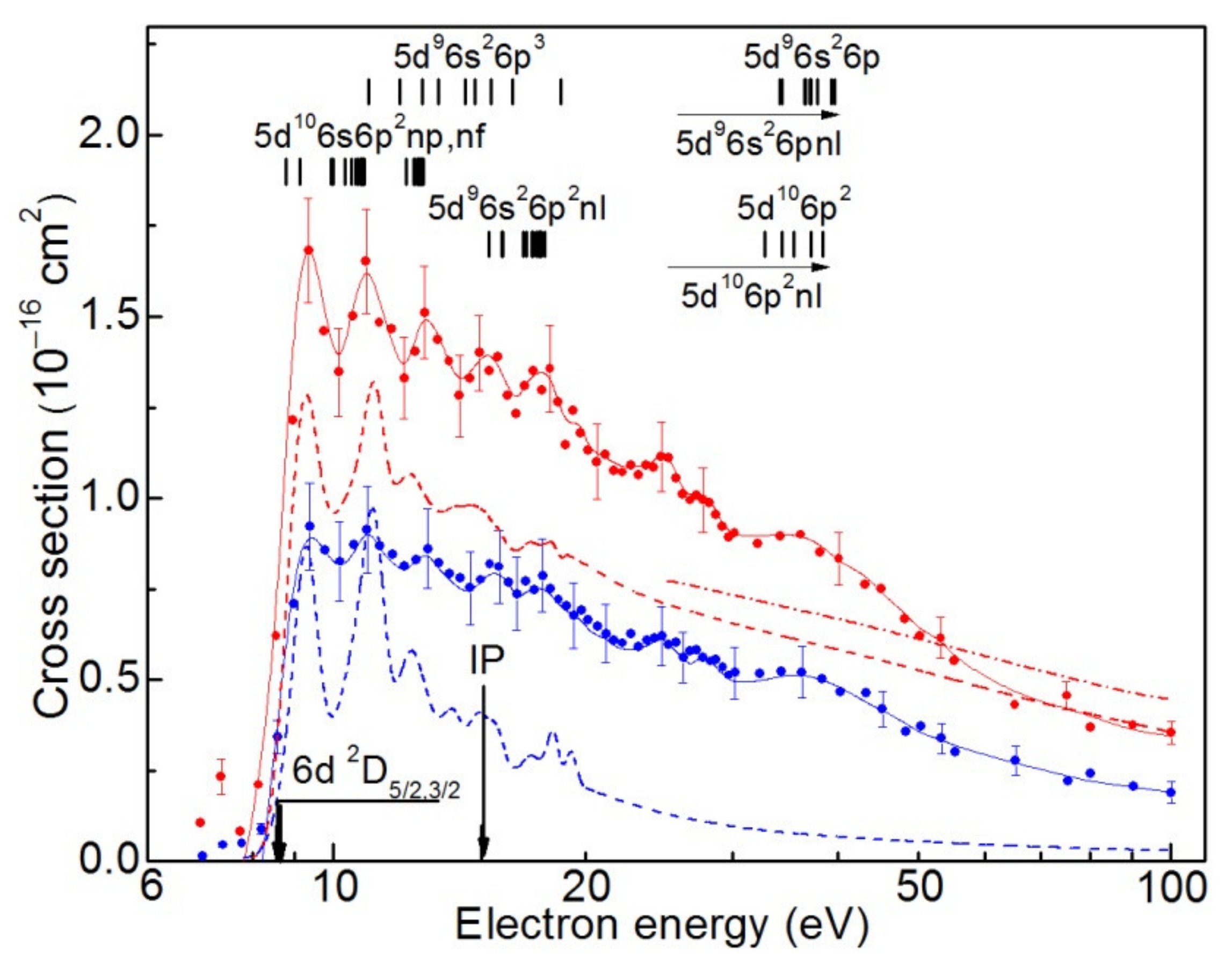
The energy dependences of the emission cross-sections of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) and $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) transitions, measured in the incident electron energy range 6–100 eV, are presented in Figure 1 with red and blue circles, respectively. The error bars in Figure 1 represent the relative uncertainties, evaluated at the 68% confidence level.

Note that both curves are measured under the same experimental conditions. In addition, in order to correctly compare the intensities of the λ143.4 nm and λ182.2 nm spectral lines, we measured the intensity I of both lines at the incident electron energy of 100 eV in the same experiment. The intensity of the λ143.4 nm line ($6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$) was found to be larger than that for the λ182.2 nm line ($6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$) by a factor of 1.8.

It can be seen from Figure 1 that the energy dependences of the emission cross-sections of both lines are similar. They rapidly increase at the thresholds and have a rather distinct similar structure up to ≈50 eV. At the higher energies (E > 50 eV), the cross-sections decrease according to the law $\sigma (E)~E^{-1}\ln E$, which is characteristic for optically allowed transitions. Note that the experimentally observed the excitation thresholds of the lines, namely E_182.2 ≈ 8.55 eV and E_143.4 ≈ 8.65 eV, correspond to the excitation of the $6d\hspace{0.17em}{}^{2}D{}_{5/2}$ and $6d\hspace{0.17em}{}^{2}D{}_{3/2}$ levels from the ground $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ level.

The observed structure can be explained by the population of the $6d\hspace{0.17em}{}^{2}D{}_{3/2}$ and $6d\hspace{0.17em}{}^{2}D{}_{5/2}$ resonance levels due to both electron decay of the atomic autoionizing states (AIS) [27,28,29,30,31,32] and radiative transitions from the higher ionic levels and AIS of the Pb⁺ ion [33]. Thus, the first three maxima in the energy range from the thresholds up to the Pb⁺ ion ionization potential (15.03 eV) are related, most likely, to the electron decay of the Pb atom $5d^{10}6s6p^{2}np$ (n ≥ 7) AIS [27,28] as well as the radiative transitions from the ionic $5d^{10}6s^{2}np,\hspace{0.17em}mf$ (n ≥ 7, m ≥ 5) levels [33]. In addition, starting from the energy ≈ 11 eV the $5d^{9}6s^{2}6p^3$ atomic AIS [27,28] also make a contribution to these maxima. The structure observed above the Pb⁺ ion ionization potential can be related to the electron decay of the atomic $5d^{9}6s^{2}6p^{2}np,\hspace{0.17em}mf$ (n ≥ 6, m ≥ 5) AIS [27,28] as well as the ionic $5d^{9}6s^{2}6pnp,\hspace{0.17em}mf$ (n ≥ 7, m ≥ 5) and $5d^{10}6p^{2}nd,\hspace{0.17em}mp$ (n ≥ 6, m ≥ 7) AIS [29,30,31,32]. Note that the $5d^{10}6s6p^{2}np$, $5d^{9}6s^{2}6p^{2}np,\hspace{0.17em}mf$, and $5d^{9}6s^{2}6p^3$ atomic AIS are formed due to the incident electron resonance capture with simultaneous excitation of one of the electrons of the Pb⁺ ion (Equation (4)). For clarity, a schematic diagram of the energy levels of the Pb⁺ and Pb²⁺ ions, as well as the transitions studied in this work, is presented in Figure 2.

The absolute value of the emission cross-section of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transition is obtained by normalizing the experimental data at the incident electron energy 100 eV, by those calculated using FAC. It should be noted that the radiative $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ179.7 nm) transition starting from the same ${}^{2}D{}_{3/2}$ level is also possible [33]. Thus, one has to take into account the branching ratio for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ transition when determining the absolute value of the emission cross-section. According to the data from Ref. [34], the branching ratio for this transition is 0.8. Proceeding from the calculated value of the excitation cross-section of 0.44 × 10^–16 cm² and the branching ratio 0.8, the absolute value of the emission cross-section of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transition is found to be (0.35 ± 0.17) × 10^–16 cm² (see

Table 1. Cross-sections σ (·10^–16 cm²) for the transitions between the $6s^{2}6p\hspace{0.17em}{}^{2}P{}^{\mathrm{o}}$ and $6s^{2}6d\hspace{0.17em}{}^{2}D$ levels at 100 eV (^a—our calculation; ^b—calculation [16]; ^c—the value obtained from the experimentally observed ratio of the line intensities 1.8). The relationship between emission (σ_em) and excitation (σ_ex) cross-sections is σ_em = BR·σ_ex (BR—the branching ratio).

Level		Data
Lower	Upper	σem	σex	BR
$6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$	$6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$	0.35	0.44 a	0.8
$6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$	$6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$	0.44	0.55 b	0.8
$6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$	$6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$	0.03	0.03 a	1
$6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$	$6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$	0.19 c	0.19	1

). Note that this value is slightly less than that from the work [15] obtained with the use of the Van Regemorter formula [35]. In addition, the branching ratio for the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ transition was not taken into account in Ref. [15]. The absolute value of the emission cross-section for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) transition is determined on account of the experimentally observed ratio of the line intensities I_143.4/I_182.2 ≈ 1.8 (at 100 eV) and is found to be (0.19 ± 0.09) × 10^–16 cm² (see Table 1).

The results of our calculation of the excitation cross-sections for the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ and $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ transitions are presented in Figure 1 as dash red and dash blue curves, respectively. As can be seen from Figure 1, the results of the calculation in both cases agree qualitatively rather well with the experimental data in the whole incident electron energy range. In the case of the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ transition, the value of the excitation cross-section is consistent with the experimental data in the electron energy range above 70 eV. At lower energies a discrepancy with experiment in the cross-section values is observed, though in the near-threshold energy range (≤16 eV), the structure observed in the experiment is reproduced rather well.

For comparison, the result of the calculation [16] for the excitation cross-section of the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ transition (when taking into account the branching ratio of 0.8) is also presented in Figure 1 by dot dash red curve. Note that the calculation [16] does not incorporate the effects of cascade transitions and the resonance contribution of autoionizing states. As it is seen from Figure 1, the behavior of both curves is similar in the energy range 25–100 eV. However, the value of the excitation cross-section from Ref. [16] is slightly larger (by a factor of not more than 1.25) than that given by our calculation. It worth to note that the cross-section value of 0.55 × 10^–16 cm² (at 100 eV) obtained in the calculation [16] is the same as given by the Van Regemorter formula [35].

As for the excitation cross-section of the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ transition calculated in this work, its value at the electron energy 100 eV (0.03·10^–16 cm²) is less by a factor of 6.3 than that followed from experimentally observed ratio of the line intensities I_143.4/I_182.2 ≈ 1.8 (0.19 × 10^–16 cm²) (see Table 1). At the same time, in the near-threshold energy range (≤16 eV) the experimentally observed structure is also reproduced rather well.

5. Conclusions

The results of experimental and theoretical study of electron-impact excitation of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) and $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transitions from the ground $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ level in the Pb⁺ ion are presented here. For correct comparison, the intensities of the λ143.4 nm and λ182.2 nm spectral lines were measured at the incident electron energy 100 eV in the same experiment.

A rather distinct structure observed in both energy dependences of the emission cross-sections results from the population of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ and $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ resonance levels, due to electron decay of the atomic $5d^{10}6s6p^{2}np$ (n ≥ 7) and $5d^{9}6s^{2}6p^3$ AIS; as well as radiative transitions from the higher $5d^{10}6s^{2}np,\hspace{0.17em}mf$ (n ≥ 7, m ≥ 5) levels of the Pb⁺ ion below the ionization potential and electron decay of the atomic $5d^{9}6s^{2}6p^{2}np,\hspace{0.17em}mf$ (n ≥ 6, m ≥ 5) and ionic $5d^{9}6s^{2}6pnp,\hspace{0.17em}mf$ (n ≥ 7, m ≥ 5), $5d^{10}6p^{2}nd,\hspace{0.17em}mp$ (n ≥ 6, m ≥ 7) AIS, above the ionization potential.

The absolute value of the emission cross-section of the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transition is obtained by normalizing the experimental data at the incident electron energy 100 eV by the calculated value using the FAC software package with taking the branching ratio of 0.8 into account. The absolute value of the emission cross-section for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}\to 6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) transition is determined on account of the experimentally observed ratio of the line intensities I_143.4/I_182.2 ≈ 1.8 (at 100 eV). The values were found to be (0.35 ± 0.17 × 10^–16 cm² for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ → $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}$ (λ143.4 nm) transition and (0.19 ± 0.09) × 10^–16 cm² for the $6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ → $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{3/2}^{\mathrm{o}}$ (λ182.2 nm) transition. Our calculation for the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{3/2}$ transition is in good agreement with the result of Ref. [16], obtained with the use of the GRASP2k package.

The calculated value of the excitation cross-section for the $6s^{2}6p\hspace{0.17em}{}^{2}P{}_{1/2}^{\mathrm{o}}\to 6s^{2}6d\hspace{0.17em}{}^{2}D{}_{5/2}$ transition at the electron energy 100 eV (0.03 × 10^–16 cm²) is less, by a factor of 6.3, than that followed from the experimentally observed ratio of the line intensities I_143.4/I_182.2 ≈ 1.8 (0.19 × 10^–16 cm²). At the same time, in the near-threshold energy range (≤16 eV), these values are about the same.

The results of our calculation agree rather well, qualitatively, with the experimental data in the whole incident electron energy range, for both radiative transitions studied in this work.