Reciprocally-Coupled Gating: Strange Loops in Bioenergetics, Genetics, and Catalysis
Abstract
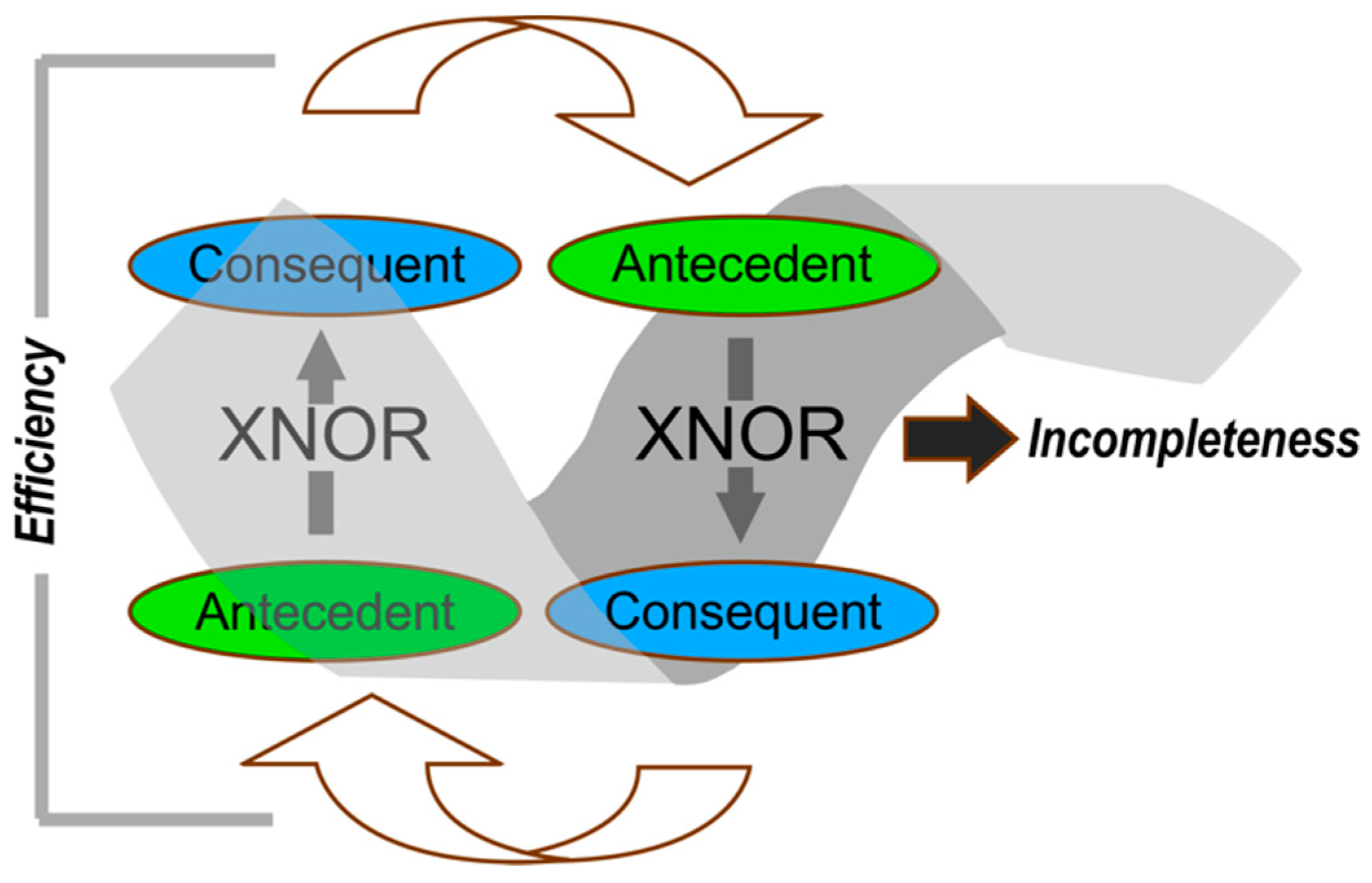
:1. Introduction
2. Biological Process Control: Feedback, Autocatalysis, Hypercycles, and Strange Loops
3. Biogenetics: Free Energy Transduction Requires Reciprocally-Coupled Gating
4. Amino Acid Physical Chemistry Drove the Origin of Genetics
5. Enzyme Catalysis Likely Evolved via Reciprocally-Coupled Gating
6. Constraints on the Emergence of New aaRS tRNA Cognate Pairs
7. Reciprocally-Coupled Gating Shaped the Growth of the Genetic Code
8. Conclusions: Strange Loops Tame Eigen’s Cliff and the Paradox of Specificity
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Dill, K.A.; Agozzino, L. Driving Forces in the Origins of Life. Open Biol. 2020, 11, 200324. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr.; Chandrasekaran, S.N.; Weinreb, V.; Li, L.; Williams, T. Combining multi-mutant and modular thermodynamic cycles to measure energetic coupling networks in enzyme catalysis. Struct. Dyn. 2017, 4, 032101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carter, C.W., Jr. High-Dimensional Mutant and Modular Thermodynamic Cycles, Molecular Switching, and Free Energy Transduction. Annu. Rev. Biophys. 2017, 46, 433–453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chandrasekaran, S.N.; Das, J.; Dokholyan, N.V.; Carter, C.W., Jr. A modified PATH algorithm rapidly generates transition states comparable to those found by other well established algorithms. Struct. Dyn. 2016, 3, 012101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weinreb, V.; Li, L.; Carter, C.W., Jr. A Master Switch Couples Mg2+-Assisted Catalysis to Domain Motion in B. stearothermophilus Tryptophanyl-tRNA Synthetase. Structure 2012, 20, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr. Escapement mechanisms: Efficient free energy transduction by reciprocally-coupled gating. Proteins Struct. Funct. Bioinform. 2019, 88, 710–717. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr. Coding of Class I and II aminoacyl-tRNA synthetases. Adv. Exp. Med. Biol.: Protein Rev. 2017, 18, 103–148. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr.; Wolfenden, R. Acceptor-stem and anticodon bases embed amino acid chemistry into tRNA. RNA Biol. 2016, 13, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr.; Wolfenden, R. tRNA Acceptor-Stem and Anticodon Bases Form Independent Codes Related to Protein Folding. Proc. Natl. Acad. Sci. USA 2015, 112, 7489–7494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolfenden, R.; Lewis, C.A.; Yuan, Y.; Carter, C.W., Jr. Temperature dependence of amino acid hydrophobicities. Proc. Natl. Acad. Sci. USA 2015, 112, 7484–7488. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr.; Wills, P.R. Interdependence, Reflexivity, Fidelity, and Impedance Matching, and the Evolution of Genetic Coding. Mol. Biol. Evol. 2018, 35, 269–286. [Google Scholar] [CrossRef]
- Wills, P.R.; Carter, C.W., Jr. Insuperable problems of an initial genetic code emerging from an RNA World. BioSystems 2018, 164, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Sapienza, P.J.; Li, L.; Williams, T.; Lee, A.L.; Carter, C.W., Jr. An Ancestral Tryptophanyl-tRNA Synthetase Precursor Achieves High Catalytic Rate Enhancement without Ordered Ground-State Tertiary Structures. ACS Chem. Biol. 2016, 11, 1661–1668. [Google Scholar] [CrossRef]
- Schulenburg, C.; Stark, Y.; Künzle, M.; Hilvert, D. Comparative Laboratory Evolution of Ordered and Disordered Enzymes. J. Biol. Chem. 2015, 290, 9310–9320. [Google Scholar] [CrossRef] [Green Version]
- Vamvaca, K.; Jelesarov, I.; Hilvert, D. Kinetics and Thermodynamics of Ligand Binding to a Molten Globular Enzyme and Its Native Counterpart. J. Mol. Biol. 2008, 382, 971–977. [Google Scholar] [CrossRef] [Green Version]
- Pervushin, K.; Vamvaca, K.; Vogeli, B.; Hilvert, D. Structure and dynamics of a molten globular enzyme. Nat. Struct. Mol. Biol. 2007, 14, 1202–1206. [Google Scholar] [CrossRef] [PubMed]
- Vamvaca, K.; Vögeli, B.; Kast, P.; Pervushin, K.; Hilvert, D. An enzymatic molten globule: Efficient coupling of folding and catalysis. Proc. Natl. Acad. Sci. USA 2004, 101, 12860–12864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wills, P.R.; Carter, C.W., Jr. Impedance matching and the choice between alternative pathways for the origin of genetic coding. Int. J. Mol. Sci. 2020, 21, 7392. [Google Scholar] [CrossRef] [PubMed]
- Blokhuis, A.; Lacoste, D.; Nghe, P. Universal motifs and the diversity of autocatalytic systems. Proc. Natl. Acad. Sci. USA 2020, 117, 25230–25236. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Gödel, Escher, Bach: An Eternal Golden Braid; Basic Books, Inc.: New York, NY, USA, 1979; p. 777. [Google Scholar]
- Kauffman, S.A. Cellular homeostasis, epigenesis and replication in randomly aggregated macromolecular systems. J. Cybern. 1971, 1, 71–96. [Google Scholar] [CrossRef]
- Eigen, M. Selforganization of Matter and the Evolution of Biological Macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M. Molecular self-organisation and the early stages of evolution. Quart Rev. Biophys 1971, 4, 149–212. [Google Scholar] [CrossRef]
- Kauffman, S.A. Autocatalytic Sets of Proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle: A Principle of Natural Self-Organization Part C: The Realistic Hypercycle. Die Nat. 1978, 65, 341–369. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle: A Principle of Natural Self-Organization Part A: Emergence of the Hypercycle. Naturwissenschaften 1977, 64, 541–565. [Google Scholar] [CrossRef]
- Hordijk, W. A History of Autocatalytic Sets: A Tribute to Stuart Kauffman. Biol. Theory 2019, 14, 224–246. [Google Scholar] [CrossRef]
- Hordijk, W. Evolution: Limited and Predictable or Unbounded and Lawless? Biol Theory 2016, 11, 187–191. [Google Scholar] [CrossRef]
- Sousa, F.L.; Hordijk, W.; Steel, M.; Martin, W.F. Autocatalytic sets in E. coli metabolism. J. Syst. Chem. 2015, 6, 4. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.I.; Steel, M.; Hordijk, W. Autocatalytic sets in a partitioned biochemical network. J. Syst. Chem. 2014, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Hordijk, W.; Wills, P.R.; Steel, M. Autocatalytic Sets and Biological Specificity. Bull. Math. Biol. 2014, 76, 201–224. [Google Scholar] [CrossRef] [Green Version]
- Hordijk, W.; Steel, M.; Kauffman, S. The Structure of Autocatalytic Sets: Evolvability, Enablement, and Emergence. Acta Biotheor. 2012, 60, 379–392. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S. What Is Life, and Can We Create It? BioScience 2013, 63, 609–610. [Google Scholar] [CrossRef] [Green Version]
- Lancet, D.; Zidovetzki, R.; Markovitch, O. Systems protobiology: Origin of life in lipid catalytic networks. J. R. Soc. Interface 2018, 15, 20180159. [Google Scholar] [CrossRef]
- Orgel, L.E. Self-organizing biochemical cycles. Proc. Natl. Acad. Sci. USA 2000, 97, 12503–12507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stubbs, R.T.; Yadav, M.; Krishnamurthy, R.; Springsteen, G.R. A plausible metal-free ancestral analogue of the Krebs cycle composed entirely of α-ketoacids. Nat. Chem. 2020, 12, 1016–1022. [Google Scholar] [CrossRef] [PubMed]
- Sobotta, J.; Geisberger, T.; Moosmann, C.; Scheidler, C.M.; Eisenreich, W.; Wächtershäuser, G.N.; Huber, C. A Possible Primordial Acetyleno/Carboxydotrophic Core Metabolism. Life 2020, 10, 35. [Google Scholar] [CrossRef] [Green Version]
- Eigen, M. Error catastrophe and antiviral strategy. Proc. Natl. Acad. Sci. USA 2002, 99, 13374–13376. [Google Scholar] [CrossRef] [Green Version]
- Szathmàry, E. The evolution of relicators. Phil. Trans. R. Soc. Lond. B 2000, 355, 1669–1676. [Google Scholar] [CrossRef]
- Koonin, E.V. The Logic. of Chance: The Nature and Origin of Biological Evolution; Pearson Education; FT Press Science: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1952, 237, 37–72. [Google Scholar]
- Gabriel, W.; Lynch, M.; Burger, R. Muller’s Ratchet and Mutational Meltdowns. Evolution 1993, 47, 1744–1757. [Google Scholar] [CrossRef] [Green Version]
- Hickinbotham, S.; Hogeweg, P. Evolution towards Extinction in Replicase Models: Inevitable unless…; Evolution of Evolution: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Cooper, A. The Inmates Are Running the Asylum: Why High-Tech Products Drive Us Crazy and How to Restore the Sanity; Sams Publishing: Indianapolis, IN, USA, 1999; p. 245. [Google Scholar]
- Wills, P.R. Autocatalysis, information, and coding. BioSystems 2001, 50, 49–57. [Google Scholar] [CrossRef]
- McCaskill, J.; Miller, J.F.; Stepney, S.; Wills, P.R. Encoding and representation of information processing in irregular computational matter. In Computational Matter; Stepney, S., Rasmussen, S., Martin, A., Eds.; Springer: Berlin, Germany, 2018; pp. 227–243. [Google Scholar]
- Wills, P.R. The generation of meaningful information in molecular systems. Phil. Trans. R. Soc. A 2016, A374, 20150016. [Google Scholar] [CrossRef] [PubMed]
- Wills, P.R.; Nieselt, K.; McCaskill, J.S. Emergence of Coding and its Specificity as a Physico-Informatic Problem. Orig. Life Evol. Biosph. 2015, 45, 249–255. [Google Scholar] [CrossRef]
- Wills, P.R. Reflexivity, Coding and Quantum Biology. BioSystems 2019, 185, 104027. [Google Scholar] [CrossRef]
- Boyer, P.D. Energy, Life, and ATP. In Nobel Lectures, Chemistry 1996–2000; Grenthe, I., Ed.; The Nobel Foundation: Singapore, 1997. [Google Scholar]
- Boyer, P.D. The ATP synthase—A splendid molecular machine. Annu. Rev. Biochem. 1997, 66, 717–749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyer, P.D. The binding change mechanism for ATP synthase—Some probabilities and possibilities. Biochim. Et Biophys. Acta 1993, 1140, 215–250. [Google Scholar] [CrossRef]
- Jencks, W.P. Reaction mechanisms, catalysis, and movement. Protein Sci. 1994, 3, 2459–2464. [Google Scholar] [CrossRef] [Green Version]
- Jencks, W.P. Utilization of Binding Energy and Coupling Rules for Active Transport and Other Coupled Vectorial Processes. Meth. Enzymol. 1989, 171, 145–164. [Google Scholar]
- Hill, T.L. Some general principles in free energy transduction. Proc. Natl Acad. Sci. USA 1983, 80, 2922–2925. [Google Scholar] [CrossRef] [Green Version]
- Hill, T.L.; Eisenberg, E. Can free energy transduction be localized at some crucial part of the enzymatic cycle? Q. Rev. Biophys. 1981, 14, 463–511. [Google Scholar] [CrossRef]
- Eisenberg, E.; Hill, T.L. A Cross-Bridge Model of Muscle Contraction. Prog. Biophys. Mol. Biol. 1978, 33, 55–82. [Google Scholar] [CrossRef]
- Warshel, A.; Bora, R.P. Perspective: Defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 2016, 144, 180901. [Google Scholar] [CrossRef] [PubMed]
- Astumian, R.D.; Mukherjee, S.; Warshel, A. The Physics and Physical Chemistry of Molecular Machines. ChemPhysChem 2016, 17, 1719–1741. [Google Scholar] [CrossRef] [Green Version]
- Prasad, B.R.; Warshel, A. Prechemistry versus preorganization in DNA replication fidelity. Proteins Struct. Funct. Bioinform. 2011, 79, 2900–2919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knapp, M.J.; Rickert, K.; Klinman, J.P. Temperature-dependent isotope effects in soybean lipoxygenase-1: Correlating hydrogen tunneling with protein dynamics. J. Am. Chem. Soc. 2002, 124, 3865–3874. [Google Scholar] [CrossRef] [PubMed]
- Villali, J.; Kern, D. Choreographing and enzyme’s dance. Curr. Opin. Chem. Biol. 2010, 14, 636–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henzler-Wildman, K.A.; Lei, M.; Vu, T.; Kerns, S.J.; Karplus, M.; Kern, D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature 2007, 450, 913–918. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.A.; Lei, M.; Vu, T.; Ott, M.; Wolf-Watz, M.; Fenn, T.; Posharski, E.; Wilson, M.A.; Petsko, G.A.; Karplus, M.; et al. Intrinsic motions along an enzymatic reaction trajectory. Nature 2007, 450, 838–849. [Google Scholar] [CrossRef]
- Pisliakov, A.V.; Cao, J.; Kamerlin, S.C.L.; Warshel, A. Enzyme millisecond conformational dynamics do not catalyze the chemical step. Proc. Natl. Acad. Sci. USA 2009, 106, 17359–17364. [Google Scholar] [CrossRef] [Green Version]
- Warshel, A.; Sharma, P.K.; Kato, M.; Xiang, Y.; Liu, H.; Olsson, M.H.M. Electrostatic Basis for Enzyme Catalysis. Chem. Rev. 2006, 106, 3210–3235. [Google Scholar] [CrossRef]
- Burbaum, J.; Schimmel, P. Structural Relationships and the Classification of Aminoacyl-tRNA Synthetases. J. Biol. Chem. 1991, 266, 16965–16968. [Google Scholar] [CrossRef]
- Burbaum, J.J.; Schimmel, P. Assembly of a Class I tRNA Synthetase from Products of an Artificially Split Gene. Biochemistry 1991, 30, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Kapustina, M.; Weinreb, V.; Li, L.; Kuhlman, B.; Carter, C.W., Jr. A Conformational Transition State Accompanies Tryptophan Activation by B. stearothermphilus Tryptophanyl-tRNA Synthetase. Structure 2007, 15, 1272–1284. [Google Scholar] [CrossRef] [Green Version]
- Kapustina, M.; Carter, C.W., Jr. Computational Studies of Tryptophanyl-tRNA Synthetase: Activation of ATP by Induced-Fit. J. Mol. Biol. 2006, 362, 1159–1180. [Google Scholar] [CrossRef] [PubMed]
- Retailleau, P.; Weinreb, V.; Hu, M.; Carter, C.W., Jr. Crystal Structure of Tryptophanyl-tRNA Synthetase Complexed with Adenosine-5’ tetraphosphate: Evidence for Distributed Use of Catalytic Binding Energy in Amino Acid Activation by Class I Aminoacyl-tRNA Synthetases. J. Mol. Biol. 2007, 369, 108–128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Retailleau, P.; Huang, X.; Yin, Y.; Hu, M.; Weinreb, V.; Vachette, P.; Vonrhein, C.; Bricogne, G.; Roversi, P.; Ilyin, V.; et al. Interconversion of ATP binding and conformational free energies by Tryptophanyl-tRNA Synthetase: Structures of ATP bound to open and closed, pre-transition conformations. J. Mol. Biol. 2003, 325, 39–63. [Google Scholar] [CrossRef]
- Weinreb, V.; Weinreb, G.; Chandrasekaran, S.N.; Das, J.; Dokholyan, N.V.; Carter, C.W., Jr. Thermodynamic impacts of combinatorial mutagenesis on protein conformational stability: Precise, high-throughput measurement by Thermofluor. BioRxiv 2019, 591495. [Google Scholar] [CrossRef]
- Weinreb, V.; Li, L.; Chandrasekaran, S.N.; Koehl, P.; Delarue, M.; Carter, C.W., Jr. Enhanced Amino Acid Selection in Fully-Evolved Tryptophanyl-tRNA Synthetase, Relative to its Urzyme, Requires Domain Movement Sensed by the D1 Switch, a Remote, Dynamic Packing Motif. J. Biol. Chem. 2014, 289, 4367–4376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chandrasekaran, S.N.; Carter, C.W., Jr. Adding torsional interaction terms to the Anisotropic Network Model improves the PATH performance, enabling detailed comparison with experimental rate data. Struct. Dyn. 2017, 4, 032103. [Google Scholar] [CrossRef] [Green Version]
- Branscomb, E.; Russell, M.J. Frankenstein or a Submarine Alkaline Vent: Who Is Responsible for Abiogenesis? Part 1: What is life–that it might create itself? BioEssays 2018, 40, 1700179. [Google Scholar] [CrossRef] [PubMed]
- Branscomb, E.; Biancalani, T.; Goldenfeld, N.; Russell, M. Escapement mechanisms and the conversion of disequilibria; the engines of creation. Phys. Rep. 2017, 677, 1–60. [Google Scholar] [CrossRef]
- Wolfenden, R. Experimental Measures of Amino Acid Hydrophobicity and the Topology of Transmembrane and Globular Proteins. J. Gen. Physiol. 2007, 129, 357–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibbs, P.R.; Radzicka, A.; Wolfenden, R. The Anomalous Hydrophilic Character of Proline. J. Am. Chem. Soc. 1991, 113, 4714–4715. [Google Scholar] [CrossRef]
- Radzicka, A.; Wolfenden, R. Comparing the Polarities of the Amino Acids: Side-Chain Distribution Coefficients between the Vapor Phase, Cyclohexane, 1-0ctanol, and Neutral Aqueous Solution. Biochemistry 1988, 27, 1664–1670. [Google Scholar] [CrossRef]
- Wolfenden, R.; Cullis, P.M.; Southgate, C.C.F. Water, Protein Folding, and the Genetic Code. Science 1979, 206, 575–577. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr.; Wills, P.R. The Roots of Genetic Coding in Aminoacyl-tRNA Synthetase Duality. Annu. Rev. Biochem. 2021, 89. in press. [Google Scholar]
- Eriani, G.; Delarue, M.; Poch, O.; Gangloff, J.; Moras, D. Partition of tRNA synthetases into two classes based on mutually exclusive sets of sequence motifs. Nature 1990, 347, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Cusack, S. Eleven down and nine to go. Nat. Struct. Biol. 1995, 2, 824–831. [Google Scholar] [CrossRef]
- Cusack, S.; Berthet-Colominas, C.; Hartlein, M.; Nassar, N.; Leberman, R. A second class of synthetase structure revealed by X-ray analysis of Escherichia coli seryl-tRNA synthetase at 2.5 A. Nature 1990, 347, 249–255. [Google Scholar] [CrossRef]
- Ruff, M.; Krishnaswamy, S.; Boeglin, M.; Poterszman, A.; Mitschler, A.; Podjarny, A.; Rees, B.; Thierry, J.C.; Moras, D. Class II Aminoacyl Transfer RNA Synthetases: Crystal Structure of Yeast Aspartyl-tRNA Synthetase Complexed with tRNAAsp. Science 1991, 252, 1682–1689. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr. Cognition, Mechanism, and Evolutionary Relationships in Aminoacyl-tRNA Synthetases. Ann. Rev. Biochem. 1993, 62, 715–748. [Google Scholar] [CrossRef]
- Carter, C.W., Jr.; Wills, P.R. Class I and II aminoacyl-tRNA synthetase tRNA groove discrimination created the first synthetase•tRNA cognate pairs and was therefore essential to the origin of genetic coding. Iubmb Life 2019, 71, 1088–1098. [Google Scholar] [CrossRef]
- Carter, C.W., Jr.; Wills, P.R. Hierarchical groove discrimination by Class I and II aminoacyl-tRNA synthetases reveals a palimpsest of the operational RNA code in the tRNA acceptor-stem bases. Nucleic Acids Res. 2018, 46, 9667–9683. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr.; Wills, P.R. Experimental Solutions to Problems Defining the Origin of Codon-Directed Protein Synthesis. BioSystems 2019, 1832019, 103979. [Google Scholar] [CrossRef]
- Rodin, A.; Rodin, S.N.; Carter, C.W., Jr. On Primordial Sense-Antisense Coding. J. Mol. Evol. 2009, 69, 555–567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodin, S.N.; Ohno, S. Two Types of Aminoacyl-tRNA Synthetases Could be Originally Encoded by Complementary Strands of the Same Nucleic Acid. Orig. Life Evol. Biosph. 1995, 25, 565–589. [Google Scholar] [CrossRef]
- Carter, C.W., Jr. Urzymology: Experimental Access to a Key Transition in the Appearance of Enzymes. J. Biol. Chem. 2014, 289, 30213–30220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Francklyn, C.; Carter, C.W., Jr. Aminoacylating Urzymes Challenge the RNA World Hypothesis. J. Biol. Chem. 2013, 288, 26856–26863. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Weinreb, V.; Francklyn, C.; Carter, C.W., Jr. Histidyl-tRNA Synthetase Urzymes: Class I and II Aminoacyl-tRNA Synthetase Urzymes have Comparable Catalytic Activities for Cognate Amino Acid Activation. J. Biol. Chem. 2011, 286, 10387–10395. [Google Scholar] [CrossRef] [Green Version]
- Pham, Y.; Kuhlman, B.; Butterfoss, G.L.; Hu, H.; Weinreb, V.; Carter, C.W., Jr. Tryptophanyl-tRNA synthetase Urzyme: A model to recapitulate molecular evolution and investigate intramolecular complementation. J. Biol. Chem. 2010, 285, 38590–38601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pham, Y.; Li, L.; Kim, A.; Erdogan, O.; Weinreb, V.; Butterfoss, G.; Kuhlman, B.; Carter, C.W., Jr. A Minimal TrpRS Catalytic Domain Supports Sense/Antisense Ancestry of Class I and II Aminoacyl-tRNA Synthetases. Mol. Cell 2007, 25, 851–862. [Google Scholar] [CrossRef] [PubMed]
- Martinez, L.; Jimenez-Rodriguez, M.; Gonzalez-Rivera, K.; Williams, T.; Li, L.; Weinreb, V.; Chandrasekaran, S.N.; Collier, M.; Ambroggio, X.; Kuhlman, B.; et al. Functional Class I and II Amino Acid Activating Enzymes Can Be Coded by Opposite Strands of the Same Gene. J. Biol. Chem. 2015, 290, 19710–19725. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.W., Jr.; Popinga, A.; Bouckaert, R.; Wills, P.R. High-Resolution, Multidimensional Phylogenetic Metrics Identify Class I Aminoacyl-tRNA Synthetase Evolutionary Mosaicity and Inter-modular‘Coupling. BioRxiv 2020, 2020, 033712. [Google Scholar]
- Chandrasekaran, S.N.; Yardimci, G.; Erdogan, O.; Roach, J.M.; Carter, C.W., Jr. Statistical Evaluation of the Rodin-Ohno Hypothesis: Sense/Antisense Coding of Ancestral Class I and II Aminoacyl-tRNA Synthetases. Mol. Biol. Evol. 2013, 30, 1588–1604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carter, C.W., Jr.; Wills, P.R. Did Gene Expression Co-evolve with Gene Replication? In Evolutionary Biology: Genome and Phenotype Evolution; Pontarotti, P., Ed.; Springer-Nature: Paris, France, 2018; Volume 9, pp. 293–313. [Google Scholar]
- Carter, C.W., Jr. The Evolution of Genetic Coding. In Scientia; Science Diffusion, Ltd.: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Goto, Y.; Katoh, T.; Suga, H. Flexizymes for genetic code reprogramming. Nat. Protoc. 2011, 6, 779–790. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.C.; Bradley, L.H.; Jinadasa, S.P.; Hecht, M.H. Cofactor binding and enzymatic activity in an unevolved superfamily of de novo designed 4-helix bundle proteins. Protein Sci. 2009, 18, 1388–1400. [Google Scholar] [CrossRef] [Green Version]
- Moffet, D.A.; Foley, J.; Hecht, M.H. Midpoint reduction potentials and heme binding stoichiometries of de novo proteins from designed combinatorial libraries. Biophys. Chem. 2003, 105, 231–239. [Google Scholar] [CrossRef]
- Kamtekar, S.; Schiffer, J.M.; Xiong, H.; Babik, J.M.; Hecht, M.H. Protein Design by Binary Patterning of Polar and Non-polar Amino Acids. Science 1993, 262, 1680–1685. [Google Scholar] [CrossRef]
- Hu, H. Wild-type and molten globular chorismate mutase achieve comparable catalytic rates using very different enthalpy/entropy compensations. Sci. China 2014, 57, 156–164. [Google Scholar] [CrossRef]
- Parra, R.G.; Schafer, N.P.; Radusky, L.G.; Tsai, M.-Y.; Guzovsky, A.B.; Wolynes, P.G.; Ferreiro, D.U. Protein Frustratometer 2: A tool to localize energetic frustration in protein molecules, now with electrostatics. Nucl. Acids Res. 2016, 44, W357. [Google Scholar] [CrossRef]
- Freibergera, M.I.; Guzovskya, A.B.; Wolynes, P.G.; Parra, R.G.; Ferreiroa, D.U. Local frustration around enzyme active sites. Proc. Natl. Acad. Sci. USA 2019, 116, 4037–4043. [Google Scholar] [CrossRef] [Green Version]
- Pauling, L. The probability of errors in the process of synthesis of protein molecules. In Festschrift Prof. Dr. Arthur Stoll; Pauling, L., Ed.; Birkhauser: Basel, UK, 1957; pp. 597–602. [Google Scholar]
- Bull, J.J.; Meyers, L.A.; Lachmann, M. Quasispecies Made Simple. PLoS Comput. Biol. 2005, 1, e61. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, J.J.; Yamane, T.; Yue, V.; Coutts, S.M. Direct Experimetnal Evidence for Kinetic Proofreading in Amino “Acylation of tRNA Ile”. Proc. Natl. Acad. Sci. USA 1976, 73, 1164–1168. [Google Scholar] [CrossRef] [Green Version]
- Fersht, A.R.; Kaethner, M.M. Enzyme Hyperspecifity. Rejection of Threonine by the Valyl-tRNA Synthetase by Misacylation and Hydrolytic Editing. Biochemistry 1976, 15, 3342–3346. [Google Scholar] [CrossRef]
- Martinis, S.A.; Boniecki, M.T. The balance between pre- and post-transfer editing in tRNA synthetases. FEBS Lett. 2010, 584, 455–459. [Google Scholar] [CrossRef] [Green Version]
- Boniecki, M.T.; Vu, M.T.; Betha, A.K.; Martinis, S.A. CP1-dependent partitioning of pretransfer and posttransfer editing in leucyl-tRNA synthetase. Proc. Natl. Acad. Sci. USA 2008, 105, 19223–19228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delarue, M. An asymmetric underlying rule in the assignment of codons: Possible clue to a quick early evolution of the genetic code via successive binary choices. RNA 2007, 13, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shore, J.; Holland, B.R.; Sumner, J.G.; Nieselt, K.; Wills, P.R. The Ancient Operational Code is Embedded in the Amino Acid Substitution Matrix and aaRS Phylogenies. J. Mol. Evol. 2019, 88, 136–150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pak, D.; Kim, Y.; Burton, Z.F. Aminoacyl-tRNA synthetase evolution and sectoring of the genetic code. Transcription 2018, 9, 205–224. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr. What RNA World? Why a Peptide/RNA Partnership Merits Renewed Experimental Attention. Life 2015, 5, 294–320. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr.; Li, L.; Weinreb, V.; Collier, M.; Gonzales-Rivera, K.; Jimenez-Rodriguez, M.; Erdogan, O.; Chandrasekharan, S.N. The Rodin-Ohno Hypothesis That Two Enzyme Superfamilies Descended from One Ancestral Gene: An Unlikely Scenario for the Origins of Translation That Will Not Be Dismissed. Biol. Direct 2014, 9, 11. [Google Scholar] [CrossRef] [Green Version]
- Kovacs, N.A.; Petrov, A.S.; Lanier, K.A.; Williams, L.D. Frozen in Time: The History of Proteins. Mol. Biol. Evol. 2017, 34, 1252–1260. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Carter, C.W., Jr. Full Implementation of the Genetic Code by Tryptophanyl-tRNA Synthetase Requires Intermodular Coupling. J. Biol. Chem. 2013, 288, 34736–34745. [Google Scholar] [CrossRef] [Green Version]
- Perona, J.J.; Gruic-Sovulj, I. Synthetic and Editing Mechanisms of Aminoacyl-tRNA Synthetases. Top. Curr. Chem. 2013. [Google Scholar] [CrossRef]
- Praetorius-Ibba, M.; Stange-Thomann, N.; Kitabatake, M.; Ali, K.; Soll, I.; Carter, C.W., Jr.; Ibba, M.; Soll, D. Ancient adaptation of the active site of tryptophanyl-tRNA synthetase for tryptophan binding. Biochemistry 2000, 39, 13136–13143. [Google Scholar] [CrossRef]
- Bullock, T.L.; Rodríguez-Hernández, A.; Corigliano, E.M.; Perona, J.J. A rationally engineered misacylating aminoacyl-tRNA synthetase. Proc. Natl. Acad. Sci. USA 2008, 105, 7428–7433. [Google Scholar] [CrossRef] [Green Version]
- Bullock, T.; Uter, N.; Nissan, T.A.; Perona, J.J. Amino Acid Discrimination by a class I aminoacyl-tRNA synthetase specified by negative determinants. J. Mol. Biol. 2003, 328, 395–408. [Google Scholar] [CrossRef]
- Carter, C.W.J. Simultaneous codon usage, the origin of the proteome, and the emergence of de-novo proteins. Curr. Opin. Struct. Biol. 2021, 68, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Deacon, T.W. Reciprocal Linkage between Self-organizing Processes is Sufficient for Self-reproduction and Evolvability. Biol. Theory 2006, 1, 136–149. [Google Scholar] [CrossRef]
- Deacon, T.W. Emergence: The Hole at the Wheel’s Hub. In The Re-Emergence of Emergence: The Emergentist Hypothesis from Science to Religion; Clayton, P., Davies, P., Eds.; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Ben-Ya’acov, U. Godel’s incompleteness theorem and Universal physical theories. J. Phys. Conf. Ser. 2019, 1391, 012067. [Google Scholar] [CrossRef]
- Jaki, S.L. On a Discovery About Godel’s Incompleteness Theorem. Paths Discov. Pontical Acad. Sci. Acta Vatican City 2006, 18, 49–60. [Google Scholar]
- Jaki, S.L. A Late Awakening to Godel in Physics. Available online: http://www.sljaki.com/texts.html (accessed on 29 December 2020).
- Feferman, S. Godel, Nagel, Minds, and Machines. J. Philos. 2009, 106, 201–219. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S. Godel and the End of Physics. Available online: http://yclept.ucdavis.edu/course/215c.S17/TEX/GodelAndEndOfPhysics.pdf (accessed on 29 December 2020).
- Dyson, F. The World on a String. New York Review of Books, 13 May 2004. [Google Scholar]
- Wright, P.E.; Dyson, H.J. Linking folding and binding. Curr. Opin. Struct. Biol. 2009, 19, 31–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deacon, T.W. Incomplete Nature; W. W. Norton & Company: New York, NY, USA, 2012. [Google Scholar]
- Deacon, T.W.; Cashman, T. Steps to a Metaphysics of Incompleteness. Theol. Sci. 2016, 14, 401–429. [Google Scholar] [CrossRef]
- Kern, T.; Schanda, P.; Brutscher, B. Sensitivity-enhanced IPAP-SOFAST-HMQC for fast-pulsing 2D NMR with reduced radiofrequency load. J. Magn. Reson. 2008, 190, 333–338. [Google Scholar] [CrossRef]
- Eisenmesser, E.Z.; Millet, O.; Labeikovsky, W.; Korzhnefv, D.M.; Wolf-Watz, M.; Bosco, D.A.; Skalicky, J.J.; Kay, L.E.; Kern, D. Intrinisic dynamics of an enzyme underlies catalysis. Nature 2005, 438, 117–137. [Google Scholar] [CrossRef]
- Luecke, H.; Schobert, B.; Richter, H.-T.; Cartailler, J.-P.; Lanyi, J.K. Structural Changes in Bacteriorhodopsin During Ion Transport at 2 Ångstrom Resolution. Science 1999, 286, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Yang, D.; Wu, M.; Guo, Y.; Guo, W.; Zhong, L.; Cai, X.; Dai, A.; Jang, W.; Shakhnovich, E.I.; et al. Common activation mechanism of class A GPCRs. eLife 2019, 8, e50279. [Google Scholar] [CrossRef]
- Menyhárd, D.K.; Pálfy, G.; Orgova, Z.; Vida, I.; Keseru, G.M.; Perczel, A. Structural impact of GTP binding on downstream KRAS signaling. Chem. Sci. 2020, 11, 9272. [Google Scholar] [CrossRef]
- Strahl, B.; Allis, C. David The language of covalent histone modifications. Nature 2000, 403, 41–45. [Google Scholar] [CrossRef]
- Kang, T.J.; Yuzawa, S.; Suga, H. Expression of Histone H3 Tails with Combinatorial Lysine Modifications under the Reprogrammed Genetic Code for the Investigation on Epigenetic Markers. Chem. Biol. 2008, 15, 1166–1174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gehring, N.H.; Roignant, J.-Y. Anything but Ordinary—Emerging Splicing Mechanisms in Eukaryotic Gene Regulation. Trends Genet. 2020, in press. [Google Scholar] [CrossRef]
- Crocker, J.; Abe, N.; Rinaldi, L.; McGregor, A.P.; Frankel, N.; Wang, S.; Alsawadi, A.; Valenti, P.; Plaza, S.; Payre, F.; et al. Low Affinity Binding Site Clusters Confer Hox Specificity and Regulatory Robustness. Cell 2015, 160, 191–203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, J.D.; Stikeleather, R.A.; Kowalik, T.F.; Lynch, M. Imposed mutational meltdown as an antiviral strategy. Evolution 2020, 74, 2549–2559. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carter, C.W., Jr.; Wills, P.R. Reciprocally-Coupled Gating: Strange Loops in Bioenergetics, Genetics, and Catalysis. Biomolecules 2021, 11, 265. https://doi.org/10.3390/biom11020265
Carter CW Jr., Wills PR. Reciprocally-Coupled Gating: Strange Loops in Bioenergetics, Genetics, and Catalysis. Biomolecules. 2021; 11(2):265. https://doi.org/10.3390/biom11020265
Chicago/Turabian StyleCarter, Charles W., Jr., and Peter R. Wills. 2021. "Reciprocally-Coupled Gating: Strange Loops in Bioenergetics, Genetics, and Catalysis" Biomolecules 11, no. 2: 265. https://doi.org/10.3390/biom11020265
APA StyleCarter, C. W., Jr., & Wills, P. R. (2021). Reciprocally-Coupled Gating: Strange Loops in Bioenergetics, Genetics, and Catalysis. Biomolecules, 11(2), 265. https://doi.org/10.3390/biom11020265




