Effect of Surface Roughness on Aggregation of Polypeptide Chains: A Monte Carlo Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lattice Models in Bulk
2.2. Lattice Models with Surfaces
2.2.1. Smooth Surface
2.2.2. Rough Surfaces
2.3. Definition of Surface Roughness
2.4. Monte Carlo Simulation
2.5. Aggregation Time τagg and Fibril Formation Time τfib
3. Results and Discussion
3.1. Effect of Smooth Surface on Aggregation Time τagg
3.1.1. Hydrophilic Surfaces
3.1.2. Hydrophobic Surfaces
3.1.3. Three Classes of Surfaces
3.2. Effect of Surface Roughness on Fibril Formation: S-Surface
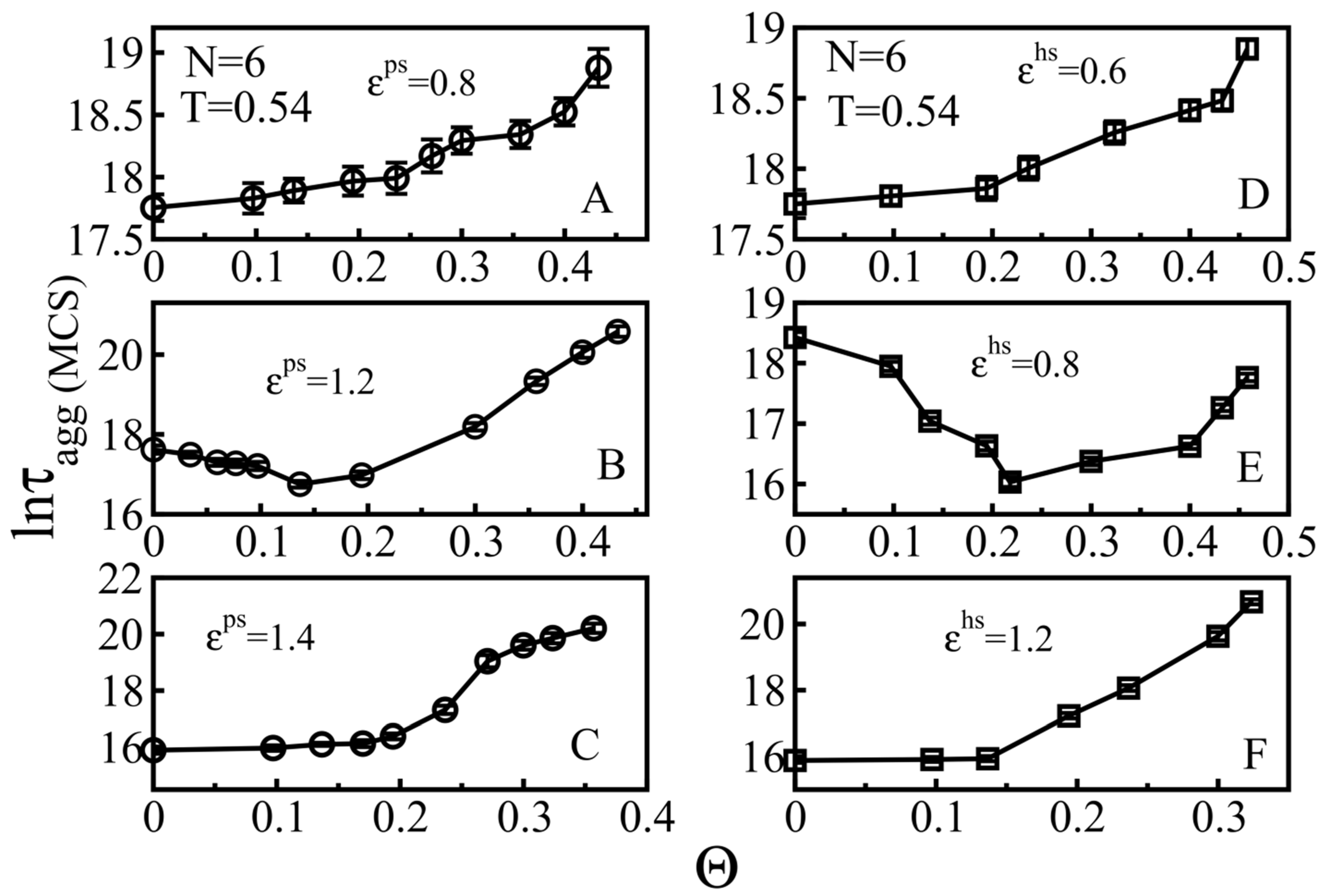
3.2.1. Weakly Absorbing Surfaces: Monotonic Dependence of the Aggregation Time on the Surface Roughness
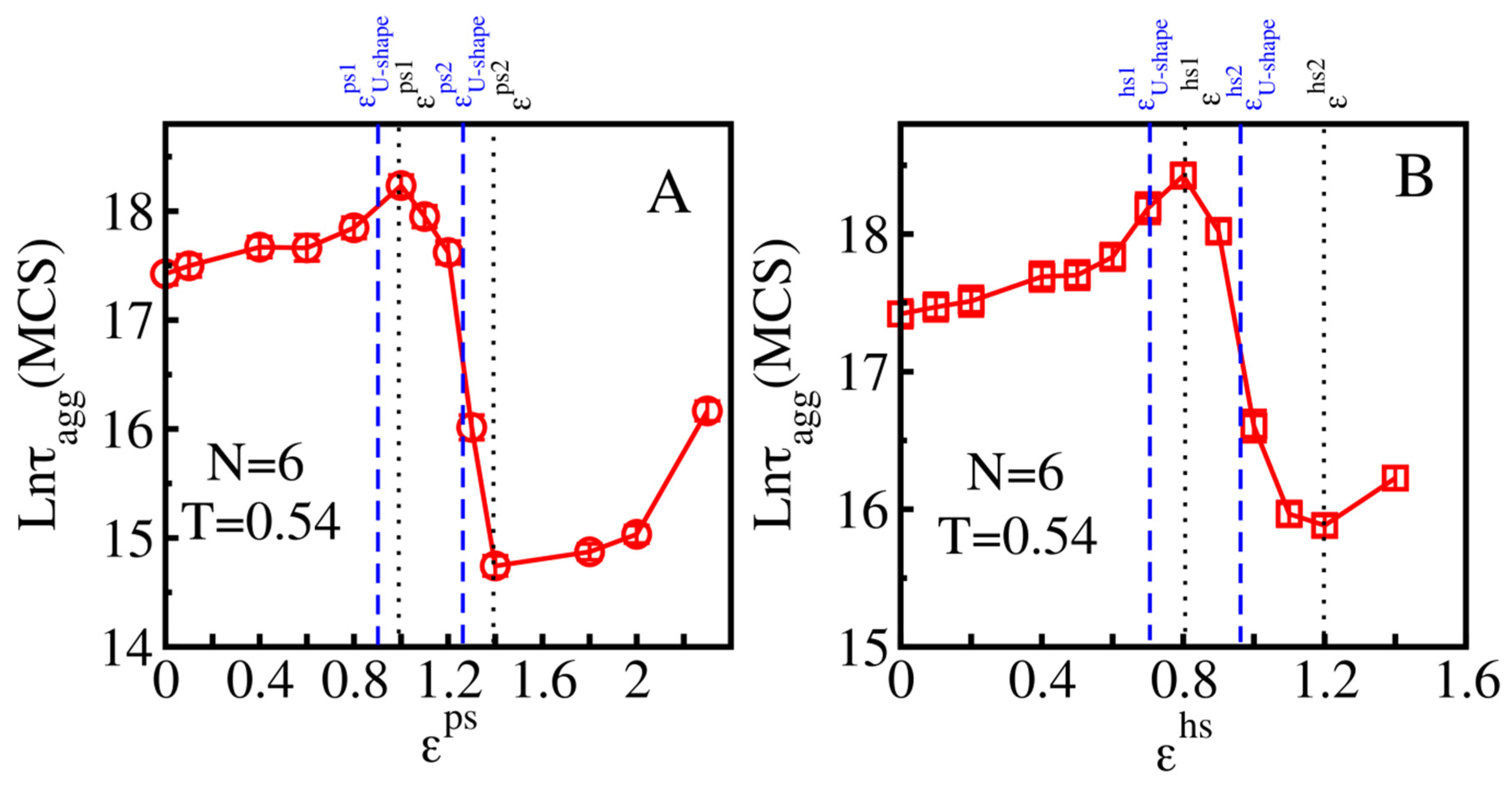
3.2.2. Medium Absorbing Surfaces: U-Shape Behavior
3.2.3. Strongly Absorbing Surfaces: Monotonic Dependence of the Aggregation Time on the Surface Roughness
3.3. Effect of Surface Roughness on Fibril Formation: D-Surface and DS-Surface Do Not Qualitatively Change the Results Obtained for S-Surfaces
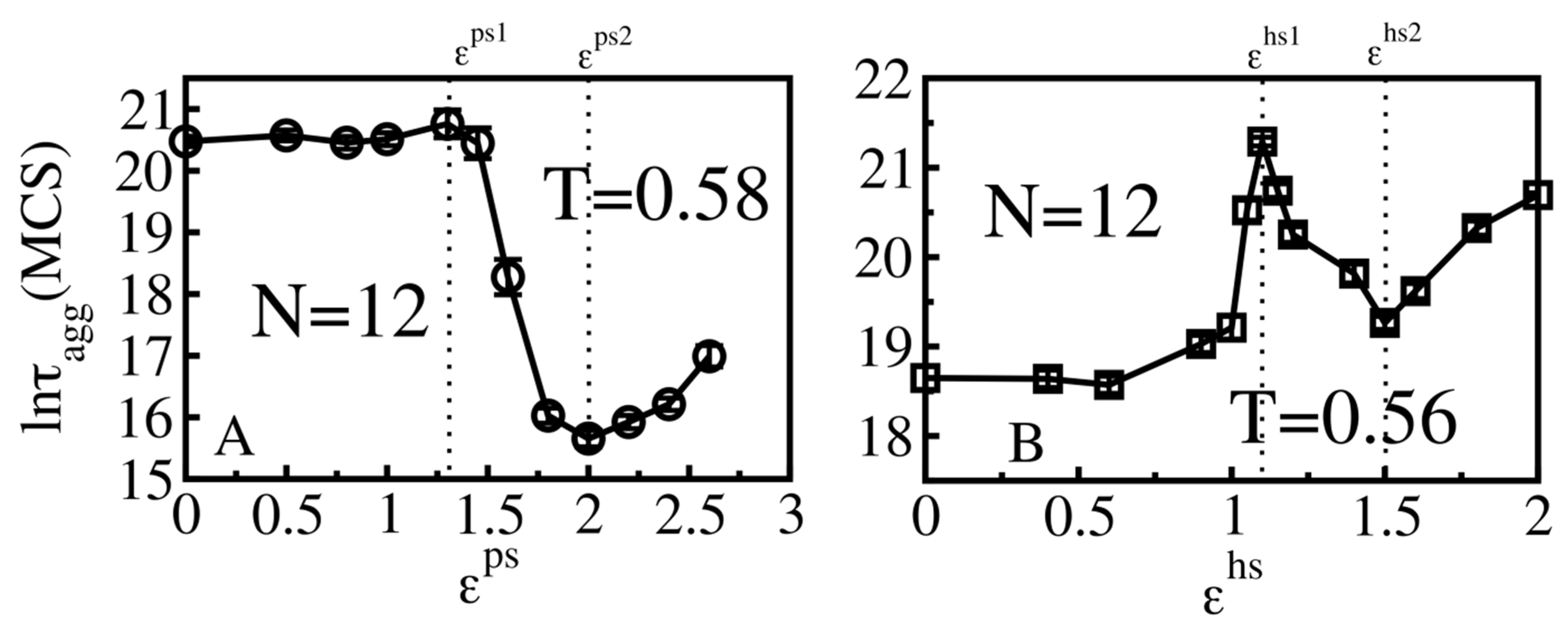
3.4. Size Effects
3.4.1. Smooth Surfaces
3.4.2. Rough Surfaces
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chiti, F.; Dobson, C.M. Protein Misfolding, Functional Amyloid, and Human Disease. Annu. Rev. Biochem. 2006, 75, 333–366. [Google Scholar] [CrossRef] [Green Version]
- Nasica-Labouze, J.; Nguyen, P.H.; Sterpone, F.; Berthoumieu, O.; Buchete, N.-V.; Coté, S.; De Simone, A.; Doig, A.J.; Faller, P.; Garcia, A.; et al. Amyloid β Protein and Alzheimer’s Disease: When Computer Simulations Complement Experimental Studies. Chem. Rev. 2015, 115, 3518–3563. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Ramamoorthy, A.; Sahoo, B.R.; Zheng, J.; Faller, P.; Straub, J.E.; Dominguez, L.; Shea, J.-E.; Dokholyan, N.V.; De Simone, A.; et al. Amyloid Oligomers: A Joint Experimental/Computational Perspective on Alzheimer’s Disease, Parkinson’s Disease, Type II Diabetes, and Amyotrophic Lateral Sclerosis. Chem. Rev. 2021, 121, 2545–2647. [Google Scholar] [CrossRef] [PubMed]
- Ellis, R. Macromolecular crowding: Obvious but underappreciated. Trends Biochem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- O’Brien, E.P.; Straub, J.E.; Brooks, B.R.; Thirumalai, D. Influence of Nanoparticle Size and Shape on Oligomer Formation of an Amyloidogenic Peptide. J. Phys. Chem. Lett. 2011, 2, 1171–1177. [Google Scholar] [CrossRef] [Green Version]
- Co, N.T.; Hu, C.-K.; Li, M.S. Dual effect of crowders on fibrillation kinetics of polypeptide chains revealed by lattice models. J. Chem. Phys. 2013, 138, 185101. [Google Scholar] [CrossRef] [Green Version]
- Musiani, F.; Giorgetti, A. Chapter Two—Protein Aggregation and Molecular Crowding: Perspectives From Multiscale Simulations. In International Review of Cell and Molecular Biology; Sandal, M., Ed.; Academic Press: Cambridge, MA, USA, 2017; Volume 329, pp. 49–77. [Google Scholar]
- Li, C.; Mezzenga, R. The interplay between carbon nanomaterials and amyloid fibrils in bio-nanotechnology. Nanoscale 2013, 5, 6207–6218. [Google Scholar] [CrossRef]
- Yang, B.; Adams, D.J.; Marlow, M.; Zelzer, M. Surface-Mediated Supramolecular Self-Assembly of Protein, Peptide, and Nucleoside Derivatives: From Surface Design to the Underlying Mechanism and Tailored Functions. Langmuir 2018, 34, 15109–15125. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Banerjee, S.; Zagorski, K.; Shlyakhtenko, L.S.; Kolomeisky, A.B.; Lyubchenko, Y.L. Molecular Model for the Surface-Catalyzed Protein Self-Assembly. J. Phys. Chem. B 2020, 124, 366–372. [Google Scholar] [CrossRef]
- Cholko, T.; Barnum, J.; Chang, C.A. Amyloid-Beta (Abeta42) Peptide Aggregation Rate and Mechanism on Surfaces with Widely Varied Properties: Insights from Brownian Dynamics Simulations. J. Phys. Chem. B 2020, 123, 5549–5558. [Google Scholar] [CrossRef]
- Keller, A.; Grundmeier, G. Amyloid aggregation at solid-liquid interfaces: Perspectives of studies using model surfaces. Appl. Surf. Sci. 2020, 506, 144991. [Google Scholar] [CrossRef]
- Galvagnion, C.; Buell, A.K.; Meisl, G.; Michaels, T.C.; Vendruscolo, M.; Knowles, T.P.; Dobson, C.M. Lipid vesicles trigger α-synuclein aggregation by stimulating primary nucleation. Nat. Chem. Biol. 2015, 11, 229–234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindberg, D.J.; Wesén, E.; Björkeroth, J.; Rocha, S.; Esbjörner, E.K. Lipid membranes catalyse the fibril formation of the amyloid-β (1–42) peptide through lipid-fibril interactions that reinforce secondary pathways. Biochim. Biophys. Acta (BBA) Biomembr. 2017, 1859, 1921–1929. [Google Scholar] [CrossRef] [PubMed]
- Morriss-Andrews, A.; Brown, F.L.H.; Shea, J.-E. A Coarse-Grained Model for Peptide Aggregation on a Membrane Surface. J. Phys. Chem. B 2014, 118, 8420–8432. [Google Scholar] [CrossRef] [PubMed]
- Butterfield, S.M.; Lashuel, H.A. Amyloidogenic Protein-Membrane Interactions: Mechanistic Insight from Model Systems. Angew. Chem. Int. Ed. 2010, 49, 5628–5654. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Li, C.; Fakhraai, Z. Kinetics of Surface-Mediated Fibrillization of Amyloid-β (12–28) Peptides. Langmuir 2018, 34, 4665–4672. [Google Scholar] [CrossRef]
- Rabe, M.; Soragni, A.; Reynolds, N.P.; Verdes, D.; Liverani, E.; Riek, R.; Seeger, S. On-Surface Aggregation of α-Synuclein at Nanomolar Concentrations Results in Two Distinct Growth Mechanisms. ACS Chem. Neurosci. 2013, 4, 408–417. [Google Scholar] [CrossRef] [Green Version]
- Cabaleiro-Lago, C.; Lynch, I.; Dawson, K.A.; Linse, S. Inhibition of IAPP and IAPP(20−29)Fibrillation by Polymeric Nanoparticles. Langmuir 2010, 26, 3453–3461. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, M.; Akhavan, O.; Ghavami, M.; Rezaee, F.; Ghiasi, S.M.A. Graphene oxide strongly inhibits amyloid beta fibrillation. Nanoscale 2012, 4, 7322–7325. [Google Scholar] [CrossRef] [PubMed]
- Ghule, A.V.; Kathir, K.M.; Suresh Kumar, T.K.; Tzing, S.-H.; Chang, J.-Y.; Yu, C.; Ling, Y.-C. Carbon nanotubes prevent 2,2,2 trifluoroethanol induced aggregation of protein. Carbon 2007, 45, 1586–1589. [Google Scholar] [CrossRef]
- Linse, S.; Cabaleiro-Lago, C.; Xue, W.-F.; Lynch, I.; Lindman, S.; Thulin, E.; Radford, S.E.; Dawson, K.A. Nucleation of protein fibrillation by nanoparticles. Proc. Natl. Acad. Sci. USA 2007, 104, 8691–8696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabaleiro-Lago, C.; Quinlan-Pluck, F.; Lynch, I.; Lindman, S.; Minogue, A.M.; Thulin, E.; Walsh, D.M.; Dawson, K.A.; Linse, S. Inhibition of Amyloid β Protein Fibrillation by Polymeric Nanoparticles. J. Am. Chem. Soc. 2008, 130, 15437–15443. [Google Scholar] [CrossRef]
- Saraiva, A.M.; Cardoso, I.; Pereira, M.C.; Coelho, M.A.N.; Saraiva, M.J.; Möhwald, H.; Brezesinski, G. Controlling Amyloid-β Peptide(1-42) Oligomerization and Toxicity by Fluorinated Nanoparticles. ChemBioChem 2010, 11, 1905–1913. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.-G.; Huynh, T.; Xia, Z.; Zhang, Y.; Fang, H.; Wei, G.; Zhou, R. Hydrophobic Interaction Drives Surface-Assisted Epitaxial Assembly of Amyloid-like Peptides. J. Am. Chem. Soc. 2013, 135, 3150–3157. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Du, H.-N.; Zhang, Z.-X.; Ji, L.-N.; Li, H.-T.; Tang, L.; Wang, H.-B.; Fan, C.-H.; Xu, H.-J.; Zhang, Y.; et al. Epitaxial Growth of Peptide Nanofilaments on Inorganic Surfaces: Effects of Interfacial Hydrophobicity/Hydrophilicity. Angew. Chem. Int. Ed. 2006, 45, 3611–3613. [Google Scholar] [CrossRef]
- Huang, R.; Su, R.; Qi, W.; Zhao, J.; He, Z. Hierarchical, interface-induced self-assembly of diphenylalanine: Formation of peptide nanofibers and microvesicles. Nanotechnology 2011, 22, 245609. [Google Scholar] [CrossRef]
- Morriss-Andrews, A.; Shea, J.-E. Kinetic pathways to peptide aggregation on surfaces: The effects of ?-sheet propensity and surface attraction. J. Chem. Phys. 2012, 136, 65103. [Google Scholar] [CrossRef]
- Shezad, K.; Zhang, K.; Hussain, M.; Dong, H.; He, C.; Gong, X.; Xie, X.; Zhu, J.; Shen, L. Surface Roughness Modulates Diffusion and Fibrillation of Amyloid-β Peptide. Langmuir 2016, 32, 8238–8244. [Google Scholar] [CrossRef]
- Nayak, A.; Dutta, A.K.; Belfort, G. Surface-enhanced nucleation of insulin amyloid fibrillation. Biochem. Biophys. Res. Commun. 2008, 369, 303–307. [Google Scholar] [CrossRef]
- Morriss-Andrews, A.; Bellesia, G.; Shea, J.-E. Effects of surface interactions on peptide aggregate morphology. J. Chem. Phys. 2011, 135, 85102. [Google Scholar] [CrossRef]
- Friedman, R.; Pellarin, R.; Caflisch, A. Amyloid Aggregation on Lipid Bilayers and Its Impact on Membrane Permeability. J. Mol. Biol. 2009, 387, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Press-Sandler, O.; Miller, Y. Molecular mechanisms of membrane-associated amyloid aggregation: Computational perspective and challenges. Biochim. Biophys. Acta (BBA) Biomembr. 2018, 1860, 1889–1905. [Google Scholar] [CrossRef] [PubMed]
- Vácha, R.; Frenkel, D. Relation between Molecular Shape and the Morphology of Self-Assembling Aggregates: A Simulation Study. Biophys. J. 2011, 101, 1432–1439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vácha, R.; Linse, S.; Lund, M. Surface Effects on Aggregation Kinetics of Amyloidogenic Peptides. J. Am. Chem. Soc. 2014, 136, 11776–11782. [Google Scholar] [CrossRef] [PubMed]
- Cabaleiro-Lago, C.; Szczepankiewicz, O.; Linse, S. The Effect of Nanoparticles on Amyloid Aggregation Depends on the Protein Stability and Intrinsic Aggregation Rate. Langmuir 2012, 28, 1852–1857. [Google Scholar] [CrossRef] [PubMed]
- Cabaleiro-Lago, C.; Quinlan-Pluck, F.; Lynch, I.; Dawson, K.A.; Linse, S. Dual Effect of Amino Modified Polystyrene Nanoparticles on Amyloid β Protein Fibrillation. ACS Chem. Neurosci. 2010, 1, 279–287. [Google Scholar] [CrossRef]
- Abeln, S.; Vendruscolo, M.; Dobson, C.M.; Frenkel, D. A Simple Lattice Model That Captures Protein Folding, Aggregation and Amyloid Formation. PLoS ONE 2014, 9, e85185. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Hall, C.K.; Voegler, A.C. Effect of denaturant and protein concentrations upon protein refolding and aggregation: A simple lattice model. Protein Sci. 1998, 7, 2642–2652. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.T.; Nguyen, P.H.; Derreumaux, P. Lattice model for amyloid peptides: OPEP force field parametrization and applications to the nucleus size of Alzheimer’s peptides. J. Chem. Phys. 2016, 144, 205103. [Google Scholar] [CrossRef]
- Sterpone, F.; Doutreligne, S.; Tran, T.T.; Melchionna, S.; Baaden, M.; Nguyen, P.H.; Derreumaux, P. Multi-scale simulations of biological systems using the OPEP coarse-grained model. Biochem. Biophys. Res. Commun. 2018, 498, 296–304. [Google Scholar] [CrossRef]
- Li, M.S.; Klimov, D.K.; Straub, J.E.; Thirumalai, D. Probing the mechanisms of fibril formation using lattice models. J. Chem. Phys. 2008, 129, 175101. [Google Scholar] [CrossRef] [Green Version]
- Co, N.T.; Lan, P.D.; Quoc Huy, P.D.; Li, M.S. Heat-induced degradation of fibrils: Exponential vs logistic kinetics. J. Chem. Phys. 2020, 152, 115101. [Google Scholar] [CrossRef] [PubMed]
- Co, N.T.; Li, M.S. New method for determining size of critical nucleus of fibril formation of polypeptide chains. J. Chem. Phys. 2012, 137, 095101. [Google Scholar] [CrossRef] [PubMed]
- Li, M.S.; Co, N.T.; Reddy, G.; Hu, C.-K.; Straub, J.E.; Thirumalai, D. Factors Governing Fibrillogenesis of Polypeptide Chains Revealed by Lattice Models. Phys. Rev. Lett. 2010, 105, 218101. [Google Scholar] [CrossRef] [PubMed]
- Betancourt, M.R.; Thirumalai, D. Pair potentials for protein folding: Choice of reference states and sensitivity of predicted native states to variations in the interaction schemes. Protein Sci. 2008, 8, 361–369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Luo, Y.; Derreumaux, P.; Wei, G. Carbon Nanotube Inhibits the Formation of β-Sheet-Rich Oligomers of the Alzheimer’s Amyloid-β(16-22) Peptide. Biophys. J. 2011, 101, 2267–2276. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Adachi, T.; Vanden Bout, D.; Zhu, X.-Y. A Mobile Precursor Determines Amyloid-β Peptide Fibril Formation at Interfaces. J. Am. Chem. Soc. 2012, 134, 14172–14178. [Google Scholar] [CrossRef]
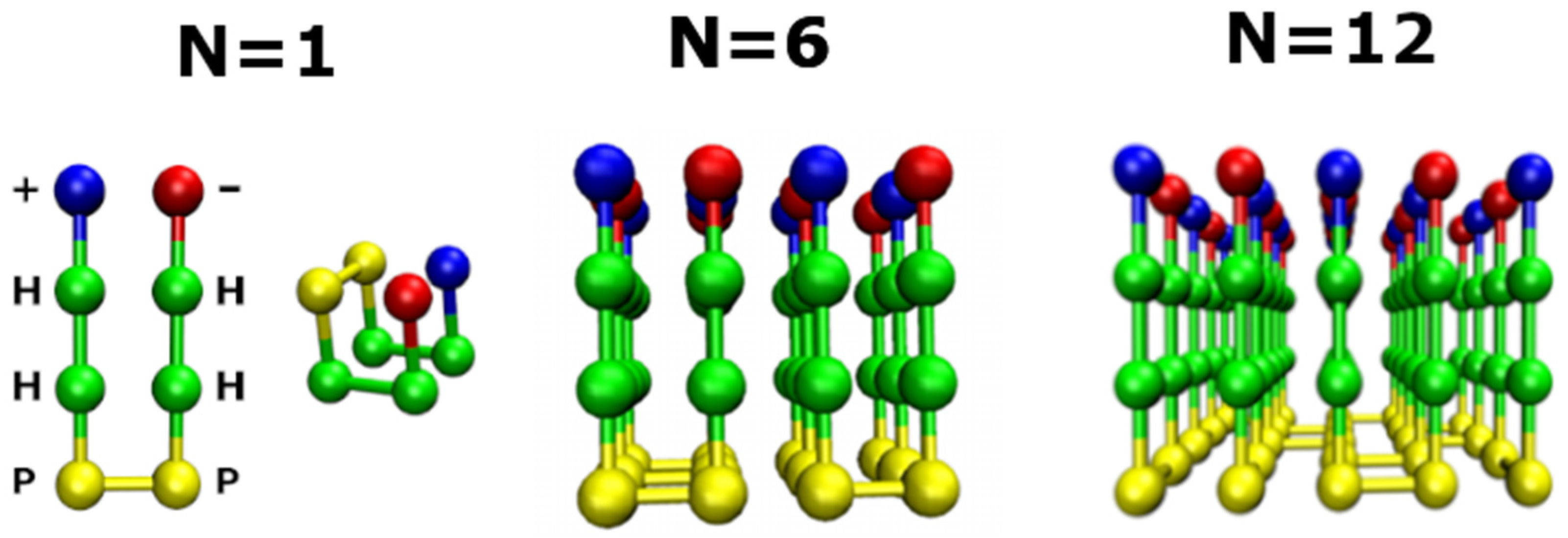
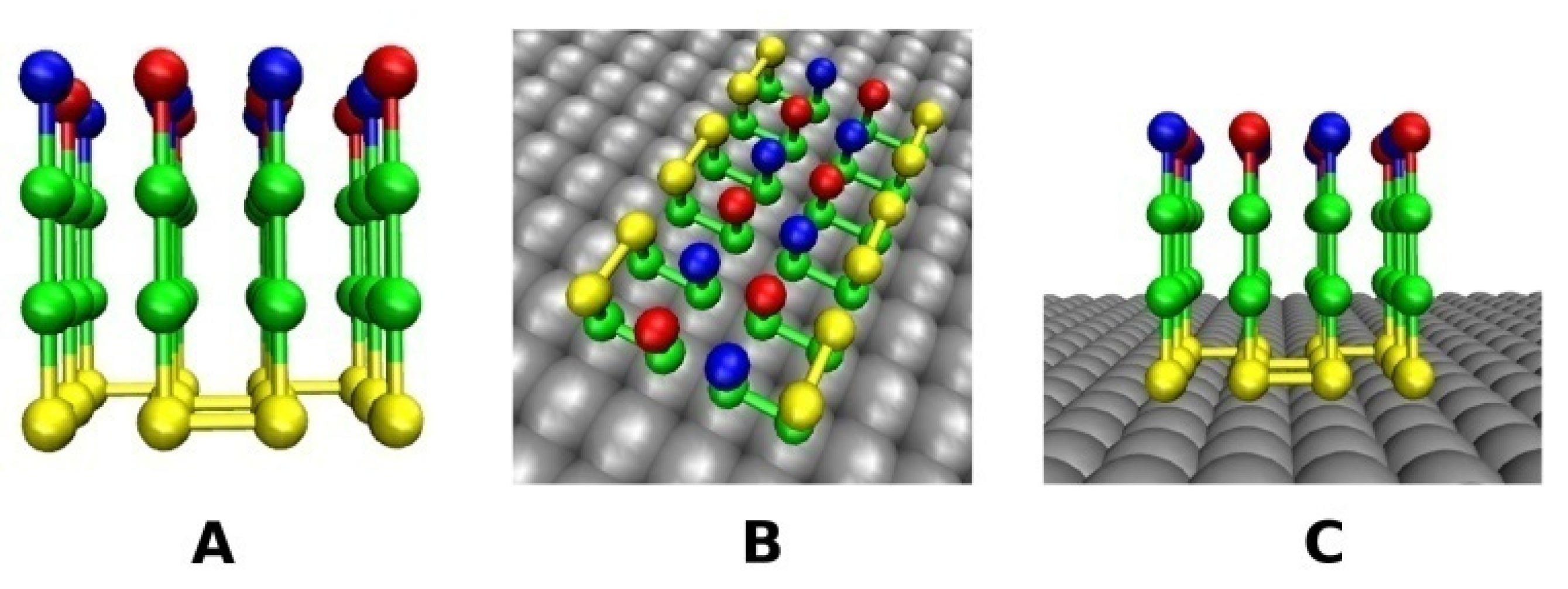
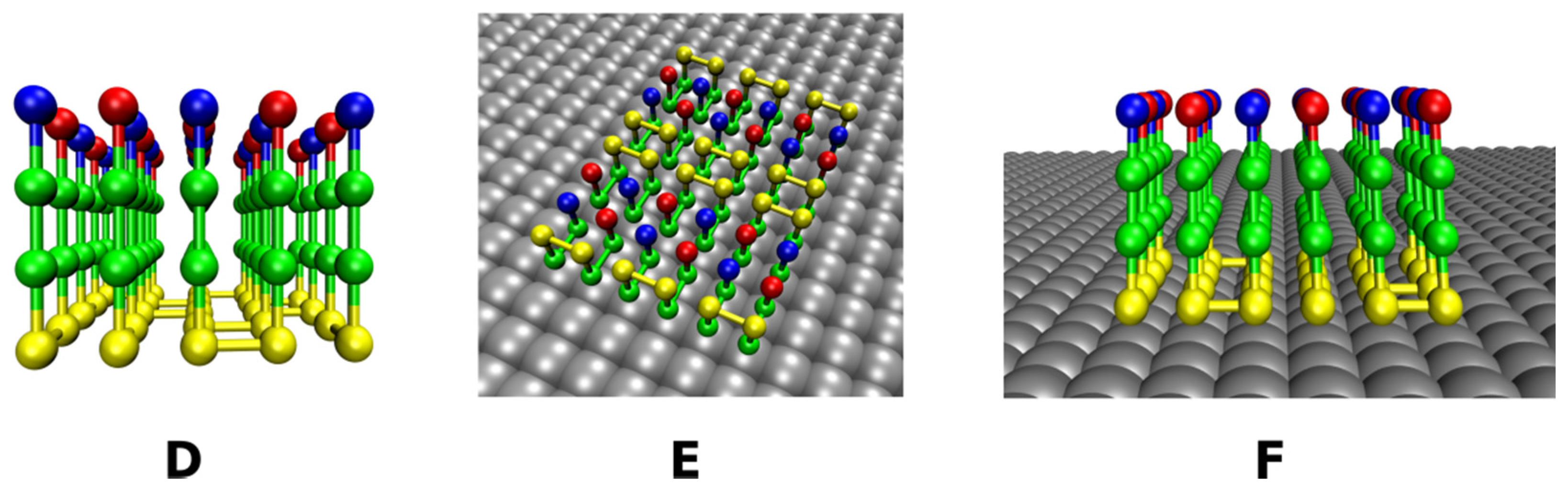
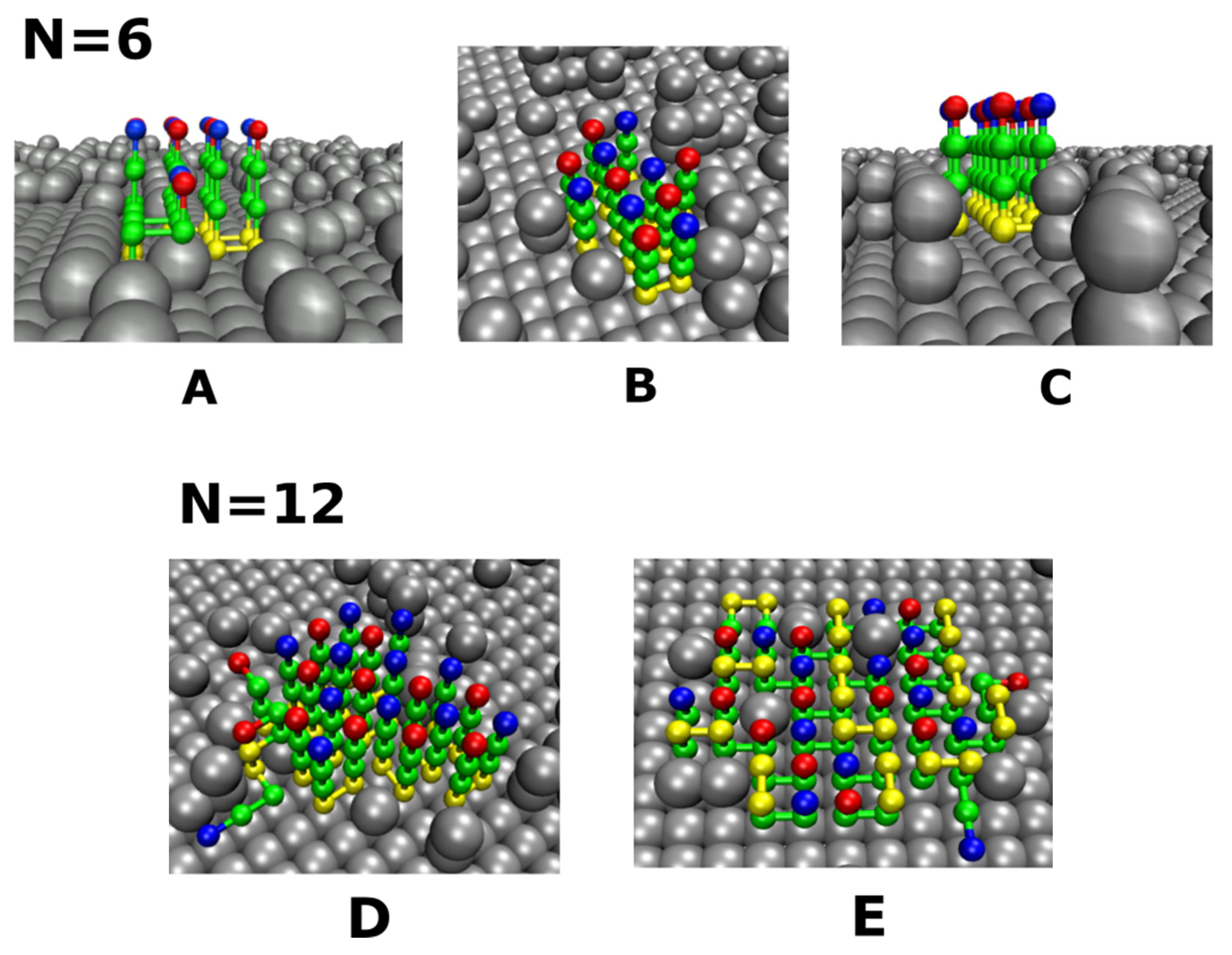



| Beads | H | P | + | − |
|---|---|---|---|---|
| H | −1.0 | 0.2 | 0.2 | 0.2 |
| P | 0.2 | −0.2 | −0.2 | −0.2 |
| + | 0.2 | −0.2 | 0.35 | −0.7 |
| − | 0.2 | −0.2 | −0.7 | 0.35 |
| Beads/Balls | H | P | + | − |
|---|---|---|---|---|
| Ps | 0.2 | −εps | −0.2 | −0.2 |
| Hs | −εhs | 0.2 | 0.2 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Co, N.T.; Li, M.S. Effect of Surface Roughness on Aggregation of Polypeptide Chains: A Monte Carlo Study. Biomolecules 2021, 11, 596. https://doi.org/10.3390/biom11040596
Co NT, Li MS. Effect of Surface Roughness on Aggregation of Polypeptide Chains: A Monte Carlo Study. Biomolecules. 2021; 11(4):596. https://doi.org/10.3390/biom11040596
Chicago/Turabian StyleCo, Nguyen Truong, and Mai Suan Li. 2021. "Effect of Surface Roughness on Aggregation of Polypeptide Chains: A Monte Carlo Study" Biomolecules 11, no. 4: 596. https://doi.org/10.3390/biom11040596
APA StyleCo, N. T., & Li, M. S. (2021). Effect of Surface Roughness on Aggregation of Polypeptide Chains: A Monte Carlo Study. Biomolecules, 11(4), 596. https://doi.org/10.3390/biom11040596






