Simulation of Calcium Dynamics in Realistic Three-Dimensional Domains
Abstract
:1. Introduction
1.1. Salivary Gland Acinar Cells
1.2. The Importance of the Spatial Structure
2. Materials and Methods
2.1. Construction of the Artificial Cells
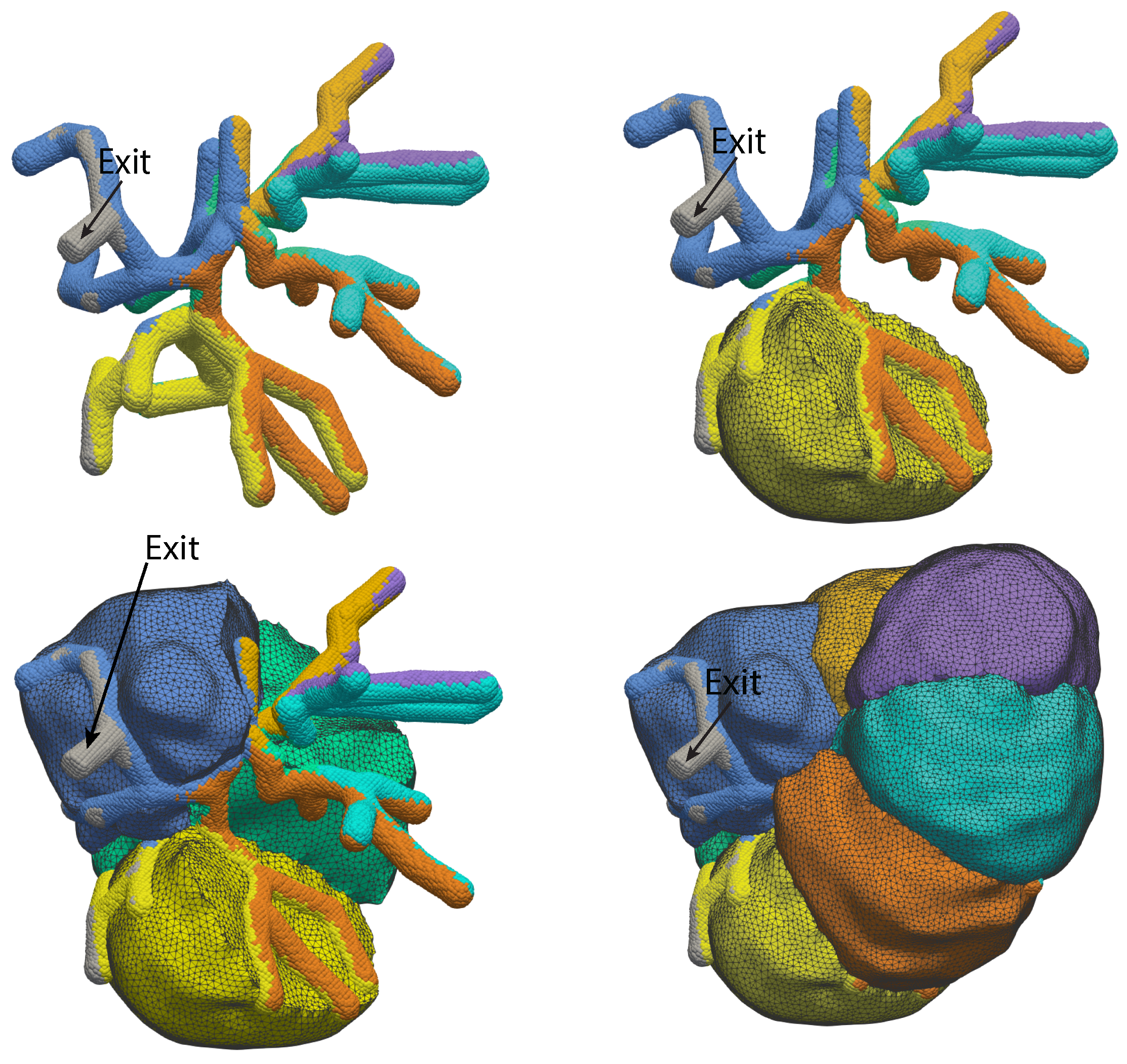
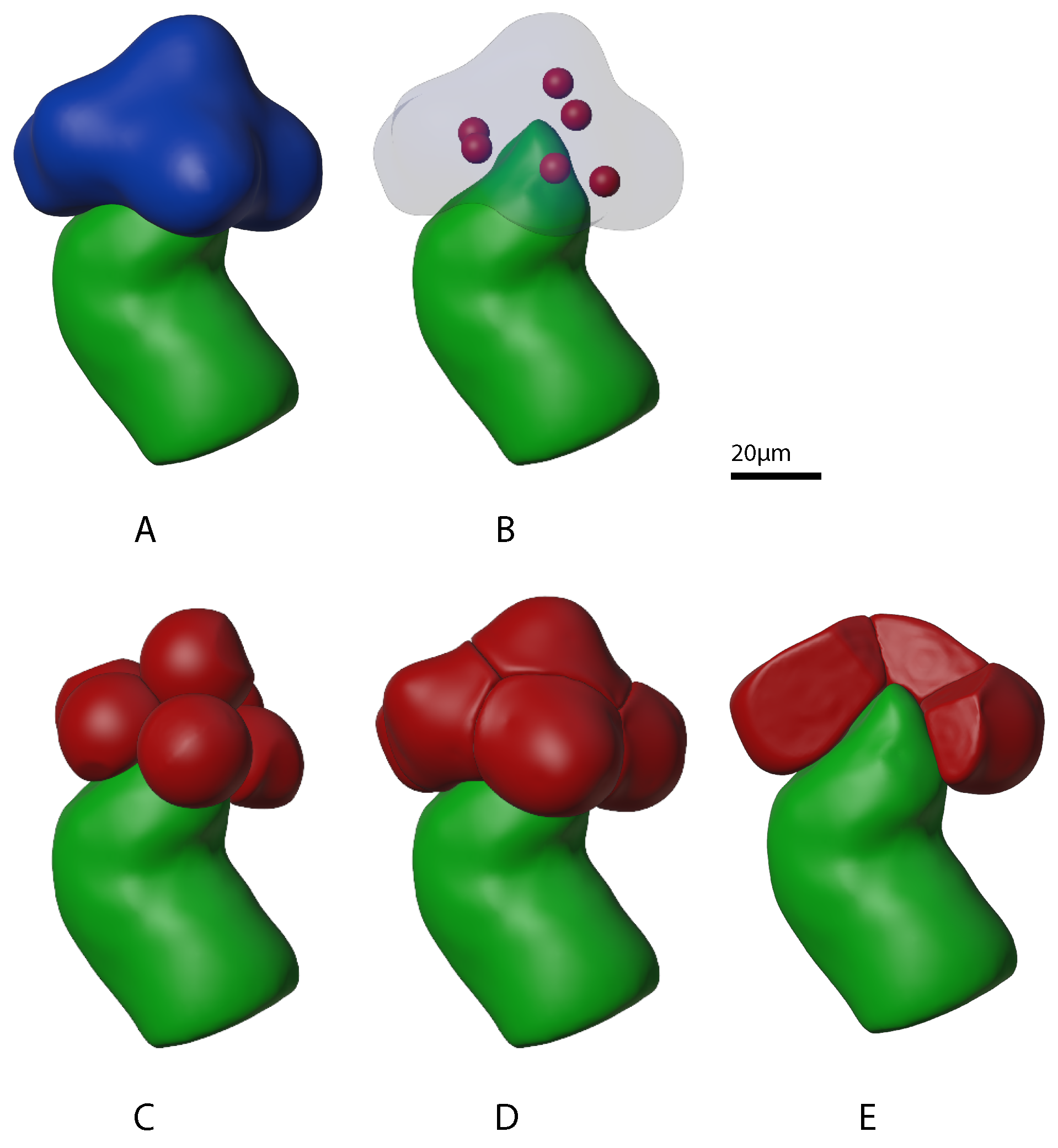
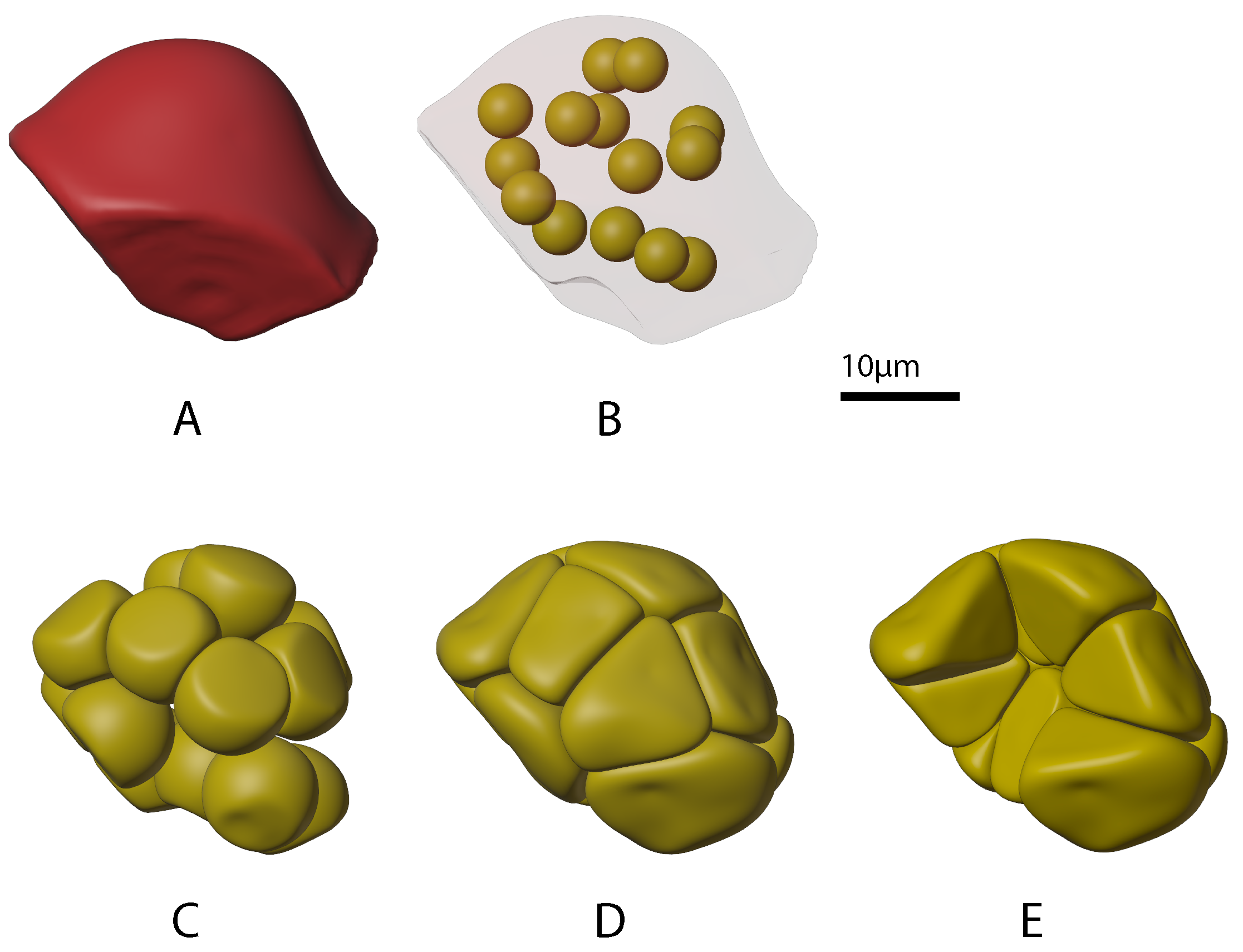
2.1.1. Growing Acini
2.1.2. Growing Acinar Cells
2.1.3. Volumetric Meshing
2.1.4. Acinus Lumen and Apical Regions
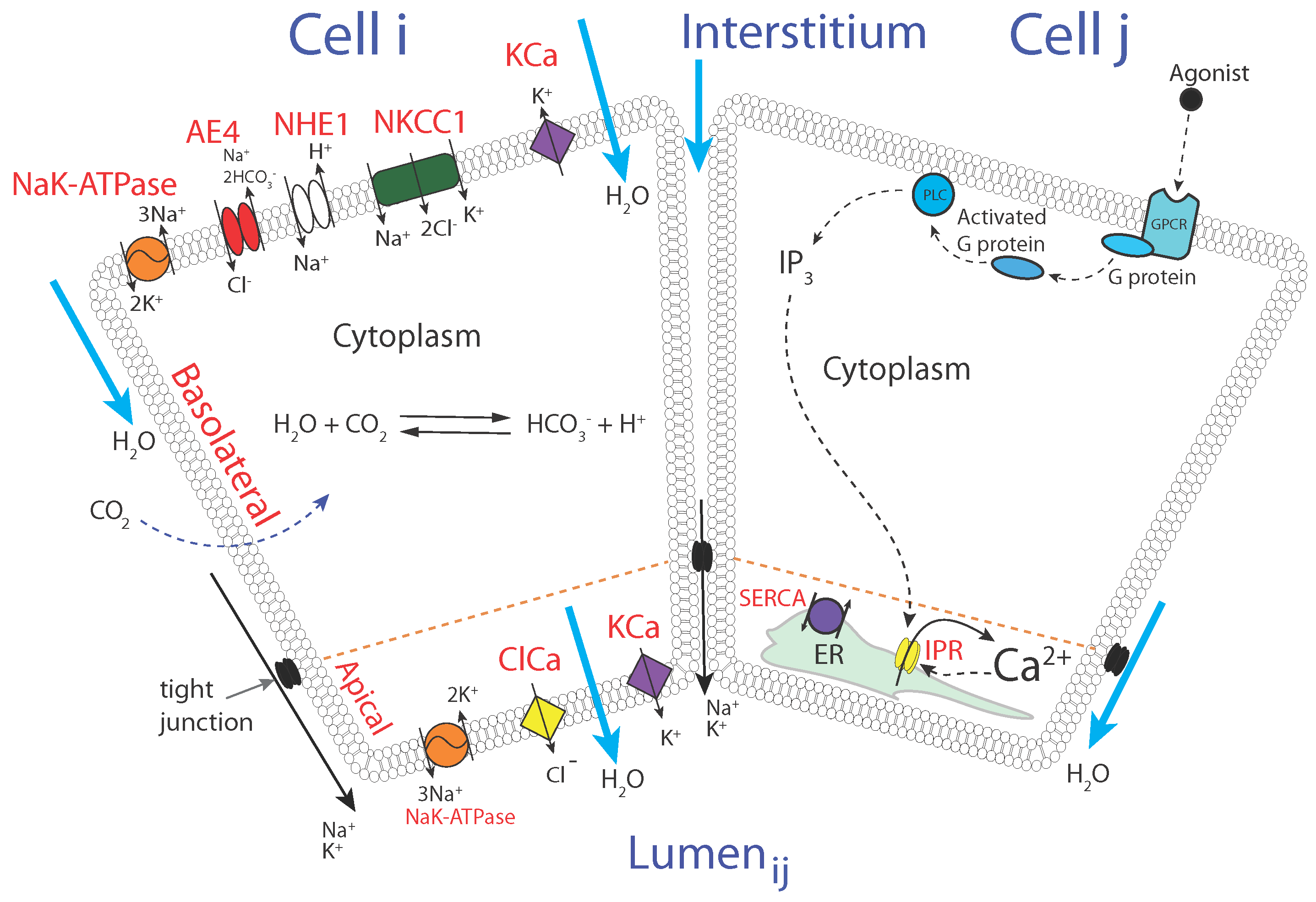
2.2. The Model
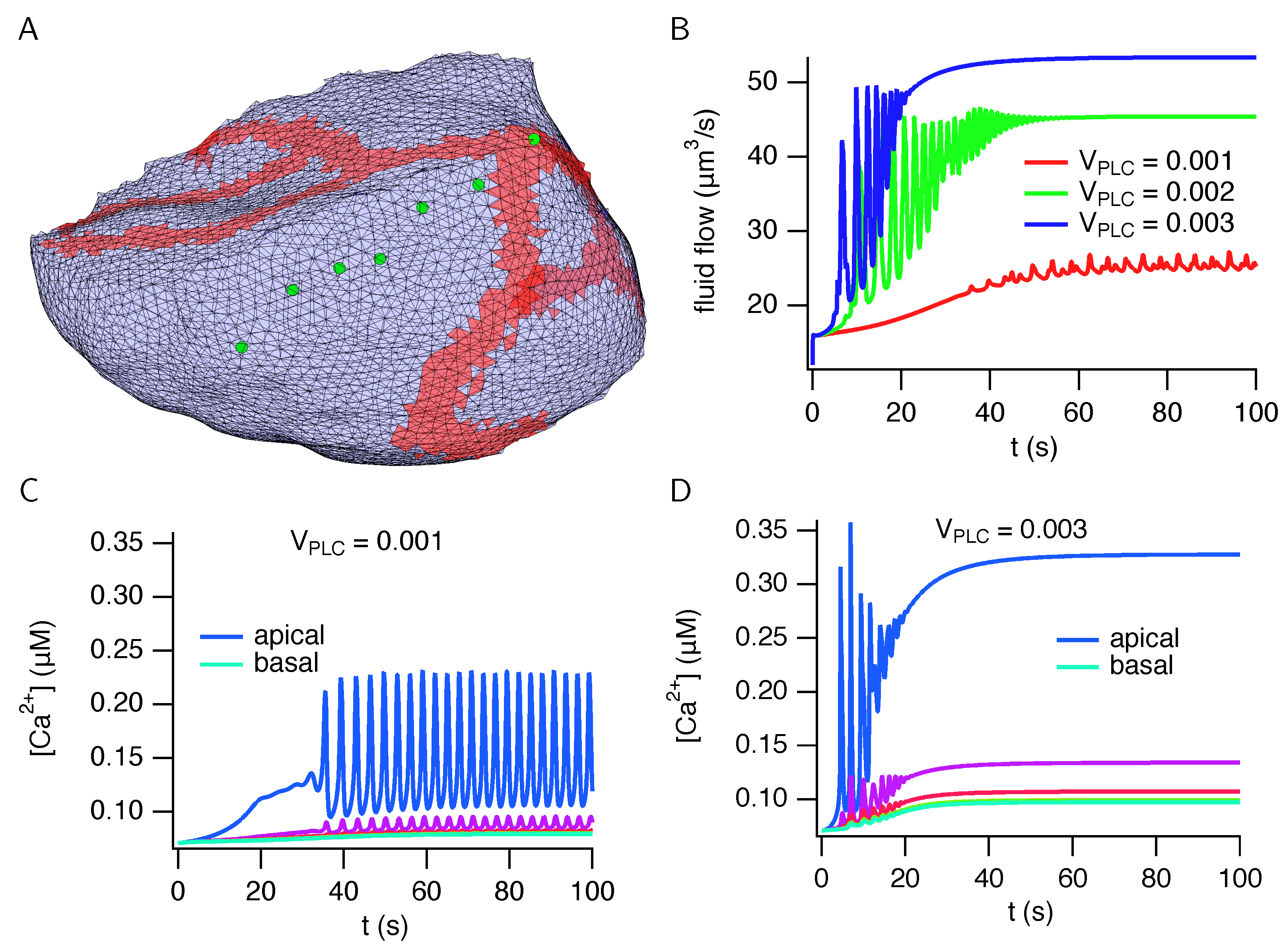
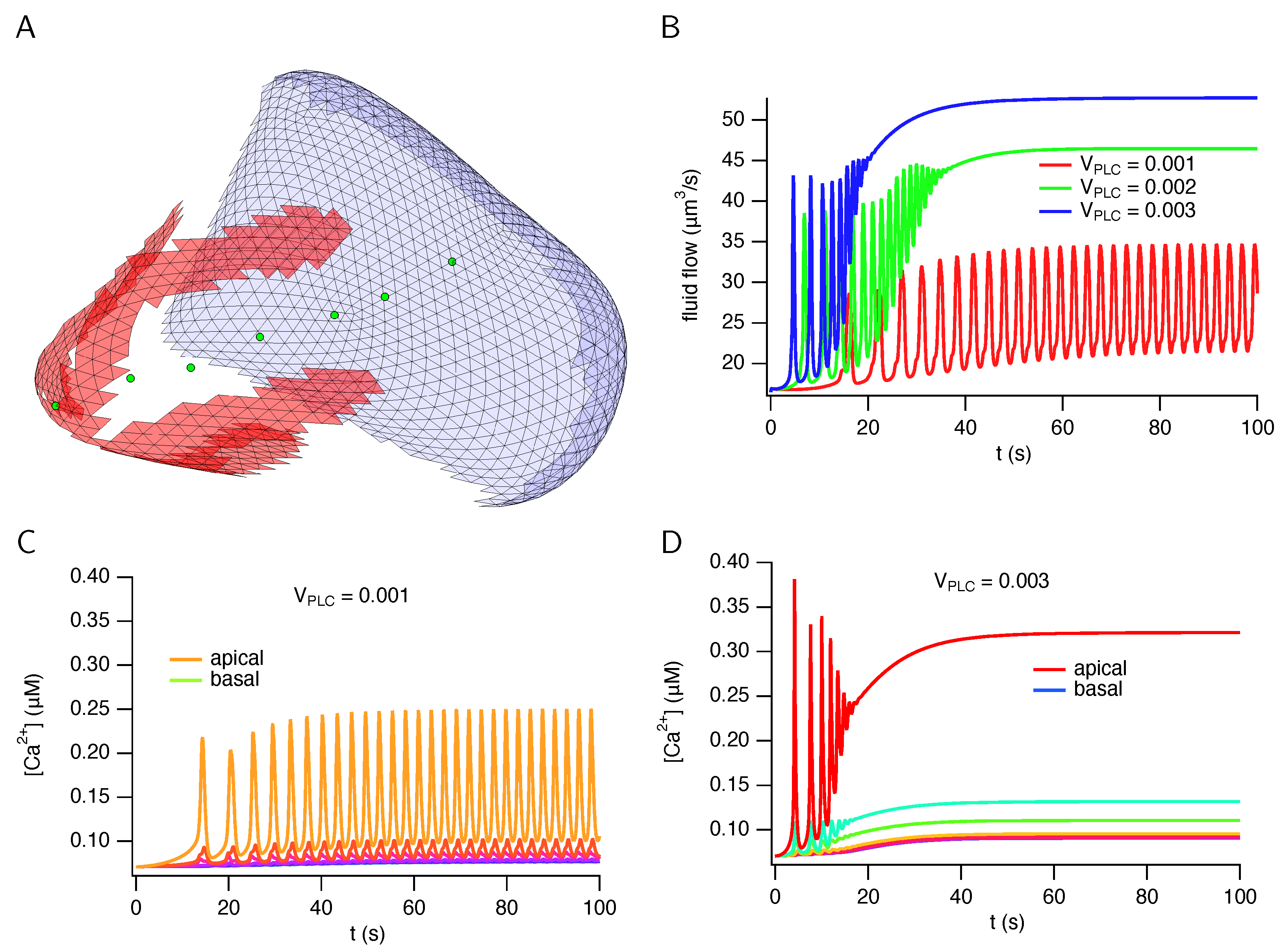
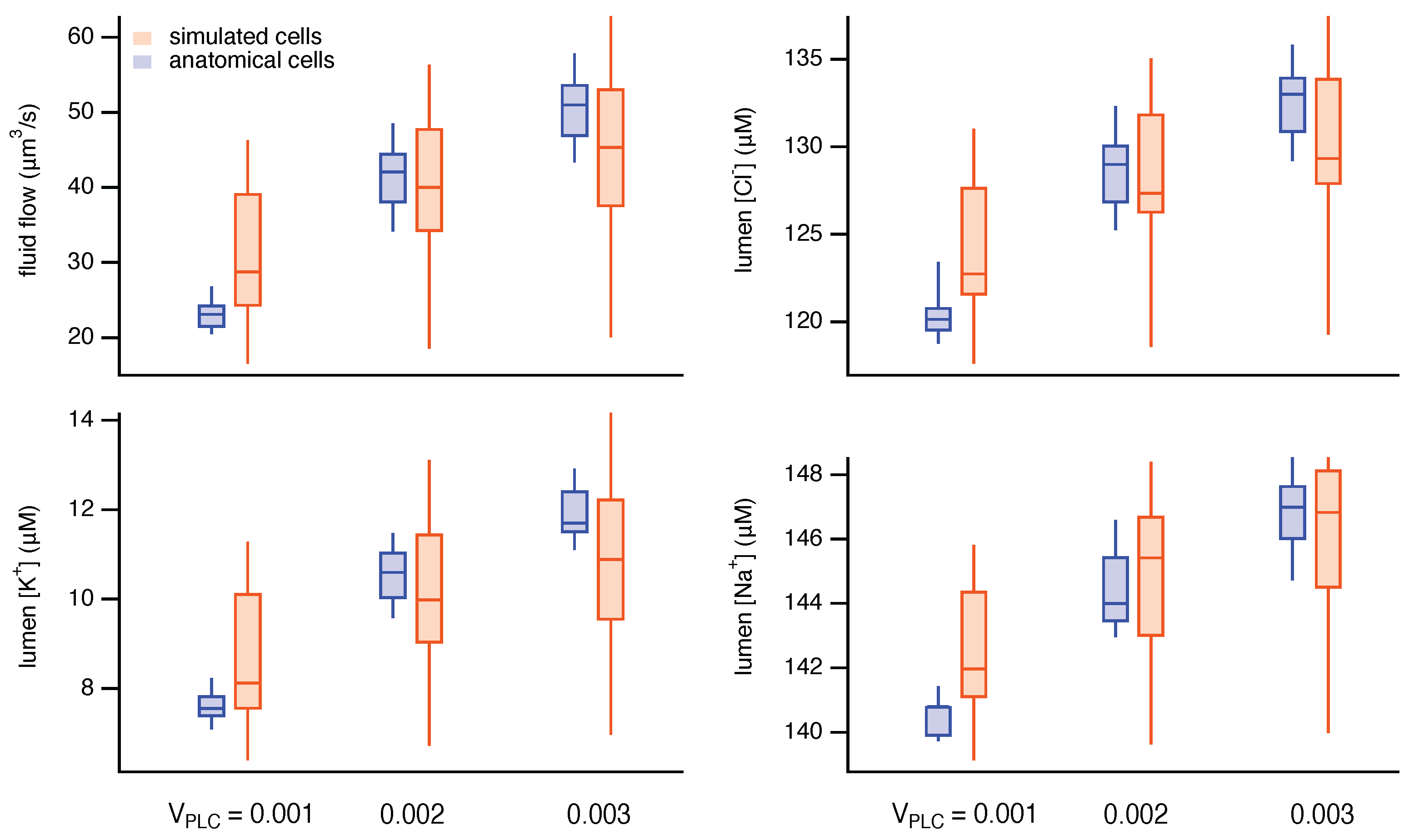
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLC | phospholipase C |
| IP | inositol trisphosphate |
| IPR | inositol trisphosphate receptor |
| ER | endoplasmic reticulum |
| SERCA | sarcoplasmic/ER ATPase |
| ClCa | -activated channel |
| KCa | -activated channel |
| NKCC1 | // cotransporter |
| NHE1 | /H exchanger |
| AE4 | anion exchanger |
References
- Berridge, M.J. Calcium oscillations. J. Biol. Chem. 1990, 265, 9583–9586. [Google Scholar] [CrossRef]
- Cobbold, P.H.; Cuthbertson, K.S. Calcium oscillations: Phenomena, mechanisms and significance. Semin. Cell Biol. 1990, 1, 311–321. [Google Scholar] [PubMed]
- Berridge, M.J. Inositol trisphosphate and calcium oscillations. Adv. Second Messenger Phosphoprot. Res. 1992, 26, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Dupont, G.; Falcke, M.; Kirk, V.; Sneyd, J. Models of Calcium Signalling; Interdisciplinary Applied Mathematics; Springer: Berlin, Germany, 2016; Volume 43. [Google Scholar] [CrossRef]
- Allbritton, N.L.; Meyer, T.; Stryer, L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science 1992, 258, 1812–1815. [Google Scholar] [CrossRef]
- Smith, G.D. Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys. J. 1996, 71, 3064–3072. [Google Scholar] [CrossRef]
- Smith, G.D.; Wagner, J.; Keizer, J. Validity of the rapid buffering approximation near a point source of calcium ions. Biophys. J. 1996, 70, 2527–2539. [Google Scholar] [CrossRef] [Green Version]
- Zeller, S.; Rüdiger, S.; Engel, H.; Sneyd, J.; Warnecke, G.; Parker, I.; Falcke, M. Modeling of the modulation by buffers of Ca2+ release through clusters of IP3 receptors. Biophys. J. 2009, 97, 992–1002. [Google Scholar] [CrossRef] [Green Version]
- Solovey, G.; Ponce Dawson, S. Observable effects of Ca2+ buffers on local Ca2+ signals. Philos. Trans. A Math. Phys. Eng. Sci. 2010, 368, 5597–5603. [Google Scholar] [CrossRef] [Green Version]
- Dupont, G.; Goldbeter, A. CaM kinase II as frequency decoder of Ca2+ oscillations. Bioessays 1998, 20, 607–610. [Google Scholar] [CrossRef]
- Sathyanarayanan, P.V.; Poovaiah, B.W. Decoding Ca2+ signals in plants. CRC Crit. Rev. Plant Sci. 2004, 23, 1–11. [Google Scholar] [CrossRef]
- Smedler, E.; Uhlén, P. Frequency decoding of calcium oscillations. Biochim. Biophys. Acta 2014, 1840, 964–969. [Google Scholar] [CrossRef] [Green Version]
- Skupin, A.; Falcke, M. From puffs to global Ca2+ signals: How molecular properties shape global signals. Chaos 2009, 19, 037111. [Google Scholar] [CrossRef] [PubMed]
- Skupin, A.A.; Thurley, K.K. Calcium signaling: From single channels to pathways. Adv. Exp. Med. Biol. 2011, 740, 531–551. [Google Scholar]
- Thul, R.; Bellamy, T.C.; Roderick, H.L.; Bootman, M.D.; Coombes, S. Calcium oscillations. Adv. Exp. Med. Biol. 2008, 641, 1–27. [Google Scholar] [PubMed]
- Thurley, K.; Skupin, A.; Thul, R.; Falcke, M. Fundamental properties of Ca2+ signals. Biochim. Biophys. Acta 2012, 1820, 1185–1194. [Google Scholar] [CrossRef] [Green Version]
- Nauntofte, B. Regulation of electrolyte and fluid secretion in salivary acinar cells. Am. J. Physiol. 1992, 263, G823–G837. [Google Scholar] [CrossRef]
- Melvin, J.E.; Yule, D.; Shuttleworth, T.; Begenisich, T. Regulation of fluid and electrolyte secretion in salivary gland acinar cells. Annu. Rev. Physiol. 2005, 67, 445–469. [Google Scholar] [CrossRef]
- Lee, M.G.; Ohana, E.; Park, H.W.; Yang, D.; Muallem, S. Molecular mechanism of pancreatic and salivary gland fluid and HCO3− secretion. Physiol. Rev. 2012, 92, 39–74. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.H.; Park, S.; Shcheynikov, N.; Muallem, S. Mechanism and synergism in epithelial fluid and electrolyte secretion. Pflug. Arch. 2014, 466, 1487–1499. [Google Scholar] [CrossRef] [Green Version]
- Proctor, G.B. The physiology of salivary secretion. Periodontol. 2000 2016, 70, 11–25. [Google Scholar] [CrossRef]
- Takano, T.; Wahl, A.M.; Huang, K.T.; Narita, T.; Rugis, J.; Sneyd, J.; Yule, D.I. Highly localized intracellular Ca2+ signals promote optimal salivary gland fluid secretion. Elife 2021, 10, e66170. [Google Scholar] [CrossRef] [PubMed]
- Vera-Sigüenza, E.; Pages, N.; Rugis, J.; Yule, D.I.; Sneyd, J. A Mathematical Model of Fluid Transport in an Accurate Reconstruction of Parotid Acinar Cells. Bull. Math. Biol. 2019, 81, 699–721. [Google Scholar] [CrossRef] [PubMed]
- Pages, N.; Vera-Sigüenza, E.; Rugis, J.; Kirk, V.; Yule, D.I.; Sneyd, J. A Model of Ca2+ Dynamics in an Accurate Reconstruction of Parotid Acinar Cells. Bull. Math. Biol. 2019, 81, 1394–1426. [Google Scholar] [CrossRef] [PubMed]
- Vera-Sigüenza, E.; Pages, N.; Rugis, J.; Yule, D.I.; Sneyd, J. A Multicellular Model of Primary Saliva Secretion in the Parotid Gland. Bull. Math. Biol. 2020, 82, 38. [Google Scholar] [CrossRef] [PubMed]
- Sneyd, J.; Vera-Sigüenza, E.; Rugis, J.; Pages, N.; Yule, D.I. Calcium Dynamics and Water Transport in Salivary Acinar Cells. Bull. Math. Biol. 2021, 83, 31. [Google Scholar] [CrossRef]
- Su, S.; Rugis, J.; Wahl, A.; Doak, S.; Li, Y.; Suresh, V.; Yule, D.; Sneyd, J. A Mathematical Model of Salivary Gland Duct Cells. Bull. Math. Biol. 2022, 84, 84. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Blender Online Community. Blender—A 3D Modelling and Rendering Package; Stichting Blender Foundation: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Oliphant, T. Python for Scientific Computing. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Millman, K.; Aivazis, M. Python for Scientists and Engineers. Comput. Sci. Eng. 2011, 13, 9–12. [Google Scholar] [CrossRef] [Green Version]
- Geuzaine, C.; Remacle, J.F. Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Sneyd, J.; Tsaneva-Atanasova, K.; Bruce, J.I.E.; Straub, S.V.; Giovannucci, D.R.; Yule, D.I. A model of calcium waves in pancreatic and parotid acinar cells. Biophys. J. 2003, 85, 1392–1405. [Google Scholar] [CrossRef]
- Palk, L.; Sneyd, J.; Patterson, K.; Shuttleworth, T.J.; Yule, D.I.; Maclaren, O.; Crampin, E.J. Modelling the effects of calcium waves and oscillations on saliva secretion. J. Theor. Biol. 2012, 305, 45–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goel, P.; Sneyd, J.; Friedman, A. Homogenization of the cell cytoplasm: The calcium bidomain equations. SIAM J. Multiscale Model. Simul. 2006, 5, 1045–1062. [Google Scholar] [CrossRef]
- Sneyd, J.; Han, J.M.; Wang, L.; Chen, J.; Yang, X.; Tanimura, A.; Sanderson, M.J.; Kirk, V.; Yule, D.I. On the dynamical structure of calcium oscillations. Proc. Natl. Acad. Sci. USA 2017, 114, 1456–1461. [Google Scholar] [CrossRef] [Green Version]
- Schneyer, L.H.; Young, J.A.; Schneyer, C.A. Salivary secretion of electrolytes. Physiol. Rev. 1972, 52, 720–777. [Google Scholar] [CrossRef]
- Giovannucci, D.R.; Bruce, J.I.E.; Straub, S.V.; Arreola, J.; Sneyd, J.; Shuttleworth, T.J.; Yule, D.I. Cytosolic Ca2+ and Ca2+-activated Cl− current dynamics: Insights from two functionally distinct mouse exocrine cells. J. Physiol. 2002, 540, 469–484. [Google Scholar] [CrossRef]
- Almassy, J.; Won, J.H.; Begenisich, T.B.; Yule, D.I. Apical Ca2+-activated potassium channels in mouse parotid acinar cells. J. Gen. Physiol. 2012, 139, 121–133. [Google Scholar] [CrossRef] [Green Version]
- Almássy, J.; Siguenza, E.; Skaliczki, M.; Matesz, K.; Sneyd, J.; Yule, D.I.; Nánási, P.P. New saliva secretion model based on the expression of Na+-K+ pump and K+ channels in the apical membrane of parotid acinar cells. Pflug. Arch. 2018, 470, 613–621. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sneyd, J.; Rugis, J.; Su, S.; Suresh, V.; Wahl, A.M.; Yule, D.I. Simulation of Calcium Dynamics in Realistic Three-Dimensional Domains. Biomolecules 2022, 12, 1455. https://doi.org/10.3390/biom12101455
Sneyd J, Rugis J, Su S, Suresh V, Wahl AM, Yule DI. Simulation of Calcium Dynamics in Realistic Three-Dimensional Domains. Biomolecules. 2022; 12(10):1455. https://doi.org/10.3390/biom12101455
Chicago/Turabian StyleSneyd, James, John Rugis, Shan Su, Vinod Suresh, Amanda M. Wahl, and David I. Yule. 2022. "Simulation of Calcium Dynamics in Realistic Three-Dimensional Domains" Biomolecules 12, no. 10: 1455. https://doi.org/10.3390/biom12101455
APA StyleSneyd, J., Rugis, J., Su, S., Suresh, V., Wahl, A. M., & Yule, D. I. (2022). Simulation of Calcium Dynamics in Realistic Three-Dimensional Domains. Biomolecules, 12(10), 1455. https://doi.org/10.3390/biom12101455





