Understanding Calmodulin Variants Affecting Calcium-Dependent Inactivation of L-Type Calcium Channels through Whole-Cell Simulation of the Cardiac Ventricular Myocyte
Abstract
:1. Introduction
2. Materials and Methods
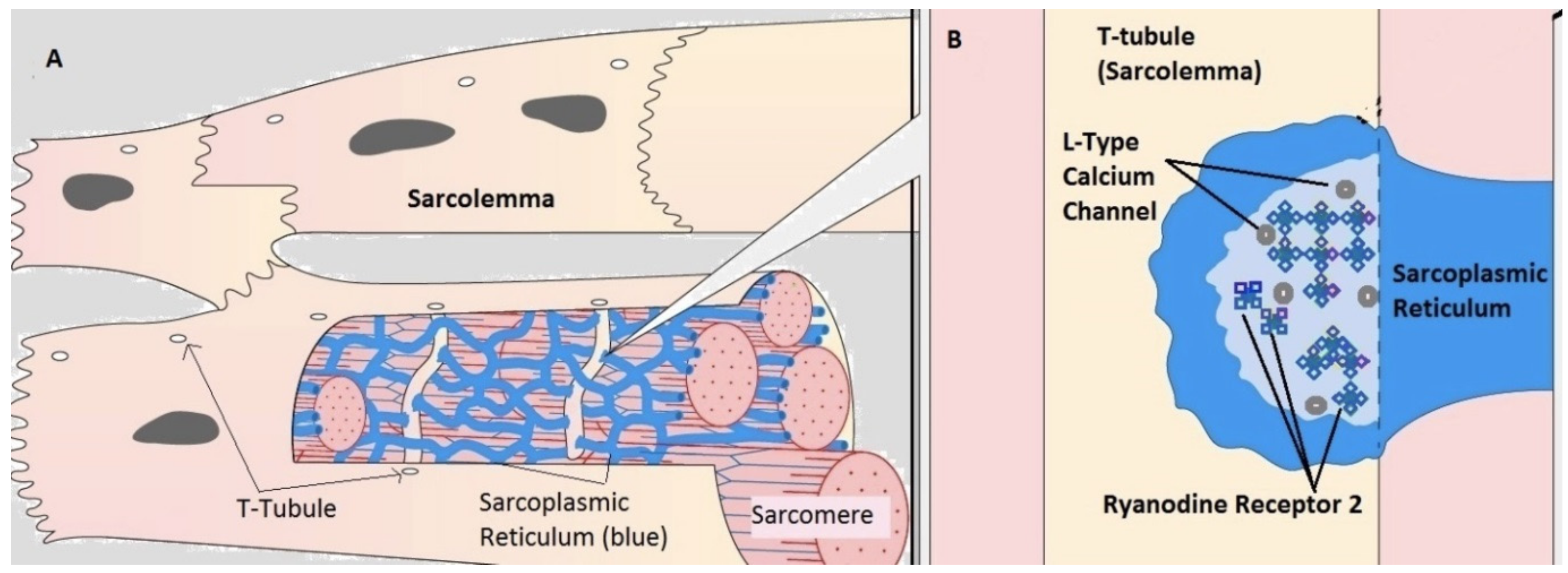
2.1. Compartmental Cellular Model
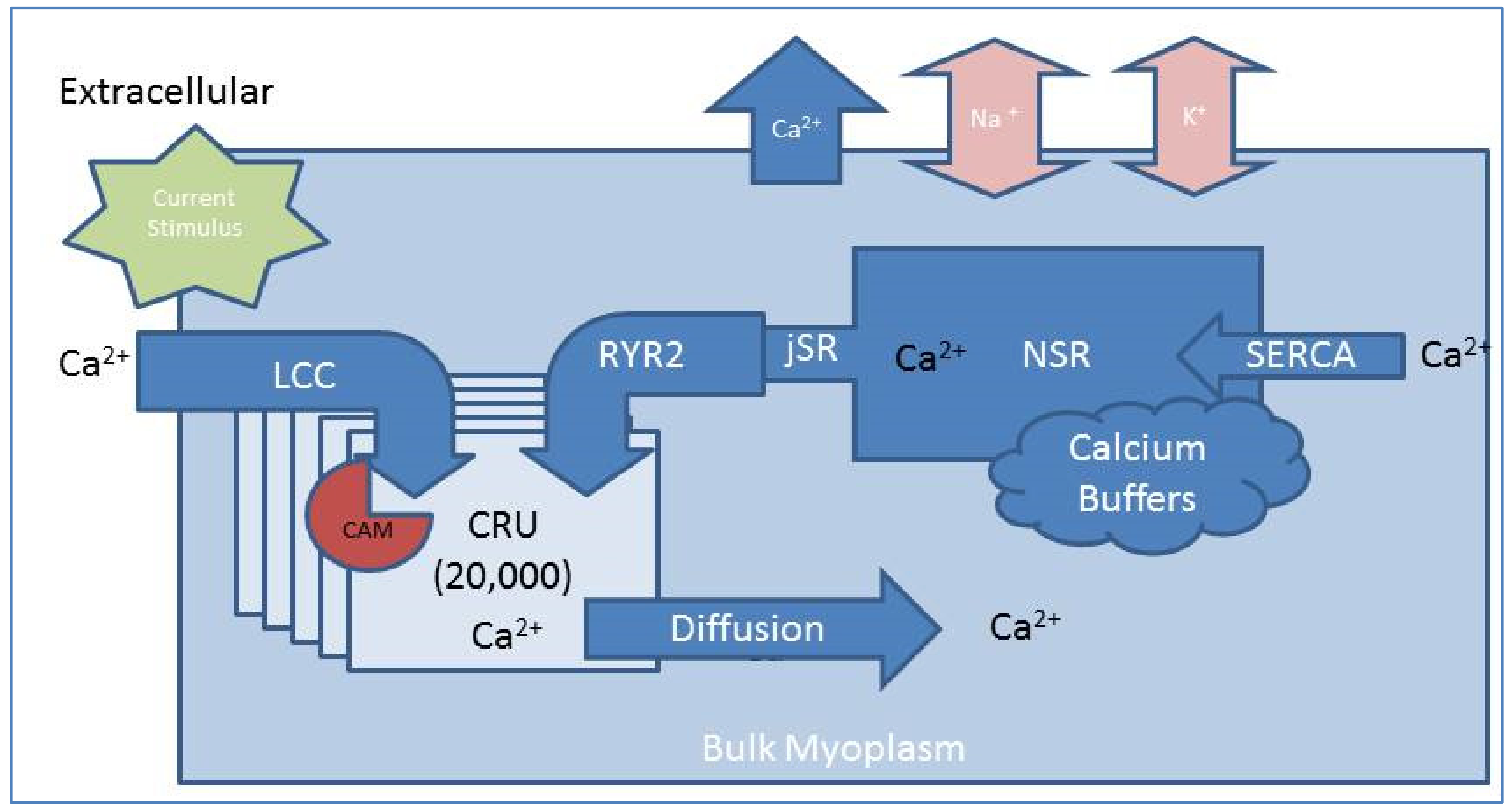
2.1.1. Calcium Release Site (CRU)
2.1.2. Ryanodine Receptor Type-2 Model
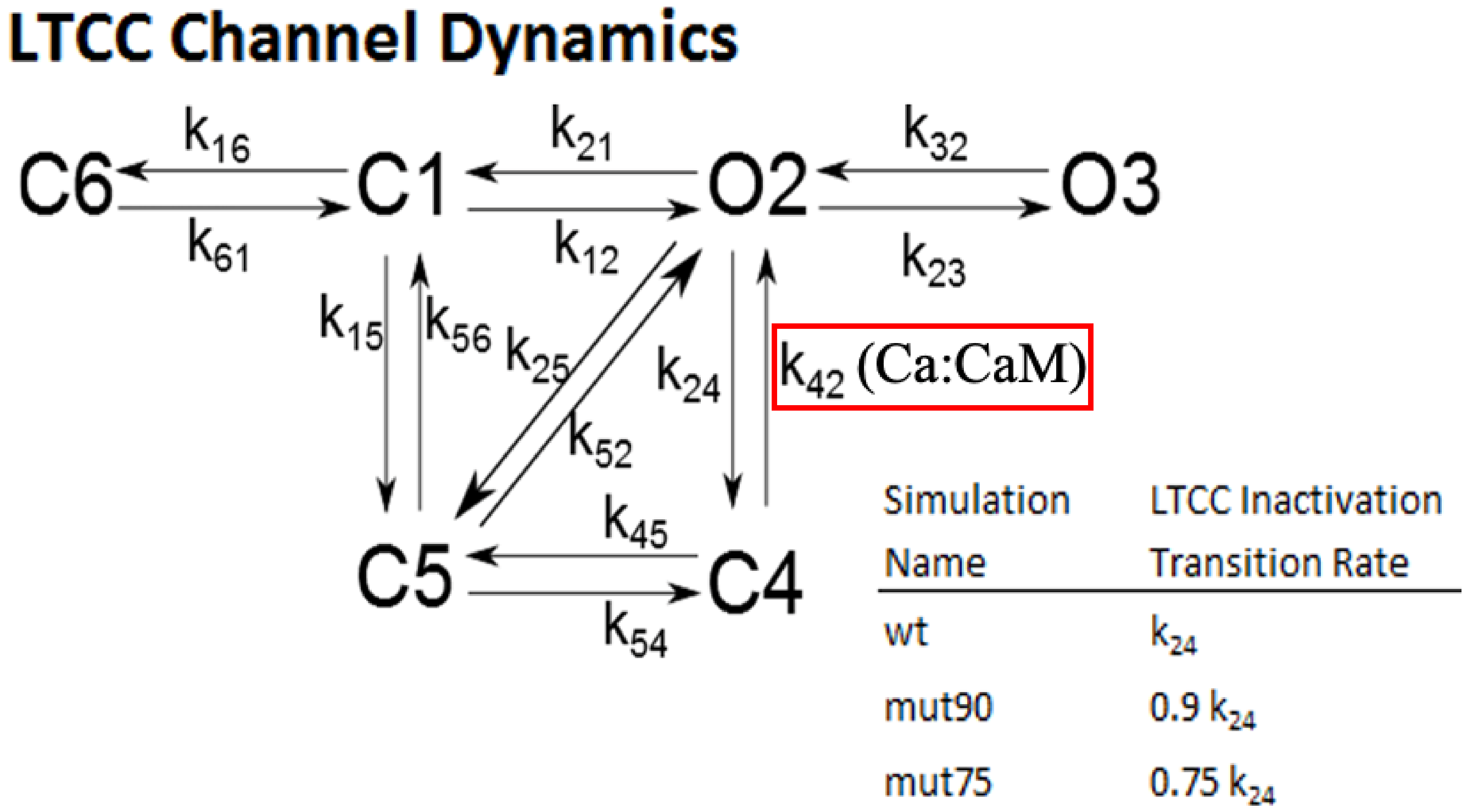
2.1.3. L-Type Calcium Channel Gating
2.2. Numerical Methods
2.3. Statistical Analysis
3. Results
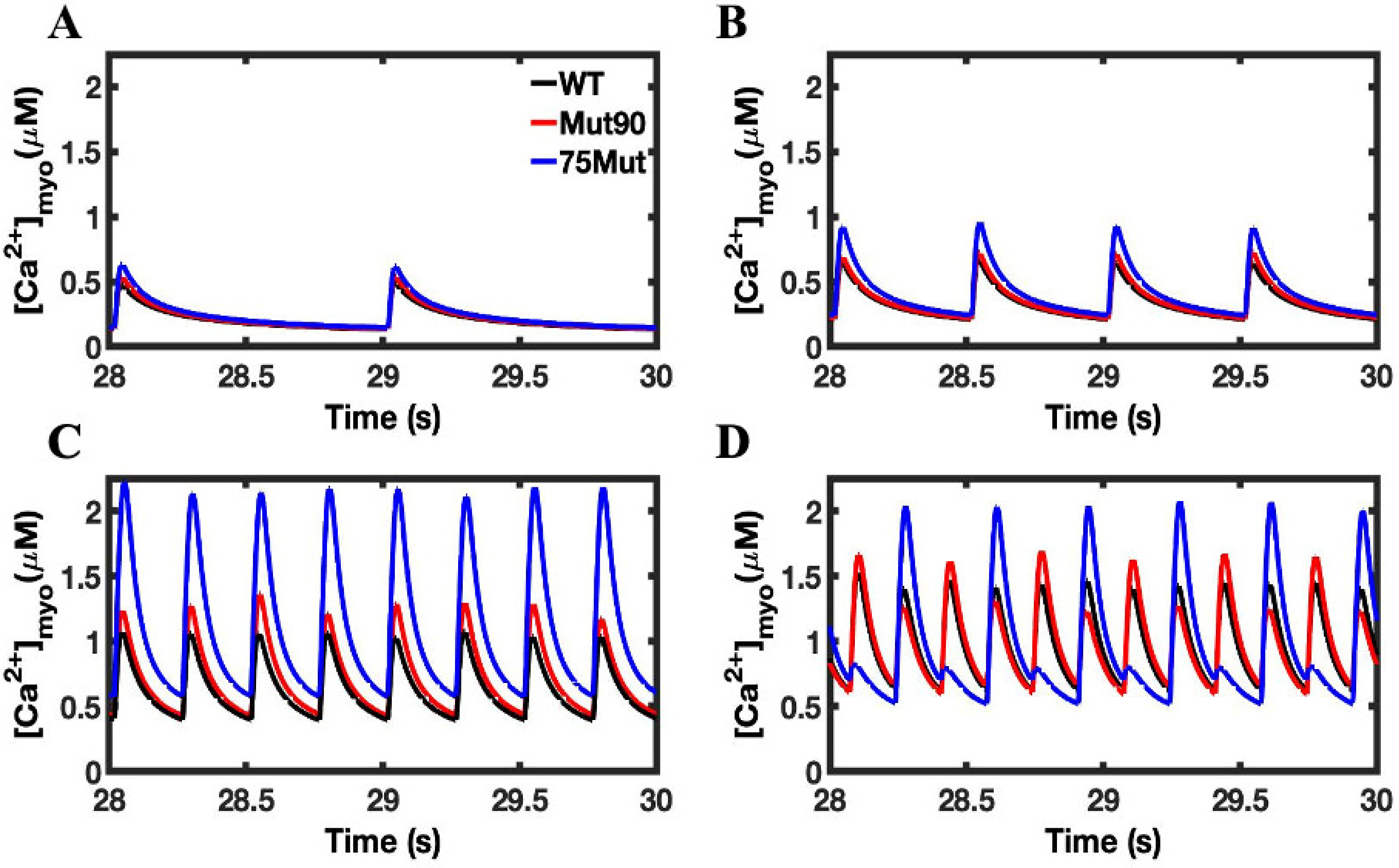
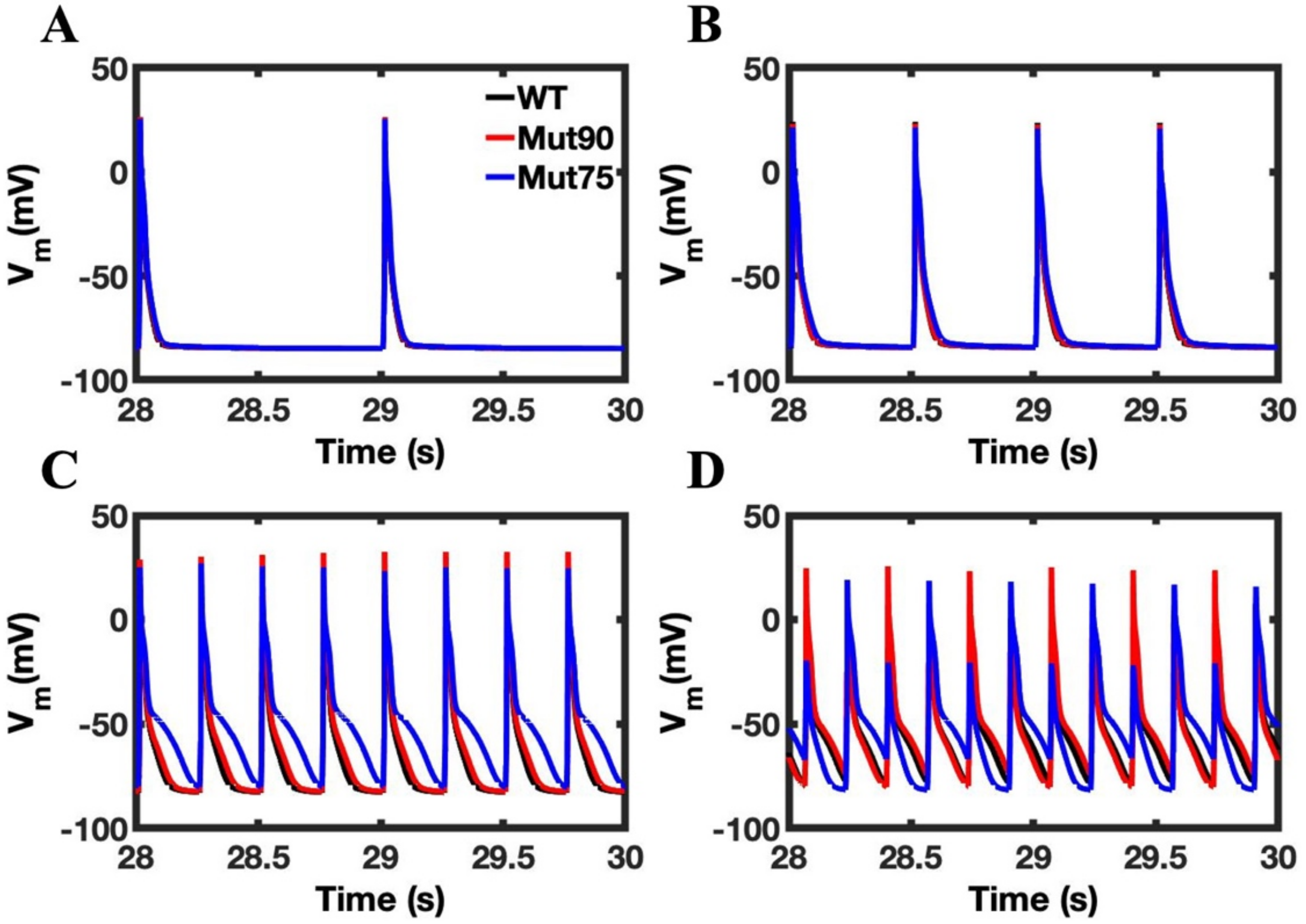
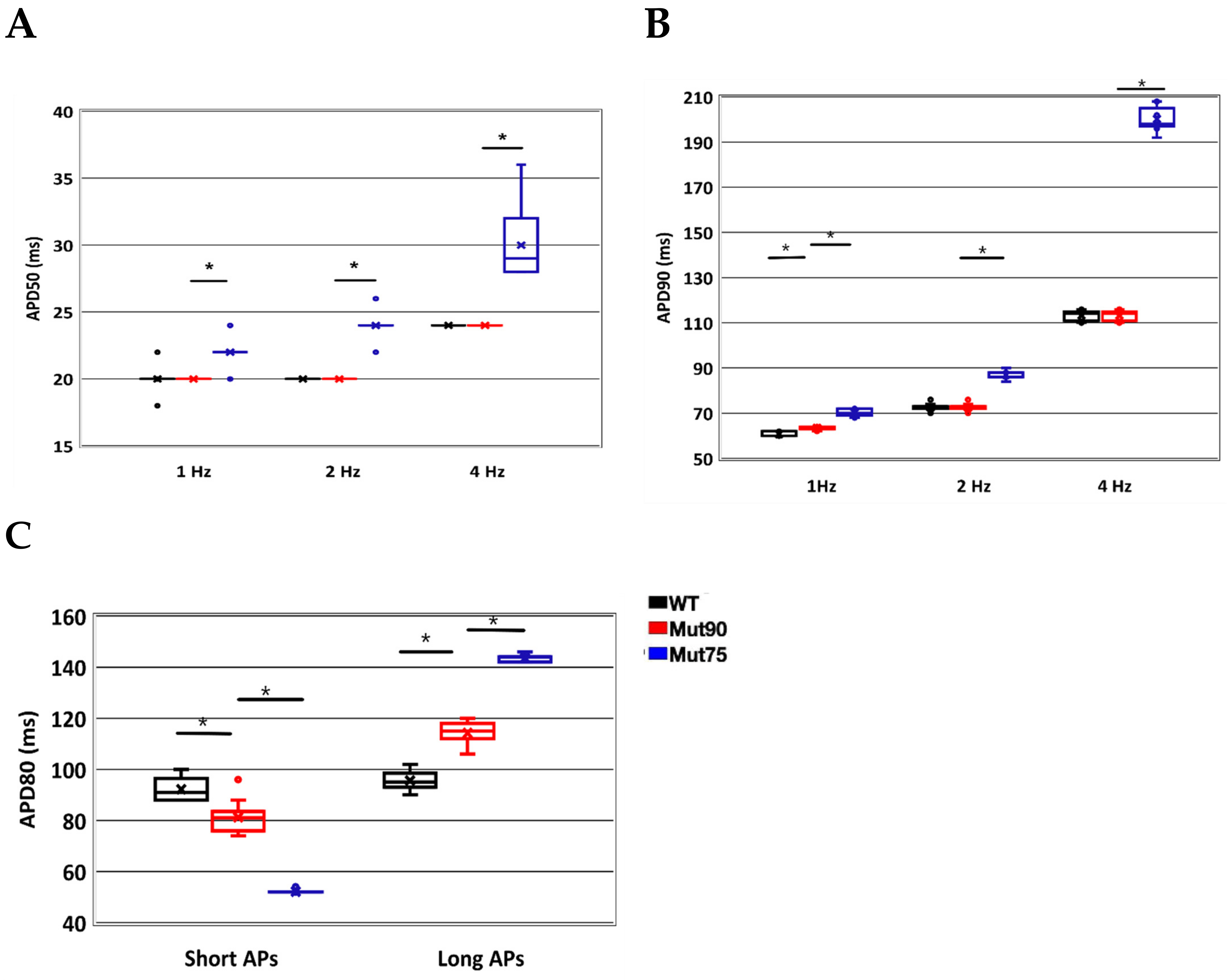
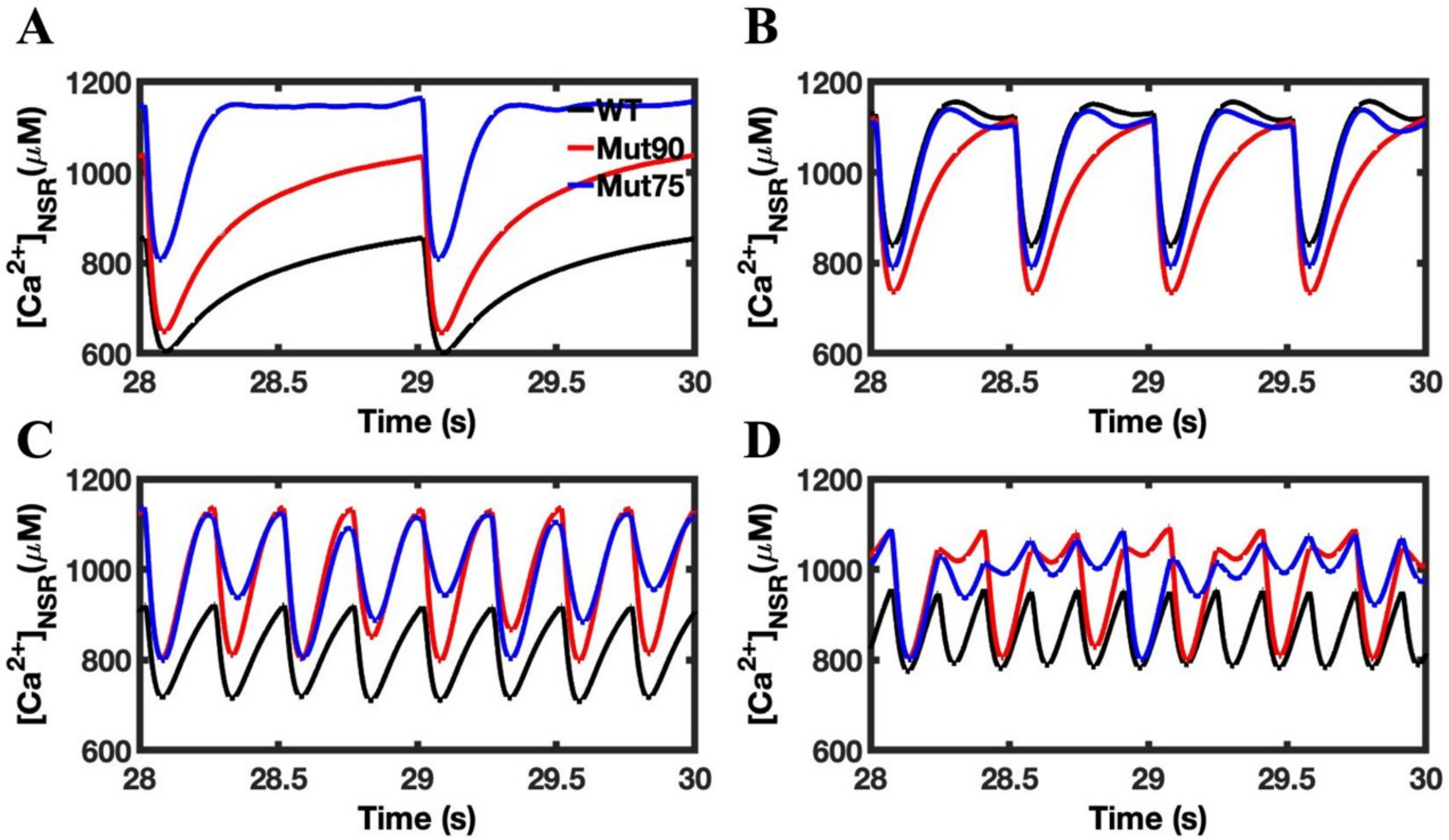
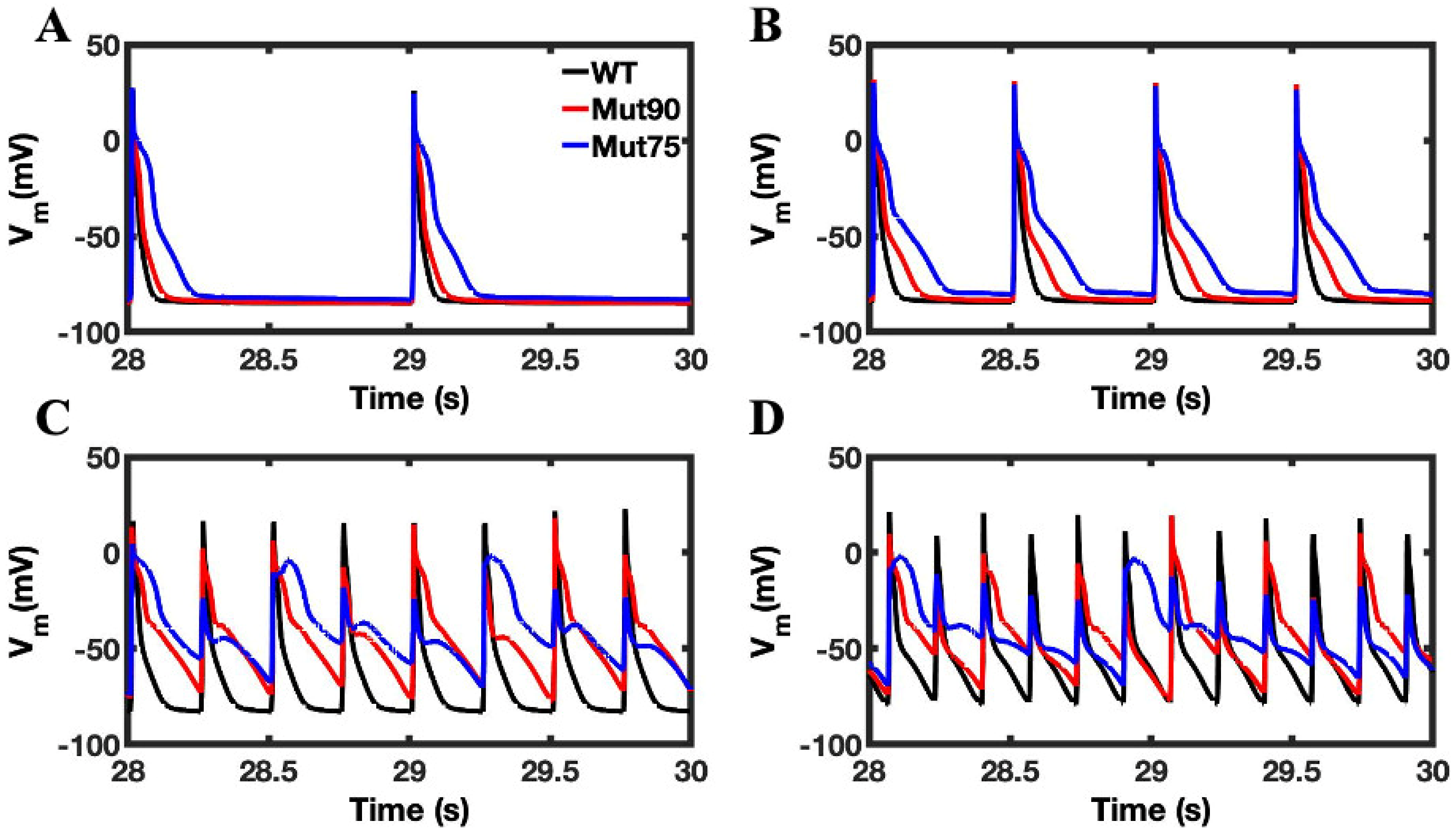
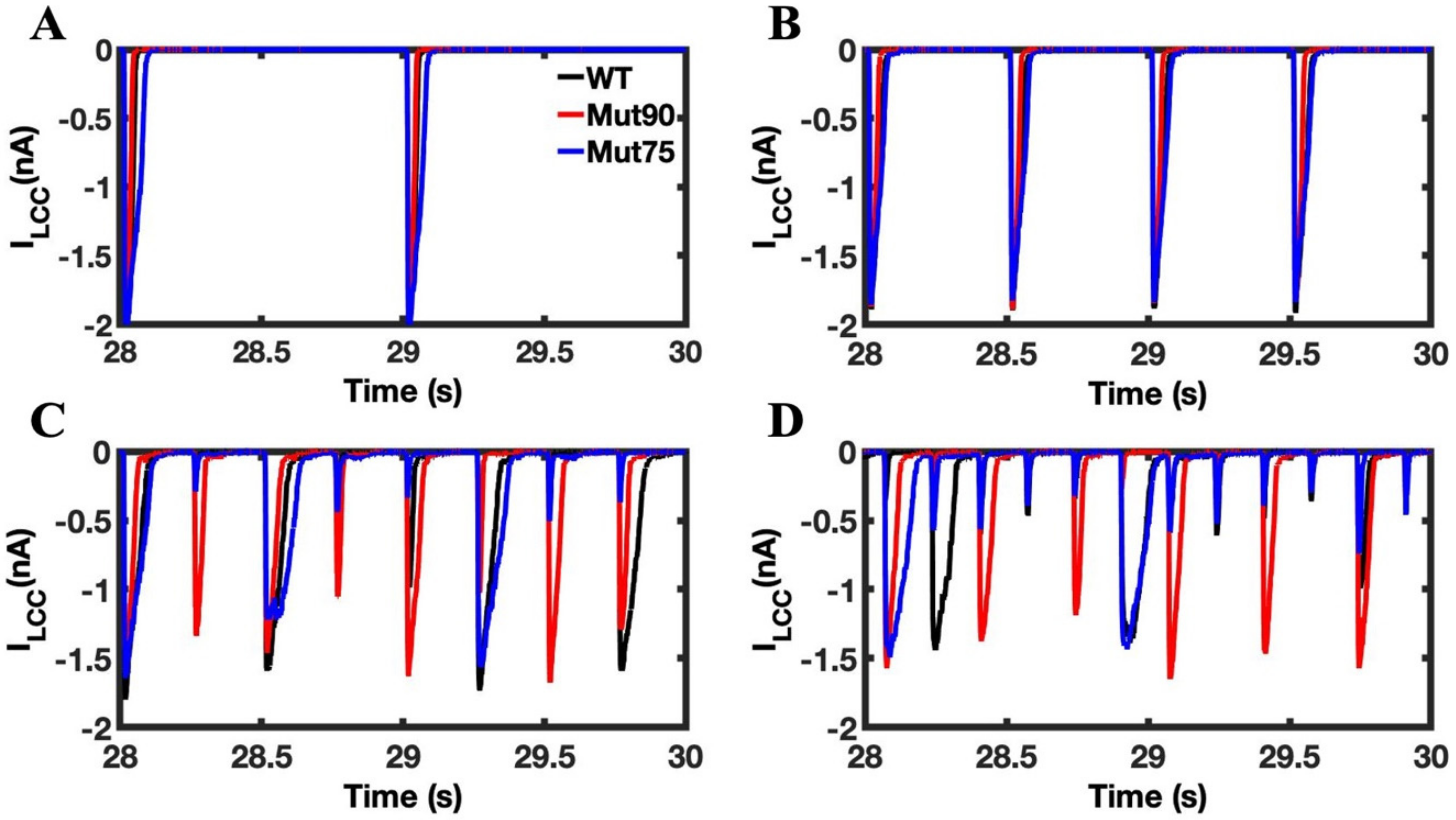
3.1. Reduction of L-Type Calcium Channel CDI Leads to Abnormal EC Coupling
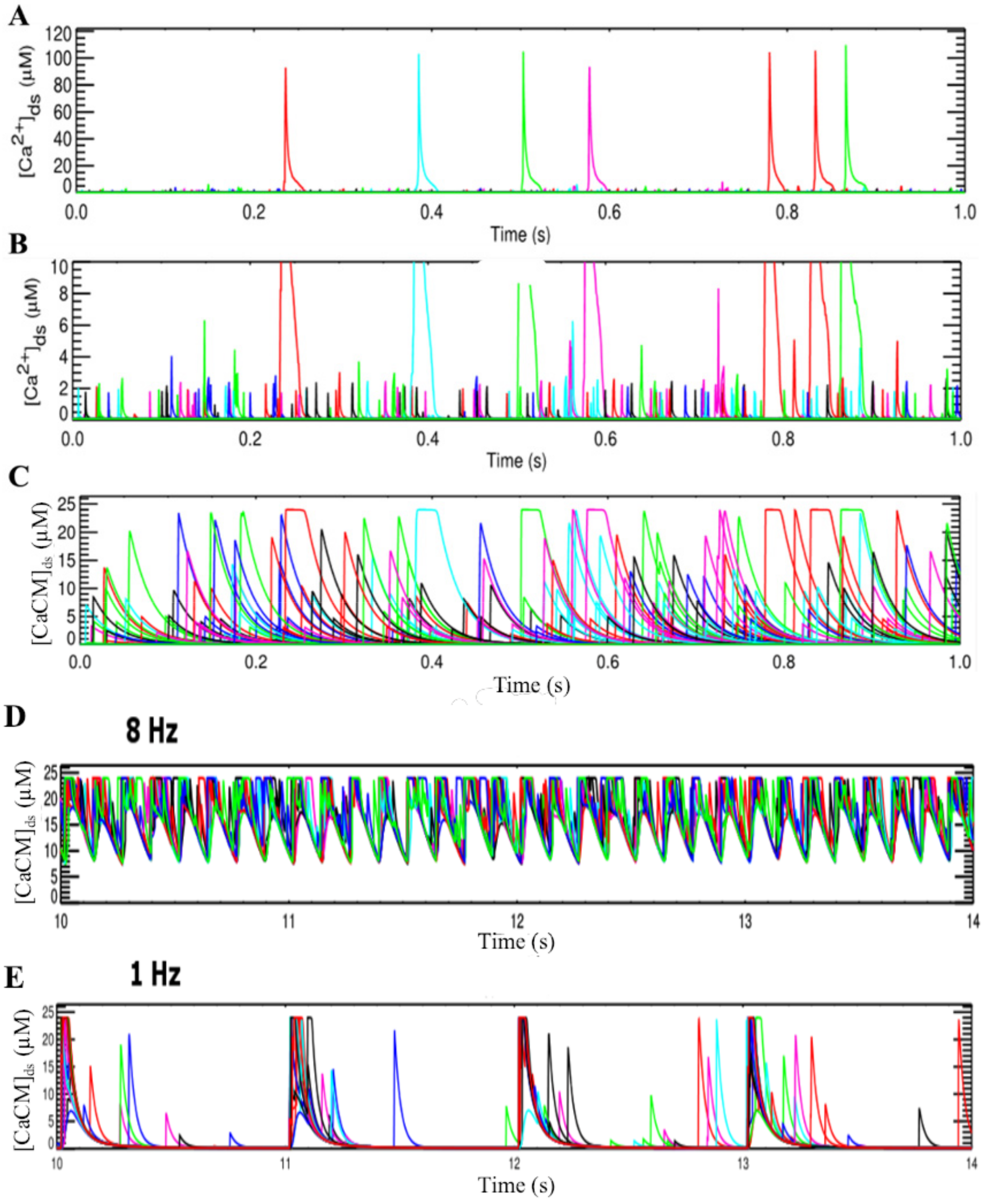
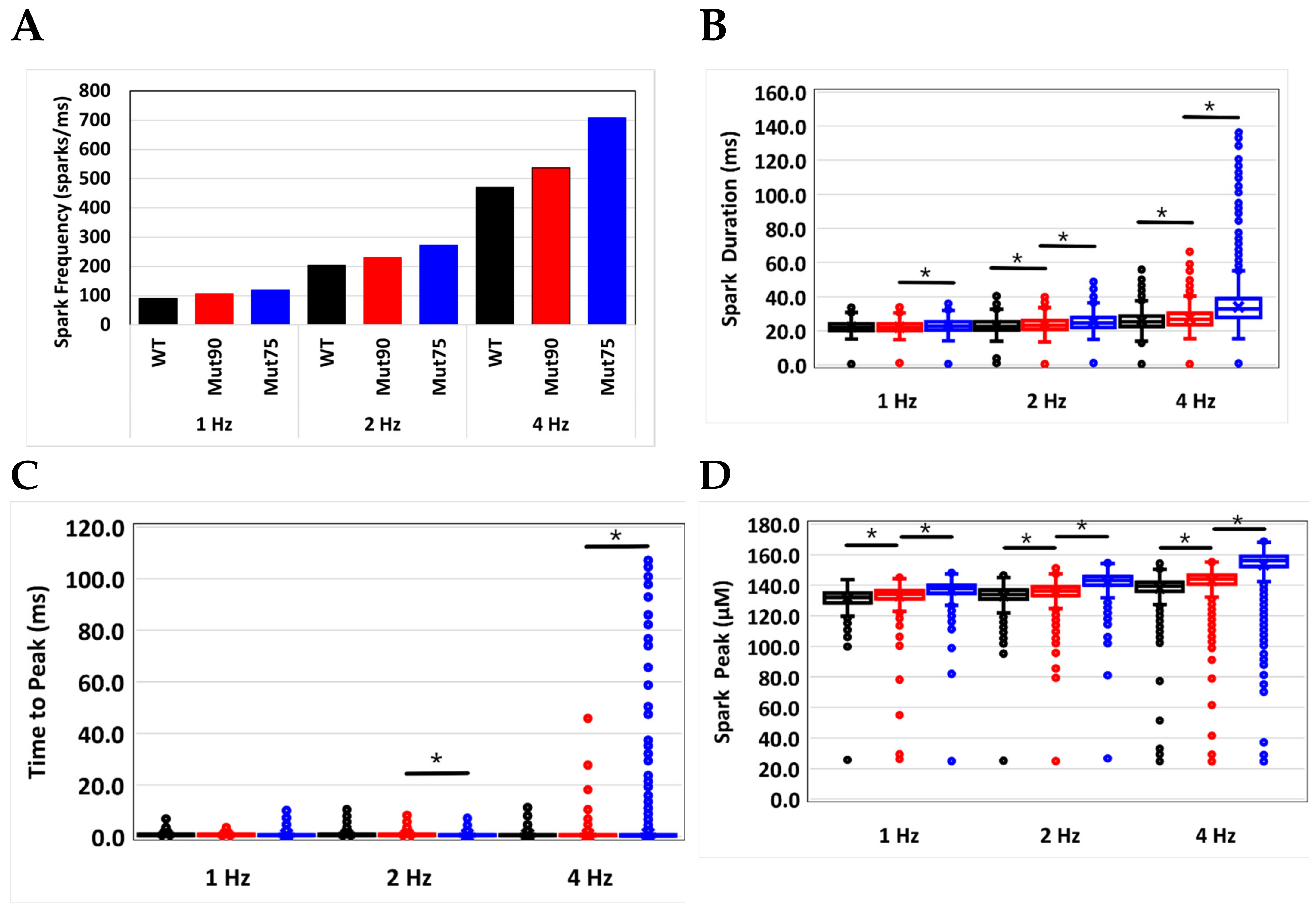
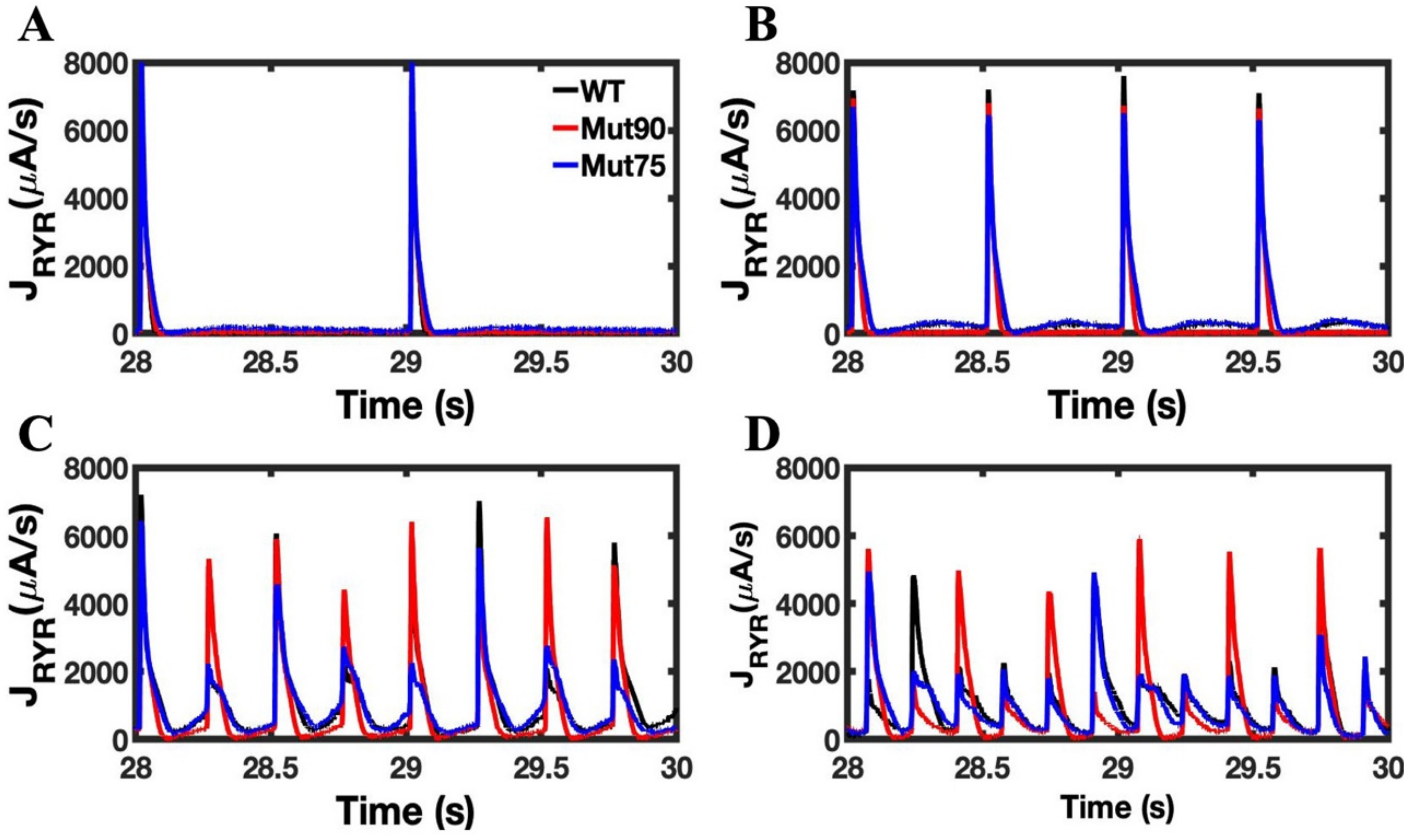
3.2. Changes in Ca2+ Spark Dynamics Underlie Arrhythmogenesis
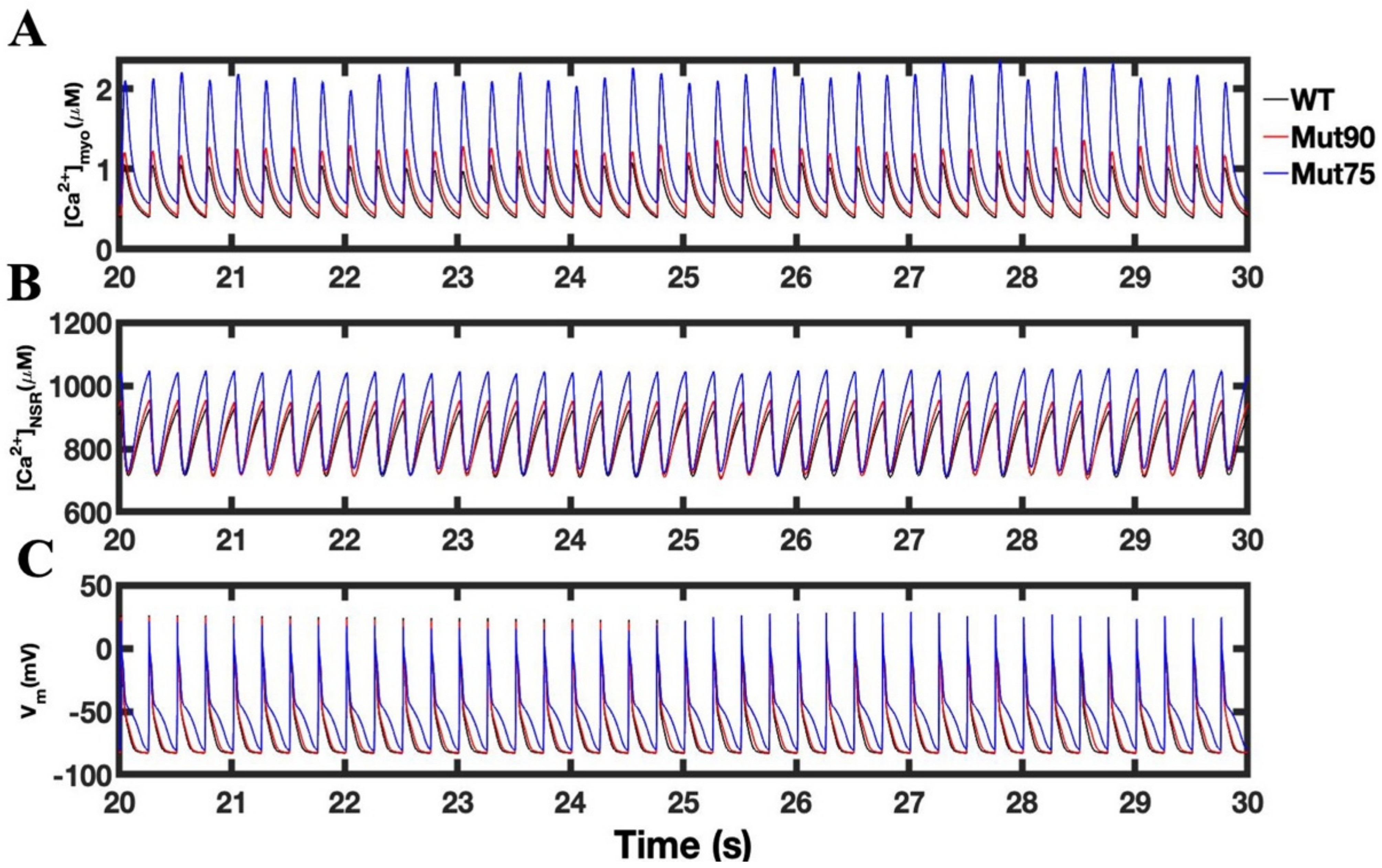
3.3. Beta-Adrenergic Stimulation Potentiates Ca2+ Overload in Myocytes with Reduced CDI
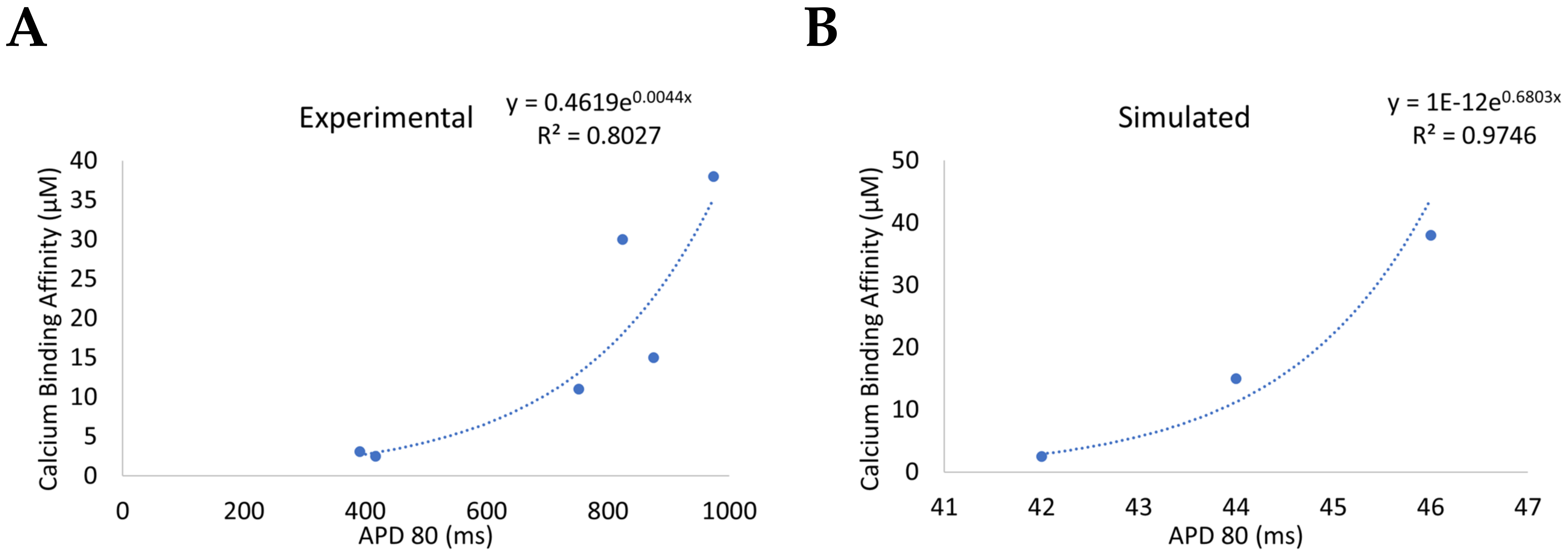
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chazin, W.J.; Johnson, C.N. Calmodulin Mutations Associated with Heart Arrhythmia: A Status Report. Int. J. Mol. Sci. 2020, 21, 1418. [Google Scholar] [CrossRef] [Green Version]
- Crotti, L.; Spazzolini, C.; Tester, D.J.; Ghidoni, A.; Baruteau, A.-E.; Beckmann, B.-M.; Behr, E.R.; Bennett, J.S.; Bezzina, C.R.; Bhuiyan, Z.A.; et al. Calmodulin mutations and life-threatening cardiac arrhythmias: Insights from the International Calmodulinopathy Registry. Eur. Heart J. 2019, 40, 2964–2975. [Google Scholar] [CrossRef] [PubMed]
- Jensen, H.H.; Brohus, M.; Nyegaard, M.; Overgaard, M.T. Human Calmodulin Mutations. Front. Mol. Neurosci. 2018, 11, 396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiménez-Jáimez, J.; Doza, J.P.; Ortega, Á.; Macías-Ruiz, R.; Perin, F.; del Rey, M.M.R.-V.; Ortiz-Genga, M.; Monserrat, L.; Barriales-Villa, R.; Blanca, E.; et al. Calmodulin 2 Mutation N98S Is Associated with Unexplained Cardiac Arrest in Infants Due to Low Clinical Penetrance Electrical Disorders. PLoS ONE 2016, 11, e0153851. [Google Scholar] [CrossRef]
- Tsai, W.-C.; Guo, S.; Olaopa, M.A.; Field, L.J.; Yang, J.; Shen, C.; Chang, C.-P.; Chen, P.-S.; Rubart, M. Complex Arrhythmia Syndrome in a Knock-In Mouse Model Carrier of the N98S Calm1 Mutation. Circulation 2020, 142, 1937–1955. [Google Scholar] [CrossRef] [PubMed]
- Søndergaard, M.T.; Liu, Y.; Larsen, K.T.; Nani, A.; Tian, X.; Holt, C.; Wang, R.; Wimmer, R.; Van Petegem, F.; Fill, M.; et al. The Arrhythmogenic Calmodulin p.Phe142Leu Mutation Impairs C-domain Ca2+ Binding but Not Calmodulin-dependent Inhibition of the Cardiac Ryanodine Receptor. J. Biol. Chem. 2017, 292, 1385–1395. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Hurtado, N.; Boczek, N.J.; Kryshtal, D.O.; Johnson, C.N.; Sun, J.; Nitu, F.R.; Cornea, R.L.; Chazin, W.J.; Calvert, M.L.; Tester, D.J.; et al. Novel CPVT-Associated Calmodulin Mutation in CALM3 (CALM3-A103V) Activates Arrhythmogenic Ca Waves and Sparks. Circ. Arrhythmia Electrophysiol. 2016, 9, e004161. [Google Scholar] [CrossRef] [Green Version]
- Yin, G.; Hassan, F.; Haroun, A.R.; Murphy, L.L.; Crotti, L.; Schwartz, P.J.; George, A.L.; Satin, J. Arrhythmogenic calmodulin mutations disrupt intracellular cardiomyocyte Ca2+ regulation by distinct mechanisms. J. Am. Heart Assoc. 2014, 3, e000996. [Google Scholar] [CrossRef] [Green Version]
- Brodland, G.W. How computational models can help unlock biological systems. Semin. Cell Dev. Biol. 2015, 47–48, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Tuszynski, J.A.; Winter, P.; White, D.; Tseng, C.-Y.; Sahu, K.K.; Gentile, F.; Spasevska, I.; Omar, S.I.; Nayebi, N.; Churchill, C.D.M.; et al. Mathematical and computational modeling in biology at multiple scales. Theor. Biol. Med. Model. 2014, 11, 52. [Google Scholar] [CrossRef]
- Hoang-Trong, T.M.; Ullah, A.; Jafri, M.S. Calcium Sparks in the Heart: Dynamics and Regulation. Res. Rep. Biol. 2015, 6, 203–214. [Google Scholar] [CrossRef] [Green Version]
- Jafri, M.S. Models of excitation-contraction coupling in cardiac ventricular myocytes. Methods Mol. Biol. 2012, 910, 309–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eisner, D.A.; Caldwell, J.L.; Kistamás, K.; Trafford, A.W. Calcium and Excitation-Contraction Coupling in the Heart. Circ. Res. 2017, 121, 181–195. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Lederer, W.J.J.; Cannell, M.B. Calcium Sparks: Elementary Events Underlying Excitation-Contraction Coupling in Heart Muscle. Science 1993, 262, 740–744. [Google Scholar] [CrossRef]
- Stuyvers, B.D.; Boyden, P.A.; Keurs, H.E.D.J. Calcium Waves. Physiological Relevance in Cardiac Function. Circ. Res. 2000, 86, 1016–1018. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Lederer, M.R.; Lederer, W.J.; Cannell, M.B. Calcium sparks and [Ca2+]i waves in cardiac myocytes. Am. J. Physiol. 1996, 270, C148–C159. [Google Scholar] [CrossRef] [PubMed]
- Capogrossi, M.C.; Houser, S.R.; Bahinski, A.; Lakatta, E.G. Synchronous occurrence of spontaneous localized calcium release from the sarcoplasmic reticulum generates action potentials in rat cardiac ventricular myocytes at normal resting membrane potential. Circ. Res. 1987, 61, 498–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miura, M.; Ishide, N.; Oda, H.; Sakurai, M.; Shinozaki, T.; Takishima, T. Spatial features of calcium transients during early and delayed afterdepolarizations. Am. J. Physiol. 1993, 265, H439–H444. [Google Scholar] [CrossRef]
- Sutanto, H.; Heijman, J. Integrative Computational Modeling of Cardiomyocyte Calcium Handling and Cardiac Arrhythmias: Current Status and Future Challenges. Cells 2022, 11, 1090. [Google Scholar] [CrossRef]
- Li, K.; Zhang, P. Clinical Advances in Congenital Long QT Syndrome. Cardiol. Discov. 2021, 1, 195–201. [Google Scholar] [CrossRef]
- Ponce-Balbuena, D.; Deschênes, I. Long QT syndrome—Bench to bedside. Heart Rhythm O2 2021, 2, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Wallace, E.; Howard, L.; Liu, M.; O’Brien, T.; Ward, D.; Shen, S.; Prendiville, T. Long QT Syndrome: Genetics and Future Perspective. Pediatr. Cardiol. 2019, 40, 1419–1430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sumitomo, N. Current topics in catecholaminergic polymorphic ventricular tachycardia. J. Arrhythmia 2016, 32, 344–351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ozawa, J.; Ohno, S.; Fujii, Y.; Makiyama, T.; Suzuki, H.; Saitoh, A.; Horie, M. Differential Diagnosis Between Catecholaminergic Polymorphic Ventricular Tachycardia and Long QT Syndrome Type 1—Modified Schwartz Score. Circ. J. Off. J. Jpn. Circ. Soc. 2018, 82, 2269–2276. [Google Scholar] [CrossRef] [Green Version]
- Saito, A.; Ohno, S.; Nuruki, N.; Nomura, Y.; Horie, M.; Yoshinaga, M. Three cases of catecholaminergic polymorphic ventricular tachycardia with prolonged QT intervals including two cases of compound mutations. J. Arrhythmia 2018, 34, 291–293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nyegaard, M.; Overgaard, M.T.; Søndergaard, M.T.; Vranas, M.; Behr, E.R.; Hildebrandt, L.L.; Børglum, A.D. Mutations in Calmodulin Cause Ventricular Tachycardia and Sudden Cardiac Death. Am. J. Hum. Genet. 2012, 91, 703–712. [Google Scholar] [CrossRef] [Green Version]
- Crotti, L.; Johnson, C.N.; Graf, E.; De Ferrari, G.M.; Cuneo, B.F.; Ovadia, M.; George, A.L. Calmodulin mutations associated with recurrent cardiac arrest in infants. Circulation 2013, 127, 1009–1017. [Google Scholar] [CrossRef] [Green Version]
- Makita, N.; Yagihara, N.; Crotti, L.; Johnson, C.N.; Beckmann, B.-M.; Roh, M.S.; Shigemizu, D.; Lichtner, P.; Ishikawa, T.; Aiba, T.; et al. Novel calmodulin mutations associated with congenital arrhythmia susceptibility. Circ. Cardiovasc. Genet. 2014, 7, 466–474. [Google Scholar] [CrossRef] [Green Version]
- Marsman, R.; Barc, J.; Beekman, L.; Alders, M.; Dooijes, D.; van den Wijngaard, A.; Ratbi, I.; Sefiani, A.; Bhuiyan, Z.; Wilde, A.; et al. A mutation in CALM1 encoding calmodulin in familial idiopathic ventricular fibrillation in childhood and adolescence. J. Am. Coll. Cardiol. 2014, 63, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Reed, G.; Boczek, N.; Etheridge, S.; Ackerman, M. CALM3 mutation associated with long QT syndrome. Heart Rhythm 2015, 12, 419–422. [Google Scholar] [CrossRef]
- Limpitikul, W.; Dick, I.; Joshi-Mukherjee, R.; Overgaard, M.; George, A.J.; Yue, D. Calmodulin mutations associated with long QT syndrome prevent inactivation of cardiac L-type Ca(2+) currents and promote proarrhythmic behavior in ventricular myocytes. J. Mol. Cell. Cardiol. 2014, 74, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.S.; Nitu, F.R.; Yang, Y.; Walweel, K.; Pereira, L.; Johnson, C.N.; Faggioni, M.; Chazin, W.J.; Laver, D.; George, A.L.; et al. Divergent regulation of ryanodine receptor 2 calcium release channels by arrhythmogenic human calmodulin missense mutants. Circ. Res. 2014, 114, 1114–1124. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Hurtado, N.; Kryshtal, D.; Hwang, H.; Johnson, C.; Chazin, W.; Boczek, N.; Tester, D.; Ye, D.; Will, M.; Ackerman, M.; et al. Calmodulin Mutation (CALM1-E141G) Associated with Long QT Syndrome Disrupts Calmodulin Calcium Binding and Impairs L-Type Ca Channel Inactivation. Heart Rhythm 2014, 11, 2135–2136. [Google Scholar] [CrossRef]
- Hoang-Trong, M.T.; Ullah, A.; Lederer, W.J.; Jafri, M.S. Cardiac Alternans Occurs through the Synergy of Voltage- and Calcium-Dependent Mechanisms. Membranes 2021, 11, 794. [Google Scholar] [CrossRef] [PubMed]
- Sobie, E.A.; Dilly, K.W.; dos Santos Cruz, J.; Lederer, W.J.; Jafri, M.S. Termination of Cardiac Ca2+ Sparks: An Investigative Mathematical Model of Calcium-Induced Calcium Release. Biophys. J. 2002, 83, 59–78. [Google Scholar] [CrossRef] [Green Version]
- Groff, J.R.; Smith, G.D. Ryanodine receptor allosteric coupling and the dynamics of calcium sparks. Biophys. J. 2008, 95, 135–154. [Google Scholar] [CrossRef] [Green Version]
- Brette, F.; Leroy, J.; Le Guennec, J.Y.; Salle, L. Ca2+ currents in cardiac myocytes: Old story, new insights. Prog. Biophys. Mol. Biol. 2006, 91, 1–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scriven, D.R.; Dan, P.; Moore, E.D. Distribution of proteins implicated in excitation-contraction coupling in rat ventricular myocytes. Biophys. J. 2000, 79, 2682–2691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walweel, K.; Gomez-Hurtado, N.; Rebbeck, R.T.; Oo, Y.W.; Beard, N.A.; Molenaar, P.; dos Remedios, C.; van Helden, D.F.; Cornea, R.L.; Knollmann, B.C.; et al. Calmodulin inhibition of human RyR2 channels requires phosphorylation of RyR2-S2808 or RyR2-S2814. J. Mol. Cell. Cardiol. 2019, 130, 96–106. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Fan, J.S.; Clark, J.W.; Palade, P.T. A model of the L-type Ca2+ channel in rat ventricular myocytes: Ion selectivity and inactivation mechanisms. J. Physiol. 2000, 529 Pt 1, 139–158. [Google Scholar] [CrossRef]
- Wagner, E.; Lauterbach, M.A.; Kohl, T.; Westphal, V.; Williams, G.S.B.; Steinbrecher, J.H.; Strreich, J.-H.; Korff, B.; Tuan, H.-T.M.; Hagen, B.; et al. Stimulation emission depletion live-cell super-resolution imaging shows proliferative remodeling of T-tubule membrane structures after myocardial infraction. Circ. Res. 2012, 111, 402–414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jurado, L.A.; Chockalingam, P.S.; Jarrett, H.W. Apocalmodulin. Physiol. Rev. 2009, 79, 661–682. [Google Scholar] [CrossRef]
- Halling, D.B.; Aracena-Parks, P.; Hamilton, S.L. Regulation of voltage-gated Ca2+ channels by calmodulin. Sci. STKE Signal Transduct. Knowl. Environ. 2005, 2005, re15. [Google Scholar] [CrossRef]
- Banerjee, R.; Yoder, J.B.; Yue, D.T.; Amzel, L.M.; Tomaselli, G.F.; Gabelli, S.B.; Ben-Johny, M. Bilobal architecture is a requirement for calmodulin signaling to Ca(V)1.3 channels. Proc. Natl. Acad. Sci. USA 2018, 115, E3026–E3035. [Google Scholar] [CrossRef] [Green Version]
- Afshar, Y.; Schmid, F.; Pishevar, A.; Worley, S. Exploiting seeding of random number generators for efficient domain decomposition parallelization of dissipative particle dynamics. Comput. Phys. Commun. 2013, 184, 1119–1128. [Google Scholar] [CrossRef]
- DeRemigio, H.; LaMar, M.D.; Kemper, P.; Smith, G.D. Markov chain models of coupled calcium channels: Kronecker representations and iterative solution methods. Phys. Biol. 2008, 5, 036003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, G.D. Modeling the Stochastic Gating of Ion Channels. Interdisciplinary Applied Mathematics. In Computational Cell Biology; Fall, C.P., Marland, E.S., Wagner, J.M., Tyson, J.J., Eds.; Springer: New York, NY, USA, 2002; Volume 20, pp. 285–319. [Google Scholar]
- Kadam, P.; Bhalerao, S. Sample size calculation. Int. J. Ayurveda Res. 2010, 1, 55–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wescott, A.P.; Jafri, M.S.; Lederer, W.J.; Williams, G.S. Ryanodine receptor sensitivity governs the stability and synchrony of local calcium release during cardiac excitation-contraction coupling. J. Mol. Cell Cardiol. 2016, 92, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Hilliard, F.A.; Steele, D.S.; Laver, D.; Yang, Z.; Le Marchand, S.J.; Chopra, N.; Piston, D.W.; Huke, S.; Knollmann, B.C. Flecainide inhibits arrhythmogenic Ca2+ waves by open state block of ryanodine receptor Ca2+ release channels and reduction of Ca2+ spark mass. J. Mol. Cell Cardiol. 2010, 48, 293–301. [Google Scholar] [CrossRef] [Green Version]
- Sikkel, M.B.; Collins, T.P.; Rowlands, C.; Shah, M.; O’Gara, P.; Williams, A.J.; Harding, S.E.; Lyon, A.R.; MacLeod, K.T. Flecainide reduces Ca2+ spark and wave frequency via inhibition of the sarcolemmal sodium current. Cardiovasc. Res. 2013, 98, 286–296. [Google Scholar] [CrossRef]
- Macquaide, N.; Tuan, H.T.; Hotta, J.; Sempels, W.; Lenaerts, I.; Holemans, P.; Hofkens, J.; Jafri, M.S.; Willems, R.; Sipido, K.R. Ryanodine receptor cluster fragmentation and redistribution in persistent atrial fibrillation enhance calcium release. Cardiovasc. Res. 2015, 108, 387–398. [Google Scholar] [CrossRef] [Green Version]
- Hove-Madsen, L.; Llach, A.; Bayes-Genís, A.; Roura, S.; Font, E.R.; Arís, A.; Cinca, J. Atrial Fibrillation Is Associated With Increased Spontaneous Calcium Release From the Sarcoplasmic Reticulum in Human Atrial Myocytes. Circulation 2004, 110, 1358–1363. [Google Scholar] [CrossRef] [Green Version]
- Badone, B.; Ronchi, C.; Kotta, M.-C.; Sala, L.; Ghidoni, A.; Crotti, L.; Zaza, A. Calmodulinopathy: Functional Effects of CALM Mutations and Their Relationship with Clinical Phenotypes. Front. Cardiovasc. Med. 2018, 5, 176. [Google Scholar] [CrossRef] [Green Version]
- Ledford, H.A.; Park, S.; Muir, D.; Woltz, R.L.; Ren, L.; Nguyen, P.T.; Sirish, P.; Wang, W.; Sihn, C.-R.; George, A.L., Jr.; et al. Different arrhythmia-associated calmodulin mutations have distinct effects on cardiac SK channel regulation. J. Gen. Physiol. 2020, 152, e202012667. [Google Scholar] [CrossRef]
- Wang, Z.; Vermij, S.H.; Sottas, V.; Shestak, A.; Ross-Kaschitza, D.; Zaklyazminskaya, E.V.; Hudmon, A.; Pitt, G.S.; Rougier, J.-S.; Abriel, H. Calmodulin binds to the N-terminal domain of the cardiac sodium channel Nav1.5. Channels 2020, 14, 268–286. [Google Scholar] [CrossRef]
- Kang, P.W.; Chakouri, N.; Diaz, J.; Tomaselli, G.F.; Yue, D.T.; Ben-Johny, M. Elementary mechanisms of calmodulin regulation of Na(V)1.5 producing divergent arrhythmogenic phenotypes. Proc. Natl. Acad. Sci. USA 2021, 118, e2025085118. [Google Scholar] [CrossRef]
- Němec, J.; Kim, J.J.; Salama, G. The link between abnormal calcium handling and electrical instability in acquired long QT syndrome--Does calcium precipitate arrhythmic storms? Prog. Biophys. Mol. Biol. 2016, 120, 210–221. [Google Scholar] [CrossRef] [Green Version]
- Giudicessi, J.R.; Ackerman, M.J. Calcium Revisited: New Insights into the Molecular Basis of Long-QT Syndrome. Circ. Arrhythmia Electrophysiol. 2016, 9, e002480. [Google Scholar] [CrossRef]
- Lin, D.-J.; Lee, W.-S.; Chien, Y.-C.; Chen, T.-Y.; Yang, K.-T. The link between abnormalities of calcium handling proteins and catecholaminergic polymorphic ventricular tachycardia. Tzu-Chi Med. J. 2021, 33, 323–331. [Google Scholar] [CrossRef]
- McCoy, M.D.; Hamre, J., 3rd; Klimov, D.K.; Jafri, M.S. Predicting Genetic Variation Severity Using Machine Learning to Interpret Molecular Simulations. Biophys. J. 2021, 120, 189–204. [Google Scholar] [CrossRef]
- Tadross, M.R.; Dick, I.E.; Yue, D.T. Mechanism of Local and Global Ca<sup>2+</sup> Sensing by Calmodulin in Complex with a Ca2+ Channel. Cell 2008, 133, 1228–1240. [Google Scholar] [CrossRef] [Green Version]
- Lai, M.; Brun, D.; Edelstein, S.J.; Le Novère, N. Modulation of calmodulin lobes by different targets: An allosteric model with hemiconcerted conformational transitions. PLoS Comput. Biol. 2015, 11, e1004063. [Google Scholar] [CrossRef] [Green Version]
- Limpitikul, W.B.; Greenstein, J.L.; Yue, D.T.; Dick, I.E.; Winslow, R.L. A bilobal model of Ca2+-dependent inactivation to probe the physiology of L-type Ca2+ channels. J. Gen. Physiol. 2018, 150, 1688–1701. [Google Scholar] [CrossRef] [Green Version]
- Kernik, D.C.; Yang, P.-C.; Kurokawa, J.; Wu, J.C.; Clancy, C.E. A computational model of induced pluripotent stem-cell derived cardiomyocytes for high throughput risk stratification of KCNQ1 genetic variants. PLoS Comput. Biol. 2020, 16, e1008109. [Google Scholar] [CrossRef]
- Bai, J.; Wang, K.; Liu, Y.; Li, Y.; Liang, C.; Luo, G.; Dong, S.; Yuan, Y.; Zhang, H. Computational Cardiac Modeling Reveals Mechanisms of Ventricular Arrhythmogenesis in Long QT Syndrome Type 8: CACNA1C R858H Mutation Linked to Ventricular Fibrillation. Front. Physiol. 2017, 8, 771. [Google Scholar] [CrossRef]
- Sadrieh, A.; Domanski, L.; Pitt-Francis, J.; Mann, S.A.; Hodkinson, E.C.; Ng, C.A.; Perry, M.D.; Taylor, J.A.; Gavaghan, D.; Subbiah, R.N.; et al. Multiscale cardiac modelling reveals the origins of notched T waves in long QT syndrome type 2. Nat. Commun. 2014, 5, 5069. [Google Scholar] [CrossRef] [Green Version]
- Grandi, E.; Puglisi, J.L.; Bers, D.M.; Severi, S. Compound mutations in Long QT syndrome assessed by a computer model. In Proceedings of the 2006 Conference on Computers in Cardiology, Valencia, Spain, 17–20 September 2006; pp. 201–204. [Google Scholar]
- Hoang-Trong, T.M.; Ullah, A.; Lederer, W.J.; Jafri, M.S. A Stochastic Spatiotemporal Model of Rat Ventricular Myocyte Calcium Dynamics Demonstrated Necessary Features for Calcium Wave Propagation. Membranes 2021, 11, 989. [Google Scholar] [CrossRef]



| Mutation * | Disease Association | Structural Domain | Activity Change | Functional Change | Ca2+ Binding Affinity | Ca2+-Dependent Inactivation ** | CaM1 | CaM2 | CaM3 |
|---|---|---|---|---|---|---|---|---|---|
| WT | none | none | none | 2.5 µM | k24 | ||||
| N54I | CPVT4 | EF Hand II adjacent | Small increase in Calcium binding in C-lobe | Significantly increased calcium waves | 3.1 µM | 0.99 × k24 | x | ||
| F90L | IVF | EF Hand III adjacent | Mediates interaction with target peptides | x | |||||
| D96V | LQT14 | EF Hand III | Moderate/High disruption of Calcium binding | Increased AP; depress LTCC inactivation | 38.0 µM | 0.74 × k24 | x | ||
| N98S | CPVT4; LQT14 | EF Hand III | Significant reduction in calcium binding | RYR2 binding disrupted at low Ca2+ | 11.0 µM | 0.92 × k24 | x | x | |
| N98I | LQT14 | EF Hand III | Reduced calcium binding | Increased RYR open probability | x | ||||
| A103V | CPVT4 | EF Hand III | x | ||||||
| D130G | LQT14 | EF Hand IV | Reduced calcium binding | Reduced RYR2 binding affinity; increased AP; impaired LTCC inactivation | 150.0 µM | 0.41 × k24 | x | x | |
| D132E | CPVT4; LQT14 | EF Hand IV | Reduced calcium binding | x | |||||
| D134H | LQT14 | EF Hand IV | Reduced calcium binding | x | |||||
| Q136P | CPVT4; LQT14 | EF Hand IV | Reduced calcium binding | x | |||||
| E141G | LQT14 | EF Hand IV adjacent | Reduced calcium binding | Impaired LTCC inactivation | x | ||||
| F142L | LQT14 | EF Hand IV adjacent | Reduced calcium binding | Reduced RYR2 binding affinity; increased AP; depress LTCC inactivation; Alter energetic coupling in C-lobe conformational dynamics | 15.0 µM | 0.89 × k24 | x | x |
| Variables | Value | Unit |
|---|---|---|
| Calmodulin | 2.4d1 | µM |
| 3.0d1 | 1/(µM.s) | |
| 7.14d1 | 1/s |
| Frequency | 1 Hz | 2 Hz | 4 Hz | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variant | WT | Mut90 | Mut75 | WT | Mut90 | Mut75 | WT | Mut90 | Mut75 |
| Spark Frequency (sparks/ms) | 89.6 | 105.9 | 119.5 | 204 | 229 | 272.9 | 470.7 | 536.5 | 707.9 |
| Spark Duration (ms) | 22.2 | 22.1 | 23.1 | 23.0 | 23.6 | 25.0 | 25.7 | 27.3 | 34.1 |
| Time to Peak (ms) | 0.78 | 0.74 | 0.73 | 0.75 | 0.75 | 0.68 | 0.71 | 0.70 | 1.02 |
| Peak Amplitude (µM) | 131.4 | 133.1 | 137.0 | 133.2 | 135.5 | 142.3 | 138.2 | 143.0 | 153.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCoy, M.D.; Ullah, A.; Lederer, W.J.; Jafri, M.S. Understanding Calmodulin Variants Affecting Calcium-Dependent Inactivation of L-Type Calcium Channels through Whole-Cell Simulation of the Cardiac Ventricular Myocyte. Biomolecules 2023, 13, 72. https://doi.org/10.3390/biom13010072
McCoy MD, Ullah A, Lederer WJ, Jafri MS. Understanding Calmodulin Variants Affecting Calcium-Dependent Inactivation of L-Type Calcium Channels through Whole-Cell Simulation of the Cardiac Ventricular Myocyte. Biomolecules. 2023; 13(1):72. https://doi.org/10.3390/biom13010072
Chicago/Turabian StyleMcCoy, Matthew D., Aman Ullah, W. Jonathan Lederer, and M. Saleet Jafri. 2023. "Understanding Calmodulin Variants Affecting Calcium-Dependent Inactivation of L-Type Calcium Channels through Whole-Cell Simulation of the Cardiac Ventricular Myocyte" Biomolecules 13, no. 1: 72. https://doi.org/10.3390/biom13010072
APA StyleMcCoy, M. D., Ullah, A., Lederer, W. J., & Jafri, M. S. (2023). Understanding Calmodulin Variants Affecting Calcium-Dependent Inactivation of L-Type Calcium Channels through Whole-Cell Simulation of the Cardiac Ventricular Myocyte. Biomolecules, 13(1), 72. https://doi.org/10.3390/biom13010072







