Alteration of Average Thickness of Lipid Bilayer by Membrane-Deforming Inclusions
Abstract
:1. Introduction
2. Methods
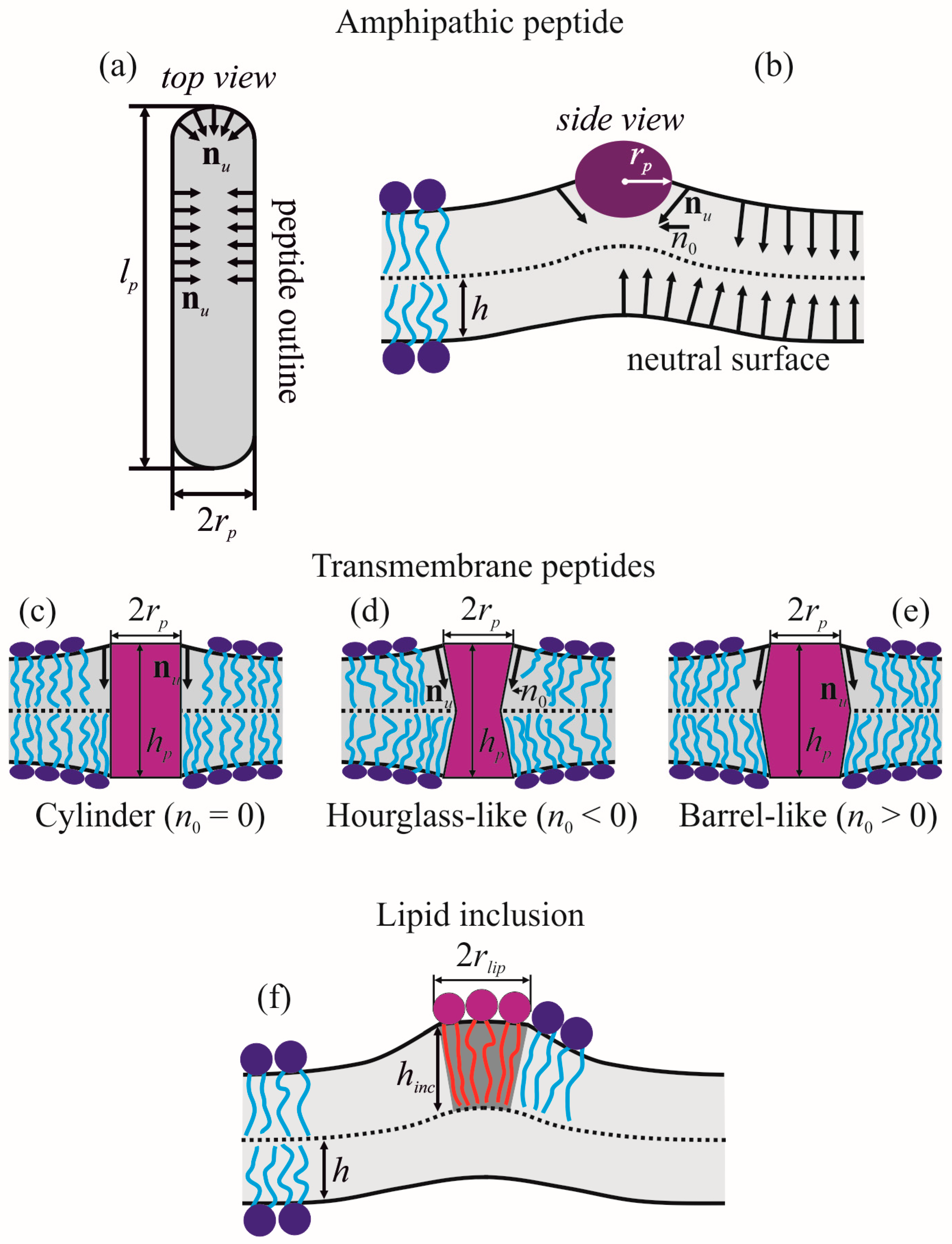
2.1. Amphipathic Peptide
2.2. Transmembrane Peptide
2.3. Lipid Inclusion
2.4. Parameters
3. Results
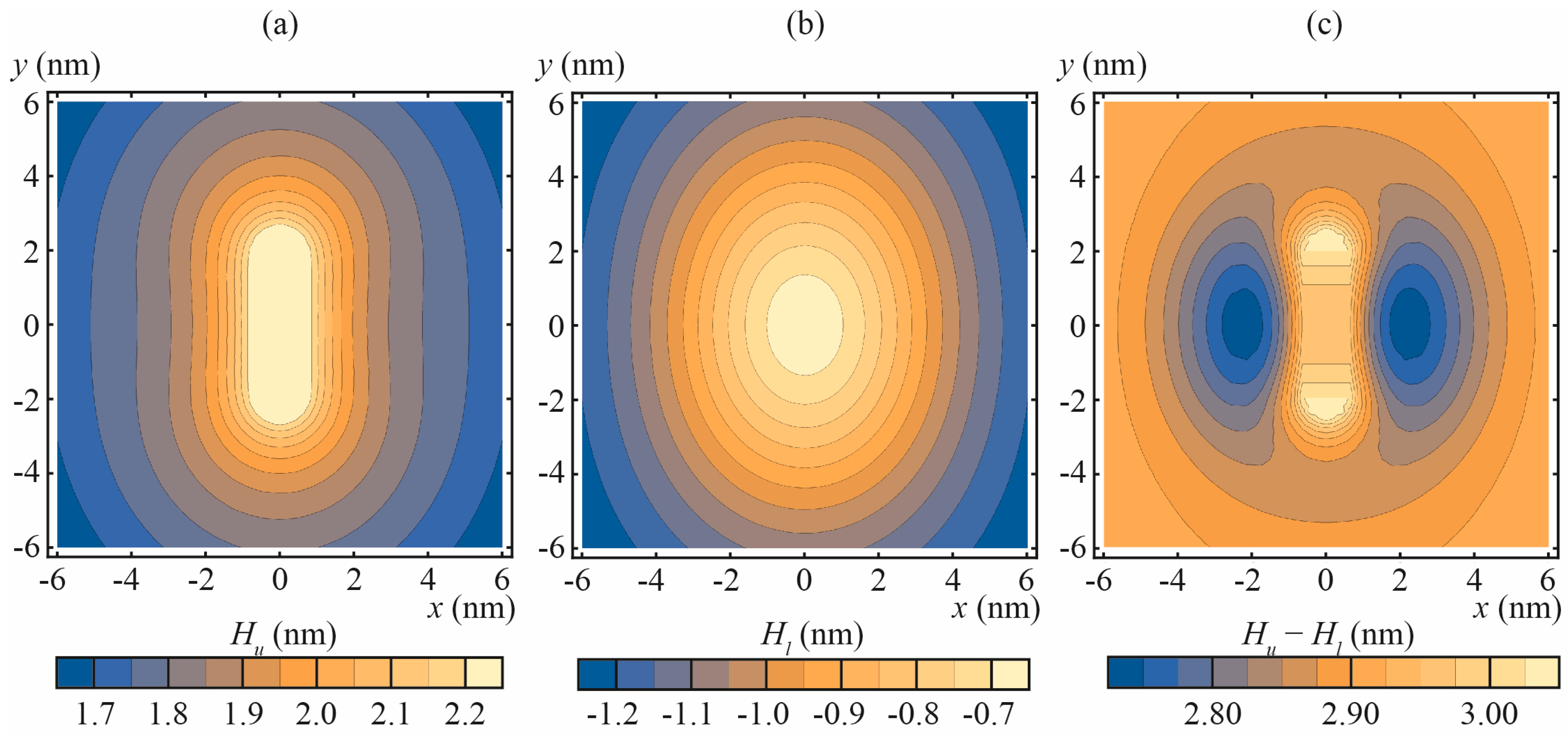
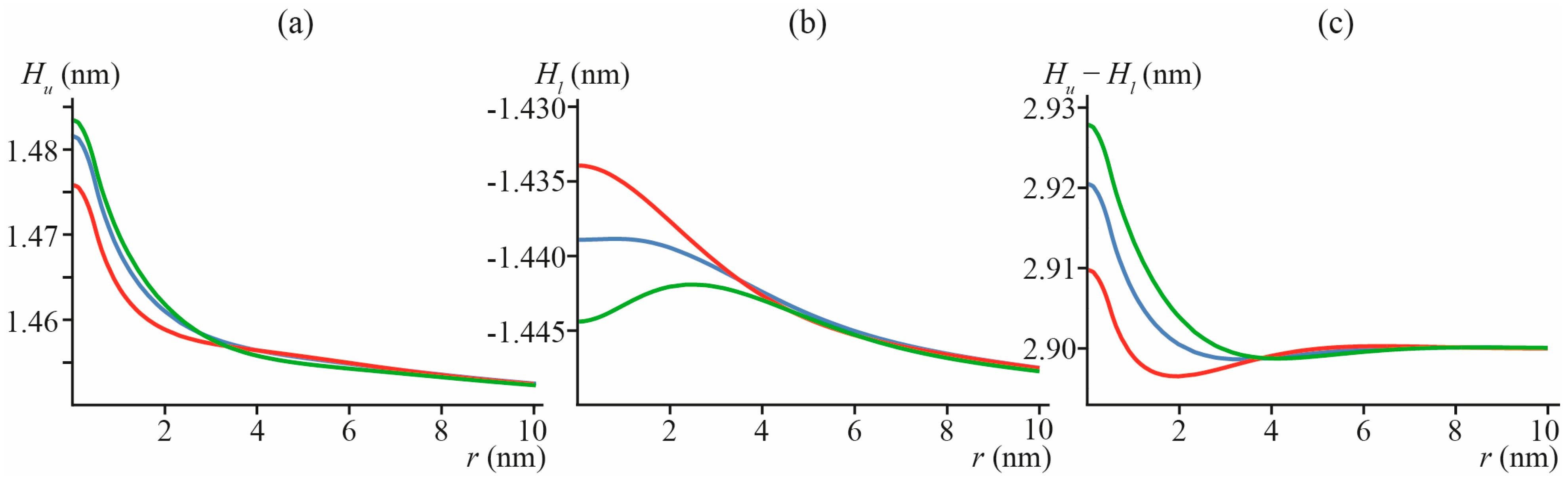
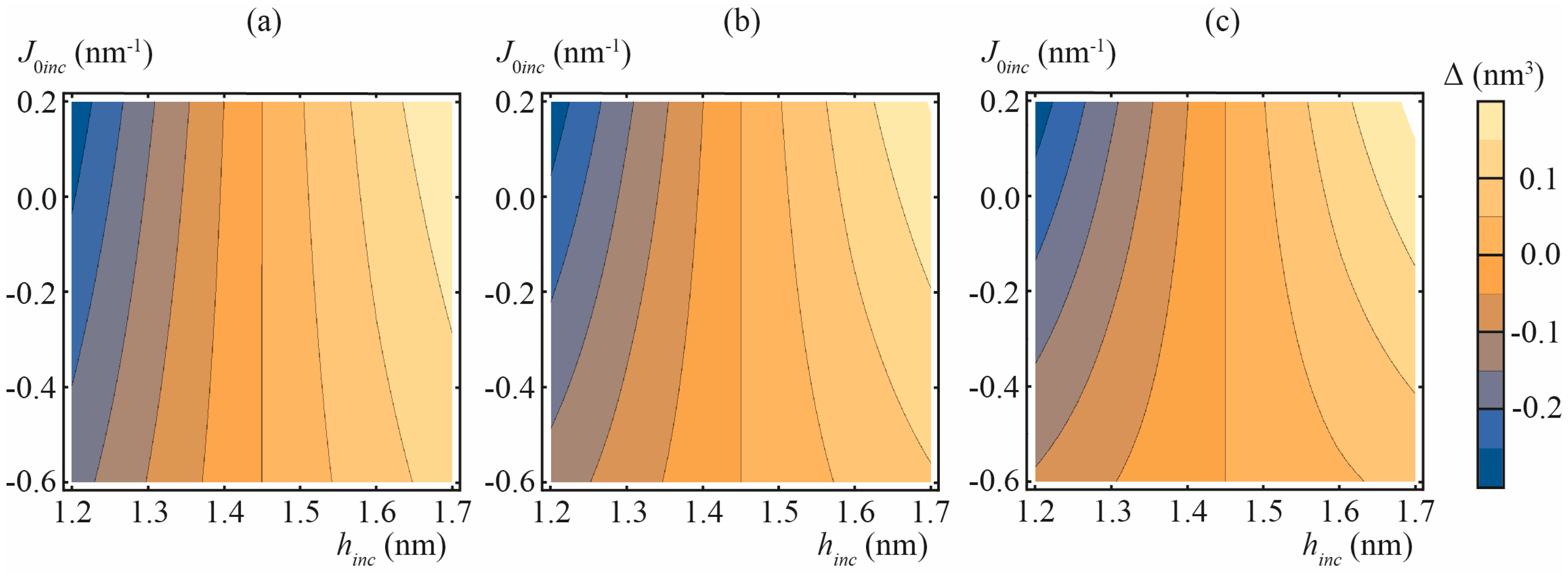
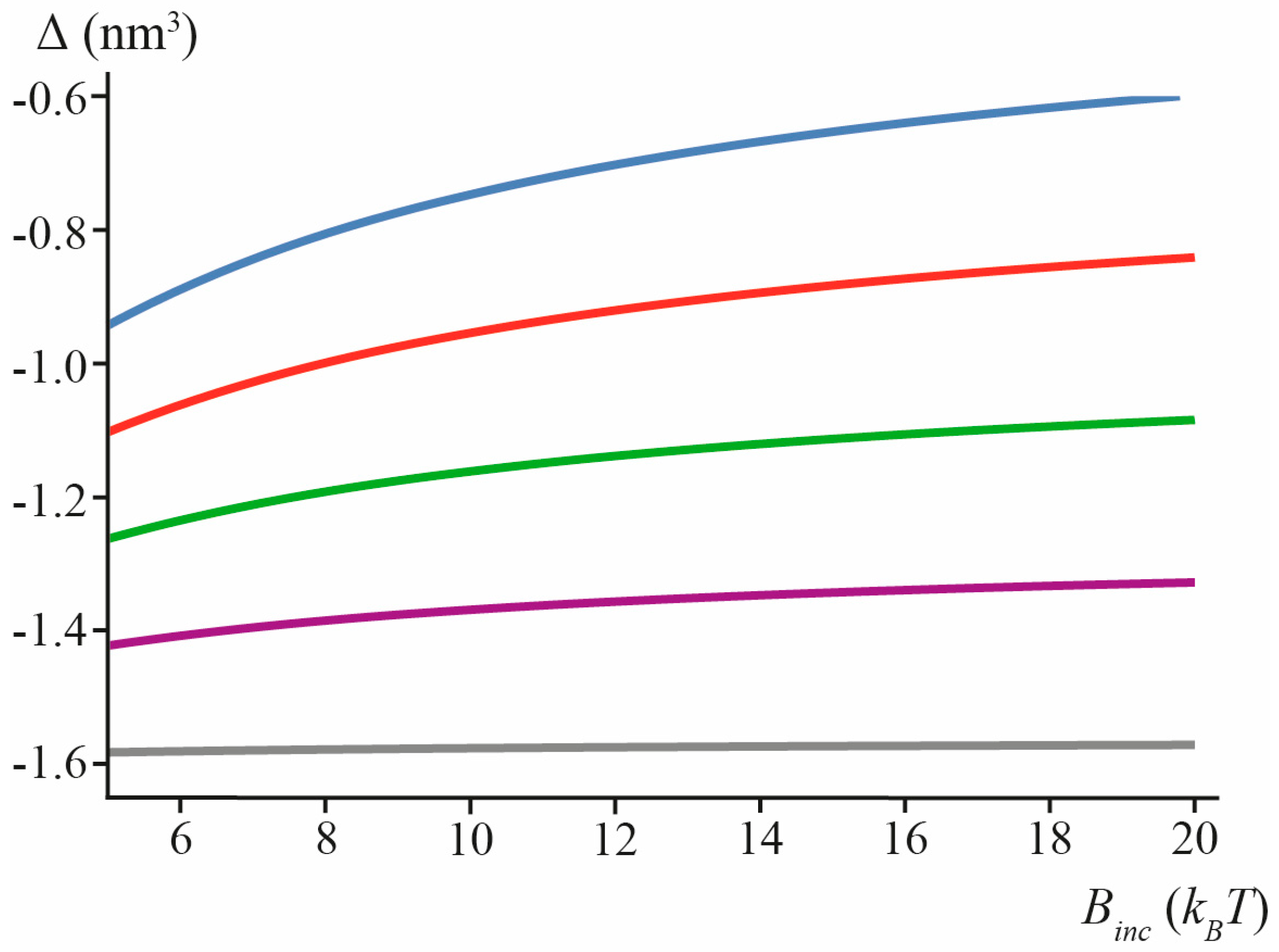
3.1. Amphipathic Peptide
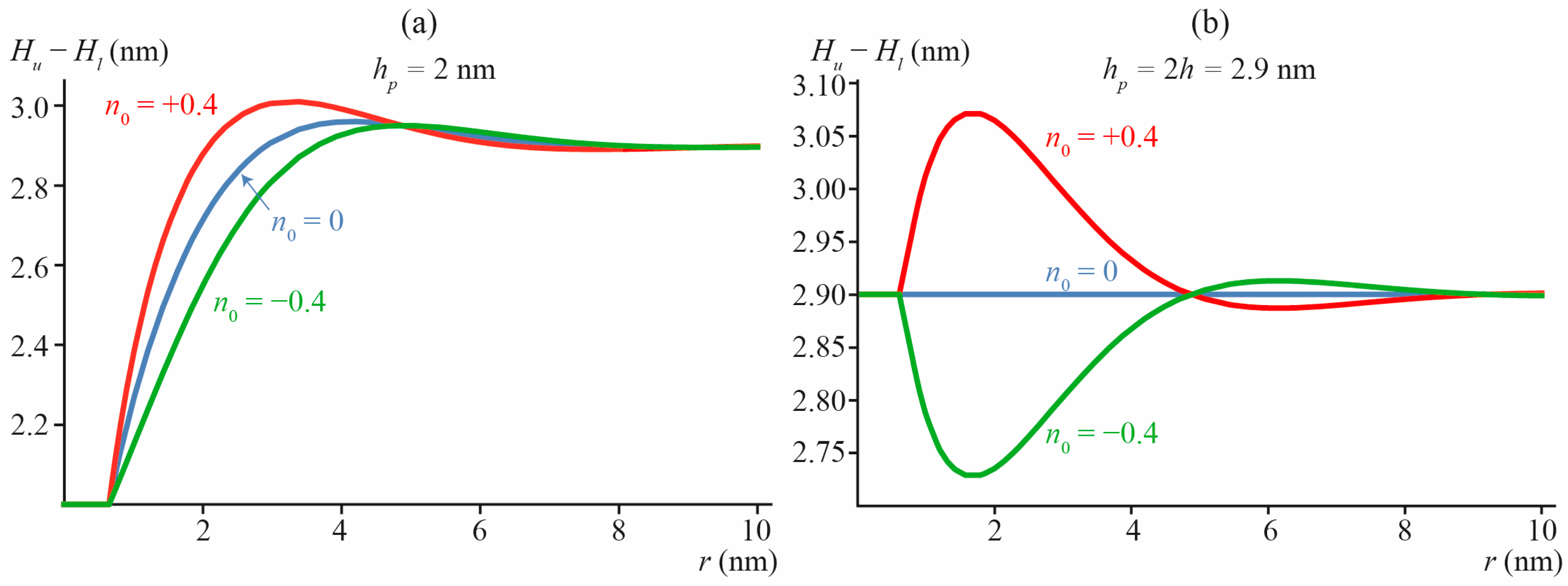
3.2. Transmembrane Peptide
3.3. Lipid Inclusion
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Evans, E.; Heinrich, V.; Ludwig, F.; Rawicz, W. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 2003, 85, 2342–2350. [Google Scholar] [CrossRef] [PubMed]
- Rawicz, W.; Olbrich, K.C.; McIntosh, T.; Needham, D.; Evans, E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000, 79, 328–339. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Peinado, C.; Dias, S.A.; Domingues, M.M.; Benfield, A.H.; Freire, J.M.; Rádis-Baptista, G.; Gaspar, D.; Castanho, M.A.R.B.; Craik, D.J.; Henriques, S.T.; et al. Mechanisms of bacterial membrane permeabilization by crotalicidin (Ctn) and its fragment Ctn (15–34), antimicrobial peptides from rattlesnake venom. J. Biol. Chem. 2018, 293, 1536–1549. [Google Scholar] [CrossRef]
- Panteleev, P.V.; Bolosov, I.A.; Balandin, S.V.; Ovchinnikova, T. Structure and biological functions of β-hairpin antimicrobial peptides. Acta Naturae 2015, 7, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Parvez, F.; Alam, J.M.; Dohra, H.; Yamazaki, M. Elementary processes of antimicrobial peptide PGLa-induced pore formation in lipid bilayers. Biochim. Biophys. Acta 2018, 1860, 2262–2271. [Google Scholar] [CrossRef]
- Sokolov, S.S.; Smirnova, E.A.; Markova, O.V.; Kireeva, N.A.; Kirsanov, R.S.; Khailova, L.S.; Knorre, D.A.; Severin, F.F. Lipophilic cations rescue the growth of yeast under the conditions of glycolysis overflow. Biomolecules 2020, 10, 1345. [Google Scholar] [CrossRef] [PubMed]
- Rokitskaya, T.I.; Khailova, L.S.; Korshunova, G.A.; Antonenko, Y.N. Efficiency of mitochondrial uncoupling by modified butyltriphenylphosphonium cations and fatty acids correlates with lipophilicity of cations: Protonophoric vs leakage mechanisms. Biochim. Biophys. Acta 2023, 1865, 184183. [Google Scholar] [CrossRef]
- Qian, S.; Wang, W.; Yang, L.; Huang, H.W. Structure of the alamethicin pore reconstructed by x-ray diffraction analysis. Biophys. J. 2008, 94, 3512–3522. [Google Scholar] [CrossRef]
- Bamberg, E.; Läuger, P. Channel formation kinetics of gramicidin A in lipid bilayer membranes. J. Membr. Biol. 1973, 11, 177–194. [Google Scholar] [CrossRef]
- Lundbæk, J.A.; Collingwood, S.A.; Ingólfsson, H.I.; Kapoor, R.; Andersen, O.S. Lipid bilayer regulation of membrane protein function: Gramicidin channels as molecular force probes. J. R. Soc. Interface 2010, 7, 373–395. [Google Scholar] [CrossRef]
- Rokitskaya, T.I.; Antonenko, Y.N.; Kotova, E.A. Photodynamic inactivation of gramicidin channels: A flash-photolysis study. Biochim. Biophys. Acta 1996, 1275, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Tevyashova, A.N.; Bychkova, E.N.; Solovieva, S.E.; Zatonsky, G.V.; Grammatikova, N.E.; Isakova, E.B.; Mirchink, E.P.; Treshchalin, I.D.; Pereverzeva, E.R.; Bykov, E.E.; et al. Discovery of amphamide, a drug candidate for the second generation of polyene antibiotics. ACS Infect. Dis. 2020, 6, 2029–2044. [Google Scholar] [CrossRef] [PubMed]
- Chulkov, E.G.; Ostroumova, O.S. Phloretin modulates the rate of channel formation by polyenes. Biochim. Biophys. Acta 2016, 1858, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.Y.; Lee, M.T.; Huang, H.W. Evidence for membrane thinning effect as the mechanism for peptide-induced pore formation. Biophys. J. 2003, 84, 3751–3758. [Google Scholar] [CrossRef] [PubMed]
- Ludtke, S.; He, K.; Huang, H. Membrane thinning caused by magainin 2. Biochemistry 1995, 34, 16764–16769. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; He, S.; Bennett, W.D.; Bilodeau, C.L.; Andersen, O.S.; Lightstone, F.C.; Ingólfsson, H.I. Atomistic characterization of gramicidin channel formation. J. Chem. Theory Comput. 2020, 17, 7–12. [Google Scholar] [CrossRef]
- Park, S.; Yeom, M.S.; Andersen, O.S.; Pastor, R.W.; Im, W. Quantitative characterization of protein–lipid interactions by free energy simulation between binary bilayers. J. Chem. Theory Comput. 2019, 15, 6491–6503. [Google Scholar] [CrossRef]
- Lillemeier, B.F.; Pfeiffer, J.R.; Surviladze, Z.; Wilson, B.S.; Davis, M.M. Plasma membrane-associated proteins are clustered into islands attached to the cytoskeleton. Proc. Natl. Acad. Sci. USA 2006, 103, 18992–18997. [Google Scholar] [CrossRef]
- Petruzielo, R.S.; Heberle, F.A.; Drazba, P.; Katsaras, J.; Feigenson, G.W. Phase behavior and domain size in sphingomyelin-containing lipid bilayers. Biochim. Biophys. Acta 2013, 1828, 1302–1313. [Google Scholar] [CrossRef]
- Zemel, A.; Ben-Shaul, A.; May, S. Perturbation of a lipid membrane by amphipathic peptides and its role in pore formation. Eur. Biophys. J. 2005, 34, 230–242. [Google Scholar] [CrossRef]
- Kondrashov, O.V.; Galimzyanov, T.R.; Pavlov, K.V.; Kotova, E.A.; Antonenko, Y.N.; Akimov, S.A. Membrane elastic deformations modulate gramicidin A transbilayer dimerization and lateral clustering. Biophys. J. 2018, 115, 478–493. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, O.V.; Kuzmin, P.I.; Akimov, S.A. Hydrophobic mismatch controls the mode of membrane-mediated interactions of transmembrane peptides. Membranes 2022, 12, 89. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, O.V.; Akimov, S.A. Regulation of antimicrobial peptide activity via tuning deformation fields by membrane-deforming inclusions. Int. J. Mol. Sci. 2022, 23, 326. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.J.; Fotiadis, D.; Scheuring, S.; Müller, S.A.; Engel, A. Electrostatically balanced subnanometer imaging of biological specimens by atomic force microscope. Biophys. J. 1999, 76, 1101–1111. [Google Scholar] [CrossRef] [PubMed]
- LeNeveu, D.M.; Rand, R.P.; Parsegian, V.A. Measurement of forces between lecithin bilayers. Nature 1976, 259, 601–603. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: San Diego, CA, USA, 2011; ISBN 978-0-12-391927-4. [Google Scholar]
- Lipowsky, R.; Sackmann, E. Handbook of Biological Physics. Chapter 11. Generic Interactions of Flexible Membranes; Elsevier Science B.V.: Amsterdam, The Netherlands, 1995; pp. 521–602. ISBN 0-444-81975-4. [Google Scholar]
- Bashkirov, P.V.; Kuzmin, P.I.; Chekashkina, K.; Arrasate, P.; Vera Lillo, J.; Shnyrova, A.V.; Frolov, V.A. Reconstitution and real-time quantification of membrane remodeling by single proteins and protein complexes. Nat. Protoc. 2020, 15, 2443–2469. [Google Scholar] [CrossRef] [PubMed]
- Vitkova, V.; Méléard, P.; Pott, T.; Bivas, I. Alamethicin influence on the membrane bending elasticity. Eur. Biophys. J. 2006, 35, 281–286. [Google Scholar] [CrossRef]
- Bereau, T.; Bennett, W.D.; Pfaendtner, J.; Deserno, M.; Karttunen, M. Folding and insertion thermodynamics of the transmembrane WALP peptide. J. Chem. Phys. 2015, 143, 243127. [Google Scholar] [CrossRef] [PubMed]
- Holt, A.; Rougier, L.; Réat, V.; Jolibois, F.; Saurel, O.; Czaplicki, J.; Killian, J.A.; Milon, A. Order parameters of a transmembrane helix in a fluid bilayer: Case study of a WALP peptide. Biophys. J. 2010, 98, 1864–1872. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Hamm, M.; Kozlov, M.M. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E 2000, 3, 323–335. [Google Scholar] [CrossRef]
- Leikin, S.; Kozlov, M.M.; Fuller, N.L.; Rand, R.P. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 1996, 71, 2623–2632. [Google Scholar] [CrossRef]
- Nagle, J.F.; Wilkinson, D.A. Lecithin bilayers. Density measurement and molecular interactions. Biophys. J. 1978, 23, 159–175. [Google Scholar] [CrossRef]
- Kondrashov, O.V.; Akimov, S.A. Effect of solid support and membrane tension on adsorption and lateral interaction of amphipathic peptides. J. Chem. Phys. 2022, 157, 074902. [Google Scholar] [CrossRef]
- Kondrashov, O.V.; Pinigin, K.V.; Akimov, S.A. Characteristic lengths of transmembrane peptides controlling their tilt and lateral distribution between membrane domains. Phys. Rev. E 2021, 104, 044411. [Google Scholar] [CrossRef]
- Hu, M.; de Jong, D.H.; Marrink, S.J.; Deserno, M. Gaussian curvature elasticity determined from global shape transformations and local stress distributions: A comparative study using the MARTINI model. Faraday Discuss. 2013, 161, 365–382. [Google Scholar] [CrossRef]
- Kollmitzer, B.; Heftberger, P.; Rappolt, M.; Pabst, G. Monolayer spontaneous curvature of raft-forming membrane lipids. Soft Matter 2013, 9, 10877–10884. [Google Scholar] [CrossRef]
- Erkan-Candag, H.; Krivic, D.; Gsell, M.A.; Aleksanyan, M.; Stockner, T.; Dimova, R.; Tiapko, O.; Groschner, K. Characterization of DAG binding to TRPC channels by target-dependent cis–trans isomerization of OptoDArG. Biomolecules 2022, 12, 799. [Google Scholar] [CrossRef]
- Morstein, J.; Impastato, A.C.; Trauner, D. Photoswitchable lipids. ChemBioChem 2021, 22, 73–83. [Google Scholar] [CrossRef]
- Frank, J.A.; Yushchenko, D.A.; Hodson, D.J.; Lipstein, N.; Nagpal, J.; Rutter, G.A.; Rhee, J.-S.; Gottschalk, A.; Brose, N.; Schultz, C.; et al. Photoswitchable diacylglycerols enable optical control of protein kinase C. Nat. Chem. Biol. 2016, 12, 755–762. [Google Scholar] [CrossRef]
- Pfeffermann, J.; Eicher, B.; Boytsov, D.; Hannesschlaeger, C.; Galimzyanov, T.R.; Glasnov, T.N.; Pabst, G.; Akimov, S.A.; Pohl, P. Photoswitching of model ion channels in lipid bilayers. J. Photochem. Photobiol. B 2021, 224, 112320. [Google Scholar] [CrossRef]
- Campelo, F.; McMahon, H.T.; Kozlov, M.M. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 2008, 95, 2325–2339. [Google Scholar] [CrossRef]
- Sodt, A.J.; Pastor, R.W. Molecular modeling of lipid membrane curvature induction by a peptide: More than simply shape. Biophys. J. 2014, 106, 1958–1969. [Google Scholar] [CrossRef]
- Kondrashov, O.V.; Galimzyanov, T.R.; Jiménez-Munguía, I.; Batishchev, O.V.; Akimov, S.A. Membrane-mediated interaction of amphipathic peptides can be described by a one-dimensional approach. Phys. Rev. E 2019, 99, 022401. [Google Scholar] [CrossRef]
- Bechinger, B.; Zasloff, M.; Opella, S.J. Structure and orientation of the antibiotic peptide magainin in membranes by solid-state nuclear magnetic resonance spectroscopy. Protein Sci. 1993, 2, 2077–2084. [Google Scholar] [CrossRef]
- Santo, K.P.; Berkowitz, M.L. Difference between magainin-2 and melittin assemblies in phosphatidylcholine bilayers: Results from coarse-grained simulations. J. Phys. Chem. B 2012, 116, 3021–3030. [Google Scholar] [CrossRef]
- Chen, C.H.; Wiedman, G.; Khan, A.; Ulmschneider, M.B. Absorption and folding of melittin onto lipid bilayer membranes via unbiased atomic detail microsecond molecular dynamics simulation. Biochim. Biophys. Acta 2014, 1838, 2243–2249. [Google Scholar] [CrossRef]
- Huang, H.W. Molecular mechanism of antimicrobial peptides: The origin of cooperativity. Biochim. Biophys. Acta 2006, 1758, 1292–1302. [Google Scholar] [CrossRef]
- Hasan, M.; Karal, M.A.S.; Levadnyy, V.; Yamazaki, M. Mechanism of initial stage of pore formation induced by antimicrobial peptide magainin 2. Langmuir 2018, 34, 3349–3362. [Google Scholar] [CrossRef]
- Fuertes, G.; Giménez, D.; Esteban-Martín, S.; Sánchez-Munoz, O.L.; Salgado, J. A lipocentric view of peptide-induced pores. Eur. Biophys. J. 2011, 40, 399–415. [Google Scholar] [CrossRef]
- Yang, L.; Weiss, T.M.; Lehrer, R.I.; Huang, H.W. Crystallization of antimicrobial pores in membranes: Magainin and protegrin. Biophys. J. 2000, 79, 2002–2009. [Google Scholar] [CrossRef] [PubMed]
- Last, N.B.; Schlamadinger, D.E.; Miranker, A.D. A common landscape for membrane-active peptides. Protein Sci. 2013, 22, 870–882. [Google Scholar] [CrossRef] [PubMed]
- Kondrashov, O.V.; Akimov, S.A. The possibility of pore formation in lipid membranes by several molecules of amphipathic peptides. Biol. Membr. 2022, 39, 384–397. [Google Scholar] [CrossRef]
- Harroun, T.A.; Heller, W.T.; Weiss, T.M.; Yang, L.; Huang, H.W. Experimental evidence for hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 1999, 76, 937–945. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondrashov, O.V.; Akimov, S.A. Alteration of Average Thickness of Lipid Bilayer by Membrane-Deforming Inclusions. Biomolecules 2023, 13, 1731. https://doi.org/10.3390/biom13121731
Kondrashov OV, Akimov SA. Alteration of Average Thickness of Lipid Bilayer by Membrane-Deforming Inclusions. Biomolecules. 2023; 13(12):1731. https://doi.org/10.3390/biom13121731
Chicago/Turabian StyleKondrashov, Oleg V., and Sergey A. Akimov. 2023. "Alteration of Average Thickness of Lipid Bilayer by Membrane-Deforming Inclusions" Biomolecules 13, no. 12: 1731. https://doi.org/10.3390/biom13121731
APA StyleKondrashov, O. V., & Akimov, S. A. (2023). Alteration of Average Thickness of Lipid Bilayer by Membrane-Deforming Inclusions. Biomolecules, 13(12), 1731. https://doi.org/10.3390/biom13121731






