Long-Time Dynamics of Selected Molecular-Motor Components Using a Physics-Based Coarse-Grained Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Systems Studied
2.2. UNRES Model of Polypeptide Chains
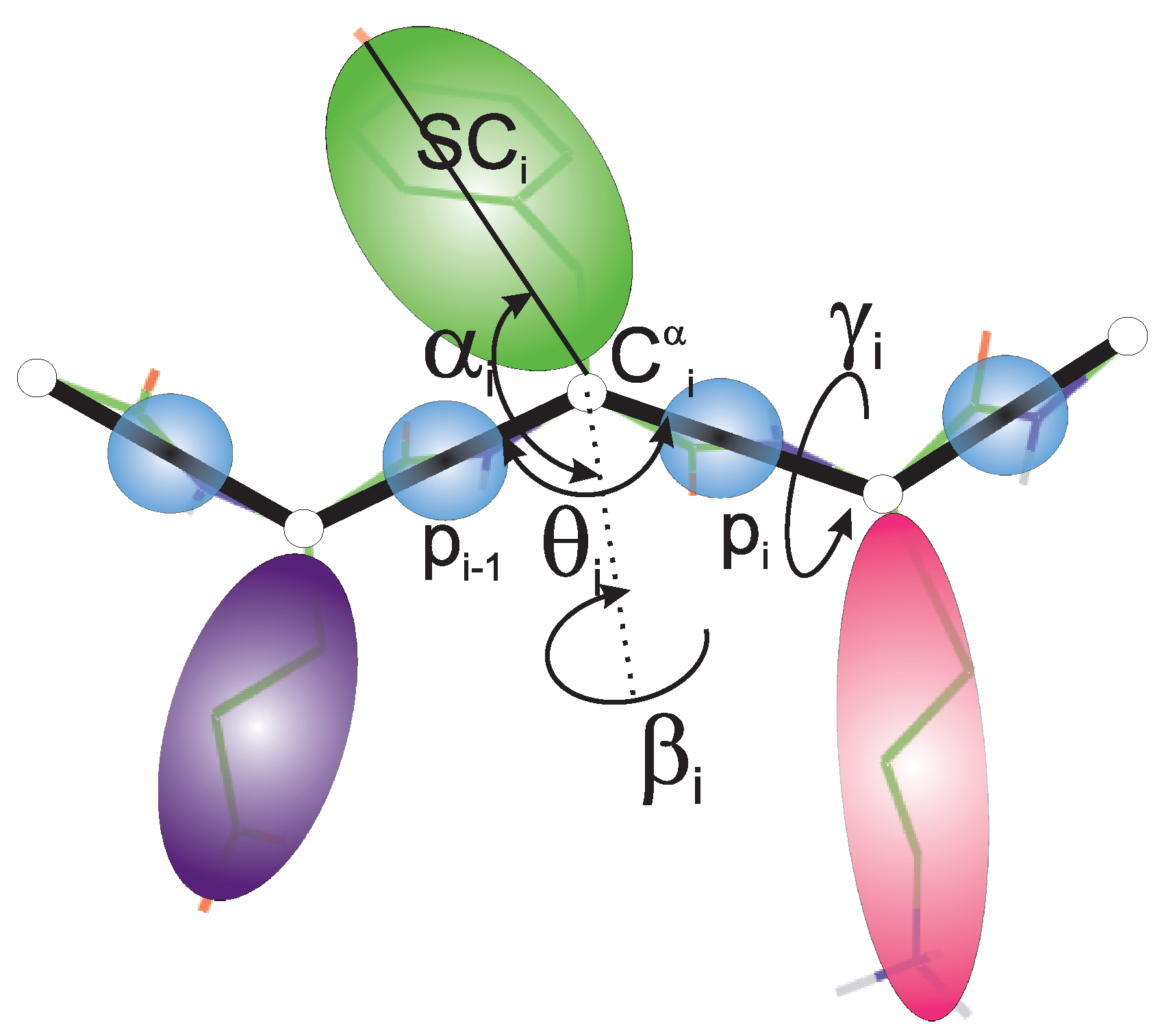
2.3. Coarse-Grained Molecular Dynamics with UNRES
2.4. Simulation Procedure
2.4.1. The 4YY2 System
2.4.2. The 6SD5 System
2.4.3. The 2BL2 System
2.5. Hardware Platform and Timing
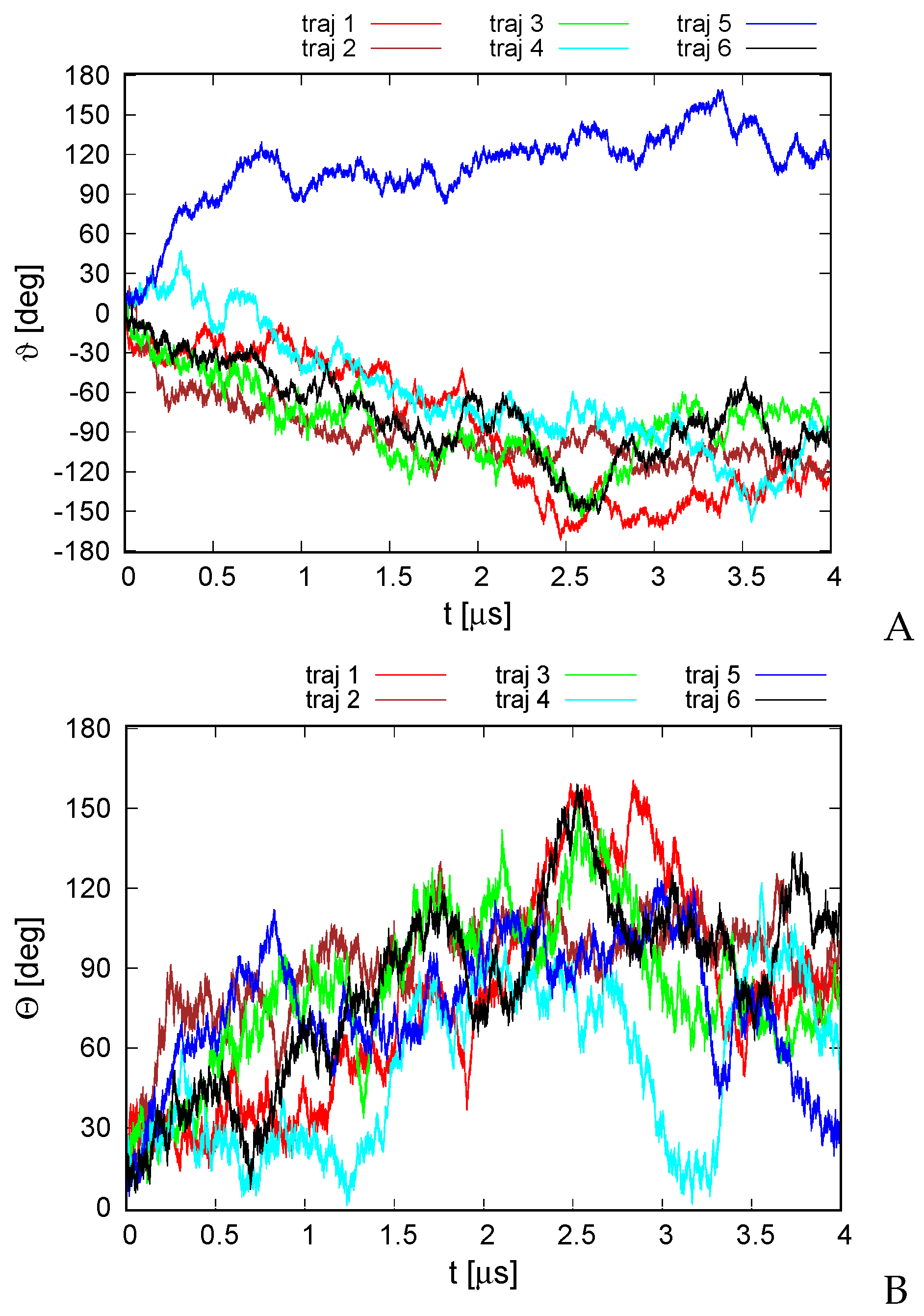
2.6. Determining the Rotation Angle
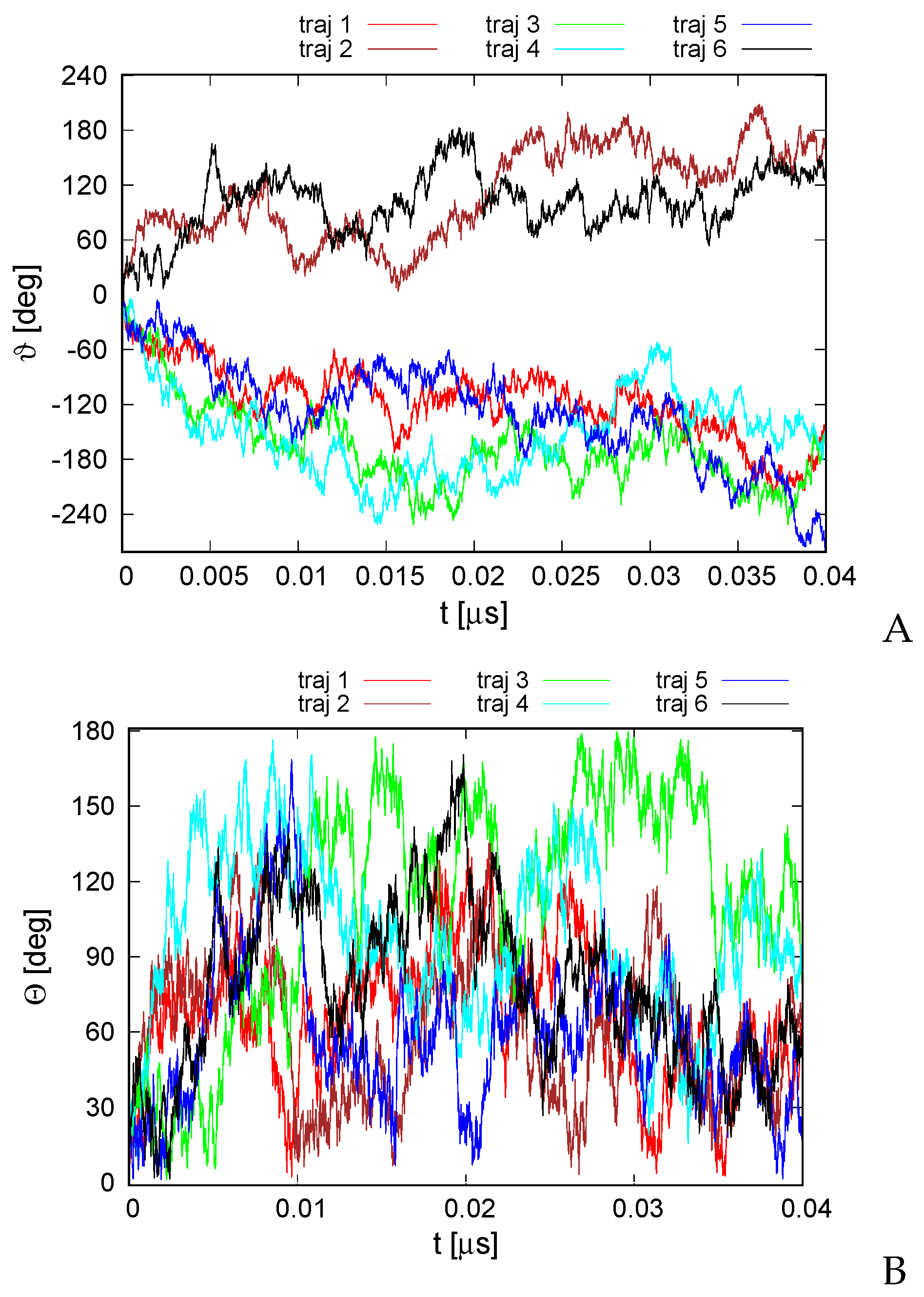
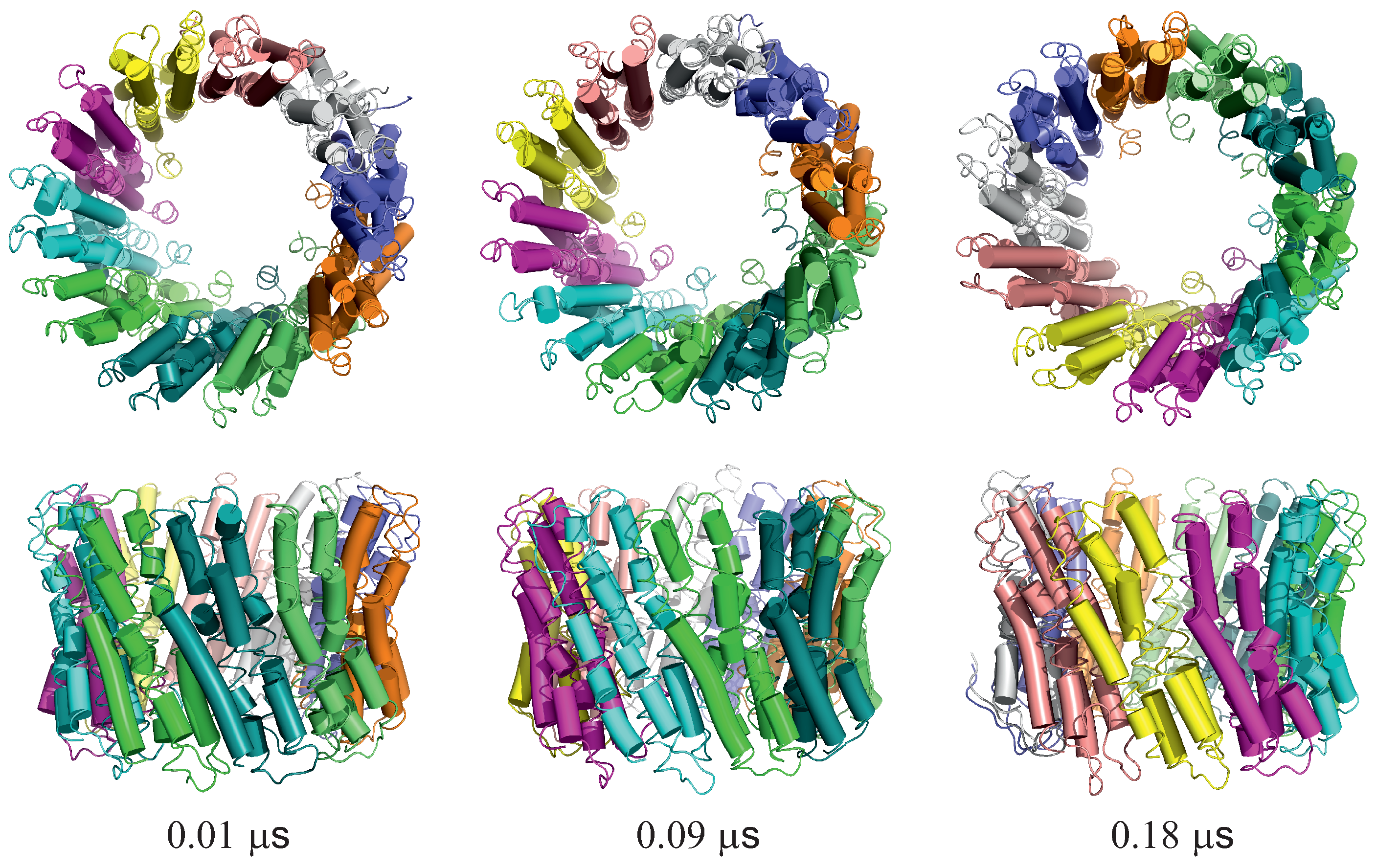
3. Results
3.1. The 4YY2 System
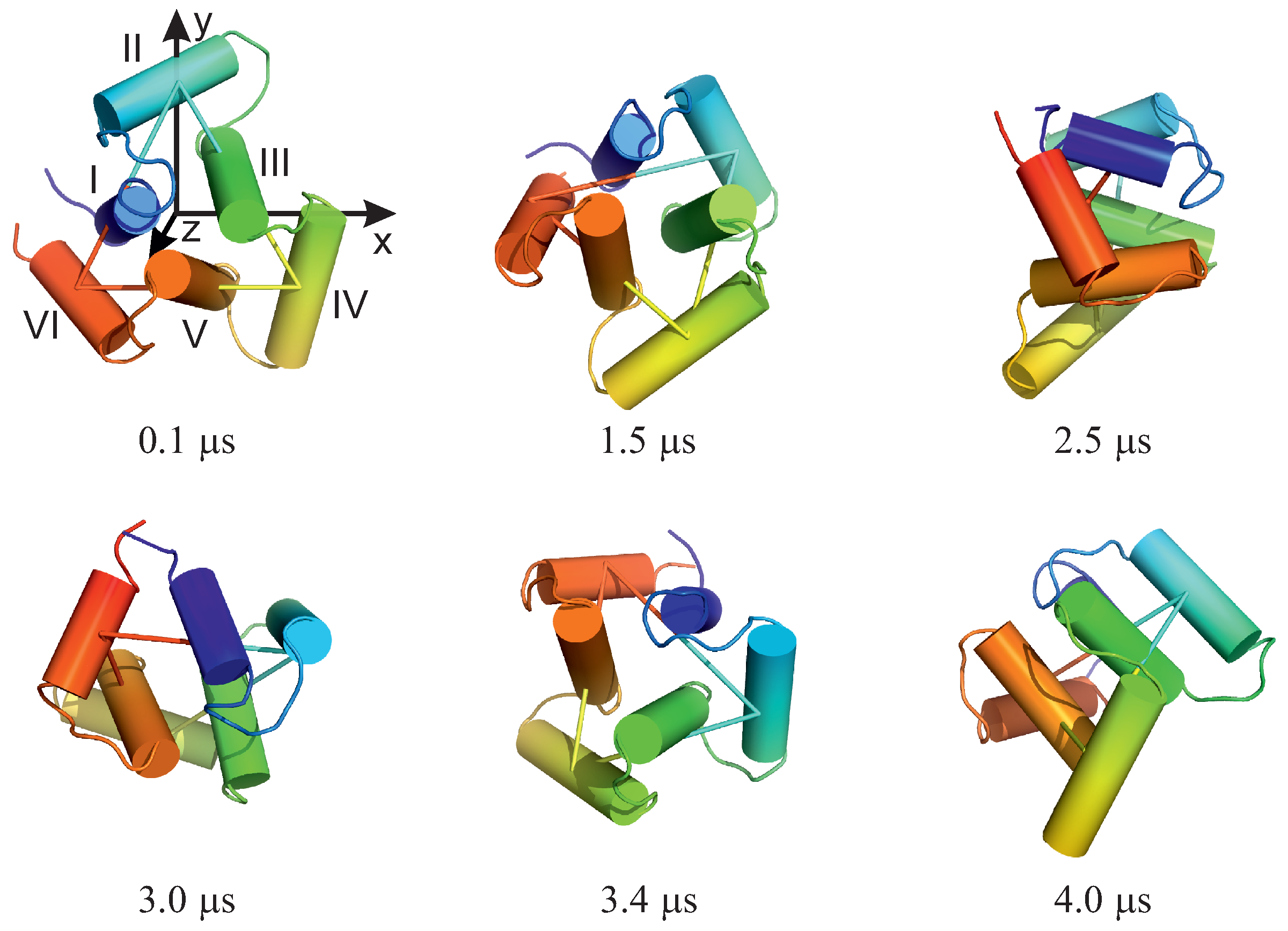
3.2. The 6SD5 System
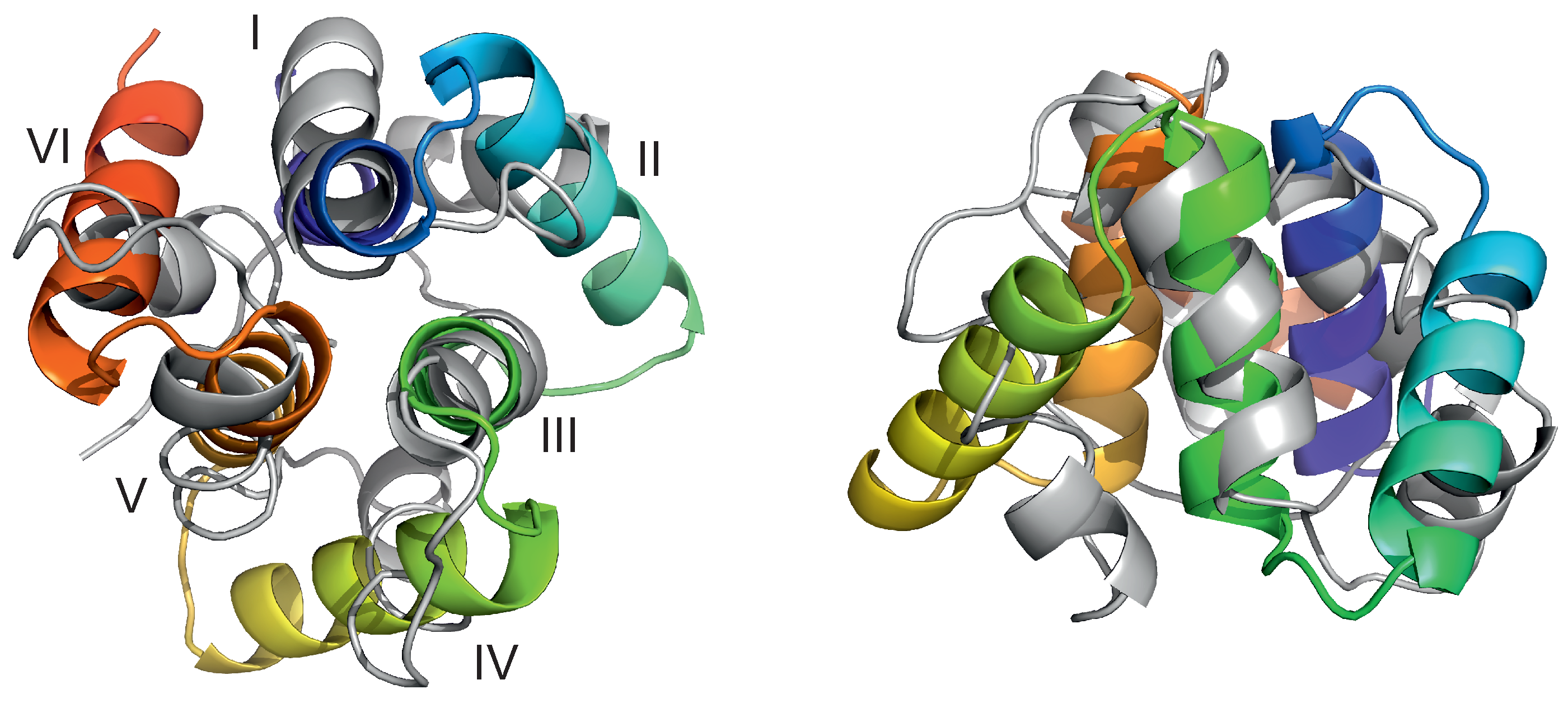
3.3. The 2BL2 System
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATP | Adenosine-5’-Tri-Phosphate |
| CHARMM-GUI | Chemistry at HARvard Macromolecular Mechanics Graphical User Interface |
| GDT_TS | Global Distance Test Total Score |
| MD | Molecular Dynamics |
| MREMD | Multiplexed Replica Exchange Molecular Dynamics |
| NVE | constant Number of particles, constant Volume, constant Energy |
| NVT | constant Number of particles, constant Volume, constant Temperature |
| PDB | Protein Data Bank |
| RMSD | Root Mean Square Deviation |
| UNRES | UNited RESidue model of proteins |
| WHAM | Weighted Histogram Analysis Method |
References
- Bustamante, C.; Chemla, Y.R.; Forde, N.R.; Izhaky, D. Mechanical processes in biochemistry. Annu. Rev. Biochem. 2004, 73, 705–748. [Google Scholar] [CrossRef] [PubMed]
- Iino, R.; Kinbara, K.; Bryant, Z. Introduction: Molecular motors. Chem. Rev. 2020, 120, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Ovalle, M.; Seale, J.S.W.; Lee, C.K.; Kim, D.J.; Astumian, R.D.; Stoddart, J.F. Molecular pumps and motors. J. Am. Chem. Soc. 2021, 143, 5569–5591. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Jia, L.; Li, S.; Li, M.; Yang, G.; Liu, N.; Ren, H.; Mou, M.; Zheng, A.; et al. The classification and therapeutic applications of molecular motors. Eur. J. Med. Chem. Rep. 2021, 3, 100009. [Google Scholar] [CrossRef]
- Cross, R.A. Mechanochemistry of the kinesin-1 ATPase. Biopolymers 2016, 105, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Karp, G. Cell and Molecular Biology: Concepts and Experiments, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2005; pp. 346–358. [Google Scholar]
- Hartman, M.A.; Spudich, J.A. The myosin superfamily at a glance. J. Cell Sci. 2012, 125, 1627–1632. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Makino, F.; Miyata, T.; Minamino, T.; Kato, T.; Namba, K. Structure of the molecular bushing of the bacterial flagellar motor. Nat. Commun. 2021, 12, 4469. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, X.; Wang, X.; Xu, C.; Chang, S.; Wu, H.; Wang, T.; Liang, H.; Gao, H.; Zhou, Y.; et al. Structural basis of assembly and torque transmission of the bacterial flagellar motor. Cell 2021, 184, 2665–2679. [Google Scholar] [CrossRef]
- Mukherjee, S.; Warshel, A. Dissecting the role of the γ-subunit in the rotary-chemical coupling and torque generation of F1-ATPase. Proc. Natl. Acad. Sci. USA 2015, 112, 2746–2751. [Google Scholar] [CrossRef]
- Mukherjee, S.; Bora, R.P.; Warshel, A. Torque, chemistry and efficiency in molecular motors: A study of the rotary-chemical coupling in F1-ATPase. Q. Rev. Biophys. 2015, 48, 395–403. [Google Scholar] [CrossRef]
- Murata, T.; Yamato, I.; Kakinuma, Y.; Leslie, A.G.W.; Walker, J.E. Structure of the rotor of the V-Type Na+-ATPase from Enterococcus hirae. Science 2005, 308, 654–659. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Hyeon, C. Energetic costs, precision, and transport efficiency of molecular motors. J. Phys. Chem. Lett. 2018, 9, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Niemi, A.J.; Peng, X.; Wilczek, F. Truncated dynamics, ring molecules, and mechanical time crystals. Phys. Rev. A 2019, 99, 023425. [Google Scholar] [CrossRef]
- Dai, J.; Niemi, A.J.; Peng, X. Classical Hamiltonian time crystals–general theory and simple examples. New J. Phys. 2020, 22, 085006. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J.; Niemi, A.J. Rotation by deformation and time-crystalline dynamics of cyclopropane molecule. New J. Phys. 2021, 23, 073024. [Google Scholar] [CrossRef]
- Wang, J.; Dai, J.; Niemi, A.J.; Peng, X. From Feynman’s ratchet to timecrystalline molecular motors. arXiv 2023, arXiv:2304.12118. [Google Scholar]
- Guichardet, A. On rotation and vibration motions of molecules. Ann. l’Inst. Henri Poincaré 1984, 40, 329–342. [Google Scholar]
- Shapere, A.; Wilczek, F. Gauge kinematics of deformable bodies. Am. J. Phys. 1989, 57, 514–518. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum time crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Shapere, A.; Wilczek, F. Classical time crystals. Phys. Rev. Lett. 2012, 109, 160402. [Google Scholar] [CrossRef] [PubMed]
- Zaletel, M.P.; Lukin, M.; Monroe, C.; Nayak, C.; Wilczek, F.; Yao, N.Y. Colloquium: Quantum and Classical Discrete Time Crystals. arXiv 2023, arXiv:2305.08904. [Google Scholar]
- Segawa, Y.; Kuwayama, M.; Hijikata, Y.; Fushimi, M.; Nishihara, T.; Pirillo, J.; Shirasaki, J.; Kubota, N.; Itami, K. Topological molecular nanocarbons: All-benzene catenane and trefoil knot. Science 2019, 365, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Courbet, A.; Hansen, J.; Hsia, Y.; Bethel, N.; Park, Y.J.; Xu, C.; Moyer, A.; Boyken, S.E.; Ueda, G.; Nattermann, U.; et al. Computational design of mechanically coupled axle-rotor protein assemblies. Science 2022, 376, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Ołdziej, S.; Pincus, M.R.; Wawak, R.J.; Rackovsky, S.; Scheraga, H.A. A united-residue force field for off-lattice protein-structure simulations. I. Functional forms and parameters of long-range side-chain interaction potentials from protein crystal data. J. Comput. Chem. 1997, 18, 849–873. [Google Scholar] [CrossRef]
- Liwo, A.; Baranowski, M.; Czaplewski, C.; Gołaś, E.; He, Y.; Jagieła, D.; Krupa, P.; Maciejczyk, M.; Makowski, M.; Mozolewska, M.A.; et al. A unified coarse-grained model of biological macromolecules based on mean-field multipole-multipole interactions. J. Mol. Model. 2014, 20, 2306. [Google Scholar] [CrossRef]
- Sieradzan, A.K.; Makowski, M.; Augustynowicz, A.; Liwo, A. A general method for the derivation of the functional forms of the effective energy terms in coarse-grained energy functions of polymers. I. Backbone potentials of coarse-grained polypeptide chains. J. Chem. Phys. 2017, 146, 124106. [Google Scholar] [CrossRef]
- Liwo, A.; Sieradzan, A.K.; Lipska, A.G.; Czaplewski, C.; Joung, I.; Żmudzińska, W.; Hałabis, A.; Ołdziej, S. A general method for the derivation of the functional forms of the effective energy terms in coarse-grained energy functions of polymers. III. Determination of scale-consistent backbone-local and correlation potentials in the UNRES force field and force-field calibration and validation. J. Chem. Phys. 2019, 150, 155104. [Google Scholar]
- Sieradzan, A.K.; Czaplewski, C.; Krupa, P.; Mozolewska, M.A.; Karczyńska, A.S.; Lipska, A.G.; Lubecka, E.A.; Gołaś, E.; Wirecki, T.; Makowski, M.; et al. Modeling the structure, dynamics, and transformations of proteins with the UNRES force field. In Protein Folding: Methods and Protocols; Muñoz, V., Ed.; Springer: New York, NY, USA, 2022; pp. 399–416. [Google Scholar]
- Antoniak, A.; Biskupek, I.; Bojarski, K.K.; Czaplewski, C.; Giełdoń, A.; Kogut, M.; Kogut, M.M.; Krupa, P.; Lipska, A.G.; Liwo, A.; et al. Modeling protein structures with the coarse-grained UNRES force field in the CASP14 experiment. J. Mol. Graph. Model. 2021, 108, 108008. [Google Scholar] [CrossRef]
- Liwo, A.; Czaplewski, C.; Sieradzan, A.K.; Lubecka, E.A.; Lipska, A.G.; Golon, Ł.; Karczyńka, A.; Krupa, P.; Mozolewska, M.A.; Makowski, M.; et al. Scale-consistent approach to the derivation of coarse-grained force fields for simulating structure, dynamics, and thermodynamics of biopolymers. In Progress in Molecular Biology and Translational Science. Computational Approaches for Understanding Dynamical Systems: Protein Folding and Assembly; Strodel, B., Barz, B., Eds.; Academic Press: London, UK, 2020; Volume 170, Chapter 2; pp. 73–122. [Google Scholar]
- Khalili, M.; Liwo, A.; Jagielska, A.; Scheraga, H.A. Molecular dynamics with the united-residue model of polypeptide chains. II. Langevin and Berendsen-bath dynamics and tests on model α-helical systems. J. Phys. Chem. B 2005, 109, 13798–13810. [Google Scholar] [CrossRef]
- Sieradzan, A.K.; Sans-Duñò, J.; Lubecka, E.A.; Czaplewski, C.; Lipska, A.G.; Leszczynski, H.; Ocetkiewicz, K.M.; Proficz, J.; Czarnul, P.; Krawczyk, H.; et al. Optimization of parallel implementation of UNRES package for coarse-grained simulations to treat large proteins. J. Comput. Chem. 2023, 44, 602–625. [Google Scholar] [CrossRef] [PubMed]
- Doyle, L.; Hallinan, J.; Bolduc, J.; Parmeggiani, F.; Baker, D.; Stoddard, B.L.; Bradley, P. Rational design of α-helical tandem repeat proteins with closed architectures. Nature 2015, 528, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.; Fong, Y.H.; Deme, J.C.; Furlong, E.J.; Kuhlen, L.; Lea, S.M. Symmetry mismatch in the MS-ring of the bacterial flagellar rotor explains the structural coordination of secretion and rotation. Nat. Microbiol. 2020, 7, 966–975. [Google Scholar] [CrossRef] [PubMed]
- Ziȩba, K.; Ślusarz, M.; Ślusarz, R.; Liwo, A.; Czaplewski, C.; Sieradzan, A.K. Extension of the UNRES coarse-grained force field to membrane proteins in the lipid bilayer. J. Phys. Chem. B 2019, 123, 7829–7839. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R. Generalized cumulant expansion method. J. Phys. Soc. Jpn. 1962, 17, 1100–1120. [Google Scholar] [CrossRef]
- Liwo, A.; Czaplewski, C.; Pillardy, J.; Scheraga, H.A. Cumulant-based expressions for the multibody terms for the correlation between local and electrostatic interactions in the united-residue force field. J. Chem. Phys. 2001, 115, 2323–2347. [Google Scholar] [CrossRef]
- Liwo, A.; Khalili, M.; Czaplewski, C.; Kalinowski, S.; Ołdziej, S.; Wachucik, K.; Scheraga, H.A. Modification and optimization of the united-residue (UNRES) potential energy function for canonical simulations. I. Temperature dependence of the effective energy function and tests of the optimization method with single training proteins. J. Phys. Chem. B 2007, 111, 260–285. [Google Scholar] [CrossRef]
- Kolinski, A.; Skolnick, J. Discretized model of proteins. I. Monte Carlo study of cooperativity in homopolypeptides. J. Chem. Phys. 1992, 97, 9412–9426. [Google Scholar] [CrossRef]
- Zaborowski, B.; Jagieła, D.; Czaplewski, C.; Hałabis, A.; Lewandowska, A.; Żmudzińska, W.; Ołdziej, S.; Karczyńska, A.; Omieczynski, C.; Wirecki, T.; et al. A maximum-likelihood approach to force-field calibration. J. Chem. Inf. Model. 2015, 55, 2050–2070. [Google Scholar] [CrossRef]
- Zwanzig, R. Memory effects in irreversible thermodynamics. Phys. Rev. 1961, 124, 983–992. [Google Scholar] [CrossRef]
- Mori, H. Transport, collective motion, and Brownian motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001; Chapter 8. [Google Scholar]
- Klippenstein, V.; Tripathy, M.; Jung, G.; Schmid, F.; van der Vegt, N.F.A. Introducing memory in coarse-grained molecular simulations. J. Phys. Chem. B 2021, 125, 4931–4954. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Czaplewski, C.; Sieradzan, A.K.; Lipska, A.G.; Samsonov, S.A.; Murarka, R.K. Theory and practice of coarse-grained molecular dynamics of biologically important systems. Biomolecules 2021, 11, 1347. [Google Scholar] [CrossRef]
- Khalili, M.; Liwo, A.; Rakowski, F.; Grochowski, P.; Scheraga, H.A. Molecular dynamics with the united-residue model of polypeptide chains. I. Lagrange equations of motion and tests of numerical stability in the microcanonical mode. J. Phys. Chem. B 2005, 109, 13785–13797. [Google Scholar] [CrossRef]
- Krupa, P.; Mozolewska, M.A.; Wiśniewska, M.; Yanping, Y.; He, Y.; Sieradzan, A.K.; Ganzynkowicz, R.; Lipska, A.G.; Karczyńska, A.; Ślusarz, M.; et al. Performance of protein-structure predictions with the physics-based UNRES force field in CASP11. Bioinformatics 2016, 32, 3270–3278. [Google Scholar] [CrossRef] [PubMed]
- Czaplewski, C.; Kalinowski, S.; Liwo, A.; Scheraga, H.A. Application of multiplexing replica exchange molecular dynamics method to the UNRES force field: Tests with α and α + β proteins. J. Chem. Theory Comput. 2009, 5, 627–640. [Google Scholar] [CrossRef]
- Kumar, S.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A.; Rosenberg, J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Murtagh, F.; Heck, A. Multivariate Data Analysis; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Trebst, S.; Troyer, M.; Hansmann, U.H. Optimized parallel tempering simulations of proteins. J. Chem. Phys. 2006, 124, 174903. [Google Scholar] [CrossRef]
- Zemla, A. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003, 13, 3370–3374. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Touw, W.G.; Baakman, C.; Black, J.; te Beek, T.A.H.; Krieger, E.; Joosten, R.P.; Vriend, G. A series of PDB related databases for everyday needs. Nucl. Acids Res. 2015, 39, D364–D368. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, LLC. The PyMOL Molecular Graphics System, Version 1.3r1. Available online: https://pymol.org/2/support.html (accessed on 4 May 2023).
- Rotkiewicz, P.; Skolnick, J. Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem. 2008, 29, 1460–1465. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Canutescu, A.A.; Dunbrack, R.L. SCWRL and MolIDE: Computer programs for side-chain conformation prediction and homology modeling. Nat. Protoc. 2008, 3, 1832–1847. [Google Scholar] [CrossRef]
- Lubecka, E.A.; Liwo, A. Introduction of a bounded penalty function in contact-assisted simulations of protein structures to omit false restraints. J. Comput. Chem. 2019, 40, 2164–2178. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Suh, D.; Sieradzan, A.K.; Czaplewski, C.; Liwo, A.; Im, W. Extenstion of CHARMM-GUI to UNICORN coarse-grained model. 2023; manuscript in preparation. [Google Scholar]
- Shepperd, S.W. Quaternion from rotation matrix. J. Guid. Control 1978, 1, 223–224. [Google Scholar] [CrossRef]
- Hanson, A.J. Visualizing Quaternions; Elsevier: London, UK, 2006. [Google Scholar]
- Williams, T.; Kelley, C. Gnuplot 4.6: An Interactive Plotting Program. 2013. Available online: http://gnuplot.sourceforge.net/ (accessed on 29 May 2023).
- Minamino, T.; Kinoshita, M.; Namba, K. Directional switching mechanism of the bacterial flagellar motor. Comput. Struct. Biotechnol. J. 2019, 17, 1075–1081. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liwo, A.; Pyrka, M.; Czaplewski, C.; Peng, X.; Niemi, A.J. Long-Time Dynamics of Selected Molecular-Motor Components Using a Physics-Based Coarse-Grained Approach. Biomolecules 2023, 13, 941. https://doi.org/10.3390/biom13060941
Liwo A, Pyrka M, Czaplewski C, Peng X, Niemi AJ. Long-Time Dynamics of Selected Molecular-Motor Components Using a Physics-Based Coarse-Grained Approach. Biomolecules. 2023; 13(6):941. https://doi.org/10.3390/biom13060941
Chicago/Turabian StyleLiwo, Adam, Maciej Pyrka, Cezary Czaplewski, Xubiao Peng, and Antti J. Niemi. 2023. "Long-Time Dynamics of Selected Molecular-Motor Components Using a Physics-Based Coarse-Grained Approach" Biomolecules 13, no. 6: 941. https://doi.org/10.3390/biom13060941
APA StyleLiwo, A., Pyrka, M., Czaplewski, C., Peng, X., & Niemi, A. J. (2023). Long-Time Dynamics of Selected Molecular-Motor Components Using a Physics-Based Coarse-Grained Approach. Biomolecules, 13(6), 941. https://doi.org/10.3390/biom13060941






