2.1. Experimental Design
This section describes the layout and purpose of each experiment performed in this study, along with the computational design. An overview of models and methods is included to provide context for understanding the experimental design. Further details of models and methods are expanded upon in their own sections further below.
The most common approach to representing MS/MS spectrum for machine learning tasks is binning of mass spectra [
4,
5,
16,
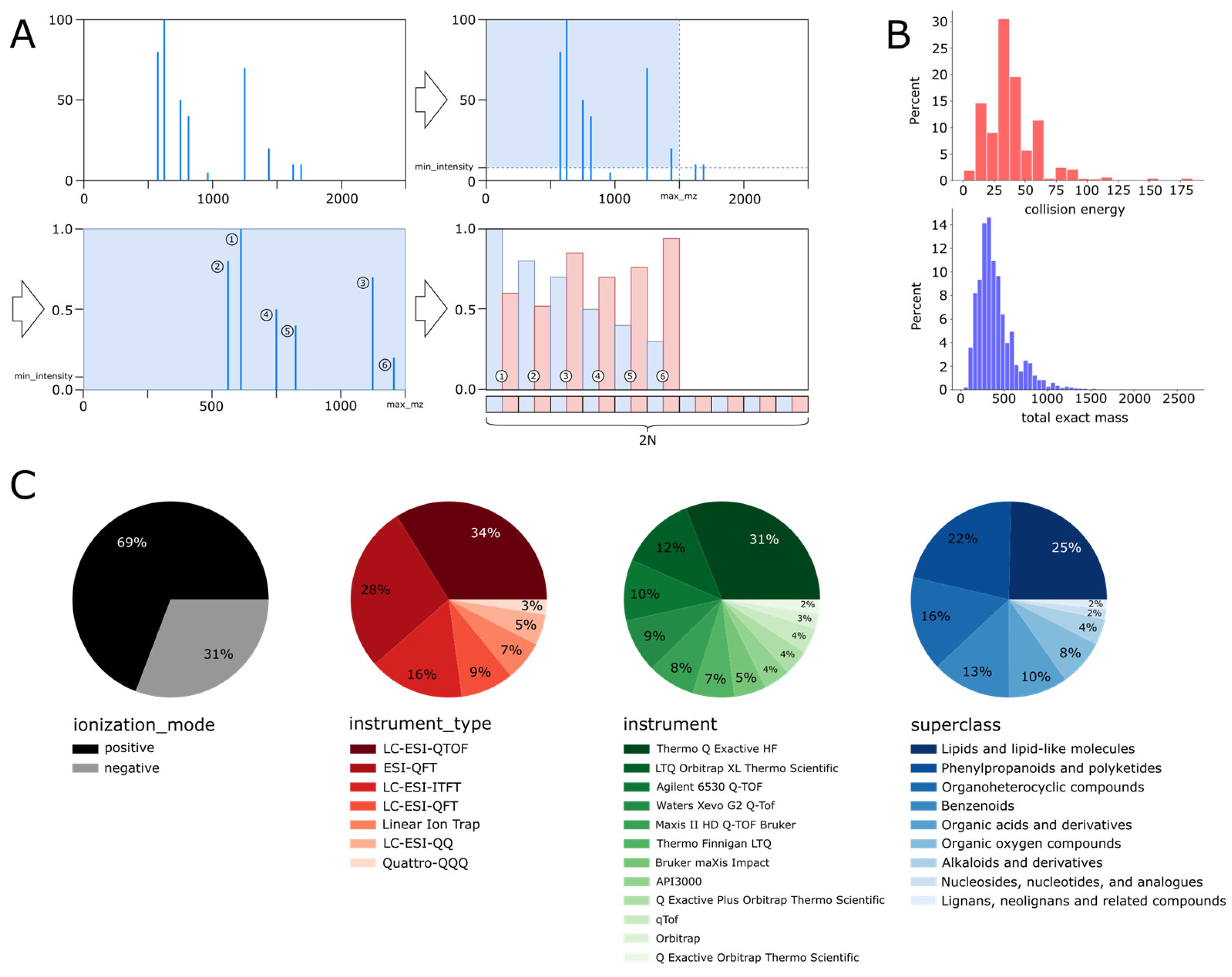
17]. Binning is most suitable for low-mass resolution instruments where discretization of mass up to 0.1 Da for large mass ranges can be used without incurring large memory overheads. However, binning is not suitable for high-mass resolution instruments where critical mass information is thrown away during the discretization process (e.g., isotope natural abundance ratios that can provide unambiguous chemical formulae) or spectrum mass ranges are limited (e.g., to less than 1000 Da precluding many larger natural products) due to memory limitations. We developed a sparse representation of the MS/MS spectrum consisting of vectorized pairs of mass and intensity values that overcome the limitations of binning by making use of the full instrument mass resolution and scan ranges while being highly memory efficient.
In
Section 3.1, we validated the suitability of sparse representation of spectra by performing machine learning experiments that involved training many classification and regression models on MoNA and HMDB datasets to predict MS/MS parameters (also referred to as factors), using MS/MS spectrum and the remaining factors as input features.
We assessed the influence of the data preprocessing parameters, e.g., the maximum number of peaks allowed in the vector representation of a spectrum, the minimum intensity of an individual peak, etc. (see
Section 2.5), as well as the BetaVAE model hyperparameters, e.g., regularization parameter beta, number of fully connected layers in the network, etc., on the reconstruction quality. The objective function of the BetaVAE model can be divided into two elements. The first is the reconstruction term, which encourages the model to learn latent representations z from the data samples x and reconstruct them accurately as x’, and the second is the KL divergence term, which encourages the inferred posterior distribution to match the prior distribution. Beta is a regularization parameter that changes the proportion of divergence term in the loss function, and if that value is greater than 1, it prioritizes learning disentangled representations of the input samples. In this experiment, we explored only the reconstruction term of the BetaVAE objective function; specifically, we investigated how model and data hyperparameters affected the reconstruction quality of the BetaVAE model. We used 4 metrics to evaluate the reconstruction quality of the data samples: cosine similarity, Euclidean distance, percentage change, and percentage difference. We used average reconstruction scores for the baseline metrics (see
Section 2.3).
In
Section 3.2, we trained classification and regression networks jointly with the Variational Autoencoder. The input for the BetaVAE model was the MS/MS spectrum, which was first compressed by the contracting encoder network to create a low-dimensional representation of the spectrum, also known as the latent representation, which was subsequently decompressed back to the spectrum by the decoder network which reconstructs the input spectrum. The compressed encoding of a spectrum was simultaneously passed to the downstream classification/regression model, and similarly to the previous experiments that involved predicting a factor associated with the MS/MS spectrum from the dataset, the input consisted of the compressed encoding of a spectrum (instead of the spectrum) and other factors from the dataset. The aim of this experiment was to verify the assertion that the latent representation of the MS/MS spectrum carries the same information as the spectrum; hence, the prediction performance achieved in the latent space should be comparable to those performed in the input space. Similar to the previous experiment, we analyzed the performance and PFI of the downstream models, and we compared the outcome with the corresponding models trained only on spectra.
In
Section 3.3, we investigated the principal relations between 10 factors associated with each MS/MS spectrum in the MoNA dataset, e.g., collision energy, instrument type, etc. On that account, we cross-correlated these factors to observe whether any pair was correlated and, if so, to what degree.
Next, we trained a set of classification and regression networks that predicted a factor from the dataset. The input to each model was a vector composed of an MS/MS spectrum concatenated with all remaining factors from the dataset, except for the factor that we used to predict, referred to as the target factor. Consequently, we had 7 classification and 3 regression task categories, depending on whether the factor was modeled as a continuous or discrete variable, e.g., a classifier that predicted the ionization mode from the spectrum and 9 remaining features, a regressor that predicted collision energy value from the spectrum and other 9 remaining features, and so on. In addition, we tuned the data preprocessing parameters for each task category to observe the impact of these parameters on the performance of the models.
Further, we trained a set of classification and regression networks jointly with the BetaVAE on the latent encoding of the spectra instead of the spectra themselves. Similar to the previous settings, the input to each model was a vector composed of a latent encoding of the MS/MS spectrum concatenated with all remaining factors from the dataset.
And finally, we analyzed trained models with regard to their performance and the permutation feature importance (PFI) [
18]. The latter metric provided us with a notion of the relative importance of the feature with respect to the target variable in the classification or regression task, i.e., to what extent the given input feature impacted the accuracy of the model, e.g., while predicting the ionization mode, what was the impact of the collision energy or precursor type on that prediction.
The above strategies provided us an opportunity to compare model performances when trained on spectra against those trained in the latent space of the BetaVAE model. In the context of the feature importance, it provided us with the ability to observe whether the latent space of the BetaVAE promoted certain factors in the classification/regression more than others and see what these factors were.
In
Section 3.4, we investigated the impact of the regularization factor beta on the points in the latent space of the BetaVAE model. The goal of the analyses was to provide insights into the latent space of the selected BetaVAE models trained on the MS/MS data, i.e., how data points were located in the latent space and how they related to the MS/MS factors, e.g., total exact mass, collision energy, etc. Visualization methods were used to build intuition about the structure of the latent space for a subset of the MoNA dataset by encoding spectra to the latent space using the encoder network and then projecting the latent space into a reduced 2D space using PCA. Moreover, we investigated if points in the latent space were distributed according to continuous factors, specifically total exact mass and collision energy. We examined if they could be clustered by any of the categorical factors, especially instrument type.
In
Section 3.5, we investigated the shape of BetaVAE and JointVAE latent spaces. We used a two-step latent traversal method to qualitatively evaluate the newly generated samples and investigate the latent space of the BetaVAE and JointVAE. First, the latent points were sampled evenly across the selected line or plane from the set of latent dimensions; second, the points were fed to the decoder network to generate the spectra). We chose to sample points in the 2D plane after fixing the third dimension in order to create a 2D grid visualization of generated spectra, which provided better intuition about the quality and shape of the latent space.
In
Section 3.6, we investigated the semantics of the latent space through interpolation. In the previous experiment, we showed examples of traversal across orthogonal directions parallel to the main axes of the latent space. However, in the high-dimensional continuous latent spaces, the linear interpolation might sample points from regions that are extremely unlikely given the Gaussian prior. Alternatively, the spherical linear interpolation (slerp), i.e., a path on the great circle of an N-dimensional sphere that corresponds to an arc linking two points, is more likely to sample in the proximity of high probability [
19]. Slerp was used to verify the BetaVAE model’s generalization ability to synthesize valid spectra not found in the training dataset. The method developed allows one to take advantage of the continuity of the chemical space, in this case, using only the mass spectrum modality of the chemical compounds and sample novel spectra.
In
Section 3.7, we investigated the suitability of current disentanglement metrics on model selection. The best metrics to measure disentanglement in generative models is an open and active area of research that does not yet have a definitive conclusion. Therefore, due to differences in definitions of the disentangled representations and the contention between researchers on how to quantify the disentanglement, we used 3 different disentanglement metrics that have been widely cited by the community to quantify the degree to which selected models achieved disentangled representations: BetaVAE [
12], FactorVAE [
20], and MIG [
21]. In our study, we evaluated metrics on MoNA and HMDB datasets and BetaVAE and JointVAE model types. First, we analyzed how much the existing disentanglement scores agreed and how much they varied across different model/preprocessing parameters. This analysis allowed us to address how important different hyperparameters were for disentanglement. Second, we analyzed whether disentanglement metrics could be used for model selection. Specifically, we focus on whether we could reliably and consistently distinguish bad and good models using the disentanglement metrics. Note that while running our experiments, we separated the impact of the regularization factor (beta in the BetaVAE model, gamma in the JointVAE models), the maximum number of peaks, and model architecture from other inductive biases, e.g., learning rate, epochs, optimizer, normalization, etc. This approach allowed us to limit the number of variables that would impact those scores but had no intrinsic value with reference to the actual representation.
In
Section 3.8, we developed an approach to uncover the factors of variations for MS/MS spectra encoded in the latent space. Unlike MNIST or other machine vision datasets, it is difficult to identify the true underlying factors of variation in mass spectrometry as the data are too complicated and high-dimensional to easily visualize and compare between samples. Therefore, we sought to develop an approach for better determining if select factors have been disentangled without the need for visual intuition. Given that the selected attributes are true factors of variation and that the BetaVAE model, in fact, achieves the disentanglement, we expect these factors to correlate with the latent variables, i.e., a coordinate Z
i of the low-dimensional latent representation Z of the spectrum. We found this method to have special applications for modalities such as mass spectra where the factors cannot be observed directly in the input space. In the correlation analysis, devised to test whether the disentanglement is true or not with reference to the assumed factors, each factor F
i must correlate with a distinct latent variable Z
j. Note that
distinct means that each factor correlates only with one latent variable exclusively (i.e., no other factors correlate with the same latent variable). In an ideal example, each factor F
i would correlate strongly with only one distinct latent variable Z
j, and the same factor would have a very weak or absent correlation with the remaining latent variables.
Next, we determined how consistent the above observation was across a subset of the MoNA dataset, and we summarized results in the form of distributions of correlation coefficients. The method developed provided us with tools to compute a comprehensive overview of all cases, helped us to conclude which factor correlated with the latent variable stronger, and provided insights into our notion of distinctiveness.
2.2. Model Design and Architecture
The classification and regression tasks used deep neural networks. Depending on the target variable and the input features, the input and the output of the models varied in size. The number of intermediate layers also varied from model to model. Therefore, the exact number and sizes of layers in the model were included in the
Supplementary Tables along with other model/training parameters and resulting metrics. Each layer was a fully connected layer followed by a batch normalization [
22] and nonlinear activation function ReLU, with the only exception for the output layer, which did not use batch normalization and consisted of a linear activation. All classification and regression models obeyed the same principle with regard to how the model was constructed.
Other experiments used the Variational Autoencoder (VAE) [
8], specifically two modifications of the basic framework, i.e., BetaVAE and JointVAE [
12,
13]. The VAE model is a deep generative model (DGM), which is able to approximate the underlying high-dimensional and complex data distribution P(X) on the given dataset X with the i.i.d. samples x. The neural network fully parameterizes the target probability distribution; thus, finding the P(X) is posed as the optimization problem that can be solved with stochastic gradient descent (SGD) [
9,
23]. The VAE model consists of the encoder network that approximates the posterior probability q(z|x) and the decoder network that approximates the likelihood probability p(x|z). The VAE optimizes the evidence lower bound, also known as the ELBO [
9].
The BetaVAE model introduces a hyperparameter beta that modifies the proportion of the Kullback–Leibler divergence component in the VAE loss function. In the special case when beta = 1, the BetaVAE reduces to the VAE model. The parameter beta is a regularization factor: when beta > 1, the network emphasizes the KL divergence more, exerting pressure on the posterior q(z|x) to match the prior p(z). This, however, comes at the cost of reconstruction quality, i.e., the bigger the beta value, the worse the reconstruction quality (Figure 4) [
12]. The BetaVAE automatically discovers independent and interpretable continuous latent representations in a completely unsupervised manner [
24], and the JointVAE extends this idea to model both continuous and discrete latent variables (at least for synthetic computer vision benchmark datasets).
The JointVAE framework learns disentangled continuous and discrete representations, i.e., it allows one to model both continuous and categorical factors. The loss function incorporates discrete and continuous KL divergence terms. However, direct optimization of the objective function often ignores the discrete component. The solution to this particular problem is to introduce a capacity parameter that is separate for the discrete and continuous channels, which controls the amount of information carried in each channel. As the training progresses, the capacity grows and encourages the gradual exploration of factors [
13].
Our implementation of the VAE models was similar to the classification and regression models, parameterized model architecture by the number of layers and their sizes as a model configuration. The VAE models consisted of a top–down encoder network and a bottom–up inference decoder network. Both encoder and decoder layers were fully connected, followed by batch normalization and nonlinear activation function ReLU. The exceptions were the last layer of the encoder, where no activation function was applied, and the output layer of the decoder, where the activation function was sigmoid and no batch normalization was used.
In tasks that involved training a downstream classification/regression model using the latent encodings of the spectra and simultaneously training the BetaVAE model, referred to before as joint training, we combined the loss functions of the downstream predictive model and the upstream autoencoder. Specifically, the loss function was a sum of the BetaVAE objective and the downstream model objective, e.g., in the case of the regressor as the downstream model, the new objective was a sum of the MSE value and the BetaVAE loss value. The architecture of the downstream classification/regression and the BetaVAE models followed the same logic as described above.
2.3. Qualitative and Quantitative Approach to Validate Models
In order to systematically quantify the performance of numerous training tasks and to be able to effectively compare resulting models, we used appropriate metrics as described in the next sections. We divided our evaluation approach into three major categories, i.e., supervised learning, spectra reconstruction, and disentanglement analysis.
2.3.1. Assessment of Supervised Models
In all supervised learning tasks, such as classification and regression, we used standard metrics to evaluate models. For classification models, accuracy, balanced accuracy, recall macro, precision macro, and F1 score were used. For regression models, MSE, RMSE, MAE, R2 (coefficient of determination), and explained variance score were used. Additionally, we used permutation feature importance (PFI) to assess the influence of the features on the model prediction. This score revealed how much information was carried within a particular feature, consequently revealing how much it contributed to the prediction.
2.3.2. Reconstruction
Evaluating VAE models can be broken down into two categories: assessing reconstruction quality and evaluating disentanglement. For the reconstruction, we use 4 different metrics, i.e., cosine similarity (cos_sim—ngular difference), Euclidean distance (eu_dist—magnitude difference), percentage change, and percentage (per_dif—absolute and relative change in value). The initial analysis of the reconstruction scores gave rise to concerns about the ambiguity of the values of the 4 different metrics. Specifically, none of the metrics revealed how a particular reconstruction output deviated from the average reconstruction, i.e., in the case when the autoencoder reconstructs averages of the samples in the dataset.
To establish a baseline value for each metric in the reconstruction task, we propose a new metric, namely average reconstruction score, that depends solely upon the data preprocessing parameters. Consequently, the average reconstruction score is not a model evaluation metric but a baseline metric. The definition of the metric is the following: given a dataset,
with samples
, find the average sample
and compute
where the
score is any of the 4 above-listed metrics. Finally, the input spectrum and reconstructed spectrum were plotted side by side for a visual comparison for qualitative reconstruction assessment.
2.3.3. Disentanglement
The most recent advances in learning disentangled representations allowed us to verify the degree to which models were able to find such representations or states with a degree of certainty otherwise. Visualization can be used as a first approximation to qualitatively assess the degree of disentanglement. Given that the inference network was trained to reconstruct samples well, i.e., the model had a small reconstruction error, we can select a set of latent points, reconstruct them with the decoder network, and compare results by plotting obtained novel data samples. Moreover, to build an intuition about the latent space, we traversed linearly through the latent space by mutating a single coordinate and keeping the remaining coordinates fixed. If the reconstructed samples showed a gradual change of a single factor, then the latent representation was considered disentangled.
While visualization is an adequate technique in the analysis only if the data samples are images, it might be inappropriate for all modalities. Another disadvantage is that the visualization does not provide any tools for automated search for models that might exhibit the desired property. Disentanglement metrics (DM) are designed to overcome this disadvantage by quantifying the disentanglement as the numerical score. In this work, we considered three scores: (1) the BetaVAE metric [
12] captures disentanglement as the accuracy of a classifier that predicts the index of a generative factor; (2) FactorVAE [
20], an improvement to the previous metric, uses majority vote classifier and accounts for the edge case in the BetaVAE metric; and (3) Mutual Information Gap (MIG) [
21], the information-theoretic score, for each factor of variation, measures the normalized gap in mutual information between the highest and the second-highest coordinate in latent representation.
2.4. Datasets and Feature Selection
In this study, we considered two tandem mass spectra (MS/MS) datasets: MoNA and HMDB [
2,
3]. The first dataset is composed of fragmentation spectra from the MoNA library and incorporates multiple factors of variation. Specifically, a combination of instrument types, range of collision energies, compound mass, and positive or negative ionization modes. The dataset was composed of 125,831 samples, whereby 86,381 were in positive ionization mode, and 38,965 were in negative ionization mode. Altogether, the dataset represented 15,956 compounds with a unique InChIKey identifier. The MoNA dataset is also extremely unbalanced with respect to instrument type category, as depicted in
Figure 1C. The major 6 distinct instrument classes constitute around 92% of the entire dataset, while the remaining 34 classes make up merely 8%.
The second dataset was picked from the HMDB library and represented fewer factors of variation. Specifically, compared to its previous counterpart, all 92,916 fragmentation spectra corresponded to a single instrument type. The dataset did not include other features, e.g., total exact mass, precursor type, precursor m/z, etc. Nevertheless, it is perfectly balanced for the ionization mode category, and collision energy values selected collision energies and were chosen. The dataset represents 15,486 unique metabolites with 6 different spectra for each compound. There are 3 spectra per ionization mode, within which each spectrum has a distinct collision energy value, i.e., 10, 20, and 40.
Both of the sets are additionally supplemented with the compound classification metadata, i.e., kingdom, superclass, class, and subclass, provided by the ClassyFire computational tool [
25].
2.5. Data Processing and Spectrum Representation
The MS/MS spectrum consists of arbitrarily many peaks located on the continuous mass-to-charge (m/z) axis. Therefore, an accurate representation of the spectrum has an inherently sparse nature. For example, spectra in the MoNA dataset had, on average, 260 peaks, with a median of 33 peaks, a minimum of 1 peak, and a maximum of 110,235 peaks. In the case of the HMDB dataset, spectra had roughly 28 peaks on average, with a median of 31 peaks, a minimum of 1 peak, and a maximum of 31 peaks.
Many machine learning models can benefit from having their input converted into a dense, vectorized form. Several preprocessing operations for modeling mass fragmentation spectra were taken and can be broken down into two categories: (1) filters that alter the inner structure of the spectrum, i.e., accept or reject peaks according to specified conditions, and (2) transformations that modify the internal values of the spectrum, without changing its structure. One filter was the minimum and the maximum possible value for the m/z, limiting the mass range. Another filter imposed a minimum peak intensity threshold. We assumed that peaks of a larger relative abundance are more likely to carry more information than peaks with a smaller relative abundance and will more likely be conserved across instruments, instrument settings, and sample matrices. We sorted peaks by their intensity value in descending order and took the top N peaks. The latter filter brings all MS/MS spectra to the same maximum length, i.e., the number of peaks per sample.
We used two transformations, one that projected intensities and m/z values into the range [0, 1] and another that used dynamic range expansion. Specifically, our preprocessing workflow was the following: First, we defined the following filtering operations:
Reject peaks below the threshold min_intensity parameter;
Reject peaks with m/z values above the max_mz parameter;
Limit the number of peaks in the spectrum to N = max_num_peaks top intensity peaks, i.e., sort peaks by the intensity value in the descending order and take the first N instances.
Second, we applied the following transformations:
Project intensity and m/z values into the range [0, 1];
Normalize intensity of peaks, i.e., rescale all peaks into the range [min_intensity, 100]. If there is only one peak, no rescaling is applied.
Finally, a spectrum was represented as a vector. Each peak was structured as a 2D vector where the first dimension was the
m/
z and the second dimension was the intensity value. To form a full spectrum, the peak vectors were concatenated in descending order with reference to intensity. The spectrum with N peaks was encoded as a vector with 2N cells.
Figure 1A depicts the spectra preprocessing pipeline. This representation of spectra allows for expressing
m/
z and intensity accurately with the real numbers. Recently, a similar dense spectral representation was applied to the analysis of proteomics data [
26].
2.6. Model Training and Hyperparameter Tuning
All experiments involving training deep neural networks utilized the Adam optimizer with a learning rate of 1 × 10−3. While training and evaluating classification models, we considered class imbalances in our datasets. To minimize the impact of class disproportions, we used a weighted random sampler approach, which ensured that a batch consisted of a similar number of instances from each class, minimizing the class disparity at the batch level. This method provided better results consistently for binary and multi-class classification tasks, even if the ratio of minor class to major class was smaller than 0.1. Other methods, such as class weights, which is a method that modifies the loss function behavior by weighting the loss of smaller classes in the case of cross-entropy, often cause unstable training observed as jittering loss function across epochs.
We used GPU implementations of metrics while evaluating our models; this way, we minimized the data transfer between GPU and CPU devices, especially in cases when the training ran entirely on the GPU. Metrics such as permutation feature importance and correlation scores were computed on the CPU. All models were trained using Intel Xeon Gold Series CPU, 500 GB of RAM, and 4 GPUs NVidia Tesla A100 with a total of 160 GB of memory. Altogether, we trained over 16,180 models, worth 2 months of continuous training: 600 classifiers, 230 regressors, and 630 classifiers trained jointly with the VAE model; 380 regressors trained jointly with the VAE model; 1220 BetaVAE models; 10,680 BetaVAE models with lower capacity; and 2430 JointVAE models.