Pulling Forces Differentially Affect Refolding Pathways Due to Entangled Misfolded States in SARS-CoV-1 and SARS-CoV-2 Receptor Binding Domain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sequences of SARS-CoV-1 and SARS-CoV-2 RBDs
2.2. Prediction of SARS-CoV-1 RBD and SARS-CoV-2 RBD Structures
2.3. Molecular Dynamics (MD) Simulation
2.4. Coarse-Grained Model and Details of Refolding Simulation
2.5. Determining Folded Trajectories and Calculating the Folding Time
2.6. Identification of Entanglements and Characterization of Misfolded Structure Through Changes in Entanglement
2.7. Identification of Folding Pathways
3. Results and Discussions
3.1. Determination of Structure of SARS-CoV-1 and SARS-CoV-2 RBDs
3.2. SARS-CoV-2 RBD Folds More Effectively Than SARS-CoV-1 RBD
3.3. SARS-CoV-2 RBD Is More Sensitive to Force Than SARS-CoV-1 RBD
3.4. Misfolded Intermediates with Altered Entanglement Are Present During Folding of SARS-CoV-1 RBD and SARS-CoV-2 RBD
3.5. External Force Helps SARS-CoV-1 RBD to Explore More Efficiently Folding Pathways, Avoiding Misfolded States with Non-Native Entanglements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baiesi, M.; Orlandini, E.; Seno, F.; Trovato, A. Exploring the correlation between the folding rates of proteins and the entanglement of their native states. J. Phys. A Math. Theor. 2017, 50, 504001. [Google Scholar] [CrossRef]
- Salicari, L.; Baiesi, M.; Orlandini, E.; Trovato, A. Folding kinetics of an entangled protein. PLoS Comput. Biol. 2023, 19, e1011107. [Google Scholar] [CrossRef] [PubMed]
- Nissley, D.A.; Jiang, Y.; Trovato, F.; Sitarik, I.; Narayan, K.B.; To, P.; Xia, Y.; Fried, S.D.; O’brien, E.P. Universal protein misfolding intermediates can bypass the proteostasis network and remain soluble and less functional. Nat. Commun. 2022, 13, 3081. [Google Scholar] [CrossRef]
- Jiang, Y.; Neti, S.S.; Sitarik, I.; Pradhan, P.; To, P.; Xia, Y.; Fried, S.D.; Booker, S.J.; O’brien, E.P. How synonymous mutations alter enzyme structure and function over long timescales. Nat. Chem. 2023, 15, 308–318. [Google Scholar] [CrossRef]
- Fernandez, J.M.; Li, H. Force-clamp spectroscopy monitors the folding trajectory of a single protein. Science 2004, 303, 1674–1678. [Google Scholar] [CrossRef]
- Li, M.S.; Hu, C.-K.; Klimov, D.K.; Thirumalai, D. Multiple stepwise refolding of immunoglobulin domain I27 upon force quench depends on initial conditions. Proc. Natl. Acad. Sci. USA 2006, 103, 93–98. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.; Zhao, X.; Li, J.; Niu, P.; Yang, B.; Wu, H.; Wang, W.; Song, H.; Huang, B.; Zhu, N.; et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: Implications for virus origins and receptor binding. Lancet 2020, 395, 565–574. [Google Scholar] [CrossRef]
- Wrapp, D.; Wang, N.; Corbett, K.S.; Goldsmith, J.A.; Hsieh, C.-L.; Abiona, O.; Graham, B.S.; McLellan, J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020, 367, 1260–1263. [Google Scholar] [CrossRef]
- Walls, A.C.; Park, Y.-J.; Tortorici, M.A.; Wall, A.; McGuire, A.T.; Veesler, D. Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein. Cell 2020, 181, 281–292.e6. [Google Scholar] [CrossRef]
- Shang, J.; Ye, G.; Shi, K.; Wan, Y.; Luo, C.; Aihara, H.; Geng, Q.; Auerbach, A.; Li, F. Structural basis of receptor recognition by SARS-CoV-2. Nature 2020, 581, 221–224. [Google Scholar] [CrossRef]
- Lan, J.; Ge, J.; Yu, J.; Shan, S.; Zhou, H.; Fan, S.; Zhang, Q.; Shi, X.; Wang, Q.; Zhang, L.; et al. Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor. Nature 2020, 581, 215–220. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.L.; Lan, P.D.; Thai, N.Q.; Nissley, D.A.; O’Brien, E.P.; Li, M.S. Does SARS-CoV-2 bind to human ACE2 more strongly than does SARS-CoV? J. Phys. Chem. B 2020, 124, 7336–7347. [Google Scholar] [CrossRef] [PubMed]
- Prentiss, M.C.; Wales, D.J.; Wolynes, P.G. The energy landscape, folding pathways and the kinetics of a knotted protein. PLoS Comput. Biol. 2010, 6, e1000835. [Google Scholar] [CrossRef] [PubMed]
- Lim, N.C.; Jackson, S.E. Molecular knots in biology and chemistry. J. Phys. Condens. Matter 2015, 27, 354101. [Google Scholar] [CrossRef]
- Vu, Q.V.; Nissley, D.A.; Jiang, Y.; O’Brien, E.P.; Li, M.S. Is Posttranslational Folding More Efficient Than Refolding from a Denatured State: A Computational Study. J. Phys. Chem. B 2023, 127, 4761–4774. [Google Scholar] [CrossRef]
- Halder, R.; Nissley, D.A.; Sitarik, I.; Jiang, Y.; Rao, Y.; Vu, Q.V.; Li, M.S.; Pritchard, J.; O’brien, E.P. How soluble misfolded proteins bypass chaperones at the molecular level. Nat. Commun. 2023, 14, 3689. [Google Scholar] [CrossRef]
- Lan, P.D.; Nissley, D.A.; Sitarik, I.; Vu, Q.V.; Jiang, Y.; To, P.; Xia, Y.; Fried, S.D.; Li, M.S.; O’Brien, E.P. Synonymous mutations can alter protein dimerization through localized interface misfolding involving self-entanglements. J. Mol. Biol. 2024, 436, 168487. [Google Scholar] [CrossRef]
- Wang, J.; Chitsaz, F.; Derbyshire, M.K.; Gonzales, N.R.; Gwadz, M.; Lu, S.; Marchler, G.H.; Song, J.S.; Thanki, N.; A Yamashita, R.; et al. The conserved domain database in 2023. Nucleic Acids Res. 2023, 51, D384–D388. [Google Scholar] [CrossRef]
- Madeira, F.; Madhusoodanan, N.; Lee, J.; Eusebi, A.; Niewielska, A.; Tivey, A.R.N.; Lopez, R.; Butcher, S. The EMBL-EBI Job Dispatcher sequence analysis tools framework in 2024. Nucleic Acids Res. 2024, 52, W521–W525. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Cianfrocco, M.A. COSMIC2: A global resource for structure prediction and structural analysis. Biophys. J. 2024, 123, 334a–335a. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Spoel, V.D. Gromacs 2020.5 Source Code; Zenodo: Geneva, Switzerland, 2021. [Google Scholar]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- O’Brien, E.P.; Christodoulou, J.; Vendruscolo, M.; Dobson, C.M. Trigger factor slows co-translational folding through kinetic trapping while sterically protecting the nascent chain from aberrant cytosolic interactions. J. Am. Chem. Soc. 2012, 134, 10920–10932. [Google Scholar] [CrossRef]
- Nissley, D.A.; O’Brien, E.P.; Christodoulou, J.; Vendruscolo, M.; Dobson, C.M. Electrostatic interactions govern extreme nascent protein ejection times from ribosomes and can delay ribosome recycling. J. Am. Chem. Soc. 2020, 142, 6103–6110. [Google Scholar] [CrossRef]
- Leininger, S.E.; Trovato, F.; Nissley, D.A.; O’Brien, E.P. Domain topology, stability, and translation speed determine mechanical force generation on the ribosome. Proc. Natl. Acad. Sci. USA 2019, 116, 5523–5532. [Google Scholar] [CrossRef]
- Eastman, P.; Friedrichs, M.; Chodera, J.D.; Radmer, R.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.-P.; Simmonett, A.C.; Harrigan, M.P.; et al. OpenMM 7: Rapid development of high-performance algorithms for molecular dynamics. PLoS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, L.; Balachandran, A.P. Knots and Physics. Phys. Today 1992, 45, 91–92. [Google Scholar] [CrossRef]
- Vu, Q.V.; Sitarik, I.; Jiang, Y.; Yadav, D.; Sharma, P.; Fried, S.D.; Li, M.S.; O’Brien, E.P. A Newly Identified Class of Protein Misfolding in All-atom Folding Simulations Consistent with Limited Proteolysis Mass Spectrometry. bioRxiv 2022. [Google Scholar] [CrossRef]
- Niemyska, W.; Millett, K.C.; Sulkowska, J.I. GLN: A method to reveal unique properties of lasso-type topology in proteins. Sci. Rep. 2020, 10, 15186. [Google Scholar] [CrossRef]
- Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; Van Gunsteren, W.F.; Mark, A.E. Peptide folding: When simulation meets experiment. Angew. Chem. Int. Ed. 1999, 38, 236–240. [Google Scholar] [CrossRef]
- Chiti, F.; Stefani, M.; Taddei, N.; Ramponi, G.; Dobson, C.M. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature 2003, 424, 805–808. [Google Scholar] [CrossRef]
- Kim, Y.E.; Hipp, M.S.; Bracher, A.; Hayer-Hartl, M.; Hartl, F.U. Molecular chaperone functions in protein folding and proteostasis. Annu. Rev. Biochem. 2013, 82, 323–355. [Google Scholar] [CrossRef]
- Gupta, A.J.; Haldar, S.; Miličić, G.; Hartl, F.U.; Hayer-Hartl, M. Active cage mechanism of chaperonin-assisted protein folding demonstrated at the single-molecule level. J. Mol. Biol. 2014, 426, 2739–2754. [Google Scholar] [CrossRef]
- Grantcharova, V.; Alm, E.J.; Baker, D.; Horwich, A.L. Mechanisms of protein folding. Curr. Opin. Struct. Biol. 2001, 11, 70–82. [Google Scholar] [CrossRef]
- Hoffmann, A.; Merz, F.; Rutkowska, A.; Zachmann-Brand, B.; Deuerling, E.; Bukau, B. Trigger factor forms a protective shield for nascent polypeptides at the ribosome. J. Biol. Chem. 2006, 281, 6539–6545. [Google Scholar] [CrossRef]
- Sekhar, A.; Rosenzweig, R.; Bouvignies, G.; Kay, L.E. Hsp70 biases the folding pathways of client proteins. Proc. Natl. Acad. Sci. USA 2016, 113, E2794–E2801. [Google Scholar] [CrossRef] [PubMed]
- Elms, P.J.; Chodera, J.D.; Bustamante, C.; Marqusee, S. The molten globule state is unusually deformable under mechanical force. Proc. Natl. Acad. Sci. USA 2012, 109, 3796–3801. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, B.; Elms, P.J.; Bustamante, C.; Marqusee, S. Direct observation of a force-induced switch in the anisotropic mechanical unfolding pathway of a protein. Proc. Natl. Acad. Sci. USA 2012, 109, 17820–17825. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Li, H. Polyprotein of GB1 is an ideal artificial elastomeric protein. Nat. Mater. 2007, 6, 109–114. [Google Scholar] [CrossRef]
- Carrion-Vazquez, M.; Oberhauser, A.F.; Fowler, S.B.; Marszalek, P.E.; Broedel, S.E.; Clarke, J.; Fernandez, J.M. Mechanical and chemical unfolding of a single protein: A comparison. Proc. Natl. Acad. Sci. USA 1999, 96, 3694–3699. [Google Scholar] [CrossRef]
- Chen, H.; Yuan, G.; Winardhi, R.S.; Yao, M.; Popa, I.; Fernandez, J.M.; Yan, J. Dynamics of equilibrium folding and unfolding transitions of titin immunoglobulin domain under constant forces. J. Am. Chem. Soc. 2015, 137, 3540–3546. [Google Scholar] [CrossRef]
- Guo, Z.; Hong, H.; Yuan, G.; Qian, H.; Li, B.; Cao, Y.; Wang, W.; Wu, C.-X.; Chen, H. Hidden intermediate state and second pathway determining folding and unfolding dynamics of GB1 protein at low forces. Phys. Rev. Lett. 2020, 125, 198101. [Google Scholar] [CrossRef]
- Lei, H.; He, C.; Hu, C.; Li, J.; Hu, X.; Hu, X.; Li, H. Single-Molecule Force Spectroscopy Trajectories of a Single Protein and Its Polyproteins Are Equivalent: A Direct Experimental Validation Based on A Small Protein NuG2. Angew. Chem. Int. Ed. 2017, 56, 6117–6121. [Google Scholar] [CrossRef]
- Su, H.; Sun, H.; Hong, H.; Guo, Z.; Yu, P.; Chen, H. Equilibrium folding and unfolding dynamics to reveal detailed free energy landscape of src SH3 protein by magnetic tweezers. Chin. Phys. B 2021, 30, 078201. [Google Scholar] [CrossRef]
- Rivera, M.; Hao, Y.; Maillard, R.A.; Baez, M. Mechanical unfolding of a knotted protein unveils the kinetic and thermodynamic consequences of threading a polypeptide chain. Sci. Rep. 2020, 10, 9562. [Google Scholar] [CrossRef]
- Rudolph, R.; Lilie, H. In vitro folding of inclusion body proteins. FASEB J. 1996, 10, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Plessa, E.; Chu, L.P.; Chan, S.H.S.; Thomas, O.L.; Cassaignau, A.M.E.; Waudby, C.A.; Christodoulou, J.; Cabrita, L.D. Nascent chains can form co-translational folding intermediates that promote post-translational folding outcomes in a disease-causing protein. Nat. Commun. 2021, 12, 6447. [Google Scholar] [CrossRef] [PubMed]
- Deuerling, E.; Bukau, B. Chaperone-assisted folding of newly synthesized proteins in the cytosol. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 261–277. [Google Scholar] [CrossRef] [PubMed]
- Pechmann, S.; Frydman, J. Evolutionary conservation of codon optimality reveals hidden signatures of cotranslational folding. Nat. Struct. Mol. Biol. 2013, 20, 237–243. [Google Scholar] [CrossRef] [PubMed]
- Wickner, S.; Maurizi, M.R.; Gottesman, S. Posttranslational quality control: Folding, refolding, and degrading proteins. Science 1999, 286, 1888–1893. [Google Scholar] [CrossRef]
- Huang, G.C.; Li, Z.Y.; Zhou, J.M.; Fischer, G. Assisted folding of D-glyceraldehyde-3-phosphate dehydrogenase by trigger factor. Protein Sci. 2000, 9, 1254–1261. [Google Scholar] [CrossRef]
- Maier, R.; Scholz, C.; Schmid, F.X. Dynamic association of trigger factor with protein substrates. J. Mol. Biol. 2001, 314, 1181–1190. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Seno, F.; Trovato, A. Sequence and structural patterns detected in entangled proteins reveal the importance of co-translational folding. Sci. Rep. 2019, 9, 8426. [Google Scholar] [CrossRef]



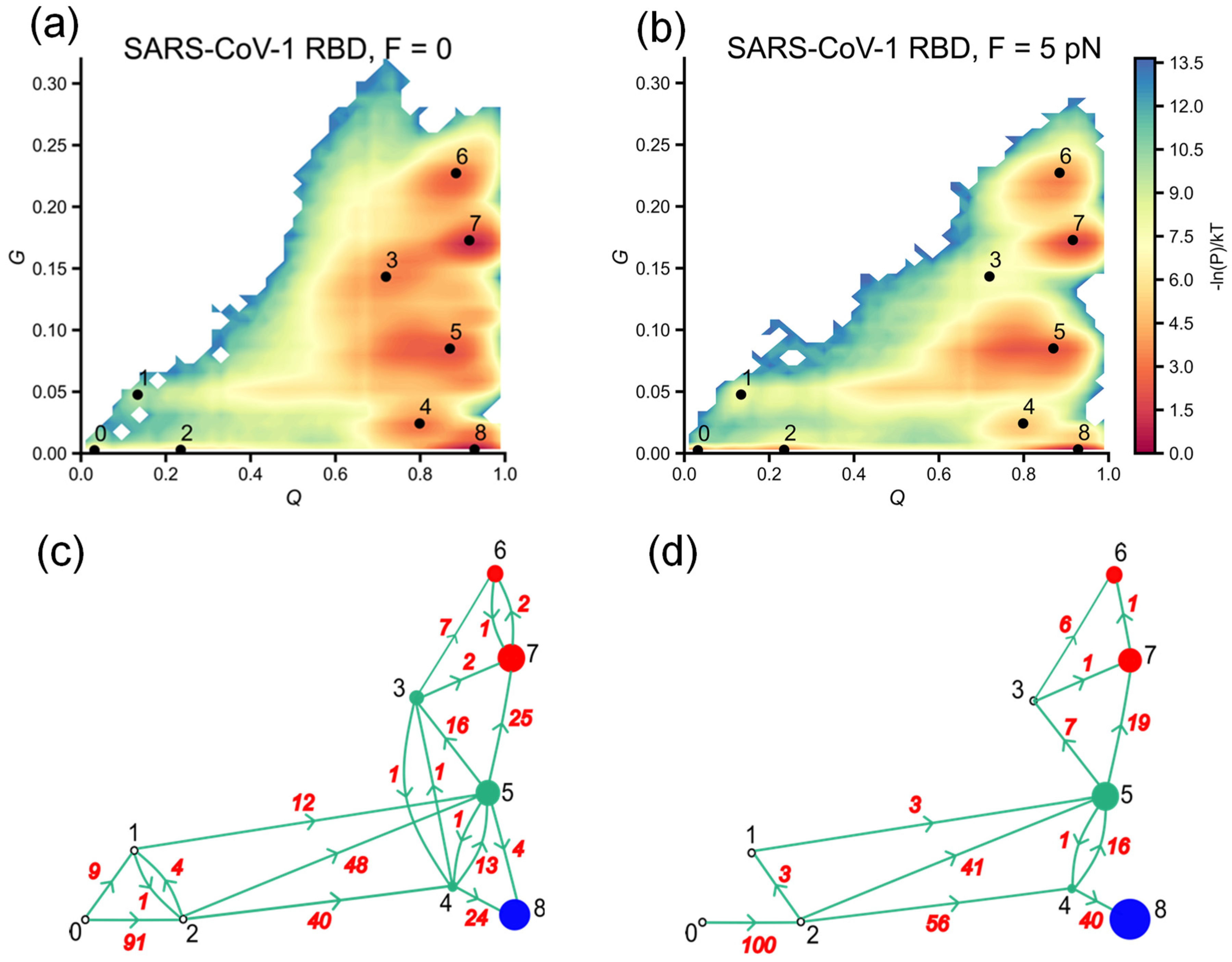
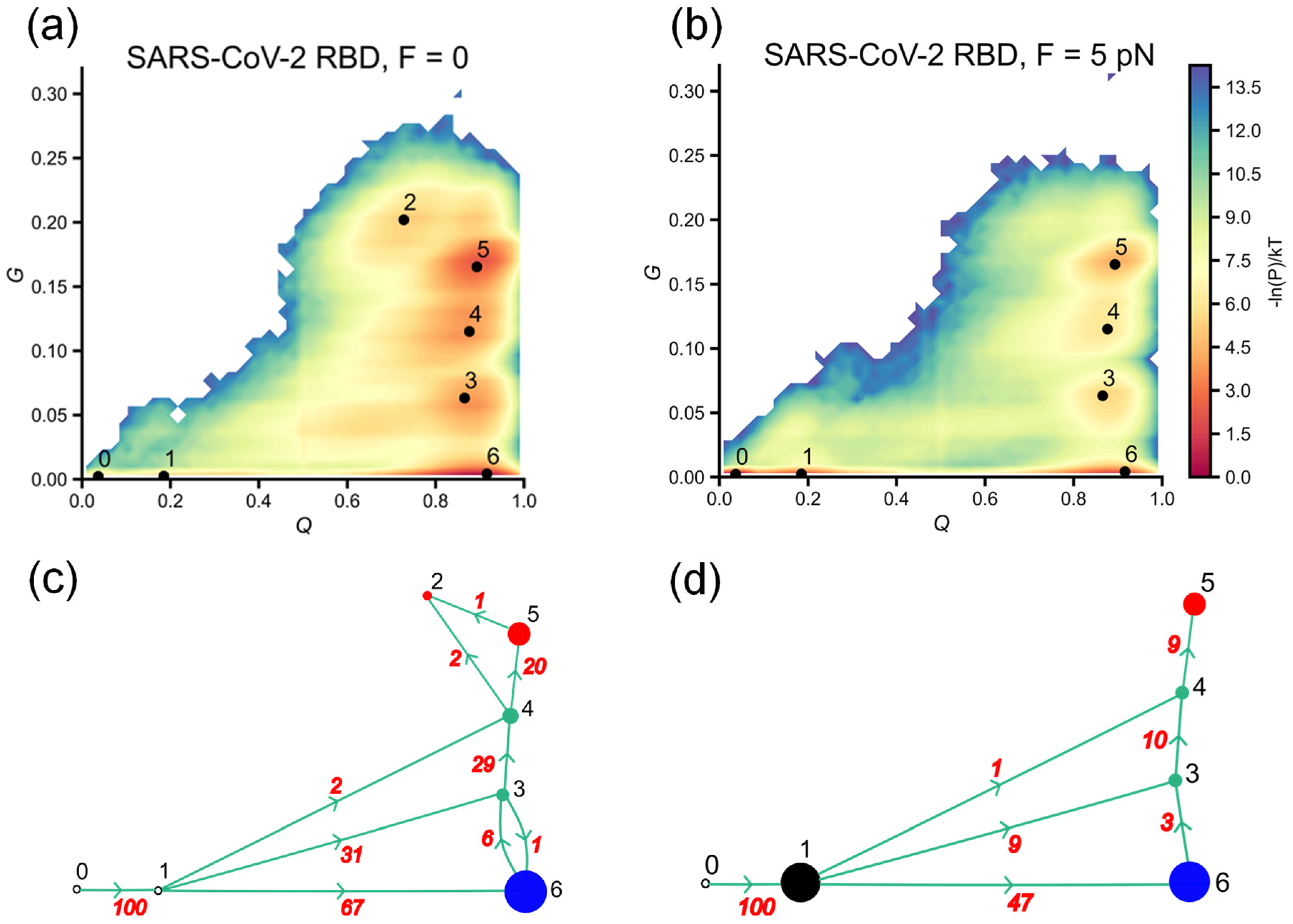
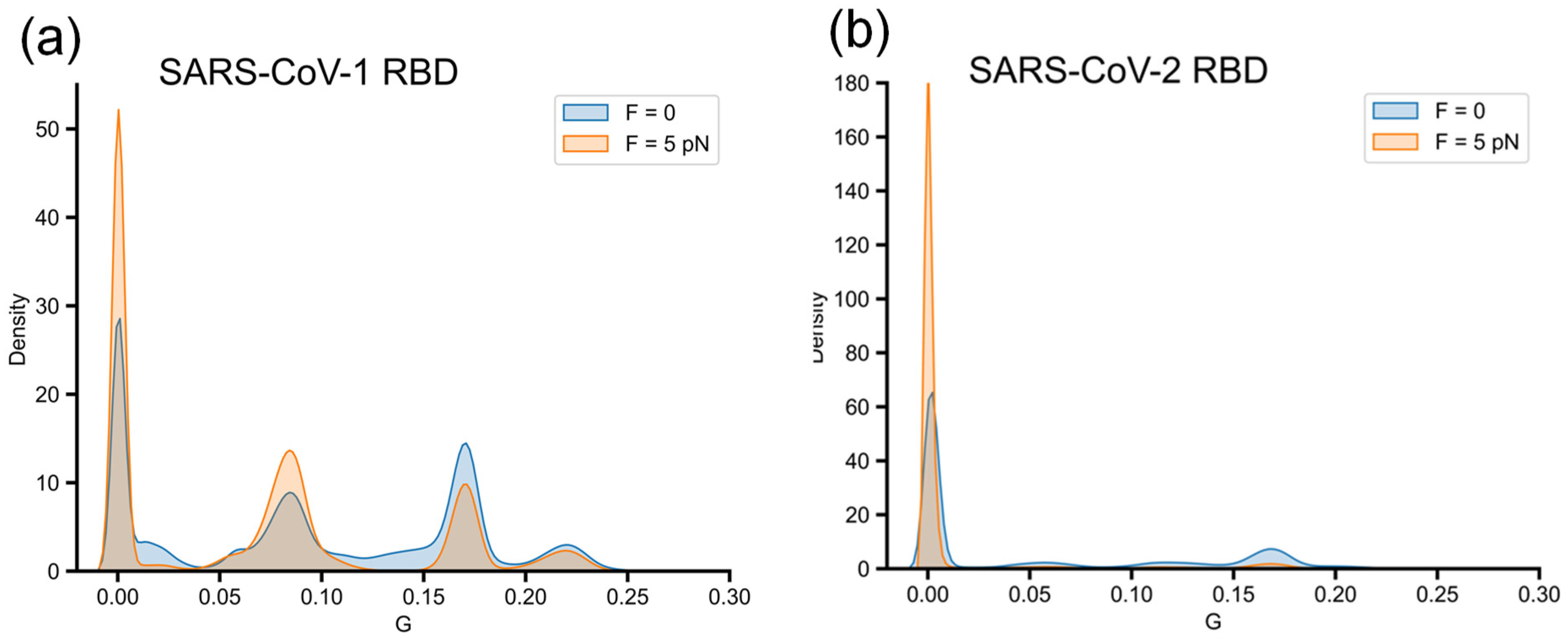
| F = 0 | F = 5 pN | ||||
|---|---|---|---|---|---|
| Protein | Qthreshold | Folded Trajectories | Folding Time (ns) | Folded Trajectories | Folding Time (ns) |
| SARS-CoV-1 RBD | 0.9306 | 56 | 369.0 | 58 | 304.95 |
| SARS-CoV-2 RBD | 0.8745 | 97 | 257.4 | 42 | 5646.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, P.D.; O’Brien, E.P.; Li, M.S. Pulling Forces Differentially Affect Refolding Pathways Due to Entangled Misfolded States in SARS-CoV-1 and SARS-CoV-2 Receptor Binding Domain. Biomolecules 2024, 14, 1327. https://doi.org/10.3390/biom14101327
Lan PD, O’Brien EP, Li MS. Pulling Forces Differentially Affect Refolding Pathways Due to Entangled Misfolded States in SARS-CoV-1 and SARS-CoV-2 Receptor Binding Domain. Biomolecules. 2024; 14(10):1327. https://doi.org/10.3390/biom14101327
Chicago/Turabian StyleLan, Pham Dang, Edward P. O’Brien, and Mai Suan Li. 2024. "Pulling Forces Differentially Affect Refolding Pathways Due to Entangled Misfolded States in SARS-CoV-1 and SARS-CoV-2 Receptor Binding Domain" Biomolecules 14, no. 10: 1327. https://doi.org/10.3390/biom14101327
APA StyleLan, P. D., O’Brien, E. P., & Li, M. S. (2024). Pulling Forces Differentially Affect Refolding Pathways Due to Entangled Misfolded States in SARS-CoV-1 and SARS-CoV-2 Receptor Binding Domain. Biomolecules, 14(10), 1327. https://doi.org/10.3390/biom14101327







