Dual-Ring SNAREpin Machinery Tuning for Fast Synaptic Vesicle Fusion
Abstract
1. Introduction
2. Materials and Methods
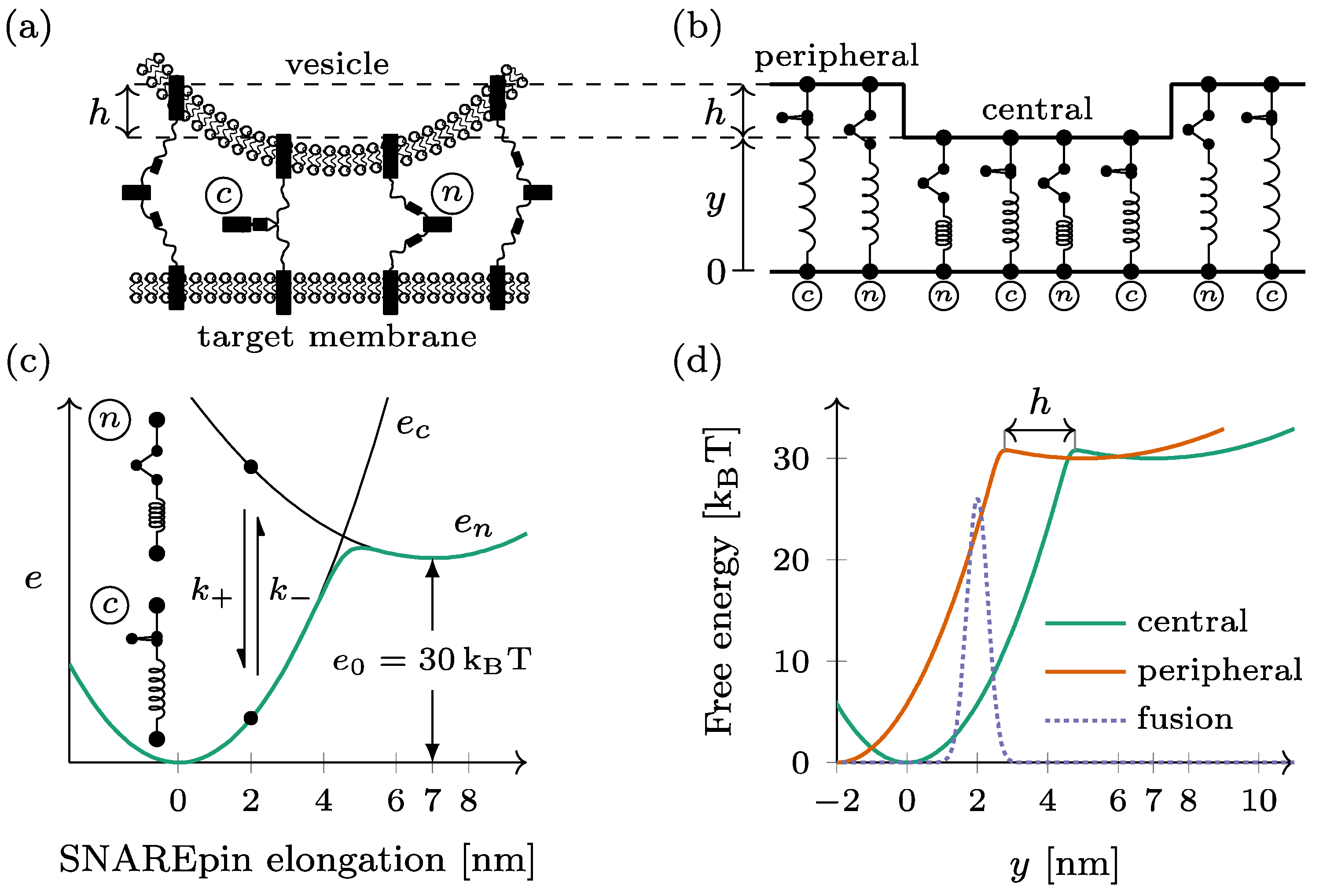
2.1. Double-Ring Mechanical Model
2.2. Fusion Dynamics
2.3. Simulations
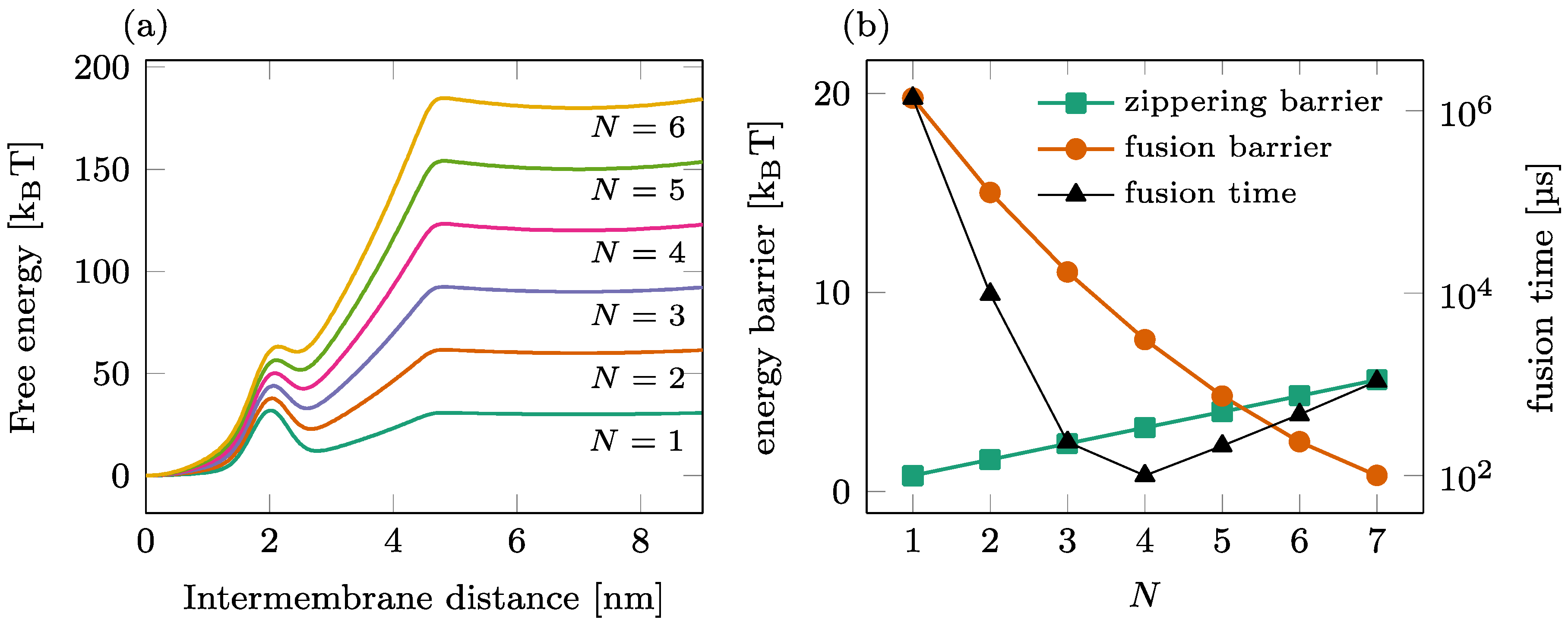
2.4. Fusion Kinetics in a Single-Ring Setting
3. Results
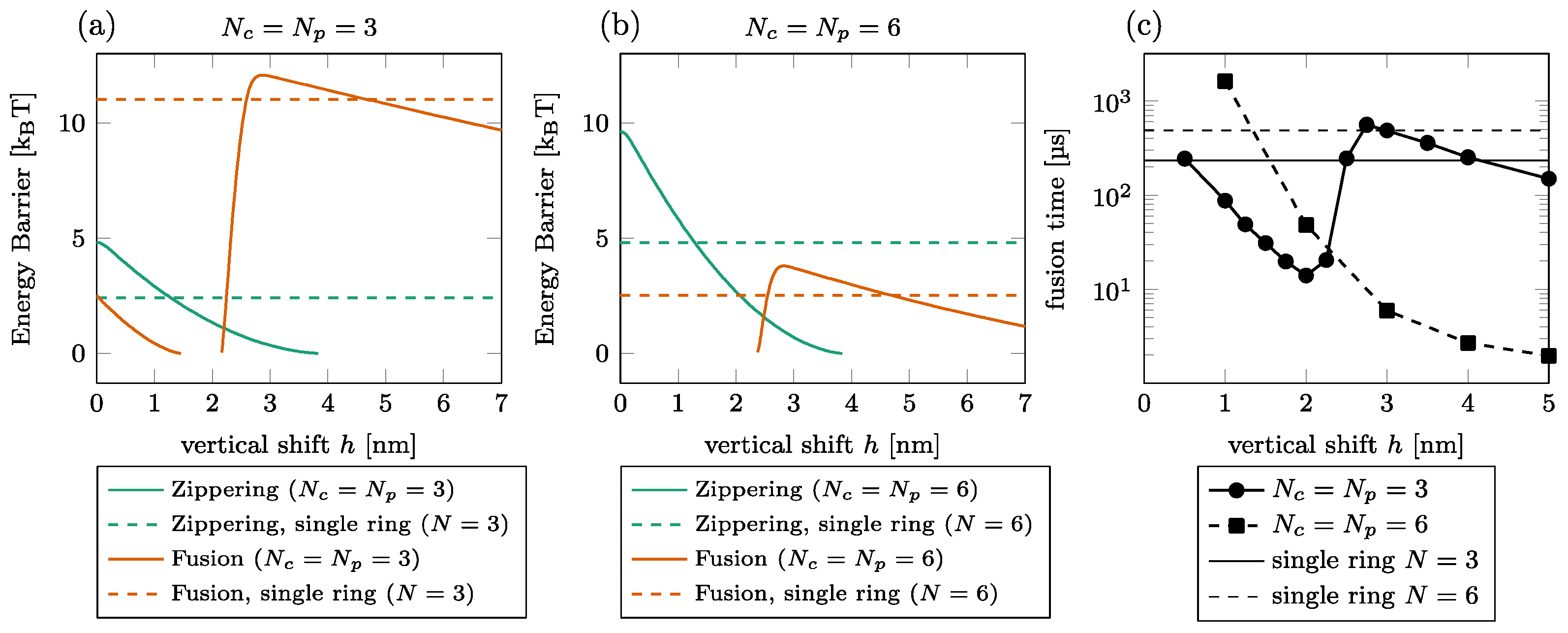
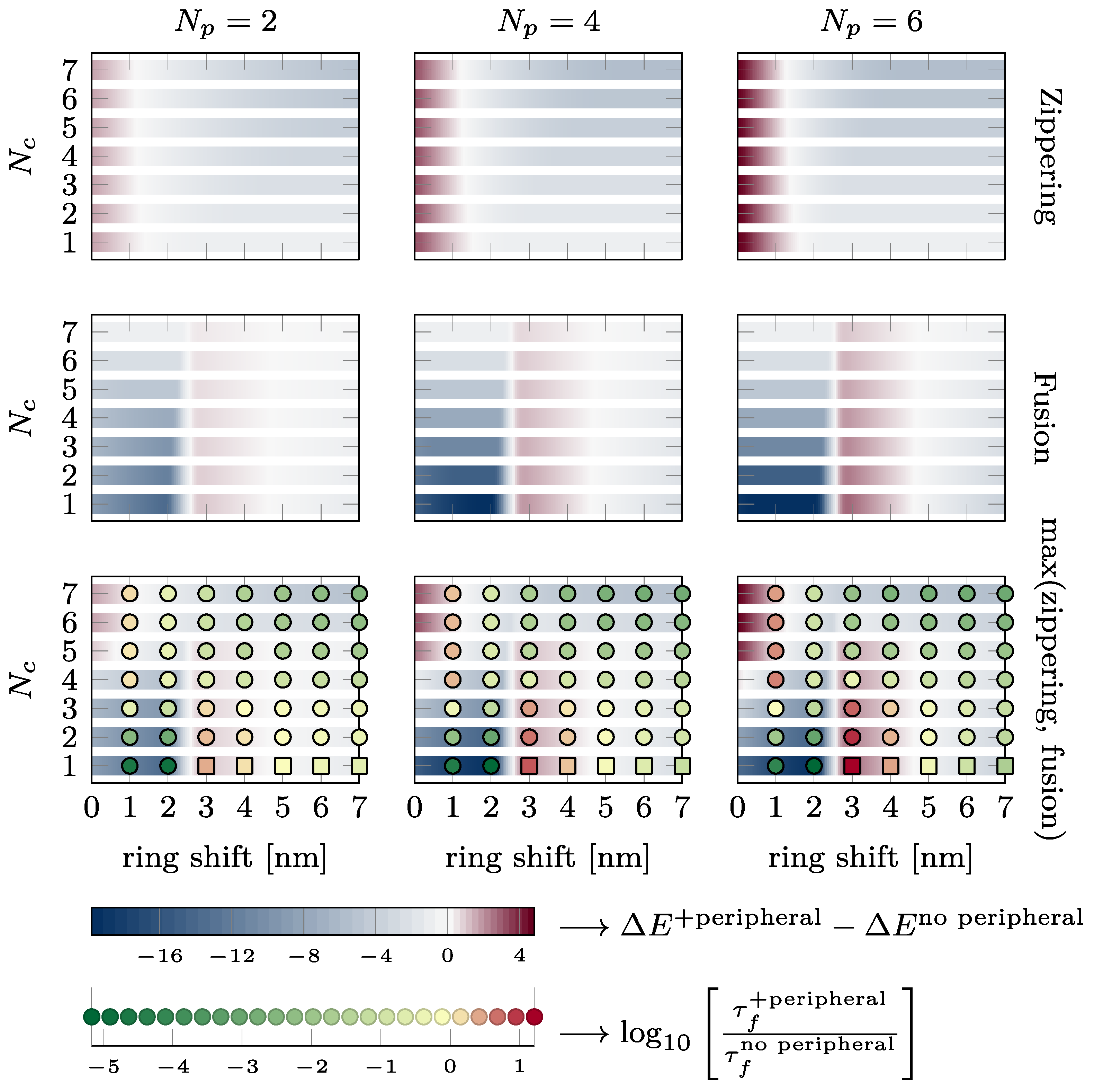
3.1. Effect of the Vertical Shift between the Two Rings
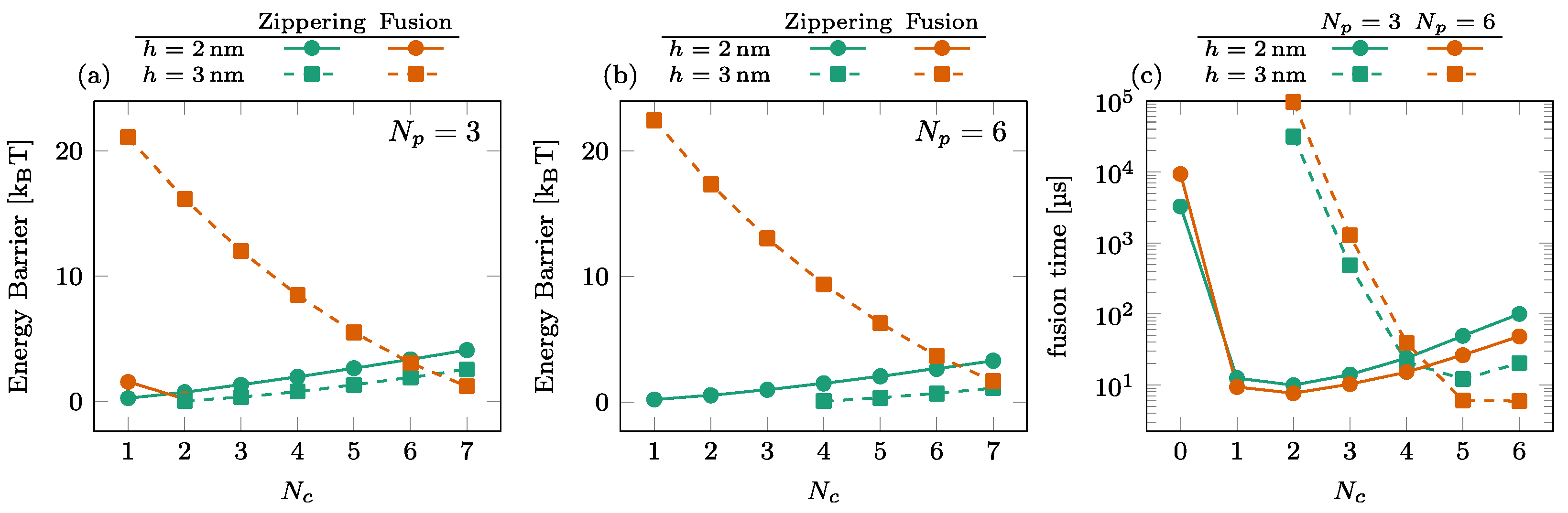
3.2. Effect of the Number of SNAREpins in the Peripheral Ring
3.3. Effect of the Number of SNAREpins in the Central Ring
3.4. Summary of the Energy Barriers and Fusion Time
4. Discussion
4.1. Role of the Vertical Shift
4.2. Energy Barrier vs. Fusion Time
4.3. Physiological Consequences
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jahn, R.; Scheller, R.H. SNAREs—Engines for membrane fusion. Nat. Rev. Mol. Cell Biol. 2006, 7, 631–643. [Google Scholar] [CrossRef] [PubMed]
- Rothman, J.E. The principle of membrane fusion in the cell (Nobel lecture). Angew. Chem. Int. Ed. Engl. 2014, 53, 12676–12694. [Google Scholar] [CrossRef] [PubMed]
- Vassilieva, E.V.; Nusrat, A. Vesicular trafficking: Molecular tools and targets. Methods Mol. Biol. 2008, 440, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Francois-Martin, C.; Bacle, A.; Rothman, J.E.; Fuchs, P.F.J.; Pincet, F. Cooperation of Conical and Polyunsaturated Lipids to Regulate Initiation and Processing of Membrane Fusion. Front. Mol. Biosci. 2021, 8, 763115. [Google Scholar] [CrossRef]
- Francois-Martin, C.; Rothman, J.E.; Pincet, F. Low energy cost for optimal speed and control of membrane fusion. Proc. Natl. Acad. Sci. USA 2017, 114, 1238–1241. [Google Scholar] [CrossRef]
- Rand, R.P.; Parsegian, V.A. Mimicry and Mechanism in Phospholipid Models of Membrane-Fusion. Annu. Rev. Physiol. 1986, 48, 201–212. [Google Scholar] [CrossRef] [PubMed]
- Rand, R.P.; Parsegian, V.A. Hydration Forces between Phospholipid-Bilayers. Biochim. Biophys. Acta 1989, 988, 351–376. [Google Scholar] [CrossRef]
- Yang, L.; Ding, L.; Huang, H.W. New phases of phospholipids and implications to the membrane fusion problem. Biochemistry 2003, 42, 6631–6635. [Google Scholar] [CrossRef]
- Sollner, T.; Bennett, M.K.; Whiteheart, S.W.; Scheller, R.H.; Rothman, J.E. A protein assembly-disassembly pathway in vitro that may correspond to sequential steps of synaptic vesicle docking, activation, and fusion. Cell 1993, 75, 409–418. [Google Scholar] [CrossRef]
- Sollner, T.; Whiteheart, S.W.; Brunner, M.; Erdjument-Bromage, H.; Geromanos, S.; Tempst, P.; Rothman, J.E. SNAP receptors implicated in vesicle targeting and fusion. Nature 1993, 362, 318–324. [Google Scholar] [CrossRef]
- Weber, T.; Zemelman, B.V.; McNew, J.A.; Westermann, B.; Gmachl, M.; Parlati, F.; Sollner, T.H.; Rothman, J.E. SNAREpins: Minimal machinery for membrane fusion. Cell 1998, 92, 759–772. [Google Scholar] [CrossRef] [PubMed]
- Mion, D.; Bunel, L.; Heo, P.; Pincet, F. The beginning and the end of SNARE-induced membrane fusion. FEBS Open Bio 2022, 12, 1958–1979. [Google Scholar] [CrossRef] [PubMed]
- Sudhof, T.C. The synaptic vesicle cycle. Annu. Rev. Neurosci. 2004, 27, 509–547. [Google Scholar] [CrossRef] [PubMed]
- Pyle, J.L.; Kavalali, E.T.; Piedras-Renteria, E.S.; Tsien, R.W. Rapid reuse of readily releasable pool vesicles at hippocampal synapses. Neuron 2000, 28, 221–231. [Google Scholar] [CrossRef]
- Heinemann, C.; Chow, R.H.; Neher, E.; Zucker, R.S. Kinetics of the secretory response in bovine chromaffin cells following flash photolysis of caged Ca2+. Biophys. J. 1994, 67, 2546–2557. [Google Scholar] [CrossRef] [PubMed]
- Schneggenburger, R.; Meyer, A.C.; Neher, E. Released fraction and total size of a pool of immediately available transmitter quanta at a calyx synapse. Neuron 1999, 23, 399–409. [Google Scholar] [CrossRef]
- Stevens, C.F.; Tsujimoto, T. Estimates for the pool size of releasable quanta at a single central synapse and for the time required to refill the pool. Proc. Natl. Acad. Sci. USA 1995, 92, 846–849. [Google Scholar] [CrossRef]
- Rosenmund, C.; Stevens, C.F. Definition of the readily releasable pool of vesicles at hippocampal synapses. Neuron 1996, 16, 1197–1207. [Google Scholar] [CrossRef] [PubMed]
- Imig, C.; Min, S.W.; Krinner, S.; Arancillo, M.; Rosenmund, C.; Sudhof, T.C.; Rhee, J.; Brose, N.; Cooper, B.H. The morphological and molecular nature of synaptic vesicle priming at presynaptic active zones. Neuron 2014, 84, 416–431. [Google Scholar] [CrossRef]
- Bera, M.; Radhakrishnan, A.; Coleman, J.; RV, K.S.; Ramakrishnan, S.; Pincet, F.; Rothman, J.E. Synaptophysin chaperones the assembly of 12 SNAREpins under each ready-release vesicle. Proc. Natl. Acad. Sci. USA 2023, 120, e2311484120. [Google Scholar] [CrossRef]
- Rothman, J.E.; Grushin, K.; Bera, M.; Pincet, F. Turbocharging synaptic transmission. FEBS Lett. 2023, 597, 2233–2249. [Google Scholar] [CrossRef] [PubMed]
- Manca, F.; Pincet, F.; Truskinovsky, L.; Rothman, J.E.; Foret, L.; Caruel, M. SNARE machinery is optimized for ultrafast fusion. Proc. Natl. Acad. Sci. USA 2019, 116, 2435–2442. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zorman, S.; Gundersen, G.; Xi, Z.; Ma, L.; Sirinakis, G.; Rothman, J.E.; Zhang, Y. Single reconstituted neuronal SNARE complexes zipper in three distinct stages. Science 2012, 337, 1340–1343. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Energetics, kinetics, and pathway of SNARE folding and assembly revealed by optical tweezers. Protein Sci. 2017, 26, 1252–1265. [Google Scholar] [CrossRef] [PubMed]
- Zorman, S.; Rebane, A.A.; Ma, L.; Yang, G.; Molski, M.A.; Coleman, J.; Pincet, F.; Rothman, J.E.; Zhang, Y. Common intermediates and kinetics, but different energetics, in the assembly of SNARE proteins. Elife 2014, 3, e03348. [Google Scholar] [CrossRef] [PubMed]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. Siam Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Caruel, M.; Truskinovsky, L. Bi-stability resistant to fluctuations. J. Mech. Phys. Solids 2017, 109, 117–141. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Zippering distance | 7 | nm | |
| Energy bias | 30 | kBT | |
| Unzippered stiffness | 1.5 | pNnm−1 | |
| Zippered stiffness | 12 | pNnm−1 | |
| FB* position | 2 | nm | |
| FB width | 0.3 | nm | |
| FB energy | 26 | kBT | |
| Drag coefficient | Nsm−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruel, M.; Pincet, F. Dual-Ring SNAREpin Machinery Tuning for Fast Synaptic Vesicle Fusion. Biomolecules 2024, 14, 600. https://doi.org/10.3390/biom14050600
Caruel M, Pincet F. Dual-Ring SNAREpin Machinery Tuning for Fast Synaptic Vesicle Fusion. Biomolecules. 2024; 14(5):600. https://doi.org/10.3390/biom14050600
Chicago/Turabian StyleCaruel, Matthieu, and Frédéric Pincet. 2024. "Dual-Ring SNAREpin Machinery Tuning for Fast Synaptic Vesicle Fusion" Biomolecules 14, no. 5: 600. https://doi.org/10.3390/biom14050600
APA StyleCaruel, M., & Pincet, F. (2024). Dual-Ring SNAREpin Machinery Tuning for Fast Synaptic Vesicle Fusion. Biomolecules, 14(5), 600. https://doi.org/10.3390/biom14050600







