An Addendum to the Chemiosmotic Theory of Mitochondrial Activity: The Role of RNA as a Proton Sink
Abstract
1. Introduction
2. RNA: The Dark Matter of Mitochondrial Energetics?
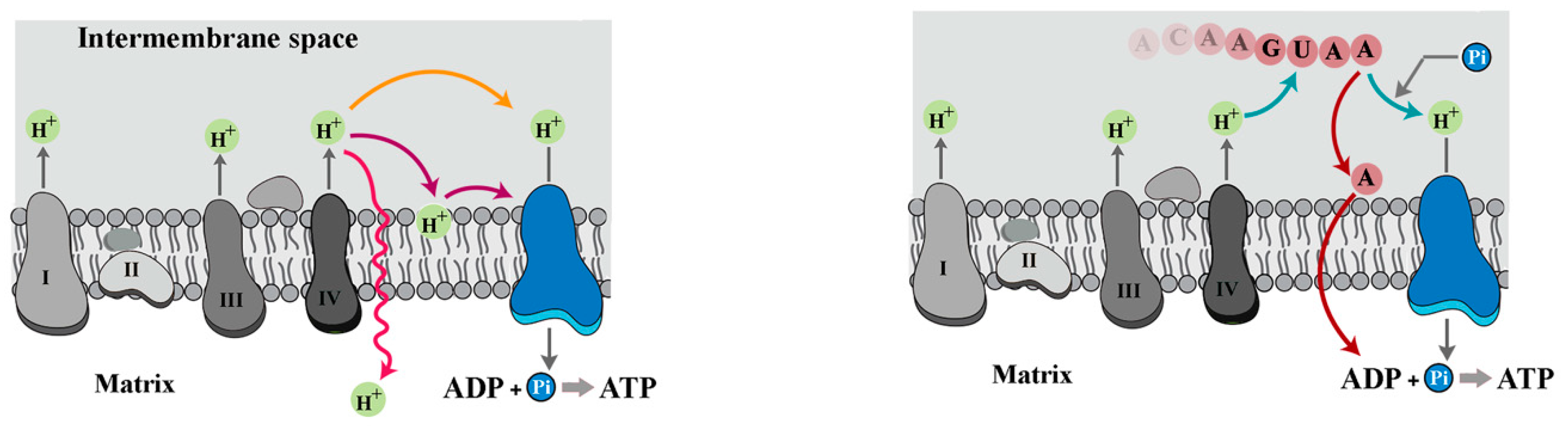
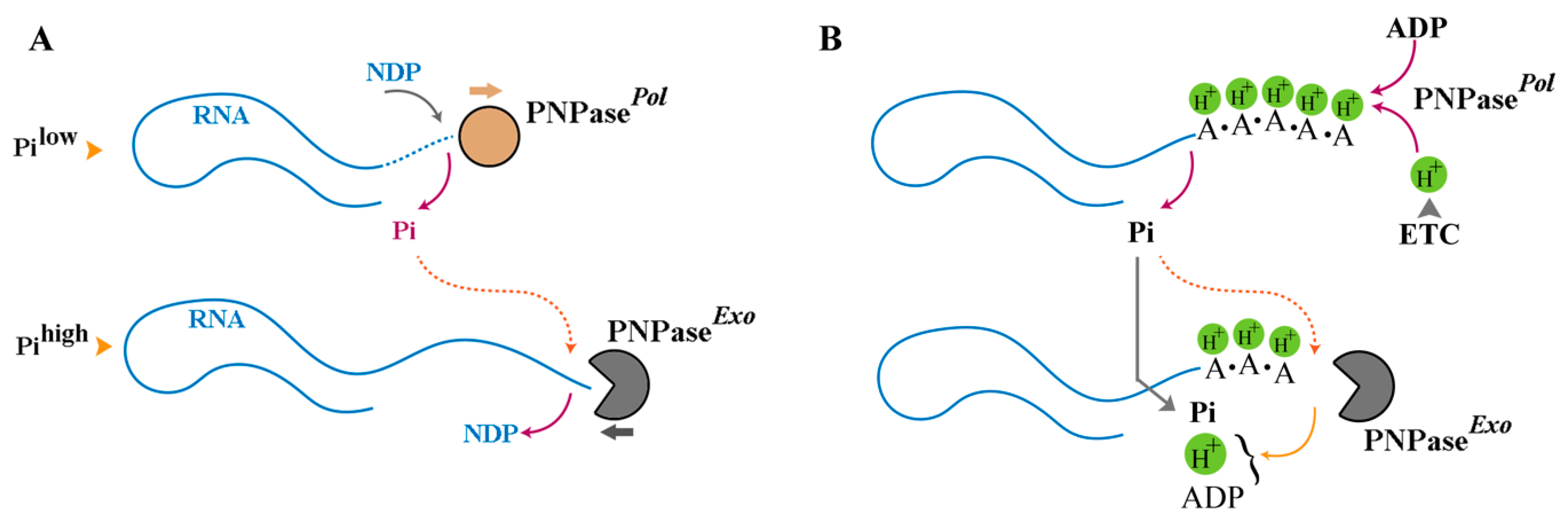
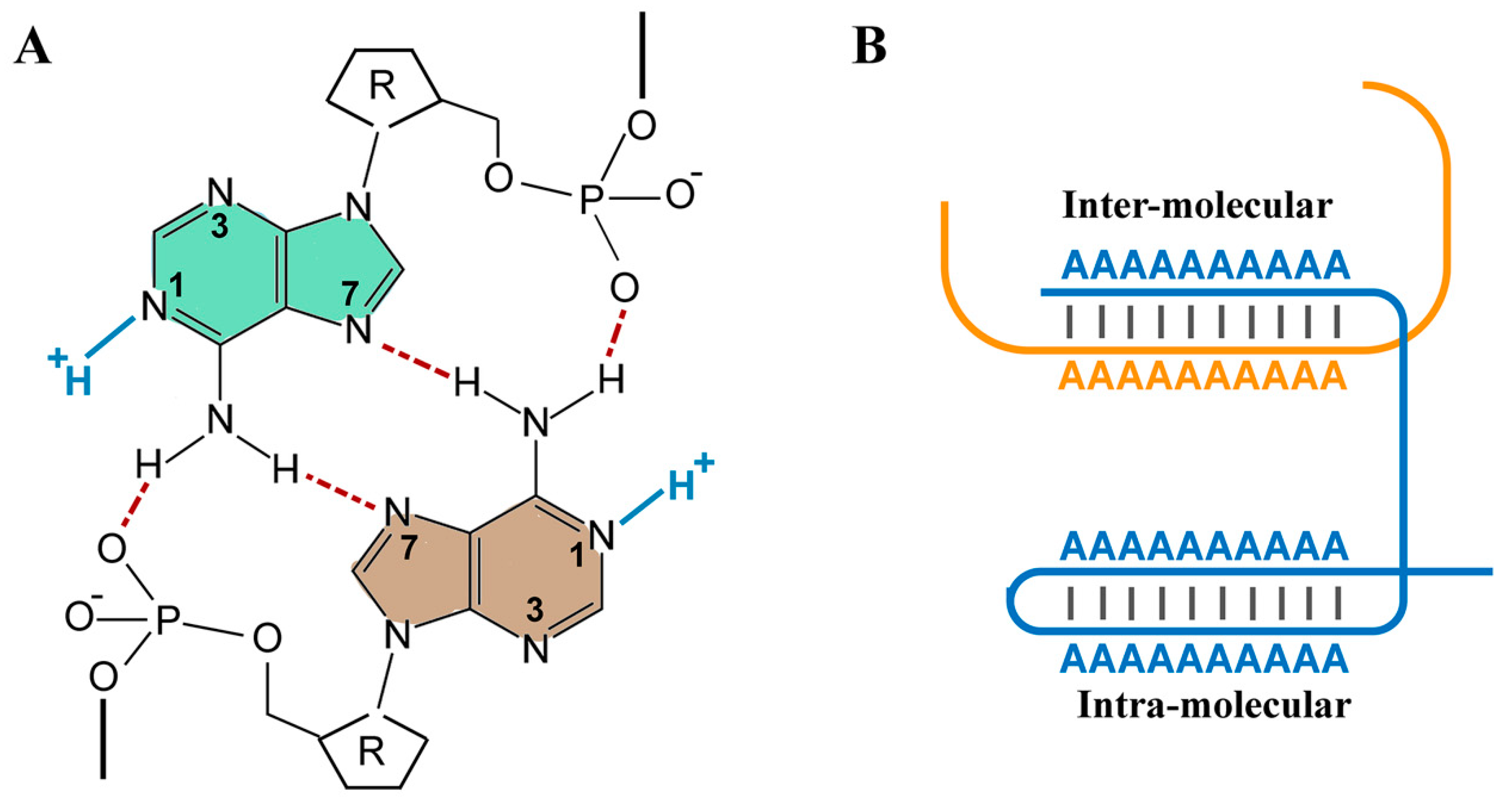
3. RNA as a Polymeric Proton Sink
4. Quantitative Underpinnings of Revised Chemiosmotic Theory
5. Mechanisms of Respiratory Control and the Revised Chemiosmotic Theory
6. Challenges and Future Directions
7. Concluding Remark
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitchell, P. Coupling of phosphorylation to electron and hydrogen transfer by a chemi-osmotic type of mechanism. Nature 1961, 191, 144–148. [Google Scholar] [CrossRef] [PubMed]
- Okuno, D.; Iino, R.; Noji, H. Rotation and structure of FoF1-ATP synthase. J. Biochem. 2011, 149, 655–664. [Google Scholar] [CrossRef]
- Kell, D.B. On the functional proton current pathway of electron transport phosphorylation. An electrodic view. Biochim. Biophys. Acta 1979, 549, 55–99. [Google Scholar] [CrossRef]
- Alexiev, U.; Mollaaghababa, R.; Scherrer, P.; Khorana, H.G.; Heyn, M.P. Rapid long-range proton diffusion along the surface of the purple membrane and delayed proton transfer into the bulk. Proc. Natl. Acad. Sci. USA 1995, 92, 372–376. [Google Scholar] [CrossRef]
- Heberle, J.; Riesle, J.; Thiedemann, G.; Oesterhelt, D.; Dencher, N.A. Proton migration along the membrane surface and retarded surface to bulk transfer. Nature 1994, 370, 379–382. [Google Scholar] [CrossRef]
- Zoratti, M.; Favaron, M.; Pietrobon, D.; Azzone, G.F. Intrinsic uncoupling of mitochondrial proton pumps. 1. Non-ohmic conductance cannot account for the nonlinear dependence of static head respiration on delta microH. Biochemistry 1986, 25, 760–767. [Google Scholar] [CrossRef]
- Divakaruni, A.S.; Brand, M.D. The regulation and physiology of mitochondrial proton leak. Physiology 2011, 26, 192–205. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, P. Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Biol. Rev. Camb. Philos. Soc. 1966, 41, 445–502. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, P. Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Biochim. Biophys. Acta 2011, 1807, 1507–1538. [Google Scholar] [CrossRef] [PubMed]
- Grzesiek, S.; Dencher, N.A. Dependency of delta pH-relaxation across vesicular membranes on the buffering power of bulk solutions and lipids. Biophys. J. 1986, 50, 265–276. [Google Scholar] [CrossRef]
- Mulkidjanian, A.Y. Proton in the well and through the desolvation barrier. Bba-Bioenergetics 2006, 1757, 415–427. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Brown, D.G. Variation in bacterial ATP level and proton motive force due to adhesion to a solid surface. Appl. Environ. Microbiol. 2009, 75, 2346–2353. [Google Scholar] [CrossRef] [PubMed]
- Morelli, A.M.; Ravera, S.; Calzia, D.; Panfoli, I. An update of the chemiosmotic theory as suggested by possible proton currents inside the coupling membrane. Open Biol. 2019, 9, 180221. [Google Scholar] [CrossRef]
- Angelova, M.I.; Bitbol, A.F.; Seigneuret, M.; Staneva, G.; Kodama, A.; Sakuma, Y.; Kawakatsu, T.; Imai, M.; Puff, N. pH sensing by lipids in membranes: The fundamentals of pH-driven migration, polarization and deformations of lipid bilayer assemblies. Biochim. Biophys. Acta Biomembr. 2018, 1860, 2042–2063. [Google Scholar] [CrossRef] [PubMed]
- Vujovic, F.; Simonian, M.; Hughes, W.E.; Shepherd, C.E.; Hunter, N.; Farahani, R.M. Mitochondria facilitate neuronal differentiation by metabolising nuclear-encoded RNA. Cell Commun. Signal 2024, 22, 450. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.W.; Oktay, Y.; Zhang, J.; Allen, E.L.; Smith, G.M.; Fan, K.C.; Hong, J.S.; French, S.W.; McCaffery, J.M.; et al. PNPASE regulates RNA import into mitochondria. Cell 2010, 142, 456–467. [Google Scholar] [CrossRef] [PubMed]
- Yehudai-Resheff, S.; Hirsh, M.; Schuster, G. Polynucleotide phosphorylase functions as both an exonuclease and a poly(A) polymerase in spinach chloroplasts. Mol. Cell Biol. 2001, 21, 5408–5416. [Google Scholar] [CrossRef] [PubMed]
- Littauer, U.Z.; Soreq, H. Polynucleotide Phosphorylase. In The Enzymes; Elsevier: Amsterdam, The Netherlands, 1982; pp. 517–553. [Google Scholar]
- Asamizu, E.; Nakamura, Y.; Sato, S.; Fukuzawa, H.; Tabata, S. A large scale structural analysis of cDNAs in a unicellular green alga, Chlamydomonas reinhardtii. I. Generation of 3433 non-redundant expressed sequence tags. DNA Res. 1999, 6, 369–373. [Google Scholar] [CrossRef]
- Gellerich, F.N.; Laterveer, F.D.; Zierz, S.; Nicolay, K. The quantitation of ADP diffusion gradients across the outer membrane of heart mitochondria in the presence of macromolecules. Biochim. Biophys. Acta 2002, 1554, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Portnoy, V.; Palnizky, G.; Yehudai-Resheff, S.; Glaser, F.; Schuster, G. Analysis of the human polynucleotide phosphorylase (PNPase) reveals differences in RNA binding and response to phosphate compared to its bacterial and chloroplast counterparts. RNA 2008, 14, 297–309. [Google Scholar] [CrossRef]
- Chen, H.W.; Rainey, R.N.; Balatoni, C.E.; Dawson, D.W.; Troke, J.J.; Wasiak, S.; Hong, J.S.; McBride, H.M.; Koehler, C.M.; Teitell, M.A.; et al. Mammalian polynucleotide phosphorylase is an intermembrane space RNase that maintains mitochondrial homeostasis. Mol. Cell Biol. 2006, 26, 8475–8487. [Google Scholar] [CrossRef]
- Stocks, J.; Gilbert, N. Nuclear RNA: A transcription-dependent regulator of chromatin structure. Biochem. Soc. Trans. 2024, 52, 1605–1615. [Google Scholar] [CrossRef] [PubMed]
- Thaplyal, P.; Bevilacqua, P.C. Experimental approaches for measuring pKa’s in RNA and DNA. Methods Enzymol. 2014, 549, 189–219. [Google Scholar] [CrossRef] [PubMed]
- Moody, E.M.; Lecomte, J.T.; Bevilacqua, P.C. Linkage between proton binding and folding in RNA: A thermodynamic framework and its experimental application for investigating pKa shifting. RNA 2005, 11, 157–172. [Google Scholar] [CrossRef]
- Izatt, R.M.; Christensen, J.J.; Rytting, J.H. Sites and thermodynamic quantities associated with proton and metal ion interaction with ribonucleic acid, deoxyribonucleic acid, and their constituent bases, nucleosides, and nucleotides. Chem. Rev. 1971, 71, 439–481. [Google Scholar] [CrossRef] [PubMed]
- Velikyan, I.; Acharya, S.; Trifonova, A.; Földesi, A.; Chattopadhyaya, J. The pKa’s of 2′-hydroxyl group in nucleosides and nucleotides. J. Am. Chem. Soc. 2001, 123, 2893–2894. [Google Scholar] [CrossRef] [PubMed]
- Legault, P.; Pardi, A. Unusual dynamics and pK(a) shift at the active site of a lead-dependent ribozyme. J. Am. Chem. Soc. 1997, 119, 6621–6628. [Google Scholar] [CrossRef]
- Narlikar, G.J.; Herschlag, D. Mechanistic aspects of enzymatic catalysis: Lessons from comparison of RNA and protein enzymes. Annu. Rev. Biochem. 1997, 66, 19–59. [Google Scholar] [CrossRef] [PubMed]
- Bevilacqua, P.C. Mechanistic considerations for general acid-base catalysis by RNA: Revisiting the mechanism of the hairpin ribozyme. Biochemistry 2003, 42, 2259–2265. [Google Scholar] [CrossRef]
- Beers, R.F.; Steiner, R.F. Titration and Spectrophotometric Studies Upon Polyadenylic Acid. Nature 1957, 179, 1076–1077. [Google Scholar] [CrossRef]
- Steiner, R.F. Polynucleotides. 3. The Behavior of Polyadenylic Acid at Acid Phs. J. Polym. Sci. 1958, 31, 53–66. [Google Scholar] [CrossRef]
- Zarudnaya, M.I.; Kolomiets, I.M.; Potyahaylo, A.L.; Hovorun, D.M. Structural transitions in poly(A), poly(C), poly(U), and poly(G) and their possible biological roles. J. Biomol. Struct. Dyn. 2019, 37, 2837–2866. [Google Scholar] [CrossRef] [PubMed]
- Rich, A.; Davies, D.R.; Crick, F.H.; Watson, J.D. The molecular structure of polyadenylic acid. J. Mol. Biol. 1961, 3, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Janik, B.; Bobst, A.M.; Sommer, R.G. Polarography of Polynucleotides. 2. Conformations of Poly(Adenylic Acid) at Acidic Ph. Biochim. Biophys. Acta 1972, 281, 152–168. [Google Scholar] [CrossRef] [PubMed]
- Santo-Domingo, J.; Demaurex, N. Perspectives on: SGP symposium on mitochondrial physiology and medicine: The renaissance of mitochondrial pH. J. Gen. Physiol. 2012, 139, 415–423. [Google Scholar] [CrossRef]
- Brand, M.D.; Felber, S.M. Membrane potential of mitochondria in intact lymphocytes during early mitogenic stimulation. Biochem. J. 1984, 217, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Hoek, J.B.; Nicholls, D.G.; Williamson, J.R. Determination of the mitochondrial protonmotive force in isolated hepatocytes. J. Biol. Chem. 1980, 255, 1458–1464. [Google Scholar] [CrossRef]
- Rieger, B.; Arroum, T.; Borowski, M.T.; Villalta, J.; Busch, K.B. Mitochondrial F1F0 ATP synthase determines the local proton motive force at cristae rims. Embo Rep. 2021, 22, e52727. [Google Scholar] [CrossRef] [PubMed]
- Seifert, E.L.; Ligeti, E.; Mayr, J.A.; Sondheimer, N.; Hajnoczky, G. The mitochondrial phosphate carrier: Role in oxidative metabolism, calcium handling and mitochondrial disease. Biochem. Biophys. Res. Commun. 2015, 464, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, F.; Prezioso, G.; Quagliariello, E.; Klingenberg, M. Kinetic study of the dicarboxylate carrier in rat liver mitochondria. Eur. J. Biochem. 1971, 22, 66–74. [Google Scholar] [CrossRef]
- Bal, W.; Kurowska, E.; Maret, W. The final frontier of pH and the undiscovered country beyond. PLoS ONE 2012, 7, e45832. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; French, S.; Evans, F.J.; Joubert, F.; Balaban, R.S. Metabolic network control of oxidative phosphorylation: Multiple roles of inorganic phosphate. J. Biol. Chem. 2003, 278, 39155–39165. [Google Scholar] [CrossRef]
- Tupper, J.T.; Tedeschi, H. Mitochondrial membrane potentials measured with microelectrodes: Probable ionic basis. Science 1969, 166, 1539–1540. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, B.; Bender, E.; Arnold, S.; Hüttemann, M.; Lee, I.; Kadenbach, B. Cytochrome c oxidase and the regulation of oxidative phosphorylation. Chembiochem 2001, 2, 392–403. [Google Scholar] [CrossRef] [PubMed]
- Kadenbach, B.; Ramzan, R.; Wen, L.; Vogt, S. New extension of the Mitchell Theory for oxidative phosphorylation in mitochondria of living organisms. Biochim. Biophys. Acta 2010, 1800, 205–212. [Google Scholar] [CrossRef]
- Kadenbach, B.; Arnold, S. A second mechanism of respiratory control. FEBS Lett. 1999, 447, 131–134. [Google Scholar] [CrossRef]
- Chance, B.; Williams, G.R. Respiratory enzymes in oxidative phosphorylation. III. The steady state. J. Biol. Chem. 1955, 217, 409–427. [Google Scholar] [CrossRef] [PubMed]
- Lardy, H.A.; Wellman, H. Oxidative phosphorylations; role of inorganic phosphate and acceptor systems in control of metabolic rates. J. Biol. Chem. 1952, 195, 215–224. [Google Scholar] [CrossRef]
- Wan, B.; Doumen, C.; Duszynski, J.; Salama, G.; Vary, T.C.; LaNoue, K.F. Effects of cardiac work on electrical potential gradient across mitochondrial membrane in perfused rat hearts. Am. J. Physiol. 1993, 265, H453–H460. [Google Scholar] [CrossRef]
- Arnold, S.; Kadenbach, B. Cell respiration is controlled by ATP, an allosteric inhibitor of cytochrome-c oxidase. Eur. J. Biochem. 1997, 249, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Bender, E.; Kadenbach, B. The allosteric ATP-inhibition of cytochrome c oxidase activity is reversibly switched on by cAMP-dependent phosphorylation. FEBS Lett. 2000, 466, 130–134. [Google Scholar] [CrossRef] [PubMed]
- Groen, A.K.; Wanders, R.J.A.; Westerhoff, H.V.; Vandermeer, R.; Tager, J.M. Quantification of the Contribution of Various Steps to the Control of Mitochondrial Respiration. J. Biol. Chem. 1982, 257, 2754–2757. [Google Scholar] [CrossRef]
- Burrows, C.J.; Muller, J.G. Oxidative Nucleobase Modifications Leading to Strand Scission. Chem. Rev. 1998, 98, 1109–1152. [Google Scholar] [CrossRef]
- Hayakawa, H.; Sekiguchi, M. Human polynucleotide phosphorylase protein in response to oxidative stress. Biochemistry 2006, 45, 6749–6755. [Google Scholar] [CrossRef] [PubMed]
- Pettit, F.H.; Roche, T.E.; Reed, L.J. Function of calcium ions in pyruvate dehydrogenase phosphatase activity. Biochem. Biophys. Res. Commun. 1972, 49, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Glancy, B.; Willis, W.T.; Chess, D.J.; Balaban, R.S. Effect of calcium on the oxidative phosphorylation cascade in skeletal muscle mitochondria. Biochemistry 2013, 52, 2793–2809. [Google Scholar] [CrossRef]
- Vilas-Boas, E.A.; Cabral-Costa, J.V.; Ramos, V.M.; Caldeira da Silva, C.C.; Kowaltowski, A.J. Goldilocks calcium concentrations and the regulation of oxidative phosphorylation: Too much, too little, or just right. J. Biol. Chem. 2023, 299, 102904. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, K.; Gohil, V.; Stuart, R.A.; Hunte, C.; Brandt, U.; Greenberg, M.L.; Schagger, H. Cardiolipin stabilizes respiratory chain supercomplexes. J. Biol. Chem. 2003, 278, 52873–52880. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Sutachan, J.J.; Plesken, H.; Kelley, R.I.; Schlame, M. Characterization of lymphoblast mitochondria from patients with Barth syndrome. Lab. Investig. 2005, 85, 823–830. [Google Scholar] [CrossRef] [PubMed]
- Ikon, N.; Ryan, R.O. Cardiolipin and mitochondrial cristae organization. Biochim. Biophys. Acta Biomembr. 2017, 1859, 1156–1163. [Google Scholar] [CrossRef] [PubMed]
- Haines, T.H.; Dencher, N.A. Cardiolipin: A proton trap for oxidative phosphorylation. FEBS Lett. 2002, 528, 35–39. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F.; Klein, R.A. Anti-electrostatic hydrogen bonds. Angew. Chem. Int. Ed. Engl. 2014, 53, 11214–11217. [Google Scholar] [CrossRef] [PubMed]
- Haines, T.H. Anionic Lipid Headgroups as a Proton-Conducting Pathway Along the Surface of Membranes—A Hypothesis. Proc. Natl. Acad. Sci. USA 1983, 80, 160–164. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Flood, A.H.; White, N.G. Recognition and applications of anion-anion dimers based on anti-electrostatic hydrogen bonds (AEHBs). Chem. Soc. Rev. 2020, 49, 7893–7906. [Google Scholar] [CrossRef] [PubMed]
- Németi, B.; Regonesi, M.E.; Tortora, P.; Gregus, Z. Polynucleotide Phosphorylase and Mitochondrial ATP Synthase Mediate Reduction of Arsenate to the More Toxic Arsenite by Forming Arsenylated Analogues of ADP and ATP. Toxicol. Sci. 2010, 117, 270–281. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farahani, R.M. An Addendum to the Chemiosmotic Theory of Mitochondrial Activity: The Role of RNA as a Proton Sink. Biomolecules 2025, 15, 87. https://doi.org/10.3390/biom15010087
Farahani RM. An Addendum to the Chemiosmotic Theory of Mitochondrial Activity: The Role of RNA as a Proton Sink. Biomolecules. 2025; 15(1):87. https://doi.org/10.3390/biom15010087
Chicago/Turabian StyleFarahani, Ramin M. 2025. "An Addendum to the Chemiosmotic Theory of Mitochondrial Activity: The Role of RNA as a Proton Sink" Biomolecules 15, no. 1: 87. https://doi.org/10.3390/biom15010087
APA StyleFarahani, R. M. (2025). An Addendum to the Chemiosmotic Theory of Mitochondrial Activity: The Role of RNA as a Proton Sink. Biomolecules, 15(1), 87. https://doi.org/10.3390/biom15010087




