Adaptive Virtual Impedance Control of a Mobile Multi-Robot System

Abstract

The capabilities of collaborative robotics have transcended the conventional abilities of decentralised robots as it provides benefits such as scalability, flexibility and robustness. Collaborative robots can operate safely in complex human environments without being restricted by the safety cages or barriers that often accompany them. Collaborative robots can be used for various applications such as machine tending, packaging, process tasks and pick and place. This paper proposes an improvement of the current virtual impedance algorithm by developing an adaptive virtual impedance controlled mobile multi-robot system focused on dynamic obstacle avoidance with a controlled planar movement. The study includes the development of a mobile multi-robot platform whereby each robot plans a path individually without a supervisor. The proposed system would implement a two-layered hierarchy for robot path planning. The higher layer generates a trajectory from the current position to the desired position, and the lower layer develops a real-time strategy to follow the generated trajectory while avoiding static and dynamic obstacles. The key contribution of this paper is the adaptive virtual impedance controller for a multi-robot system that will maintain movement stability and improve the motion behaviour in a dynamic environment.

1. Introduction

Mobile ground robots are widely used for various tasks in indoor environments. The addition of multiple mobile ground robots is introduced to improve the efficiency of certain tasks, thus creating a multi-robot system. This paper introduces a multi-robot system that is collaborative and autonomous, where each robot has its own local task or goal, but the robots collaborate on global tasks such as mapping. This paper develops a movement algorithm for a multi-robot system with the ability to avoid obstacles while maintaining movement stability.

The motion of a mobile robot is based on the forward kinematics and the inverse kinematics. The kinematics models are needed to control the linear and angular velocities in order to complete the control task for the mobile robot [1]. Extensive research has been conducted in the field of autonomous mobile robot navigation [2,3,4,5]. Navigation is a complex task and involves various techniques to gather and decode information. There are several adequate path planning algorithms that have been developed for mobile robot systems [6]. This paper implemented the A* path planner because it considers the lowest cost per iteration move to be taken [7]. A* determines the closest possible path from starting position to the goal point, making this an optimal search algorithm. Moreover, A* solves a given problem by evaluating all possible paths to determine the path that leads to the goal point fastest.

Previously developed motion control algorithms allow a mobile robot to avoid static and dynamic obstacles [8,9], while navigating in an indoor environment. Obstacle avoidance algorithms, such as the potential field method [10,11,12], have been widely used. The concept of this method is to fill the workspace of the robot with an artificial potential field in which the robot is attracted towards the goal and repulsed away from the obstacles. Previously, this method was used to plan a path for a mobile robot in static environments [13], but it has several shortcomings, such as the inability to reach a goal when it is near an obstacle. Moreover, the robot cannot navigate through a narrow line of obstacles due to the large repulsive field generated. Further drawbacks include motion oscillations near obstacles and local minima. However, in many implementations, the environment is dynamic and thus this method is not considered by the paper. Another popular obstacle avoidance algorithm is fuzzy control [14,15]. However, it has poor system control accuracy and, due to the algorithm lacking systematicity, the control goal cannot be defined. Model predictive control [16,17] is effectively used to overcome the trajectory tracking problem since it reduces the tracking error along the desired trajectory. Model predictive control predicts upcoming disturbances and plans upcoming actions accordingly. The algorithm improves the steady-state response which reduces the offset error and increases control accuracy.

This paper considers the virtual impedance algorithm for obstacle avoidance and local motion control in a multi-robot dynamic environment. Impedance control is used in dynamic environments because it relates the force and the position. The impedance control algorithm aims to set the dynamics of the system to a desired impedance defined by the user. This is the main difference since impedance control is used with an external force feedback [18]. A repulsive force is generated from the obstacles, pushing the mobile ground robot away from the obstacles, but also away from the goal. The method compensates for the repulsive force by generating an attractive force towards the goal. The attractive and repulsive forces act as a spring and damper with the parameters, K and D, to define the strength of the forces. The total force acting on the mobile ground robot is the sum of the attractive and repulsive forces.

The traditional virtual impedance algorithm only generates an attractive force towards the goal and a situation could occur whereby the attractive force and repulsive forces are equal [19]. Moreover, traditional virtual impedance control is susceptible to cause movement instability and oscillations near obstacles. This paper proposes a two-layered navigation strategy that incorporates a global path planner [20], together with an improved adaptive virtual impedance algorithm to overcome these problems. The main contribution of this paper is the improvement in motion behaviour and movement stability of a multi-robot system navigating in a dynamic indoor environment.

This paper is organised as follows: Section 2 describes the traditional virtual impedance control algorithm. Section 3 introduces the new improved adaptive virtual impedance control method. Section 4 defines the mathematical equations used in the model-based control strategy. Section 5 describes the parameters of the adaptation algorithm used to improve the movement behaviour of a mobile multi-robot system. Section 6 presents the simulated results together with real-world results obtained from experiments. Section 7 concludes the paper and presents the perspectives of the work.

2. Virtual Impedance Control in a Multi-Robot Environment

The virtual impedance method considers a mobile robot moving in a multi-robot environment to be submitted to the following forces:

• A repulsive force between the mobile robot and both the obstacles and the other mobile robots;
• An attractive force between the mobile robot and the reference trajectory.
• Leading to different types of interactions:
• Interactions between robots;
• Interactions between robots and obstacles;
• Interactions between robots and reference trajectories.

Figure 1 shows the different interactions of a system with two mobile robots.

Each interaction is defined by a couple of parameters, K and D, representing the stiffness and the damping of the corresponding force [21]. The dynamic behaviour of a robot $i$ in a multi-robot environment is given by [22]:

$$M_i{\ddot{X}}_i=U_i+V_i$$

(1)

with $i$ = 1…nb and nb the number of robots.

where:

$U_{\mathrm{i}}$: represents the attractive forces between the robot $i$ and its reference trajectory.

$V_i$: concerns the repulsive forces between the robot $i$ and the objects in its vicinity, including fixed and dynamic objects.

$U_i$ is given by:

$$U_i=-K_{traj}^i\left(X_i-X_d^i\right)-D_{traj}^i\left({\dot{X}}_i-{\dot{X}}_d^i\right)$$

(2)

$V_i$ is given by:

$$V_i=V_i^{mobiles}+V_i^{obstacles}$$

(3)

with

$$V_i^{mobiles}={\displaystyle \sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}\{\begin{array}{c}\begin{array}{c}{K}_{ij}^{mobiles}\left(R_{robot}^i-\Vert X_i-X_j\Vert \right)\frac{\left(X_i-X_j\right)}{\Vert X_i-X_j\Vert }+D_{ij}^{mobiles}\left({\dot{X}}_i-{\dot{X}}_j\right)\\ \mathrm{if} \Vert X_i-X_j\Vert <R_{robot}^i\end{array}\\ 0 if not\end{array}$$

(4)

and

$$V_i^{obstacles}={\displaystyle \sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{nbs}\{\begin{array}{c}\begin{array}{c}{K}_{ij}^{obstacles}\left(R_{robot}^i-\Vert X_i\Vert \right)\frac{\left(X_i\right)}{\Vert X_i\Vert }+D_{ij}^{obstacles}\left({\dot{X}}_i\right)\\ \mathrm{if} \Vert X_i\Vert <R_{robot}^i\end{array}\\ 0 if not\end{array}$$

(5)

where:

$M_i$: the virtual mass of the mobile robot.

$X_i$: the current x position of the mobile robot.

$X_d$: the desired x position of the reference trajectory.

K: stiffness tuning parameter.

D: damping tuning parameter.

$R_{robot}^i$: set of parameters defining the sensing envelope of the mobile robot.

The expressions of $V_i^{mobiles}$ and $V_i^{obstacles}$ show that a robot is taken into account only if it is in the interaction zone of the robot $i$ defined by $R_{robot}^i$.

Moreover, the interactions of the robot $i$ with the obstacles are computed based on the information issued from the sensors (ultrasonic, IR or LiDAR) with which the robot is equipped, given that the environment is supposed to be unknown and dynamic. The update of the robot trajectory is based on the integration of Equation (1) with each sampling time. The movement of the robot at its next position is only allowed if it respects the avoiding security constraint [19] given by:

$$X_i=\left\{\begin{array}{c}new position if d_{j,i}>L_{block}\\ X_i if not\end{array}\right\}$$

(6)

Figure 2 illustrates the interactions between robot $i$ and an obstacle, as well as the virtual sensing envelope.

Where $d_{j,i}$ is the distance between the robot $i$ and the obstacle, static or dynamic, and $L_{block}$ is the security distance defined within the virtual sensing envelope.

The development of the multi-robot system with the two-layered navigation strategy is based on the block diagram shown in Figure 3.

Simultaneous localisation and mapping (SLAM) is used to build a map of the environment with the data received from the sensors [23]. The global path planner uses the newly created map for trajectory planning. The entire block diagram is duplicated for a second, third or fourth robot added to the environment.

The kinematic model shown in Figure 4, takes the velocity of the mobile robot and transforms it into the generalised coordinate vector by the following equation [24]:

$$\begin{array}{c}{x}_{t+\mathsf{\Delta }}=x_t+V_C\mathsf{\Delta }\cos \left({\theta }_t\right)\\ y_{t+\mathsf{\Delta }}=y_t+V_C\mathsf{\Delta }\sin \left({\theta }_t\right)\\ {\theta }_{t+\mathsf{\Delta }}={\theta }_t+{\mathsf{\omega }}_C\mathsf{\Delta }\end{array}$$

(7)

The velocity of the mobile robot can then be taken from each wheel velocity. The linear velocity of the mobile robot is expressed as:

$$V_C=\frac{r\left({\mathsf{\omega }}_{\mathrm{R}}+{\mathsf{\omega }}_{\mathrm{L}}\right)}{2}$$

(8)

The angular velocity of the mobile robot is expressed as:

$${\mathsf{\omega }}_C=\frac{r\left({\mathsf{\omega }}_{\mathrm{R}}-{\mathsf{\omega }}_{\mathrm{L}}\right)}{L}$$

(9)

where:

${\mathrm{V}}_{\mathrm{L}},{\mathrm{V}}_{\mathrm{R}}:$ left wheel and right wheel velocity, respectively.

$x, y:$ relative position of the mobile robot in inertia frame.

θ: relative heading of the mobile robot in inertia frame.

$L:$ distance between left and right wheel.

$r:$ radius of wheel.

$V_C$: mobile robot’s centre linear velocity in a global reference frame from the two differential driving wheels.

${\mathsf{\omega }}_C$: mobile robot’s centre angular velocity in a global reference frame from the two differential driving wheels.

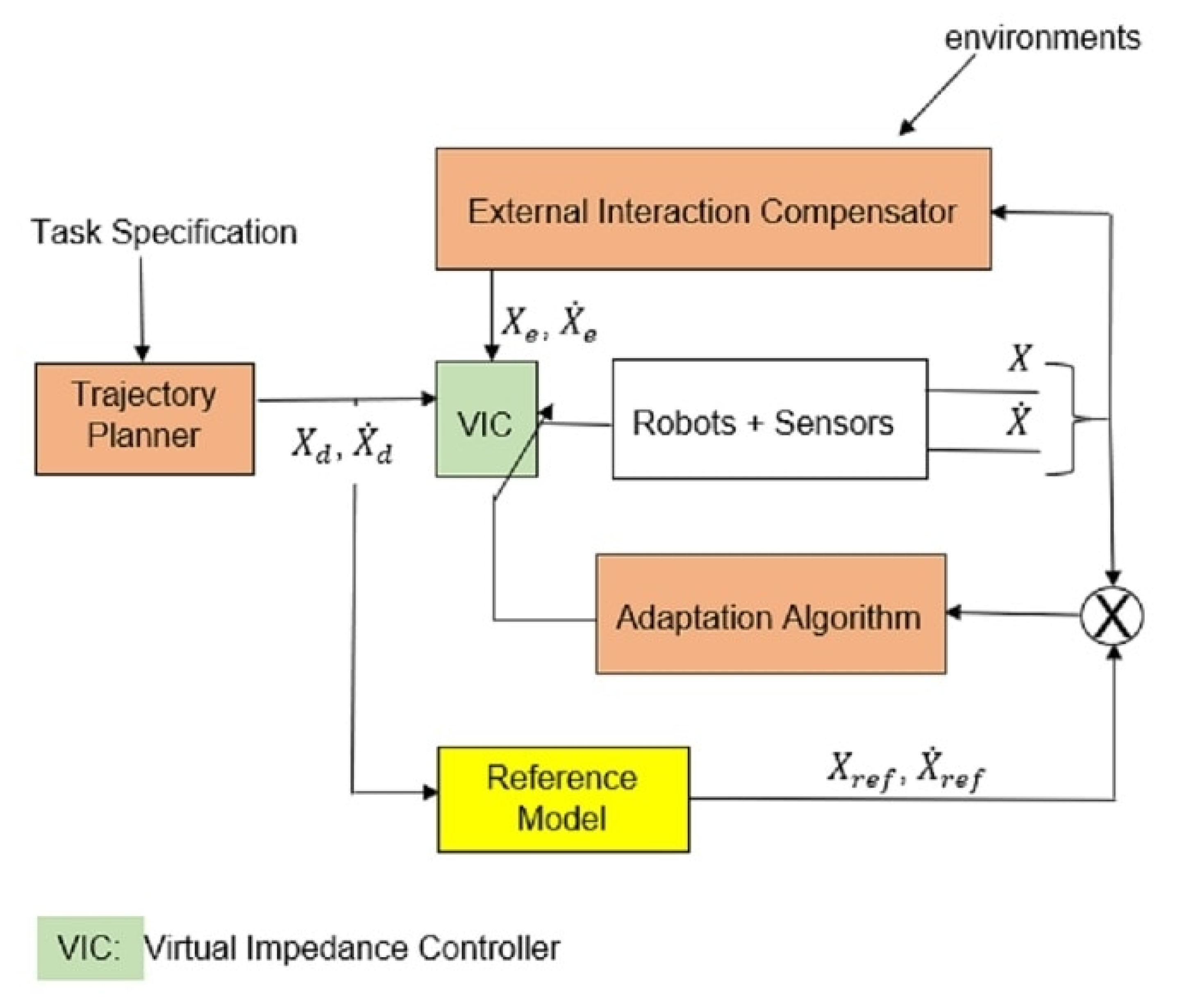
The multi-robot system with the virtual impedance controller is represented in the block diagram in Figure 5.

With this two-layered navigation strategy, the robot generates an attractive force towards the planned trajectory until the goal is reached. The attractive force is stable because the global trajectory planner plans an obstacle-free path from the starting position. The robot only generates a repulsive force if an obstacle (static or dynamic) enters into its security zone (defined within the sensing envelope). This is different from the potential field method that generates a repulsive force from an obstacle, no matter the position of the mobile robot. These forces can be controlled with the damping and stiffness parameters in order to find a good balance so that the robot will always avoid obstacles, yet remain attracted to the planned trajectory. However, the orientation of the robot becomes unstable as the robot reacts to the repulsive forces whilst being attracted to the reference trajectory. The oscillations are highlighted when the robot is subjected to multiple repulsive forces generated from multiple obstacles (static or dynamic).

3. Improved Adaptive Virtual Impedance Control

A new adaptive virtual impedance method is proposed in Figure 6 to overcome the instability problem of the conventional virtual impedance method. The improved control method aims to remove the orientation oscillations that occur when the mobile robot approaches obstacles.

The virtual impedance controller is modified by adding an adaptation algorithm and reference model for stable dynamic behaviour [25,26,27]. The dynamic behaviour of the robot is given by the following equation:

$$M·\ddot{x}=K·\left(x_{traj}-x\right)+D·\left({\dot{x}}_{traj}-\dot{x}\right)+K_e\left(x_e-x\right)+D_e\left({\dot{x}}_e-\dot{x}\right)$$

(10)

with

$x$: the robot position vector.

$x_{traj}$: the trajectory position vector.

$x_e$: the obstacle position vector in the environment.

In state space form, the dynamic equation is written as follows:

$${\dot{X}}_i=A{X}_i+B_1{u}_d+{\displaystyle \sum }_{j=1}^n{B}_{2j}{X}_j$$

(11)

with

$$X_i=\left[\begin{array}{c}{x}_i\\ {\dot{x}}_i\end{array}\right]; X_j=\left[\begin{array}{c}{x}_{ej}\\ {\dot{x}}_{ej}\end{array}\right]; u_d=\left[\begin{array}{c}{x}_{traj}\\ {\dot{x}}_{traj}\end{array}\right]$$

(12)

$u_d$ and $X_j$ represent the input vectors to the system.

$$A=\left[\begin{array}{cc}0& 1\\ K_1/M& D_1/M\end{array}\right]; B_1=\left[\begin{array}{cc}0& 1\\ K_i/M& D_i/M\end{array}\right]; B_{2j}=\left[\begin{array}{cc}0& 1\\ K_{ej}/M& D_{ej}/M\end{array}\right]$$

(13)

$$K_1=K_i+{\displaystyle \sum }_{j=1}^n{K}_{ej}; D_1=D_i+{\displaystyle \sum }_{j=1}^n{D}_{ej}$$

(14)

The matrix $B_{2j}$ is added when another mobile robot is added to the environment. Additional mobile robots can be added by adding more matrices. The current position of the robot, positions of obstacles and the position of the desired trajectory are used to formulate Equations (10) and (11). Next, we will look at the same system, but with two degrees of freedom (dof).

The extension of a system with two dof is defined using the new state vector $X$ given by:

$${\tilde{X}}_i={\left[x_i {\dot{x}}_i y_i {\dot{y}}_i\right]}^T$$

(15)

${\tilde{u}}_d$ and ${\tilde{X}}_j$ represent the input vectors of the system, with:

$${\tilde{u}}_d={\left[x_d {\dot{x}}_d y_d {\dot{y}}_d\right]}^T and {\tilde{X}}_j={\left[x_j {\dot{x}}_j y_j {\dot{y}}_j\right]}^T$$

(16)

The new state space equation is given by:

$${\dot{\tilde{X}}}_i=\tilde{A}{\tilde{X}}_i+{\tilde{B}}_1{\tilde{u}}_d+{\displaystyle \sum }_{j=1}^n{\tilde{B}}_{2j}{\tilde{X}}_j$$

(17)

with

$$\tilde{A}=\left[\begin{array}{cc}A& {\mathbf{0}}_{2.2}\\ {\mathbf{0}}_{2.2}& A\end{array}\right]; {\tilde{B}}_1=\left[\begin{array}{cc}{B}_1& {\mathbf{0}}_{2.2}\\ {\mathbf{0}}_{2.2}& B_1\end{array}\right]; {\tilde{B}}_{2j}=\left[\begin{array}{cc}{B}_{2j}& {\mathbf{0}}_{2.2}\\ {\mathbf{0}}_{2.2}& B_{2j}\end{array}\right]$$

(18)

and where ${\mathbf{0}}_{2.2}$ is a 2 × 2 zero matrix.

The 2 × 2 zero matrix is added because it represents the linear transformation, which transforms all the vectors to the zero vector. Equation (17) uses both the x and y positions and the matrices used are 4 × 4. The damping and stiffness parameters, K and D, can be tuned in the A and $B_1$ matrices to achieve different results. Increasing the K parameter will result in greater attractive and repulsive forces. The value of the damping parameter will influence the rate at which the robot recovers to the desired trajectory. A good balance between these parameters is required to achieve the desired motion behaviour.

The position and the speed of the robot are determined by the integration of Equation (17). The speed and acceleration are bounded by the actuators used on the physical robot in a real-world scenario.

4. Reference Model-Based Control Strategy

A reference model is defined in order to control the dynamic behaviour of the robot on its reference trajectory; this reference model is shown in the lower block in Figure 6.

The reference model is defined by a second-order differential equation as follows:

$$x_{ref}=-2\xi {\omega }_n{\dot{x}}_{ref}-{\omega }_n^2{\ddot{x}}_{ref}+{\omega }_n^2{x}_d+2\xi {\omega }_n{x}_d$$

(19)

If we defined the different state and control variables

$$X={\left[ x_{ref} {\dot{x}}_{ref} \right]}^T and u_d={\left[ x_d {\dot{x}}_d \right]}^T$$

(20)

Equation (11) is written in state space form as follows:

$$\dot{X}= A_{ref}X+B_{ref}{u}_d$$

(21)

with

$$A_{ref}=\left[\begin{array}{cc}0& 1\\ -{\omega }_n^2& -2\xi {\omega }_n\end{array}\right] and B_{ref}=\left[\begin{array}{cc}0& 0\\ {\omega }_n^2& 2\xi {\omega }_n\end{array}\right]$$

(22)

Now, we extend this representation to a system with two dof with ${\tilde{X}}_{ref}$ the state vector defined as follows:

$${\tilde{X}}_{ref}={\left[x_{ref} {\dot{x}}_{ref} y_{ref} {\dot{y}}_{ref}\right]}^T$$

(23)

The new state space equation is written as follows:

$${\dot{\tilde{X}}}_{ref}={\grave{A}}_g{\tilde{X}}_{ref}+{\grave{B}}_g{\tilde{u}}_d$$

(24)

where:

$${\tilde{u}}_d=\left[x_d {\dot{x}}_d y_d {\dot{y}}_d\right]$$

(25)

with ${\grave{A}}_g$ and ${\grave{B}}_g$ given by:

$${\grave{A}}_g=\left[\begin{array}{cc}{A}_{ref}& {\mathbf{0}}_{2.2}\\ {\mathbf{0}}_{2.2}& A_{ref}\end{array}\right] and {\grave{B}}_g=\left[\begin{array}{cc}{B}_{ref}& {\mathbf{0}}_{2.2}\\ {\mathbf{0}}_{2.2}& B_{ref}\end{array}\right]$$

(26)

The control architecture proposed in Figure 6 shows that the system (robot and controller) is submitted to both the action of the environment (obstacles and other robots) that generates repulsive forces and to the attractive force generated by the error between the actual robot position and the desired position given by the desired trajectory. Each robot has the same control architecture. The parameters of the controller are adapted in real time such that each robot mimics the reference model [28,29].

The parameters, K and D, of each controller are adapted by the minimisation of the cost function defined, on one hand, by the quadratic error between the robot state vector with the reference model state vector and, on the other hand, by a constraint related in respect to a minimal security distance with the obstacles and with the other robots. The cost function is defined by:

$$J_i=\frac{1}{2}{\Vert X_i-X_{ref}\Vert }^2+\frac{1}{2}{\displaystyle \sum }_{\begin{array}{c}j=1\\ i\ne j\end{array}}^n{\lambda }_i\left(d_{sec}^2-d_{i,j}^2\right){\delta }_{i,j}$$

(27)

where:

${\delta }_{i,j}=1$ if $d_{i,j}<=R_j$ and $\delta =0$ otherwise.

${\lambda }_i$: a positive scalar used for the penalisation of the constraint related to the security distance.

$d_{sec}$: the security distance with respect to the distance between the robots.

$d_{i,j}$: the distance between the robot $i$ and the robot $j$ ($j$ = 1…nb and nb the number of robots. ($j$ ≠ $i$)).

$R_j$: represents the boundary of the detection envelope of robot $i$.

5. Parameters of Adaptation Algorithm

The adaptation of the parameters, K and D, implies the computation of the gradient of $J_i$, obtained as follows [30], given that $p=K_i, D_i, M_i, K_{ij}^{obstacles},\dots$

$$\frac{\partial J_i}{\partial p}=\frac{\partial J_i}{\partial {\tilde{X}}_i} \frac{\partial {\tilde{X}}_i}{\partial p}+{\displaystyle \sum }_{j=1}^n\frac{\partial J_i}{\partial d_{i,j}} \frac{\partial d_{i,j}}{\partial p}$$

(28)

The distance $d_{i,j}$ is defined as follows:

${\tilde{X}}_i$ and ${\tilde{X}}_j$ represent the state vectors of the robots $i$ and $j$.

$$\frac{\partial d_{i,j}}{\partial p}=\frac{\partial d_{i,j}}{\partial {\tilde{X}}_i} \frac{\partial {\tilde{X}}_i}{\partial p}$$

(29)

Combining Equations (28) and (29) leads to:

$$\frac{\partial J_i}{\partial p}=(\frac{\partial J_i}{\partial {\tilde{X}}_i}+{\displaystyle \sum }_{j=1}^n\frac{\partial J_i}{\partial d_{i,j}} \frac{\partial d_{i,j}}{\partial {\tilde{X}}_i})\frac{\partial {\tilde{X}}_i}{\partial p}$$

(30)

with

$$\frac{\partial J_i}{\partial {\tilde{X}}_i}=\left({\tilde{X}}_i-{\tilde{X}}_{ref}\right)$$

(31)

$$\frac{\partial J_i}{\partial d_{i,j}}=-{\lambda }_i{d}_{i,j}$$

(32)

and

$$\frac{\partial d_{i,j}}{\partial {\tilde{X}}_i}=({\tilde{X}}_i-{\tilde{X}}_j)$$

(33)

$\frac{\partial {\tilde{X}}_i}{\partial p}$ is obtained by the derivation of Equation (17), leading to:

$$\frac{\partial {\tilde{X}}_i}{\partial p}=\frac{\partial \tilde{A}}{\partial p}{\tilde{X}}_i+\frac{\partial {\tilde{B}}_1}{\partial p}{\tilde{u}}_d+{\displaystyle \sum }_{j=1}^n\frac{\partial {\tilde{B}}_2}{\partial p}{\tilde{X}}_j$$

(34)

For instance, by considering the parameters, $K_i$ and $D_i,$ for the reference trajectory, Equation (34) is rewritten as follows:

$$\frac{\partial {\tilde{X}}_i}{\partial K_i}=\frac{\partial \tilde{A}}{\partial K_i}{\tilde{X}}_i+\frac{\partial {\tilde{B}}_1}{\partial K_i}{\tilde{u}}_d$$

(35)

$$\frac{\partial {\tilde{X}}_i}{\partial D_i}=\frac{\partial \tilde{A}}{\partial D_i}{\tilde{X}}_i+\frac{\partial {\tilde{B}}_1}{\partial D_i}{\tilde{u}}_d$$

(36)

with $\frac{\partial \tilde{A}}{\partial K_i}, \frac{\partial \tilde{A}}{\partial D_i}, \frac{\partial {\tilde{B}}_1}{\partial K_i}, \frac{\partial {\tilde{B}}_1}{\partial D_i}$, which are represented by the following matrices:

$$\frac{\partial \tilde{A}}{\partial K_i}=\left[\begin{array}{ccc}0& 0& \begin{array}{cc}0& 0\end{array}\\ -1/M& 0& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}0\\ -1/M\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\right]$$

(37)

$$\frac{\partial \tilde{A}}{\partial D_i}=\left[\begin{array}{ccc}0& 0& \begin{array}{cc}0& 0\end{array}\\ 0& -1/M& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ -1/M\end{array}\end{array}\end{array}\right]$$

(38)

with

$$\frac{\partial {\tilde{B}}_1}{\partial K_i}=-\frac{\partial \tilde{A}}{\partial K_i}, \frac{\partial {\tilde{B}}_1}{\partial D_i}=-\frac{\partial \tilde{A}}{\partial D_i}$$

(39)

Let us define $a_1=\frac{\partial \tilde{A}}{\partial K_i}and{a}_2=\frac{\partial \tilde{A}}{\partial D_i}.$

Therefore

$$\frac{\partial {\tilde{X}}_i}{\partial K_i}=a_1\left({\tilde{X}}_i-u_d\right)$$

(40)

$$\frac{\partial {\tilde{X}}_i}{\partial D_i}=a_2\left({\tilde{X}}_i-u_d\right)$$

(41)

The gradient method is used to compute the new parameter as follows:

$$P_{new}=P_{old}-\mathsf{ƞ}\frac{\partial J}{\partial p}{|}_{P_{old}}$$

(42)

Equation (42) is used to update the specific parameter chosen to represent $P_{old}$.

6. Results

The results of the implemented adaptive virtual impedance control algorithm are presented below. The adaptive virtual impedance control algorithm forms part of the two-layered navigation strategy implemented by the paper. The global (higher) layer uses the A * path planner to plan a collision-free path to the goal using a pre-gathered grid map of the indoor environment. The local (lower) level uses the control algorithm for dynamic behaviour when avoiding the unknown static and dynamic obstacles that enter into the sensing envelope of the mobile robot.

The following simulation introduces an unknown obstacle (red block) into the environment. During the simulation, the robot makes use of its two-layered navigation strategy to plan a path and avoid obstacles during its navigation towards the goal. The motion behaviour and orientation oscillations when avoiding obstacles were closely observed.

At the start of navigation simulation 1, the implemented robot plans a collision-free path to the goal point using the A* path planner (Figure 7a) unaware of the unknown obstacle (red block). The robot detects the obstacle 2m away, but the control algorithm only generates a repulsive force from the obstacle when it enters into the security zone (1 m), as seen in Figure 7b. The movement of the robot experiences some instabilities due to the attractive and repulsive forces acting on it (Figure 7c). The improved adaptive virtual impedance method generates an attractive force toward the planned trajectory instead of the goal point, this can clearly be seen in Figure 7d. The robot returns to the desired trajectory that was planned at the start, instead of moving directly toward the goal. The A* star path planner does not re-plan a path during navigation. When an unknown obstacle enters the sensing envelope of the mobile robot, the generated repulsive force is far greater than the attractive force. This is to guarantee that the mobile robot avoids the obstacle. The parameters used during navigation simulation 1 are presented in

Table 1. Navigation simulation 1 parameters.

K	D	R	S
(stiffness (N/m))	(damping (N s/m))	(sensing envelope (m))	(security zone (m))
3	4	2	1
M	r	L	Lidar
(virtual mass (Kg))	(wheel radius (mm))	(distance between wheels (mm))	(scan angles (rads))
1	33	160	π, 5π/6, 2π/3, π/2, π/3, π/6, 2π

. The stable movement and motion behaviour of the mobile robot can be seen in the Supplementary Material (Video S1).

Next, a real-world experiment was conducted. A similar floor layout was created by placing obstacles in similar positions to match those in the simulation. The reason for conducting the experiment was to test the adaptive virtual impedance algorithm in a real-world scenario. The same parameters were used during the real-world experiment.

The robot pre-plans a collision-free path to the goal in Figure 8a. The robot detects the red obstacle in Figure 8b and relies on the control algorithm to avoid the obstacle. The mobile robot avoided the red obstacle and returned to the planned path before moving to the goal (Figure 8c). The path planned by the mobile can be seen in the Supplementary Material (Video S2). The movement behaviour of the mobile robot when avoiding the red obstacle can be seen in the Supplementary Material (Video S3).

The data on the graphs in Figure 9 illustrate how the mobile robot reacts to detecting the unknown obstacle. The orientation of the mobile robot experiences minor oscillations, in both the simulation (Figure 9a) and real world (Figure 9b) when detecting the unknown obstacle. This is due to the avoidance algorithm of the robot, as it generates a repulsive force from the newly detected obstacle. The movement of the robot is improved from the conventional virtual impedance method and the results show a stable linear velocity with good motion behaviour.

The next experiment introduces a dynamic obstacle in the environment. The mobile robot plans a similar path from the starting position to the goal as in the previous simulation. The results of this simulation, in which the two-layered navigation strategy reacts to an unknown dynamic obstacle entering the sensing and security zone of the mobile robot, are presented below.

The implemented robot pre-plans a collision-free path to the goal in Figure 10a. As the mobile robot moves along the desired trajectory in Figure 10b, a dynamic obstacle moves in front of the mobile robot. The orientation of the robot experiences minor oscillations (Figure 10c), as the algorithm generates a repulsive force from the newly detected dynamic obstacle. Since the obstacle is moving away from the mobile robot, the mobile robot recovers quickly and moves toward the goal point along the planned path (Figure 10d). The reference model in the adaptive virtual impedance algorithm ensures that the desired behaviour in the transition phases is respected. The mobile robot moves back to the planned path as soon as the dynamic obstacle moves out of the security zone of the mobile robot and no longer obscures the path along the desired trajectory. The two-layered navigation strategy only makes use of the global path planner at the start of the simulation. The desired trajectory is not re-planned during the simulation. It is evident that the implemented robot took longer to return to the desired trajectory when a dynamic obstacle is in the close vicinity of the robot. The simulation tested the localisation, path planning and obstacle avoidance capabilities of the mobile robot in a dynamic environment. The parameters used during navigation simulation 2 are presented in

Table 2. Navigation simulation 2 parameters.

K	D	R	S
(stiffness (N/m))	(damping (N s/m))	(sensing envelope (m))	(security zone (m))
3	4	2	1
M	r	L	Lidar
(virtual mass (Kg))	(wheel radius (mm))	(distance between wheels (mm))	(scan angles (rads))
1	33	160	π, 5π/6, 2π/3, π/2, π/3, π/6, 2π

.

In Figure 11a the mobile robot pre-plans a collision-free path to the goal. As the mobile robot approaches the goal, a human representing a dynamic obstacle, moves in front of the mobile robot (Figure 11b). The dynamic obstacle continues to move away from the mobile robot in Figure 11c. Once the dynamic obstacle moved away, the mobile robot was able to recover and reach the goal. The movement behaviour of the mobile robot when detecting and avoiding a dynamic obstacle can be seen in the Supplementary Material (Video S4).

As seen in Figure 12a, the angular velocity oscillates when a dynamic obstacle enters into the sensing envelope of the mobile robot. The angular velocity is volatile around the 14 s mark in Figure 12b due to the presence of the dynamic obstacle as the robot tries to return to the planned path.

The following simulation implements multiple mobile robots. Each robot plans a path to its own goal point and uses the adaptive virtual impedance controller to avoid collisions.

The simulation in Figure 13 implements multiple mobile robots. Each robot plans a path to its own goal point at the start (Figure 13a) and uses the adaptive virtual impedance controller to avoid collisions (Figure 13b). The simulation illustrated the avoidance capability of each mobile robot when their planned paths intersect (Figure 13c). The result shows that the robots avoid collisions easier when the other dynamic obstacle detected is another mobile robot with the implemented two-layered navigation strategy (Figure 13d). The result demonstrated that the mobile robots avoided a collision and each robot recovered to its own planned path. The mobile robots successfully implemented the two-layered navigation strategy in a dynamic multi-robot environment and maintained the desired behaviour with movement stability.

7. Conclusions and Future Work

The A* path planner successfully planned paths for single and multiple mobile robots in an environment with known and unknown obstacles. An optimal path with a desired trajectory toward the goal was generated for each mobile robot. It was noted that the A* path planner did not re-plan a new path once unknown obstacles were detected. This is a characteristic of the path planner that was welcomed, since the research aimed at developing a local motion control algorithm that would recover to the original path after avoiding an obstacle.

The conventional virtual impedance control method was improved to overcome drawbacks, such as severe oscillations in motion behaviour. The improved adaptive virtual impedance algorithm was implemented with the A* path planner in a two-layered navigation strategy. The obtained results show stable motion behaviour with good accuracy in environments with known obstacles. The introduction of a static unknown obstacle resulted in minor oscillations in motion behaviour. However, this had no effect on the travelled path and the motion remained smooth throughout. The mobile robot accurately recovered to the desired trajectory after avoiding the obstacle.

The motion behaviour of the mobile robot in a multi-robot dynamic environment experienced prolonged oscillations because of the unpredictability of dynamic obstacles. This can be reduced to a degree, by changing the stiffness and damping parameters. The system avoids local minima by applying the two-layered navigation strategy with the adaptive virtual impedance control method.

Real-world experiments were conducted using the TurtleBot 3 Burger. The obtained results validated the ones obtained in simulations. Successful experiments tested the two-layered navigation strategy with unknown and dynamic obstacles.

The autonomous collaborative robot system could have many different applications such as smart manufacturing or working in an environment with humans. Clinical arenas, such as hospitals and wellness centres, could benefit from collaborative mobile robotics. Such a robot system can aid in disinfecting areas, moving equipment, carrying medicine [31], and even automate wheelchairs. The avoidance algorithm can be further developed to avoid dynamic obstacles from all angles. This can be useful if the system is applied within an environment with humans that have unpredictable movement behaviours.

An auto-adaptive path planning method [32] can be introduced to improve the path planning capabilities of the multi-robot system. Previous research shows that the robot can change its own configurations to perform auto-adapted path planning corresponding to the environmental variation. This method can increase the probability of completing the path planning, especially in a large dynamic multi-robot environment.

Further work can be carried out when the robot is equipped with a manipulator. The orientation of the mobile robot then becomes critical. The movement and control algorithm for a gripper requires further development of the current navigation algorithm in this paper. The orientation of the mobile robot is critical for the gripper to be able to pick up objects.

Further research regarding a real-time neural network method is on-going. The main idea is to map a set of conventional neural networks to map the adaptive virtual impedance method.