Design of a Labriform-Steering Underwater Robot Using a Multiphysics Simulation Environment
Abstract
:1. Introduction
2. Materials and Methods
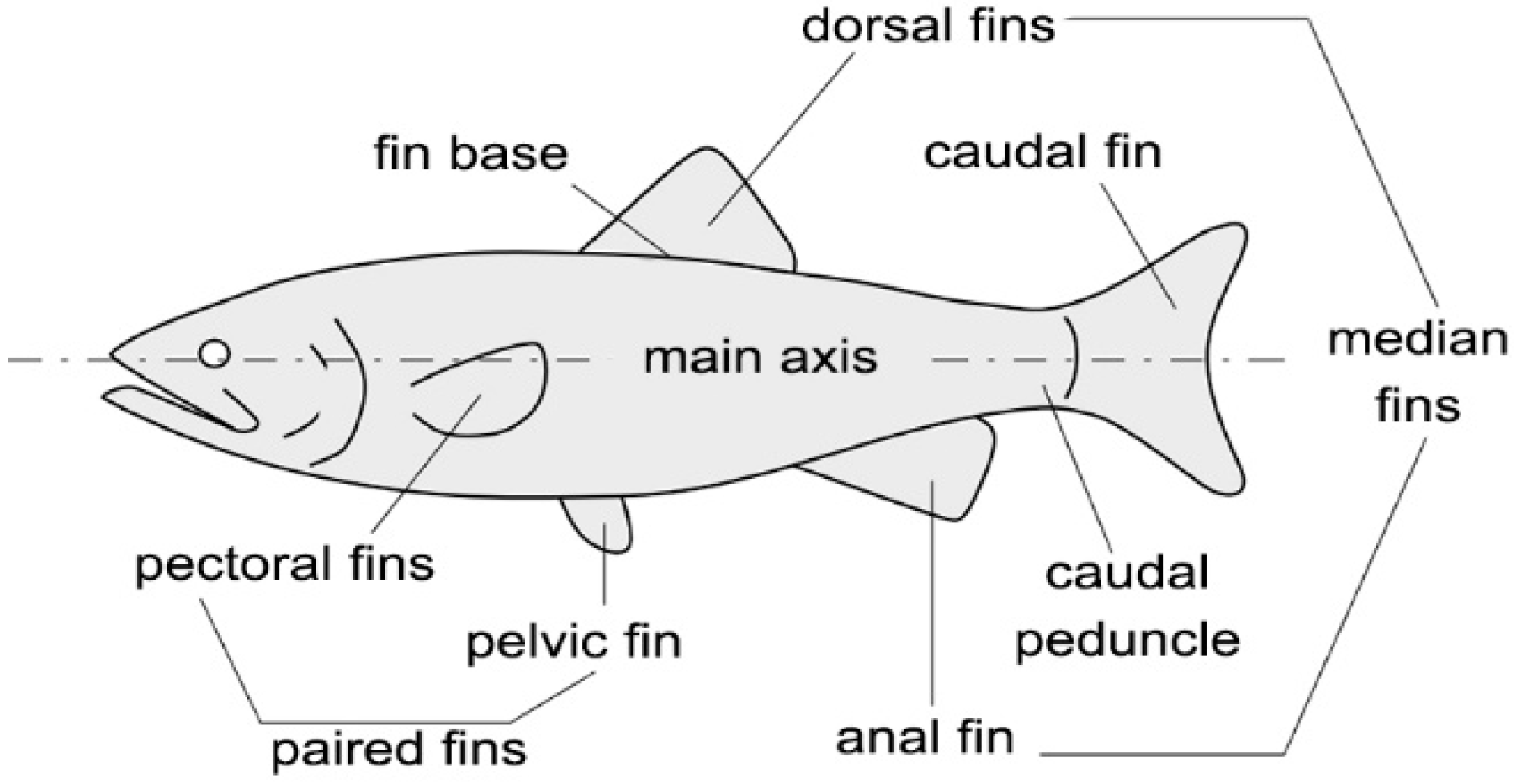
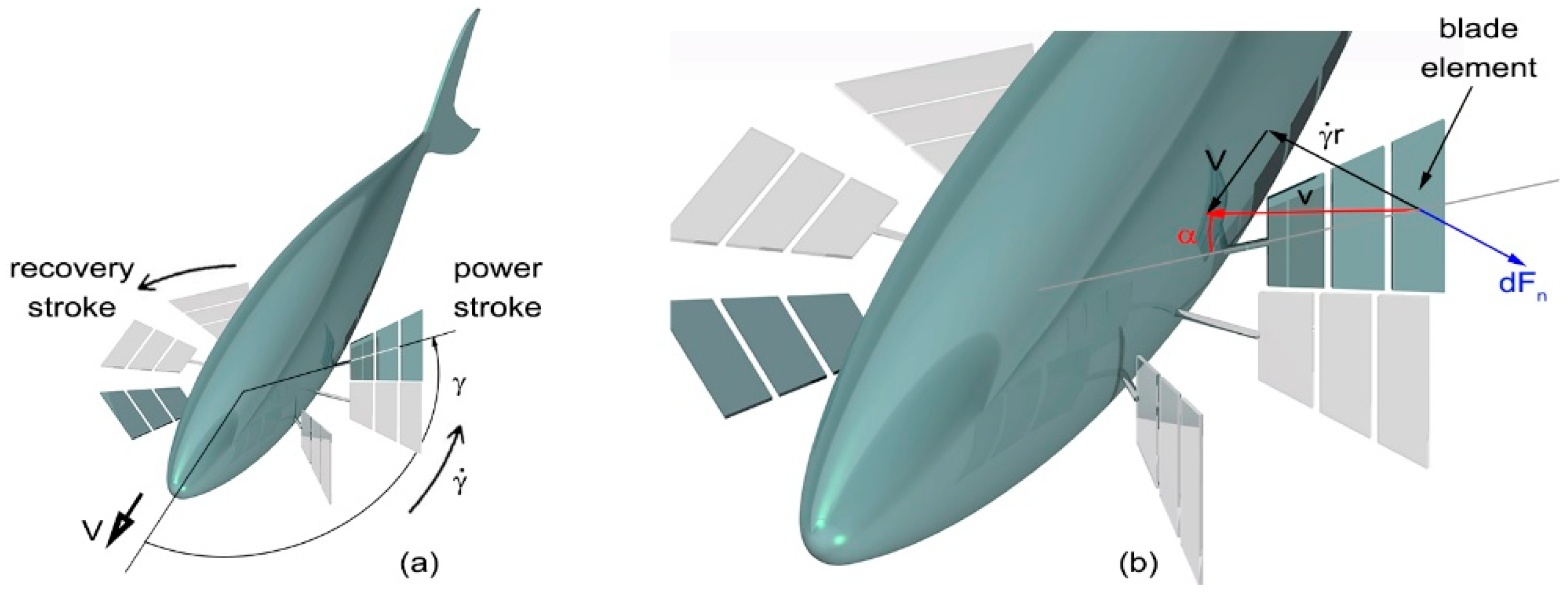
2.1. Mechanics of Drag-Based Labriform Swimming and Blade-Element Theory
- Drag force is due to pressure drag only, whereas the effects of viscosity are negligible.
- During the power stroke, the distal two-thirds of the fin are perpendicular to the horizontal plane.
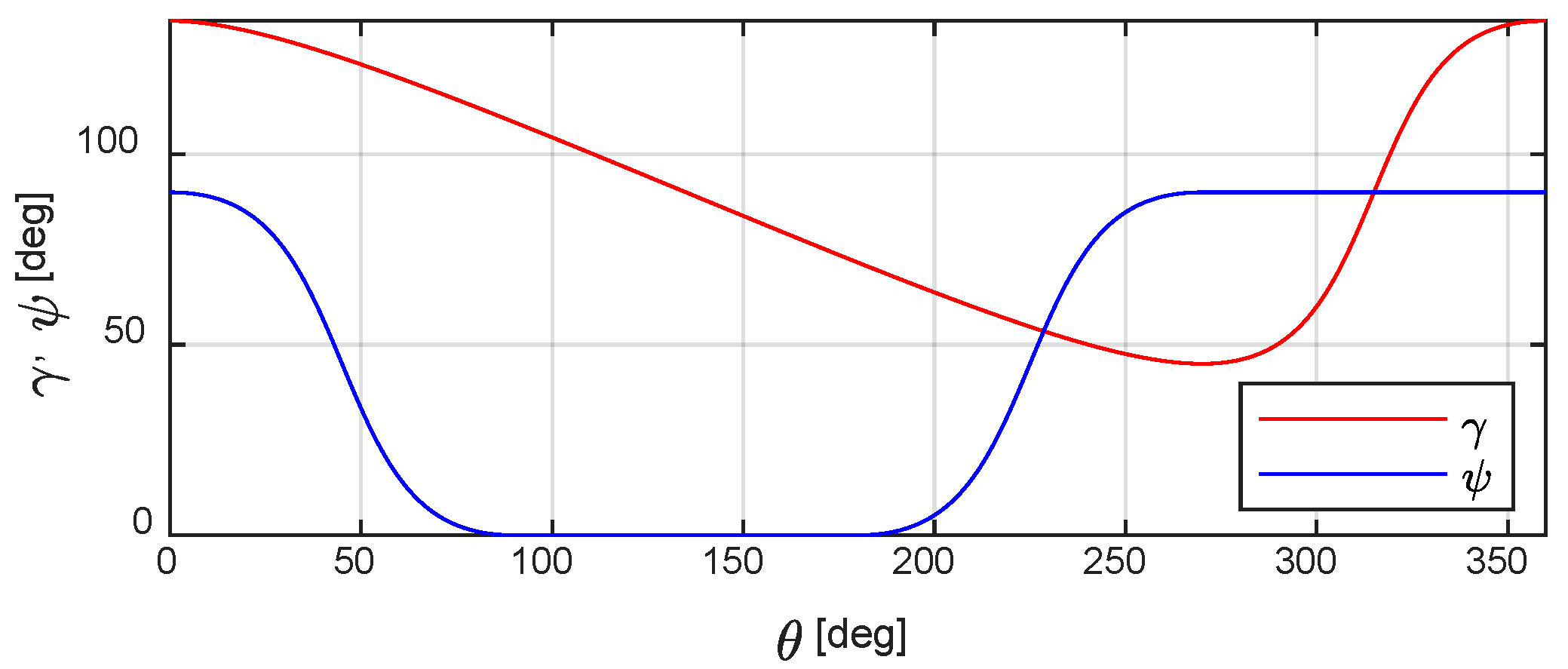
- The rowing rotation around the fish yaw axis is about 90 degrees.
- At the end of the power stroke, as the fin moves forward, its distal two-thirds form a small angle with the horizontal plane (about 10–20 degrees).
- The power stroke is about three times faster than the recovery stroke.
- A blade-element approach is used to analyze pectoral fin mechanics in drag-based labriform swimming.
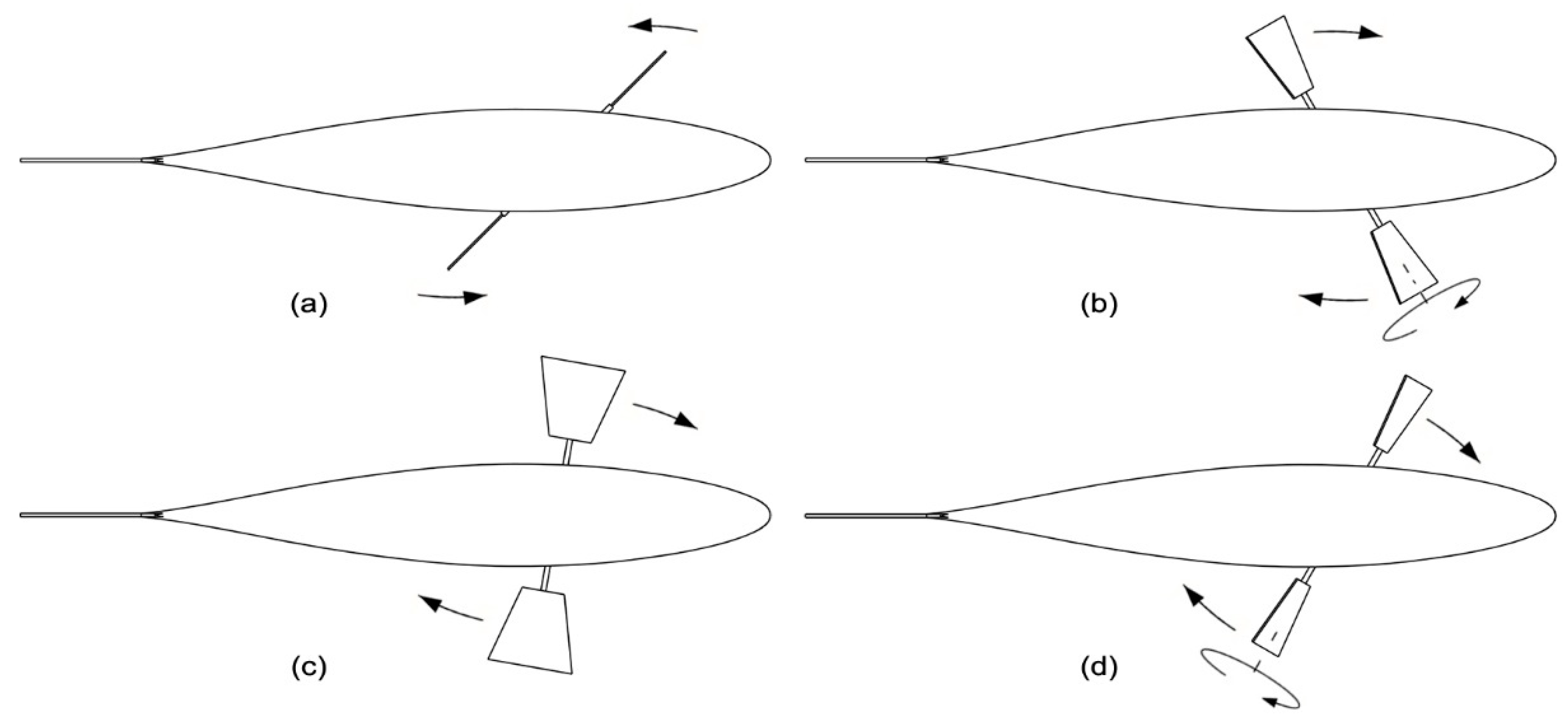
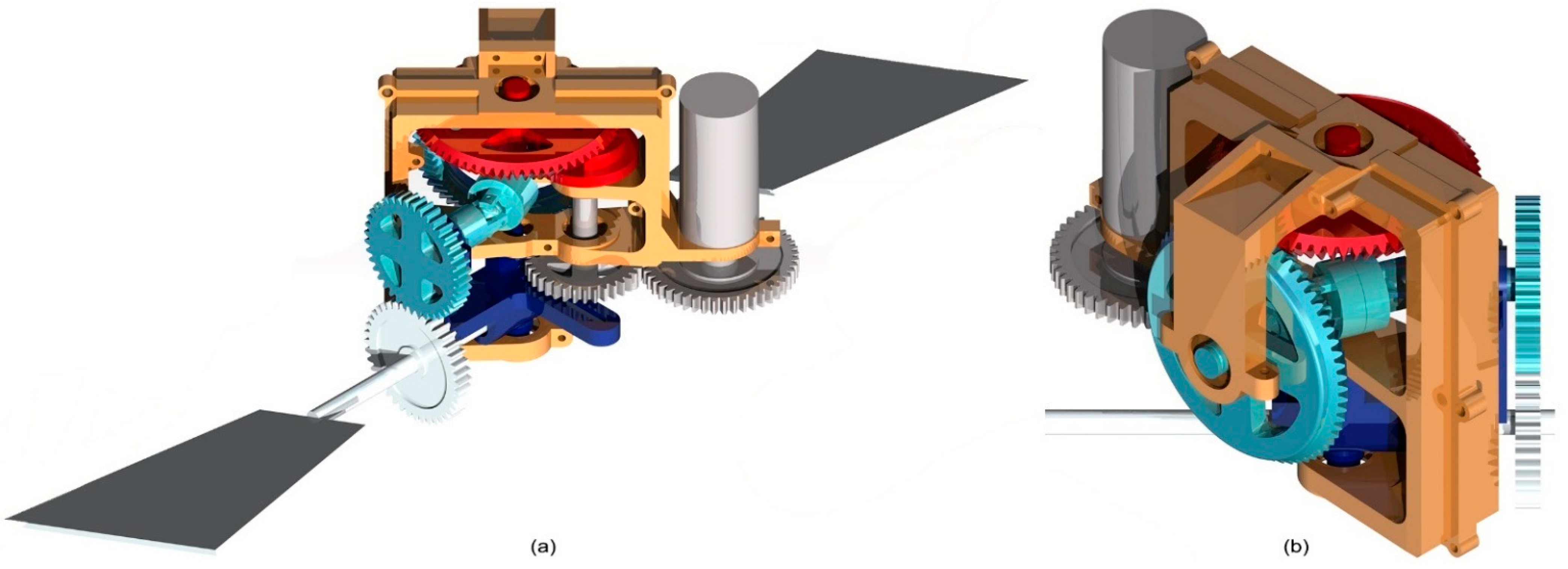
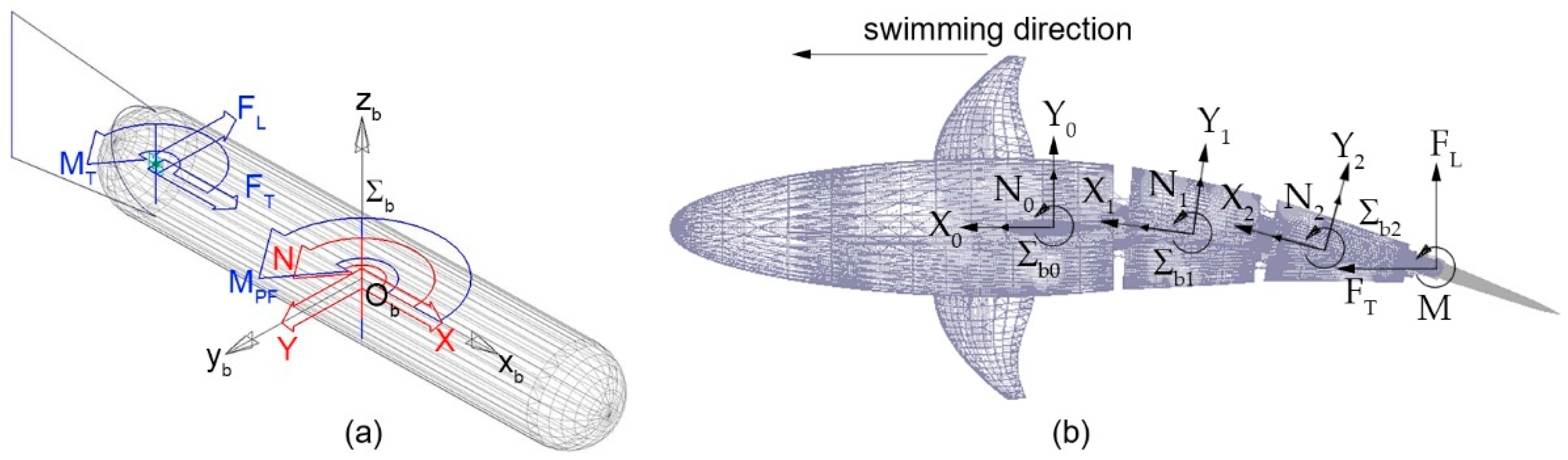
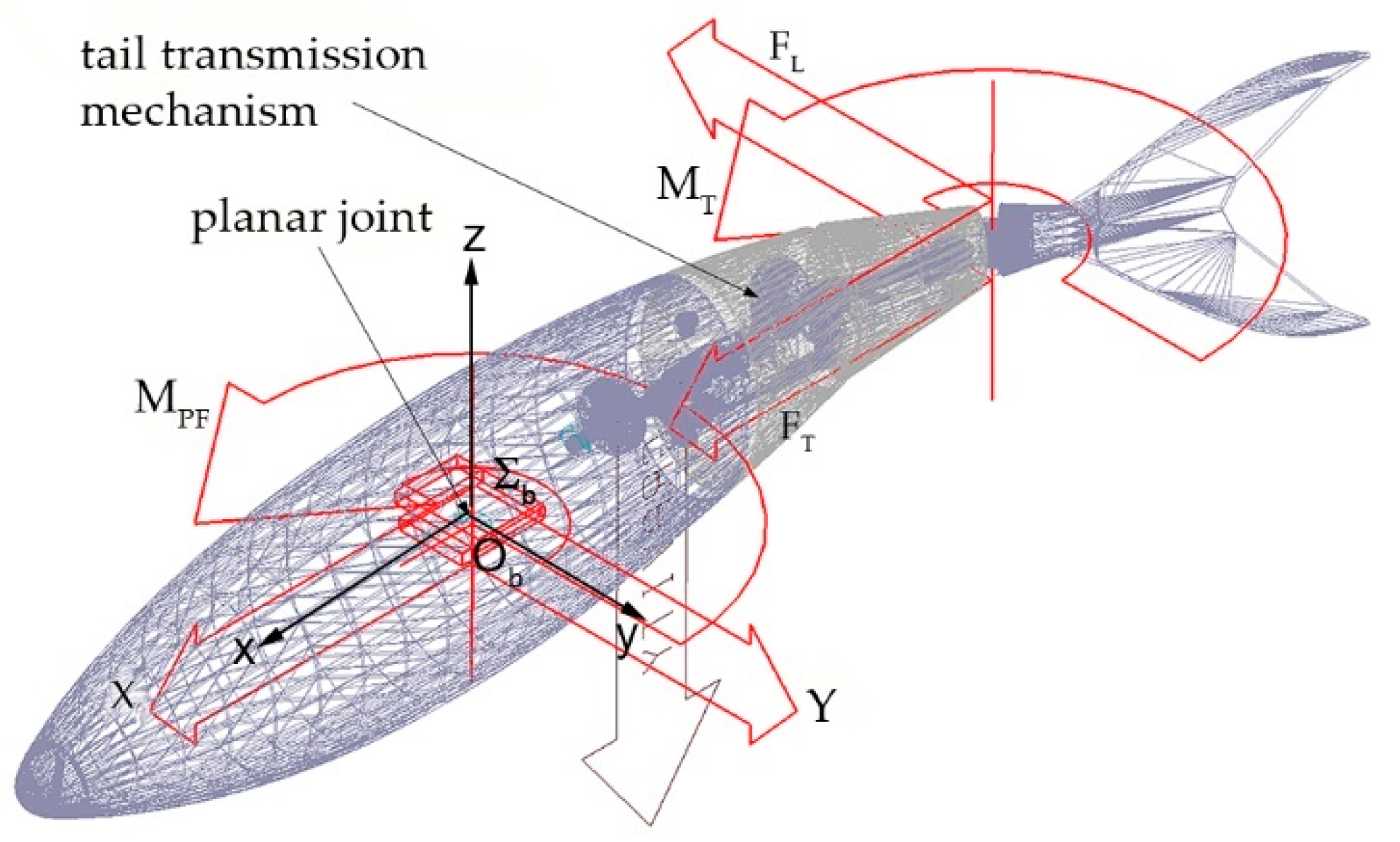
2.2. Functional Design of the Transmission System
- Phase 1—the power stroke, Figure 4a: the pitching rotation is blocked, and the fin is kept perpendicular to the horizontal plane, while it spins about the yaw axis at high angular velocity.
- Phase 2—feathering recovery stroke, Figure 4b: the fin turns around its pitch axis until it is flat on the horizontal plane; at the same time, it rotates slowly about the fish yaw axis in the opposite direction with respect to the power stroke.
- Phase 3—main recovery stroke, Figure 4c: the rotation about the pitch axis is blocked and the fin is kept parallel the horizontal plane, while it continues to move slowly in the reverse direction with respect to the power stroke.
- Phase 4—unfeathering recovery stroke, Figure 4d: the fin turns about its pitch axis until it is perpendicular to the horizontal plane; at the same time, the fin slows down along the last part of the rotation about the yaw axis, preparing for the upcoming power stroke.
3. Results
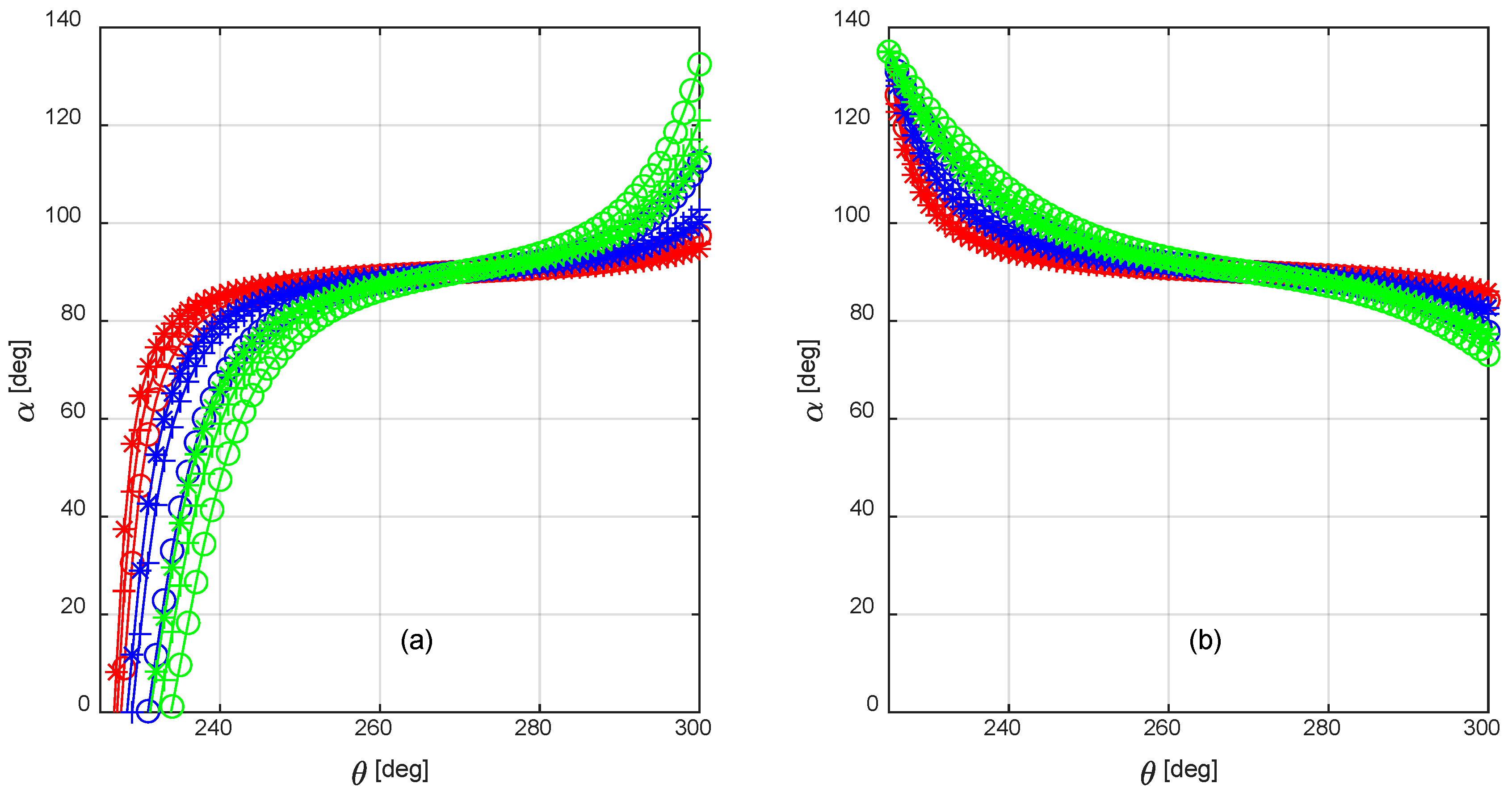
3.1. Preliminary Analysis of the Transmission Mechanism
3.2. Multibody Analysis
3.3. Mechanism Prototyping and Mechatronic Components
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scaradozzi, D.; Palmieri, G.; Costa, D.; Pinelli, A. BCF swimming locomotion for autonomous underwater robots: A review and a novel solution to improve control and efficiency. Ocean Eng. 2017, 130, 437–453. [Google Scholar] [CrossRef]
- Sfakiotakis, M.; Lane, D.; Davies, J. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef] [Green Version]
- Costa, D.; Palmieri, G.; Scaradozzi, D.; Callegari, M. Experimental Validation of a Bio-Inspired Thruster. J. Dyn. Syst. Meas. Control 2021, 143, 081004. [Google Scholar] [CrossRef]
- Costa, D.; Palmieri, G.; Palpacelli, M.C.; Callegari, M.; Scaradozzi, D. Design of a bio-inspired underwater vehicle. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Costa, D.; Palmieri, G.; Palpacelli, M.C.; Scaradozzi, D.; Callegari, M. Design of a Carangiform Swimming Robot through a Multiphysics Simulation Environment. Biomimetics 2020, 5, 46. [Google Scholar] [CrossRef]
- Blake, R.W. The mechanics of labriform locomotion I. Labriform locomotion in the angelfish (Pterophyllum eimekei): An analysis of the power stroke. J. Exp. Biol. 1979, 82, 255–271. [Google Scholar] [CrossRef]
- Vogel, S. Life in Moving Fluids: The Physical Biology of Flow; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Kato, N.; Furushima, M. Pectoral fin model for maneuver of underwater vehicles. In Proceedings of the Symposium on Autonomous Underwater Vehicle Technology, Monterey, CA, USA, 2–6 June 1996. [Google Scholar]
- Westneat, M.W.; Walker, J.A. Applied aspects of mechanical design, behavior, and performance of pectoral fin swimming in fishes. In Proceedings of the Special Session on Bio-Engineering Research Related to Autonomous Underwater Vehicles, Durham, NH, USA, 10–11 September 1997; Available online: https://apps.dtic.mil/sti/pdfs/ADA330550.pdf#page=157 (accessed on 21 November 2021).
- Naser, F.A.; Rashid, M.T. Design, modeling, and experimental validation of a concave-shape pectoral fin of labriform-mode swimming robot. Eng. Rep. 2019, 1, e12082. [Google Scholar] [CrossRef]
- Sitorus, P.E.; Nazaruddin, Y.Y.; Leksono, E.; Budiyono, A. Design and implementation of paired pectoral fins locomotion of labriform fish applied to a fish robot. J. Bionic Eng. 2009, 6, 37–45. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, Z.; Du, R. The design and prototyping of a wire-driven robot fish with pectoral fins. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013. [Google Scholar]
- Li, Z.; Ge, L.; Xu, W.; Du, Y. Turning characteristics of biomimetic robotic fish driven by two degrees of freedom of pectoral fins and flexible body/caudal fin. Int. J. Adv. Robot. Syst. 2018, 15, 1729881417749950. [Google Scholar] [CrossRef]
- Behbahani, S.B.; Tan, X. Bio-inspired flexible joints with passive feathering for robotic fish pectoral fins. Bioinspiration Biomim. 2016, 11, 036009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, N.; Gupta, A.; Mukherjee, S. A dynamic model for underwater robotic fish with a servo actuated pectoral fin. SN Appl. Sci. 2019, 1, 659. [Google Scholar] [CrossRef] [Green Version]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drucker, E.G.; Walker, J.A.; Westneat, M.W. Mechanics of pectoral fin swimming in fishes. Fish Physiol. 2005, 23, 369–423. [Google Scholar]
- Lauder, G.V.; Jayne, B.C. Pectoral fin locomotion in fishes: Testing drag-based models using three-dimensional kinematics. Am. Zool. 1996, 36, 567–581. [Google Scholar] [CrossRef]
- Fischer, I.S.; Paul, R.N. Kinematic Displacement Analysis of a Double-Cardan-Joint Driveline. J. Mech. Des. 1991, 113, 263–271. [Google Scholar] [CrossRef]
- Costa, D.; Palmieri, G.; Callegari, M.; Scaradozzi, D. Multi-body Analysis of a Bio-inspired Underwater Robot. In Advances in Italian Mechanism Science; Mechanisms and Machine Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 68. [Google Scholar]
- Antonelli, G. Underwater Robots: Motion and Force Control of Vehicle-Manipulator Systems; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Fossen, T.I. Marine Control System-Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Costa, D.; Palmieri, G.; Palpacelli, M.-C.; Panebianco, L.; Scaradozzi, D. Desing of a Bio-inspired Autonomous Underwater Robot. J. Intell. Robot. Syst. 2018, 91, 181–192. [Google Scholar] [CrossRef]
- Prandtl, L.; Tietjens, O.G.; Den Hartog, J.P. Applied Hydro-And Aeromechanics; Dover: New York, NY, USA, 1957; Volume 35. [Google Scholar]
- Scaradozzi, D.; Conte, G.; De Capua, G.P.; Sorbi, L.; Luciani, C.; De Cecco, P.G.; Sorci, A. Innovative technology for studying growth areas of Posidonia oceanica. In Proceedings of the 2009 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, Crema, Italy, 25 September 2009; pp. 71–75. [Google Scholar]





| - | Power Stroke | Recovery Stroke | ||
|---|---|---|---|---|
| Time | Time 1 | Time 2 | Time 3 | Time 4 |
| Yaw rotation | Driven—fast | Driven—slow | Driven—slow | Driven—slow |
| Yaw angle γ 1 | 45° -> 135° | 135° -> 108.5° | 108.5° -> 71.5° | 71.5° -> 45° |
| Pitch rotation | Blocked | Driven | Blocked | Driven |
| Pitch angle φ | Trimmed at 90° | 90° -> 0° | Trimmed at 0° | 0° -> 90° |
| 0.5 | [0.8–1.2] |
| Motor Frequency | Swimming Speed | |||
|---|---|---|---|---|
| 0.125 BL/s | 0.25 BL/s | 0.50 BL/s | 1 BL/s | |
| 0.5 Hz | 3.16 | 7.17 | 12.25 | 14.93 |
| 1 Hz | 1.46 | 3.15 | 7.15 | 12.17 |
| 1.5 Hz | 0.98 | 1.97 | 4.44 | 9.35 |
| 2 Hz | 0.75 | 1.45 | 3.13 | 7.09 |
| 3 Hz | 0.53 | 0.96 | 1.94 | 4.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, D.; Scoccia, C.; Palpacelli, M.; Callegari, M.; Scaradozzi, D. Design of a Labriform-Steering Underwater Robot Using a Multiphysics Simulation Environment. Robotics 2022, 11, 11. https://doi.org/10.3390/robotics11010011
Costa D, Scoccia C, Palpacelli M, Callegari M, Scaradozzi D. Design of a Labriform-Steering Underwater Robot Using a Multiphysics Simulation Environment. Robotics. 2022; 11(1):11. https://doi.org/10.3390/robotics11010011
Chicago/Turabian StyleCosta, Daniele, Cecilia Scoccia, Matteo Palpacelli, Massimo Callegari, and David Scaradozzi. 2022. "Design of a Labriform-Steering Underwater Robot Using a Multiphysics Simulation Environment" Robotics 11, no. 1: 11. https://doi.org/10.3390/robotics11010011








