Mixed Position and Twist Space Synthesis of 3R Chains
Abstract
1. Introduction
2. The 3R Serial Chain
2.1. Forward and Inverse Kinematics of the 3R Chain
2.2. Space of Potential Twists of the End-Effector
3. Twist Spaces of Dimension 3 for the Serial 3R Chain
3.1. Finite and Infinitesimal Motion
3.2. Kinematic Generators of a Twist System
3.3. Feasible Screw Systems for the 3R Serial Chain
3.4. Proofs of Feasibility
3.5. The 3R Chain as a Kinematic Generator of Twists
4. Synthesis with a Specified Twist Space
Solving the System of Equations
5. Design for Lower-Dimensional Twist Spaces
6. Design for Fully Specified Twist Space
6.1. Example 2: Arbitrary Finite Motion and General Twist System
6.2. Example 3: Invariant Twist System–Motion within a Subgroup of SE(3)
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sandor, G.; Freudenstein, F. Higher-order plane motion theories in kinematic synthesis. J. Eng. Ind. 1967, 89, 223–230. [Google Scholar] [CrossRef]
- Kramer, R.S.S. Selective precision synthesis of planar mechanisms satisfying position and velocity constraints. Mech. Mach. Theory 1979, 14, 161–170. [Google Scholar]
- Holte, J.; Chase, T.; Erdman, A. Approximate velocities in mixed exact-approximate position synthesis of mechanisms. AMSE J. Mech. Des. 2001, 123, 388–394. [Google Scholar] [CrossRef]
- Sathyadev, D.; Soni, A. Synthesis of planar mechanisms for coupler tangent-line envelope generation: An alternative to coupler point-path generation. ASME J. Mech. Des. 1988, 110, 122–129. [Google Scholar] [CrossRef]
- Chen, P.; Roth, B. A unified theory for the finitely and infinitesimally separated position problems of kinematic synthesis. ASME J. Eng. Ind. 1969, 91, 203–208. [Google Scholar] [CrossRef]
- Chen, P.; Roth, B. Design equations for finitely and infinitesimally separated position synthesis of binary link and combined link chains. ASME J. Eng. Ind. 1969, 91, 209–219. [Google Scholar] [CrossRef]
- Tsai, L.W.; Roth, B. Design of dyads with helical, cylindrical, spherical, revolute and prismatic joints. Mech. Mach. Theory 1972, 7, 85–102. [Google Scholar] [CrossRef]
- Robson, N.; McCarthy, J. Second order task specifications used in the geometric design of spatial mechanical linkages. Int. J. Mod. Eng. 2010, 11, 5–11. [Google Scholar]
- Robson, N.; Chen, B. Geometric Design with Multiple Realizable Motion Directions in the Vicinity of a Planar Mechanism-Environment Contact. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference IDETC/CIE 2018, Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar]
- Moon, H.; Robson, N.; Langari, R. Approximating elbow constrained hand paths via kinematic synthesis with contact specifications. In Advances in Robot Kinematics; Lenarcic, J., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Robson, N.; Soh, G.S. Kinematic Synthesis of Planar Multi-limb Mechanisms for Multi-directional Interaction with Bodies in the Environment. In Advances in Robot Kinematics 2018; Lenarcic, J., Parenti-Castelli, V., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 356–363. [Google Scholar]
- Hasanzadeh, N.; Gosh, S.; Robson, N.; Perez-Gracia, A. Velocity-field tasks for in-hand manipulative synthesis. In Advances in Robot Kinematics; Merlet, J., Lenarcic, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Robson, N.; Ghosh, S.; Soh, G.S. Kinematic Synthesis and Design of the Robust Closed Loop Articulated Minimally actuated (CLAM) Hand. Robotica 2019, 38, 1921–1939. [Google Scholar] [CrossRef]
- Tian, C.; Fang, Y.; Ge, Q.J. Structural synthesis of parallel manipulators with coupling sub-chains. Mech. Mach. Theory 2017, 118, 84–99. [Google Scholar] [CrossRef]
- Lee, E.; Mavroidis, C. Solving the geometric design problem of spatial 3r robot manipulators using polynomial homotopy continuation. ASME J. Mech. Des. 2002, 124, 652–661. [Google Scholar] [CrossRef][Green Version]
- Lee, E.; Mavroidis, C. An elimination procedure for solving the geometric design of spatial 3r manipulators. ASME J. Mech. Des. 2006, 128, 142–146. [Google Scholar] [CrossRef]
- Lee, E.; Mavroidis, C.; Merlet, J. Five precision point synthesis of spatial rrr manipulators using interval analysis. ASME J. Mech. Des. 2004, 126, 842–850. [Google Scholar] [CrossRef]
- Hauenstein, J.D.; Wampler, C.W.; Pfurner, M. Synthesis of three-revolute spatial chains for body guidance. Mech. Mach. Theory 2017, 110, 61–72. [Google Scholar] [CrossRef]
- Gibson, C.; Hunt, K. Geometry of screw systems–2: Classification of screw systems. Mech. Mach. Theory 1990, 25, 11–27. [Google Scholar] [CrossRef]
- Selig, J.M. Geometric Fundamentals of Robotics Monographs in Computer Science, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Carricato, M.; Zlatanov, D. Persistent Screw Systems. Mech. Mach. Theory 2014, 73, 296–313. [Google Scholar] [CrossRef]
- Carricato, M.; Rico-Martinez, J. Persistent screw systems. In Advances in Robot Kinematics: Motion in Man and Machine; Lenarcic, J., Stanisic, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 185–194. [Google Scholar]
- Carricato, M.; Rico-Martinez, J. Persistent screw systems of Dimension 3. In Proceedings of the 13th World Congress in Mechanism and Machine Science, Guanajuato, Mexico, 19–23 June 2011. [Google Scholar]
- Huynh, P.; Hervé, J.M. Equivalent Kinematic Chains of Three Degree-of-Freedom Tripod Mechanisms with Planar-Spherical Bonds. J. Mech. Des. 2005, 127, 95–102. [Google Scholar] [CrossRef]
- Tsai, M.; Lee, H. On the Special Bases of Two- and Three-Screw Systems. ASME J. Mech. Des. 1993, 115, 540–546. [Google Scholar] [CrossRef]
- Donelan, P.; Gibson, C. On the hierarchy of Screw Systems. Acta Appl. Math. 1993, 32, 267–296. [Google Scholar] [CrossRef]


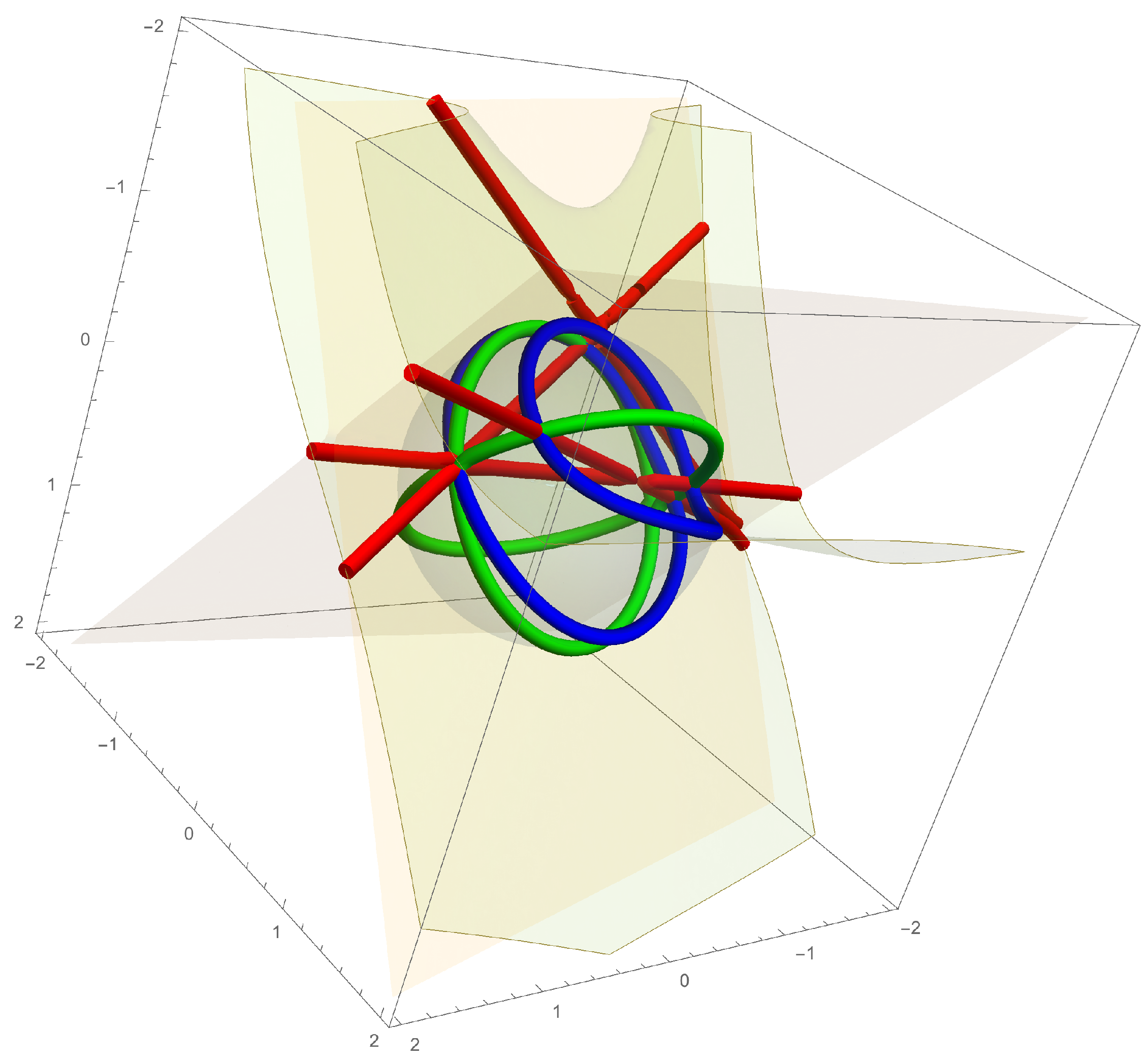
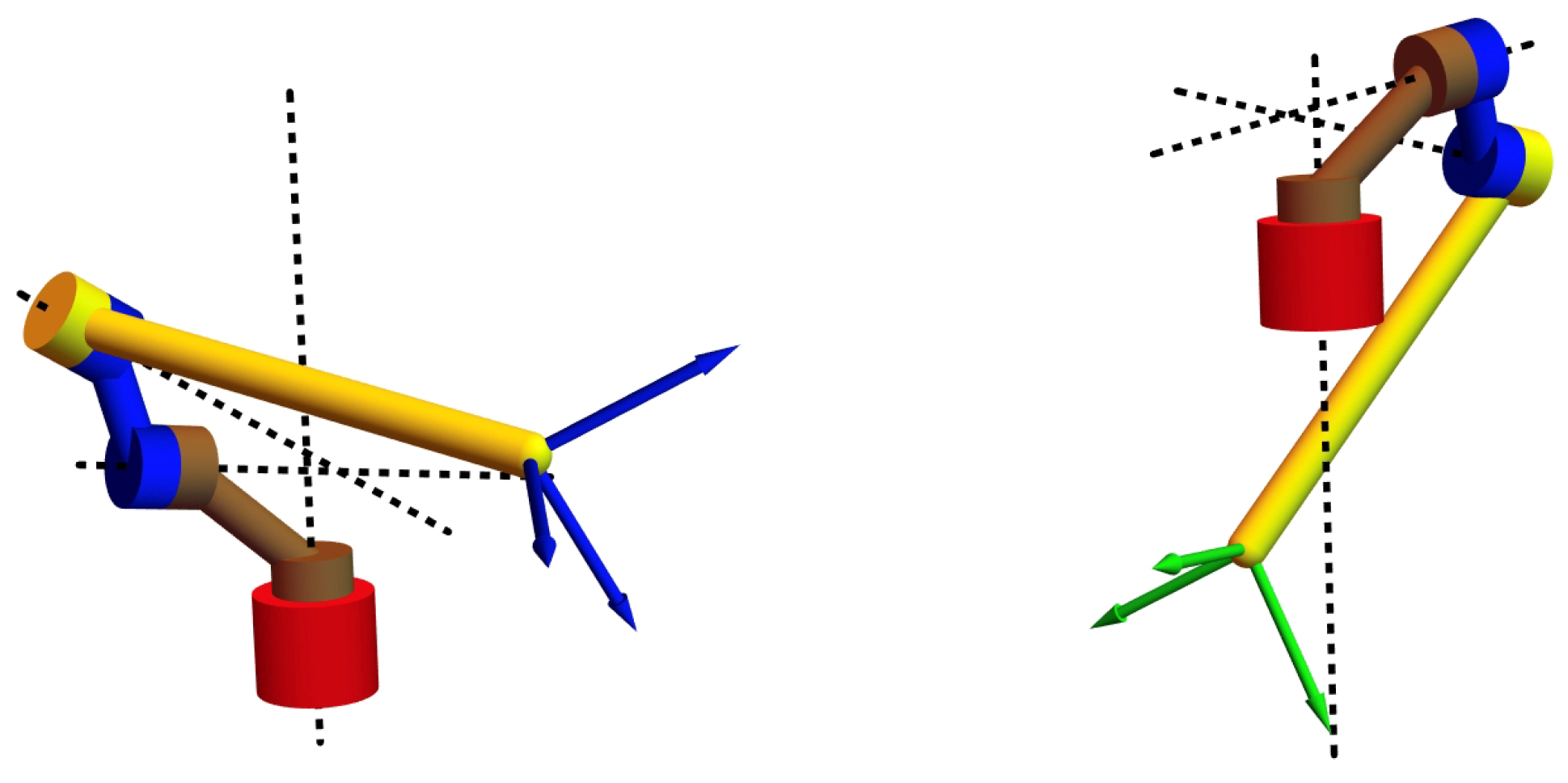

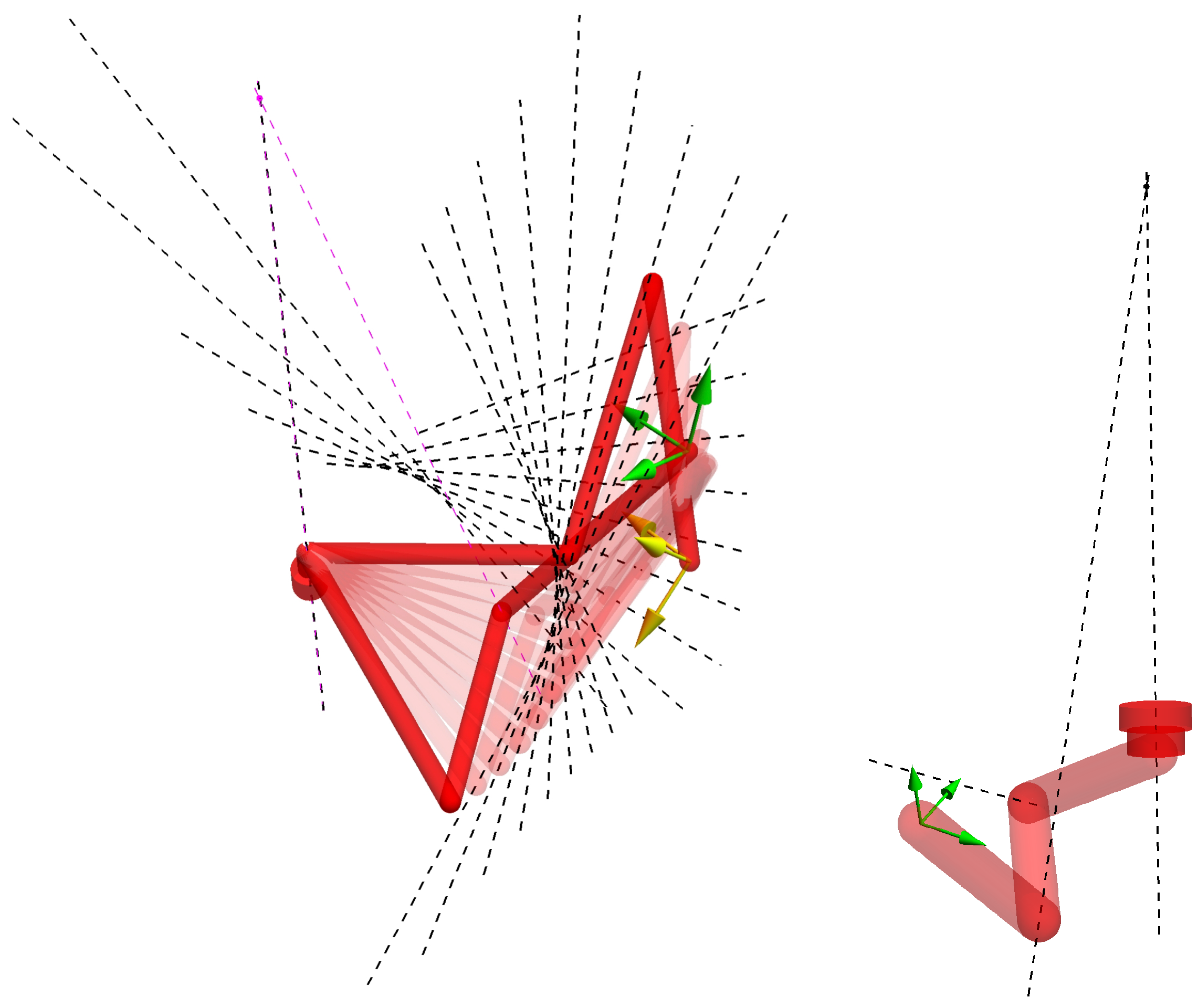
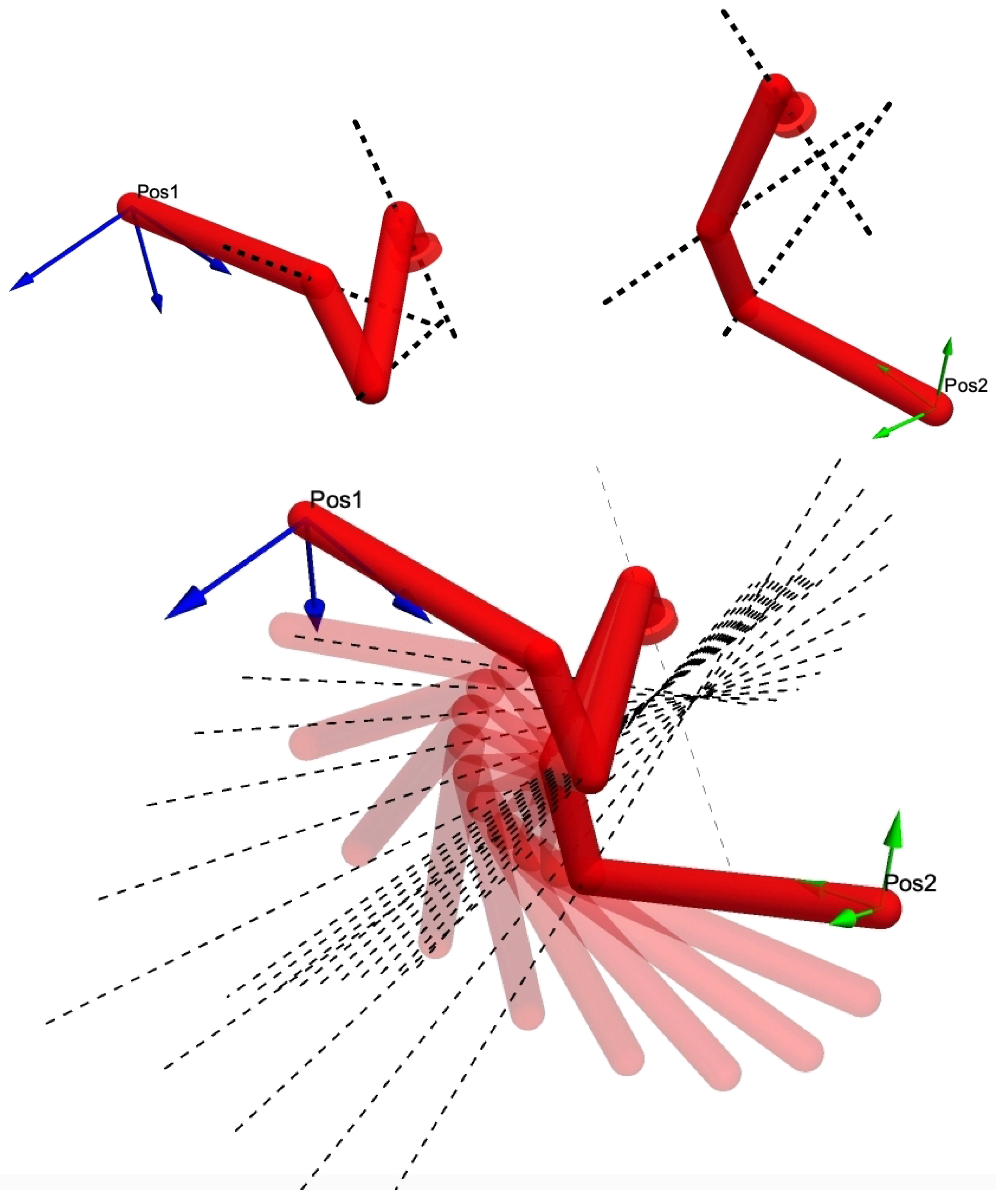
| Completion Group | Gibson Hunt Type | Normal Form | Invariance | Feasible | |||
|---|---|---|---|---|---|---|---|
| ∞ | ∞ | ∞ | Invariant | NO | |||
| 0 | 0 | 0 | Invariant | YES | |||
| 0 | ∞ | ∞ | Invariant | YES | |||
| h | ∞ | ∞ | Invariant | NO | |||
| 0 | ∞ | ∞ | Variable | NO | |||
| 0 | ∞ | ∞ | Persistent | NO | |||
| h | h | ∞ | Variable | NO | |||
| 0 | 0 | ∞ | Variable | YES | |||
| ∞ | Variable | YES | |||||
| ∞ | Variable | YES | |||||
| h | h | h | Variable | NO | |||
| Variable | YES | ||||||
| Variable | YES | ||||||
| Position | End-Effector Twists |
|---|---|
| Axes | Plücker Coordinates |
|---|---|
| Position | End-Effector Twists |
|---|---|
| Axes | Plücker Coordinates |
|---|---|
| Position | End-Effector Twists |
|---|---|
| Axes | Plücker Coordinates |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanzadeh, N.; Perez-Gracia, A. Mixed Position and Twist Space Synthesis of 3R Chains. Robotics 2022, 11, 13. https://doi.org/10.3390/robotics11010013
Hassanzadeh N, Perez-Gracia A. Mixed Position and Twist Space Synthesis of 3R Chains. Robotics. 2022; 11(1):13. https://doi.org/10.3390/robotics11010013
Chicago/Turabian StyleHassanzadeh, Neda, and Alba Perez-Gracia. 2022. "Mixed Position and Twist Space Synthesis of 3R Chains" Robotics 11, no. 1: 13. https://doi.org/10.3390/robotics11010013
APA StyleHassanzadeh, N., & Perez-Gracia, A. (2022). Mixed Position and Twist Space Synthesis of 3R Chains. Robotics, 11(1), 13. https://doi.org/10.3390/robotics11010013





