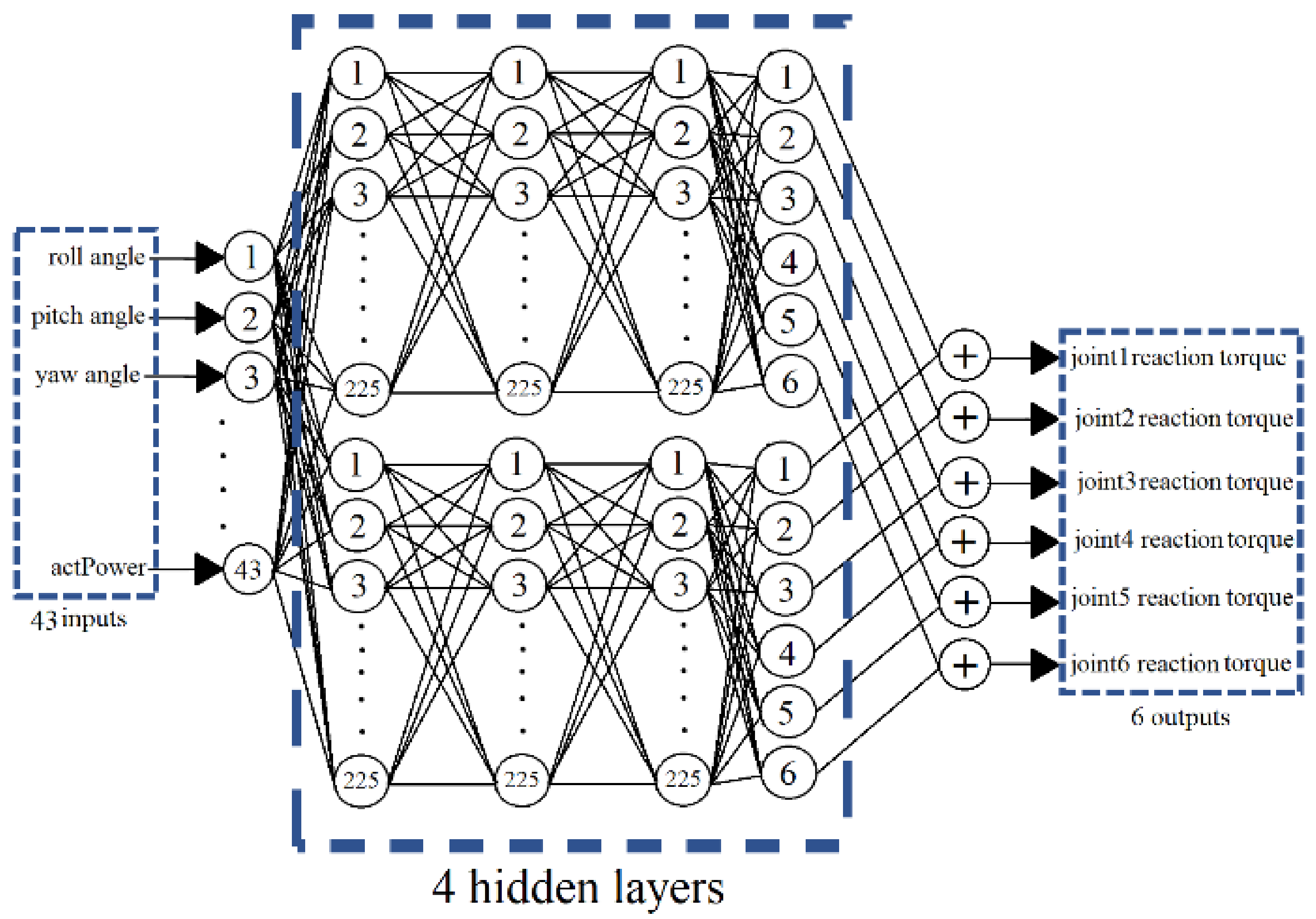
1. Introduction
Reinforcement Learning allows the system to learn by interacting with the environment. There is no need for a large number of labeled samples, and the system learns as it accumulates experience. Since its introduction, RL has shown great potential in many applications.
This study addresses the direct application of Reinforcement Learning (RL) to the joint force control of an articulated robot to follow pre-specified trajectories. The RL controller uses a neural network to compute the required joint torque. It requires no knowledge of an underlying dynamic robot model and needs no complex inverse kinematics calculation. From the application point of view, a neural network-based robot arm controller is desirable. However, very few available RL robot control examples have addressed the direct torque control of articulated robots. Searching through the literature, one finds that most available results dealt only with the kinematic trajectory planning and left the torque control problem to the controller that came with the robot. Many related results have based their control on model-based inverse dynamic cancellation and used RL to learn the control parameters [
1,
2]. The others that did address direct joint torque were for SCARA robots with only two links [
2,
3]. Considering how humans learn to control their limbs, it is still desirable to know if one can train the robot arm the way we train ourselves to use our arm.
Learning control has been around for a long time. In 1995, Nuttin and Van Brussel proposed a learning controller to increase the insertion speed in consecutive peg-into-hole operations; the learning controller could perform the same without increasing the contact force level [
4]. In 1997, Schaal examined the types of learning problems that benefit from demonstration [
5]. He compared the performance of various learning algorithms on an anthropomorphic robotic arm. In 2006, Peters and Schaal demonstrated the efficiency of Reinforcement Learning in teaching a SARCOS Master Arm to hit a baseball [
6]. In 2007, he also performed the Reinforcement Learning approach on the anthropomorphic robotic arm simulation in operational space control [
7]. In 2010, Kober et al. explained the technique of learning mappings from circumstances to meta-parameters by using Reinforcement Learning. He showed two robot movement applications: throwing darts and table tennis hitting [
8]. In 2016, Gu et al. showed that a Deep Reinforcement Learning algorithm based on the off-policy training of Deep Q-Functions could scale to complex 3D manipulation tasks for a robot [
9]. In 2017, Liu et al. proposed an RL learning control for the robotic insertion task [
10]. In 2018, Luo et al. used Guided Policy Search in the peg-in-hole insertion in a deformable hole [
1].
Many RL approaches are available. The Deep Deterministic Policy Gradients (DDPG) is a state-of-the-art algorithm to simultaneously train the Deep Q Network and the Deep Policy Network. DDPG achieves good performance in continuous control problems by integrating the Deterministic Policy Gradient algorithm. From a comparative viewpoint, the difference between the Stochastic- and Deterministic Policy Gradient is that the Stochastic Policy Gradient integrates over both state and action spaces. In contrast, the Deterministic Policy Gradient only integrates over the state space. Consequently, the Deterministic Policy Gradient requires fewer samples than the Stochastic Policy Gradient, especially if the action space has few dimensions [
11]. Survey papers at various stages of development on RL are already available. Kormushev provided a summary describing the RL application in the real world industry [
12], and Wang et al. published a review of recent theoretical development [
13]. There is also the convergence issue with the training algorithm. When Silver et al. first proposed the deterministic policy gradient (DPG) algorithm [
11], they required a linear compatible function as the state-action value function. The DDPG proposed by Lillicrap et al. [
14] uses a deep neural network (DNN) as a function approximator. The nonlinear approximator introduces a risk of trapping in the local optimal. Many literature results have shown that the main issue is the compatibility between the actor and critic networks. To avoid this situation, DDPG introduces the noisy state-action value function. Many research efforts have been devoted to exploring ways to improve convergence [
15,
16,
17,
18,
19,
20,
21,
22]. There are also alternative approaches to DDPG for continuous-time reinforcement learning. Ghavamzadeh and Mahadevan [
23] developed a generalization of the MAXQ for continuous-time semi-Markov decision processes. Tiganj et al. [
24] developed a logarithmically-compressed time scale model for the future to establish a scale-invariant timeline to overcome the discretization problem. Research by Jiao and Oh [
25] proposed using separate threads to execute the “behavior” and the “update policy.” In this research, we adopted the method proposed by [
14] to add noise to the actor policy to ensure value function compatibility.
This study used a HIWIN RA605 robotic arm for the target experiment. We defined the simulation’s target trajectory, reward function, policy, and actor-critic network structures. After many trials, it became clear that the direct application of RL to multi-link articulated robot trajectory control without an underlining model is more complicated than one expects. A recent study directly applied the deep learning controller to emulate the inverse dynamics action [
26]. They handled the nonlinear behavior by applying the learning control on the separate axis with all the other axes fixed. However, they still used model-based supervised learning. In addition, their effort to train all the axes can be too great for practical implementation. Instead, our study based the training on the trajectory without needing a dynamic model. One can therefore train the RL network along a specific path. We describe the proposed network structure and the result of the training.
This study also compared the control with the Model Predictive Control (MPC), another popular control method, to demonstrate the control effectiveness. MPC based the design on a system model. Instead of conventional feedback, it determines the control action by optimizing a performance index over a finite time horizon [
27]. Many previous researchers have proposed different MPC methods. In 2014, Nikdel designed an MPC controller to control a single-degree-of-freedom shape memory alloy (SMA) actuated rotary robotic arm to track the desired joint angle [
28]. MPC discovered practices in dynamic and unpredictable environments such as chemical plants and oil refineries [
29], as well as power system balancing [
30]. More recently, the MPC has also begun to find applications in the control of autonomous vehicles [
31] and robotic trajectory control [
32,
33,
34]. In 2016, Best et al. applied MPC to robot joint control. The dynamic model-based control of a soft robot shows significant improvement over the regular controller [
35]. In 2017, Lunni et al. applied a Nonlinear Model Predictive Controller (NMPC) to an aerial robotic arm for tracking desired 3D trajectories. They demonstrated online use of the NMPC controller with limited computational power [
36]. In 2018, Guechi et al. proposed a combination of MPC and feedback linearization control for a two-link robotic arm [
37,
38]. In the same year, Car et al. applied an MPC-based position control to an unmanned aerial vehicle (UAV). The onboard computer running linear MPC-based position control communicates through a serial port with the low-level altitude controller [
39].
This paper describes using RL to control a HIWIN RA605 robotic arm. The task is for the robot arm to follow a desired trajectory while maintaining a specific attitude for the end effector. We propose a split network structure that allows for the direct application of RL to robot trajectory control. We also compare the control performance to a Twin Delayed Deep Deterministic Policy Gradient (TD3) network and an MPC. The results show that the proposed RL structure can achieve articulated robot control without the help of an accurate robot model. The RL trajectory is oscillatory but instinctively avoids the singularity and requires no background model. The behavior is similar to a human holding out their hand. Although the TD3 controller still converges, it oscillates around a noticeable offset. The MPC is smooth but requires a system model and additional treatments to avoid singularities.
2. Theoretical Background
2.1. Deep Deterministic Policy Gradient (DDPG)
The popular DDPG was first used in this study to train the RL network. The standard reinforcement learning algorithm considers the problem of an agent interacting with an environment . The policy for the agent’s action at state is represented by a probability distribution , where represents the state space and represents the action space. Assuming that the actions can be parameterized with parameters ; the parameterized policy becomes which selects the action in state with parameters by interacting with the environment. At each time step , the agent receives a reward for its action, and the return from a state is defined by the sum of the discounted future reward . As a result, the expected return, or the value function, for the action becomes . The goal of the agent is to maximize the value function by updating and . To allow an iterative learning process, one can express the value function in a recursive form: . One can omit the inner expectation if one chooses a deterministic policy as , and reduces the value function to an expression that depends only on the environment such as . It is now possible to use an off-policy algorithm to learn with a greedy policy .
The standard RL algorithm is not directly applicable to continuous action space due to the need for optimization at every time step. DDPG thus resolves into an actor-critic model structure. The actor specifies the deterministic policy by mapping the states to a specific action. The critic then learns the value function using the Bellman equation. The policy gradient of the expected return can be expressed as:
The basic algorithm for DDPG is shown in Algorithm 1.
Algorithm 1: DDPG
Update the parameters of
, which is
, to maximize
.
Update and , where is a factor between 0 and 1.
2.2. The Modified DDPG Method
As mentioned before, the algorithm in the previous subsection adopted the greedy policy to optimize for each time step and is unsuitable for applying to continuous-time robotic motion control. Therefore, modifying the algorithm into an applicable actor-critic algorithm is necessary.
In the DDPG algorithm, is used to represent the decision-making policy that determines the corresponding action in the state . The decision of the action by does not result directly from the information of the state and would require two steps to determine. Suppose there are five possible discrete actions, will first decide on the most probable action and use it as its decision. Nevertheless, due to the greedy selection, the final choice may not be the same as the action with the highest possibility.
In this paper, the action consists of six joint torques; there is an infinitely possible choice of actions because the torque is a continuous variable. As a result, the possibility of all activities being covered cannot be covered. Instead of using to determine the most probable action, the algorithm resolves to using to directly determine the action , which consists of the six joint torques, based on the states . The algorithm also added noise to the action to ensure value function compatibility.
The modified DDPG method (DDPG-1) algorithm is shown as Algorithm 2.
Algorithm 2: DDPG-1
Update the parameters of
, which is
to minimize
.
Update the parameters of
, which is
to maximize
.
Using the DDPG-1 method, one can consistently update the parameters of the critic and the policy consistently during training to obtain the optimized critic and policy . For each training step, the action selected is , where is the noise for value function compatibility. We also explored the TD3 algorithm, but it did not provide too much improvement.
2.3. The Differential Kinematics
The robotic control is slightly more complicated than the standard control systems. Unlike the regular control system that directly takes the control error for feedback, the control system needs to adequately translate the trajectory error in the task space into the various joint torques. In other words, there is a transformation of the measurement from the “task space” into the “joint space,” and the translation involves the differentiation of the Jacobian matrices, which, in turn, introduces Coriolis accelerations. The robotic control system will need to cancel or suppress this nonlinear effect. In a common end-following task, the position and attitude of the robot end-effector in the Cartesian coordinate system contain three position values (, , ) and three attitude angles (,,), for a total of six degrees of freedom. For an RA 605 robotic arm with six joints, the controller will need to perform the inverse kinematics and compute the nonlinear dynamic forces for cancellation and exercise the control. One of the goals of this research is to use a deep learning network for the inverse dynamic model and directly control the robotic arm.
4. Model Predictive Control [11,12]
As described before, MPC is based on the system dynamic model. The robot is described by Equation (9). Define the control law, Equation (10), to cancel the nonlinear effect:
The system reduces to a feedback-linearized system (11).
In the MPC, we apply a proportional-derivative (PD) controller given by Equation (12) to stabilize the robotic arm system:
where
is the vector of joint variables to reflect the desired trajectory. Consider a time interval
, where
is the timeslot of the prediction. From Equation (10), we can develop the following two prediction models [
12]:
If the target joint angle is
, a simplified MPC design is to define a one-horizon time quadratic cost function to stabilize the system as:
where
is the predicted angular position error, and
is the predicted angular velocity error. In Equation (7), the timeslot
and weight
are positive real control parameters to be designed. To minimize
, one introduces the prediction model Equation (13) into Equation (14) and lets the partial derivative
equal 0. Considering that the robot slowly follows the trajectory, the resulting control becomes:
where
and
are:
By allowing the target joint angle to change over time, and from Equation (8), we obtain a more general control law:
From Equations (9), (10), and (18), a block diagram of the MPC controller and the robotic arm system can be shown in
Figure 6, where
are the target joint angles in the joint-space.
The main goal of the control is for the joint angles to follow their targets according to the second-order dynamics specified by the transfer function , where is a damping factor and is a natural frequency by design.
Modeling of the Robotic Arm System
The HIWIN Technologies Corporation provided the RA605 robot arm for the D-H table, which can be readily incorporated into the “rvctools” Robotics toolbox in MATLAB for simulation purposes. It is also possible to obtain the system parameters for the dynamic model of the robot.
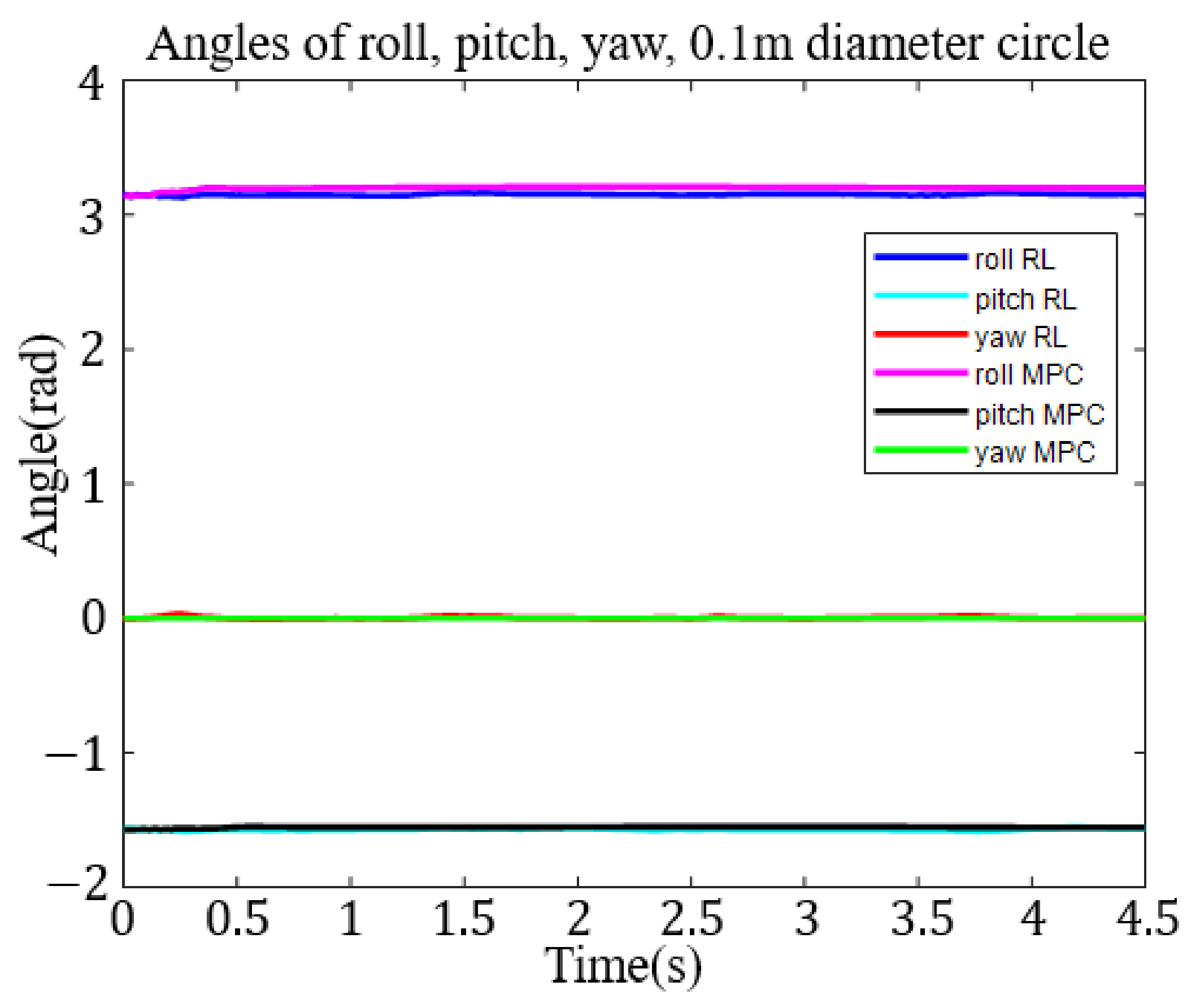
This research applied the DDPG to the RL training algorithm. We built an RA605 robotic arm model within the MATLAB simulation environment and, for generality purposes, four different target trajectories: a small circle trajectory (0.1 m diameter), a larger circle trajectory (0.2 m diameter), a small square trajectory (0.1 m side length) and a big square trajectory (0.2 m side length),
Figure 7. To demonstrate the ability of six-axis trajectory control, we fixed the roll, pitch, and yaw angles of the end effector at
,
, and 0 rad, respectively.
6. Conclusions
This paper proposes a split network structure for the direct application of RL to robotic trajectory following control. We first show that it is possible to train the RL network to directly mimic the inverse dynamic cancellation action without the help of a precise system model. The RL uses the modified DDPG algorithm as the underlying learning algorithm, and the tests follow four different target trajectories. The 0.1 m circle trajectory spent 343,070 s and 22,228 episodes training. It took 65,783 s and 4378 episodes to learn the 0.2 m circle trajectory. The 0.1 m square trajectory took 186,100 s to train, while the 0.2 m square trajectories took 129,040 s.
This study also compares RL performance to MPC performance. The RL control inherently avoids exercising violent movements while passing through the singularities and still succeeds in handling large and complicated trajectory situations. The MPC requires an accurate system model and is straightforward in implementation. However, it cannot avoid singularity without additional treatment and fails to control in large and complicated trajectory situations.
Comparing the two methods shows that RL successfully makes the robotic arm go through the target trajectory without excessive joint angle movements. MPC does not need time for training and achieves smoother control, but it requires an accurate system model. The authors will also try to implement the controller in an experiment for future verification.