Simulation-Based Comparison of Novel Automated Construction Systems

Abstract

As automated construction processes require large workspaces and high payloads, the use of cables is a reasonable approach to span wide distances and share loads. Therefore, a cable-driven parallel robot is a suitable choice for automated masonry construction. Another possible robotic system for this task consists of a set of cooperative drones, each connected to the end effector and the payload by a cable. Because of the similarities between the two robotic systems, the same object-oriented programmed software can be used for trajectory planning and subsequent investigations, making minor adjustments. The implemented optimizing path planning algorithm takes into account the physical boundaries, motion time, collision avoidance and energy requirements. Thus, a simulation-based comparison of the characteristics of both systems can be made. In this paper, the necessary physical models for both the drone system and the cable robot are derived in detail. Based on the common framework, this paper presents a comparison between the two robotic systems, defining two different scenarios. The first scenario demonstrates the functioning of the optimizer approach. The second scenario is used to compare the two systems. For this purpose, the trajectories for all 1720 masonry units of the first floor of a house are optimized. The analysis of the results shows that both systems can transport heavy loads, with the cable robot having advantages on smaller sites, while the drone system covers larger distances for the price of slower performance and higher energy consumption.

1. Introduction and State of the Art

In the modern component manufacturing industry, the use of CAx software is widespread, especially in automated series production. The advantages are an improved quality, reduced costs and shorter manufacturing time. In contrast, the design and construction of buildings are mostly individual and thus still require the execution of work on site, typically based on traditional manual processes using printed two-dimensional technical drawings. However, in recent years, digital process chains are also being developed in the construction of modern buildings using the Building Information Modeling (BIM) method [1]. Analogous to the process in component manufacturing, one core method of BIM is the digital modeling of buildings. The modeling in BIM is based on parameterizable objects, functions and logics. Further advantages for the user include the creation of requirements and drawing plans, the possibility to calculate costs, simplified scheduling and the visualization of the building. At the end of the modeling process, manufacturing data can be generated from the digital models. These data sets might serve in the future as the basis for automating certain work processes and executing them by using different robots [2,3].

Notably, a major challenge in the design of automated construction systems is the extremely large volume of typical sites, which has to be covered by the automated construction solutions. Conventional robot arms fail, which is why special robot arms of large scale or mobile platform bases have been presented [4]. Furthermore, the typical mass of construction elements is a challenge for those robot systems employing serial kinematic structures.

Alternatively, the use of multiple cables is an efficient approach to share payloads and to span large distances. Therefore, the concept of automated masonry using a cable-driven parallel robot (CDPR) has been presented recently [5,6]; see Figure 1a. CDPRs are a special form of a parallel manipulator and thus share fundamental kinematical properties with hexapods. The workspace of the CDPR is spanned by a mobile frame which makes it attractive for construction processes. Within this workspace, the end effector of the robot can be freely positioned in all six degrees of freedom by individually changing the length and tension of the cables. The cables run from motor-controlled cable winches via guiding pulleys to anchor points on the end effector. The guiding pulleys are attached to the frame, either fixed or on movable mechanisms. The actual task of the cable robot for masonry works is then to pick up the bricks e.g., at an automated mortar system, and to place them in the defined poses according to BIM model data. Typically, this should be done in the shortest possible time. The CDPR has two properties that make it particularly suitable for this application. On the one hand, overactuation (e.g., using more actuated cables than the end effector’s number of Degrees-of-Freedom) can be used to enhance the stiffness of the system, which is crucial for outdoor applications. On the other hand, the movable masses are extremely low as these are essentially limited to the end-effector and the payload. Still, a CDPR has drawbacks, where the most obvious drawback is the high number of cables that may even run below the end effector level, which introduces a risk of collisions with already built structures or moving objects. This has to be handled, e.g., by vertically moving pulleys. Moreover, cables are unilateral constraints in general. This needs to be considered while path planning and control. In addition, the purchasing costs as well as the setup costs for the assembly and disassembly of the cable robot must be taken into account, when checking the economic feasibility [7]. Still, a first prototype for automated masonry has been presented and technically validated [8,9] as shown in Figure 1a, including an automated mortar station which delivers masonry units to the CDPR using a lifter. Notably, this prototype is designed for single-storey experiments and thus only the lower pulleys are actuated to move vertically. Due to their advantages, CDPR have been investigated also for other relevant construction processes such as 3D printing of concrete [10,11,12,13,14] or curtain wall installation as demonstrated in the EU project, Hephaestus [15].

In contrast, a multicopter or drone is a spatially unlimited applicable robotic system with comparatively low set-up costs. Since the beginning of their development, multicopters have been used to transport lightweight objects. A significant application example is a camera-carrying drone. In the film and advertising industry, drones are now predominantly used instead of helicopters because they offer much more versatile camera settings and are significantly less expensive. At large events, camera drones are used by the police and event organizers to monitor the event area and direct the stream of visitors. Another application scenario, although not yet as widespread, can be found in agriculture. Here, drones are used for example as an equipment carrier for pest control [16]. In the construction industry, drones are primarily used for land surveying, documenting the progress of construction work or assessing damage of hard-to-reach places or areas [17,18,19]. Additionally, they are used for active monitoring of construction sites to achieve an increase in construction site safety. For an overview, see [20]. All previously mentioned use cases have in common that the payload of the drone is comparatively small.

Over the years, however, the payload for drones increased continuously, so that, nowadays, heavy-lift drones with a maximum payload of up to $100\mathrm{kg}$ can be purchased. The reason for this are, among other things, increasingly better lithium-ion batteries, which enable the use of more powerful motors [21]. Due to these developments, drones are thus becoming increasingly interesting for the transportation of heavy loads or for the use in internal logistics [22]. Research in the field of alternative energy sources, such as the use of a fuel cell, may increase the operating time in the future [23]. A multicopter might be equipped with an end effector that is able to pick up a payload. Essentially, three different approaches are pursued; see [24]. In the simplest case, the end effector is firmly connected to the drone [25,26,27,28]. However, when using underactuated drones, this method has the disadvantage that the payload cannot be fully oriented. One way to overcome the underactuation is to use a rigidly mounted end effector in combination with a full- or overactuated multicopter [29]. A different approach discussed in [30,31] is the use of drones with robotics arms. This second approach also allows the independent movement of the payload in all six degrees-of-freedom. The approaches described so far are particularly suitable for the transport and/or manipulation of lightweight objects.

One disadvantage, however, is that the payload is usually located very close to the drone. This might be an issue in specific applications (e.g., in cluttered environments). Therefore, another frequently investigated use case is the transport of a payload that is connected to a drone via a cable. This allows the adjustment of the distance between the drone and the payload almost arbitrarily. As a major advantage, by using multiple, cooperating drones connected to a common payload using cables, the maximum payload weight can be drastically increased and the maneuverability can be enhanced. In the past, drone cooperation has already been investigated repeatedly. In [32], the transport of a payload, which is still considered as a point mass, is investigated using two drones. However, this does not increase the controllability and, furthermore, the drones have to be far enough apart. If the distance of the drones is increased, the cable forces increase as well since the system is closer to a singularity of the second kind. The transport of a rigid beam using two quadrocopters is demonstrated in [33]. With the use of three or more drones, the payload is kinematically underconstrained [34] but statically determined with the help of gravity. Moreover, it can be fully controlled, as the three drones in total have more controllable degrees of freedom than the end effector. As examples, flight maneuvers with three drones are presented in [35,36,37]. When using three or more drones, there is also the possibility to reconfigure them in space without moving the payload. With these maneuvers in null space, the properties of the system can be influenced. This fact and the relation to cable robots is considered in [38]. The goal of planning an optimal trajectory in terms of the cable angles and energy efficiency is considered in [39]. Path planning under external disturbances is shown in [40]. Planning a trajectory for the specific task of flying through a window is the subject of the work [41]. In addition, [42] deals with highly dynamic trajectories. The procedure of lifting the payload is analyzed in [43,44].

In the scope of this paper, another possible scenario would be using cooperating drones on large construction sites to handle internal logistics or to do simple construction tasks, such as the automated masonry already mentioned, see Figure 1b. Unlike cable robots, drones are not locally bound. Furthermore, the space and infrastructure requirements on the construction site are easy to provide.

Accordingly, while both systems use cables to share the load of high payloads, they still have inherent technological differences, leading to differing characteristics when used for automated masonry. As for this application, both systems have only been tested in very early technological stages, but might be very promising to be developed within future research projects, it is reasonable to create approaches to evaluate and compare their potential performances in automated masonry using simulation tools. Thus, this contribution aims at comparing the two presented cable-based systems in predefined scenarios using numerical model-based simulations. Due to the model-based approach, the physical models for both the drone system and the cable robot need to be derived in detail. Based on a software framework, the two robotic systems are evaluated, defining two different scenarios. The first scenario demonstrates the applicability and capabilities of the optimizer approach. The second scenario is used to compare the two systems in terms of several performance indices such as required construction time and energy requirements.

The paper is structured as follows: In Section 2, the methodical approach and the used optimization framework are presented. Section 3 introduces the cost functions used for the path planning algorithm. The approach is then demonstrated in Section 4 to optimize trajectories for a cable robot and a system of cooperating drones. The optimization results and the different characteristics of both systems are discussed. The paper is summarized in Section 5.

2. Methodological Approach

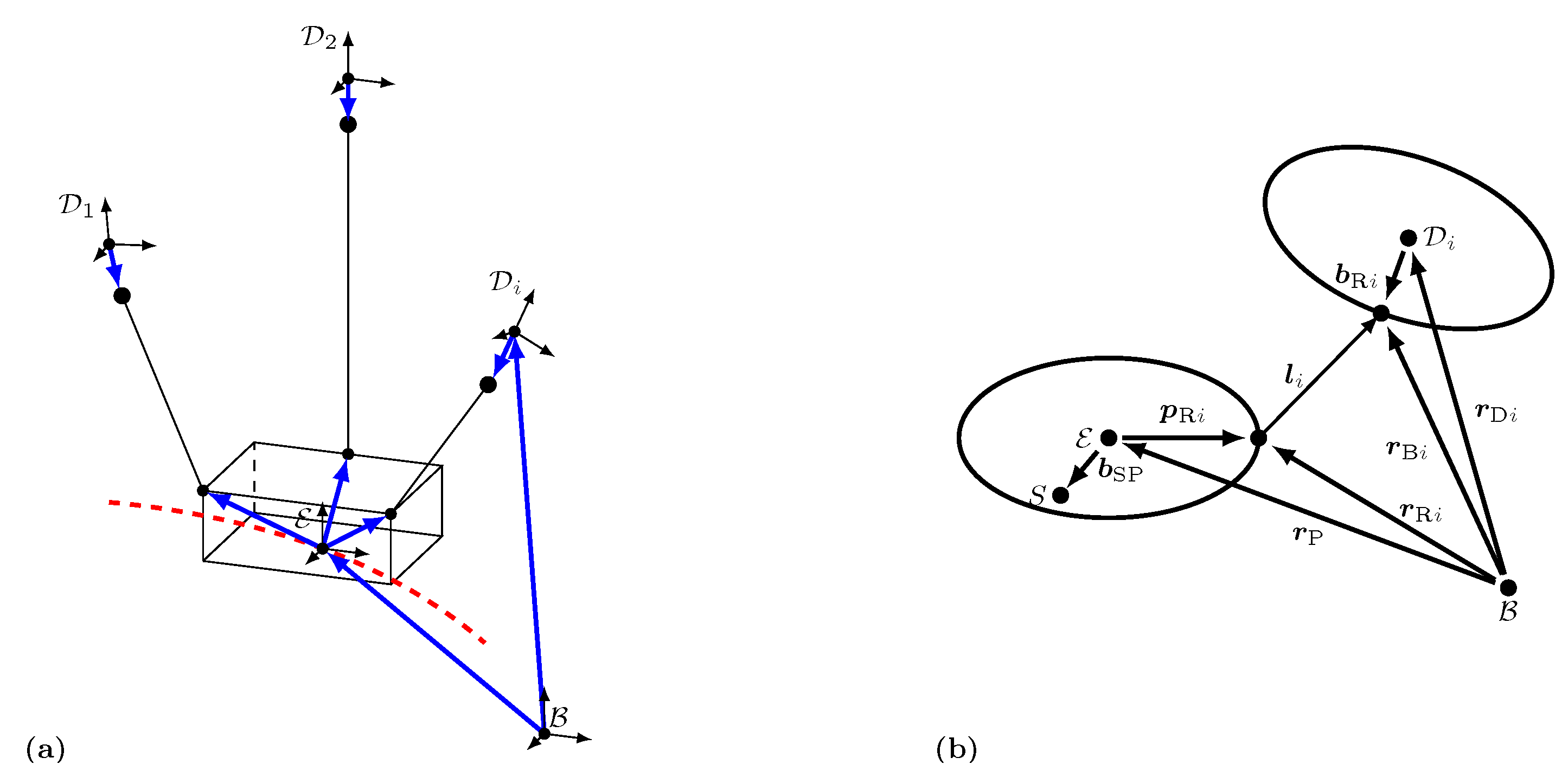
2.1. Setup of the Software Framework

As introduced, the analysis of the robot systems is supported by a software framework implemented as a generic trajectory optimization tool. To be as flexible as possible, the framework uses an object-oriented architecture. Through the object-based software design the workflow of the transport of a masonry unit can be split up into several trajectories, in which each movement such as lifting, moving to a target position, placing down and moving back to the starting position becomes an own independent optimization problem with its own parameterization. Note that BIM data are used to provide the information required for this purpose, which among other things, include the target position and orientation of each brick used in the building. For this purpose, a BIM postprocessing algorithm was created to derive masonry laying plans from a given BIM model.

Figure 2 shows the general workflow using the framework.

The core of the framework includes a number of optimization algorithms, both from the Optimization Toolbox and the Global Optimization Toolbox of MATLAB^® [45]. For trajectory optimizations, which require the tuning of multiple parameters per spline-segment, a global optimizer is useful, such as a Particle Swarm Optimizer. On the other hand, a gradient-based optimizer might reduce computational costs and can be applied in special cases, e.g., when a spatial fixed trajectory should be time-optimized only. Based on this, cost functions representing technical criteria can be created. These can be evaluated for a number of trajectories. The properties and parameters of each trajectory can be defined independently, including the definition of the start and target position (e.g., based on the BIM data provided), the specification of the robot used and its properties, the optimized parameters, the cost functions to be applied per trajectory, the static objects that must be considered for collision avoidance as well as the definition of the payload. For each trajectory, the parameters and properties are updated before the optimization starts. As multiple cost functions might be needed, they are added to a single overall cost function using weights which allows to vary their influence.

Due to the object-oriented approach, only the models for the individual physical behavior of the robot and the corresponding cost functions have to be adapted to compare automated construction system for a given masonry laying plan.

2.2. Parametrization of Trajectories

A trajectory describes the motion of the robot and its components over time. Accordingly, it contains information about the pose and its time derivatives. In general, the trajectory will be optimized in the world reference frame based on the framework in Section 2.1. The mathematical description of the trajectory must be defined in a consistent manner that allows the variation of its parameters by the chosen numerical optimizer. For this issue, splines—i.e., a chain of interconnected polynomials with common knots—are a popular choice. The coefficients of the polynomials are determined by the numerical solution of a system of equations $\mathit{A}\mathit{x}=\mathit{b}$, whereby the vector $\mathit{b}$ contains initial variables, some of which are optimization parameters. By changing these parameters using an optimization algorithm, a different trajectory is generated which can be evaluated with respect to the cost functions. The total costs are the sum of the individual costs, where each individual cost function evaluates a single technical criterion of the trajectory such as time, energy requirements and avoidance of collisions.

To allow for a precise masonry process including the required intermediate pose measurements, alignment processes and masonry process steps (such as application of mortar), the transportation task is decomposed into 15 consecutive segments for each masonry unit. For each partial step, an individual trajectory is created and registered for the optimization process.

Table 1. Transportationsequence for each masonry unit.

Trajectory	Function	Payload	Time [s]
1	Measuring the dimensions of the masonry unit	no	32.7
2	Slowly move down to the pickup position	no	9.12
3	Pick up the masonry unit	no	5.54
4	Slowly move up half a meter	yes	4.89
5	Move up to transition height	yes	optimized
6	Transition through workspace to target	yes	optimized
7	Move down to half a meter above target position	yes	optimized
8	Measuring the target position	yes	20.64
9	Slowly move down half a meter	yes	2.62
10	Placing down the masonry unit	yes	11.78
11	Slowly move up half a meter	no	1.31
12	Move up to transition height	no	optimized
13	Transition through workspace	no	optimized
14	Move down to half a meter above next masonry unit	no	optimized
15	Wait until the mortar system has finished	no	externally defined

gives an detailed overview.

Essentially, the trajectories differ in whether the end effector is currently transporting a masonry unit or not and whether the time for a path segment is optimized or not. A full collision check is performed for all path segments. In the case of the cable robot, both the pulleys of the lower cables and the mortar system must be raised with increasing height in order to avoid a collision between cables and the already completed part of the masonry which is also reflected by a trajectory computed for each moving pulley. In the measuring process during trajectory 1 and 8, the end effector is aligned over the start and target position using laser sensors. While most of the other trajectories are predefined due to process conditions, the duration of trajectory 15 is defined by the external mortaring system. In addition to a fixed time $t_{\mathrm{M}}$, which the mortar system needs to apply the mortar, the lifting of the mortar system also requires a certain time $t_{\mathrm{H}}$. The time $t_{\mathrm{c},15}$ that the cable robot has to wait is therefore calculated by

$$t_{\mathrm{c},15}=t_{\mathrm{M}}+t_{\mathrm{H}}-\sum _{i=1}^{14}{t}_i.$$

(1)

In case of the drone system, the risk of a cable collision with the already completed part of the masonry is reduced as there are no cables below the current masonry layer. Accordingly, the mortar system must not be lifted. Thus, the duration $t_{\mathrm{d},15}$ of the 15th trajectory is calculated for the drone system as

$$t_{\mathrm{d},15}=t_{\mathrm{M}}-\sum _{i=1}^{14}{t}_i.$$

(2)

In case $t_{\mathrm{c},15}$ or $t_{\mathrm{d},15}$ becomes negative, the 15th trajectory is skipped and its duration is set to zero. As long as a single trajectory is independent from the other ones, the evaluation sequence is arbitrary which can be very beneficial for parallelization of the computations.

Dependent on the robotic system, up to $f_{\mathrm{P}}=6$ degrees-of-freedom (DOF) of the platform pose ${\widehat{\mathit{r}}}_{\mathrm{P}}$ can be independently specified over time by splines. All trajectories with the exception of trajectories 6 and 13 have no additional knots between their start and target position and are therefore represented by a single segment. As for trajectories 6 and 13, a certain variability of the trajectory is demanded, but a high number of spline segments would increase the number of optimization variables. Hence, three spline segments were chosen to compromise between flexibility and computation time. For the trajectories, the following constraints are given:

• At start: Position is given, the velocity and all higher order time derivatives are set to zero, i.e., no optimization parameters.
• At first and second knot: Position, velocity and acceleration are parameters, subject to numerical optimization, i.e., three parameters in total, per DOF and knot. In the case of six DOFs, this leads to 18 parameters per knot. Jerk and higher order time derivatives are set to zero.
• At goal: Position is given, the velocity and all higher order time derivatives are set to zero, i.e., no optimization parameters.

A trajectory with $n_{\mathrm{k}}$ additional knots has $3f_{\mathrm{P}}{n}_{\mathrm{k}}$ optimization parameters for the description of the movement. As already introduced, the transition time per path segment can be defined as an optimization parameter. This adds up to $n_{\mathrm{k}}+1$ additional parameters. To evaluate the cost functions and do a proper collision check for a trajectory, each spline is discretized in $n_{\mathrm{s}}$ time steps along the spline where $t_{\mathrm{s}}\left(k\right)$, $k\in \{1,\dots ,n_{\mathrm{s}}\}$ is a specific time step.

2.3. Definition of the Optimization Parameters

The resulting optimized trajectory for a robotic system massively depends on the specific technical criteria such as low transition time, low energy consumption and collision avoidance. Each property that should be taken into account or optimized is considered as a criterion $\chi$, valued by costs at the end of each optimization step. The costs of each criterion $\chi$ are calculated as the sum of a cost value ${\mathcal{V}}_{\chi }$, multiplied by the weight ${\mathcal{W}}_{\chi }$, and a penalty term ${\mathcal{P}}_{\chi }$. While the cost value ${\mathcal{V}}_{\chi }$ rates a continuous optimization parameter, the penalty term ${\mathcal{P}}_{\chi }$ is only non-zero when physical boundaries are not met. Note that tasks (such as of collision avoidance) may include both summands. Furthermore, the weights contain the respective physical units, such that the costs for each $\chi$ become dimensionless. The value of the total costs ${\mathcal{V}}_{\mathrm{total}}$ for a trajectory is computed by summing up each single costs of a criterion $\chi$. Therefore, the task to find the best trajectory in terms of the defined cost functions can be formulated as the unconstrained optimization problem

$$\min \sum _{\chi }({\mathcal{W}}_{\chi }·{\mathcal{V}}_{\chi }+{\mathcal{P}}_{\chi }).$$

(3)

This approach allows the multi-criteria optimization procedure to have very different weightings in order to meet a wide range of priorities, such as productivity (time optimization), economic efficiency (energy optimization) or safety (collision avoidance). Moreover, it is simple to understand and enables for flexible tuning to represent individual preferences. Note that the criteria (cost functions) in general are within a conflict, since the improvement of one cost function at some point (e.g., a short transition time) will degrade another (e.g., cable forces). However, the criteria are physically independent and cannot be transformed into each other. Hence, the weighting factors are arbitrary and influenced by the subjectivity of the user. Moreover, the subjectivity influences the solution which is considered as optimal. A useful approach for future work would be the investigation of Pareto optimal methods. Here, a quantity of solutions to the optimization problem is determined, where an improvement of one cost value results in a degradation of another. This quantity, which consists of all optimal compromises, is called Pareto front. This front allows an individual selection of an optimal solution under given preferences for the optimization criteria [46].

Here, the following criteria are considered as cost functions:

• Trajectory time: The robot motion should be as fast as possible. This can be achieved by defining ${\mathcal{V}}_{\mathrm{time}}=\sum t_{\mathrm{S}}$. Since the time has no upper boundary, it follows ${\mathcal{P}}_{\mathrm{time}}=0$.
• Maximum end effector position, velocity and acceleration: For each time step in which the boundaries of the position, velocity or acceleration of the end effector are exceeded, the associated penalty term ${\mathcal{P}}_{\mathrm{pos}}$, ${\mathcal{P}}_{\mathrm{vel}}$ or ${\mathcal{P}}_{\mathrm{acc}}$ is charged. The boundaries of the position are derived from the robot’s frame, the ones of the velocity and acceleration depend on the motor specifications but can also be limited for safety reasons. A limitation in task space is intuitive.
• Actuator forces: In the case of the cable robot, the costs ${\mathcal{V}}_{\mathrm{Force}}$ include the cable forces as a major criterion. The physical boundaries $f_{\min }$ and $f_{\max }$ of the cable forces should not be exceeded to avoid cable breaks and cable slackness, respectively [47]. Therefore, the penalty term ${\mathcal{P}}_{\mathrm{force}}$ is added whenever a cable force violates the boundaries. In the case of the cable robot, the necessary cable forces are generated by the torque of the winch motors. As the winches have masses, they introduce their own dynamics and boundaries. Hence, the additional cost value ${\mathcal{V}}_{\mathrm{torque}}$ as well as the penalty term ${\mathcal{P}}_{\mathrm{torque}}$ are defined. Note that, for simplicity, the motor torque limits are considered constant. The modeling of complex motor effects, such as field weakening, iron losses or temperature dependencies is part of future work. In the case of the drone system, the forces are generated by propellers. This leads to the cost function ${\mathcal{V}}_{\omega }$ and the penalty term ${\mathcal{P}}_{\omega }$.
• Power and energy consumption: An electrical power source has technically defined limitations. To protect the source from overload, the total power demand needs to be limited. This is taken into account by the penalty term ${\mathcal{P}}_{\mathrm{power}}$. A cost value ${\mathcal{V}}_{\mathrm{power}}$ might be used, e.g., to consider thermal load. Within this work such effects are neglected, i.e., ${\mathcal{V}}_{\mathrm{power}}=0$. The energy consumption is one out of many factors which influence the economic efficiency of a robotic system. Hence, this parameter can also be considered by a cost function ${\mathcal{V}}_{\mathrm{energy}}$. Since there is often no physical boundary, it usually follows ${\mathcal{P}}_{\mathrm{energy}}=0$.
• Self-collision of the robots: For both robotic systems, the self-collision of cables are investigated. Whenever a cable collision is detected, the penalty term ${\mathcal{P}}_{\mathrm{CaCa}}$ is assigned to the costs. In the case of the drone system, the self-collisions of drones are considered as well and, if necessary, are taken into account by the penalty term ${\mathcal{P}}_{\mathrm{DD}}$.
• Collisions of the robot with its environment: This includes collisions between objects in the workspace and

  -

  the end effector or payload (ObEE),

  -

  the drones (ObD) and

  -

  the cables (CaOb).

  Note that collisions between cables and the end effector (CaEE) can be treated as CaOb collisions.

During the optimization process the penalty terms are used as follows: If a boundary violation for the considered cost function occurs, a constant penalty value is applied as given e.g., in Table 3. Consequently, the optimizer tends to move in the direction of penalty-free trajectories, i.e., solutions where ${\mathcal{P}}_{\chi }=0$. At the end of the optimization, a penalty-free trajectory is considered valid.

3. Modeling and Cost Functions

This section discusses the fundamentals to represent the relevant technical criteria by appropriate cost functions for optimization of the trajectories. Both the cable robot and the multicopter drone system are presented.

3.1. Modeling of the Platform Dynamics

The feasibility of a trajectory depends on the ability of the robotic system to apply the required forces to the platform. The derivation of the necessary equations is based on the schematic illustration in Figure 3.

The unit consisting of the actual end effector—which is an actuated gripping device plus the required sensors (as shown e.g., in [8])—and the masonry unit to be transported is called a platform. Accordingly, its properties differ depending whether the platform is moving a masonry unit to its goal position or returning empty to the mortaring station, which is why they must be recalculated at the beginning of each trajectory. Each rigid body $\mathcal{K}$ can be described by the Newton–Euler equation

$$\underset{{\widehat{\mathit{M}}}_{\mathcal{K}}}{\underbrace{\left[\begin{array}{cc}{m}_{\mathcal{K}}\mathit{E}& {\tilde{\mathit{b}}}_{\mathrm{S}\mathcal{K}}^{\mathrm{T}}\\ m_{\mathcal{K}}{\tilde{\mathit{b}}}_{\mathrm{S}\mathcal{K}}& {\mathrm{\Theta }}_{\mathcal{K}}\end{array}\right]}}\underset{{\ddot{\widehat{\mathit{r}}}}_{\mathcal{K}}}{\underbrace{\left[\begin{array}{c}{\ddot{\mathit{r}}}_{\mathcal{K}}\\ {\dot{\mathit{\omega }}}_{\mathcal{K}}\end{array}\right]}}=\underset{{\widehat{\mathit{f}}}_{\mathcal{K}}^{\mathrm{c}}}{\underbrace{\left[\begin{array}{c}-m_{\mathcal{K}}{\tilde{\mathit{\omega }}}_{\mathcal{K}}{\tilde{\mathit{\omega }}}_{\mathcal{K}}{\mathit{b}}_{\mathrm{S}\mathcal{K}}\\ -{\tilde{\mathit{\omega }}}_{\mathcal{K}}{\mathrm{\Theta }}_{\mathcal{K}}{\mathit{\omega }}_{\mathcal{K}}\end{array}\right]}}+\underset{{\widehat{\mathit{f}}}_{\mathcal{K}}^{\mathrm{e}}}{\underbrace{\left[\begin{array}{c}{\mathit{f}}_{\mathcal{K}}^{\mathrm{e}}\\ {\mathit{\tau }}_{\mathcal{K}}^{\mathrm{e}}\end{array}\right]}}+\underset{{\widehat{\mathit{f}}}_{\mathcal{K}}^{\mathrm{z}}}{\underbrace{\left[\begin{array}{c}{\mathit{f}}_{\mathcal{K}}^{\mathrm{z}}\\ {\mathit{\tau }}_{\mathcal{K}}^{\mathrm{z}}\end{array}\right]}}.$$

(4)

Now, the platform P is considered, i.e., $\mathcal{K}=\mathrm{P}$. The platform dynamics with its mass $m_{\mathrm{P}}$ are described in the platform-fixed coordinate system $\mathcal{E}$. The origin of the coordinate system is centrally fixed below the gripping unit. Hence, if a masonry unit is fixed in the gripper, $\mathcal{E}$ coincides with the center of the masonry unit’s bottom. Note that this holds for all masonry units within the building employed in this work. The inertia of the platform ${\mathrm{\Theta }}_{\mathrm{P}}$ with respect to the coordinate system $\mathcal{E}$ is obtained considering the inertia of the end effector ${\mathrm{\Theta }}_{\mathrm{S}}$ and the masonry unit with respect to their centers of gravity and the Steiner–Huygens relation, if a masonry unit is gripped. The vector ${\mathit{b}}_{\mathrm{SP}}$ points from the platform’s coordinate system to its center of mass. The matrix $\mathit{E}\in {\mathbb{R}}^{3\times 3}$ is an identity matrix. The second time derivative ${\ddot{\widehat{\mathit{r}}}}_{\mathrm{P}}$ of the pose ${\widehat{\mathit{r}}}_{\mathrm{P}}$ consists of the second time derivative of the position vector ${\mathit{r}}_{\mathrm{P}}$ and the first time derivative of the angular velocity ${\mathit{\omega }}_{\mathrm{P}}$. The platform dynamics in Equation (4) can be summarized using the mass matrix ${\widehat{\mathit{M}}}_{\mathrm{P}}$, the vector ${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{c}}$, which is composed of the Coriolis and centrifugal force ${\mathit{f}}_{\mathrm{P}}^{\mathrm{c}}=-m_{\mathrm{P}}{\tilde{\mathit{\omega }}}_{\mathrm{P}}{\tilde{\mathit{\omega }}}_{\mathrm{P}}{\mathit{b}}_{\mathrm{SP}}$ and torque ${\mathit{\tau }}_{\mathrm{P}}^{\mathrm{c}}=-{\tilde{\mathit{\omega }}}_{\mathrm{P}}{\mathrm{\Theta }}_{\mathrm{P}}{\mathit{\omega }}_{\mathrm{P}}$, the vector ${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{e}}$, which is composed of the applied force ${\mathit{f}}_{\mathrm{P}}^{\mathrm{e}}$ and torque ${\mathit{\tau }}_{\mathrm{P}}^{\mathrm{e}}$, and the vector ${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}$, which is composed of the constraint force ${\mathit{f}}_{\mathrm{P}}^{\mathrm{z}}$ and torque ${\mathit{\tau }}_{\mathrm{P}}^{\mathrm{z}}$. Products of type $\tilde{\mathit{a}}\mathit{b}$ with the skew-symmetric matrix

$$\tilde{a}=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]$$

(5)

correspond to the cross product $a\times b$. With respect to Equation (4), the constraint force at the platform can be calculated for a given trajectory by

$${\widehat{f}}_{\mathrm{P}}^{\mathrm{z}}={\widehat{M}}_{\mathrm{P}}\left({\widehat{r}}_{\mathrm{P}}\right){\ddot{\widehat{r}}}_{\mathrm{P}}-{\widehat{f}}_{\mathrm{P}}^{\mathrm{c}}\left({\widehat{r}}_{\mathrm{P}},{\dot{\widehat{r}}}_{\mathrm{P}}\right)-{\widehat{f}}_{\mathrm{P}}^{\mathrm{e}}\left({\widehat{r}}_{\mathrm{P}},{\dot{\widehat{r}}}_{\mathrm{P}}\right).$$

(6)

The constraint force ${\widehat{f}}_{\mathrm{P}}^{\mathrm{z}}$ must be applied by the cables, which are attached to the platform. The kinematic modeling (both for a CDPR and the drone system) is similar to conventional Stewart Gough platforms. As rotation requirements of the platform are limited, simply roll-pitch-yaw angles have been applied. Kinematic modeling details can be found in [48]. Note that, for the drone system, the base points are moving. Each cable in the parallel mechanism is described by the vector $l_i=r_{\mathrm{B}i}-r_{\mathrm{P}}-p_{\mathrm{R}i}$. Here, the vector $p_{\mathrm{R}i}$ points from the platform’s coordinate system to the attachment point $R_i$ of the i-th cable, while the vector $r_{\mathrm{B}i}$ points from the origin of the world reference frame $\mathcal{B}$ to the point $B_i$. The cable attachment point $R_i$ can also be described with regard to the origin of the world refence frame $\mathcal{B}$ by the vector $r_{\mathrm{R}i}$. In the case of a cable robot, at point $B_i$ the i-th cable enters the workspace. In the case of a drone system, the i-th cable is fixed at the i-th drone at this point. While in the case of the drone system the platform is connected to each drone by a cable of the constant length $l_{0,i}={∥{\mathit{l}}_i∥}_2$, the cable length is variable in the case of a cable robot. The resulting constraint conditions are given by the algebraic equation

$$\mathit{g}=\left[\begin{array}{c}{g}_1\\ g_2\\ ⋮\\ g_{n_{\mathrm{C}}}\end{array}\right]=\left[\begin{array}{c}\frac{1}{2}\left({\mathit{l}}_1^{\mathrm{T}}{\mathit{l}}_1-l_{0,1}^2\right)\\ \frac{1}{2}\left({\mathit{l}}_2^{\mathrm{T}}{\mathit{l}}_2-l_{0,2}^2\right)\\ ⋮\\ \frac{1}{2}\left({\mathit{l}}_{n_{\mathrm{C}}}^{\mathrm{T}}{\mathit{l}}_{n_{\mathrm{C}}}-l_{0,n_{\mathrm{C}}}^2\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right].$$

(7)

Equation (7) states that each of the $n_{\mathrm{C}}$ cables reduces the platform’s degrees-of-freedom by one. It is well known that the constraint forces can be expressed by ${\widehat{\mathit{f}}}^{\mathrm{z}}={\mathit{C}}^{\mathrm{T}}\mathit{\lambda }$, where the matrix is calculated by $\mathit{C}=\frac{\partial \mathit{g}}{\partial \widehat{\mathit{r}}}$. Note that the constraints introduced by the cables are holonomic, since they are not velocity dependent. The result shows that the reaction forces point in the direction of the cables. Thus, each cable force ${\mathit{f}}_{\mathrm{R}i}$ can be described by the unit cable vector ${\mathit{\upsilon }}_{\mathrm{R}i}$ multiplied by the magnitude of the cable force $f_{\mathrm{R}i}$. Therefore, the constraint forces can be expressed as

$${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}=-\underset{{\mathit{A}}^{\mathrm{T}}}{\underbrace{\left[\begin{array}{ccc}{\mathit{\upsilon }}_{\mathrm{R}1}& \dots & {\mathit{\upsilon }}_{\mathrm{R}{n}_{\mathrm{C}}}\\ {\tilde{\mathit{p}}}_{\mathrm{R}1}{\mathit{\upsilon }}_{\mathrm{R}1}& \dots & {\tilde{\mathit{p}}}_{\mathrm{R}{n}_{\mathrm{C}}}{\mathit{\upsilon }}_{\mathrm{R}{n}_{\mathrm{C}}}\end{array}\right]}}\left[\begin{array}{c}{f}_{\mathrm{R}1}\\ ⋮\\ f_{\mathrm{R}{n}_{\mathrm{C}}}\end{array}\right],\mathrm{with}{\mathit{\upsilon }}_{\mathrm{R}i}=\frac{{\mathit{f}}_{\mathrm{R}i}}{{∥{\mathit{f}}_{\mathrm{R}i}∥}_2}\iff {\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}=-\underset{{\mathit{P}}^{\mathrm{T}}}{\underbrace{\left[\begin{array}{ccc}\mathit{E}& \dots & \mathit{E}\\ {\tilde{\mathit{p}}}_{\mathrm{R}1}& \dots & {\tilde{\mathit{p}}}_{\mathrm{R}{n}_{\mathrm{C}}}\end{array}\right]}}\left[\begin{array}{c}{\mathit{f}}_{\mathrm{R}1}\\ ⋮\\ {\mathit{f}}_{\mathrm{R}{n}_{\mathrm{C}}}\end{array}\right].$$

(8)

Since the assumed ideal cables cannot apply any torque, there are not any direct constraint torques. Equation (8) can be solved for the actual cable forces e.g., by using the Moore–Penrose pseudoinverse of ${\mathit{P}}^{\mathrm{T}}$. Note that, for the cable robot, an active-set method is used to compute the scalar cable forces using ${\mathit{A}}^{\mathrm{T}}$, which is a common approach for CDPRs [49]. As long as the end effector is in the workspace, the algorithm generates forces between the given limits $f_{\min }$ and $f_{\max }$ [49]. Further, note that the cable force calculation is a separate algorithm (e.g., based on active set optimization), which is called by the trajectory optimizer to validate a trajectory for feasible cable forces at each time step. Typically, when low forces are demanded, this will lead to cable forces close to or even at $f_{\min }$ for some cables. Therefore, in practice, $f_{\min }$ is chosen slightly above the physically required value to leave a margin for control purposes. Since all cables need a minimum tension $f_{\min }$ to avoid slackness and obtain a valid solution, the costs for the cables forces can be taken into account by

$${\mathcal{V}}_{\mathrm{force}}=\frac{1}{n_{\mathrm{C}}{n}_{\mathrm{s}}}\left(\sum _{k=1}^{n_{\mathrm{s}}}\sum _{i=1}^{n_{\mathrm{C}}}\frac{f_{\mathrm{R}i}\left(k\right)-f_{\min }}{f_{\max }-f_{\min }}\right).$$

(9)

Every time the cable forces are beyond $f_{\min }$ or $f_{\max }$ a penalty term ${\mathcal{P}}_{\mathrm{force}}$ is added and ${\mathcal{V}}_{\mathrm{force}}$ is not assigned. Therefore, the costs for this criterion cannot be negative. Note that this also holds for similar cost functions. Considering singularities, three kinds need to be taken into account for parallel robots as explained in [49]. Serial singularities (first kind) can be neglected from a practical point of view, since the cable lengths are fixed for the drone system and will never drop to zero for the CDPR. Parallel singularities (second kind), which coincide with a loss of rank within the platform’s Jacobian ${\mathit{A}}^{\mathrm{T}}$, will cause an error when trying to compute cable forces, leading to a penalty. Consequently, the optimizer will avoid such configurations throughout a trajectory, even if they exist. Moreover, the CDPR design has been analyzed for feasible cable forces throughout the required workspace [48]. Architectural singularities (third kind) are avoided by carefully choosing the design parameters of the system. For the drone, for example, the cables are arranged on the platform in such a way that two cables never converge at one point. Furthermore, the only desired rotation is about the vertical axis in order to place a masonry unit. Note that this is done by a rotational gripper in the case of the CDPR. This reduces the set of required configurations drastically from a practical point of view.

3.2. Modeling of the Drone Dynamics

The considered drone system consists of a platform $\mathcal{K}=P$ with the mass $m_{\mathrm{P}}$ and $i=1,\dots ,n_{\mathrm{C}}$ drones $D_i$ with the mass $m_{\mathrm{D}}$ and the inertia ${\mathrm{\Theta }}_{\mathrm{D}}$. Within this work, we considered quadrotors for a first implementation and verification of the optimization algorithm. Based on the object-oriented structure of the optimization framework, the quadrotor can be easily replaced by more complex drones in future work. The coordinate system of each drone ${\mathcal{D}}_i$ is located at its respective center of mass. The pose of a drone is defined by the vector ${\widehat{\mathit{r}}}_{\mathrm{D}i}$. The vector ${\mathit{b}}_{\mathrm{R}i}$ points from the center of the coordinate system ${\mathcal{D}}_i$ to the cable attachment point of the drone. The orientation of each drone is described by Cardan angles (axes $x,y,z$ and angles ${\alpha }_{\mathrm{D}i},{\beta }_{\mathrm{D}i},{\gamma }_{\mathrm{D}i}$), where, by definition, the angle around the drone-fixed $z_{\mathrm{D}i}$-axis ${\gamma }_{\mathrm{D}i}$ is zero for all times. This leads to the transformation matrix ${}^{0{\mathcal{D}}_i}\mathit{T}={\mathit{T}}_x\left({\alpha }_{\mathrm{D}i}\right){\mathit{T}}_y\left({\beta }_{\mathrm{D}i}\right)$. Since the derivation of the inverse model is the same for every drone, the index i is omitted from now on in this section. The Cardan angles ${\alpha }_{\mathrm{D}}$ and ${\beta }_{\mathrm{D}}$ are related to the angular velocity ${\mathit{\omega }}_{\mathrm{D}}$ by the so-called kinematic Cardan equation. For the representation of the angular velocity ${\mathit{\omega }}_{\mathrm{D}}$ in the coordinate system of the drone, it holds

$$\left[\begin{array}{c}{\dot{\alpha }}_{\mathrm{D}}\\ {\dot{\beta }}_{\mathrm{D}}\\ {\dot{\gamma }}_{\mathrm{D}}\end{array}\right]=\frac{1}{cos\left({\beta }_{\mathrm{D}}\right)}\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\left({\beta }_{\mathrm{D}}\right)& 0\\ -sin\left({\beta }_{\mathrm{D}}\right)& 0& cos\left({\beta }_{\mathrm{D}}\right)\end{array}\right]\left[\begin{array}{c}{}^{\mathcal{D}}{\omega }_{\mathrm{D}x}\\ {}^{\mathcal{D}}{\omega }_{\mathrm{D}y}\\ {}^{\mathcal{D}}{\omega }_{\mathrm{D}z}\end{array}\right].$$

(10)

The drones must be able to carry the required forces at any time. To check whether a trajectory is feasible, the rotor angular velocities of all motors must be determined and evaluated for each drone at each time step. This implies that an inverse model of the system dynamics must be found based on Equations (4) and (8). For the drone modeling simplified equations are used. This implies the consideration of a drone as a rigid body using the thrust of each propeller as a direct input value. The thrust $F_{\mathrm{A}}$ and the drag ${\tau }_{\mathrm{W}}$ of each propeller are each approximated by quadratic functions [50]

$$\begin{array}{cc}\hfill F_{\mathrm{A},p}& =c_{\mathrm{T}}{\omega }_p^2,\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill {\tau }_{\mathrm{w},p}& =c_{\mathrm{W}}{\omega }_p^2,\hfill \end{array}$$

(11b)

in terms of the propeller speed ${\omega }_p$, $p=\mathrm{M}1,\dots ,\mathrm{M}4$. The parameter $c_{\mathrm{T}}$ is the thrust and the parameter $c_{\mathrm{W}}$ is the drag coefficient. These quantities depend mainly on the propeller used, but also on other factors such as the shape of the drone frame, which influences the air flow at the mounting position of the motor. The translational movement of a drone follows from Equation (4). Using the mass $m_{\mathrm{D}}$, the acceleration due to the gravity g and the total thrust of all propellers $F_{\mathrm{A}}$ leads to

$$m_{\mathrm{D}}\left[\begin{array}{c}{\ddot{x}}_{\mathrm{D}}\\ {\ddot{y}}_{\mathrm{D}}\\ {\ddot{z}}_{\mathrm{D}}\end{array}\right]=\left[\begin{array}{c}{F}_{\mathrm{A}}sin\left({\beta }_{\mathrm{D}}\right)\\ -F_{\mathrm{A}}cos\left({\beta }_{\mathrm{D}}\right)sin\left({\alpha }_{\mathrm{D}}\right)\\ F_{\mathrm{A}}cos\left({\alpha }_{\mathrm{D}}\right)cos\left({\beta }_{\mathrm{D}}\right)\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ -m_{\mathrm{D}}g\end{array}\right]-\left[\begin{array}{c}{f}_{\mathrm{R}x}^{\mathrm{z}}\\ f_{\mathrm{R}y}^{\mathrm{z}}\\ f_{\mathrm{R}z}^{\mathrm{z}}\end{array}\right],$$

(12)

since ${\mathit{f}}_{\mathrm{D}}^{\mathrm{c}}=\mathbf{0}$ due to ${\mathit{b}}_{\mathrm{SD}}=\mathbf{0}$. Equation (12) can directly be solved for the Cardan angles

$${\alpha }_{\mathrm{D}}=-arctan\left(\frac{m_{\mathrm{D}}{\ddot{y}}_{\mathrm{D}}+f_{\mathrm{R}y}^{\mathrm{z}}}{m_{\mathrm{D}}\left({\ddot{z}}_{\mathrm{D}}+g\right)+f_{\mathrm{R}z}^{\mathrm{z}}}\right),$$

(13a)

$${\beta }_{\mathrm{D}}=arctan\left(cos\left({\alpha }_{\mathrm{D}}\right)\frac{m_{\mathrm{D}}{\ddot{x}}_{\mathrm{D}}+f_{\mathrm{R}x}^{\mathrm{z}}}{m_{\mathrm{D}}\left({\ddot{z}}_{\mathrm{D}}+g\right)+f_{\mathrm{R}z}^{\mathrm{z}}}\right),$$

(13b)

and the norm of the total thrust

$$F_{\mathrm{A}}=\sqrt{{\left({\ddot{x}}_{\mathrm{D}}{m}_{\mathrm{D}}+f_{\mathrm{R}x}^{\mathrm{z}}\right)}^2+{\left({\ddot{y}}_{\mathrm{D}}{m}_{\mathrm{D}}+f_{\mathrm{R}y}^{\mathrm{z}}\right)}^2+{\left(\left({\ddot{z}}_{\mathrm{D}}+g\right)m_{\mathrm{D}}+f_{\mathrm{R}z}^{\mathrm{z}}\right)}^2}.$$

(14)

Under the assumption that the Coriolis and centrifugal forces can be neglected, the rotational movement of a drone follows from Equation (4) and is given by

$${\mathrm{\Theta }}_{\mathrm{D}}\left[\begin{array}{c}{}^{\mathcal{D}}{\dot{\omega }}_{\mathrm{D}x}\\ {}^{\mathcal{D}}{\dot{\omega }}_{\mathrm{D}y}\\ {}^{\mathcal{D}}{\dot{\omega }}_{\mathrm{D}z}\end{array}\right]=\left[\begin{array}{c}{c}_{\mathrm{T}}\left({\omega }_{\mathrm{M}2}^2-{\omega }_{\mathrm{M}4}^2\right)r_{\mathrm{D}}\\ -c_{\mathrm{T}}\left({\omega }_{\mathrm{M}1}^2-{\omega }_{\mathrm{M}3}^2\right)r_{\mathrm{D}}\\ -c_{\mathrm{W}}\left({\omega }_{\mathrm{M}1}^2-{\omega }_{\mathrm{M}2}^2+{\omega }_{\mathrm{M}3}^2-{\omega }_{\mathrm{M}4}^2\right)\end{array}\right]+\left[\begin{array}{c}-{\tau }_{\mathrm{R}x}\\ {\tau }_{\mathrm{R}y}\\ 0\end{array}\right].$$

(15a)

Note that this equation provides a direct link between the angular velocity of the drone ${\mathit{\omega }}_{\mathrm{D}}$ in the drone-fixed coordinate system and the motor speeds. In Equation (15a), $r_{\mathrm{D}}$ is the radius of the drone, defined as the distance in the $xy$-plane of the drone between the z-axis of the coordinate system $\mathcal{D}$ and the axis of rotation of each propeller. The vector ${\mathit{\tau }}_{\mathrm{R}}$ is the constraint torque with its elements

$$\begin{array}{cc}\hfill {\tau }_{\mathrm{R}x}& =b_{\mathrm{R}z}\left(f_{\mathrm{R}y}^{\mathrm{z}}cos\left({\alpha }_{\mathrm{D}}\right)+f_{\mathrm{R}z}^{\mathrm{z}}sin\left({\alpha }_{\mathrm{D}}\right)\right),\hfill \end{array}$$

(15b)

$$\begin{array}{cc}\hfill {\tau }_{\mathrm{R}y}& =b_{\mathrm{R}z}\left(f_{\mathrm{R}x}^{\mathrm{z}}cos\left({\beta }_{\mathrm{D}}\right)+f_{\mathrm{R}y}^{\mathrm{z}}sin\left({\alpha }_{\mathrm{D}}\right)sin\left({\beta }_{\mathrm{D}}\right)-f_{\mathrm{R}z}^{\mathrm{z}}cos\left({\alpha }_{\mathrm{D}}\right)sin\left({\beta }_{\mathrm{D}}\right)\right).\hfill \end{array}$$

(15c)

Equation (15) can now be solved for the angular velocity of each motor

$${\mathit{\omega }}_p=\left[\begin{array}{c}{\omega }_{\mathrm{M}1}\\ {\omega }_{\mathrm{M}2}\\ {\omega }_{\mathrm{M}3}\\ {\omega }_{\mathrm{M}4}\end{array}\right]=\frac{0.5}{\sqrt{r_{\mathrm{D}}{c}_{\mathrm{T}}{c}_{\mathrm{W}}}}\left[\begin{array}{c}\sqrt{r_{\mathrm{D}}{c}_{\mathrm{W}}{F}_{\mathrm{A}}+2c_{\mathrm{W}}{\tau }_{\mathrm{R}y}-2{\mathrm{\Theta }}_{\mathrm{D}y}{c}_{\mathrm{W}}{\dot{\omega }}_{\mathrm{D}y}-r_{\mathrm{D}}{\mathrm{\Theta }}_{\mathrm{D}z}{c}_{\mathrm{T}}{\dot{\omega }}_{\mathrm{D}z}}\\ -\sqrt{r_{\mathrm{D}}{c}_{\mathrm{W}}{F}_{\mathrm{A}}+2c_{\mathrm{W}}{\tau }_{\mathrm{R}x}+2{\mathrm{\Theta }}_{\mathrm{D}x}{c}_{\mathrm{W}}{\dot{\omega }}_{\mathrm{D}x}+r_{\mathrm{D}}{\mathrm{\Theta }}_{\mathrm{D}z}{c}_{\mathrm{T}}{\dot{\omega }}_{\mathrm{D}z}}\\ \sqrt{r_{\mathrm{D}}{c}_{\mathrm{W}}{F}_{\mathrm{A}}-2c_{\mathrm{W}}{\tau }_{\mathrm{R}y}+2{\mathrm{\Theta }}_{\mathrm{D}y}{c}_{\mathrm{W}}{\dot{\omega }}_{\mathrm{D}y}-r_{\mathrm{D}}{\mathrm{\Theta }}_{\mathrm{D}z}{c}_{\mathrm{T}}{\dot{\omega }}_{\mathrm{D}z}}\\ -\sqrt{r_{\mathrm{D}}{c}_{\mathrm{W}}{F}_{\mathrm{A}}-2c_{\mathrm{W}}{\tau }_{\mathrm{R}x}-2{\mathrm{\Theta }}_{\mathrm{D}x}{c}_{\mathrm{W}}{\dot{\omega }}_{\mathrm{D}x}+r_{\mathrm{D}}{\mathrm{\Theta }}_{\mathrm{D}z}{c}_{\mathrm{T}}{\dot{\omega }}_{\mathrm{D}z}}\end{array}\right].$$

(16)

It has to be stated that the inversion of the drone’s model only succeeds if ${\mathit{r}}_{\mathrm{B}i}^{\left(n\right)}={\mathit{r}}_{\mathrm{D}i}^{\left(n\right)}$ holds for the n-th time derivative. Hence, the vector ${\mathit{b}}_{\mathrm{RD}}$ should be as short as possible. With the knowledge of all cable forces ${\mathit{f}}_{\mathrm{R}i}$, the trajectory of the cable attachment point and the relating time derivatives can be calculated by

$${\mathit{r}}_{\mathrm{B}i}^{\left(n\right)}={\mathit{r}}_{\mathrm{R}i}^{\left(n\right)}+l_{0,i}{\mathit{\upsilon }}_{\mathrm{R}i}^{\left(n\right)}.$$

(17)

In cases where two or more drones are used, Equation (8) leads to an underdetermined system of linear equations. As already mentioned, its solution can be found by

$${\mathit{f}}_{\mathrm{R}}={\left({\mathit{P}}^{\mathrm{T}}\right)}^{+}{\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}+\left(\mathit{E}-{\left({\mathit{P}}^{\mathrm{T}}\right)}^{+}{\mathit{P}}^{\mathrm{T}}\right){\mathit{\lambda }}_0,$$

(18)

where ${\left({\mathit{P}}^{\mathrm{T}}\right)}^{+}\in {\mathbb{R}}^{3n_{\mathrm{D}}\times 6}$ is the Moore–Penrose inverse, ${\mathit{E}}_{3n_{\mathrm{D}}\times 3n_{\mathrm{D}}}$ the identity matrix and ${\mathit{\lambda }}_0\in {\mathbb{R}}^{3n_{\mathrm{D}}\times 1}$ an arbitrary vector. The time derivatives of ${\mathit{f}}_{\mathrm{R}}$ can be calculated by differentiating first (8) with respect to time using the Leibniz rule

$${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}\left(n\right)}=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\mathit{P}}^{\mathrm{T}\left(k\right)}\left(x\right){\mathit{f}}_{\mathrm{R}}^{(n-k)}\left(x\right),$$

(19)

and solving this equations analogous to the procedure of (18) afterwards, concerning that the vectors ${\mathit{\lambda }}_i$ for the time derivatives are chosen equal to zero.

For the modeling of the drone dynamics, it is assumed that the coordinate axes of $\mathcal{E}$ are aligned with the platform’s principal axes of inertia. This also holds for the homogeneous masonry unit. Assuming that a masonry unit is always gripped centrally, this yields ${\mathit{b}}_{\mathrm{S}}={\left[\begin{array}{ccc}0& 0& {\mathit{b}}_{\mathrm{S}z}\end{array}\right]}^{\mathrm{T}}$ and ${\mathrm{\Theta }}_{\mathrm{P}}=\mathrm{diag}\left({\mathrm{\Theta }}_{\mathrm{P}xx},{\mathrm{\Theta }}_{\mathrm{P}yy},{\mathrm{\Theta }}_{\mathrm{P}zz}\right)$. Note that ${\mathit{b}}_{\mathrm{S}}$ and ${\mathrm{\Theta }}_{\mathrm{P}}$ have to be recalculated for every trajectory. Additionally, by default the platform performs only rotations around the body-fixed $z_{\mathrm{P}}$-axis. Thus, the orientation of the platform can be described by the matrix ${\mathit{T}}_{\mathrm{P}}\left({\gamma }_{\mathrm{P}}\right)$. That means that there is the direct relation ${\omega }_{\mathrm{P}}={\dot{\gamma }}_{\mathrm{P}}$ between the angular velocity and the time derivative of the platform angle around the z-axis. This simplifies Equation (6) into

$${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}={\widehat{\mathit{M}}}_{\mathrm{P}}{\ddot{\widehat{\mathit{r}}}}_{\mathrm{P}}-{\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{e}},\mathrm{with}{\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{c}}=\mathbf{0}.$$

(20)

The necessary time derivatives of Equation (20) in Equation (19) can be calculated by

$${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}\left(n\right)}={\widehat{\mathit{M}}}_{\mathrm{P}}{\widehat{\mathit{r}}}_{\mathrm{P}}^{\left(n+2\right)},$$

(21)

since the product ${\dot{\widehat{\mathit{M}}}}_{\mathrm{P}}{\ddot{\widehat{\mathit{r}}}}_{\mathrm{P}}$ of the time derivative of the mass matrix

$${\dot{\widehat{\mathit{M}}}}_{\mathrm{P}}=\left[\begin{array}{cc}\mathbf{0}& m_{\mathrm{P}}{\dot{\tilde{\mathit{b}}}}_{\mathrm{S}}^{\mathrm{T}}\\ m_{\mathrm{P}}{\dot{\tilde{\mathit{b}}}}_{\mathrm{S}}& {\dot{\mathrm{\Theta }}}_{\mathrm{P}}\end{array}\right]=\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tilde{\mathit{\omega }}}_{\mathrm{P}}{\mathrm{\Theta }}_{\mathrm{P}}-{\mathrm{\Theta }}_{\mathrm{P}}{\tilde{\mathit{\omega }}}_{\mathrm{P}}\end{array}\right]$$

(22)

and the acceleration vector ${\ddot{\widehat{\mathit{r}}}}_{\mathrm{P}}={\left[\begin{array}{cccc}{\ddot{\mathit{r}}}_{\mathrm{P}}& 0& 0& {\dot{\omega }}_{\mathrm{P}z}\end{array}\right]}^{\mathrm{T}}$ is always zero. This follows because

$${\tilde{\mathit{\omega }}}_{\mathrm{P}}{\mathrm{\Theta }}_{\mathrm{P}}-{\mathrm{\Theta }}_{\mathrm{P}}{\tilde{\mathit{\omega }}}_{\mathrm{P}}=\left[\begin{array}{ccc}0& {\omega }_{\mathrm{P}z}\left({\mathrm{\Theta }}_{\mathrm{P}xx}-{\mathrm{\Theta }}_{\mathrm{P}yy}\right)& 0\\ {\omega }_{\mathrm{P}z}\left({\mathrm{\Theta }}_{\mathrm{P}xx}-{\mathrm{\Theta }}_{\mathrm{P}yy}\right)& 0& 0\\ 0& 0& 0\end{array}\right].$$

(23)

Moreover, the time derivatives of the vector of the applied force ${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{e}\left(n\right)}$ are always zero, since the constant gravitational force is the only applied force which is taken into account.

Note that the calculation of the propeller speeds ${\mathit{\omega }}_p$ in Equation (16) depends on ${\dot{\mathit{\omega }}}_{\mathrm{D}}$. Solving Equation (10) for ${\mathit{\omega }}_{\mathrm{D}}$ states that the calculation of ${\dot{\mathit{\omega }}}_{\mathrm{D}}$ requires the second time derivatives ${\ddot{\alpha }}_{\mathrm{D}}$ and ${\ddot{\beta }}_{\mathrm{D}}$. Therefore, Equation (13) must be differentiated twice, which means that the fourth time derivative ${\mathit{r}}_{\mathrm{D}}^{\left(4\right)}={\mathit{r}}_{\mathrm{B}}^{\left(4\right)}$ has to be determined. Furthermore, it follows from Equations (8) and (17) that ${\mathit{\upsilon }}_{\mathrm{B}}^{\left(4\right)}$ and ${\mathit{f}}_{\mathrm{R}}^{\left(4\right)}$ must also be known. Equation (18) states that this requires knowledge of the fourth time derivative of the constraint force ${\widehat{\mathit{f}}}_{\mathrm{P}}^{\mathrm{z}}$. Finally, it follows from Equation (21) that the sixth time derivative of the platform pose ${\widehat{\mathit{r}}}_{\mathrm{P}}$ is needed. For each trajectory and its six time derivatives, the boundary conditions at the beginning and end of the trajectory must be defined (i.e., two times a set of one plus six conditions) to ensure continuity, resulting in a total of 14 boundary conditions per DOF. Using polynomials for the trajectory, a polynomial of the 13th order provides 14 coefficients. Solving a system of these 14 unknown coefficients and the 14 boundary conditions thus defines the trajectory meeting all conditions at the start, the end and in all time derivatives. An example of the use of a polynomial function for a trajectory can be found in [51].

Equation (16) leads to the cost function

$${\mathcal{V}}_{\omega }=\frac{1}{n_{\mathrm{s}}{n}_{\mathrm{D}}{n}_{\mathrm{M}}}{\left(\sum _{k=1}^{n_{\mathrm{s}}}\sum _{i=1}^{n_{\mathrm{D}}}\sum _{j=1}^{n_{\mathrm{M}}}\frac{{\omega }_{\mathrm{M},i,j}\left(k\right)-{\omega }_{\mathrm{M},\min }}{{\omega }_{\mathrm{M},\max }-{\omega }_{\mathrm{M},\min }}\right)}^3.$$

(24)

If the actual speed ${\omega }_{\mathrm{M}}$ is above the maximum speed ${\omega }_{\mathrm{M},\max }$ or below minimum speed ${\omega }_{\mathrm{M},\min }$, the penalty term ${\mathcal{P}}_{\omega }$ is applied and ${\mathcal{V}}_{\omega }$ is not assigned.

3.3. Modeling of the Cable Robot’s Winch Dynamics, Power and Energy Consumption

Winch dynamics: The moment of inertia of the drive train, reduced to the winch side, is computed as

$$J=J_{\mathrm{W}}+J_{\mathrm{C}}+J_{\mathrm{M}}{i}_{\mathrm{G}}^2+J_{\mathrm{G}}{i}_{\mathrm{G}}^2,$$

(25)

by taking into account the moment of inertia of the winch $J_{\mathrm{W}}$, the clutch $J_{\mathrm{C}}$, the motor shaft $J_{\mathrm{M}}$ and the gearbox $J_{\mathrm{G}}$ with its gear ratio $i_{\mathrm{G}}$. Using the winch drum radius $r_{\mathrm{W}}$ and the cable acceleration ${\ddot{q}}_{\mathrm{R}}$, one finds for the total motor torque of the i-th cable

$${\tau }_{\mathrm{t},i}=\frac{f_{\mathrm{R},i}{r}_{\mathrm{W}}}{i_{\mathrm{G}}{\eta }_{\mathrm{G}}}+\frac{J{\ddot{q}}_{\mathrm{R}i}}{i_{\mathrm{G}}{\eta }_{\mathrm{G}}{r}_{\mathrm{W}}}.$$

(26)

The friction of the overall drive train is modeled by an overall efficiency ${\eta }_{\mathrm{G}}$ (theefficiency ${\eta }_{\mathrm{G}}$ can be derived from the manufacturer’s catalog data at full load of the gearbox). As the drive train torques are limited by ${\tau }_{\mathrm{t},\max }$, a penalty ${\mathcal{P}}_{\mathrm{torque}}$ is set in case ${\tau }_{\mathrm{t},i}$ exceeds the capabilities. Note that, in this work, ${\mathcal{V}}_{\mathrm{torque}}=0$.

Power and energy consumption: The used electric motors are highly efficient permanent magnet synchronous motors. The detailed electric modeling of the motor is simplified by a power balance approach. The mechanical winch power per cable at time step k can be computed as

$$P_{\mathrm{M},i}\left(k\right)={\tau }_{\mathrm{t},i}\left(k\right){\omega }_{\mathrm{W},i}\left(k\right),$$

(27)

where ${\omega }_{\mathrm{W},i}$ is the angular velocity of the i-th winch drum. Considering the motor’s phase to phase winding resistance $R_{\mathrm{pp}}$ and its motor torque constant $k_{\mathrm{t}}$ from the specifications in the data sheet, the copper losses

$$P_{\mathrm{C},i}=\frac{3}{2}{\left(\frac{{\tau }_{\mathrm{t},i}}{k_{\mathrm{t}}}\right)}^2{R}_{\mathrm{pp}}$$

(28)

can be computed [52]. Note that the motor has three phases and is star connected. Taking into account also the inverter efficiency ${\eta }_{\mathrm{ESC}}$ and the recuperation efficiency ${\eta }_{\mathrm{R}}$ leads to the total, needed or recuperated winch power

$$P_{\mathrm{W},i}=\left\{\begin{array}{cc}(P_{\mathrm{M},i}{\eta }_{\mathrm{G}}+P_{\mathrm{C},i}){\eta }_{\mathrm{ESC}}{\eta }_{\mathrm{R}}\hfill & \mathrm{for}{P}_{\mathrm{M},i}+P_{\mathrm{C},i}<0\hfill \\ (P_{\mathrm{M},i}\frac{1}{{\eta }_{\mathrm{G}}}+P_{\mathrm{C},i})\frac{1}{{\eta }_{\mathrm{ESC}}}\hfill & \mathrm{for}{P}_{\mathrm{M},i}+P_{\mathrm{C},i}\ge 0\hfill \end{array}\right..$$

(29)

For every time step, an overall power

$$P\left(k\right)=\sum _{i=1}^{n_{\mathrm{c}}}{P}_{\mathrm{W},i}\left(k\right)$$

(30)

can be computed. In case $P\left(k\right)$ exceeds the maximum power $P_{\max }$ provided by the power source at any time step k, a penalty ${\mathcal{P}}_{\mathrm{power}}$ is set. From the power requirements over time, the energy consumption is approximated using the trapezoidal rule [53]

$$E_{\mathrm{total}}=\sum _{k=2}^{n_{\mathrm{s}}}\frac{P\left(k\right)+P(k-1)}{2}\mathrm{\Delta }t,$$

(31)

where $\mathrm{\Delta }t=\frac{t_{\mathrm{total}}}{n_{\mathrm{s}}}$ is the step size of a time step. If used, the total energy consumption defines its costs ${\mathcal{V}}_{\mathrm{energy}}=E_{\mathrm{total}}$. Later on $E_{\mathrm{total}}$ is used to compare both systems. Notably, neither ${\mathcal{V}}_{\mathrm{power}}$, ${\mathcal{V}}_{\mathrm{energy}}$ nor ${\mathcal{P}}_{\mathrm{energy}}$ is employed within the optimization and is thus set to zero.

The considered CDPR has eight cables in each corner of the frame, which are guided into the workspace using pivoting deflection pulleys. The four lower pulleys (see Equation (47), ${}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}1}{,}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}2}{,}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}5}{,}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}6}$) can be moved vertically. They are lifted as soon as a layer of masonry units has been finished. The movement needed is done between trajectories 14 and 15. Therefore, it is assumed that these pulleys are attached to slides that may move along vertical rails, powered by external drives. The dynamic effects and power consumption is neglected. Note that the details on the modeling of these effects can be found in [48]. The actuated sliding motion of the pulleys under cable tension and alongside a trajectory has already been demonstrated [54].

3.4. Modeling of Collisions

The following collision detection formalisms are based on geometric considerations. The necessary fundamentals can be found in [55].

Self-collision of the robot and collisions of the robot with its environment: For collision avoidance, all relevant objects such as drones, end effector, payload and static obstacles are represented by cuboid geometries called Axis-Aligned Bounding Boxes (AABB) [56]. As these boxes are aligned with the three axes of the inertial system, both distance computations as well as collision checks are massively simplified. In case relevant rotations of the bodies involved are planned, the AABBs can be replaced by so-called Oriented Bounding Boxes (OBB) [56] for the price of slightly increased computation costs.

Collision on AABBs can be trivially checked using the Separating Axis Theorem [56]. Two convex objects can not collide if a separating (hyper-)plane and its normal—the separating axis—exist. Accordingly, if in at least one axis no overlap of the boxes can be found—which is trivial to check per-axis of the inertial system—the AABBs do not collide. Given two AABBs 1 and 2, their center coordinates ${\mathit{r}}_1={[x_1,y_1,z_1]}^{\mathrm{T}}$ and ${\mathit{r}}_2={[x_2,y_2,z_2]}^{\mathrm{T}}$ as well as their halfwidth extends $e_{1x},e_{1y},e_{1z}$ and $e_{2x},e_{2y},e_{2z}$, respectively, the following distances can be computed

$$\begin{array}{cc}\hfill d_x& =\mathrm{abs}(x_1-x_2)-(e_{1\mathrm{x}}+e_{2\mathrm{x}}),\hfill \\ \hfill d_y& =\mathrm{abs}(y_1-y_2)-(e_{1\mathrm{y}}+e_{2\mathrm{y}}),\hfill \\ \hfill d_z& =\mathrm{abs}(z_1-x_2)-(e_{1\mathrm{z}}+e_{2\mathrm{z}}).\hfill \end{array}$$

(32)

If all distances $d_x,d_y,d_z$ become negative at the same time, a collision occurs. This allows to check the potential collisions $\chi \in \left\{\mathrm{DD},\mathrm{ObEE},\mathrm{ObD}\right\}$ where, in case of collision, ${\mathcal{P}}_{\mathrm{DD}},{\mathcal{P}}_{\mathrm{ObEE}}$ or ${\mathcal{P}}_{\mathrm{ObD}}$, respectively, receives penalty terms.

Furthermore, the distance of the AABBs is checked to support the convergence of the optimizer. Thus, the costs of ${\mathcal{V}}_{\mathrm{DD}},{\mathcal{V}}_{\mathrm{ObEE}}$ and ${\mathcal{V}}_{\mathrm{ObD}}$ are calculated by observing the smallest distance

$$d_{ij}=\sqrt{d_x^2+d_y^2+d_z^2}$$

(33)

of each two AABBs, which generally is the distance of the two closest corners. The costs

$${\mathcal{V}}_{\chi }=\frac{1}{n_{\mathrm{s}}{n}_{\mathrm{oo}}}\left(\sum _{i=1}^{n_{\mathrm{o}}-1}\sum _{j=1+i}^{n_{\mathrm{o}}}\sum _{k=1}^{n_{\mathrm{s}}}1-\frac{d_{ij}\left(k\right)}{d_{\min }}\right),n_{\mathrm{oo}}=\left(\genfrac{}{}{0pt}{}{n_{\mathrm{o}}}{2}\right),\chi \in \left\{\mathrm{DD},\mathrm{ObEE},\mathrm{ObD}\right\}.$$

(34)

are respectively assigned as long as the condition $0\le d_{ij}\left(k\right)\le d_{\min }$ is met. Distances of two AABBs larger than a predefined distance $d_{\min }$ are treated as uncritical. In this case ($d_{ij}\left(k\right)>d_{\min }$), ${\mathcal{V}}_{\mathrm{DD}}$, ${\mathcal{V}}_{\mathrm{ObEE}}$ and ${\mathcal{V}}_{\mathrm{ObD}}$ are set to zero to avoid negative cost values. Note that the binomial coefficient $n_{\mathrm{oo}}$ equals the number of collision checks for $n_{\mathrm{o}}$ obstacles.

Self-collision of cables: The method for detecting self-collisions of cables takes advantage of the fact that the end effector follows a continuous path. Whether during the last time step $\mathrm{\Delta }t$ a collision might have happened or not, can be checked by simple geometric considerations using the given quantities in Figure 4a.

Accordingly, it is assumed that the time interval is chosen sufficiently small so that the motion can be considered as linear between two time steps. Two cables $S_i$ and $S_j$ are shown in the platform-fixed coordinate system $\mathcal{E}$ for the two successive time steps $t_k$ and $t_{k+1}$. In this coordinate system, the vectors ${\mathit{p}}_{\mathrm{R}i}$ and ${\mathit{p}}_{\mathrm{R}j}$ to the end effector’s cable attachment points $R_i=R_{i,k}=R_{i,k+1}$ and $R_j=R_{j,k}=R_{j,k+1}$ are constant. However, the cable attachment points at the drones $B_i$ and $B_j$ with their associated vectors ${\mathit{r}}_{\mathrm{B}i}$ and ${\mathit{r}}_{\mathrm{B}j}$ move relatively to the end effector within the time step on an circular arc with the radius $l_0$. Thereby, the cable $S_i$ sweeps out the sector area $K_i$ defined by the three points $R_i$, $B_{i,k}$ and $B_{i,k+1}$ while the cable $S_j$ sweeps out the sector area $K_j$ defined by the three points $R_j$, $B_{j,k}$ and $B_{j,k+1}$. Thus, for a collision test, the four cable vectors

$${\mathit{l}}_{i,k}={\mathit{r}}_{\mathrm{B}i,k}-{\mathit{r}}_{\mathrm{R}i},{\mathit{l}}_{i,k+1}={\mathit{r}}_{\mathrm{B}i,k+1}-{\mathit{r}}_{\mathrm{R}i},{\mathit{l}}_{j,k}={\mathit{r}}_{\mathrm{B}j,k}-{\mathit{r}}_{\mathrm{R}j},{\mathit{l}}_{j,k+1}={\mathit{r}}_{\mathrm{B}j,k+1}-{\mathit{r}}_{\mathrm{R}j}$$

(35)

must be defined. Given that the two sector areas are not parallel to each other, a point of intersection between the sector area $K_i$ and the cable $S_j$ as well as between the sector area $K_j$ and the cable $S_i$ can always be calculated for each time step. A collision can only be entirely excluded if the calculated points of intersection $D_{i,k}$ and $D_{i,k+1}$ between the sector area $K_i$ and the cable $S_j$ as well as the calculated points of intersection $D_{j,k}$ and $D_{j,k+1}$ between the sector area $K_j$ and the cable $S_i$ are all outside the sector areas.

For the actual collision check, the two sector areas are treated as planes, expressed by their normal form ${\left(\mathit{x}-\mathit{p}\right)}^{\mathrm{T}}\mathit{n}=0$. Here, $\mathit{x}$ is the vector to an arbitrary point on the plane, $\mathit{p}$ is the vector to the cable attachment point of the considered sector area and $\mathit{n}$ is the normal vector of the plane. In a first step, the intersection points $D_{i,k}$ and $D_{i,k+1}$ between the plane $K_i$ and the cable $S_j$ expressed by the vector ${\mathit{l}}_j$ are calculated separately for the two time steps $t_k$ and $t_{k+1}$. For this purpose, the vector $\mathit{x}$ in the normal form of the plane is successively substituted by the parametric equation of the cables. The vector ${\mathit{r}}_{\mathrm{R}i}$ is chosen as $\mathit{p}$. This yields the two vectors

$$\begin{array}{cc}\hfill {\mathit{d}}_{i,k}& ={\mathit{r}}_{\mathrm{R}j}+s_{j,k}{\mathit{l}}_{j,k},\mathrm{with}{s}_{j,k}=\frac{{\left({\mathit{r}}_{\mathrm{R}i}-{\mathit{r}}_{\mathrm{R}j}\right)}^{\mathrm{T}}{\mathit{n}}_i}{{\mathit{l}}_{j,k}^{\mathrm{T}}{\mathit{n}}_i},\hfill \end{array}$$

(36a)

$$\begin{array}{cc}\hfill {\mathit{d}}_{i,k+1}& ={\mathit{r}}_{\mathrm{R}j}+s_{j,k+1}{\mathit{l}}_{j,k+1},\mathrm{with}{s}_{j,k+1}=\frac{{\left({\mathit{r}}_{\mathrm{R}i}-{\mathit{r}}_{\mathrm{R}j}\right)}^{\mathrm{T}}{\mathit{n}}_i}{{\mathit{l}}_{j,k+1}^{\mathrm{T}}{\mathit{n}}_i}\hfill \end{array}$$

(36b)

of the intersection points $D_i$. The first condition

$$C_{1i,k}:\left(0<s_{j,k}\le 1\right),C_{1i,k+1}:\left(0<s_{j,k+1}\le 1\right)$$

(37)

checks separately for each time step whether the point of intersection is within the free cable section between the last pulley on frame side and the platform. Otherwise a collision can be excluded. If one of the conditions $C_{1i,k}$ or $C_{1i,k+1}$ is fulfilled, the second step is to check if the calculated points of intersection are inside the sector area. For this, the sector area is defined by its parametric equation ${\mathit{x}}_i={\mathit{p}}_{\mathrm{R}i}+s_{i,k}{\mathit{l}}_{i,k}+s_{i,k+1}{\mathit{l}}_{i,k+1}$, with the affine coordinates of a point $s_{i,k}$ and $s_{i,k+1}$. Inserting the points of intersection ${\mathit{d}}_{i,k}$ and ${\mathit{d}}_{i,k+1}$ from Equation (36) in the parametric equation leads to their position vectors

$$\begin{array}{cc}\hfill {\mathit{s}}_{\mathrm{D},i,k}& ={\mathit{S}}_i^{+}\left({\mathit{d}}_{i,k}-{\mathit{r}}_{\mathrm{R}i}\right){\mathit{s}}_{\mathrm{D},i,k}\in {\mathbb{R}}^{2\times 1},\hfill \end{array}$$

(38a)

$$\begin{array}{cc}\hfill {\mathit{s}}_{\mathrm{D},i,k+1}& ={\mathit{S}}_i^{+}\left({\mathit{d}}_{i,k+1}-{\mathit{r}}_{\mathrm{R}i}\right){\mathit{s}}_{\mathrm{D},i,k+1}\in {\mathbb{R}}^{2\times 1}.\hfill \end{array}$$

(38b)

Herein, the matrix ${\mathit{S}}_i^{+}$ is the pseudo inverse of the matrix ${\mathit{S}}_i=\left[\begin{array}{cc}{\mathit{l}}_{i,k}& {\mathit{l}}_{i,k+1}\end{array}\right]$. The intersection point is within the sector area, provided that for the two timesteps the conditions

$$\begin{array}{cccc}\hfill C_{2i,k}:& \left(\left({\mathit{s}}_{\mathrm{D},i,k}\left(1\right)>0\right)\wedge \left({\mathit{s}}_{\mathrm{D},i,k}\left(2\right)>0\right)\right),\hfill & \hfill C_{3i,k}:& {∥{\mathit{S}}_i{\mathit{s}}_{\mathrm{D},i,k}∥}_2\le l_0\hfill \end{array}$$

(39)

$$\begin{array}{cccc}\hfill C_{2i,k+1}:& \left(\left({\mathit{s}}_{\mathrm{D},i,k+1}\left(1\right)>0\right)\wedge \left({\mathit{s}}_{\mathrm{D},i,k+1}\left(2\right)>0\right)\right),\hfill & \hfill C_{3i,k+1}:& {∥{\mathit{S}}_i{\mathit{s}}_{\mathrm{D},i,k+1}∥}_2\le l_0\hfill \end{array}$$

(40)

are true. This procedure must be repeated for the sector area $K_j$ and the cable $S_i$. This results in the conditions $C_{1j,k},C_{2j,k}$ and $C_{3j,k}$ for the time step $t_k$ and $C_{1j,k+1},C_{2j,k+1}$ and $C_{3j,k+1}$ for the time step $t_{k+1}$. The overall condition can be defined as

$$\begin{array}{cc}\hfill C_{\mathrm{ges}}=& \left(C_{1i,k}\wedge C_{2i,k}\wedge C_{3i,k}\right)\vee \left(C_{1i,k+1}\wedge C_{2i,k+1}\wedge C_{3i,k+1}\right)\vee \hfill \\ \hfill & \left(C_{1j,k}\wedge C_{2j,k}\wedge C_{3j,k}\right)\vee \left(C_{1j,k+1}\wedge C_{2j,k+1}\wedge C_{3j,k+1}\right).\hfill \end{array}$$

(41)

Finally it can be stated that

• a collision can be excluded, if $C_{\mathrm{ges}}=0$ and that
• a collision has happened within the chosen time step, if $C_{\mathrm{ges}}=1$.

Provided that a collision took place, it can be useful to repeat the collision check with a reduced step size. In the case of a cable collision, the penalty ${\mathcal{P}}_{\mathrm{CaCa}}$ is added. For cable–cable collisions, no costs are calculated, which is why ${\mathcal{V}}_{\mathrm{CaCa}}=0$. Inspired by Gouttefarde [57] and due to its simplicity, an approach easy to implement was chosen. More sophisticated approaches can be found in [58,59,60,61].

Cable–obstacle collisions: For a collision check between a cable and an obstacle according to Figure 4b, all $f=1,\dots ,6$ faces of a AABB are checked individually for a collision with every cable i. The vector ${\mathit{c}}_f$ points to the center of each face, which can be derived using the halfwidth extends ${\mathit{e}}_{\mathrm{f}}={\left[\begin{array}{ccc}{e}_{\mathrm{f}x}& e_{\mathrm{f}y}& e_{\mathrm{f}z}\end{array}\right]}^{\mathrm{T}}$ of the AABB. Analogous to the procedure for a collision of type $\chi =\mathrm{CaCa}$, each face of the AABB is defined as a plane in its normal form ${\left({\mathit{x}}_i-{\mathit{c}}_f\right)}^{\mathrm{T}}{\mathit{n}}_f=0$. The cable under consideration $S_i$ is again expressed by its vector ${\mathit{l}}_i$. With these two definitions, each point of intersection

$${\mathit{d}}_{i,f}={\mathit{r}}_{\mathrm{R}i}+s_{i,f}{\mathit{l}}_i,\mathrm{with}{s}_{i,f}=\frac{{\left({\mathit{c}}_f-{\mathit{r}}_{\mathrm{R}i}\right)}^{\mathrm{T}}{\mathit{n}}_f}{{\mathit{l}}_i^{\mathrm{T}}{\mathit{n}}_f},f=1,\dots ,6,i=1,\dots ,n_{\mathrm{c}}$$

(42)

is calculated for all $n_{\mathrm{c}}$ cables. From the center of each face, the vector

$${\mathit{q}}_{i,f}=\left[\begin{array}{c}{q}_{i,f,x}\\ q_{i,f,y}\\ q_{i,f,z}\end{array}\right]=\left({\mathit{d}}_{i,f}-{\mathit{c}}_{\mathrm{f}}\right)$$

(43)

points to the point of intersection of the considered cable and face. Provided that the conditions

$$\begin{array}{cc}\hfill C_1& :\left(\left(|q_{i,f,x}|\le e_{\mathrm{f}x}\right)\wedge \left(|q_{i,f,y}|\le e_{\mathrm{f}y}\right)\wedge \left(|q_{i,f,z}|\le e_{\mathrm{f}z}\right)\right),\hfill \end{array}$$

(44a)

$$\begin{array}{cc}\hfill C_2& :{∥{\mathit{d}}_{i,f}-{\mathit{r}}_{\mathrm{R}i}∥}_2\le l_0\hfill \end{array}$$

(44b)

are both satisfied, there is a collision and the procedure is terminated with the penalty term ${\mathcal{P}}_{\mathrm{CaOb}}$ for the considered cable. In contrast to the cable–cable collision, for the cable–obstacle collision a cost function is defined. For this purpose, for each cable $i=1,\dots ,n_{\mathrm{c}}$ the closest distance to one of the surfaces of all objects $j=1,\dots ,n_{\mathrm{o}}$ is defined by

$$d_{ij}=\underset{\forall f}{min}\left({∥{\mathit{d}}_{i,j,f}-{\mathit{c}}_{i,j,f}∥}_2\right)$$

(45)

This leads to the total cable–obstacle collision costs for one time step

$${\mathcal{V}}_{\mathrm{CaOb}}=\frac{1}{n_{\mathrm{c}}{n}_{\mathrm{s}}{n}_{\mathrm{o}}}\left(\sum _{i=1}^{n_{\mathrm{c}}}\sum _{j=1}^{n_{\mathrm{o}}}\sum _{k=1}^{n_{\mathrm{s}}}1-\frac{d_{ij}\left(k\right)}{d_{\min }}\right).$$

(46)

Here, analogous to Equation (34), the value of $d_{\min }$ specifies a boundary above which the costs are zero.

4. Discussion of the Optimization Results

The following scenarios under consideration deal with the automatic construction of a building consisting of 1720 calcium silicate units. These mainly include calcium silicate masonry units of the type 6DF [62,63], as well as flat lintels and masonry units to compensate height differences. Note that, for all units, the optimization has ended penalty-free for both systems, i.e., all undesired events could be avoided and all final optimization runs terminated with valid trajectories.

In the first scenario, a drone system with three quadrocopters as shown in Figure 1b is used to transport the payload past some already erected buildings to the actual construction site. In this case, the optimizer is forced to plan a path which avoids collisions. The scenario is used to verify the functioning of the implemented algorithms. The drone system used in this first scenario has the parameters listed in

Table 2. Drone system parameters.

Parameter	Value
Number and type of drones	$n_{\mathrm{D}}=3$ quadrocopters
Platform mass	$m_{\mathrm{P}}=20\mathrm{kg}$
Drone mass	$m_{\mathrm{D}}=14.26\mathrm{kg}$
Masonry unit mass	$m_{\mathrm{B}}=10.7\mathrm{kg}$–$53.7\mathrm{kg}$
Length of the i-th cable	$l_{0,i}=5.7\mathrm{m}$
Vector from the drone’s center of gravity to the attachment point of the cable	${\mathit{b}}_{\mathrm{R}i}={\left[\begin{array}{ccc}0\mathrm{m}& 0\mathrm{m}& -0.04\mathrm{m}\end{array}\right]}^{\mathrm{T}}$
Tensor of inertia of the drone	${\mathrm{\Theta }}_{\mathrm{D}}\approx \mathrm{diag}\left(0.33{\mathrm{kgm}}^2,0.33{\mathrm{kgm}}^2,0.78{\mathrm{kgm}}^2\right)$
Tensor of inertia of the platform	${\mathrm{\Theta }}_{\mathrm{P}}\approx \mathrm{diag}\left(0.2{\mathrm{kgm}}^2,0.2{\mathrm{kgm}}^2,0.2{\mathrm{kgm}}^2\right)$
Thrust coefficient	$c_{\mathrm{T}}$ = 7.243 $·{10}^{-4}{\mathrm{Ns}}^2/{\mathrm{rad}}^2$
Drag coefficient	$c_{\mathrm{W}}=3.137·{10}^{-5}{\mathrm{Nms}}^2/{\mathrm{rad}}^2$
Rotor speed	${\omega }_{\mathrm{M}},\max =560\mathrm{rad}/\mathrm{s}$
Vector to the cable attachment points of the platform	$\begin{array}{c}{\mathit{p}}_{\mathrm{R}1}={\left[\begin{array}{ccc}0.34\mathrm{m}& -0.1525\mathrm{m}& 0.6\mathrm{m}\end{array}\right]}^{\mathrm{T}}\\ {\mathit{p}}_{\mathrm{R}2}={\left[\begin{array}{ccc}0\mathrm{m}& 0.305\mathrm{m}& 0.6\mathrm{m}\end{array}\right]}^{\mathrm{T}}\\ {\mathit{p}}_{\mathrm{R}3}={\left[\begin{array}{ccc}-0.34\mathrm{m}& -0.1525\mathrm{m}& 0.6\mathrm{m}\end{array}\right]}^{\mathrm{T}}\end{array}$

. Notably, with the given drone system, the platform is kinematically underconstrained [34], which means that the system might oscillate in case of disturbances. Applicable control approaches are subject to future work, where e.g., flatness-based approaches are promising [64].

To identify and compare the advantages and disadvantages of each robotic system, the second scenario deals with the optimization of the entire construction process for all 1720 masonry units for this drone system and the cable robot presented in Figure 1a. For the optimization process, all trajectories are employed as given in Table 1. Note that the mass of the platform is subject to instantaneous changes after gripping the masonry unit between trajectories 3 and 4 and after placing the masonry unit between trajectories 10 and 11. This inevitably leads to discontinuities, e.g., in cable forces or propeller speeds. Such discontinuities might as well lead to theoretically infinite accelerations, e.g., at the motors of the drones. However, since the simulation framework is using an open loop physical model and calculates each trajectory independently, this does not lead to problems within the simulation. The effects of this short time period were assumed to be negligible in terms of energy consumption and overall construction time. Thus, a modeling of such effects was not included within this work. Future work includes the modeling of the contact forces when gripping or releasing a masonry unit.

The cable robot’s parameters are given in [48]. The most important ones are

$$\begin{array}{cc}\hfill [{}^{\mathcal{E}}{\mathit{p}}_{\mathrm{R}1}\cdots {}^{\mathcal{E}}{\mathit{p}}_{\mathrm{R}8}]& =\left[\begin{array}{cccccccc}0.51& -0.51& 0.51& -0.51& 0.51& -0.51& 0.51& -0.51\\ -0.0315& -0.0315& -0.445& -0.445& 0.0315& 0.0315& 0.445& 0.445\\ 0.714& 0.714& 0.324& 0.324& 0.714& 0.714& 0.324& 0.324\end{array}\right]\mathrm{m},\hfill \\ \hfill \left[\begin{array}{c}{}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}1}\cdots {}^{\mathcal{B}}{\mathit{r}}_{\mathrm{B}8}\end{array}\right]& =\left[\begin{array}{cccccccc}4.8& -4.8& 4.33& -4.33& 4.8& -4.8& 4.33& -4.33\\ -6.996& -6.996& -7.096& -7.096& 6.996& 6.996& 7.096& 7.096\\ 0.5& 0.5& 5.1875& 5.1875& 0.5& 0.5& 5.1875& 5.1875\end{array}\right]\mathrm{m},\hfill \\ \hfill {}^{\mathcal{B}}\mathit{b}{}_{\mathrm{SP}}& ={\left[\begin{array}{ccc}-0.0078& -0.0074& 0.4059\end{array}\right]}^{\mathrm{T}}\mathrm{m},\hfill \\ \hfill {}^{\mathcal{B}}\theta {}_{\mathrm{S}}& =\left[\begin{array}{ccc}11.0424& 0.3203& 0.4189\\ 0.3203& 10.8053& 0.3697\\ 0.4189& 0.3697& 9.8329\end{array}\right]\mathrm{kg}{\mathrm{m}}^2.\hfill \end{array}$$

(47)

The end effectors of both systems differ in their ability to rotate the masonry unit. In the case of the drone system, the rotation comes from the absolute positioning of the drones. In comparison, the end effector of the cable robot can actively rotate a masonry unit. For this reason, the end effector of the drone system can be built much lighter since the rotation unit, using a powerful electric motor, heavy bearings and an extra frame [9], is omitted. Moreover, the frame of the end effector for the drone can be built using more lightweight elements since the expected cable forces are lower in comparison to the CDPR and the cables are not tensed against each other. Additionally, five cable attachment points and five cable force sensors are not needed. Therefore, it is assumed that the weight $m_{\mathrm{EE}}=100\mathrm{kg}$ of the end effector of the cable robot can be reduced to $m_{\mathrm{EE}}=20\mathrm{kg}$ for the drone system.

Notably, in both scenarios, the 6th trajectory—which is basically the motion across the site—of the 1000th masonry unit is discussed in more detail with its starting position A and its target position B. Apart from the lateral movement from its starting position ${\mathit{r}}_{\mathrm{P}},\mathrm{A}$ to its target position ${\mathit{r}}_{\mathrm{P}},\mathrm{B}$, the masonry unit is additionally rotated by $\phi =-{90}^{\circ }$ around the $z_{\mathrm{P}}$-axis. Hereby, the target position and the rotation angle result from the masonry laying plan. Note that cable angles ${\alpha }_{\mathrm{S}},{\beta }_{\mathrm{S}}$ are used for evaluation. These angles are defined as the Cardan angles analog to Section 3.2, such that the initial unit cable vector ${\mathit{\upsilon }}_{\mathrm{R}0}={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{\mathrm{T}}$ is mapped to ${\mathit{\upsilon }}_{\mathrm{R}i}$.

First scenario: For the first scenario, the 6th trajectory starts at point A with ${\mathit{r}}_{\mathrm{P},\mathrm{A}}={\left[\begin{array}{ccc}30\mathrm{m}& -6\mathrm{m}& 2.45\mathrm{m}\end{array}\right]}^{\mathrm{T}}$ and ends at point B with ${\mathit{r}}_{\mathrm{P},\mathrm{B}}={\left[\begin{array}{ccc}2.8625\mathrm{m}& 3.9\mathrm{m}& 2.45\mathrm{m}\end{array}\right]}^{\mathrm{T}}$ passing two additional knots $S_1$ and $S_2$. These knots with their vectors ${\mathit{r}}_{\mathrm{P},\mathrm{S}1}$ and ${\mathit{r}}_{\mathrm{P},\mathrm{S}2}$ are optimized as well as the platform’s velocity and acceleration at these points. The relative position of the drones to each other is influenced by the definition of the vector ${\mathit{\lambda }}_0$ in Equation (18). The choice

$${\mathit{\lambda }}_0=\left[\begin{array}{c}{\mathit{\lambda }}_{0,1}\\ {\mathit{\lambda }}_{0,2}\\ {\mathit{\lambda }}_{0,3}\end{array}\right]{\lambda }_{\mathrm{S}},{\mathit{\lambda }}_{0,1}=\left[\begin{array}{c}sin\left({60}^{\circ }\right)\\ -cos\left({60}^{\circ }\right)\\ 1\end{array}\right],{\mathit{\lambda }}_{0,2}=\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right],{\mathit{\lambda }}_{0,3}=\left[\begin{array}{c}-sin\left({60}^{\circ }\right)\\ -cos\left({60}^{\circ }\right)\\ 1\end{array}\right].$$

(48)

results in solutions where the drones are as close as possible to an angle of ${120}^{\circ }$ around the $z_{\mathrm{P}}$-axis to each other. The scalar value ${\lambda }_{\mathrm{S}}\in \mathbb{R}$ can be used to adjust the spreading between the drones, since the force ${\mathit{f}}_{\mathrm{R}}$ calculated with Equation (18) is the one that has the smallest distance to ${\mathit{\lambda }}_0$ with respect to Euclidean norm. Therefore, an increasing value ${\lambda }_{\mathrm{S}}$ results in a greater distance between the drones.

The optimization is done using the introduced Particle Swarm Optimizer of MATLAB^® with its default settings [65] and the parameters of the cost functions as shown in

Table 3. Optimization parameters for the drone system.

Cost Function	Cost	Weight	Penalty	Limits
Time	1	$1\frac{1}{\mathrm{s}}$	-	-
Propeller speed	1	21,952	10,000	$5\dots 560\mathrm{rad}/\mathrm{s}$
DD	1	1	$1·{10}^5$	$d_{\min }=1\mathrm{m}$
ObEE	1	1	1000	$d_{\min }=0.1\mathrm{m}$
ObD	1	0	$1·{10}^6$	$d_{\min }=0.1\mathrm{m}$
CaCa	1	0	$1·{10}^6$	$d_{\min }=0.1\mathrm{m}$
CaOb	1	1	$1·{10}^6$	$d_{\min }=0.1\mathrm{m}$
Position end effector	1	0	1000	$r_{\mathrm{P}},\mathrm{z}=0\dots 4.5\mathrm{m}$
Velocity end effector	1	0	1000	$|v_{\max }|=3\frac{\mathrm{m}}{\mathrm{s}}$
Acceleration end effector	1	0	1000	$|a_{\max }|=5\frac{\mathrm{m}}{{\mathrm{s}}^2}$

.

Note that the comparatively high value of ${\mathcal{W}}_{\omega }$ results from the power of three in Equation (24) and the need for small drone angles ${\alpha }_{\mathrm{D}}$ and ${\beta }_{\mathrm{D}}$ to meet the assumption ${\mathit{r}}_{\mathrm{B}i}^{\left(n\right)}\approx {\mathit{r}}_{\mathrm{D}i}^{\left(n\right)}$. Figure 5 shows the optimization result for trajectories 4 to 10.

As desired, the optimized trajectories avoid all obstacles.

For the 6th trajectory, the transition time is reduced by the optimizer from initially $t_{\mathrm{t}}=50\mathrm{s}$ to $t_{\mathrm{t}}\approx 27.02\mathrm{s}$. The platform is with ${\widehat{\mathit{r}}}_{\mathrm{P},\mathrm{A}}^{\left(i\right)}={\widehat{\mathit{r}}}_{\mathrm{P},\mathrm{B}}^{\left(i\right)}=\mathbf{0}$ in perfect rest at the start and target position. The optimizer changed the initial position, velocity and acceleration vectors of the platform at the additional knot S1 and S2 to the vectors given in

Table 4. Optimizationresult for the 1000th masonry unit for scenario 1 at the knots S1 and S2 of trajectory 6.

Knot	Position	Velocity	Acceleration
Knot S1 at $t_{\mathrm{S}1}\approx 10.81\mathrm{s}$	${\mathit{r}}_{\mathrm{P},\mathrm{S}1}\approx \left[\begin{array}{c}16.32\\ 2.08\\ 2.45\end{array}\right]\mathrm{m}$	${\dot{\mathit{r}}}_{\mathrm{P},\mathrm{S}1}\approx \left[\begin{array}{c}-0.96\\ 0.16\\ -0.08\end{array}\right]\frac{\mathrm{m}}{\mathrm{s}}$	${\ddot{\mathit{r}}}_{\mathrm{P},\mathrm{S}1}\approx \left[\begin{array}{c}0.861\\ -0.10\\ 0.10\end{array}\right]\frac{\mathrm{m}}{{\mathrm{s}}^2}$
Knot S2 at $t_{\mathrm{S}2}\approx 16.21\mathrm{s}$	${\mathit{r}}_{\mathrm{P},\mathrm{S}2}\approx \left[\begin{array}{c}11.57\\ 2.82\\ 2.33\end{array}\right]\mathrm{m}$	${\dot{\mathit{r}}}_{\mathrm{P},\mathrm{S}2}\approx \left[\begin{array}{c}-1.26\\ 0.17\\ 0.03\end{array}\right]\frac{\mathrm{m}}{\mathrm{s}}$	${\ddot{\mathit{r}}}_{\mathrm{P},\mathrm{S}2}\approx \left[\begin{array}{c}-0.03\\ -0.01\\ 0.00\end{array}\right]\frac{\mathrm{m}}{{\mathrm{s}}^2}$

. To obtain a better impression of the actual platform and drone speeds, the calculated position of the drone’s cable attachment points are additionally highlighted at constant time intervals. For the rotation of the masonry unit, the whole end effector has to be rotated. Therefore, the drones must change their absolute position to each other in a coordinated manner.

This fact can be seen in Figure 5 by the intersections of their flight paths. Moreover, the relative alignment of the drones at approximately ${120}^{\circ }$ is clearly visible. After the optimization, the spreading factor has the value ${\lambda }_{\mathrm{S}}\approx 33.06$. This value is mainly affected by two cost functions. The costs of the rotor speeds ${\mathcal{V}}_{\omega }$ are increasing as ${\lambda }_{\mathrm{S}}$ becomes larger and, thus, the optimizer tries to achieve the smallest possible ${\lambda }_{\mathrm{S}}$. The cost function ${\mathcal{V}}_{\mathrm{DD}}$ has the opposite effect and increases when ${\lambda }_{\mathrm{S}}$ decreases, as the AABBs get closer. Thus, ${\lambda }_{\mathrm{S}}$ can be influenced by the weights of ${\mathcal{W}}_{\omega }$ and ${\mathcal{W}}_{\mathrm{DD}}$.

The associated cable and drone angles are shown in Figure 6a–c.

As an example, the curves for the drone D2 are considered in more detail at the start and target position. From Equation (48), it follows that at the starting point, the cable vector of this drone lies within a plane parallel to the $yz$-plane of the inertial frame, pointing in positive y- and z-direction. This requires a single rotation around the x-axis of the inertial frame with ${\alpha }_{\mathrm{S}2}<0^{\circ }$ and ${\beta }_{\mathrm{S}2}=0^{\circ }$. To achieve a stable system behavior while hovering, the drone must be tilted less than the cable and, therefore, $|{\alpha }_{\mathrm{D}2}|<|{\alpha }_{\mathrm{S}2}|$ must hold. Both conditions are confirmed by the angles calculated by the optimizer. At the target position, the drone D2 is oriented in such way that the cable lies within a plane parallel to the $xz$-plane of the inertial frame, pointing in positive x- and z-direction. This requires a single rotation with ${\beta }_{\mathrm{S}2}>0^{\circ }$ and ${\alpha }_{\mathrm{S}2}=0^{\circ }$. Furthermore, $|{\beta }_{\mathrm{D}2}|<|{\beta }_{\mathrm{S}2}|$ must hold. These considerations are also confirmed by the results in Figure 6b. The same procedure can be used to check the other cable and drone angles at the start and target positions. During the trajectory, maximum angles of ${\alpha }_{\mathrm{S},\mathrm{D}},{\beta }_{\mathrm{S},\mathrm{D}}<{15}^{\circ }$ occur. The differences between the cable and drone angles are $\mathrm{\Delta }{\alpha }_{\mathrm{S},\mathrm{D}}=|{\alpha }_{\mathrm{S}}-{\alpha }_{\mathrm{D}}|<6^{\circ }$ and $\mathrm{\Delta }{\beta }_{\mathrm{S},\mathrm{D}}=|{\beta }_{\mathrm{S}}-{\beta }_{\mathrm{D}}|<6^{\circ }$. The results of the required rotor speeds are shown in the Figure 6d–f separately for each drone. It can be seen that, due to the arrangement of the cables at the end effector, all drones must carry the same load in stationary case. To reach ${\alpha }_{\mathrm{S}2}<0^{\circ }$ and $|{\alpha }_{\mathrm{D}2}|<|{\alpha }_{\mathrm{S}2}|$, the rotor speeds of drone D2 must satisfy the conditions ${\omega }_{\mathrm{M}1}={\omega }_{\mathrm{M}3}$ and ${\omega }_{\mathrm{M}2}>{\omega }_{\mathrm{M}4}$. This is the only possibility to generate a counter reaction torque to the constraint torque applied by the cable. For the given trajectory, only small differences in rotor speed of about $|{\omega }_p|\approx {\omega }_{\mathrm{M}0}\pm 15\mathrm{rad}/\mathrm{s}$ from the hovering speed are necessary. The hovering speed can be derived for the stationary case from Equation (16), which simplifies to

$${\omega }_{\mathrm{M}0}=\sqrt{\frac{\left(m_{\mathrm{D}}+\frac{m_{\mathrm{P}}}{3}\right)g}{4c_{\mathrm{T}}}}.$$

(49)

For the 1000th masonry unit the hovering speed is ${\omega }_{\mathrm{M}0}\approx 308.47\mathrm{rad}/\mathrm{s}$. The curves of both the cable and drone angles as well as the rotor speeds have the desired smooth curve. In total, the optimization result of scenario 1 shows that the path planning framework works as expected. This means that a penalty-free solution for a complex maneuver was found.

Second scenario: The second scenario is a comparison between the drone system already presented and a cable robot. The cable robot mainly consists of a base frame to which pulleys are attached. The cables enter the actual workspace via pulleys. The platform is moved by changing the length or tension, respectively, of each of the $n_{\mathrm{c}}$ cables in a coordinated manner [66]. For the drone system, the movement of the platform results from the movement of each individual drone for constant cable lengths. The masonry units are fed to the construction area via an automated mortar system. Since the mortar system is also responsible for applying the mortar in addition to feeding the masonry units, it is also used for the drone system. For a comparison of both robotic systems, the trajectories for all 1720 masonry units of the first floor are optimized and compared in terms of time required and energy used. Due to the natural boundaries drawn by the workspace of the cable robot frame, the danger of a personal injury is little. Since it can be assumed that there are no obstacles in the workspace other than the masonry units already placed, the masonry units are transferred from the start to the target position using straight trajectories. As this simplifies numerous operations, and to maintain comparability, this trajectory shape is also used for the drone system. Accordingly, for the cable robot, the only optimization parameter is the transition time, which is why a gradient-based optimization method is suitable. For this purpose, the optimizer fmincon of MATLAB^® is used with its default settings [67]. The parameters for the cost function are listed in

Table 5. Optimization parameters for the cable robot.

Costfunction	Cost	Weight	Penalty	Limits
Time	1	$1\frac{1}{\mathrm{s}}$	-	-
Cable force	1	0	10,000	$150\dots 4500\mathrm{N}$
Cable velocity limits	1	0	1000	$6\frac{\mathrm{m}}{\mathrm{s}}$
ObEE	1	0	1000	$d_{\min }=0.1\mathrm{m}$
CaCa	1	0	1000	-
CaEE	1	0	1000	$d_{\min }=0.1\mathrm{m}$
CaOb	1	0	1000	$d_{\min }=0.1\mathrm{m}$
Position end effector	1	0	1000	$r_{\mathrm{P},\mathrm{z}}=0\dots 4.5\mathrm{m}$
Velocity end effector	1	0	1000	$|v_{\max }|=3\frac{\mathrm{m}}{\mathrm{s}}$
Acceleration end effector	1	0	1000	$|a_{\max }|=5\frac{\mathrm{m}}{{\mathrm{s}}^2}$
Motor torque	1	0	1000	${\tau }_{\mathrm{t}}=-10\dots 110\mathrm{Nm}$
Power	1	0	1000	$P_{\max }=\mathrm{32,000}\mathrm{W}$

.

Although a lower cable force limit of $150\mathrm{N}$ seems to be excessive, it is well chosen from practical experience (and thus also include a practically identified safety margin for control purposes). The drone system has the same characteristic as in the first scenario. In addition to the actual transition time $t_{\mathrm{t}}$, the spreading factor ${\lambda }_{\mathrm{S}}$ is also optimized. In this case, as in scenario 1, a particle swarm optimization is preferred. The parameters of the cost functions are the same as in Table 3, with the exception that ${\mathcal{W}}_{\chi }=0$ for $\chi =\in \left\{\mathrm{ObD},\mathrm{CaOb}\right\}$.

Figure 7 and Figure 8 show the optimization results for trajectories 4 to 10.

For both systems, the optimization results in the desired straight trajectories. Based on the AABBs for the end effector and the masonry unit, the result shows the different rotation methods for the masonry unit around the platform’s $z_{\mathrm{P}}$-axis. For the cable robot, it can be seen that the end effector maintains its orientation throughout the transportation while the masonry unit rotates. For the drone system, however, the rotation of the masonry unit is the same as that of the end effector to which the masonry unit is attached. For both systems, the expected change in the size of the AABBs can be seen during the rotation. Furthermore it is obvious that the cables of the cable robot are blocking relevant volumes within workspace during the motion. This increases the risk of cable collisions, to be avoided by the optimizer. For the scenario at hand, the lower pulleys have already reached a certain height. Note that the pulleys are lifted with a rising building between two masonry units of different layers. Moreover, the transfer position of the mortar system is lifted accordingly. In contrast, the cables of the drone system are always above the end effector. Hence, cable collisions with an obstacle are almost impossible if a certain laying plan is maintained.

The resulting cable forces are presented for the cable robot in Figure 9. Analogously, the rotor speeds for the drone system are shown in Figure 10d–f.

For the cable robot, the highest calculated cable forces are below $f_{\mathrm{R},\max }$. This means that the optimizer was not able to accelerate the trajectory any further due to the defined penalties, although the cable robot still has cable force reserves. For both systems, the curves show a smooth course, with the exception of the transition during gripping or placing the masonry unit. The force of gravity of the platform varies in dependence of the actual masonry unit mass. For the cable robot this varies between $F_{\mathrm{G},\mathrm{P}}=1050\mathrm{N}$ and $F_{\mathrm{G},\mathrm{P}}=1508\mathrm{N}$ and for the drone system between $F_{\mathrm{G},\mathrm{D}}=301\mathrm{N}$ and $F_{\mathrm{G},\mathrm{D}}=723\mathrm{N}$. Due to the movement of the drones along with the platform, the cable forces are only slightly more than one-third of $F_{\mathrm{G},\mathrm{D}}$ each. In the case of the cable robot, the cables often have a unsuitable flat angle at the platform due to the cable pulleys fixed at the frame. As a result, the net cable forces of the cable robot to carry the platform tend to be in the lower kN range and are thus many times larger than the cable forces of the drone system. Another reason for the high cable forces is that the lower cables additionally pull the platform downwards. Therefore, it follows that the cables of the drone system are subjected to much less stress. On the other hand, however, each drone of the drone system has to carry its own weight on top of the platform’s weight. Depending on the platform’s mass, this results in the hovering speeds $|{\omega }_{\mathrm{M}0}|\approx 308.18\dots 362.59\mathrm{rad}/\mathrm{s}$ which are, compared to the theoretical speed for applying the force of gravity, slightly increased. The deviation depends on the spreading factor ${\lambda }_{\mathrm{S}}$. Using the lift coefficient, the theoretically required force per drone of $F_{\mathrm{A}}\approx 275.16\mathrm{N}$ to $F_{\mathrm{A}}\approx 380.90\mathrm{N}$ can be calculated. The significantly better ratio of the force needed to carry the platform is solely due to the cable angles at the platform.

Despite the significantly larger necessary cable forces, the cable robot is more efficient due to its drive concept. With the given quantities of the cable robot, the resulting force per watt of applied power can be calculated for the stationary case. Using Equations (26)–(29) leads to the relation

$${\eta }_{\mathrm{cable}}=\frac{\left[N\right]}{\left[W\right]}=\frac{2{\left(i_{\mathrm{G}}{\eta }_{\mathrm{G}}{k}_{\mathrm{t}}\right)}^2{\eta }_{\mathrm{ESC}}}{3r_{\mathrm{W}}^2{R}_{\mathrm{P}}{f}_{\mathrm{R}}}\approx \frac{2{\left(10·0,8941·1.4\right)}^2·0.95}{3·0.{135}^2·0.12f_{\mathrm{R}}}=\frac{45374.5}{f_{\mathrm{R}}}.$$

(50)

From the manufacturer’s data sheet for the drive unit of the drone system the same relationship can be derived with

$${\eta }_{\mathrm{drone}}=\frac{\left[N\right]}{\left[W\right]}=\frac{4\sqrt{c_{\mathrm{T}}^3}}{2c_{\mathrm{W}}\sqrt{F_{\mathrm{A}}}}\approx \frac{1.243}{\sqrt{F_{\mathrm{A}}}}.$$

(51)

Common to both systems is that the ratio decreases with an increasing force. A comparison of the ratios ${\eta }_{\mathrm{cable}}$ and ${\eta }_{\mathrm{drone}}$ is done for the initial position of the 1000th masonry unit, which can be seen in Figure 9 and Figure 10. For the cable force $f_{\mathrm{R}1}=1586\mathrm{N}$, one can calculate ${\eta }_{\mathrm{cable}}=28.61\mathrm{N}/\mathrm{W}$, which is over 329 times more effective than the ratio of ${\eta }_{\mathrm{drone}}=0.087\mathrm{N}/\mathrm{W}$ for the total thrust of $F_{\mathrm{A}}=205\mathrm{N}$ of the drone D2. Another advantage of the cable robot is its ability to recuperate energy when lowering or decelerating the masonry unit. Recuperation of stored kinetic or potential energy is currently not realistic in the case of the drone system.

Integral comparison and conclusion: From the optimization results, it follows that the overall construction time for all 1720 masonry units is $t_{\mathrm{C}}=58.85\mathrm{h}$ for the cable robot and $t_{\mathrm{D}}=83.09\mathrm{h}$ in the case of the drone system. Hence, the drone system requires approximately $\mathrm{\Delta }t=24.4\mathrm{h}$ more time, which corresponds to a value of over $41\%$. With a total of $25.48\mathrm{h}$, a lot of time is needed for the measurement processes during trajectories 1 and 8. Therefore, the actual time for moving the platform from A to B is comparatively small compared to the waiting and measurement time. Especially for the drone system, this has a very negative effect due to the high energy demand. The drone system with $E_{\mathrm{D}}=602.15\mathrm{kWh}$ requires more than 44 times as much energy as the cable robot with $E_{\mathrm{C}}=13.68\mathrm{kWh}$. This fact is mainly due to the bad ratio of applied power to the resulting lift force. In practice, this results in 186 battery changes for each drone during construction. Assuming that two minutes are needed to change the batteries of all three drones, this task would add another $t_{\mathrm{B}}=6.2\mathrm{h}$ to the construction time. Looking at the recuperated energy of the cable robot, the amount of energy over all masonry units is $E_{\mathrm{rec}}=7.94\mathrm{kWh}$, which is about $36.72\%$. Accordingly, the recuperation capability contributes significantly to the low energy consumption of the cable robot.

Another disadvantage of the drone system is its significantly more complex positioning. While the positioning of the end effector in the case of the cable robot can be directly determined with a high accuracy via the cable lengths, complex methods must be applied to determine the position of the drone system. Conceivable options are, for instance, the usage of satellite navigation with the application of real-time kinematic positioning or an optical tracking system. In addition, the platform with only three cables is statically indeterminate in the case of the drone system, which is why it can always be stimulated to make undesired movements by disturbances such as wind. In contrast, the platform of the cable robot with eight cables is even statically overdetermined. The drone system, however, has its advantages when it comes to flexibility, beginning with its much faster setup time. Moreover the drone system has great advantages whenever spatially flexible transports over long distances are required, as in the application of scenario 1. Here, the cable robot is not an alternative. The same applies to very large buildings. Here, the frame of the cable robot, the mortar system and the pulleys would have to be constantly readjusted. Due to the limited workspace and the unsuitable cable angles, it is even important for the cable robot that the masonry is centered in the construction space of the cable robot (which might have a climbing frame to support e.g., high rise buildings). In conclusion, it can be said that both systems are suitable for transporting heavy loads, whereas the cable robot might as well transport masonry units significantly heavier than in this scenario. In conclusion, due to the discussed differences in their characteristics, their fields of application also differ widely. While the cable robot is predestined for the movement of very heavy loads within a defined and limited workspace with a very high accuracy and/or over a long time period, a drone system has its advantages above all when the transportation has to take place over longer distances for a limited period of time.

5. Conclusions and Outlook

This paper dealt with the investigation of two different robotic systems for automated masonry construction. The comparison is based on an object-oriented programmed framework for model-based dynamical path planning. The main advantage of the object-oriented approach is the easy adaption of the framework to different scenarios, new robots or cost functions that have to be taken into account. Overall, the software tool has proven to be an efficient tool for the investigation of robots which transport a common load using cables.

The optimization result greatly depends on the definition of the cost functions and penalty terms. While the penalty terms ensure that physical boundaries are met and collisions are avoided, the quality of a penalty-free trajectory is rated by the total scalar value of the cost function itself. For the consideration of the physical boundaries like cable forces, motor limits or energy consumption, the inverse model of each robotic system was derived in detail. Additionally, the modeling for cable–cable collisions as well as cable–obstacle collisions and robot–obstacle collisions were presented. The optimization of a first scenario demonstrated the full functionality of the optimizer for transporting a payload in a complex environment using a drone system.

In a second scenario, the construction of the first floor of a building was compared for both a cable robot as well as a drone system by optimizing the trajectories of all 1720 masonry units. The result shows, on the one hand, that both robotic systems are able to transport heavy loads, but on the other hand, that they have also great differences in their characteristics. The major differences are the energy consumption and the overall construction time. These lead to different fields of applications for the two systems.

In the future, the resulting optimization data for the drone system has to be validated using a dynamic physical simulation model, which contains less simplifications. This implies, for example, that the drones cable attachment points may not coincide with their center of gravity. Moreover, the acting Coriolis and centrifugal forces of rotating parts like the propellers should be considered. In case the deviations between the rotor speed determined by the optimizer and the resulting propeller speeds from the accurate simulation model are too big, the inverse model has to be investigated for the cause. In a further step, a prototype of the drone system has to be set up. In the case of the cable robot, the next step is to validate the calculated data on a full erected prototype. This includes mainly the cable forces and the energy consumption. To speed up the overall construction time, one future investigation will deal with the improvement of the positioning process of the end effector while gripping or placing the masonry units. This should be reached by optimizing the measurement routine of the laser sensors, in order to speed up the detection of the masonry unit’s pose, as well as the detection of the erected building structure.