Feasibility and Application of the B.E.A.T. Testbed for Assessing the Effects of Lower Limb Exoskeletons on Human Balance
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Apparatus
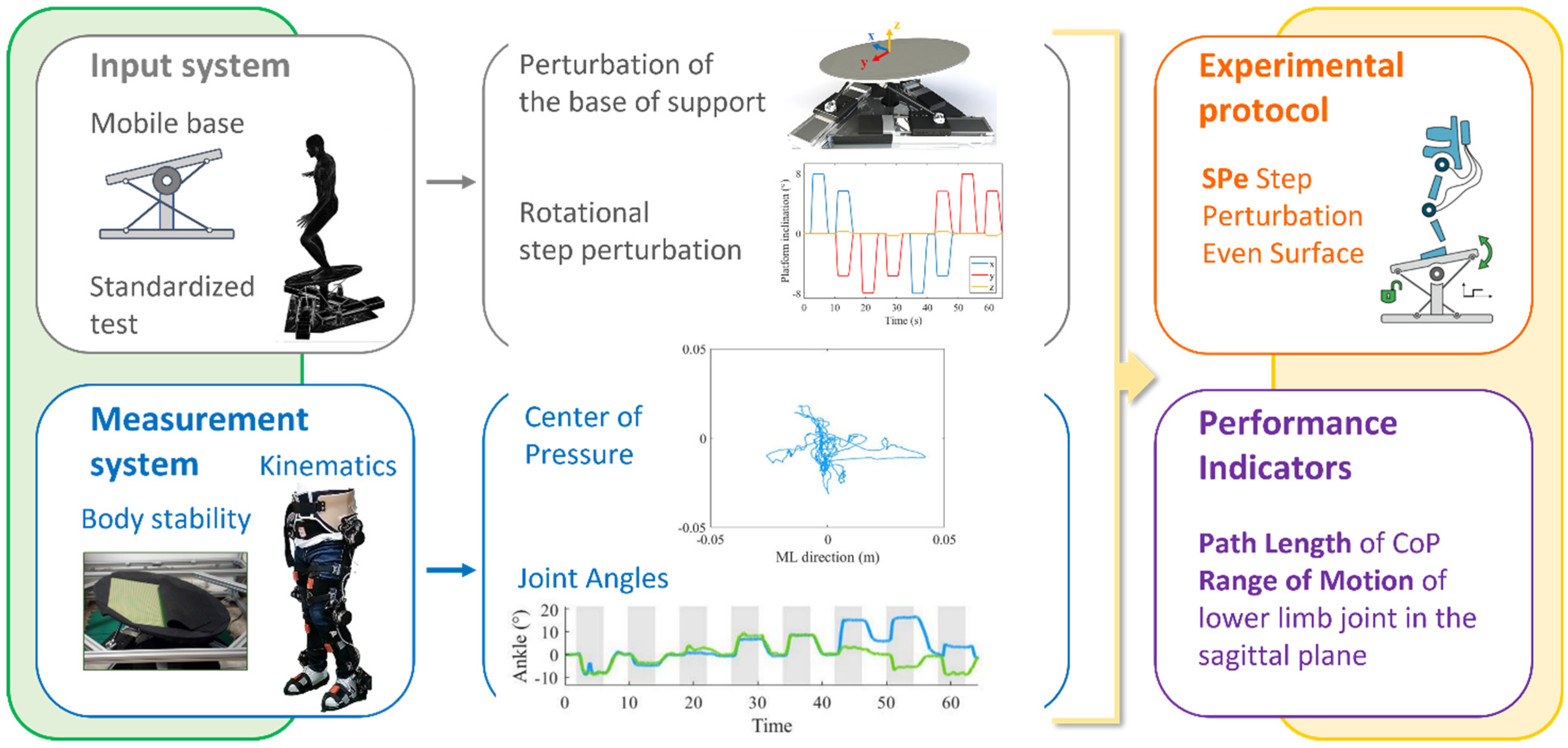
2.2.1. The B.E.A.T. System
2.2.2. The EXO-H2
2.2.3. Kinematic Measurement System
2.3. Experimental Protocol
2.4. Data Analysis
2.5. Statistical Analysis
3. Results
3.1. Feasibility of the Performance Indicators
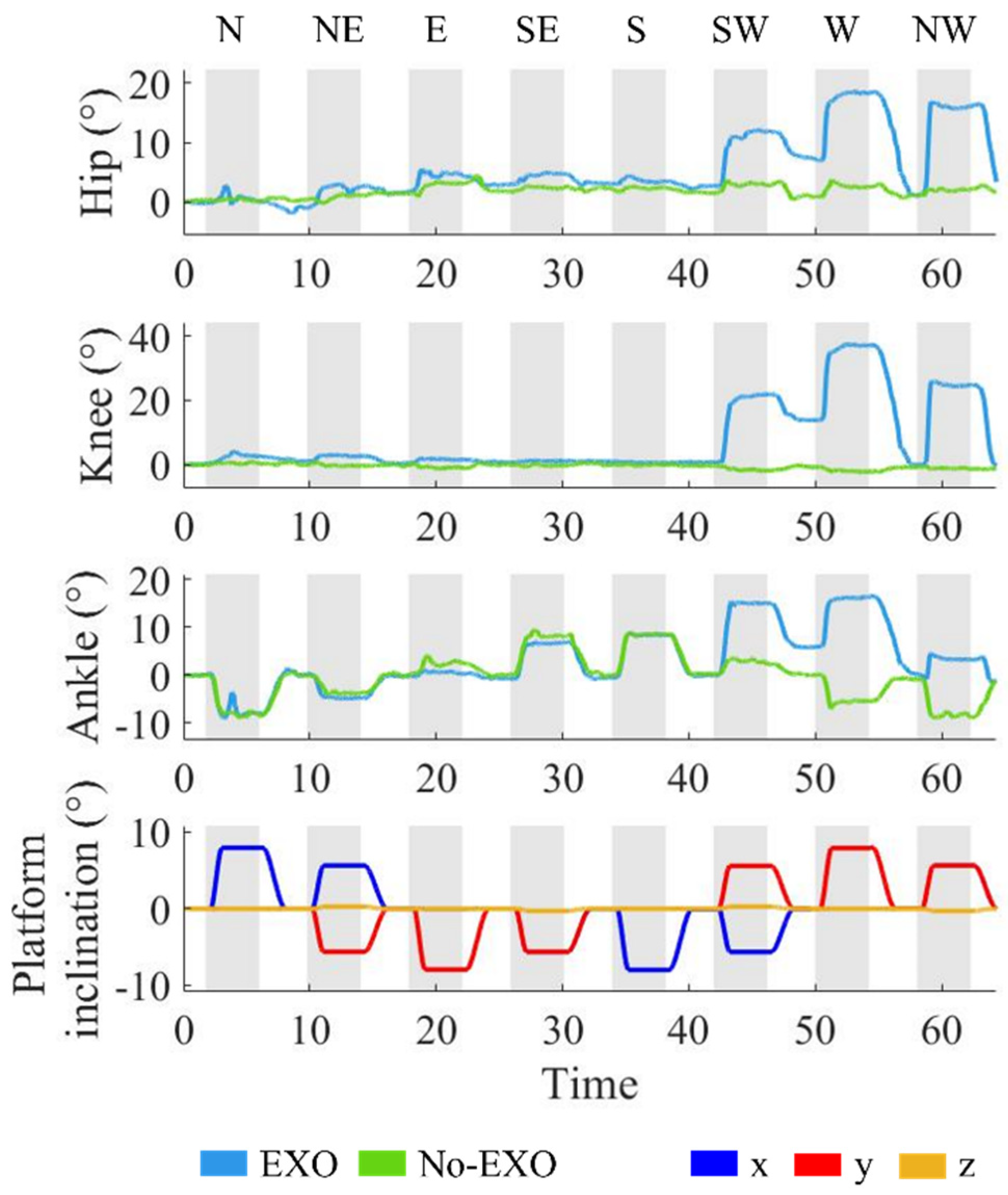
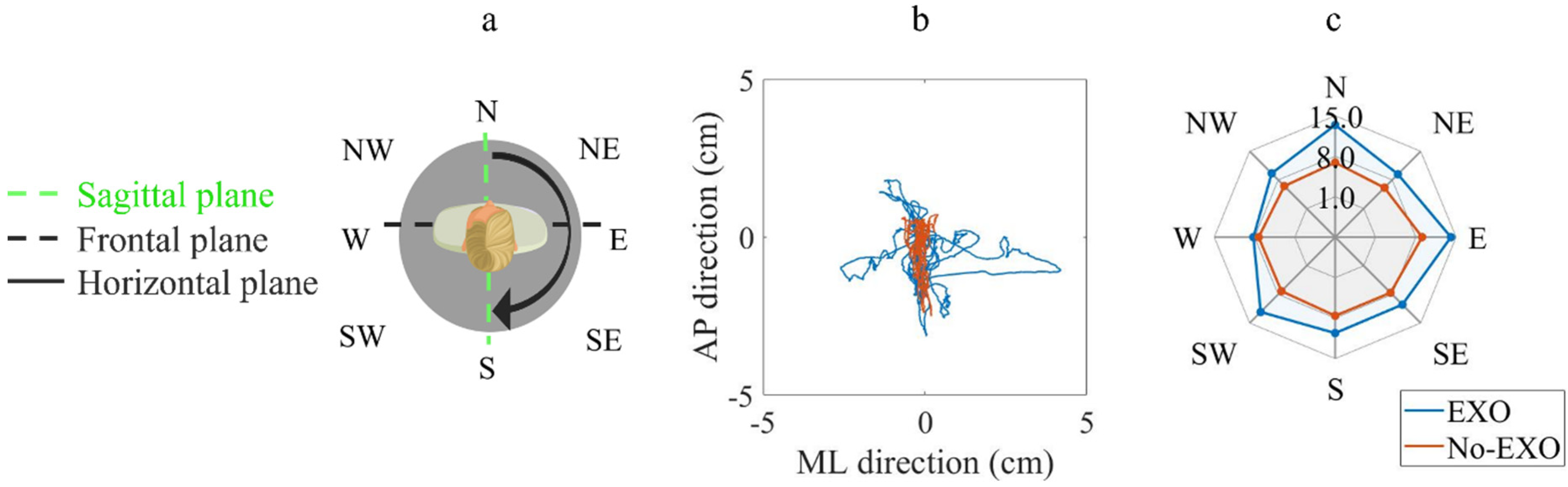
3.2. Case Study: Influence of Exoskeleton Mechanical Constraints on the Postural Strategies
4. Discussion
4.1. Feasibility of the Performance Indicators
4.2. Case study: Influence of Exoskeleton Mechanical Constraints on the Postural Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dollar, A.M.; Herr, H. Lower Extremity Exoskeletons and Active Orthoses: Challenges and State-of-the-Art. IEEE Trans. Robot. 2008, 24, 144–158. [Google Scholar] [CrossRef]
- Cardona, M.; Destarac, M.; Cena, C.G. Robotics for Rehabilitation: A State of the Art. In Exoskeleton Robots for Rehabilitation and Healthcare Devices; SpringerBriefs in Applied Sciences and Technology; Springer: Singapore, 2020; pp. 1–11. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, W.; Zhang, W.; Ding, X. A Review on Lower Limb Rehabilitation Exoskeleton Robots. Chin. J. Mech. Eng. 2019, 32, 1–11. [Google Scholar] [CrossRef]
- Gálvez-Zúñiga, M.A.; Aceves-López, A. A Review on Compliant Joint Mechanisms for Lower Limb Exoskeletons. J. Robot. 2016, 2016, 5751391. [Google Scholar] [CrossRef]
- Torricelli, D.; Rodriguez-Guerrero, C.; Veneman, J.F.; Crea, S.; Briem, K.; Lenggenhager, B.; Beckerle, P. Benchmarking Wearable Robots: Challenges and Recommendations from Functional, User Experience, and Methodological Perspectives. Front. Robot. AI 2020, 7, 561774. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, W.; Shi, D.; Ding, X. Design of hip joint assistant asymmetric parallel mechanism and optimization of singularity-free workspace. Mech. Mach. Theory 2018, 122, 389–403. [Google Scholar] [CrossRef]
- Olivier, J.; Ortlieb, A.; Bertusi, P.; Vouga, T.; Bouri, M.; Bleuler, H. Impact of ankle locking on gait implications for the design of hip and knee exoskeletons. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 618–622. [Google Scholar] [CrossRef]
- Stegall, P.; Winfree, K.; Zanotto, D.; Agrawal, S.K. Rehabilitation exoskeleton design: Exploring the effect of the anterior lunge degree of freedom. IEEE Trans. Robot. 2013, 29, 838–846. [Google Scholar] [CrossRef]
- Browning, R.C.; Modica, J.R.; Kram, R.; Goswami, A. The effects of adding mass to the legs on the energetics and biomechanics of walking. Med. Sci. Sports Exerc. 2007, 39, 515–525. [Google Scholar] [CrossRef]
- De Witt, J.K.; Hagan, R.D.; Cromwell, R.L. The effect of increasing inertia upon vertical ground reaction forces and temporal kinematics during locomotion. J. Exp. Biol. 2008, 211, 1087–1092. [Google Scholar] [CrossRef][Green Version]
- Pennycott, A.; Wyss, D.; Vallery, H.; Riener, R. Effects of added inertia and body weight support on lateral balance control during walking. IEEE Int. Conf. Rehabil. Robot. 2011, 2011, 5975415. [Google Scholar] [CrossRef]
- Noble, J.W.; Prentice, S.D. Adaptation to unilateral change in lower limb mechanical properties during human walking. Exp. Brain Res. 2005, 169, 482–495. [Google Scholar] [CrossRef]
- Zanotto, D.; Akiyama, Y.; Stegall, P.; Agrawal, S.K. Knee Joint Misalignment in Exoskeletons for the Lower Extremities: Effects on User’s Gait. IEEE Trans. Robot. 2015, 31, 978–987. [Google Scholar] [CrossRef]
- Ringhof, S.; Patzer, I.; Beil, J.; Asfour, T.; Stein, T. Does a Passive Unilateral Lower Limb Exoskeleton Affect Human Static and Dynamic Balance Control? Front. Sports Act Living 2019, 1, 22. [Google Scholar] [CrossRef] [PubMed]
- Luger, T.; Seibt, R.; Cobb, T.J.; Rieger, M.A.; Steinhilber, B. Influence of a passive lower-limb exoskeleton during simulated industrial work tasks on physical load, upper body posture, postural control and discomfort. Appl. Ergon. 2019, 80, 152–160. [Google Scholar] [CrossRef]
- Bessler, J.; Schaake, L.; Bidard, C.; Buurke, J.H.; Lassen, A.E.B.; Nielsen, K.; Saenz, J.; Vicentini, F. COVR—Towards Simplified Evaluation and Validation of Collaborative Robotics Applications Across a Wide Range of Domains Based on Robot Safety Skills. Biosyst. Biorobotics 2018, 22, 123–126. [Google Scholar] [CrossRef]
- Torricelli, D.; Pons, J.L. EUROBENCH: Preparing Robots for the Real World. Biosyst. Biorobotics 2018, 22, 375–378. [Google Scholar] [CrossRef]
- COST ACTION CA16116 WEARABLE ROBOTS FOR AUGMENTATION, ASSISTANCE OR SUBSTITUTION OF HUMAN MOTOR FUNCTIONS | Jan F Veneman | 5 Updates | 1 Publications | Research Project. Available online: https://www.researchgate.net/project/COST-Action-CA16116-Wearable-Robots-for-Augmentation-Assistance-or-Substitution-of-Human-Motor-Functions (accessed on 12 October 2021).
- Zampogna, A.; Mileti, I.; Palermo, E.; Celletti, C.; Paoloni, M.; Manoni, A.; Mazzetta, I.; Costa, G.D.; Pérez-López, C.; Camerota, F.; et al. Fifteen Years of Wireless Sensors for Balance Assessment in Neurological Disorders. Sensors 2020, 20, 3247. [Google Scholar] [CrossRef] [PubMed]
- Ferber-Viart, C.; Ionescu, E.; Morlet, T.; Froehlich, P.; Dubreuil, C. Balance in healthy individuals assessed with Equitest: Maturation and normative data for children and young adults. Int. J. Pediatr. Otorhinolaryngol. 2007, 71, 1041–1046. [Google Scholar] [CrossRef] [PubMed]
- Broglio, S.P.; Sosnoff, J.J.; Rosengren, K.S.; McShane, K. A Comparison of Balance Performance: Computerized Dynamic Posturography and a Random Motion Platform. Arch. Phys. Med. Rehabil. 2009, 90, 145–150. [Google Scholar] [CrossRef]
- Ionescu, E.; Morlet, T.; Froehlich, P.; Ferber-Viart, C. Vestibular assessment with Balance Quest: Normative data for children and young adults. Int. J. Pediatr. Otorhinolaryngol. 2006, 70, 1457–1465. [Google Scholar] [CrossRef]
- Lees, A.; Vanrenterghem, J.; Barton, G.; Lake, M. Kinematic response characteristics of the CAREN moving platform system for use in posture and balance research. Med. Eng. Phys. 2007, 29, 629–635. [Google Scholar] [CrossRef]
- Taborri, J.; Salvatori, S.; Mariani, G.; Rossi, S.; Patane, F. BEAT: Balance Evaluation Automated Testbed for the standardization of balance assessment in human wearing exoskeleton. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 and IoT, MetroInd 4.0 and IoT 2020—Proceedings, Roma, Italy, 3–5 June 2020; pp. 526–531. [Google Scholar] [CrossRef]
- Patane, F.; Cappa, P. A 3-DOF parallel robot with spherical motion for the rehabilitation and evaluation of balance performance. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 19, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Taborri, J.; Mileti, I.; Del Prete, Z.; Rossi, S.; Palermo, E. Yaw Postural Perturbation Through Robotic Platform: Aging Effects on Muscle Synergies. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 916–921. [Google Scholar] [CrossRef]
- Mileti, I.; Taborri, J.; Rossi, S.; Del Prete, Z.; Paoloni, M.; Suppa, A.; Palermo, E. Measuring age-related differences in kinematic postural strategies under yaw perturbation. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bortole, M.; Venkatakrishnan, A.; Zhu, F.; Moreno, J.C.; Francisco, G.E.; Pons, J.L.; Contreras-Vidal, J.L. The H2 robotic exoskeleton for gait rehabilitation after stroke: Early findings from a clinical study. J. Neuroeng. Rehabil. 2015, 12, 54. [Google Scholar] [CrossRef] [PubMed]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Cappa, P.; Patanè, F.; Rossi, S.; Petrarca, M.; Castelli, E.; Berthoz, A. Effect of changing visual condition and frequency of horizontal oscillations on postural balance of standing healthy subjects. Gait Posture 2008, 28, 615–626. [Google Scholar] [CrossRef] [PubMed]
- Cicchetti, D.V. Guidelines, Criteria, and Rules of Thumb for Evaluating Normed and Standardized Assessment Instruments in Psychology. Psychol. Assess. 1994, 6, 284–290. [Google Scholar] [CrossRef]
- Zampogna, A.; Mileti, I.; Martelli, F.; Paoloni, M.; Del Prete, Z.; Palermo, E.; Suppa, A. Early balance impairment in Parkinson’s Disease: Evidence from Robot-assisted axial rotations. Clin. Neurophysiol. 2021, 132, 2422–2430. [Google Scholar] [CrossRef]
- Grassi, L.; Rossi, S.; Studer, V.; Vasco, G.; Motta, C.; Patanè, F.; Castelli, E.; Rossi, S.; Cappa, P. Quantification of postural stability in minimally disabled multiple sclerosis patients by means of dynamic posturography: An observational study. J. Neuroeng. Rehabil. 2017, 14, 4. [Google Scholar] [CrossRef]
- Blenkinsop, G.M.; Pain, M.T.G.; Hiley, M.J. Balance control strategies during perturbed and unperturbed balance in standing and handstand. R. Soc. Open Sci. 2017, 4, 161018. [Google Scholar] [CrossRef]
- Sung, P.S.; Schalk, B.; Camp, R.; Park, M.S. Gender difference of hip-ankle compensations following a novel trip perturbation in young adults. Clin. Biomech. 2020, 80, 105194. [Google Scholar] [CrossRef]
- Batcir, S.; Shani, G.; Shapiro, A.; Alexander, N.; Melzer, I. The kinematics and strategies of recovery steps during lateral losses of balance in standing at different perturbation magnitudes in older adults with varying history of falls. BMC Geriatr. 2020, 20, 249. [Google Scholar] [CrossRef]
- Chumacero-Polanco, E.; Yang, J. Validation of an ankle-hip model of balance on a balance board via kinematic frequency-content. Gait Posture 2020, 82, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Morasso, P. Centre of pressure versus centre of mass stabilization strategies: The tightrope balancing case. R. Soc. Open Sci. 2020, 7, 200111. [Google Scholar] [CrossRef] [PubMed]
- Fasola, J.; Vouga, T.; Baud, R.; Bleuler, H.; Bouri, M. Balance Control Strategies during Standing in a Locked-Ankle Passive Exoskeleton. IEEE Int. Conf. Rehabil. Robot. 2019, 2019, 593–598. [Google Scholar] [CrossRef]
- Tokur, D.; Grimmer, M.; Seyfarth, A. Review of balance recovery in response to external perturbations during daily activities. Hum. Mov. Sci. 2019, 69, 102546. [Google Scholar] [CrossRef] [PubMed]
- Paillard, T. Cross-Education Related to the Ipsilateral Limb Activity on Monopedal Postural Control of the Contralateral Limb: A Review. Front. Physiol. 2020, 11, 496. [Google Scholar] [CrossRef]
- Mandalidis, D.G.; Karagiannakis, D.N. A comprehensive method for assessing postural control during dynamic balance testing. MethodsX 2020, 7, 100964. [Google Scholar] [CrossRef]
- Keith, T.R.; Condon, T.A.; Phillips, A.; McKeon, P.O.; King, D.L. Postural control strategies are dependent on reach direction in the star excursion balance test. Int. J. Athl. Ther. Train. 2016, 21, 33–39. [Google Scholar] [CrossRef]
- O’Connor, S.M.; Kuo, A.D. Direction-dependent control of balance during walking and standing. J. Neurophysiol. 2009, 102, 1411–1419. [Google Scholar] [CrossRef]
- Shao, Y.; Zhang, W.; Su, Y.; Ding, X. Design and optimisation of load-adaptive actuator with variable stiffness for compact ankle exoskeleton. Mech. Mach. Theory 2021, 161, 104323. [Google Scholar] [CrossRef]


| N | NE | E | SE | S | SW | W | NW | |
|---|---|---|---|---|---|---|---|---|
| ROM of Joint Angles | ||||||||
| Left | ||||||||
| Hip | 0.91 | 0.95 | 0.96 | 0.96 | 0.97 | 0.97 | 0.98 | 0.78 |
| Knee | 0.93 | 0.97 | 0.98 | 0.95 | 0.94 | 0.99 | 0.99 | 0.86 |
| Ankle | 0.84 | 0.97 | 0.97 | 0.94 | 0.91 | 0.99 | 0.96 | 0.65 |
| Right | ||||||||
| Hip | 0.91 | 0.97 | 0.97 | 0.80 | 0.93 | 0.98 | 0.94 | 0.96 |
| Knee | 0.92 | 0.99 | 0.99 | 0.79 | 0.97 | 0.95 | 0.96 | 0.99 |
| Ankle | 0.86 | 0.95 | 0.98 | 0.81 | 0.93 | 0.93 | 0.95 | 0.94 |
| CoP | ||||||||
| PL | 0.69 | 0.93 | 0.95 | 0.94 | 0.89 | 0.96 | 0.95 | 0.94 |
| PLML | 0.75 | 0.94 | 0.94 | 0.94 | 0.92 | 0.96 | 0.95 | 0.95 |
| PLAP | 0.68 | 0.90 | 0.82 | 0.91 | 0.85 | 0.91 | 0.84 | 0.90 |
| N | NE | E | SE | S | SW | W | NW | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Joint Angle (°) | ||||||||||
| L | Hip | No-EXO | 1.8 ± 0.9 | 4.8 ± 4.2 * | 6.2 ± 4.8 ** | 4.5 ± 3.9 ** | 2.7 ± 2.2 | 5.1 ± 5.5 | 5.1 ± 6.6 | 3.2 ± 2.4 |
| EXO | 1.9 ± 1.0 | 10.3 ± 7.3 | 15.2 ± 6.0 | 12.1 ± 6.1 | 1.9 ± 0.8 | 2.3 ± 1.7 | 4.6 ± 2.5 | 4.8 ± 1.6 | ||
| Knee | No-EXO | 2.8 ± 3.7 | 7.0 ± 8.7 * | 9.5 ± 10.4 ** | 7.2 ± 8.8 ** | 2.8 ± 2.9 | 6.3 ± 10.9 | 6.7 ± 12.6 | 3.6 ± 4.1 | |
| EXO | 1.8 ± 1.1 | 16.2 ± 13.7 | 26.4 ± 10.6 | 23.1 ± 10.2 | 2.1 ± 1.4 | 2.3 ± 1.0 | 2.7 ± 1.4 | 2.9 ± 1.3 | ||
| Ankle | No-EXO | 8.6 ± 1.9 | 5.5 ± 1.9 | 5.9 ± 5.5 ** | 10.1 ± 4.9 ** | 9.8 ± 1.9 | 6.4 ± 5.2 | 5.0 ± 4.6 | 8.4 ± 0.6 | |
| EXO | 7.2 ± 2.2 | 6.8 ± 4.6 | 16.0 ± 4.0 | 18.3 ± 4.4 | 8.0 ± 2.2 | 3.1 ± 2.2 | 5.1 ± 1.7 | 7.5 ± 2.1 | ||
| R | Hip | No-EXO | 1.9 ± 1.2 | 4.4 ± 5.7 | 4.9 ± 6.2 | 4.2 ± 4.1 | 2.5 ± 1.3 | 7.4 ± 6.0 | 8.8 ± 7.0 | 10.8 ± 6.1 |
| EXO | 2.5 ± 2.7 | 3.4 ± 1.2 | 4.0 ± 1.8 | 2.8 ± 1.3 | 2.0 ± 1.8 | 11.6 ± 4.4 | 14.9 ± 5.2 | 12.5 ± 4.9 | ||
| Knee | No-EXO | 3.0 ± 4.0 | 6.5 ± 11.6 | 7.0 ± 11.7 | 4.9 ± 7.2 | 2.7 ± 1.6 | 10.4 ± 12.9 ** | 13.1 ± 14.3 ** | 10.8 ± 13.3 ** | |
| EXO | 3.0 ± 3.7 | 2.5 ± 1.6 | 2.1 ± 0.9 | 1.5 ± 0.4 | 2.7 ± 2.4 | 23.5 ± 10.0 | 30.4 ± 9.6 | 24.6 ± 10.2 | ||
| Ankle | No-EXO | 6.9 ± 2.8 | 6.3 ± 4.1 | 6.4 ± 6.1 | 8.9 ± 4.1 | 8.1 ± 2.7 | 7.9 ± 6.3** | 7.2 ± 4.1 ** | 7.7 ± 2.8 | |
| EXO | 7.6 ± 2.3 | 5.8 ± 1.7 | 3.3 ± 2.7 | 7.0 ± 2.3 | 9.9 ± 1.9 | 16.9 ± 5.9 | 14.7 ± 4.5 | 8.3 ± 2.7 | ||
| CoP (cm) | ||||||||||
| PL | No-EXO | 7.9 ± 3.5 | 7.7 ± 3.5 | 7.8 ± 2.3 ** | 7.2 ± 1.3 * | 6.9 ± 0.9 ** | 8.5 ± 2.0 | 8.4 ± 2.9 | 7.0 ± 2.1 * | |
| EXO | 7.0 ± 1.9 | 10.0 ± 2.6 | 13.2 ± 3.5 | 11.5 ± 3.4 | 9.1 ± 1.9 | 10.8 ± 2.6 | 10.2 ± 2.8 | 9.0 ± 1.6 | ||
| PLML | No-EXO | 4.8 ± 1.4 | 5.6 ± 2.2 | 6.2 ± 2.0 ** | 5.5 ± 1.2 * | 4.6 ± 0.5 * | 6.7 ± 2.2 | 7.0 ± 2.6 | 5.3 ± 1.6 * | |
| EXO | 4.7 ± 1.2 | 8.0 ± 2.0 | 11.1 ± 3.2 | 8.8 ± 2.8 | 6.1 ± 1.7 | 8.6 ± 2.7 | 8.5 ± 2.9 | 7.0 ± 1.9 | ||
| PLAP | No-EXO | 5.1 ± 3.1 | 4.2 ± 2.5 | 3.7 ± 1.2 * | 3.6 ± 0.8 * | 4.1 ± 0.9 * | 3.8 ± 1.0 * | 3.4 ± 1.1 | 3.5 ± 1.3 | |
| EXO | 4.1 ± 1.3 | 4.5 ± 1.2 | 5.0 ± 1.5 | 5.8 ± 1.5 | 5.3 ± 0.6 | 5.0 ± 0.8 | 4.0 ± 0.8 | 4.3 ± 0.9 | ||
| EXO | No-EXO | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | NE | E | SE | S | SW | W | NW | N | NE | E | SE | S | SW | W | NW | |
| N | ●● ●● | ●●● ●● | ●●● ●● | ● ●○ | ●●● ●● | ●●● ●● | ●● ●● | ▲ | ▲ | ▲ | ▲ ▲ | |||||
| NE | ●● ●● | ● ●● | ● | ● ● ● | ● ●●● | ● ●●● | ● ●● | ▲ ▲ | ||||||||
| E | ●●● ●● | ● ●● | ●● ●● | ●● ● ●● | ●●● ●●● | ●●● ●●● | ●●● ●● ●● | ▲ | ▲ | |||||||
| SE | ●●● ●● | ● | ●● ●● | ●●● ● ●● | ●●● ●●● | ●●● ●●● | ●●● ●● | ▲ | ▲ | ▲ △ | ▲ | ▲ ▲ | ||||
| S | ● ●○ | ●● ● ● | ●● ● ●● | ●●● ● ●● | ● ●●● ●● | ●● ●● | ●● | ▲ △ | ▲ | ▲ ▲△ | ||||||
| SW | ●●● ●● | ● ●●● | ●●● ●●● | ●●● ●●● | ● ●●● ●● | ●● ○ | ● ●○ | ▲ | ▲ | ▲ | ||||||
| W | ●●● ●● | ●● ●●● | ●●● ●●● | ●●● ●●● | ●● ●●○ | ●● | ● ● ●● | ▲ ▲ | ▲ ▲ | ▲ ▲ | ▲ ▲△ | ▲ ▲ ▲ | ||||
| NW | ●● ●● | ●● ●● | ●●● ●● ●● | ●●● ●● | ●● ○ | ●● ● | ● ● ●● | ▲ ▲ ▲ | ||||||||
| Legend | ROM | CoP | ||||
|---|---|---|---|---|---|---|
| Hip | Knee | Ankle | PL | PLML | PLAP | |
| Left | ▲● | ▲● | ▲● | ▲● | ▲● | △○ |
| Right | ▲● | ▲● | ▲● | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mileti, I.; Taborri, J.; Rodriguez-Cianca, D.; Torricelli, D.; Rossi, S.; Patanè, F. Feasibility and Application of the B.E.A.T. Testbed for Assessing the Effects of Lower Limb Exoskeletons on Human Balance. Robotics 2022, 11, 151. https://doi.org/10.3390/robotics11060151
Mileti I, Taborri J, Rodriguez-Cianca D, Torricelli D, Rossi S, Patanè F. Feasibility and Application of the B.E.A.T. Testbed for Assessing the Effects of Lower Limb Exoskeletons on Human Balance. Robotics. 2022; 11(6):151. https://doi.org/10.3390/robotics11060151
Chicago/Turabian StyleMileti, Ilaria, Juri Taborri, David Rodriguez-Cianca, Diego Torricelli, Stefano Rossi, and Fabrizio Patanè. 2022. "Feasibility and Application of the B.E.A.T. Testbed for Assessing the Effects of Lower Limb Exoskeletons on Human Balance" Robotics 11, no. 6: 151. https://doi.org/10.3390/robotics11060151
APA StyleMileti, I., Taborri, J., Rodriguez-Cianca, D., Torricelli, D., Rossi, S., & Patanè, F. (2022). Feasibility and Application of the B.E.A.T. Testbed for Assessing the Effects of Lower Limb Exoskeletons on Human Balance. Robotics, 11(6), 151. https://doi.org/10.3390/robotics11060151










