Planar Model for Vibration Analysis of Cable Rehabilitation Robots
Abstract
:1. Introduction
2. Mathematical Model for the Free Vibrations
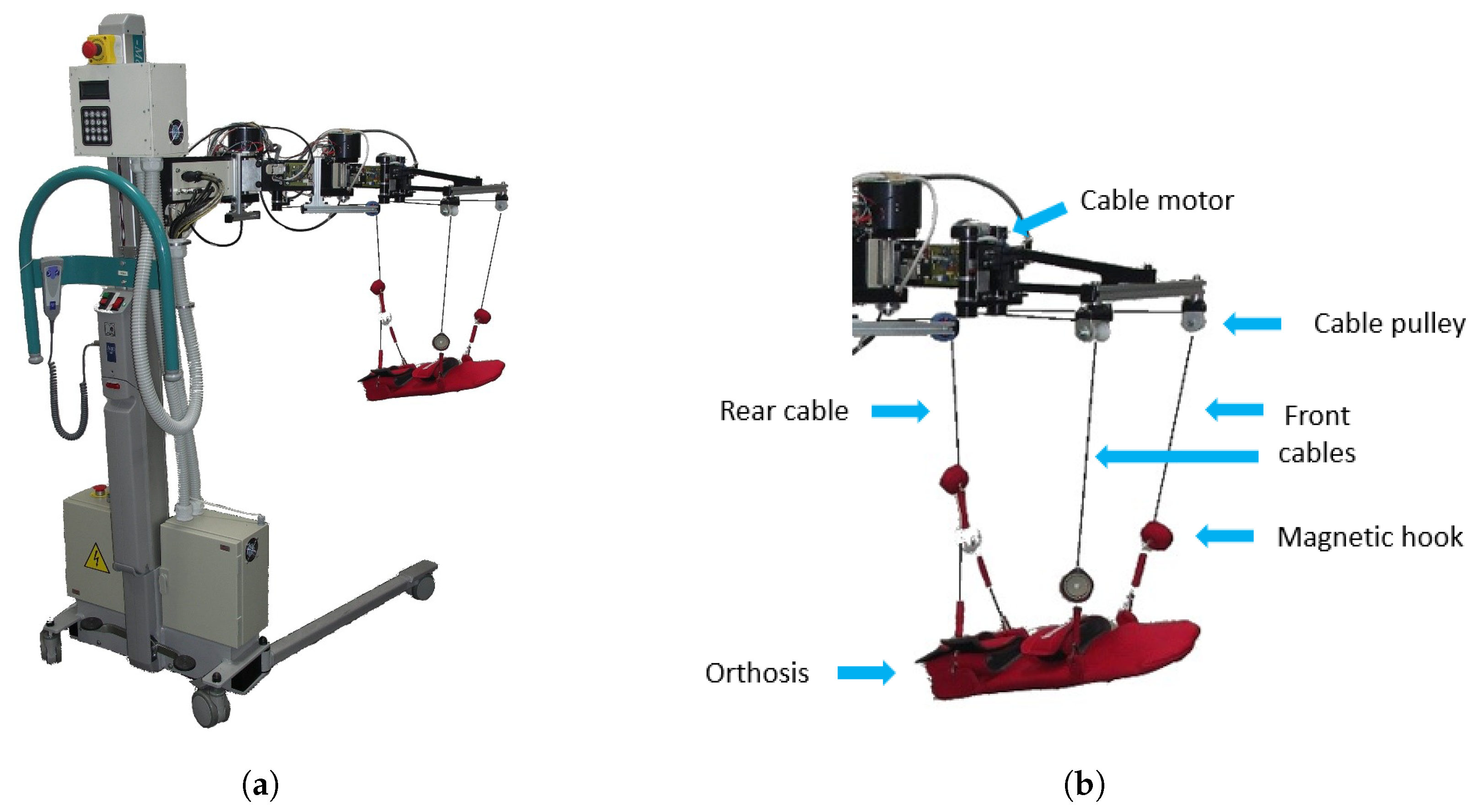
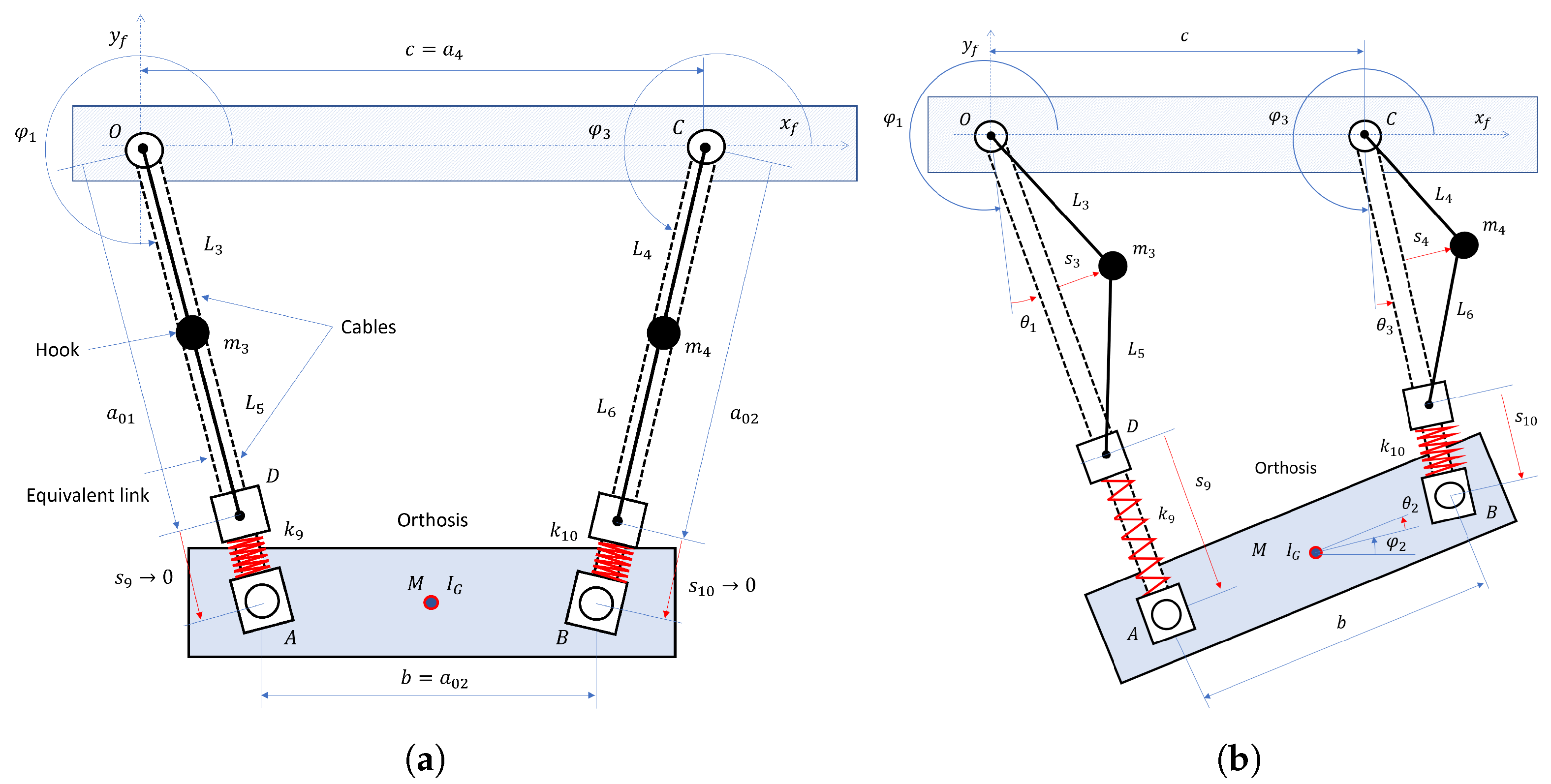
2.1. Planar Model
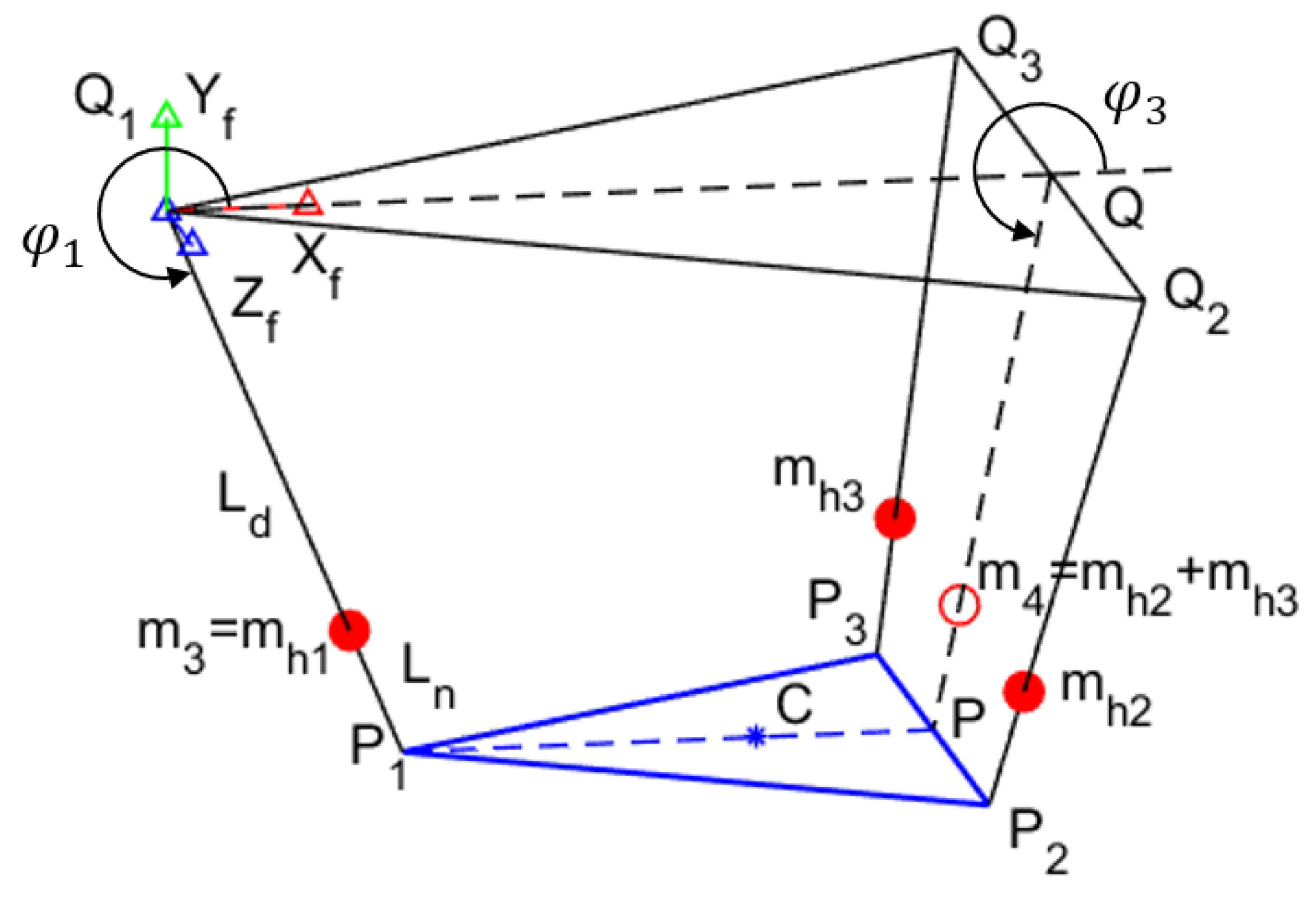
2.2. 3D Simplified Model
3. Numerical Results
3.1. Transverse Modes of Vibration
3.2. Longitudinal Modes of Vibration
3.3. Modes of Vibration of the 3D System
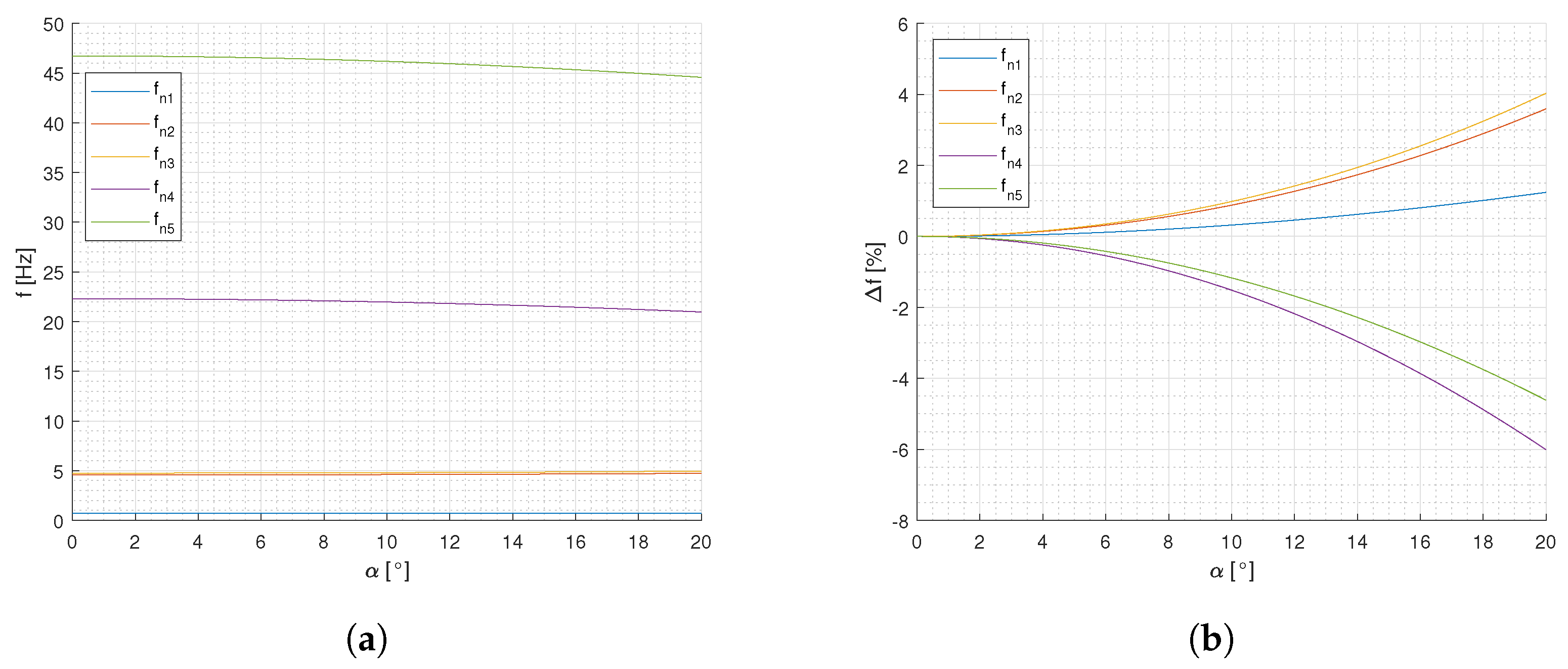
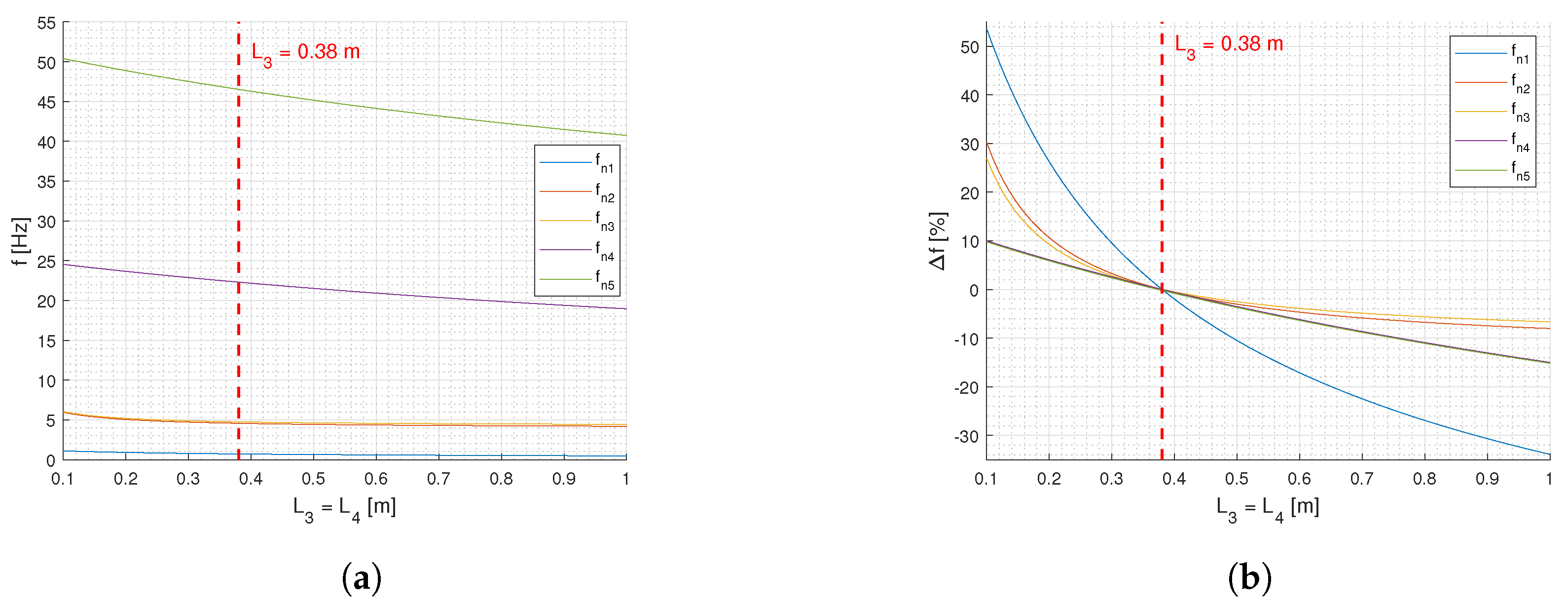
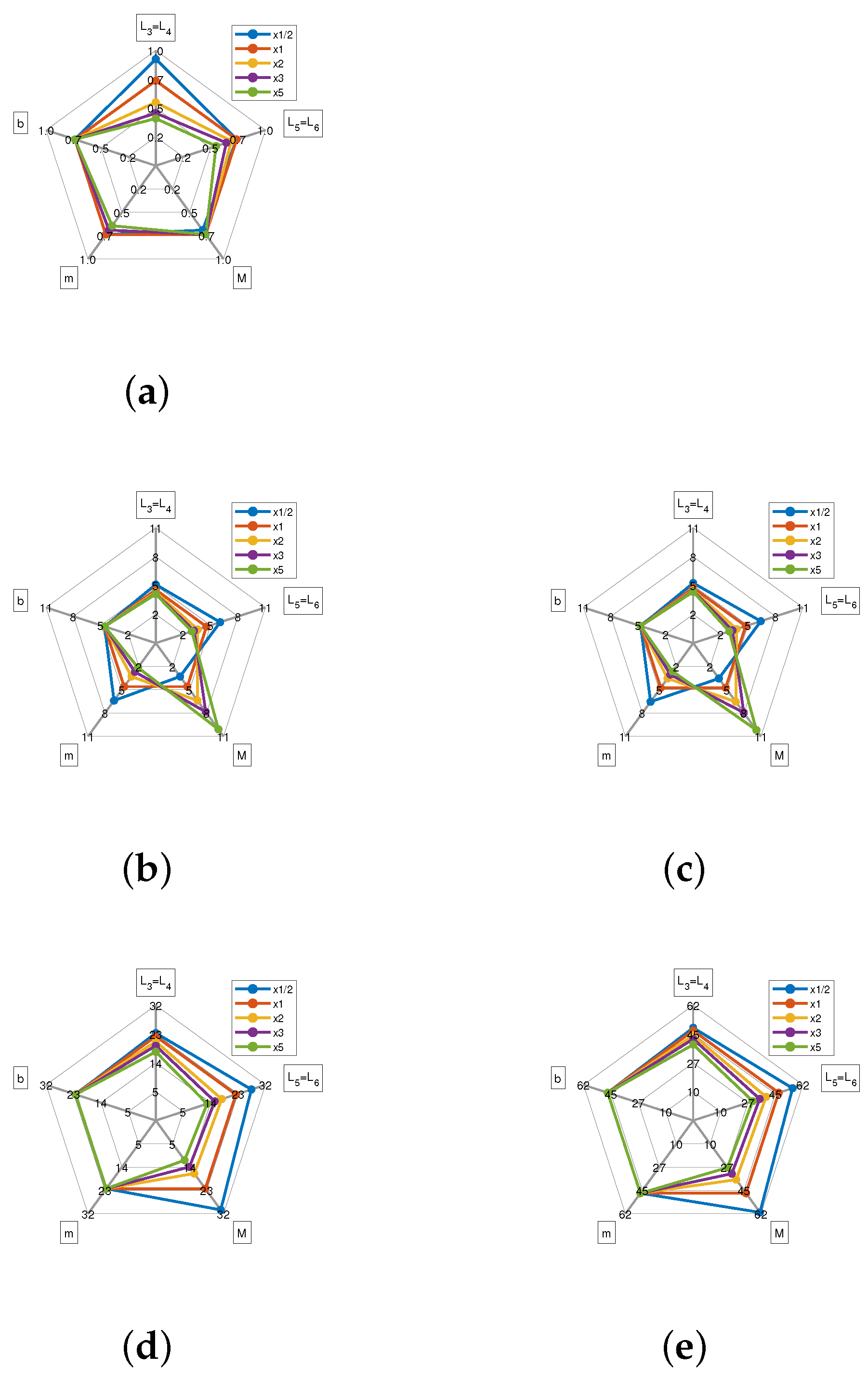
3.4. Influence of Parameters on Natural Frequencies
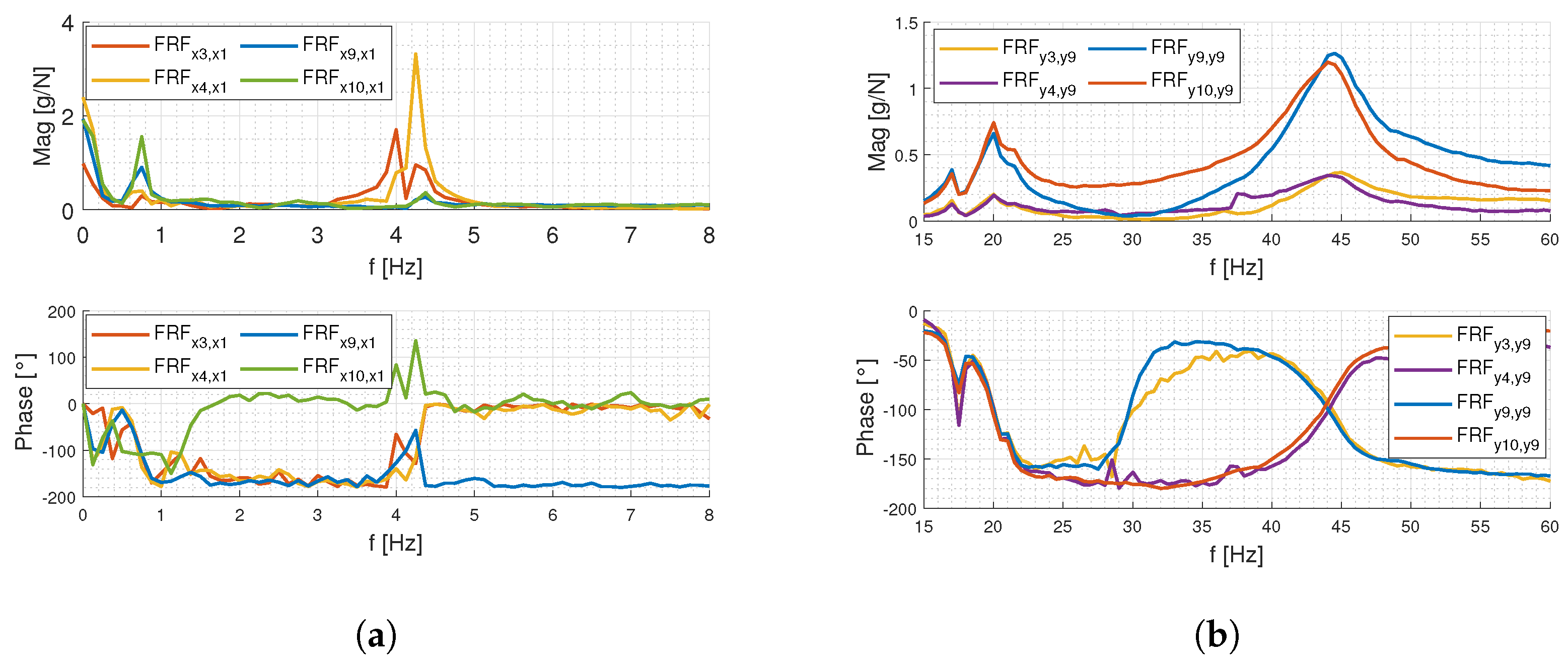
4. Experimental Test and Validation
5. Frequency Content of the Input Motion
6. Conclusive Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Babaiasl, M.; Mahdioun, S.H.; Jaryani, P.; Yazdani, M. A review of technological and clinical aspects of robot-aided rehabilitation of upper-extremity after stroke. Disabil. Rehabil. Assist. Technol. 2016, 11, 263–280. [Google Scholar] [CrossRef] [PubMed]
- Maciejasz, P.; Eschweiler, J.; Gerlach-Hahn, K.; Jansen-Troy, A.; Leonhardt, S. A survey on robotic devices for upper limb rehabilitation. J. Neuroeng. Rehabil. 2014, 11, 1–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cieza, A.; Causey, K.; Kamenov, K.; Hanson, S.W.; Chatterji, S.; Vos, T. Global estimates of the need for rehabilitation based on the Global Burden of Disease study 2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 2006–2017. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, B.; Artemiadis, P. A review of robot-assisted lower-limb stroke therapy: Unexplored paths and future directions in gait rehabilitation. Front. Neurorobot. 2020, 14, 19. [Google Scholar] [CrossRef] [Green Version]
- Weber, L.M.; Stein, J. The use of robots in stroke rehabilitation: A narrative review. NeuroRehabilitation 2018, 43, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Bertani, R.; Melegari, C.; De Cola, M.C.; Bramanti, A.; Bramanti, P.; Calabrò, R.S. Effects of robot-assisted upper limb rehabilitation in stroke patients: A systematic review with meta-analysis. Neurol. Sci. 2017, 38, 1561–1569. [Google Scholar] [CrossRef]
- Chien, W.T.; Chong, Y.Y.; Tse, M.K.; Chien, C.W.; Cheng, H.Y. Robot-assisted therapy for upper-limb rehabilitation in subacute stroke patients: A systematic review and meta-analysis. Brain Behav. 2020, 10, e01742. [Google Scholar] [CrossRef] [PubMed]
- Narayan, J.; Kalita, B.; Dwivedy, S.K. Development of robot-based upper limb devices for rehabilitation purposes: A systematic review. Augment. Hum. Res. 2021, 6, 1–33. [Google Scholar] [CrossRef]
- Zuccon, G.; Lenzo, B.; Bottin, M.; Rosati, G. Rehabilitation robotics after stroke: A bibliometric literature review. Expert Rev. Med Devices 2022, 19, 405–421. [Google Scholar] [CrossRef]
- Moshaii, A.A.; Najafi, F. A review of robotic mechanisms for ultrasound examinations. Ind. Robot. Int. J. 2014, 41, 373–380. [Google Scholar] [CrossRef]
- Nelles, G. Cortical reorganization-effects of intensive therapy. Restor. Neurol. Neurosci. 2004, 22, 239–244. [Google Scholar] [PubMed]
- Bütefisch, C.; Hummelsheim, H.; Denzler, P.; Mauritz, K.H. Repetitive training of isolated movements improves the outcome of motor rehabilitation of the centrally paretic hand. J. Neurol. Sci. 1995, 130, 59–68. [Google Scholar] [CrossRef] [PubMed]
- French, B.; Thomas, L.H.; Coupe, J.; McMahon, N.E.; Connell, L.; Harrison, J.; Sutton, C.J.; Tishkovskaya, S.; Watkins, C.L. Repetitive task training for improving functional ability after stroke. Cochrane Database Syst. Rev. 2016, 11, CD006073. [Google Scholar] [CrossRef] [Green Version]
- Bayona, N.A.; Bitensky, J.; Salter, K.; Teasell, R. The role of task-specific training in rehabilitation therapies. Top. Stroke Rehabil. 2005, 12, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Xie, S.Q.; Das, R.; Zhu, G.L. Control strategies for effective robot assisted gait rehabilitation: The state of art and future prospects. Med. Eng. Phys. 2014, 36, 1555–1566. [Google Scholar] [CrossRef]
- Oujamaa, L.; Relave, I.; Froger, J.; Mottet, D.; Pelissier, J.Y. Rehabilitation of arm function after stroke. Literature review. Ann. Phys. Rehabil. Med. 2009, 52, 269–293. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Bottin, M.; Russo, M.; Rosati, G.; Laribi, M.; Petuya, V. Requirements and Solutions for Motion Limb Assistance of COVID-19 Patients. Robotics 2022, 11, 45. [Google Scholar] [CrossRef]
- Prasad, R.; El-Rich, M.; Awad, M.; Hussain, I.; Jelinek, H.; Huzaifa, U.; Khalaf, K. A Framework for Determining the Performance and Requirements of Cable-Driven Mobile Lower Limb Rehabilitation Exoskeletons. Front. Bioeng. Biotechnol. 2022, 10, 920462. [Google Scholar] [CrossRef]
- Gopura, R.; Bandara, D.; Kiguchi, K.; Mann, G.K. Developments in hardware systems of active upper-limb exoskeleton robots: A review. Robot. Auton. Syst. 2016, 75, 203–220. [Google Scholar] [CrossRef]
- Bruckmann, T.; Pott, A. Cable-Driven Parallel Robots; Springer: Berlin/Heidelberg, Germany, 2012; Volume 12. [Google Scholar]
- Khosravi, M.A.; Taghirad, H.D. Dynamic modeling and control of parallel robots with elastic cables: Singular perturbation approach. IEEE Trans. Robot. 2014, 30, 694–704. [Google Scholar] [CrossRef]
- Kawamura, S.; Kino, H.; Won, C. High-speed manipulation by using parallel wire-driven robots. Robotica 2000, 18, 13–21. [Google Scholar] [CrossRef]
- Mao, Y.; Jin, X.; Dutta, G.G.; Scholz, J.P.; Agrawal, S.K. Human movement training with a cable driven arm exoskeleton (CAREX). IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Rosati, G.; Gallina, P.; Masiero, S. Design, implementation and clinical tests of a wire-based robot for neurorehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 560–569. [Google Scholar] [CrossRef] [PubMed]
- Ball, S.J.; Brown, I.E.; Scott, S.H. A planar 3DOF robotic exoskeleton for rehabilitation and assessment. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 4024–4027. [Google Scholar]
- Perry, J.C.; Rosen, J.; Burns, S. Upper-limb powered exoskeleton design. IEEE/ASME Trans. Mechatron. 2007, 12, 408–417. [Google Scholar] [CrossRef]
- Laribi, M.; Ceccarelli, M.; Sandoval, J.; Bottin, M.; Rosati, G. Experimental Validation of Light Cable-Driven Elbow-Assisting Device L-CADEL Design. J. Bionic Eng. 2022, 19, 416–428. [Google Scholar] [CrossRef]
- Zuccon, G.; Bottin, M.; Ceccarelli, M.; Rosati, G. Design and performance of an elbow assisting mechanism. Machines 2020, 8, 68. [Google Scholar] [CrossRef]
- Rosati, G.; Gallina, P.; Masiero, S.; Rossi, A. Design of a new 5 dof wire-based robot for rehabilitation. In Proceedings of the 9th International Conference on Rehabilitation Robotics, ICORR 2005, Chicago, IL, USA, 28 June–1 July 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 430–433. [Google Scholar]
- Xu, P.; Li, J.; Li, S.; Xia, D.; Zeng, Z.; Yang, N.; Xie, L. Design and Evaluation of a Parallel Cable-Driven Shoulder Mechanism With Series Springs. J. Mech. Robot. 2022, 14, 031012. [Google Scholar] [CrossRef]
- Xu, Z.; Xie, L. Cable-Driven Flexible Exoskeleton Robot for Abnormal Gait Rehabilitation. J. Shanghai Jiaotong Univ. Sci. 2022, 27, 231–239. [Google Scholar] [CrossRef]
- Seyfi, N.; Keymasi Khalaji, A. Robust control of a cable-driven rehabilitation robot for lower and upper limbs. ISA Trans. 2022, 125, 268–289. [Google Scholar] [CrossRef]
- Zhong, B.; Guo, K.; Yu, H.; Zhang, M. Toward Gait Symmetry Enhancement via a Cable-Driven Exoskeleton Powered by Series Elastic Actuators. IEEE Robot. Autom. Lett. 2022, 7, 786–793. [Google Scholar] [CrossRef]
- Shoaib, M.; Asadi, E.; Cheong, J.; Bab-Hadiashar, A. Cable driven rehabilitation robots: Comparison of applications and control strategies. IEEE Access 2021, 9, 110396–110420. [Google Scholar] [CrossRef]
- Rosati, G.; Cenci, S.; Boschetti, G.; Zanotto, D.; Masiero, S. Design of a single-dof active hand orthosis for neurorehabilitation. In Proceedings of the 2009 IEEE International Conference on Rehabilitation Robotics, Kyoto, Japan, 23–26 June 2009; pp. 161–166. [Google Scholar]
- Zuccon, G.; Tang, L.; Doria, A.; Bottin, M.; Minto, R.; Rosati, G. The Effect of Pulleys and Hooks on the Vibrations of Cable Rehabilitation Robots. In Mechanisms and Machine Science, Proceedings of the Advances in Italian Mechanism Science, Naples, Italy, 7–9 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; Volume 122, pp. 273–281. [Google Scholar]
- Kozak, K.; Zhou, Q.; Wang, J. Static analysis of cable-driven manipulators with non-negligible cable mass. IEEE Trans. Robot. 2006, 22, 425–433. [Google Scholar] [CrossRef]
- Riehl, N.; Gouttefarde, M.; Krut, S.; Baradat, C.; Pierrot, F. Effects of non-negligible cable mass on the static behavior of large workspace cable-driven parallel mechanisms. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2193–2198. [Google Scholar]
- Rosati, G.; Andreolli, M.; Biondi, A.; Gallina, P. Performance of cable suspended robots for upper limb rehabilitation. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 385–392. [Google Scholar]
- Jiang, Q.; Kumar, V. Determination and stability analysis of equilibrium configurations of objects suspended from multiple aerial robots. J. Mech. Robot. 2012, 4, 021005. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cossalter, V.; Doria, A.; Mitolo, L. Inertial and modal properties of racing motorcycles. SAE Trans. 2002, 111, 2461–2468. [Google Scholar]
- Cossalter, V.; Doria, A.; Basso, R.; Fabris, D. Experimental analysis of out-of-plane structural vibrations of two-wheeled vehicles. Shock Vib. 2004, 11, 433–443. [Google Scholar] [CrossRef] [Green Version]
- Verbeke, J.; Debruyne, S. Vibration analysis of a UAV multirotor frame. In Proceedings of the ISMA 2016 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 19–21 September 2016; pp. 2401–2409. [Google Scholar]
- Belotti, R.; Caneva, G.; Palomba, I.; Richiedei, D.; Trevisani, A. Model updating in flexible-link multibody systems. J. Phys. Conf. Ser. 2016, 744, 012073. [Google Scholar] [CrossRef] [Green Version]
- Doria, A.; Cocuzza, S.; Comand, N.; Bottin, M.; Rossi, A. Analysis of the compliance properties of an industrial robot with the Mozzi axis approach. Robotics 2019, 8, 80. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]







| Parameter | Value |
|---|---|
| (kg · m) | |
| M (kg) | |
| (kg) | |
| g (m/s) | |
| (m) | |
| (m) | |
| (m) | |
| (m) | |
| (rad) | |
| (rad) | 0 |
| Transverse (Hz) | Mode I | 0.720 | 0.720 | 0 |
| Mode II | 4.571 | 4.571 | 0 | |
| Mode III | 4.756 | 4.756 | 0 | |
| Longitudinal (Hz) | Mode IV | 19.868 | 22.305 | 12.27 |
| Mode V | 41.622 | 46.725 | 12.26 |
| Mode I | Mode II | Mode III | Mode IV | Mode V | |
|---|---|---|---|---|---|
| f (Hz) | 0.731 | 3.846 | 4.078 | 18.414 | 35.753 |
| (mm) | Mode | Analytical (Hz) | Experimental (Hz) | Experimental | ||
|---|---|---|---|---|---|---|
| 0.25 | Transverse | I | 0.842 | 0.834 | 0.455 | 0.95% |
| II | 4.858 | 4.407 | 0.656 | 9.28% | ||
| III | 5.028 | 4.735 | 0.574 | 5.83% | ||
| Longitudinal | IV | 23.261 | 19.878 | 5.868 | 14.54% | |
| V | 48.729 | 44.578 | 5.938 | 8.52% | ||
| 0.38 | Transverse | I | 0.720 | 0.715 | 1.491 | 0.69% |
| II | 4.571 | 3.977 | 0.530 | 12.99% | ||
| III | 4.756 | 4.280 | 0.637 | 10.01% | ||
| Longitudinal | IV | 22.305 | 19.688 | 4.818 | 11.73% | |
| V | 46.725 | 44.121 | 5.268 | 5.57% | ||
| 0.50 | Transverse | I | 0.644 | 0.634 | 0.816 | 1.55% |
| II | 4.432 | 3.725 | 0.548 | 15.95% | ||
| III | 4.646 | 4.056 | 0.701 | 12.70% | ||
| Longitudinal | IV | 21.520 | 19.218 | 3.178 | 10.70% | |
| V | 45.079 | 42.126 | 4.675 | 6.55% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuccon, G.; Doria, A.; Bottin, M.; Rosati, G. Planar Model for Vibration Analysis of Cable Rehabilitation Robots. Robotics 2022, 11, 154. https://doi.org/10.3390/robotics11060154
Zuccon G, Doria A, Bottin M, Rosati G. Planar Model for Vibration Analysis of Cable Rehabilitation Robots. Robotics. 2022; 11(6):154. https://doi.org/10.3390/robotics11060154
Chicago/Turabian StyleZuccon, Giacomo, Alberto Doria, Matteo Bottin, and Giulio Rosati. 2022. "Planar Model for Vibration Analysis of Cable Rehabilitation Robots" Robotics 11, no. 6: 154. https://doi.org/10.3390/robotics11060154
APA StyleZuccon, G., Doria, A., Bottin, M., & Rosati, G. (2022). Planar Model for Vibration Analysis of Cable Rehabilitation Robots. Robotics, 11(6), 154. https://doi.org/10.3390/robotics11060154









