Virtual UR5 Robot for Online Learning of Inverse Kinematics and Independent Joint Control Validated with FSM Position Control †
Abstract
:1. Introduction
2. Methods for Virtual Robot Design
2.1. Virtual Robotics Laboratory
2.2. 3D Modeling of the UR5 Robot with Blender
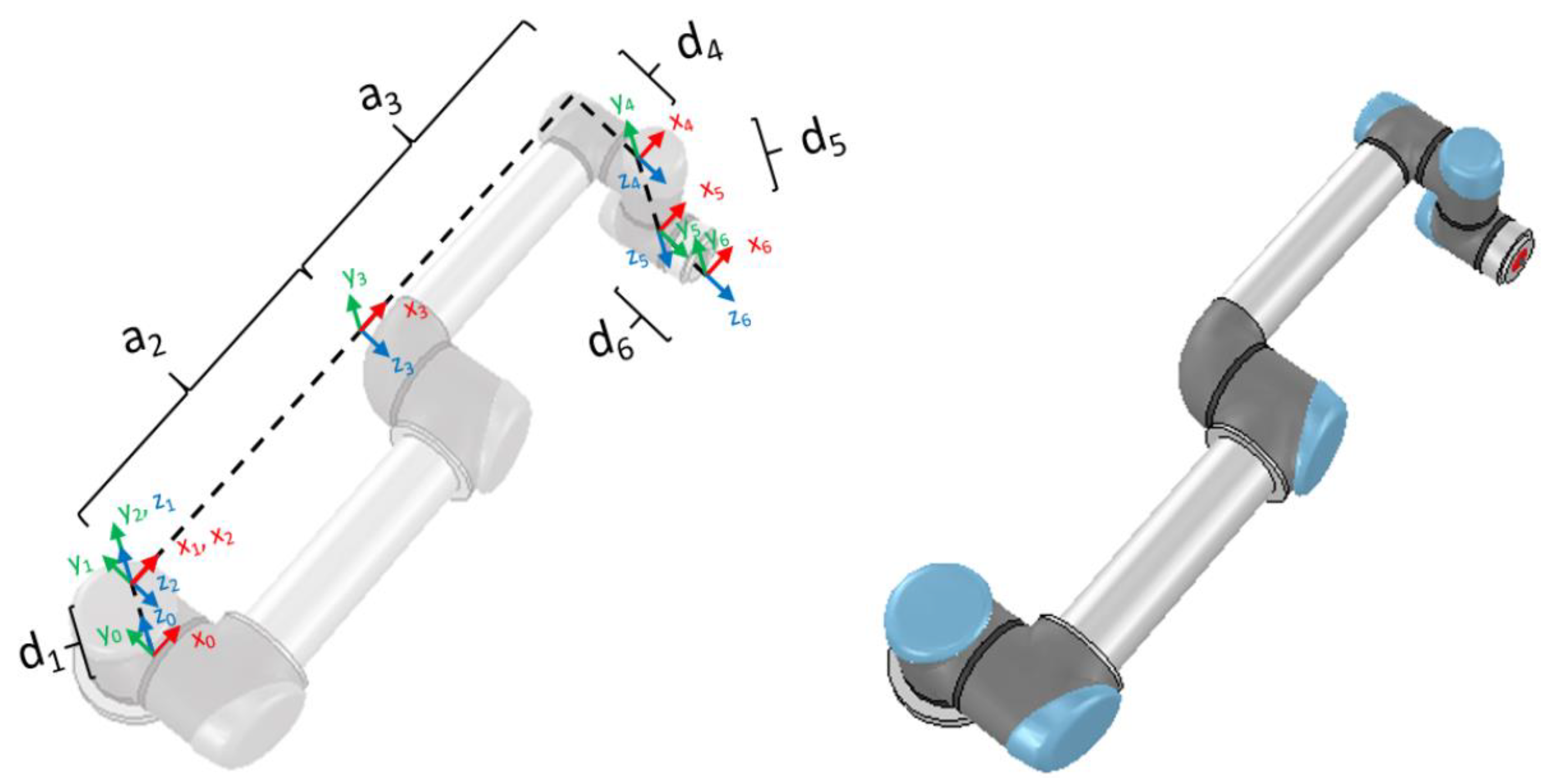
2.3. Kinematics of the UR Robot
3. Methods for Virtual Robot Control
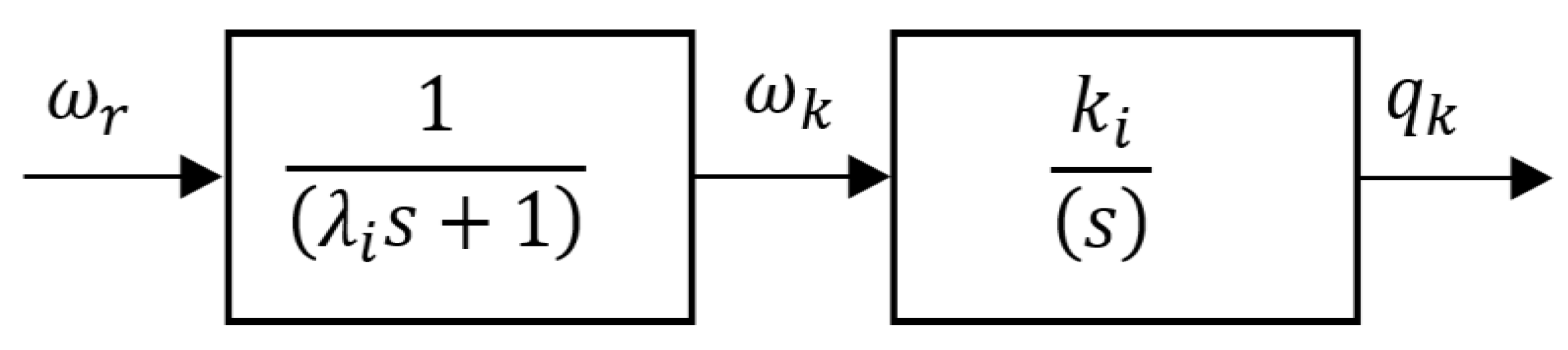
3.1. Speed Servo Control of DC Motors
3.2. PID Joint Position Control
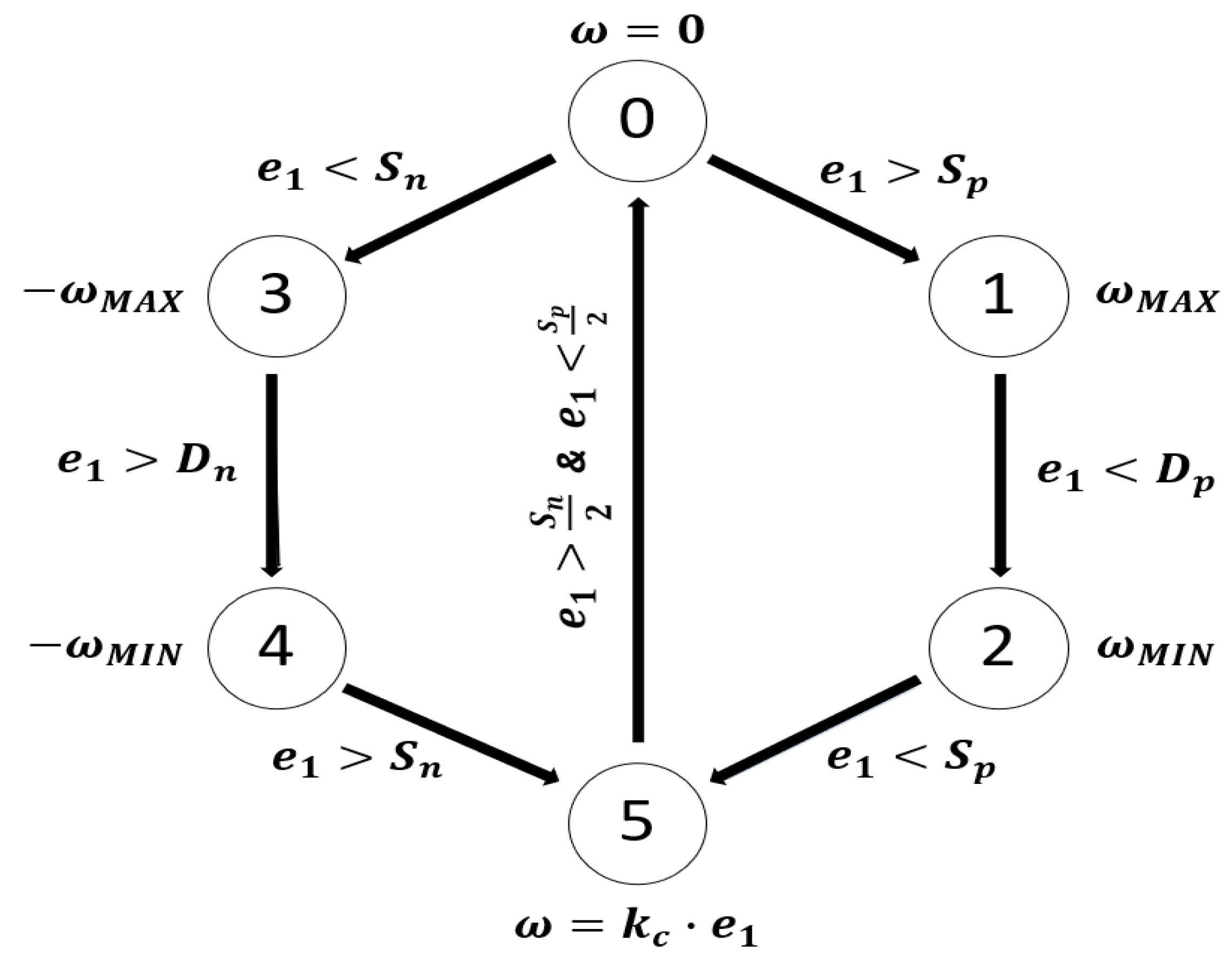
3.3. Finite State Machine for Joint Position Control
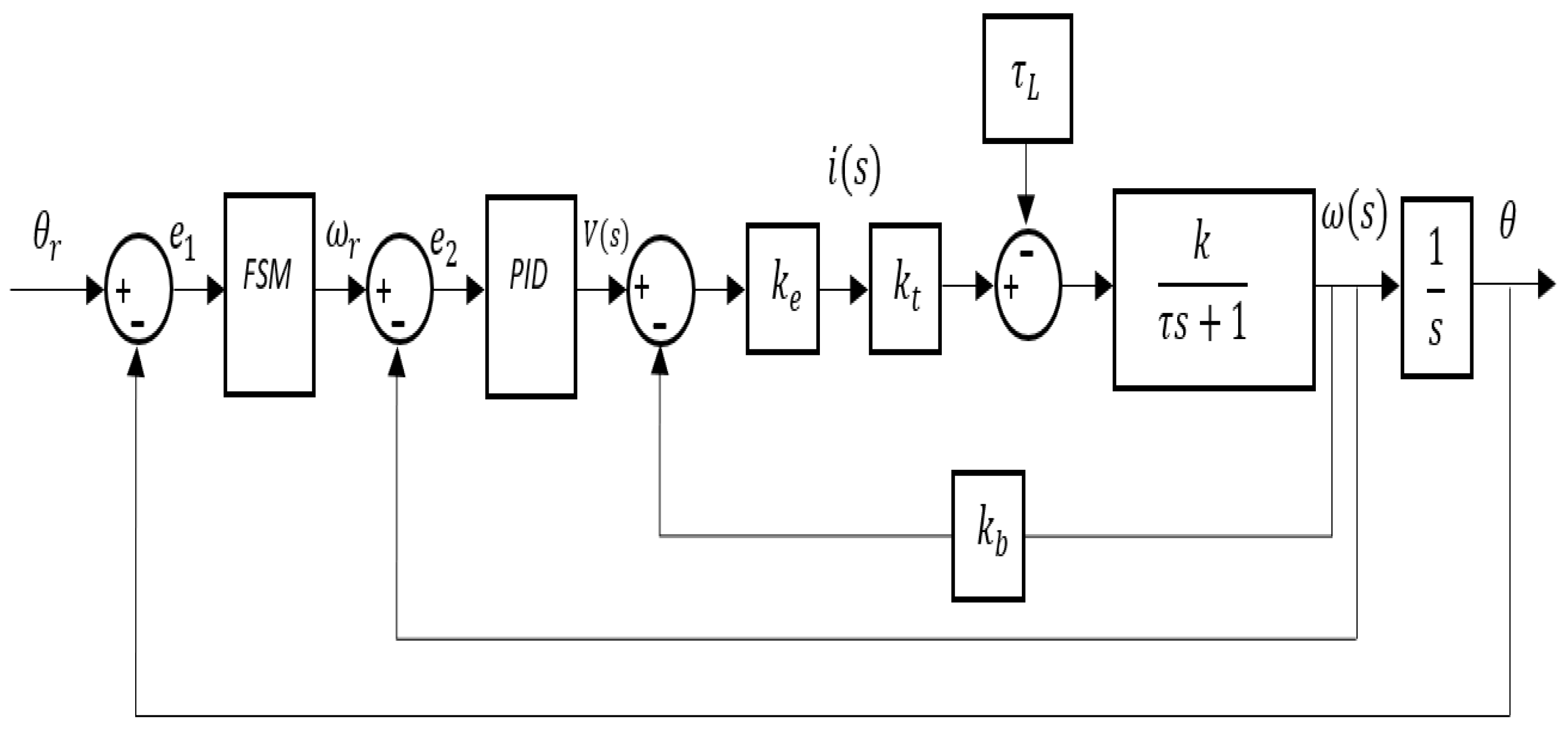
3.3.1. Cascade FSM-IMC-PID for Position and Speed Control
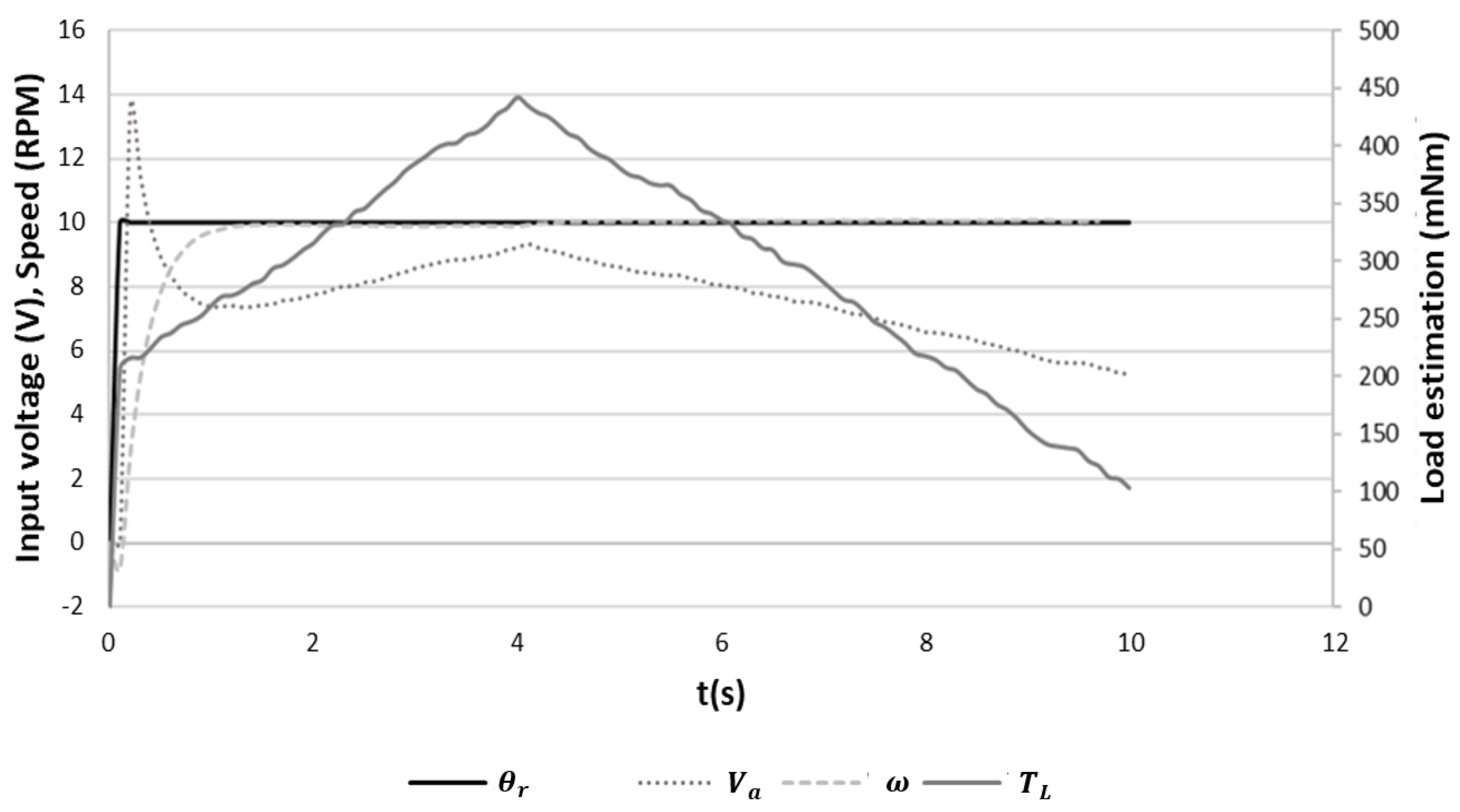
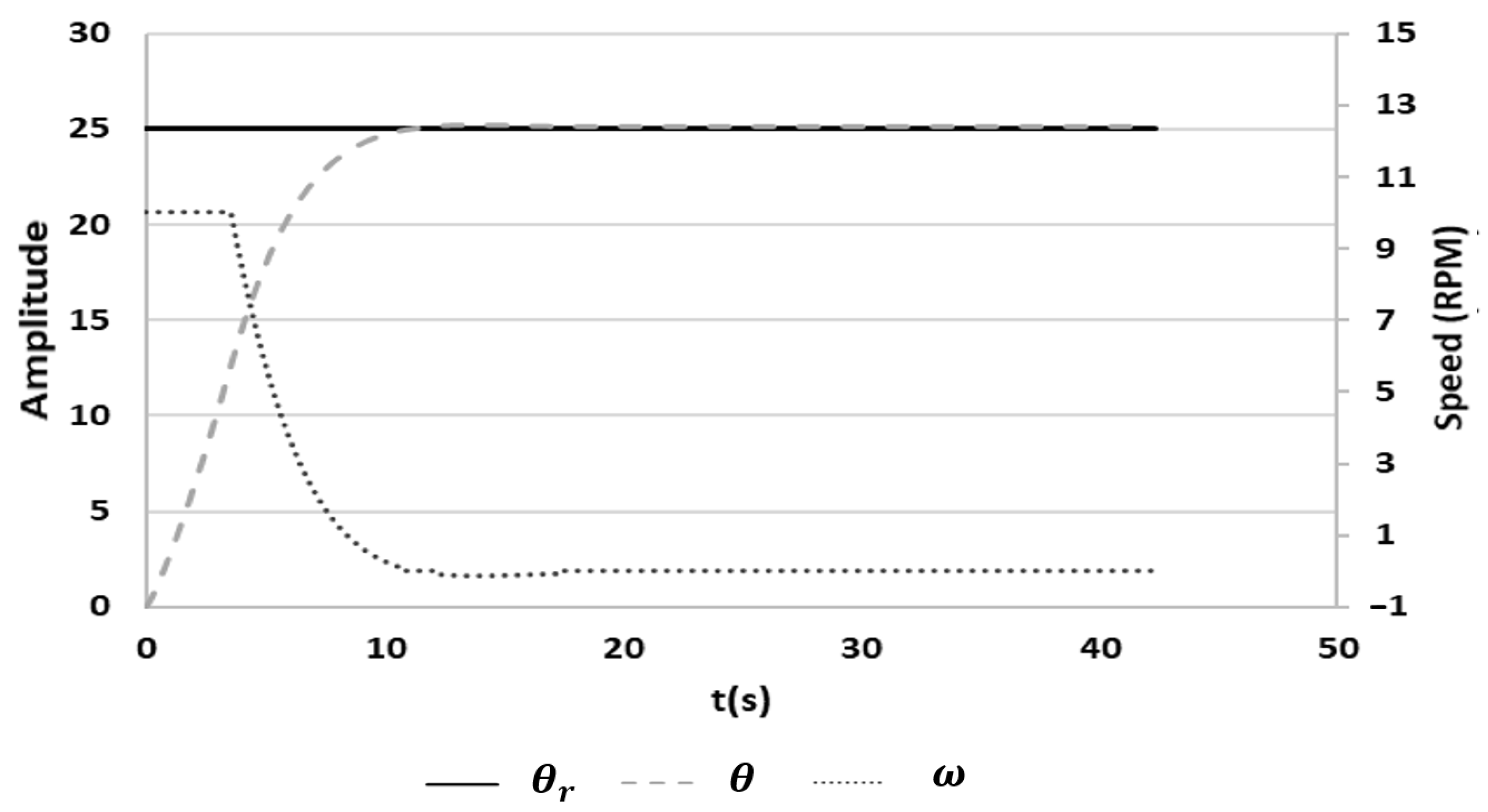
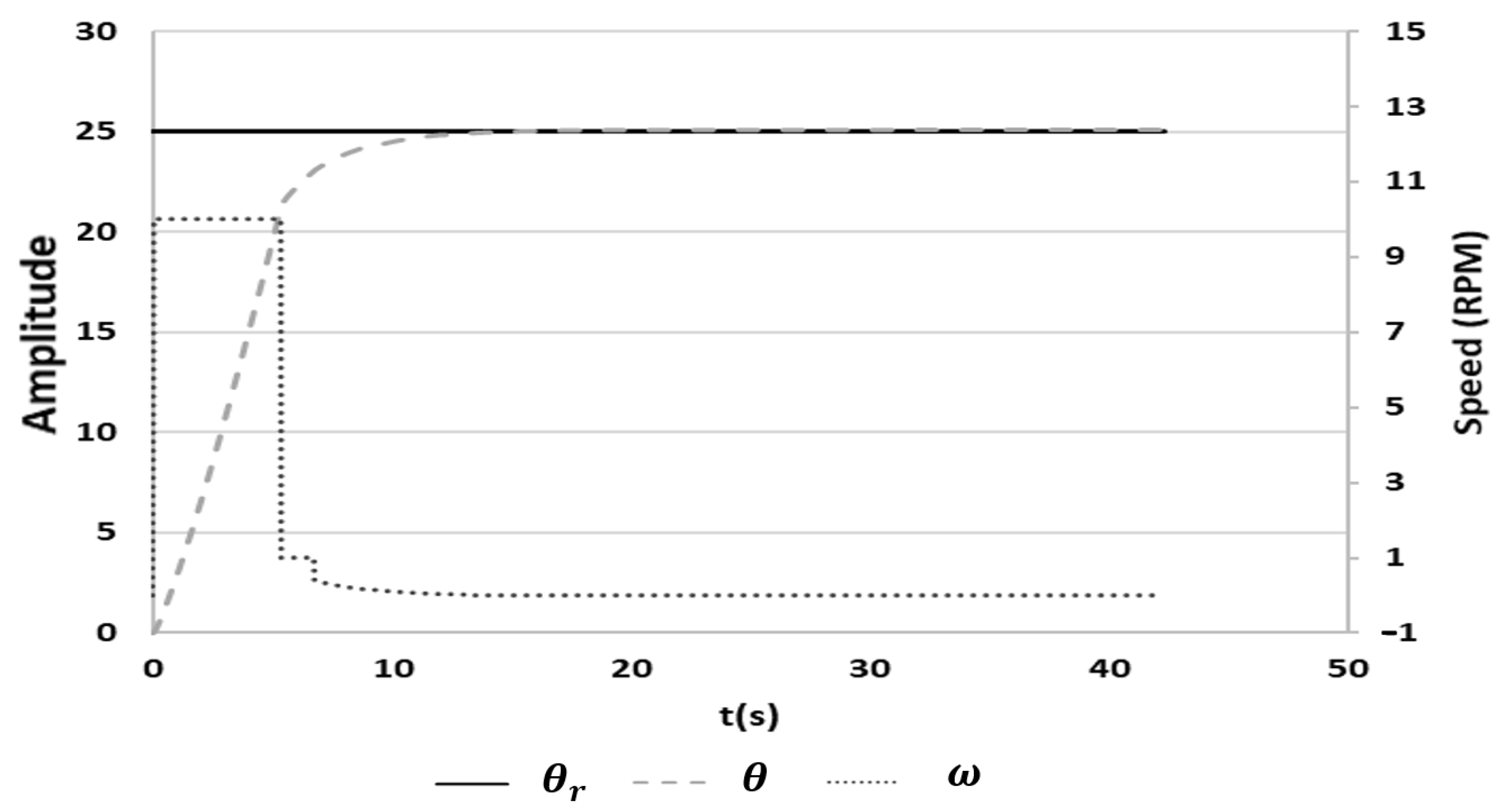
3.3.2. Response of the FSM-IMC-PID Controller
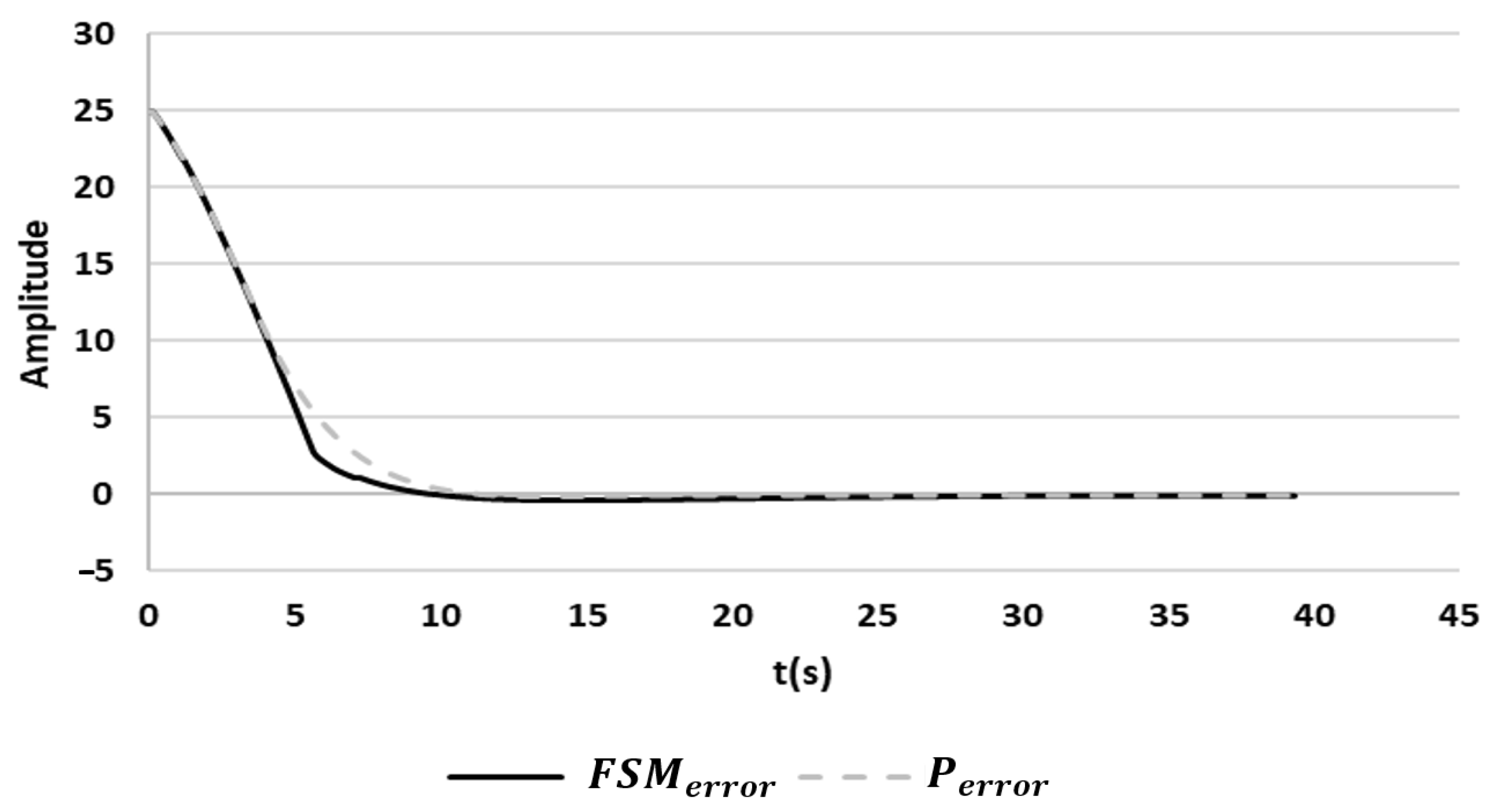
3.3.3. Comparison of FSM versus Proportional Controller
4. Results and Discussion
4.1. Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Olszewska, J.I. The Virtual Classroom: A New Cyber Physical System. In Proceedings of the 2021 IEEE 19th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2021; pp. 187–192. [Google Scholar] [CrossRef]
- Pivoto, D.G.S.; de Almeida, L.F.F.; Da Rosa Righi, R.; Rodrigues, J.J.P.C.; Lugli, A.B.; Alberti, A.M. Cyber-physical systems architectures for industrial internet of things applications in Industry 4.0: A literature review. J. Manuf. Syst. 2021, 58, 176–192. [Google Scholar] [CrossRef]
- Leng, J.; Zhang, H.; Yan, D.; Liu, Q.; Chen, X.; Zhang, D. Digital twin-driven manufacturing cyber-physical system for parallel controlling of smart workshop. J. Ambient. Intell. Humaniz. Comput. 2018, 10, 1155–1166. [Google Scholar] [CrossRef]
- Pérez, L.; Rodríguez-Jiménez, S.; Rodríguez, N.; Usamentiaga, R.; García, D.F. Digital Twin and Virtual Reality Based Methodology for Multi-Robot Manufacturing Cell Commissioning. Appl. Sci. 2020, 10, 3633. [Google Scholar] [CrossRef]
- Wuttke, H.D.; Henke, K.; Hutschenreuter, R. Digital twins in remote labs. In Cyber-Physical Systems and Digital Twins; Springer: New York, NY, USA, 2019; pp. 289–297. [Google Scholar] [CrossRef]
- Verner, I.M.; Cuperman, D.; Gamer, S.; Polishuk, A. Training Robot Manipulation Skills through Practice with Digital Twin of Baxter. Int. J. Online Biomed. Eng. 2019, 15, 58–70. [Google Scholar] [CrossRef]
- Rukangu, A.; Tuttle, A.; Johnsen, K. Virtual reality for remote controlled robotics in engineering education. In Proceedings of the IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops, VR Workshops 2021, Lisbon, Portugal, 27 March–1 April 2021; pp. 751–752. [Google Scholar]
- Tselegkaridis, S.; Sapounidis, T. Simulators in educational robotics: A Review. Educ. Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Hao, C.; Zheng, A.; Wang, Y.; Jiang, B. Experiment Information System Based on an Online Virtual Laboratory. Future Internet 2021, 13, 27. [Google Scholar] [CrossRef]
- Cobo, E.B.; Andaluz, V.H. Virtual Training System for Robotic Applications in Industrial Processes. In Augmented Reality, Virtual Reality, and Computer Graphics; AVR. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2021; Volume 12980, pp. 717–734. [Google Scholar] [CrossRef]
- Cogurcu, Y.E.; Douthwaite, J.A.; Maddock, S. Augmented Reality for Safety Zones in Human Robot Collaboration. EG UK Comput. Graph. Vis. Comput. 2022, 1–7. [Google Scholar]
- Alkhedher, M.; Mohamad, O.; Alavi, M. An interactive virtual laboratory for dynamics and control systems in an undergraduate mechanical engineering curriculum—A case study. Glob. J. Eng. Educ. 2021, 23, 55–61. [Google Scholar]
- Arenas, F.; Martell, F.; Sanchez, I.Y.; Paredes, C.A. Virtual laboratory for online learning of UR5 robotic arm inverse kinematic and joint motion control. In Proceedings of the 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 9–10 December 2021. [Google Scholar]
- Talli, A.; Meti, V.K. Design, simulation, and analysis of a 6-axis robot using robot visualization software. IOP Conf. Ser. Mater. Sci. Eng. 2020, 872, 12040. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Y. Design and simulation of robotic arm with light weight and heavy Load. In Proceedings of the 2nd World Conference on Mechanical Engineering and Intelligent Manufacturing: WCMEIM, Shanghai, China, 22–24 November 2019; pp. 537–540. [Google Scholar] [CrossRef]
- Rout, J.; Agrawal, S.; Choudhury, B.B. Modeling and control of a six-wheeled mobile robot. Information and Communication Technology for Competitive Strategies. In Proceedings of the Third International Conference on ICTCS 2017, Udaipur, India, 16–17 December 2017; pp. 323–331. [Google Scholar] [CrossRef]
- Villalobos, J.; Sanchez, I.Y.; Martell, F. Singularity Analysis and Complete Methods to Compute the Inverse Kinematics for a 6-DOF UR/TM-Type Robot. Robotics 2022, 11, 137. [Google Scholar] [CrossRef]
- Jahnavi, K.; Sivraj, P. Teaching and learning robotic arm model. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT 2017), Kerala, India, 6–7 July 2017; pp. 1570–1575. [Google Scholar] [CrossRef]
- Villalobos, J.; Sanchez, I.Y.; Martell, F. Alternative Inverse Kinematic Solution of the UR5 Robotic Arm. In Advances in Automation and Robotics Research; LACAR 2021. Lecture Notes in Networks and Systems; Moreno, H.A., Carrera, I.G., Ramírez-Mendoza, R.A., Baca, J., Banfield, I.A., Eds.; Springer: Cham, Switzerland, 2022; Volume 347. [Google Scholar]
- Sailan, K.; Kuhnert, K.D. DC motor angular position control using PID controller for the porpuse of controlling the hydraulic pump. In Proceedings of the International Conference on Control, Engineering & Information Technology, Sousse, Tunisia, 4–7 June 2013; pp. 22–26. [Google Scholar]
- Arenas, F.; Martell, F.; Sanchez, I.Y. Discrete Time DC Motor Model For Load Torque Estimation For PID-IMC Speed Control. Mechatron. Syst. Control. 2022, 50, 102–108. [Google Scholar] [CrossRef]
- Huang, G.; Lee, S. Pc-based PID speed control in DC motor. International conference on audio, language and image processing. In Proceedings of the International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2008; pp. 400–407. [Google Scholar]
- Ihechiluru, S.; Enwerem, C.O. Performance assessment of a model-based dc motor scheme. Appl. Model. Simul. 2019, 3, 145–153. [Google Scholar]
- Ahmed, U.O.; Patrick, A.A.; Kwembe, B.A. DC Motor Speed Control using Internal Model Controller Industrial Transformation Strategy. Int. J. Eng. Adv. Technol. 2020, 9, 300–306. [Google Scholar] [CrossRef]
- Al Tahtawi, A.R.; Somantri, Y.; Haritman, E. Design and Implementation of PID Control-based FSM Algorithm on Line Following Robot. JTERA (J. Teknol. Rekayasa) 2016, 1, 23–30. [Google Scholar] [CrossRef]






| i | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 0 | 0 | ||
| 3 | 0 | 0 | ||
| 4 | 0 | |||
| 5 | 0 | |||
| 6 | 0 | 0 |
| Performance Index | FSM | % | |
|---|---|---|---|
| ISE | 74,466.68 | 78,257.19 | 4.84 |
| IAE | 4498.84 | 4814.55 | 6.56 |
| ITAE | 11,561.20 | 13,548.74 | 14.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arenas-Rosales, F.; Martell-Chavez, F.; Sanchez-Chavez, I.Y.; Paredes-Orta, C.A. Virtual UR5 Robot for Online Learning of Inverse Kinematics and Independent Joint Control Validated with FSM Position Control. Robotics 2023, 12, 23. https://doi.org/10.3390/robotics12010023
Arenas-Rosales F, Martell-Chavez F, Sanchez-Chavez IY, Paredes-Orta CA. Virtual UR5 Robot for Online Learning of Inverse Kinematics and Independent Joint Control Validated with FSM Position Control. Robotics. 2023; 12(1):23. https://doi.org/10.3390/robotics12010023
Chicago/Turabian StyleArenas-Rosales, Filemon, Fernando Martell-Chavez, Irma Y. Sanchez-Chavez, and Carlos A. Paredes-Orta. 2023. "Virtual UR5 Robot for Online Learning of Inverse Kinematics and Independent Joint Control Validated with FSM Position Control" Robotics 12, no. 1: 23. https://doi.org/10.3390/robotics12010023
APA StyleArenas-Rosales, F., Martell-Chavez, F., Sanchez-Chavez, I. Y., & Paredes-Orta, C. A. (2023). Virtual UR5 Robot for Online Learning of Inverse Kinematics and Independent Joint Control Validated with FSM Position Control. Robotics, 12(1), 23. https://doi.org/10.3390/robotics12010023






