Abstract
Over the last years, a rapid evolution of unmanned aerial vehicle (UAV) usage in various applications has been observed. Their use in indoor environments requires a precise perception of the surrounding area, immediate response to its changes, and, consequently, a robust position estimation. This paper provides an implementation of navigation algorithms for solving the problem of fast, reliable, and low-cost inventorying in the logistics industry. The drone localization is achieved with a particle filter algorithm that uses an array of distance sensors and an inertial measurement unit (IMU) sensor. Navigation is based on a proportional–integral–derivative (PID) position controller that ensures an obstacle-free path within the known 3D map. As for the full 3D coverage, an extraction of the targets and then their final succession towards optimal coverage is performed. Finally, a series of experiments are carried out to examine the robustness of the positioning system using different motion patterns and velocities. At the same time, various ways of traversing the environment are examined by using different configurations of the sensor that is used to perform the area coverage.
Keywords:
UAV; localization; particle filter; logistics; inventorying; 3D coverage; OctoMap; indoor environments 1. Introduction
The unmanned aerial vehicles market is currently facing a large growth and is estimated to further advance in the upcoming years. Drones were initially used for military applications, a fact that creates several ethical and legal challenges, as well as concerns about the invasion of privacy that may occur with their usage. Nowadays, most of the UAVs are autonomous and operate in dynamic environments, without the need for a specialized operator. The scientific community considers drones as an emerging technology, since their capabilities allow the development of more and more innovative robotic applications.
Some typical applications of UAVs are the following:
- The inspection and maintenance of large areas or buildings, such as bridges, tunnels, underground mines, etc.
- The provision of humanitarian aid in inaccessible regions after natural disasters.
- The continuous inventorying in large warehouses, without the need for human intervention.
- The management and inspection of agricultural lands.
- The transport of small-volume packages.
The current paper focuses on the problem of autonomous inventorying in any indoor, three-dimensional space. Manual inventorying by personnel is a painful process, related to burdens on the workers health, due to the repeated movements they are asked to make for elongated time spans. Furthermore, in any procedure in which humans are involved, possible errors may exist, especially due to mental or physical fatigue. By using drones, this procedure becomes much simpler and, in theory, more precise, since every product’s position can be determined within a few centimeters’ accuracy. The autonomous inventorying from a drone consists of the following technical subproblems: (a) the drone localization in the indoor environment; (b) the position estimation of the products’ tags; and (c) the full and autonomous 3D area coverage.
Drone localization describes the calculation of the position and the orientation of the robot within a known map. The usage of UAVs in indoor environments is of great interest, due to the fact that a Global Positioning System (GPS) sensor that could directly provide the pose cannot be used. Any action that the drone is performing inside the environment requires a precise perception of the surrounding area and direct response to its changes, as well as stable and safe navigation. Apart from the robust localization, the UAV must follow a predetermined flight plan, shaped according to points of interest in the map. In this way, the full 3D coverage of the area can be established. In order to achieve full 3D coverage, the existence of an accessible and finite path is assumed, whose points are suitable for accessing all products via the desired detection sensors.
The successful achievement of autonomous aerial vehicle inventorying in an indoors environment is not an easy task, since it comprises several components, the most important of which are localization, path planning, and navigation. Concerning localization, the indoor environments are usually cluttered with obstacles, as well as being dynamic, since moving actors may exist in them (e.g., humans). These facts pose a challenge to the efficient and sound sensor integration and fusion, as several sensors (LiDARs, sonars, IMUs, cameras, radars, etc.) must be properly calibrated to operate in such complex environments and then be synchronized and ultimately fused. This is a necessity since indoor localization lacks support from GPS signals, making harder the correct pose identification of the drone. Furthermore, since aerial vehicles are concerned, the localization degrees of freedom are now six (x,y,z, , , ), instead of three (x,y, ) of the 2D plane, a fact that allows for more errors to exist/accumulate that can potentially lead to collisions with 3D obstacles. Where path planning is concerned, most of the algorithmic solutions require exponentially more computational resources when the dimensions increase (in our case, from two to three). Furthermore, if the environment is cluttered, special care must be taken to evaluate the 3D model of the drone against the 3D obstacles, so as to produce obstacle-free and safe paths, something that also is computationally intensive. Finally, navigation in 3D environments must again deal with dynamic obstacles (therefore, local planning is obligatory), environmental constraints, and 3D vehicle dynamics, which are much more complex in nature from their 2D counterparts, as the system (air) can induce severe disturbances in the UAV motion.
The aim of this paper is to present a complete approach on an autonomous aerial vehicle localization, path planning, and navigation towards the full 3D coverage of a known map, targeted at the logistics domain. The drone used is equipped with a distance sensors array, a laser altimeter sensor, and an IMU. The localization system is based on a particle filter algorithm that combines the distance and the IMU measurements to estimate the pose in real time. An obstacle-free path planning inside the 3D map is achieved using the RRT* (Rapidly exploring Random Tree) algorithm [1] through the Open Motion Planning Library (OMPL). The path that occurs can be smoothed by using B-spline functions. The navigation of the UAV is performed with a PID position controller. Finally, in order to achieve full coverage, a subsampling method is used to detect the points that offer the maximum visibility of objects. By having these points, we use the nearest neighbor algorithm in combination with hill climbing search to reduce the total distance and provide the UAV with the final trajectory to follow. In order to evaluate the coverage, we are using a simplified, simulated radio frequency identification (RFID) antenna, which presumably detects the products when they are in its field of view and finally calculates the percentage of the covered vertical surfaces.
The whole implementation relies on the Robot Operating System (ROS) [2], which offers a message-passing interface that provides structured communication between different software packages and components. It also deals with the allocation of resources, such as memory and processor time, among others, and allows for solving standard robotic problems using preexisting libraries. The environment in which the drone operates is considered known (no simultaneous localization and mapping (SLAM) is performed), and its map is available in OctoMap format [3].
The rest of the paper is structured as follows. Initially, in Section 2, the state-of-the-art in the fields of autonomous aerial vehicles localization, navigation, and full 3D coverage is provided. In Section 3, the algorithms and tools employed in this work are described, whereas in Section 4, the implementation of the proposed solution is described in detail. Finally, Section 5 presents the experimental results, and Section 6 contains a conclusion of the work and proposes possible future work.
2. Related Work
In recent years, plenty of approaches have been presented in order to deal with the problem of UAV localization, navigation, and coverage path planning. The solutions that have been proposed vary mostly in the type of sensors that are available on the drone and the environment map representation. We are going to examine some approaches on these problems separately.
2.1. Localization
The most common way to deal with localization issues for drones is using an RGB-D camera, due to their low cost and weight. Perez-Grau et al. [4] proposed the use of the classic Monte Carlo localization (MCL) algorithm [5] in combination with a red green blue-depth (RGB-D) camera for visual odometry and point cloud matching, as well as radio-based sensors localized within the known 3D map. The use of multiple monocular cameras with an existent 3D point-cloud map was presented in [6]. A simultaneous tracking and rendering approach, based in a monocular camera, appeared in [7]. There, real-time localization with limited hardware in a known mesh map of the environment was achieved using a semi-direct image alignment technique. Nevertheless, research also exists regarding localization using IMU measurements fused with a position generation mechanism. In [8], the authors mitigated the noise induced by the system and erroneous IMU measurements by using sporadic position measurements from a four-beacons ultrawide band (UWB) system, leading to improved localization results of the end-point of a robotic arm, as well as to lower execution times. A similar technique was suggested in [9], where IMU measurements and a UWB positioning system were fused using an unscented Kalman filter (UKF), improving the overall positioning accuracy.
Localization of RFID tags was performed in [10] with a ground robot that performs SLAM in an indoor environment. The work presented in detail the way the RFID technology works in robotic problems. Beul et al. [11] used a micro aerial vehicle (MAV) equipped with a dual 3D laser scanner, three stereo camera pairs, an IMU, and an RFID reader to deal with the problem of the autonomous inventorying in large warehouses. Every acquired 3D scan is represented as a multiresolution grid and is aligned to the map that has already been created. As for the drone navigation, the A* algorithm in combination with a reactive obstacle avoidance system is used. A similar approach was presented in [12], where a 3D lidar handles the self-localization and mapping problems and the MAV is capable of flying up to 7.8 m/s. The positioning of passive RFID tags with a UAV is achieved through a flying ultra-high-frequency (UHF) RFID reader and a synthetic aperture radar (SAR)-based localization processing in [13]. This work is related to outdoor environments and the drone trajectory is directly provided by a Global Navigation Satellite System (GNSS).
In the previous approaches, the UAVs could keep a safe distance from the surrounding obstacles. However, in [14], an MAV that is capable of autonomously navigating through a dark and smoke-filled environment of a ship was presented. The vehicle can navigate in narrow passages autonomously by using its two onboard computers, a forward-looking RGB-D camera and a downward-looking optical flow camera for pose and velocity estimation, respectively. Also, a point laser and a sonar sensor are used for height estimation.
2.2. 3D Coverage Planning and Control
Coverage path planning is about creating a path that passes from all the points of interest in an environment, while avoiding all obstacles. As presented in [15], there are six requirements:
- The robot must move through all the points in the target area covering it completely.
- The robot must fill the region without overlapping paths.
- Continuous and sequential operation without any repetition of paths is required.
- The robot must avoid all obstacles.
- Simple motion trajectories (e.g., straight lines or circles) should be used (for simplicity in control).
- An “optimal” path is desired under available conditions.
This problem can be solved either with a heuristic approach or a complete one. An offline planner that computes an efficient coverage trajectory is presented in [16]. A grid-based decomposition of the map is performed in order to pick positions for the drone. Then, a wavefront algorithm calculates all coverage paths with the minimum number of turns and chooses the one with the minimum total cost. Finally, cubic splines are used to provide smooth trajectories to the UAV. Bircher et al. [17] presented a three-dimensional coverage path planning for aerial inspection. One viewpoint for every triangle of the mesh of the environment is selected to ensure the complete coverage. Without focusing on minimizing the number of waypoints, an iterative resampling scheme is employed to minimize the total cost of the trajectory. Another approach in inspection cases was presented in [18]. A coverage path planning algorithm with adaptive viewpoint sampling constructs accurate 3D models of complex large structures using a UAV. Using the sensor models, an offline path is created and a prediction of coverage percentage is calculated. A different approach was presented in [19], where a neural network architecture is able to represent a dynamically varying environment. The workspace is discretized into squares and a real-time path planning is achieved, even in unstructured environments. A heuristic approach was presented in [20], where the energy restrictions are taken into account and the optimal speed for minimizing the energy consumption is calculated.
In [21] the coverage problem was discretized into generating potential target locations. These, along with the drones poses (which are dynamic), are added as nodes in a common graph, whose edges denote allowed motion paths. Then, a graph neural network is trained and employed to perform full coverage on the growing and changing graph. In [22], the authors proposed a coverage controller for an autonomous UAV that calculates coverage plans for 3D objects (surface-based). There, the plans consist of graphs, whose edges are probability constraints, which, via the unscented transformation, formulate the coverage as an optimal control problem, allowing the concurrent optimization of the drone’s motion and camera control inputs. Similarly, in [23], the authors classify regions of interest into clusters, for each of which they use an exact formulation based on mixed linear programming to obtain approximate optimal point-to-point paths that fully cover the solution space. In [24], the coverage path planning problem is optimized towards minimizing the energy consumption by reducing the route’s turns, using a precise tracking of energy consumption for a number of different drone actions (takeoff, cruise, hover, etc.). Similarly, in [25], the authors dealt with power consumption in the form of constraints. Specifically, they proposed a double deep-Q learning approach that generates coverage-oriented paths, containing a control policy that optimizes the routes given random start positions and varying power constraints. Finally, in [26], an ant colony system (ACS)-based algorithm was proposed to generate sufficiently good paths to fully cover the required regions, and approximately optimal solutions towards minimizing the exploration time consumption were performed.
2.3. Novelty Statement
The contribution of this work in comparison with the existing state-of-the-art techniques can be summarized to the following statements. First, the UAV is equipped with the minimum number of sensors that can be used, i.e., range sensors and an IMU. That leads to a small quantity of information that is available for localization purposes, without the use of any external sources that provide additional data from the indoor environment. This approach constitutes the solution low-cost in comparison to similar methodologies that reside on LiDAR range finders (LRFs), RGB, or RGB-D cameras. The main contribution of this work lies in the way of implementing an OctoMap full-coverage path planning by solving the traveling salesman problem (TSP) in 3D space, while ensuring the optimization of the trajectory length. Specifically, we target the logistics domain, where the usual tasks are the inventorying of the products or the search of the position of a specific product. Our approach differs to the others mentioned in the state of the art section, since the vast majority of them treats coverage as a horizontal problem (2D, or 2.5D, i.e., to cover the surface of an area). In our work, we implement vertical coverage approaches, as the products are usually placed in high shelves, at different heights. Therefore, the proposed algorithm computes targets near the vertical obstacles of the OctoMap, along with their normal vectors perpendicular to the obstacles. Then, optimal full path traversing calculation is proposed for two different coverage strategies (horizontal and vertical), whose performance is evaluated against different coverage sensor field of view (FOV) properties. Also, the drone’s navigation within the OctoMap is proposed, which relies solely on the localization system output, ensuring object collision avoidance and easy adaptability to any kind of UAV, irrespective of its sensors.
3. Theoretical Background
In this section, a short description of the utilized tools and concepts is presented, necessary to establish a knowledge base for the implementation description.
3.1. Principles of the UAV Operation
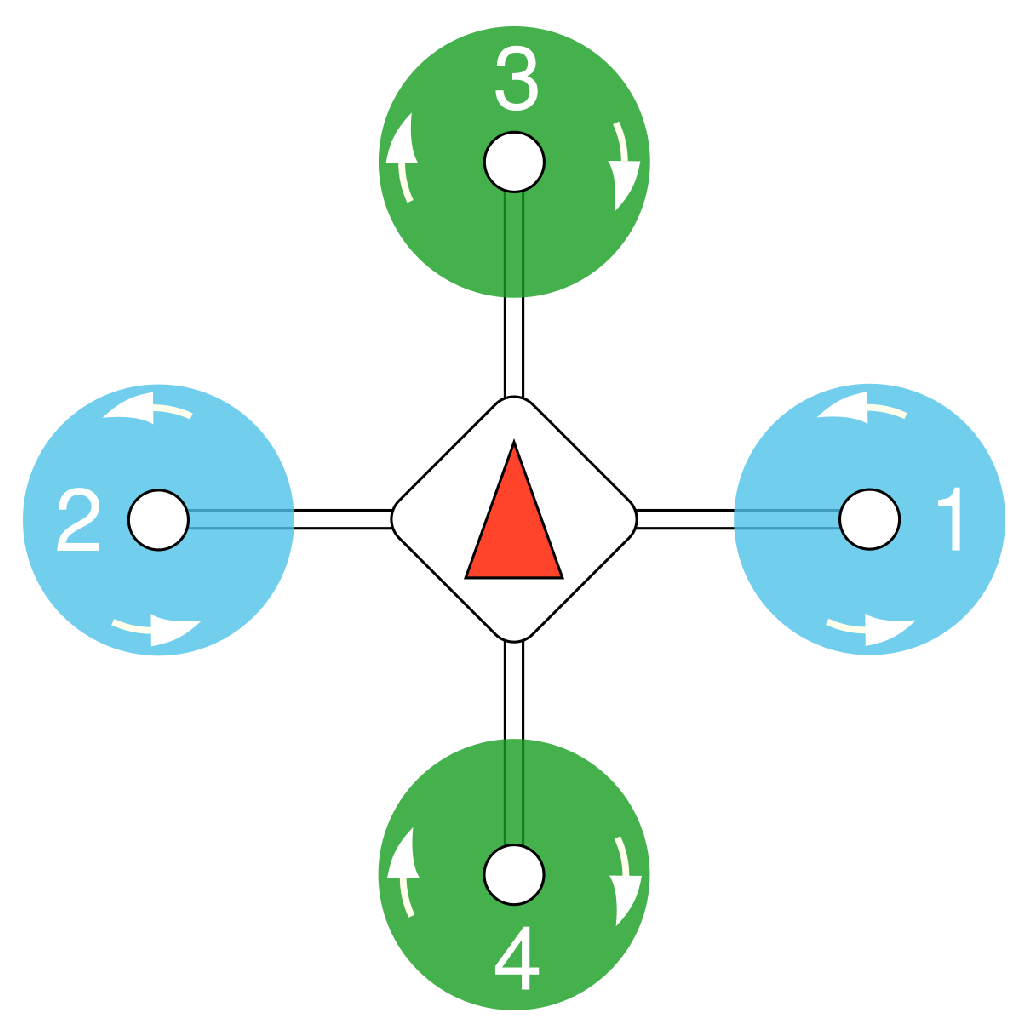
The UAVs are classified into different categories, depending on the number and the formation of their rotors. In this project, we are using a quadcopter, which is a type of drone that is lifted and propelled by four rotors; it is shown in Figure 1. Each propeller has a variable and independent speed which allows a full range of movements. A quadcopter can achieve six degrees of freedom, but only by planning maneuvers that make use of its four controllable degrees of freedom. The most useful operations of the drone used in this project are the following:
Figure 1.
Quadcopter format.
- Altitude hold/hover: Staying in the same 2D position while airborne.
- Take-off and landing.
- Headless mode: Keeping the heading stable, no matter which direction the drone moves.
- Waypoint navigation: Using localization methods to navigate to an intermediate location on a travel path.
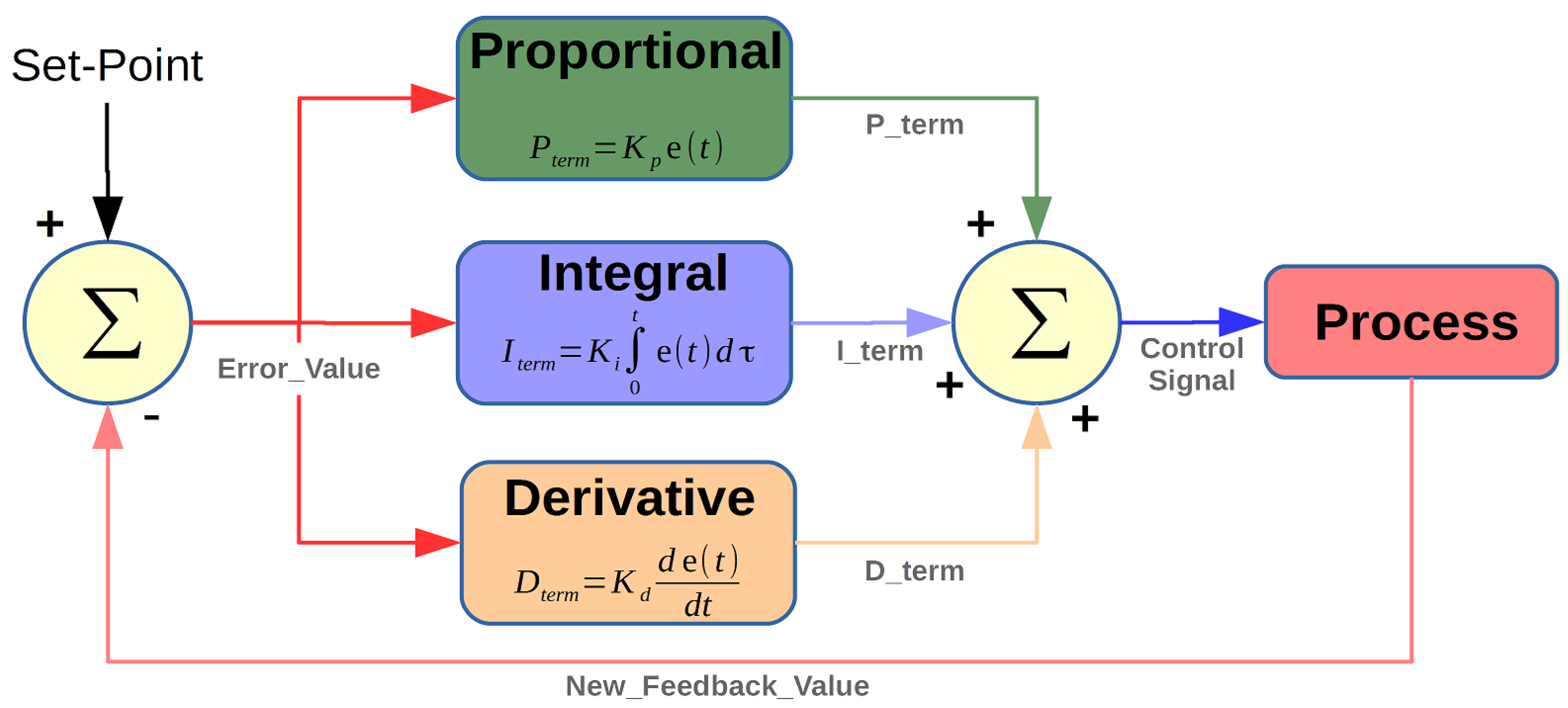
3.2. PID Controller
A proportional–integral–derivative controller is an algorithm used in industrial control applications to regulate temperature, flow, pressure, speed, and other process variables. PID control is a well-established way of driving a system towards a target position. It uses closed-loop control feedback to keep the actual output from a process as close to the target output as possible. Its operation is displayed in Figure 2.
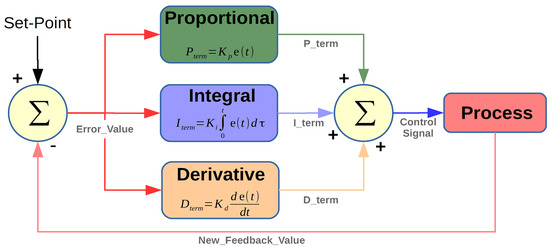
Figure 2.
PID operation (https://se.mathworks.com/matlabcentral/mlc-downloads/downloads/submissions/58257/versions/2/screenshot.png, Source) (accessed on 22 May 2024).
The controller output depends on three basic control behaviors, the proportional, the integral, and the derivative one. Each one of these terms is separately tuned and affects the output in a different way. The P-controller gives output, which is proportional to current error, the I-controller integrates the error over a period of time until the error value reaches zero, and the D-controller’s output depends on error rate of change with respect to time. Each of these terms is multiplied with a constant that can be determined with various methods.
3.3. OctoMap
The OctoMap library [3] provides a way to represent a 3D environment in a way that is suitable for robotic applications. The map implementation is based on an octree, which provides great advantages. It is capable of representing both the known and the unknown space, as well as of extending the map with new information at any time. The map updating is performed in a probabilistic way, due to the sensors’ noise and the chance of dealing with dynamic objects in the environment. An important feature of OctoMap is that it can be multiresolution, suitable for plenty of applications. Last, but not least, its octree representation leads to a compact format, both in disk and in memory.
3.4. Open Motion Planning Library
The Open Motion Planning Library [27] contains plenty of motion planning algorithms suitable for robotic applications. The algorithms it contains, (RRTs, Probabilistic Roadmaps (PRMs), etc.), are sampling-based and operate on very abstractly defined state spaces. It is open source and is widely used by the scientific community, both for education and research reasons. The basic concept of OMPL is the space decomposition into states and the use of a graph that contains these states as nodes. The graph’s edges denote all the feasible paths in the environment. The state format depends on the object of the occasion, for example, in our case, a state consists of the variables that describe the position in three axes, as well as the orientation of the object.
4. Implementation
This section discusses the implementation of the localization, navigation, and 3D coverage methodology.
4.1. Drone Localization
Drone localization is referred to as the problem of estimating the position and the orientation of the UAV within a known 3D map of an indoor environment, which has been previously acquired using a 3D SLAM approach. Due to the lack of GPS, the operation of drones in such environments is of great interest, as there is a need to take advantage of all the available sensors and resources. In our case, the UAV consists of an array of distance sensors placed circumferentially to the drone, an IMU, and a laser altimeter. Our approach implements the MCL algorithm, which is based on a particle filter. Specifically, the exact type of particle filter used is the bootstrap filter, a form of the sequential Monte Carlo algorithm. The core idea is to evaluate a set of states, using a specific weighting parameter, and consider the one with the highest weight as the currently correct state. Each particle is described by a state vector as follows:
In the general case, and also exist in the state vector, but in the current work it is assumed that these variables are close to zero when the drone reaches the poses where the products are visible to the detection sensor.
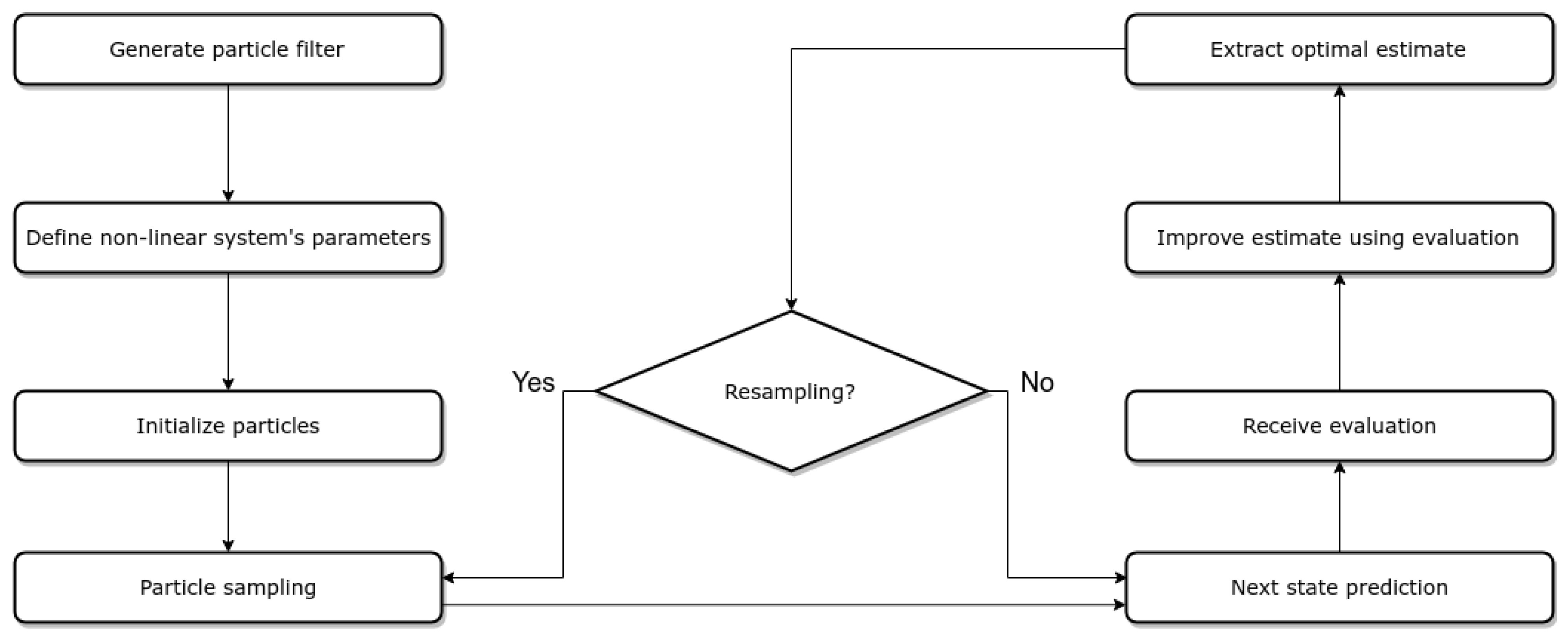
The particle filter approach requires as input the previous set of particles, a motion, and a measurement model for the specific UAV. The process followed by the particle filter is described in Figure 3.
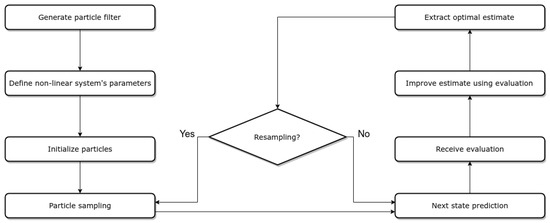
Figure 3.
Particle filter process.
As for the filter initialization, this depends on the prior knowledge of the initial position. If this is known and given as a parameter, the particles are initialized around this position given a Gaussian distribution described by a known standard deviation (position tracking localization). In the case of not having any information about the initial position, the particles are distributed in the whole map with a normal distribution (global localization). In both cases, the associated weights of N particles are all equally initialized to .
Regarding the motion model, there is the need to calculate the robot’s motion over time, as we have no direct source of odometry. The obvious solution would be to use visual odometry from the RGB camera, but since the controller was developed in a simulated environment, such an approach was not possible. The combination of the IMU measurements and the laser altimeter, as well as the velocity commands, can provide a robust motion estimation. The timestamped messages from these sources are handled by the ApproximateTime Policy of ROS Message Filters https://wiki.ros.org/message_filters (accessed on 22 May 2024), as this provides a time-adaptive algorithm to merge these measurements.
The value in the state vector is directly provided by the IMU and the z by the height altimeter. Given this, we transform the linear velocity vector from the robot frame to the world frame, as shown in Equation (2). This value is then integrated over time to estimate the drone’s motion, which is added to the previous state vector (Equation (3)). The final estimation is published to the proper ROS topic and handled by the motion model, in order to sample the particle set in every step of the filter execution.
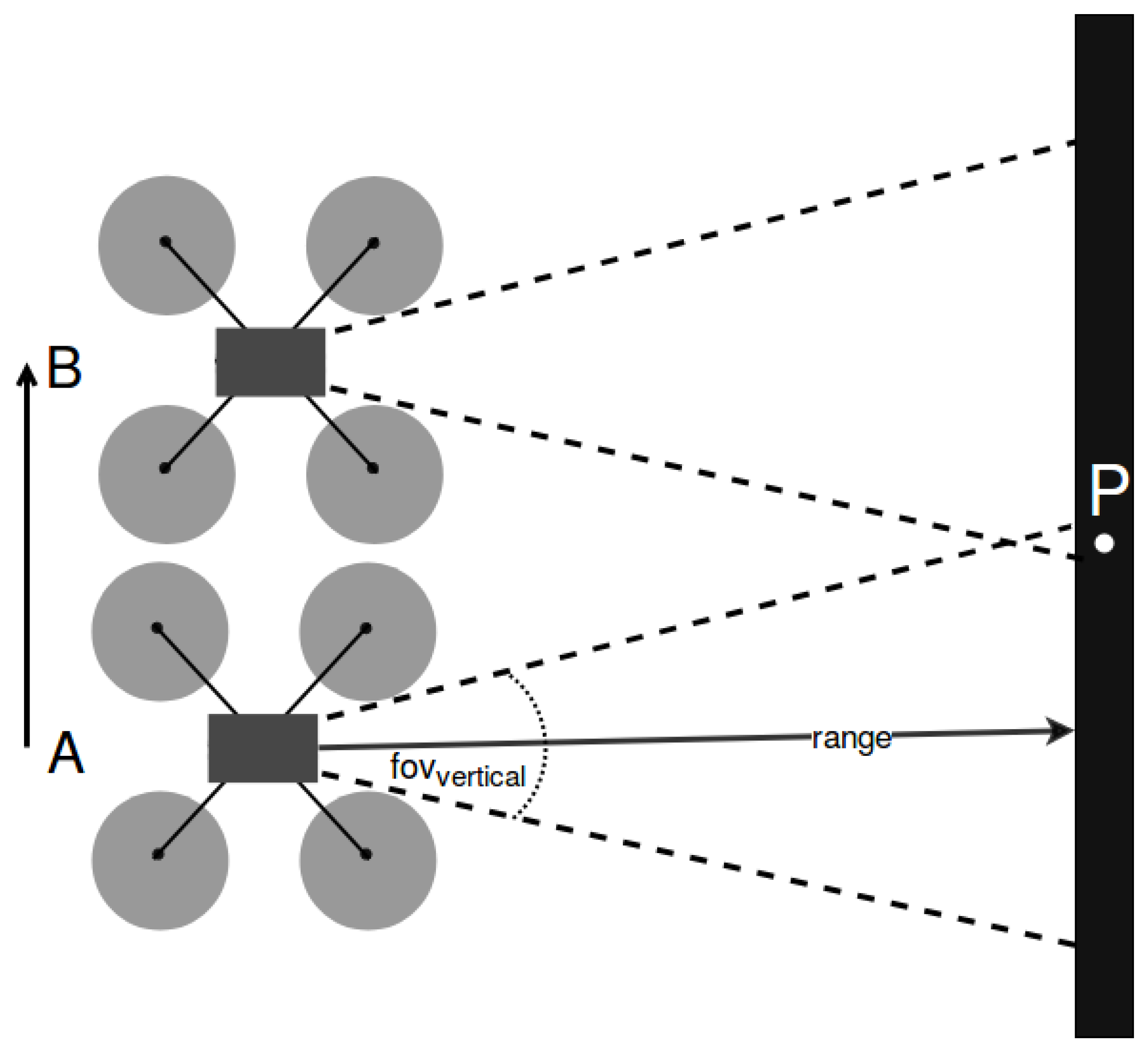
The measurement model uses the simultaneous data point acquisition of the eight rays on the range finder around the UAV, as shown in Figure 4.

Figure 4.
Range finder used by the UAV (https://www.terabee.com/shop/lidar-tof-multi-directional-arrays/teraranger-tower-evo/, Source) (accessed on 22 May 2024).
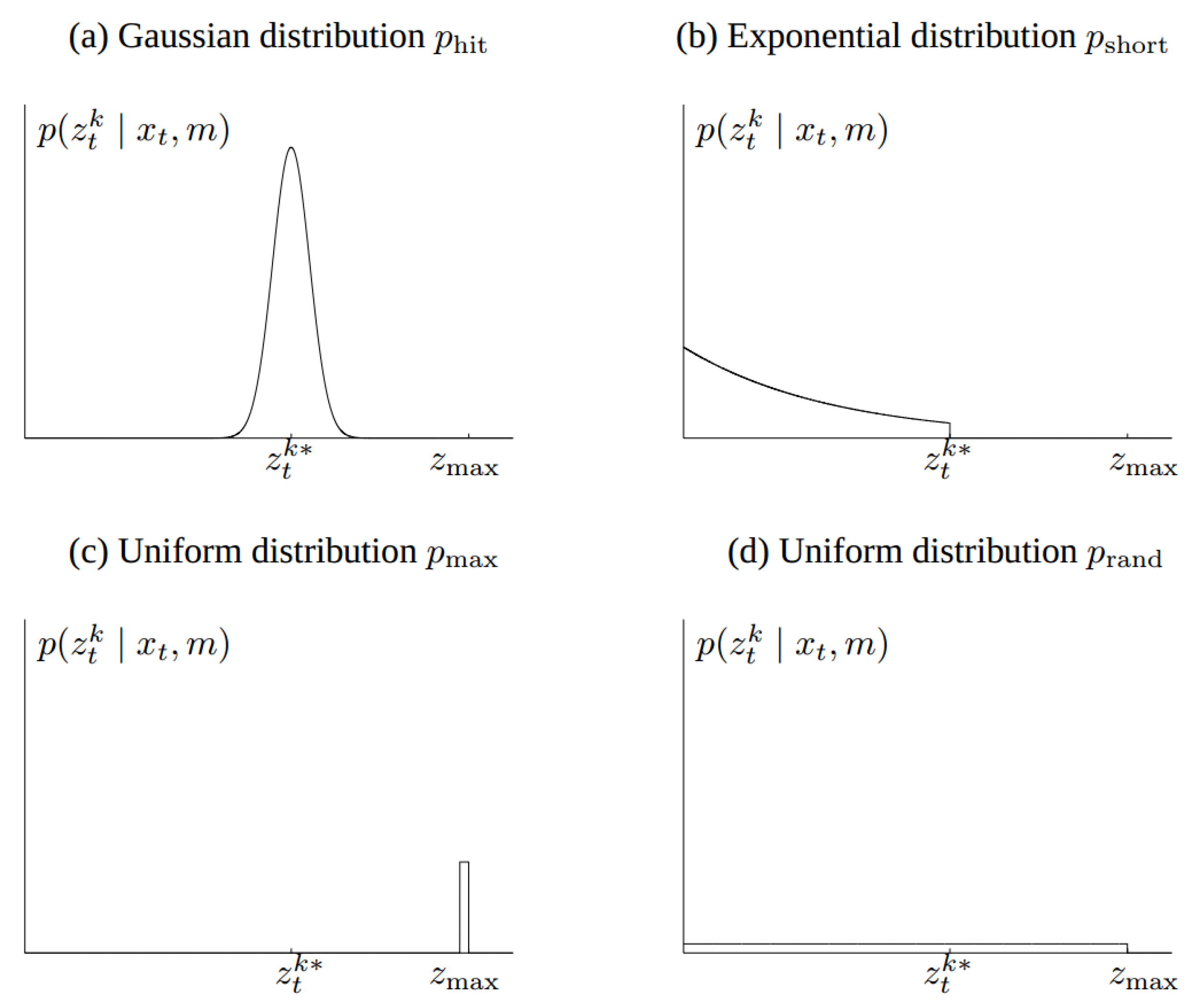
Formally, the measurement model is defined as a conditional probability distribution , where is the robot pose, is the measurement at time t, and m is the map of the environment, as is described in [28]. In that way, noise existence is taken into account for the calculations. Four types of measurement errors are incorporated in our model and are described below. Figure 5 displays the distribution functions that describe the measurement model.
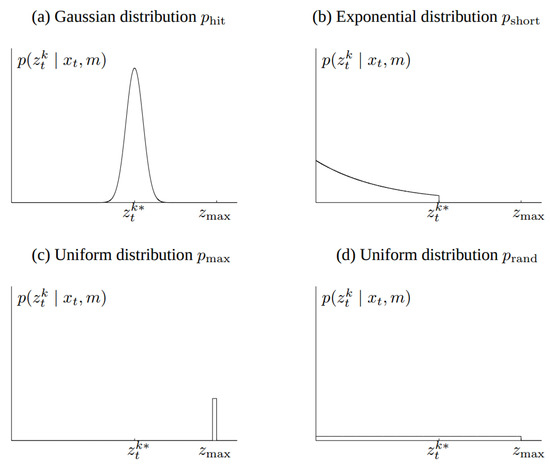
Figure 5.
Measurement model description.
Correct range with local measurement noise: Even if the sensor correctly calculates the distance from the nearest object, the value returned may be affected by some noise. The latter is due to the limited sensor resolution, the atmospheric influences, etc. This noise is modeled by a Gaussian distribution, as shown in Figure 5a. The measurement probability is described in Equations (4) and (5).
Unexpected objects: The environments in which the moving robots operate are dynamic, while the maps are static. As a result, any object that is not included in a map may be the cause for the distance sensors to calculate really small ranges several times. A simple method to overcome this issue is to consider these ranges as noise. An exponential distribution is used to describe this case, as shown in Equation (6). The parameter is an intrinsic parameter of the measurement model. We obtain the following equation for :
Failures: Sometimes obstacles are not detected. For example, sonar sensors fail when they measure on a steep angle, and laser range finders cannot measure in bright light or black, light-absorbing objects. Maximum range measurements are also a typical sensor failure, when the result is the maximum allowable value . This case is modeled with a point-mass distribution centered at , as shown in Figure 5c and described below:
Random measurements: Range finders occasionally output some random inexplicable measurements. For simplicity, we model such measurements using a uniform distribution spread over the entire sensor measurement range , depicted in Figure 5d.
The aforementioned distributions are combined using a weighted average, defined by the coefficients and , whose sum must be equal to 1.
Since the models have been fully described and the data preprocessing has been completed, the particle filter is created. The number of particles is defined as a system parameter, and it remains constant throughout the filter execution and provides a balance between the calculation accuracy and the computing load. Each particle is sampled according to its weight via the roulette wheel methodology. Using the motion model and the previous state, we can calculate the difference in the robot pose, which is then added to each particle’s state. This transform is applied in every particle, along with a portion of noise related to the specific motion model, and changes its position and orientation within the 3D map. The new state is now evaluated by using the measurement model, and every particle’s weight is modified.
The final position estimation is determined by the mean of the best of the particles with the highest weight value. The percentage of the particles that contribute in the final estimation is a parameter of the localization system and can be easily modified.
The number of particles N remains the same throughout the algorithm execution. As a result, some of them end up with zero weight and do not contribute in the final pose estimation. For this reason, a process called Resampling is applied every time the deviation of the particles’ weights () is less than the half of the total number of particles, as shown in Equation (9) [29]. describes the distribution equality of the particles in space and this process aims to focus on the space areas that matter the most. In order to cover the space of samples in a more systematic fashion than an independent random sampler, the low-variance sampling strategy [30] is applied.
4.2. Drone Navigation
In order to achieve safe and stable navigation throughout the environment, a cascaded PID approach is implemented. The controller used is designed to receive as input the UAV’s current position and the target position. Its output is their difference, which is then transformed to the necessary velocity commands. The position controller feeds another PID controller that is responsible for converting these commands to the rotor force that is required for the UAV to move towards the right direction with the right speed.
The target positions come from a set of waypoints that lead to the final goal through an obstacle-free and smooth path. The waypoints consist of four variables, x, y, z, , as it is assumed that for each waypoint, . In order to ensure the path smoothness, we make use of the OMPL library, which provides motion planning solutions for environments of any dimension. For our case, the selected 3D environment (a simulated library) is used to calculate state vectors that will lead to the desired goal, given the MCL pose estimation. Each of these waypoints are checked that are within the map bounds and do not lead to any undesired collision. The UAV is considered as a moving object with fixed dimensions, and a safe distance is kept from every object in the environment.
The initial path is created with the RRT* algorithm [31], which ensures its convergence in a finite time. In the case that the start or goal state coincide with an insecure position, we want to automatically find a nearby state that is valid, so motion planning can be performed. Given the allowed distance for both states and the maximum number of attempts, the states may be switched to a safer and valid position, if needed. This process samples the states within a neighborhood controlled by the distance parameter and returns one that can be accepted.
Each geometric path is evaluated by a metric S that indicates the smoothness of it. The closer S is to 0, the smoother the path is. We apply steps of smoothing with B-splines, while maintaining the path validity. At each step, the path is subdivided and states along it are updated such that the smoothness is improved. Fewer steps are applied if no progress is detected. This set of state vectors is then sent to the UAV controller, until the final goal is reached. In Figure 6, the input path is shown in red and the optimized output path is shown in blue.
Figure 6.
Path smoothing with B-splines.
An example of a path planning procedure performing obstacle avoidance is visible in Figure 7.

Figure 7.
Drone path planning and obstacle avoidance.
Regarding the UAV motion, we employ a proportional–derivative (PD) controller for each one of the state vector variables, x, y, z, , , and . Initially, while keeping the orientation stable, we control the position variables until the UAV reaches the position goal. Once it approaches the goal within an accepted distance, the position variables remain stable and a PD controller attempts to control the value, while keeping the and variables equal to 0. This happens in order to achieve a more stable motion. We also apply a speed limit for the drone movement for experimental reasons.
We define the error function for the position and rotation variables as follows:
Even though a PID controller would allow a better control of the UAV in real life, the whole project takes place in a simulated environment. For this reason, the I part of the controller remains equal to zero as there are no unexpected disturbances, such as wind, that will cause instability issues for the UAV. and parameters were defined as dynamic ROS parameters, which means that they could be modified during the execution. The value of is chosen as the maximum value that allows the UAV to reach the goal in a quick and stable way and was experimentally configured. The same happens for . Its value remains really small to avoid instability, due to instant changes.
The final controller formula is described in the following equations.
The output of the controller is converted from world frame to the robot frame using the rotation formula described in Equation (15).
where is the current angle of the UAV.
The previous process is repeated consecutively for each one of the subgoals that lead to the final goal. Once the UAV reaches the final one, it enters a hovering mode, until the next goal is received.
4.3. 3D Coverage Formulation
The underlying idea of 3D coverage of a known space is that every point of interest must be within the UAV’s FOV at least once. The drone is equipped with an RFID reader with specific, but configurable, characteristics, as follows:
- Range.
- Horizontal and vertical field of view (described in angles).
- Scope (orthogonal or circular).
- A unit vector that describes the orientation of the reader.
The evaluation of the coverage process must be based on a metric that is robust and reliable. The coverage assessment derives from the number of nodes covered by the sensor over the total number of visible nodes in the initial map. While this metric relies on the quality of the map, it can provide an overview of the coverage performance.
Apart from a numeric value, a new OctoMap with the covered surface is created and can provide a useful insight into the points that are hard to cover or are even unreachable by the drone. A partially covered map is displayed in Figure 8, and a fully covered space is evident in Figure 9.

Figure 8.
Ongoing coverage.

Figure 9.
Full coverage.
4.4. Targets Extraction in a Known OctoMap towards Full 3D Coverage
In order to achieve a full 3D coverage within an OctoMap, it is necessary to define all the waypoints that the drone should traverse through in order to accomplish the full coverage. A waypoint is described by the coordinates in 3D space (x,y,z) and an orientation vector.
These positions are all located within a bounding box around the map’s obstacles, in order to reduce the boundary noise coming from the mapping process in surfaces, such as the roof of the environment. We applied a subsampling procedure with a fixed step over the x-axis and y-axis. A different step is used for the z-axis, as shown in Equation (17).
Its value depends on the RFID range and the vertical field of view and ensures that every point of interest will be within the sensor’s FOV at least twice. As shown in Figure 10, the point P will be visible by the UAV’s sensor when its z-coordinate is equal to A and also when it is equal to B. Next, each of these points is validated as a pose is safe for the robot, by checking if this point exists in an obstacle, or if the nearest obstacle exists at a distance smaller than a predefined threshold. The output of this procedure is a set of points in 3D space that are adjacent to obstacles, but safe as possible targets of the drone.
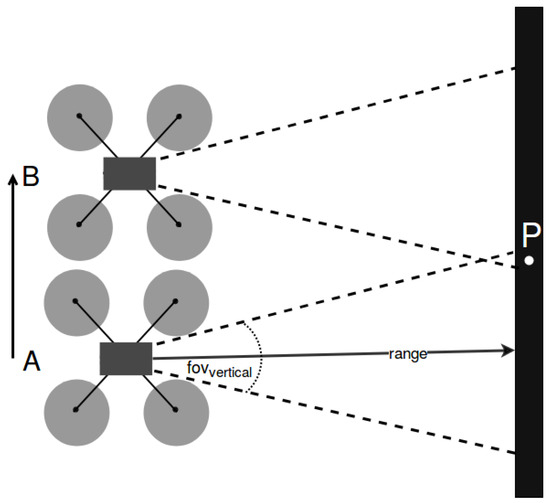
Figure 10.
Point P remains visible from both heights, A and B, where .
Once these tentative targets have been specified, they should be reordered in a way that minimizes the total distance of the trajectory and optimizes the UAV’s route. It is also necessary to exclude the targets that may be nonsafe for the UAV. The following checks are performed:
- The target is an occupied OctoMap node.
- The target’s position belongs in occupied space from the OctoMap projection in Occupancy Grid Map.
- There are obstacles at a close distance.
- Every target is directly accessible by at least another accessible target.
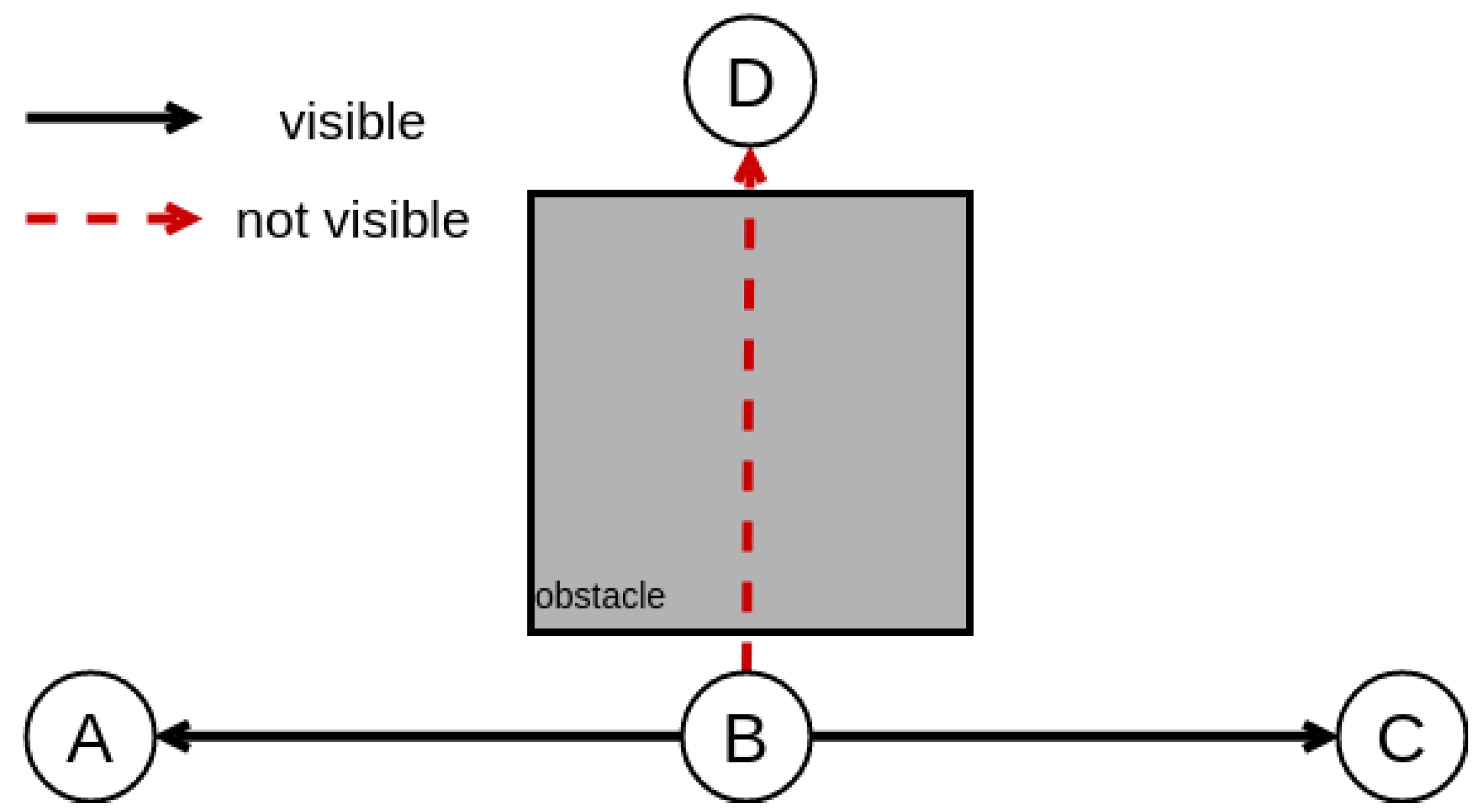
Regarding the last check, the map representation may cause some targets to be surrounded by an obstacle of the environment and, thus, to not be accessible by the UAV. For this reason, we need to ensure direct visibility between all the targets. This is achieved by applying a nearest neighbor search in all points recursively, ensuring that each waypoint can be directly accessed by another without the interference of any obstacle, as can be seen in Figure 11. Specifically, a UAV located in node B can directly move to nodes A and C. However, it cannot move to node D, even though their absolute distance is the same as .
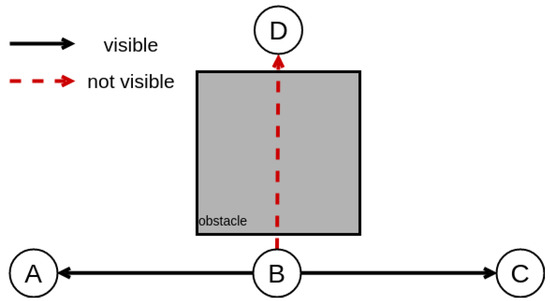
Figure 11.
Direct visibility between nodes.
Apart from the (x, y, z) values, there is a need to define the optimal orientation that maximizes the area covered. This requires the knowledge of the orientation vector and the surface’s normal vector. For each position, we examine every angle, starting from with a step equal to degrees. We define as the vector that describes the robot’s orientation vector and as the surface’s normal vector.
For a specific position A and an angle , we apply the OctoMap ray-casting functionality to determine the coordinates of a position B, which belongs on the surface and is the center of the sensor’s FOV. These two points provide us . As for , it is calculated using the getNormals function of OctoMap on point B. The coverage percentage C is given by the dot product of the normalized vectors.
The result of the process described is a set of targets in the format of that will lead to full 3D coverage. The values of and are considered to be zero, in order to ensure slow maneuvering and high precision.
4.5. Targets Succession towards Optimal Coverage
Optimal coverage requires minimization of the total distance that the drone will traverse, while ensuring that all points of interest will be covered, which is essentially the TSP in 3D space. This is denoted as the task to find, for a finite number of points whose pairwise distances are known, the shortest route connecting them. As in every other NP-hard problem, the greater the number of points, the harder it becomes to solve.
A naive approach would be to employ a search or an optimization algorithm (e.g., gradient descent or hill climbing), so as to iteratively find a (locally) optimal solution. Nevertheless, this approach would be time-inefficient due to the large number of possible targets, especially for realistic scenarios, such as large warehouses.
In order to reduce the number of targets and therefore minimize the algorithmic processing time, another approach was followed. First, the entirety of targets are grouped by different heights (position in the z axis), ignoring their orientation vector. This leads to horizontal slices of targets, which all have the same z but different , essentially mapping the three-dimensional points to a two-dimensional plane. The outcome of this is a set of points. A nondirectional graph is then created to represent the new targets. Each vertex contains an value and each edge describes the Euclidean distance from one position to another. Two nodes are connected on the condition that their distance is lower than 75% of the coverage sensor’s range.
The calculation of the optimal path resides on a combination of the nearest neighbor and the hill climbing algorithms, in order to take advantage of neighboring targets heuristically. The A* search algorithm [32] was used to calculate the pairwise distance between all nodes in the graph.
Two nodes can be consecutive on the condition that they are directly visible to one another. This can be calculated with the computeRayKeys function of the OctoMap library. Provided that all targets have been extracted from a subsampling process, the minimum distance between two positions is known and equal to the sampling step.
Starting from a random point N, its distance from the neighbors and is calculated. If is equal to the sampling step, this point is considered as the next one in the succession process. Otherwise, a random node is selected, and since the direct-visibility criterion is met, its distance is calculated. Then, an iterative search is performed for the next best target, until the nodes’ distance is minimum or a specific finite number of iterations has been reached.
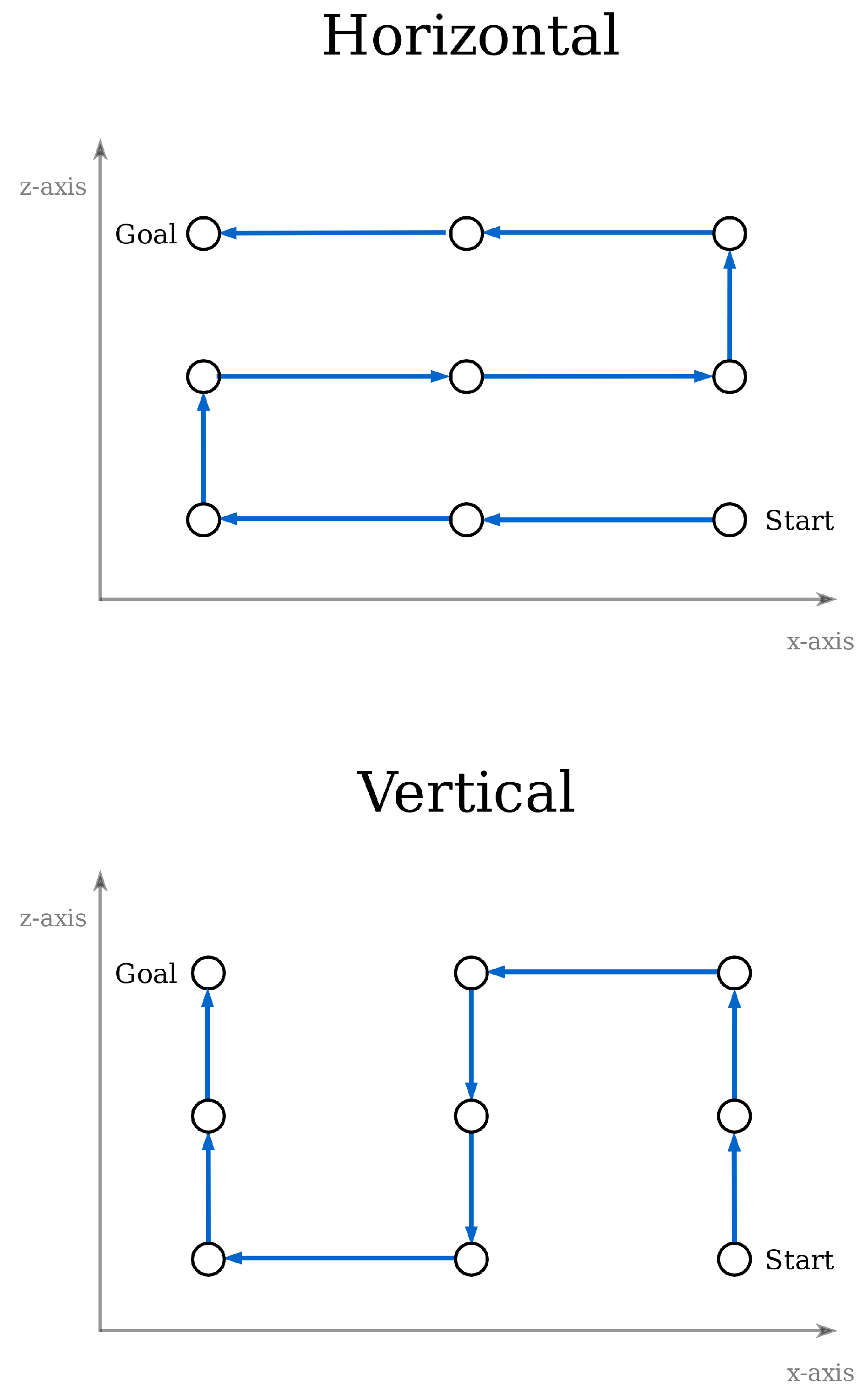
Since an optimal path in the two-dimensional space has been found, the solution can now be transferred to the 3D space. Two methods are applied for this transformation, the vertical and horizontal connection of waypoints, as shown in Figure 12.
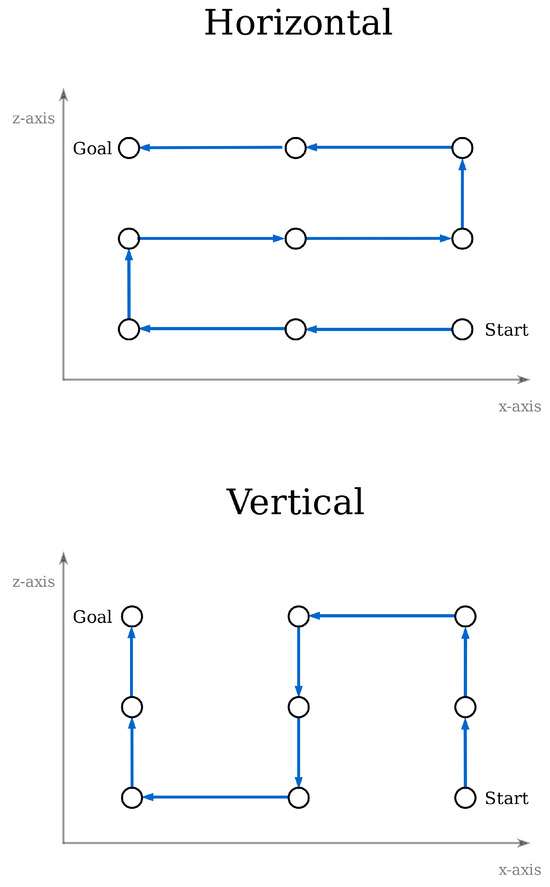
Figure 12.
Path transformation from 2D to 3D—horizontal vs. vertical method.
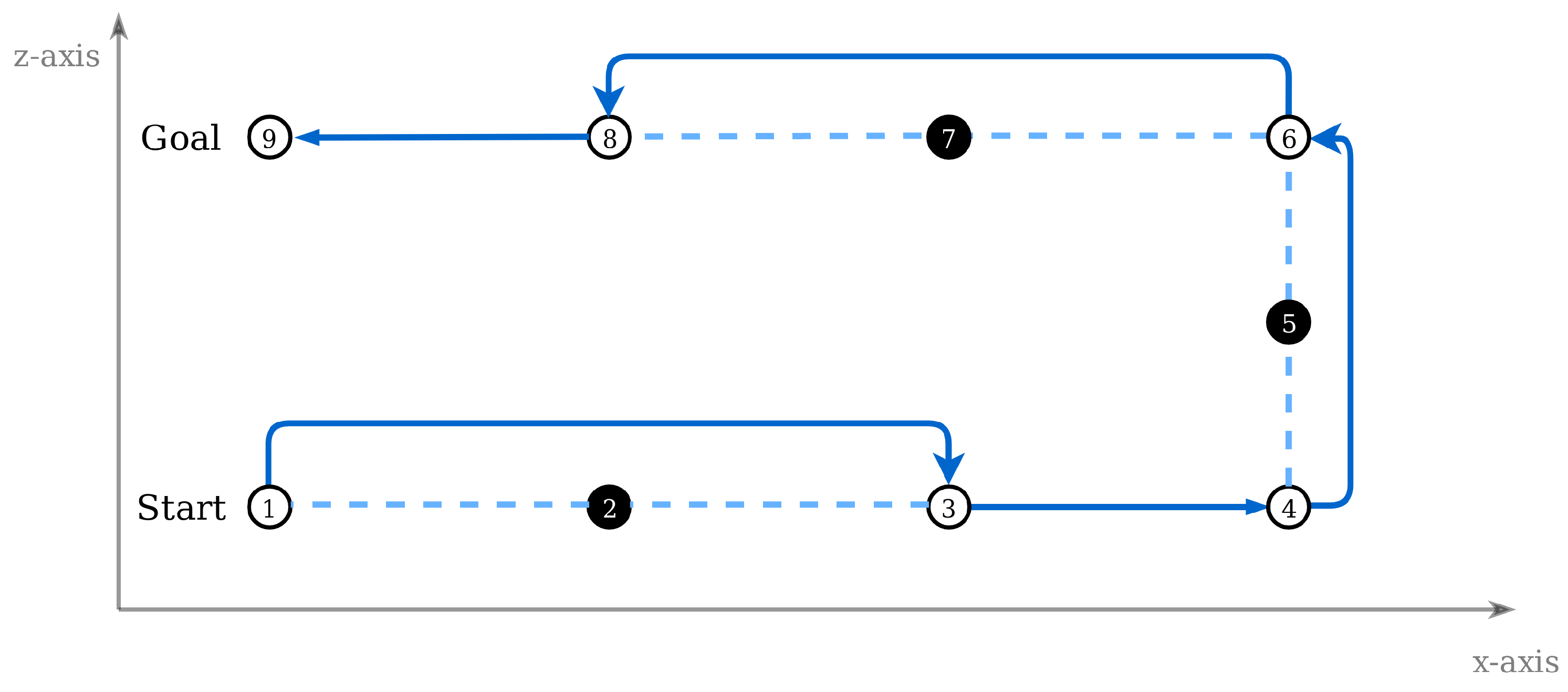
There is one last step involved in the path processing. All targets are sequentially checked, and those that are redundant are removed. A node is considered to be redundant when it is located between two other nodes in the same direction, either x, y, or z, and their distance is equal to the sampling step. Figure 13 depicts this procedure, where targets 2, 5, and 7 are omitted, leading to the same goal with six targets instead of the initial set of nine. The benefits of this process are (i) the reduction of waypoints and, thus, less data saved in memory, and (ii) smoother and continuous drone movement, as fewer speed reductions that are performed in each goal will be needed.
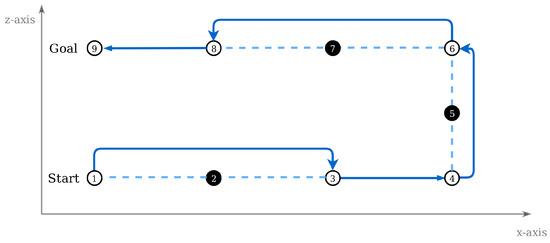
Figure 13.
Omitting redundant targets in path processing.
Once the final set of targets has been defined, the drone is now able to traverse through them. As aforementioned, the OMPL library with the RRT* algorithm is responsible for creating local paths between two successive targets. An assumption was made regarding the targets succession: the UAV does not need to reach the target’s position exactly, but needs to be within a specific range in order to consider the node visited and receive the next goal. This range is defined as a system parameter and is equal to for translation and for rotation. Once all nodes have been visited, the UAV returns to its initial position.
5. Experimental Results
In order to evaluate the proposed approaches’ performance, two separate experiments were performed, both in simulated environments in Gazebo. The first set of experiments concern the drone localization performance, whereas the second evaluates the full-coverage algorithms in terms of coverage percentage and time elapsed. All experiments were simulated and executed on a personal computer, equipped with an Intel Core i7-7500 processor, an Intel HD 620 Graphics card, and 8 GB of RAM, whilst the operating system was Ubuntu 16.04, 64 bit. Concerning the software libraries used, these included ROS Kinetic, Gazebo 7.0.0, OctoMap 1.8.1, and OMPL 1.2.1.
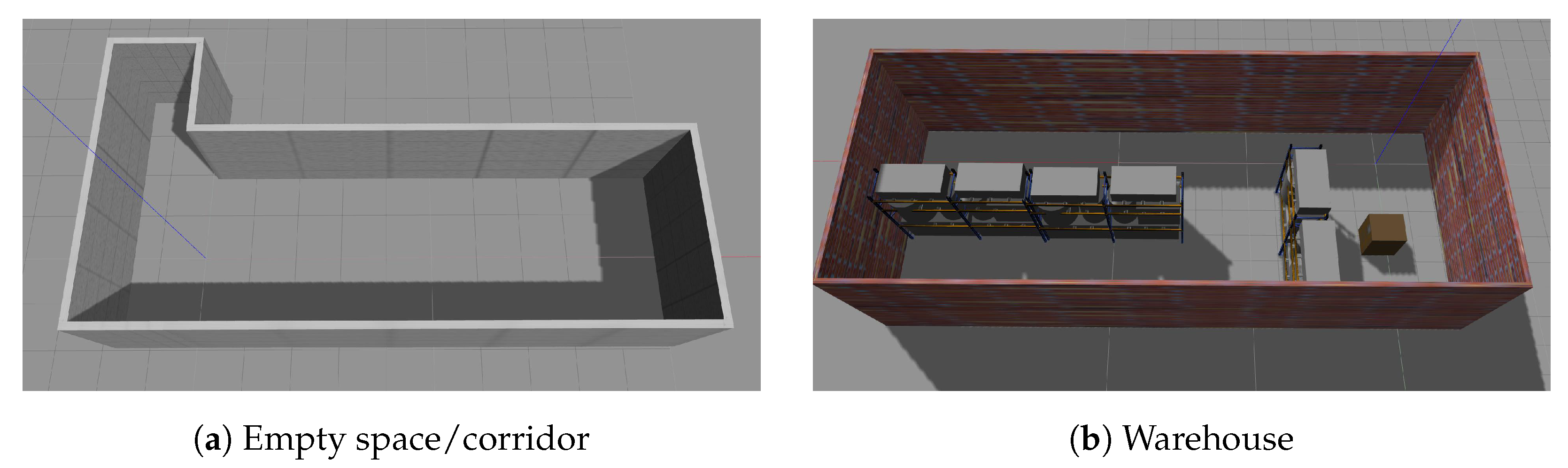
Two different environments were used to perform the experiments in the Gazebo simulator, the corridor and the warehouse, as shown in Figure 14a,b. The corridor’s dimensions are , while the warehouse’s are . The drone used was acquired from the Hector Quadrotor ROS stack, https://wiki.ros.org/hector_quadrotor (accessed on 22 May 2024). This specific model comprises an IMU, a barometer for simulating the pressure in different heights, a sonar altimeter sensor, a separate magnetometer, and a GPS receiver. Also, the developers provide optional camera and LiDAR sensors according to the requirements of each application. In our work, we used the predefined parameters of the drone’s kinematic and dynamic models [33], but the sensor parameters were modified to our needs (e.g., different ranges, FOVs, etc.). Specifically, the drone was equipped with a simulated TeraRanger Tower sensor array https://www.terabee.com/shop/lidar-tof-range-finders/teraranger-tower-evo/ (accessed on 22 May 2024), offering eight laser beams circumferentially to the drone with a maximum range of 14 m, a laser altimeter (by modifying the parameters of the given sonar altimeter), and the default IMU. Finally, since in our approach only localization is performed, the 3D maps were generated a priori using the RTAB-Map 3D SLAM https://introlab.github.io/rtabmap/ (accessed on 22 May 2024) [34] and a simulated Turtlebot robot https://wiki.ros.org/turtlebot_gazebo (accessed on 22 May 2024).
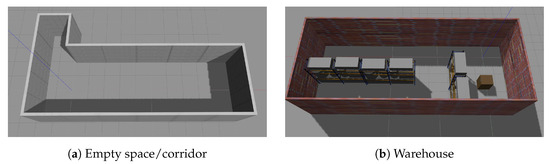
Figure 14.
Environments used for full-coverage experiments.
5.1. Localization Experiments
The purpose of these experiments is to calculate the difference between the position estimation of the localization system and the ground truth position. The latter is provided by the GazeboRosP3D plugin http://docs.ros.org/electric/api/gazebo_plugins/html/group__GazeboRosP3D.html (accessed on 22 May 2024) in the Gazebo simulator, and it sends that information to the ROS topic. The localization module exports its position estimation to the ROS topic. In order to compare the results, both topics were recorded using the rosbag http://wiki.ros.org/rosbag (accessed on 22 May 2024), tools and were processed offline.
The localization module was tested for three different types of motion: (i) straight line; (ii) spiral; (iii) meander, and three different maximum velocity values. For each experiment, five iterations were performed, and their mean was calculated.
The entirety of particles was used to export the final position belief. The parameters used for the localization algorithm are described in Table 1 and were experimentally defined. These values were kept stable throughout the simulations.

Table 1.
Parameters values used for the localization module.
During the simulations, the position error in every axis was recorded, as well as the orientation error with the corresponding timestamp. Using these data, the following metrics were calculated:
5.1.1. Moving in a Straight Line
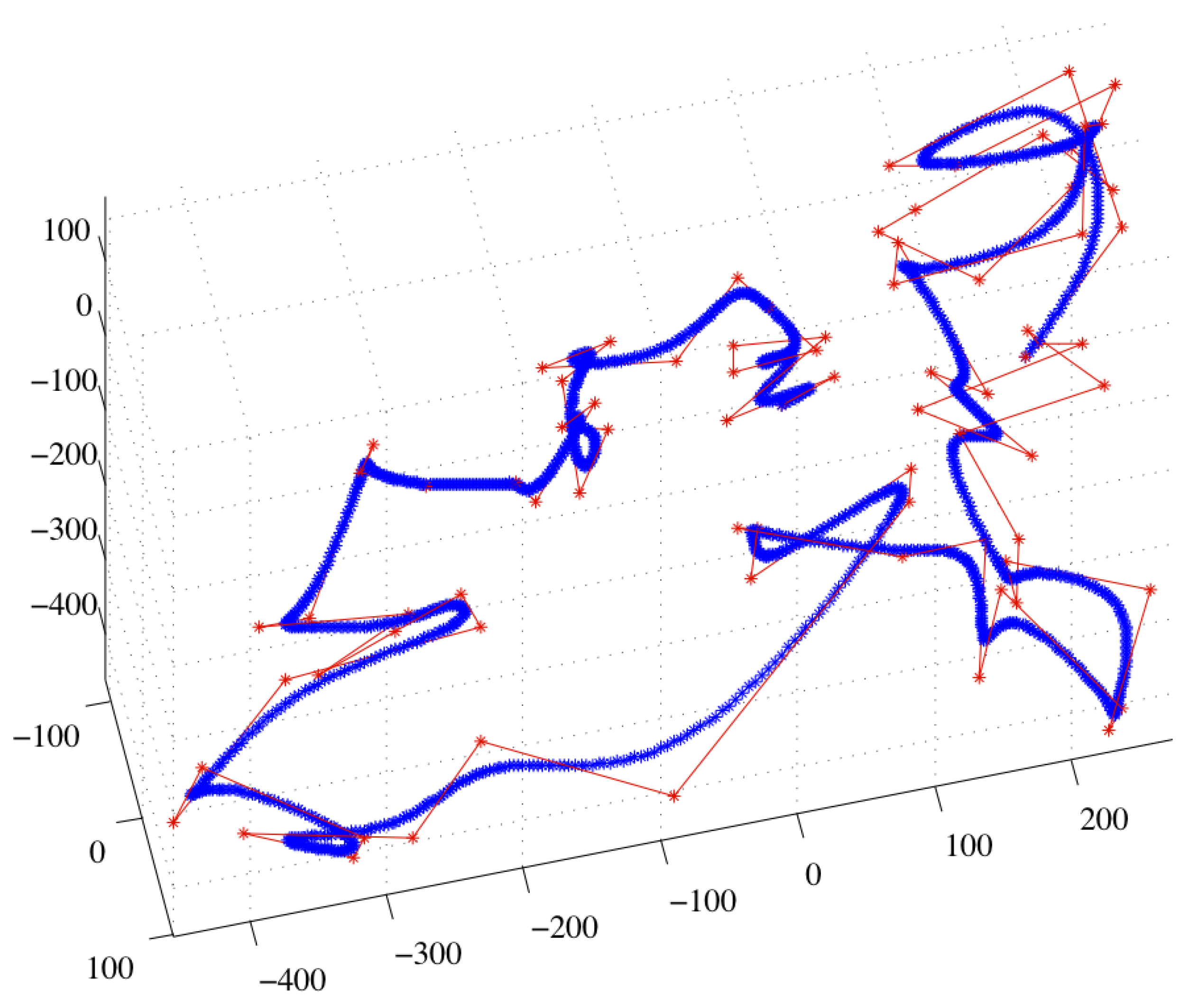
Straight movement was tested in two different environments, a corridor and a warehouse. The drone, after reaching a specific height, had to move through several targets and enter the hovering mode in the last one. Figure 15a,b depict this motion in both environments.

Figure 15.
Moving in a straight line.
In this case, the orientation error was also calculated, but since it was almost zero in all tests, regardless of the environment and the moving speed, it is not included in the results tables. This behavior was expected, since the drone does not perform any turns and the orientation is directly received from the IMU sensor. As shown in Table 2, the lowest position error appears when the drone moves with the lowest speed, both in the corridor and the warehouse. Apart from the main value, the maximum value also remains low, whereas when the UAV flies with the high speed, the position error can be instantaneously high.

Table 2.
Average metric values of position error (in meters). Green cells indicate the lowest error for the specific velocity setup.
5.1.2. Moving in a Spiral Pattern
The next case examined is movement in a spiral pattern. Specifically, the drone was moving in a circular path directed upwards, since every target was in a higher position than its previous. During these tests, the orientation was kept stable and the same as the initial one. Therefore, the following simulations examine the system, while the drone changes its x, y, and z coordinates at the same time. The environments used were an empty room and a warehouse (Figure 16).

Figure 16.
Moving in a spiral line.
The localization results are presented in Table 2 and Table 3 for each case. The orientation error is mentioned only for the warehouse, as for the empty environment it remained almost zero in all tests. Despite the fact that the position is constantly changing, the estimation remains stable. Specifically, moving with a normal velocity results in a lower position error in all cases, as well as the slow speed tests. Also, the orientation error may present momentary higher values, but its mean remains low, and as a result, the localization system does not become affected.

Table 3.
Average metric values of orientation error (in radians). Green cells indicate the lowest error for the specific velocity setup.
5.1.3. Moving in a Meander Pattern
The last case examined is moving in a meander pattern. The drone followed a set of targets, which are depicted in Figure 17a,b for each environment. The order of succession is from the low and outer points towards the inner and higher ones. Also, during this movement, the drone’s orientation changes in every target, aiming for the next one.

Figure 17.
Moving in a meander.
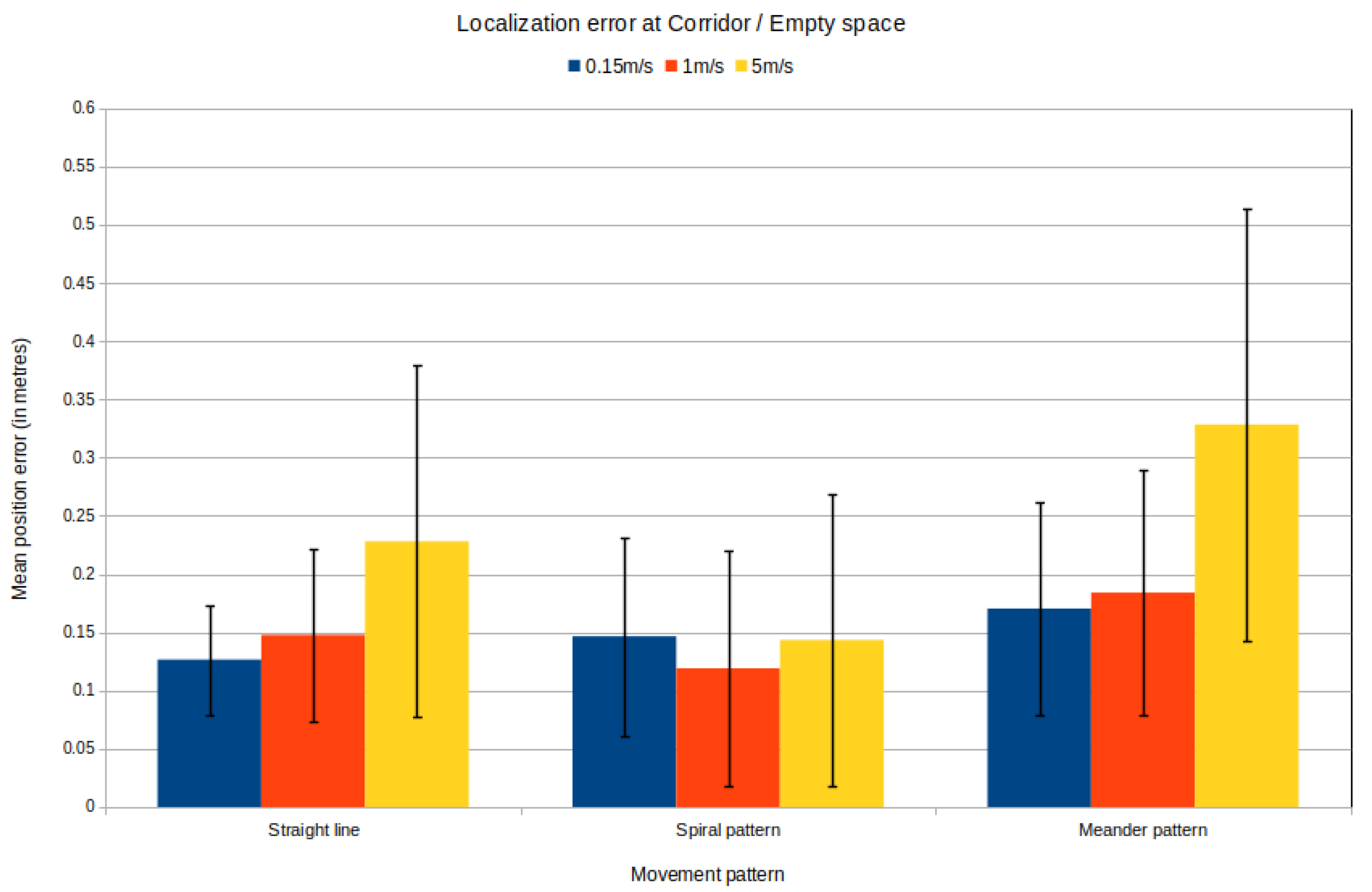
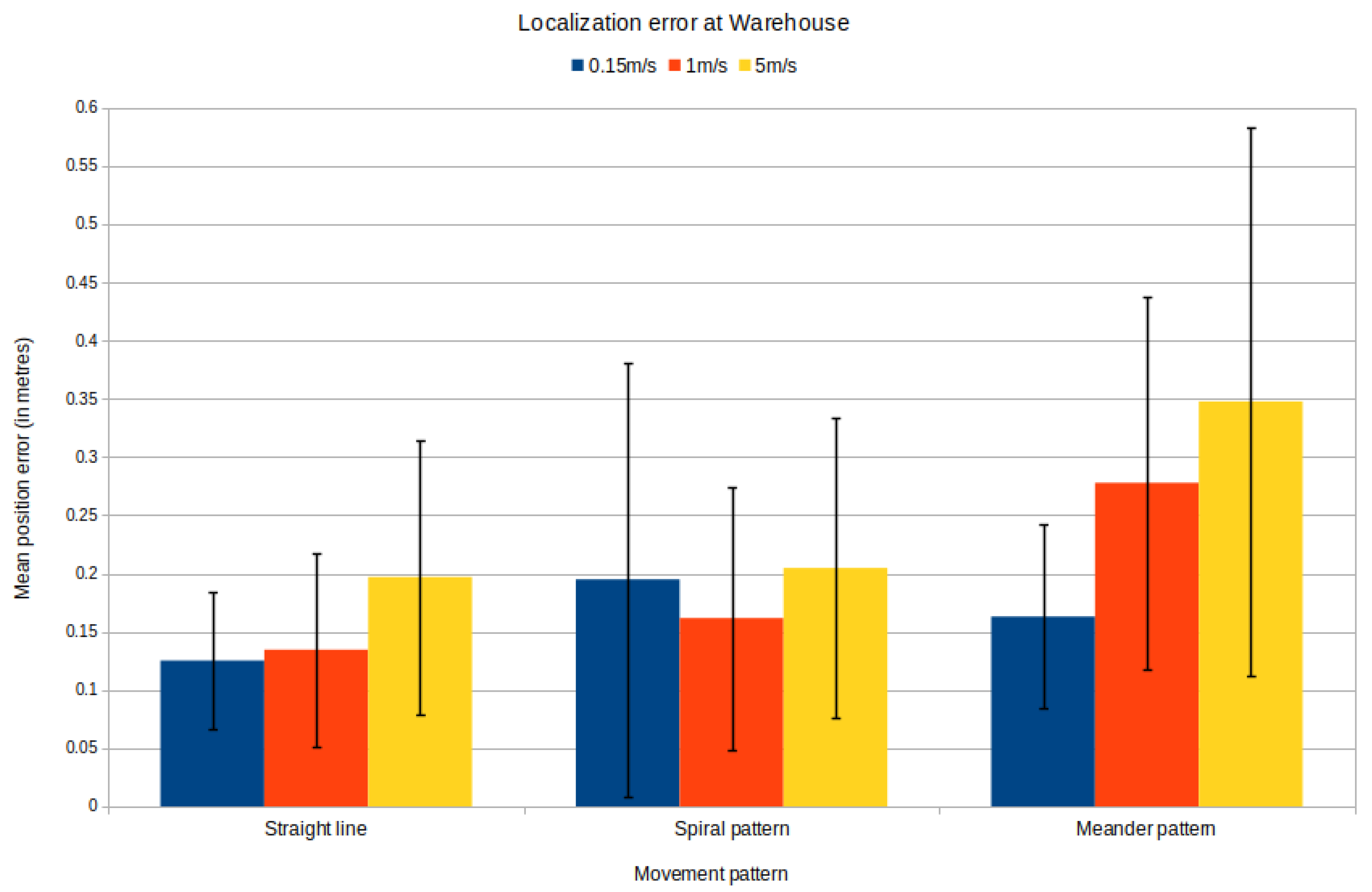
This case presents the highest error from all the previous experiments, as shown in Figure 18 and Figure 19. Nevertheless, the small velocity also leads to the lowest position and orientation error. It is worth noting that during the high speed movement, the error presents a high variance, leading to a nonstable motion.
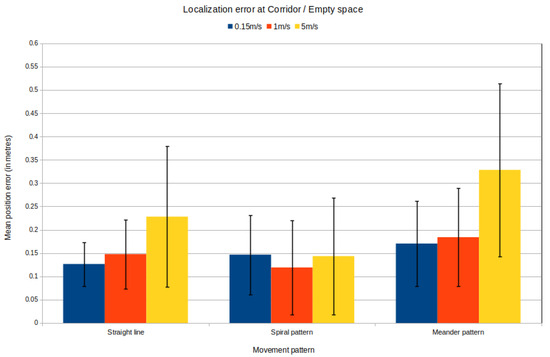
Figure 18.
Localization errors in corridor/empty space.
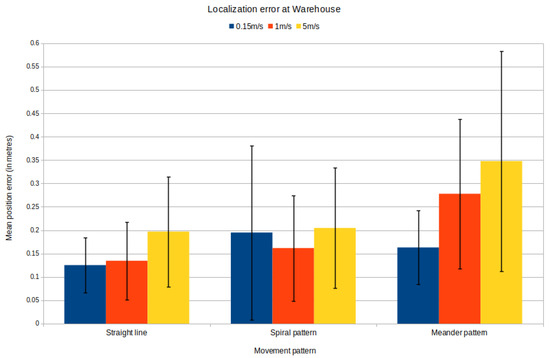
Figure 19.
Localization errors in warehouse.
5.2. Full-Coverage Experiments
The purpose of the full-coverage experiments is the calculation of the area percentage that was covered within the environment, as well as the time needed for this process. Again, the experiments were conducted in the corridor and the warehouse environments, and the sensor responsible for covering the environment was a simplified, simulated RFID antenna in two variations (narrow and wide), described by the parameters shown in Table 4.

Table 4.
RFID antenna parameters.
In order to define the set of waypoints that the drone had to visit, different sampling steps were used depending on the environment and the sensor type used in each case. We applied a shorter sampling step for the corridor in comparison to the warehouse environment, due to their size difference. Applying a larger step for small areas, such as the corridor, will result in a small number of waypoints that cannot ensure truly full coverage.
Given the waypoints, a prior coverage estimation is executed. For each position and for the specific angle that was chosen, we calculate the number of OctoMap nodes that are within the sensor’s FOV at least once. The result of this is divided over the total number of nodes that the map contains to output the Coverage Estimation. But the real area that will be covered after the coverage process is obviously larger. This is due to the fact that the drone, while moving between different targets, also crosses other areas that have not been explicitly defined, leading to more nodes within the FOV than expected. We define this as Real Coverage.
A comparison is made between the results that occurred using the horizontal (slice) and the vertical (lift) method of connection, as described in Section 4.5. It is necessary to ensure that the localization system is working and is supporting safe and stable navigation throughout the environment. The maximum speed used in all experiments is the slow one, as it provides the lowest error for every type of movement, according to Section 5.1.
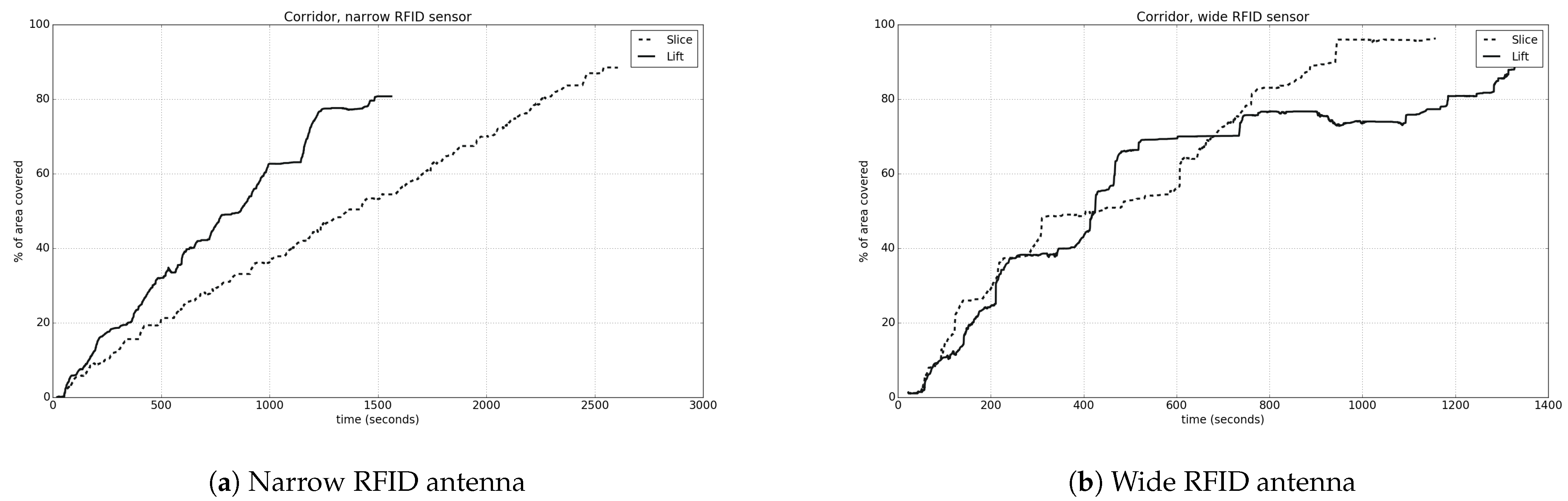
To begin with, all the experiments for the corridor environment will be examined. In Figure 20a,b, the coverage percentage in relation to time is depicted, comparing the connection of targets for both narrow and wide RFID type. The results are shown in detail in Table 5.
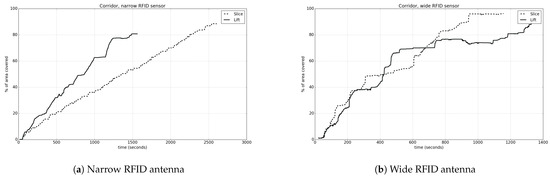
Figure 20.
Coverage percentage in relation to time for the corridor environment.

Table 5.
Assessing full coverage for corridor environment.
We observe that when using a wide sensor type, the coverage results are better, and full coverage is achieved in a shorter period of time, as expected. In the case of using a narrow sensor type, there is a linear correlation between the coverage percentage and time, while in the opposite case, the coverage curve is similar to the logarithmic.
It is worth noting the difference that exists between the different ways of connecting the targets, according to the sensor type. Specifically, when the sensor has a narrow FOV, the vertical connection leads to a lower coverage percentage, but needs more time to be completed. In contrast, when using a wide FOV, the horizontal connection of waypoints leads to a higher percentage of covered area with a faster process. The difference observed between the coverage estimation and the real one arises due to the fact that the drone surpasses more positions in the environment than the limited predefined goals that have been calculated. This way, it is able to detect more targets that had not been included in the target set.
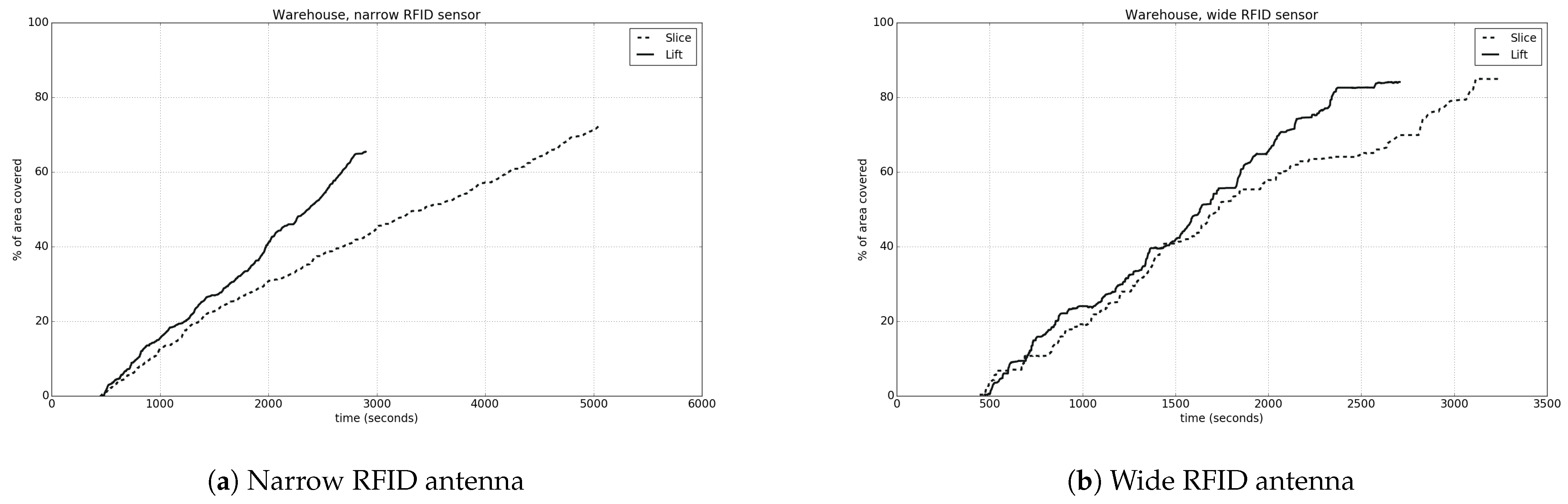
Figure 21a,b and Table 6 present the results for the warehouse environment. In this case, the sampling step used was higher than the previous one, since the environment is larger in size. For both sensor types, we observe that the coverage curves also have the same attitude as before. Irrespective of the wide or narrow field of view, using the vertical connection leads to a more quick completion of the coverage process. Nevertheless, when the horizontal connection is used, the final coverage percentage is higher. On the other hand, when this is combined with a narrow FOV, there is a great difference in the total time needed, due to the many different height levels that the drone must reach. In all cases, it is typical that there is a difference between the real coverage and its estimation.
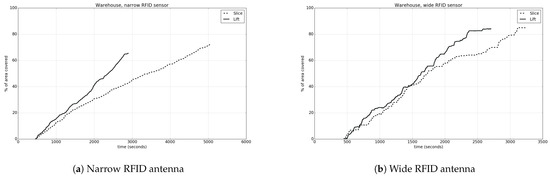
Figure 21.
Coverage percentage in relation to time for the warehouse environment.

Table 6.
Assessing full coverage for warehouse environment.
In the warehouse, as it presents a more complex environment with several features, the total coverage percentage is less than the ideal for full coverage. This happens due to the 3D map’s peculiarities, i.e., the existence of points–nodes that cannot be detected by the drone and were also not removed with the post-processing procedure previously described.
5.3. Practical Considerations
At this point, it is important to state that when the aforementioned approach is to be deployed in a real drone, several additional steps have to be followed for the performance to be optimal.
5.3.1. IMU Calibration Procedure
The first regards the IMU calibration, which was omitted from our experiments as the drone was simulated in Gazebo. In reality, prior to the drone deployment, a careful calibration of the IMU must be performed so as to avoid large errors or drifts and to ensure accurate sensor readings. The most common approach to calibrate an IMU initiates with visiting the IMU manual in order to better understand the parameters that mostly affect the specific device. Then, the IMU should be placed in a stable, horizontal position and perform calibration of the individual sensors that it contains. For example, zero-rate bias and scale factor calibration should be performed for the gyroscope, zero-g bias and scale factor calibration should be performed for the accelerometer, and magnetometer calibration should be executed (if applicable). Then, the calibration parameters must be applied in the real hardware and be validated. Finally, the IMUs usually require a periodical calibration to be performed, since they are affected by environmental factors such as temperature or aging.
5.3.2. Computational Resources Requirements
Another important issue to discuss regards the computational resources needed to deploy the suggested methodology, since real drones are usually equipped with embedded devices having significantly less power than the PC used in our experiments. Even though modern embedded devices have become quite small in size, require minimal power consumption, and are quite powerful, it makes sense to provide some comments regarding the computational requirements of each algorithm. Our approach consists of the following software modules:
- Drone navigation using RRT* and a PID controller: The RRT* algorithm is expected to have a slower performance in a computationally weaker system; nevertheless, the increase in computation time is considered negligible, since RRT* (a) ensures convergence in a finite time, and (b) can be parameterized so as to perform fewer iterations. Concerning the PID, since its operation resides in the utilization of closed-form equations, no performance reduction is expected.
- Drone localization using a particle filter: As known, the performance of a particle filter is directly affected by the number of particles selected. Furthermore, it makes sense that the computational requirements to execute the particle filter linearly increase to the selected number of particles, as the same computations need to occur for each particle. This being said, it must be noted that our solution implements position tracking localization, where the initial drone pose is considered known at the start of the experiment and the particle filter keeps track of the future poses, given the drone controls and the sensors measurements. The position tracking localization problem requires significantly fewer particles than the global localization problem, where the initial drone position is unknown and a large number of particles is spread in the unoccupied areas of the environment. In the latter case, the position estimator algorithm performance would decrease quadratically to the environment’s dimensions. Conclusively, since we implement position tracking, the computational requirements will increase if an embedded device is to be used, but this problem can be mitigated by decreasing the number of the particles, with no expected performance loss in the position estimation.
- Calculation of targets towards full 3D coverage: The targets extraction process given an Octomap includes the subsampling of the 3D space, the filtering of the samples that are near the vertical walls (which need to be covered), and the calculation of the orientation vector vertical to the wall for all of them. All of these algorithms require a single pass on all samples (algorithmic complexity ); thus, no significant computational increase is expected. Concerning the computation of the optimal path that traverses the aforementioned targets, the combination of nearest neighbor and hill climbing algorithms is applied. Since the second algorithm is usually computationally intensive, the performance is expected to significantly drop. Nevertheless, in the logistics applications the environment is considered static; therefore, the total path calculation can be performed only once, and not necessarily using the drone’s resources. Then, the computed path can be utilized as is in the future deployments of the drone.
5.3.3. Parameters Value Determination
Regarding the parameters used throughout the experiments, their values should be set according to a systematic approach or a specific line of thought. Specifically:
- Localization—Number of particles: The number of particles should be large enough to accommodate the complexity of the environment and the possible errors of the measurement and motion models, but not too large, since significant computational resources will be needed.
- Localization—, , , , , coefficients: These are intrinsic parameters of the measurement device; therefore, when a real sensor is used, they should be either acquired from the sensor’s manual or be experimentally defined.
- Navigation—PID coefficients: When a real drone is to be used, the PID coefficients need to be set. The common practice is to perform an initial selection of the P, I, and D gains either based on the system dynamics or by using a method to specify the initial parameters, such as the Zeiger–Nichols [35]. Then, the parameters must be fine-tuned experimentally by using performance metrics like overshoot, rise time, settling time, etc.
5.3.4. Acceptable Coverage Rates
In the experiments section, two path traversal methodologies were described in order to perform full 3D coverage of the vertical surfaces, the horizontal and the vertical approach. There, we showcased that the horizontal strategy is recommended since in all conditions it reached coverage rates of over 90%, in comparison to the vertical strategy. This raises a question: Is the 90% coverage rage acceptable in realistic conditions? The acceptable percentage of coverage rate actually depends on the specific logistics application and the parameters of the coverage sensor used. For example, if a warehouse includes large boxes that need to be inventoried, there is no need for a high percentage of coverage (e.g., >80%), as the drone would detect most (if not all) of the boxes due to their size. On the contrary, if the warehouse contains many smaller packages, a high coverage rate is mandatory (e.g., >95%), since several packages will remain undetected. Finally, if a logistics application requires a very high coverage rate (e.g., >99%), the parameters of the target sampling algorithm can be altered (e.g., the sampling step) for the drone to be forced to perform denser coverage. Of course, this would lead to quite large deployment times; therefore, the exact parameterization must be performed according to the customer’s requirements. Finally, it should be stated that, realistically, 100% will never be reached, since targets placed in narrow parts of the environment will always exist, a fact that prevents the drone from reaching them due to its physical dimensions. Nevertheless, in reality, products will be placed on surfaces/shelves that do not exist in very narrow areas; thus, coverage rates lower than 100% do not result in loss of information.
6. Conclusions-Future Work
This work presents an autonomous system for solving the problem of low-cost and fast inventorying using a UAV. Initially, the localization problem was solved by implementing a particle filter algorithm that uses solely the distance measurements and the IMU sensor. Also, the full-coverage problem of a 3D known map was solved by first selecting the targets that the drone must traverse through and then reordering them in order to optimize the total path.
Overall, the main factors that affect the localization system are the speed of movement as well as the path pattern followed. When the drone is traveling with the slow speed, the position estimation is robust and the error is within accepted range. With regard to full coverage, using a sensor with a wide horizontal and vertical FOV is preferred, as it leads to a quicker and more complete coverage process. When the targets are connected in a vertical way, the coverage time is much less than the horizontal one, which leads to a higher final percentage of area covered.
This provides a good starting point for discussion and further research. Further studies should investigate the implementation of the adaptive Monte Carlo localization (AMCL) for a UAV, which will reduce the processing power needed and will also solve the global localization problem. Also, in order to use this system with a real drone, the implementation of visual odometry is essential. Additionally, if the localization precision is concerned, the utilization of more advanced methods should be considered, and/or the employment of external (environmental) position tracking systems like UWB, that, in collaboration with the existing sensors, would offer smaller localization errors. Of course, this course of action would increase the total cost of the solution. Finally, a thorough comparison of these methods to the proposed one should be made, so as to infer if the complexity/cost increase is justified against the accuracy benefits.
Another comment on the decisions made in this work is that a PID controller was implemented towards the proper navigation of the drone. This decision was made since (a) PID is quite simpler in implementation and understanding in comparison to more advanced techniques, (b) it is quite robust in simple scenarios where no significant external disturbances are expected (despite their general sensitivity to noise), a fact that applies in indoor scenarios, (c) it is computationally cheap to implement, and (d) established approaches towards its manual or automatic tuning exist. Nevertheless, it should be stated that more advanced controllers should be used and evaluated towards their inferiority to the PID, such as the linear quadratic regulator (LQR) [36] or the model predictive control (MPC) [37], which have been proven to perform better in a wide variety of applications/environments.
Regarding the coverage system, plenty of additional modules could be created. A real-time coverage method could be implemented that, by using the area that has already been covered and the time limitations, will be able to define the next targets that will lead to better results and not just follow the initial plan. It is also interesting to research the existence of patterns and the usage of topological features in an environment. In addition, multiple drone coverage shall be of great interest, as their synchronization will lead to a really fast and effective full coverage. Last, but not least, it is important to research the power needs of a drone that strongly affect the flight plan.
Author Contributions
Conceptualization: K.T., E.T., and A.L.S.; methodology: K.T., E.T., and A.L.S.; software: K.T. and E.T.; validation: K.T. and E.T.; investigation: K.T.; writing—original draft preparation: K.T. and E.T.; writing—review and editing: E.T. and A.L.S.; visualization: K.T.; supervision: E.T. and A.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karaman, S.; Frazzoli, E. Sampling-based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Morgan, Q.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In ICRA Workshop on Open Source Software; 2009; Volume 3, p. 5. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=ROS%3A+An+open-source+Robot+Operating+System&btnG= (accessed on 22 May 2024).
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An Efficient Probabilistic 3D Mapping Framework Based on Octrees. Autonomous Robots. 2013. Available online: http://octomap.github.io (accessed on 22 May 2024).
- Perez-Grau, F.J.; Caballero, F.; Viguria, A.; Ollero, A. Multi-sensor three-dimensional Monte Carlo localization for long-term aerial robot navigation. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417732757. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Dellaert, F.; Thrun, S. Monte Carlo Localization: Efficient Position Estimation for Mobile Robots. Aaai/Iaai 1999, 1, 343–349. [Google Scholar]
- Stewart, A.D.; Newman, P. LAPS-localisation using appearance of prior structure: 6-DoF monocular camera localisation using prior pointclouds. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 2625–2632. [Google Scholar]
- Ok, K.; Greene, W.N.; Roy, N. Simultaneous tracking and rendering: Real-time monocular localization for MAVs. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4522–4529. [Google Scholar]
- D’ippolito, F.; Garraffa, G.; Sferlazza, A.; Zaccarian, L. A hybrid observer for localization from noisy inertial data and sporadic position measurements. Nonlinear Anal. Hybrid Syst. 2023, 49, 101360. [Google Scholar] [CrossRef]
- You, W.; Li, F.; Liao, L.; Huang, M. Data fusion of UWB and IMU based on unscented Kalman filter for indoor localization of quadrotor UAV. IEEE Access 2020, 8, 64971–64981. [Google Scholar] [CrossRef]
- Antonis, D.; Stavroula, S.; Emmanouil, T.; Loukas, P. Robotics Meets RFID for Simultaneous Localization (of Robots and Objects) and Mapping (SLAM)-A Joined Problem. In Wireless Power Transmission for Sustainable Electronics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; pp. 175–222. [Google Scholar] [CrossRef]
- Beul, M.; Krombach, N.; Nieuwenhuisen, M.; Droeschel, D.; Behnke, S. Autonomous Navigation in a Warehouse with a Cognitive Micro Aerial Vehicle; Springer International Publishing: Cham, Switzerland, 2017; pp. 487–524. ISBN 978-3-319-54927-9. [Google Scholar]
- Beul, M.; Droeschel, D.; Nieuwenhuisen, M.; Quenzel, J.; Houben, S.; Behnke, S. Fast Autonomous Flight in Warehouses for Inventory Applications. IEEE Robot. Autom. Lett. 2018, 3, 3121–3128. [Google Scholar] [CrossRef]
- Buffi, A.; Motroni, A.; Nepa, P.; Tellini, B.; Cioni, R. A SAR-Based Measurement Method for Passive-Tag Positioning With a Flying UHF-RFID Reader. IEEE Trans. Instrum. Meas. 2019, 68, 845–853. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, S.; Jain, S.; Dubey, G.; Roth, S.; Maeta, S.M.; Nuske, S.T.; Wu, Y.; Scherer, S. Robust Autonomous Flight in Constrained and Visually Degraded Shipboard Environments. J. Field Robot. 2017, 34, 25–52. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Nam, L.H.; Huang, L.; Li, X.J.; Xu, J.F. An approach for coverage path planning for UAVs. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; pp. 411–416. [Google Scholar]
- Bircher, A.; Kamel, M.S.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Three-dimensional coverage path planning via viewpoint resampling and tour optimization for aerial robots. Auton. Robot. 2015, 40, 11. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Gan, D.; Dias, J.; Zweiri, Y.; Seneviratne, L. Coverage Path Planning with Adaptive Viewpoint Sampling to Construct 3D Models of Complex Structures for the Purpose of Inspection. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7047–7054. [Google Scholar] [CrossRef]
- Yang, S.X.; Luo, C. A neural network approach to complete coverage path planning. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2004, 34, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Di Franco, C.; Buttazzo, G. Coverage Path Planning for UAVs Photogrammetry with Energy and Resolution Constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Tolstaya, E.; Paulos, J.; Kumar, V.; Ribeiro, A. Multi-robot coverage and exploration using spatial graph neural networks. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8944–8950. [Google Scholar]
- Papaioannou, S.; Kolios, P.; Theocharides, T.; Panayiotou, C.G.; Polycarpou, M.M. Unscented optimal control for 3d coverage planning with an autonomous uav agent. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 703–712. [Google Scholar]
- Chen, J.; Du, C.; Zhang, Y.; Han, P.; Wei, W. A clustering-based coverage path planning method for autonomous heterogeneous UAVs. IEEE Trans. Intell. Transp. Syst. 2021, 23, 25546–25556. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, Y.; Briceno, S.; Mavris, D.N. Energy-constrained multi-UAV coverage path planning for an aerial imagery mission using column generation. J. Intell. Robot. Syst. 2020, 97, 125–139. [Google Scholar] [CrossRef]
- Theile, M.; Bayerlein, H.; Nai, R.; Gesbert, D.; Caccamo, M. UAV coverage path planning under varying power constraints using deep reinforcement learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1444–1449. [Google Scholar]
- Chen, J.; Ling, F.; Zhang, Y.; You, T.; Liu, Y.; Du, X. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Sucan, I.A.; Moll, M.; Kavraki, L.E. The Open Motion Planning Library. IEEE Robot. Autom. Mag. 2012, 19, 72–82. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Liu, J.S. Metropolized independent sampling with comparisons to rejection sampling and importance sampling. Stat. Comput. 1996, 6, 113–119. [Google Scholar] [CrossRef]
- Douc, R.; Cappe, O. Comparison of resampling schemes for particle filtering. In ISPA 2005, Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis, Zagreb, Croatia, 15–17 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 64–69. [Google Scholar] [CrossRef]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Department of Computer Science, Iowa State University: Ames, IA, USA, 1999. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. SSC4 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Johannes, M.; Sendobry, A.; Kohlbrecher, S.; Klingauf, U.; Von Stryk, O. Comprehensive simulation of quadrotor uavs using ros and gazebo. In Simulation, Modeling, and Programming for Autonomous Robots, Proceedings of the Third International Conference, SIMPAR 2012, Tsukuba, Japan, 5–8 November 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 400–411. [Google Scholar]
- Mathieu, L.; Michaud, F. RTAB-Map as an open-source lidar and visual simultaneous localization and mapping library for large-scale and long-term online operation. J. Field Robot. 2019, 36, 416–446. [Google Scholar]
- Hang, C.C.; Åström, K.J.; Ho, W.K. Refinements of the Ziegler—Nichols tuning formula. IEEE Proc. D (Control. Theory Appl.) 1991, 138, 111–118. [Google Scholar] [CrossRef]
- Norman, L.; Sandell, N.J.A.M.; Athans, M. Robustness results in linear-quadratic Gaussian based multivariable control designs. IEEE Trans. Autom. Control 1981, 26, 75–93. [Google Scholar]
- Qin, J.S.; Badgwell, T.A. An Overview of Industrial Model Predictive Control Technology; AIche Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1997; Volume 93, pp. 232–256. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).