Imitation Learning from a Single Demonstration Leveraging Vector Quantization for Robotic Harvesting
Abstract
1. Introduction
- We implement a one-shot IL agent that is capable of mushroom harvesting using a straightforward sensorial stream that is cheap to obtain. The agent operates directly on RGB images from a single camera embedded within the palm of the gripper with no pre-processing, other than downscaling, and the position coordinates of the cartesian robot carrying the gripper. Our method requires no 3D information or camera calibration. No engineering work needs to be carried out apart from collecting ~20 mins worth of data.
- We introduce a Vector Quantization module that is shown to provide significant performance improvement in terms of mushroom picking success rates. We benchmark against [10], a one-shot IL method that was tested on toy tasks in highly controlled conditions without distractors. Our method is sufficiently robust to achieve a 100% success rate in mushroom picking in a realistic environment in the presence of distractors.
- We test our approach on a real robot, featuring a soft, pneumatically actuated gripper, shown in Figure 1, and mushrooms of varying sizes. To the best of our knowledge, this is the first implementation of a one-shot IL pipeline on a real setup for mushroom harvesting. This is in contrast to [11], where the IL pipeline required 80 demonstrations and it was only tested in simulated environments.
2. Background and Related Work
3. Materials and Methods
3.1. Imitation Learning Architecture
3.2. Experiments
3.2.1. Mushroom Picking Environment
3.2.2. Robotic System
3.2.3. Data Collection
- The target mushroom is randomly placed on the soil and a number of other mushrooms are randomly placed around it. All mushrooms are 30–50 mm in cap diameter.
- The gripper is manually moved in a position that allows for firm grasping, i.e., with the fingers around the target mushroom.
- The gripper is then moved upwards in a conical spiral with its position and the corresponding image from the in-hand camera recorded at regular intervals. Each observation–relative target position () is stored. The radius and the slope of the conical spiral are randomized in each data collection.
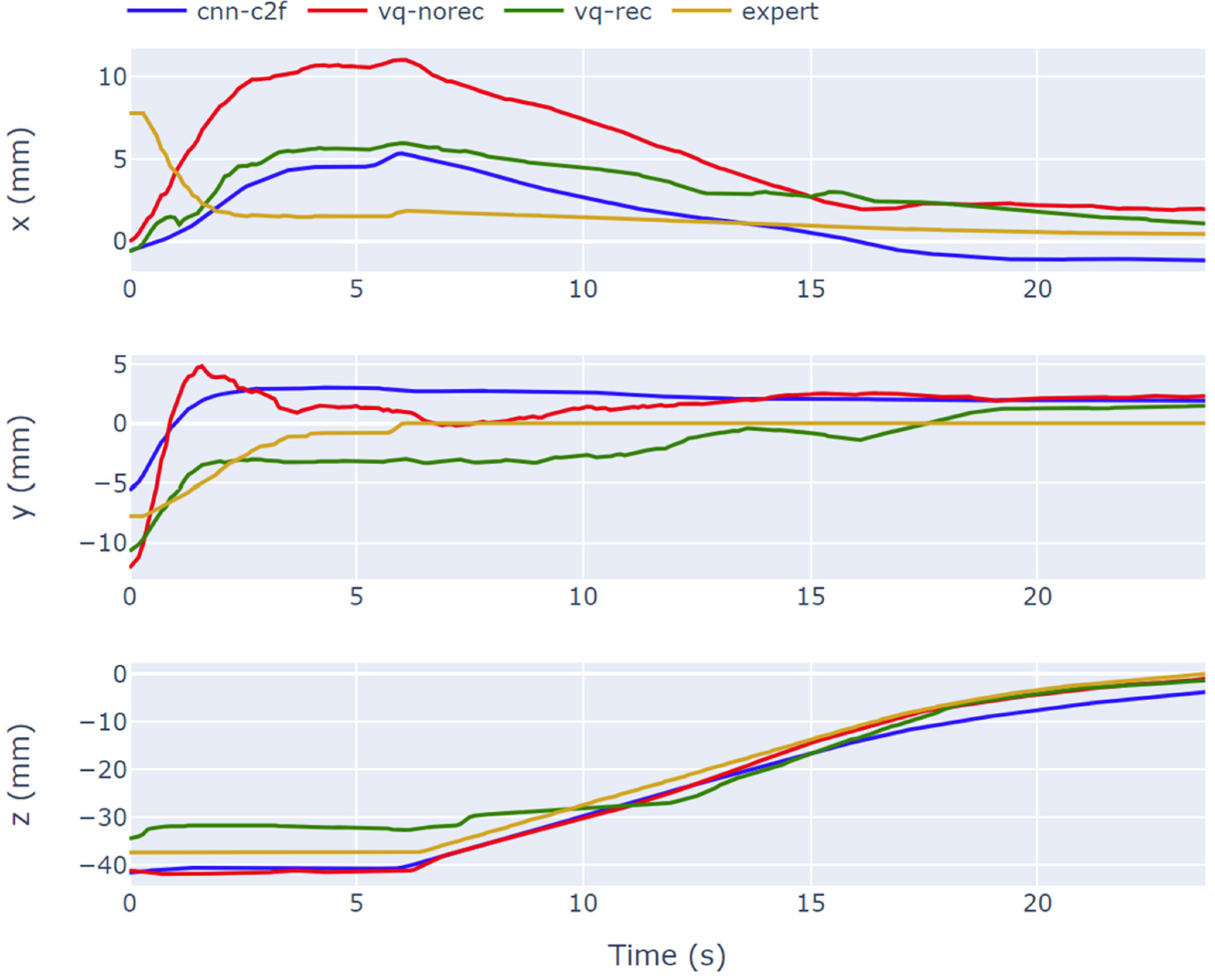
3.2.4. Benchmarks
- A convolutional model following the coarse-to-fine approach of [10] from which our own approach draws inspiration. We refer to this approach as cnn-c2f.
- A simpler variant of our approach where the Image Decoder and the respective loss have been removed to establish the merit of using the Vector Quantization module. This approach is termed vq-norec.
- A non-IL based approach where visual servoing is accomplished leveraging YOLOv5 [39], a well-trusted object detector to detect the mushrooms on the scene, and a controller is programmed to move the gripper to minimize the error between the center of the image and the center of the bounding box of the mushroom closer to the center of the image. This approach is detailed in [8] and we refer to it as yolo-vs.
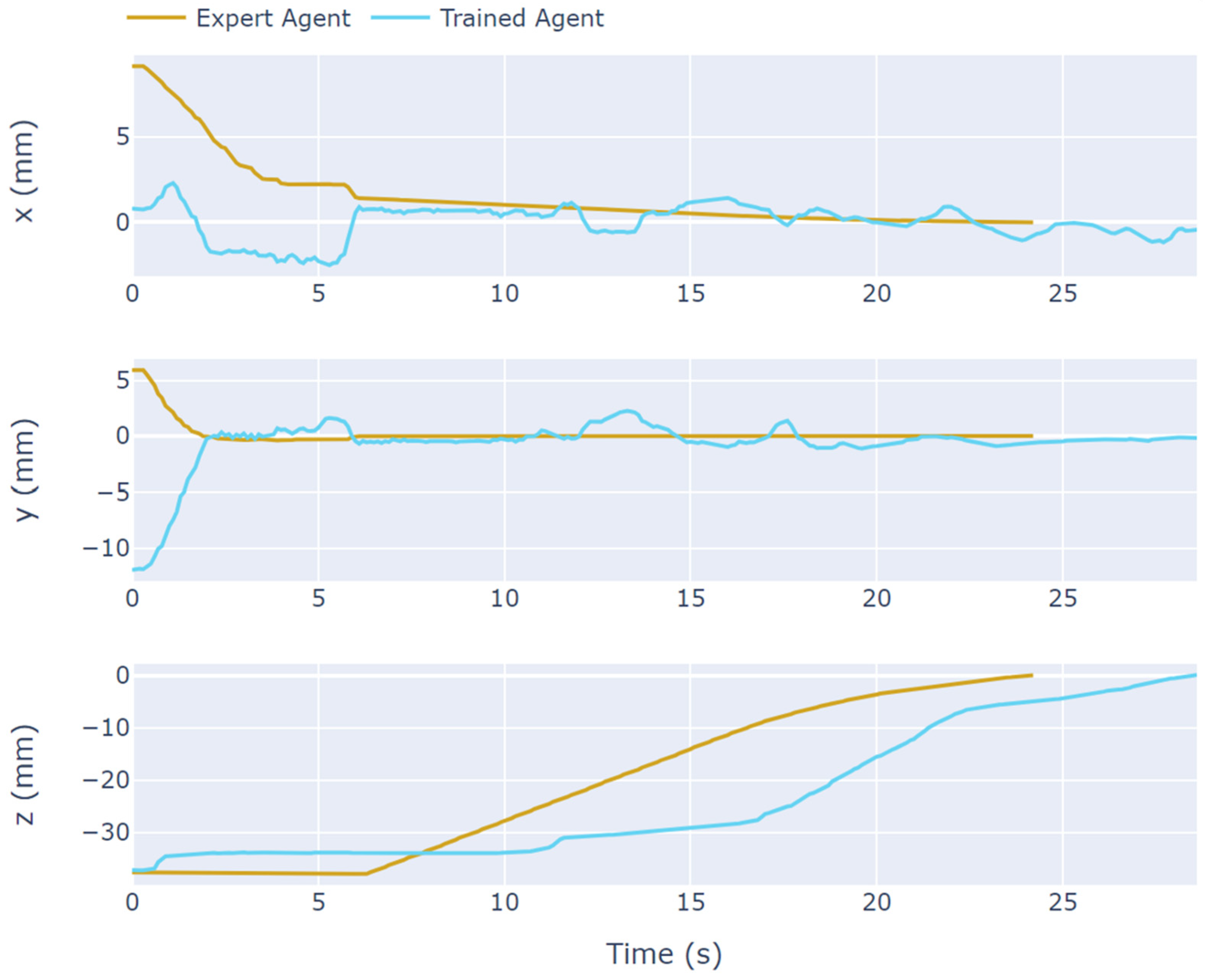
4. Results
5. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, Y.; Chen, X.; Edu, C.X.B.; Schulman, J.; Abbeel, P.; Edu, P.B. Benchmarking Deep Reinforcement Learning for Continuous Control. arXiv 2016, arXiv:1604.06778. [Google Scholar]
- Ravichandar, H.; Polydoros, A.S.; Chernova, S.; Billard, A. Recent Advances in Robot Learning from Demonstration. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 297–330. [Google Scholar] [CrossRef]
- Huang, M.; He, L.; Choi, D.; Pecchia, J.; Li, Y. Picking dynamic analysis for robotic harvesting of Agaricus bisporus mushrooms. Comput. Electron. Agric. 2021, 185, 106145. [Google Scholar] [CrossRef]
- Carrasco, J.; Zied, D.C.; Pardo, J.E.; Preston, G.M.; Pardo-Giménez, A. Supplementation in Mushroom Crops and Its Impact on Yield and Quality. AMB Express 2018, 8, 146. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Ji, J.; Cai, H.; Chen, H. Modeling and Force Analysis of a Harvesting Robot for Button Mushrooms. IEEE Access 2022, 10, 78519–78526. [Google Scholar] [CrossRef]
- Mohanan, M.G.M.M.G.; Salgaonkar, A.S.A. Robotic Mushroom Harvesting by Employing Probabilistic Road Map and Inverse Kinematics. BOHR Int. J. Internet Things Artif. Intell. Mach. Learn. 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Yin, H.; Yi, W.; Hu, D. Computer Vision and Machine Learning Applied in the Mushroom Industry: A Critical Review. Comput. Electron. Agric. 2022, 198, 107015. [Google Scholar] [CrossRef]
- Mavridis, P.; Mavrikis, N.; Mastrogeorgiou, A.; Chatzakos, P. Low-Cost, Accurate Robotic Harvesting System for Existing Mushroom Farms. IEEE/ASME Int. Conf. Adv. Intell. Mechatron. AIM 2023, 2023, 144–149. [Google Scholar] [CrossRef]
- Bissadu, K.D.; Sonko, S.; Hossain, G. Society 5.0 Enabled Agriculture: Drivers, Enabling Technologies, Architectures, Opportunities, and Challenges. Inf. Process. Agric. 2024; in press. [Google Scholar] [CrossRef]
- Johns, E. Coarse-to-Fine Imitation Learning: Robot Manipulation from a Single Demonstration. Proc. IEEE Int. Conf. Robot. Autom. 2021, 2021, 4613–4619. [Google Scholar] [CrossRef]
- Porichis, A.; Vasios, K.; Iglezou, M.; Mohan, V.; Chatzakos, P. Visual Imitation Learning for Robotic Fresh Mushroom Harvesting. In Proceedings of the 2023 31st Mediterranean Conference on Control and Automation, MED 2023, Limassol, Cyprus, 26–29 June 2023; pp. 535–540. [Google Scholar] [CrossRef]
- Ng, A.Y.; Russel, S.J. Algorithms for Inverse Reinforcement Learning. In Proceedings of the ICML ’00 17th International Conference on Machine Learning, San Francisco, CA, USA, 29 June–2 July 2000; pp. 663–670. [Google Scholar]
- Finn, C.; Levine, S.; Abbeel, P. Guided Cost Learning: Deep Inverse Optimal Control via Policy Optimization. arXiv 2016, arXiv:1603.00448. [Google Scholar]
- Das, N.; Bechtle, S.; Davchev, T.; Jayaraman, D.; Rai, A.; Meier, F. Model-Based Inverse Reinforcement Learning from Visual Demonstrations. arXiv 2021, arXiv:2010.09034. [Google Scholar]
- Haldar, S.; Mathur, V.; Yarats, D.; Pinto, L. Watch and Match: Supercharging Imitation with Regularized Optimal Transport. arXiv 2022, arXiv:2206.15469. [Google Scholar] [CrossRef]
- Sermanet, P.; Lynch, C.; Chebotar, Y.; Hsu, J.; Jang, E.; Schaal, S.; Levine, S.; Brain, G. Time-Contrastive Networks: Self-Supervised Learning from Video. In Proceedings of the IEEE International Conference on Robotics and Automation, Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 1134–1141. [Google Scholar]
- Ho, J.; Ermon, S. Generative Adversarial Imitation Learning. Adv. Neural. Inf. Process Syst. 2016, 29, 4572–4580. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2014, 63, 139–144. [Google Scholar] [CrossRef]
- Dadashi, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Wasserstein, O.P.P. Primal Wasserstein Imitation Learning. In Proceedings of the ICLR 2021—Ninth International Conference on Learning Representations, Virtual, 4 May 2021. [Google Scholar]
- Pomerleau, D.A. ALVINN: An Autonomous Land Vehicle in a Neural Network. Adv. Neural. Inf. Process Syst. 1988, 1, 305–313. [Google Scholar]
- Rahmatizadeh, R.; Abolghasemi, P.; Boloni, L.; Levine, S. Vision-Based Multi-Task Manipulation for Inexpensive Robots Using End-to-End Learning from Demonstration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 3758–3765. [Google Scholar] [CrossRef]
- Florence, P.; Lynch, C.; Zeng, A.; Ramirez, O.A.; Wahid, A.; Downs, L.; Wong, A.; Lee, J.; Mordatch, I.; Tompson, J. Implicit Behavioral Cloning. In Proceedings of the 5th Conference on Robot Learning, PMLR, Zurich, Switzerland, 29–31 October 2018; pp. 158–168. [Google Scholar]
- Janner, M.; Li, Q.; Levine, S. Offline Reinforcement Learning as One Big Sequence Modeling Problem. Adv. Neural. Inf. Process Syst. 2021, 2, 1273–1286. [Google Scholar] [CrossRef]
- Shafiullah, N.M.; Cui, Z.; Altanzaya, A.A.; Pinto, L. Behavior Transformers: Cloning $ k $ Modes with One Stone. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 16 May 2022; pp. 22955–22968. [Google Scholar]
- Zhao, T.Z.; Kumar, V.; Levine, S.; Finn, C. Learning Fine-Grained Bimanual Manipulation with Low-Cost Hardware. In Proceedings of the Proceedings of Robotics: Science and Systems, Daegu, Republic of Korea, 23 April 2023. [Google Scholar]
- Shridhar, M.; Manuelli, L.; Fox, D. Perceiver-Actor: A Multi-Task Transformer for Robotic Manipulation. In Proceedings of the 6th Conference on Robot Learning (CoRL), Auckland, New Zealand, 14–18 December 2022. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. arXiv 2020, arXiv:2006.11239. [Google Scholar]
- Pearce, T.; Rashid, T.; Kanervisto, A.; Bignell, D.; Sun, M.; Georgescu, R.; Macua, S.V.; Tan, S.Z.; Momennejad, I.; Hofmann, K.; et al. Imitating Human Behaviour with Diffusion Models. arXiv 2023, arXiv:2301.10677. [Google Scholar]
- Chi, C.; Feng, S.; Du, Y.; Xu, Z.; Cousineau, E.; Burchfiel, B.; Song, S. Diffusion Policy: Visuomotor Policy Learning via Action Diffusion. arXiv 2023, arXiv:2303.04137. [Google Scholar] [CrossRef]
- Perez, E.; Strub, F.; De Vries, H.; Dumoulin, V.; Courville, A. FiLM: Visual Reasoning with a General Conditioning Layer. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, New Orleans, LA, USA, 2–7 February 2018; pp. 3942–3951. [Google Scholar] [CrossRef]
- Vitiello, P.; Dreczkowski, K.; Johns, E. One-Shot Imitation Learning: A Pose Estimation Perspective. arXiv 2023, arXiv:2310.12077. [Google Scholar]
- Valassakis, E.; Papagiannis, G.; Di Palo, N.; Johns, E. Demonstrate Once, Imitate Immediately (DOME): Learning Visual Servoing for One-Shot Imitation Learning. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Kyoto, Japan, 23–27 October 2022; pp. 8614–8621. [Google Scholar] [CrossRef]
- Park, J.; Seo, Y.; Liu, C.; Zhao, L.; Qin, T.; Shin, J.; Liu, T.-Y. Object-Aware Regularization for Addressing Causal Confusion in Imitation Learning. Adv. Neural. Inf. Process Syst. 2021, 34, 3029–3042. [Google Scholar]
- Kujanpää, K.; Pajarinen, J.; Ilin, A. Hierarchical Imitation Learning with Vector Quantized Models. In Proceedings of the International Conference on Machine Learning, Chongqing, China, 27–29 October 2023. [Google Scholar]
- Van Den Oord, A.; Vinyals, O.; Kavukcuoglu, K. Neural Discrete Representation Learning. arXiv 2017, arXiv:1711.00937. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Toyer, S.; Wild, C.; Emmons, S.; Fischer, I.; Research, G.; Lee, K.-H.; Alex, N.; Wang, S.; Luo, P.; et al. An Empirical Investigation of Representation Learning for Imitation. arXiv 2021, arXiv:2205.07886. [Google Scholar]
- Pagliarani, N.; Picardi, G.; Pathan, R.; Uccello, A.; Grogan, H.; Cianchetti, M. Towards a Bioinspired Soft Robotic Gripper for Gentle Manipulation of Mushrooms. In Proceedings of the 2023 IEEE International Workshop on Metrology for Agriculture and Forestry, MetroAgriFor, Pisa, Italy, 6–8 November 2023; pp. 170–175. [Google Scholar] [CrossRef]
- Jocher, G.; Chaurasia, A.; Stoken, A.; Borovec, J.; Kwon, Y.; Michael, K.; Fang, J.; Yifu, Z.; Wong, C.; Montes, D.; et al. Ultralytics/Yolov5: V7.0—YOLOv5 SOTA Realtime Instance Segmentation; Zenodo; CERN: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]

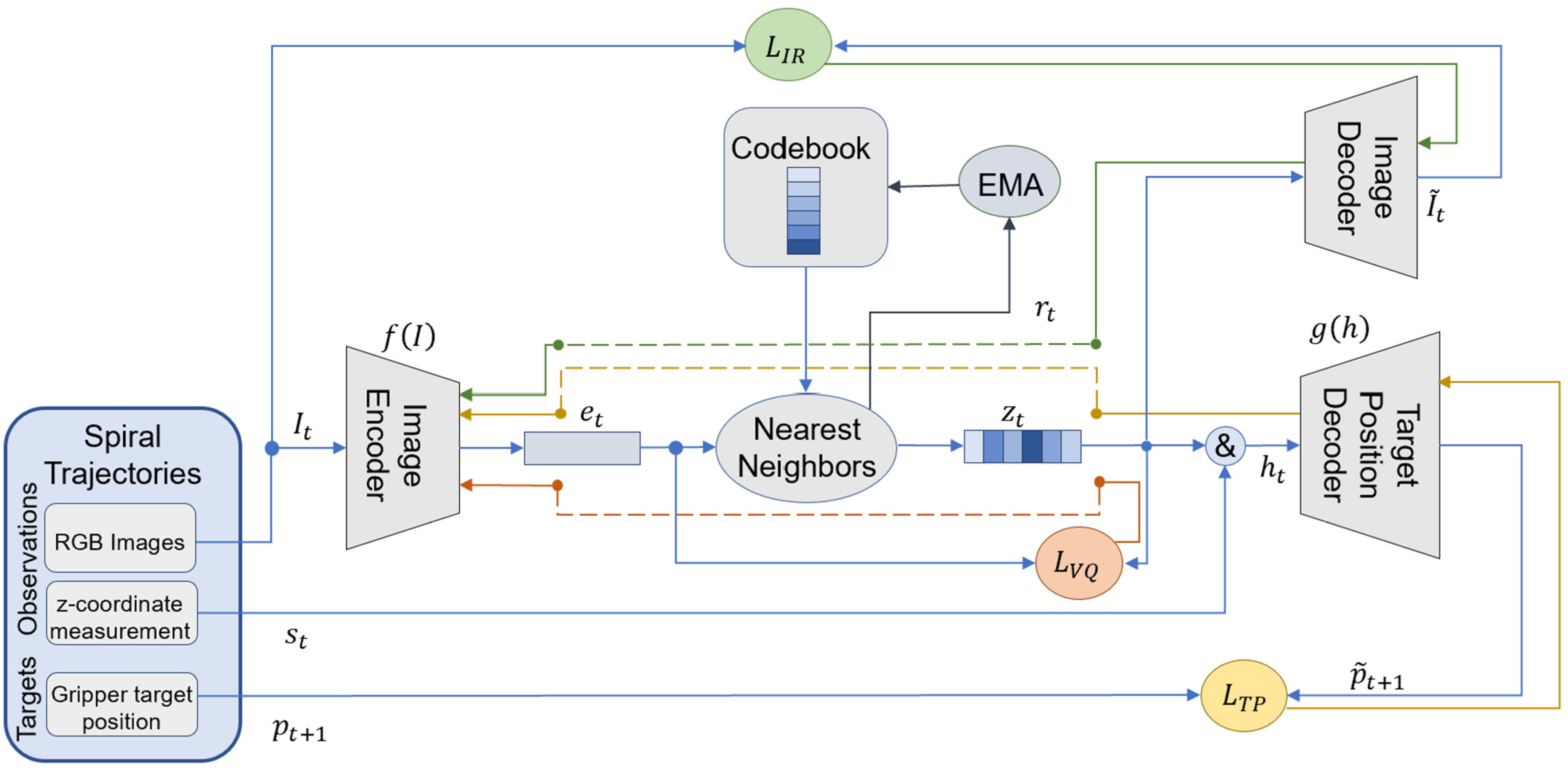









| Model Component | Type | Layers/Parameters |
|---|---|---|
| Image Encoder | Convolutional Neural Network | Conv layer 1: 20 channels, 5 × 5, stride 2 Conv layer 2: 10 channels, 3 × 3, stride 2 |
| Vector Quantizer | EMA-based Quantizer | Embedding Vocabulary size: 1024 |
| Embedding dimension: 10 Embedding width/height: 14 × 21 | ||
| Target Position Decoder | Recurrent Neural Network | Sequence length: 5 Hidden layer 1: 1024 Hidden layer 2: 1024 |
| Image Decoder | Convolutional Neural Network | Deconv layer 1: 20 channels, 3 × 3, stride 2 Deconv layer 2: 3 channels, 5 × 5, stride 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porichis, A.; Inglezou, M.; Kegkeroglou, N.; Mohan, V.; Chatzakos, P. Imitation Learning from a Single Demonstration Leveraging Vector Quantization for Robotic Harvesting. Robotics 2024, 13, 98. https://doi.org/10.3390/robotics13070098
Porichis A, Inglezou M, Kegkeroglou N, Mohan V, Chatzakos P. Imitation Learning from a Single Demonstration Leveraging Vector Quantization for Robotic Harvesting. Robotics. 2024; 13(7):98. https://doi.org/10.3390/robotics13070098
Chicago/Turabian StylePorichis, Antonios, Myrto Inglezou, Nikolaos Kegkeroglou, Vishwanathan Mohan, and Panagiotis Chatzakos. 2024. "Imitation Learning from a Single Demonstration Leveraging Vector Quantization for Robotic Harvesting" Robotics 13, no. 7: 98. https://doi.org/10.3390/robotics13070098
APA StylePorichis, A., Inglezou, M., Kegkeroglou, N., Mohan, V., & Chatzakos, P. (2024). Imitation Learning from a Single Demonstration Leveraging Vector Quantization for Robotic Harvesting. Robotics, 13(7), 98. https://doi.org/10.3390/robotics13070098







