Artistic Robotic Painting Using the Palette Knife Technique

Abstract

This paper presents a novel robotic painting system able to create artworks using the palette knife technique. The implementation of this method with a robotic system is particularly challenging, since the robot needs to precisely manipulate the palette knife to pick up and release the color on the canvas. The painting system comprises a 6-DOF collaborative robot, a camera to acquire the information on the color position, and several algorithms for the artistic rendering of the images and for the planning of the trajectories that the robot has to follow. During the painting process the user can modify multiple parameters: both software, for example, stroke position and orientation, and hardware, for example, palette knife inclination and height, to obtain different stroke effects. Finally, the experimental results are discussed by analyzing the artworks painted by the novel robotic system.

1. Introduction

Art in its multiple forms is practiced by all human cultures; it is the fulfillment of the human desire to express emotions and creativity. The society of the 21st Century has managed to achieve a remarkable technological knowledge. Even though art and technology seem to be very far apart from each other, if combined together, they can create a new concept of art known as robotic art [1].

Robotic art involves many disciplines [2] such as dance, music, theater, and painting. This work focuses on robotic painting art: technology, that is, machines, robots, computers and sensors, are used for drawing and painting. One of the first artists to apply this novel concept of art was the Swiss sculptor Jean Tinguely (1925–1991) [3]. In the 1950s he started the development of a series of generative works called Métamatics, a collection composed of machines generating complex and random patterns. In the 1970s the English professor Harold Cohen (1928–2016) developed AARON [4], a computer program that draws and paints stylized images from its programmed “imagination”. The algorithm was implemented in Harold Cohen’s painting machine and received a great attention from international exhibitions and art galleries, including the Tate Gallery in London. In recent years many examples of machines and robots for artistic painting can be found in literature, each using different methodologies and techniques to produce artworks.

In 2006 Calinon et al. [5] developed an interesting humanoid robot capable of drawing portraits. The system consists of a four degree-of-freedom (DOF) robotic arm and an algorithm based on face detection and image reconstruction. In 2008 Aguilar and Lipson [6] proposed a robotic system that can produce paintings using a 6-DOF arm and an algorithm for the brushstroke positioning. In 2009 Lu et al. [7] presented a robotic system that performs automated pen-ink drawing based on visual feedback.

In the last decade many artists used manipulators or robots to create artistic graphics and paintings. Some of them implemented advanced algorithms that achieved excellent results, such as the painting robot eDavid by Deussen et al. [8,9]. eDavid is one of the most impressive examples of robot artists, capable of reproducing non-photorealistic images, using visual feedback and complex algorithms to simulate the human painting process. Another interesting example is given by Tresset et al. [10], who developed Paul, a robotic installation that produces observational face drawings guided by visual feedback. Furthermore, in 2016 Luo et al. [11] proposed a robot capable of painting colorful pictures with a visual control system like human artists. Two other interesting examples of robotic painting are proposed by Scalera et al.: the first uses the spray painting technique [12], commonly found in the industrial environment for aesthetic and protection [13,14]; the second is the first robotic painting system adopting the watercolor technique [15,16]. Other recent examples include the works presented by Karimov et al. [17], who developed a robot capable of creating full-color images aimed at reproducing a human-like style, and by Igno et al. [18], who proposed a robotic system focused on painting artworks by image regions. Moreover, Song et al. [19] presented an impedance-controlled pen-drawing system capable of creating art on arbitrary surfaces. Vempati et al. developed Paint Copter [20], an unmanned aerial vehicle capable of spray painting on complex 3D surfaces. Moreover, Ren and Kry [21] investigated the trajectory generation for light paintings with a quadrotor robot.

Several examples of robotic systems for artistic painting that use many different tools, that is, pens, pencils and brushes, can be found in the literature. To the best of the author’s knowledge, no examples of robotic systems using the palette knife painting technique have been developed yet. This technique is characterized by tools called palette knives, which are used to transfer the color to the canvas. Using such tools with a robotic painting system is a challenging task, since not only the positions, but also the orientations of the palette knife have to be accurately planned for the painting process. In this context, Okaichi [22] managed to model and 3D simulate the palette knife technique, but the algorithms have not been experimentally implemented in a robotic application yet.

This paper proposes a new robotic system capable of painting artworks using the palette knife technique, shown in Figure 1. The system consists of a 6-axis robotic arm equipped for palette knife painting, a camera for the acquisition of the position of the paint, and a series of algorithms for image processing and trajectory planning. The system receives a digital reference image as input, which is then processed by two different algorithms, introducing an artistic contribution. The first one concerns the image low frequencies, the other one is used to emphasize the information on the high frequencies. The image frequencies are related to the rate of change of intensity per pixel: high frequencies return information about the image details and edges, whereas low frequencies about large and uniform areas. The data extracted from the input image is converted into paths that are reproduced by the robot. The main contributions of this work can be summarized as follows: (a) the development of a novel robotic painting system capable of paining artworks using the palette knife technique, (b) the implementation of image processing and path planning algorithms that accounts for the orientation of the palette knife during paining, and (c) the experimental validation of the system.

The paper is organized as follows: in Section 2 the painting knife technique is briefly illustrated. In Section 3 the robotic painting system developed in this work is presented. Section 4 describes the algorithms used for image processing and trajectory planning. Section 5 reports the experimental results, whereas Section 6 discusses the conclusions and possible future developments of the paper.

2. Palette Knife Painting Technique

The palette knife painting technique employs tools—called palette knives—made of a flexible steel blade fixed into wooden handles to mix and apply paint on the canvas (Figure 1b). Palette knives come in an array of shapes and sizes, each allowing the artist to create a great variety of strokes and effects. These tools were originally used for mixing paint on the palette. However, since the 1800s palette knives have also been used for painting [23]. In that period of time artists such as Rembrandt and Goya used palette knives in addition to brushes to create intricate details and effects. It was not until the 19th Century that the technique became extremely popular, in particular thanks to Gustave Courbet, who began to use knives to apply paint in his landscapes. However, it was only in the 20th Century that several artists began to experiment artworks entirely painted with the knife technique.

Palette knives are useful for applying paint on white canvas or on an existing layer of dry paint. Usually, it is not necessary to dilute the paint, but this gives a more vibrant color tonality. The blade allows the painter to spread the paint onto the canvas with a smooth motion. The tool orientation and inclination are crucial to determine the stroke effects, which can be grouped in different categories [24]:

• Hard line: It produces strokes with clear edges. Using the palette knife tip, thin or wide lines (Figure 2a,b) can be drawn depending on the applied pressure. Hard edges area can be drawn with the long side of the palette knife: tilting the tool to one side and pulling strongly to the other side produces a painted area with a hard edge.
• Soft edge: It regards the edge blending between two colors. Squizzle allows to soften two colors together using the tip of the palette knife, whereas the cuddle allows to pull the colors softly together with the bottom of the palette knife.
• Swoosh: It produces strokes with slightly unclear edges by means of pressing downwards the palette knife bottom side. Using only one paint tonality the light swoosh and heavy swoosh (Figure 2c,d) can be drawn by changing the pressure applied to the palette knife.

The developed robotic painting system uses the swoosh technique to fill up large areas, whereas hard lines are used to draw the edges and the details.

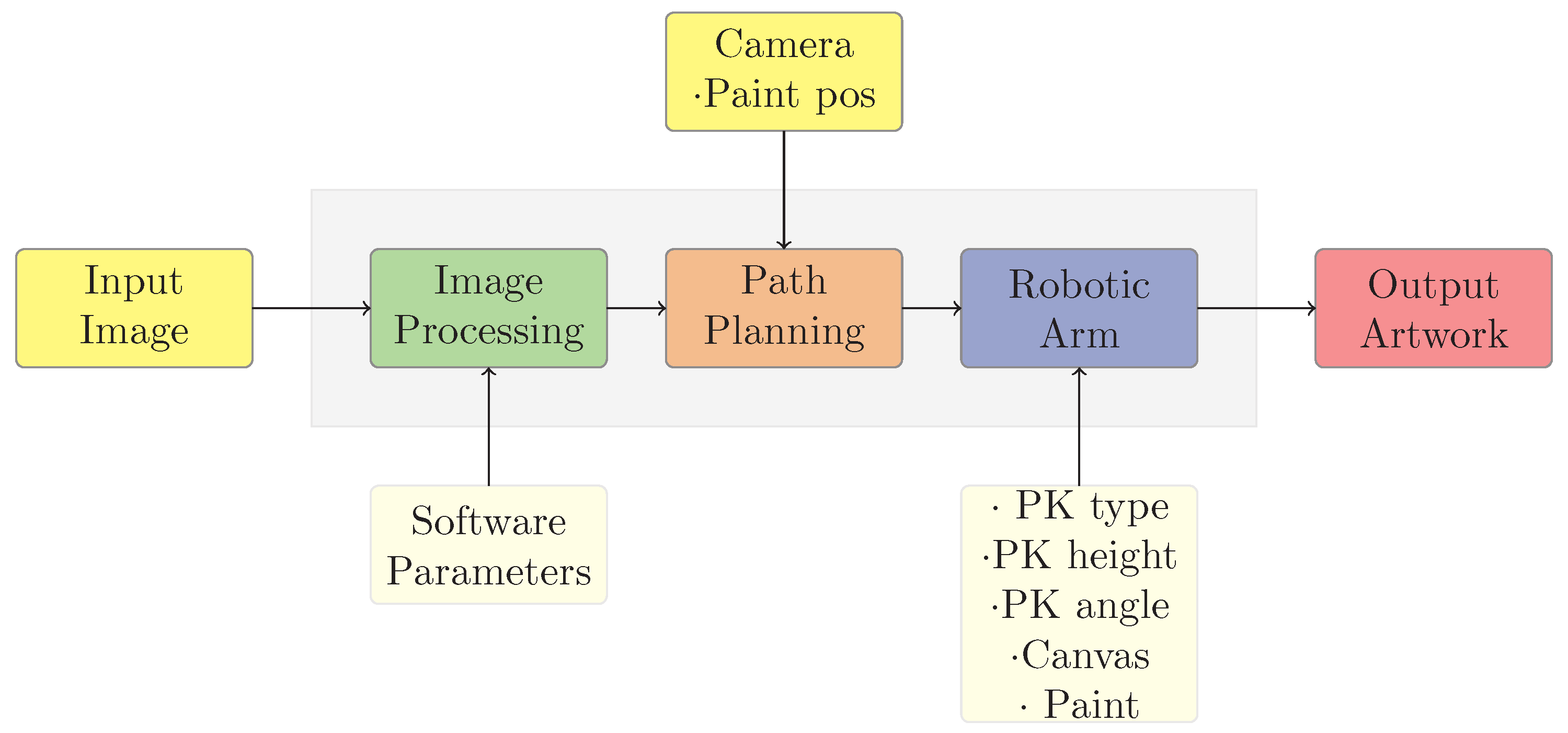
3. Robotic Painting System

This section provides an overview of the architecture of the robotic painting system, which consists of both software, that is, trajectory planning and image processing algorithms, and hardware components, that is, palette knife type (PK type in Figure 3), canvas, and paint. The robot used in this work is a UR10 collaborative robot by Universal Robots. This type of robot was chosen since its collaborative features allow a human operator to work side by side with the manipulator during the painting process. For the user it is indeed important to have access to the robot proximity to check the correct execution of the artwork, provide color when needed, adjust the dilution of the color, clean the palette knife and eventually change it. The robot is equipped for painting purposes and it is provided with acrylic or tempera colors and painting paper, as shown in Figure 1a. A custom tool designed in SolidWorks and 3D printed using an Ultimaker 2+ allows the palette knife to be mounted on the robot end-effector (Figure 1b). Furthermore, a Logitech C310 webcam allows the user to obtain the paint position coordinates on the working surface by clicking on the color image in a live camera stream.

The software for image processing and path planning is implemented in a user friendly graphical interface developed in MATLAB App Designer. The robotic painting system receives a digital image as input; the most common file formats can be loaded (PNG, JPG, BMP). The reference image is processed using different non-photorealistic rendering techniques explained in details in Section 4. Then, the sequence of paths to be completed by the robot is planned in the operative space. The robot is controlled with the proprietary UR Script Programming Language, which includes built-in functions that monitor and control I/O and robot movements. The motion commands are sent to the robot controller using the TCP/IP protocol. An overview of the system is shown in Figure 3.

Since the robot interacts with its surroundings, it needs to know exact geometrical information (poses) about the working surface, the canvas position, the tool size, and the color palette position. The following paragraphs provide an overview on the calibrations required by the robotic system to properly operate in the painting environment—tool center point, painting surface and camera. All calibrations are performed in static conditions and, therefore, the compliance of the palette knife does not influence the results. However, small errors due to the compliance of the palette knife during calibration are considered negligible for the aims of this work.

3.1. Tool Center Point Calibration

The tool center point calibration allows to identify the change of coordinates between the center of the robot end-effector and the tool center point (TCP) using translations and rotations. Paining knives can be identified with a tag number, in this work only the painting knife "41 Pastello" (Figure 1b) is used, therefore this calibration has to be performed only once. If a different tool with a different shape is taken into account, a new TCP calibration is required. Figure 4 shows a schematic of the tool mounted on the robot flange. Three reference frames are available: the canvas $〈x,y,z〉$, the robot flange $〈x^{\prime },y^{\prime },z^{\prime }〉$ and the palette knife $〈x^{″},y^{″},z^{″}〉$. The TCP is namely the $O^{″}$ position and orientation with respect to the robot flange reference frame $〈x^{\prime },y^{\prime },z^{\prime }〉$, consequently it defines the position and the orientation of $〈x^{″},y^{″},z^{″}〉$.

Thanks to the design of the palette knife support (Figure 1b), the blade is kept parallel to the robot flange $y^{\prime }$ axis; moreover the $y^{″}$, $z^{″}$ and $y^{\prime }$, $z^{\prime }$ are co-planar as in Figure 4. Due to this, the TCP calibration is required to define only two parameters: the translation $l_y$ and the translation $l_z$. During the painting process the tool poses are referred to the frame $〈x^{″},y^{″},z^{″}〉$, therefore to minimize the position error the TCP has to be determined with high accuracy. In order to handle rotations more easily, the TCP is set on the blade tip. In Figure 4 ${\alpha }_{draw}$ is the angle between the palette knife $y^{″}$ axis and the canvas plane, whereas $\Delta h$ is the distance between the TCP $O^{″}$ and the canvas. $\Delta h$, considered with its absolute value, assumes negative values since the palette knife has to press on the canvas flexing itself in order to perform the stroke.

If the procedure is done manually the result may vary depending on the skills of the operator. Luo and Wang [25] and Hallenberg [26] proposed two different methodologies to achieve a tool center point calibration by applying computer vision and image processing techniques. The calibration proposed in this paper is a hybrid system halfway between the manual procedure and the methodologies recalled above: thanks to the camera set on the top of the robot working surface a fast and flexible calibration procedure, feasible for many different palette knives with different shapes and dimensions, can be integrated in the software. The procedure to perform the calibration is given below:

• Approximately measure $l_y$ and $l_z$ and set the values.
• $y^{″}$ calibration: rotate the tool around the newly defined $z^{″}$ check if the center of rotation coincides with the tip of the painting knife. If not, correct the $l_y$ value and check again.
• $z^{″}$ calibration: rotate the tool around the newly defined $x^{″}$ check if the center of rotation coincides with the tip of the painting knife. If not, correct the $l_z$ value and check again.

Steps (2) and (3) are extremely delicate, therefore a more detailed analysis is required. In order to adjust the $l_y$ translation, it is necessary to perform a rotation around $z^{″}$ by ${90}^{\circ }$. During this process the $z^{″}$ axis must be orthogonal to the camera, hence ${\alpha }_{draw}=0$. Figure 5 shows the three possible cases from the camera point of view: $l_y$ overestimation, $l_y$ underestimation or $l_y$ correct estimation. The blue dot is the desired TCP position on the painting knife tip, whereas the red point is the actual TCP position, its location is due to the used $l_y$ parameter. $〈x_1^{\prime },y_1^{\prime },z_1^{\prime }〉$ and $〈x_2^{\prime },y_2^{\prime },z_2^{\prime }〉$ represent the orientation of the robot flange before and after the rotation. Figure 5a shows a $l_y$ overestimation, and Figure 5b an underestimation. Therefore, it is required to estimate this error and correct the $l_y$ value in order to obtain the case shown in Figure 5c.

The error along the y axis $\Delta e_y$ can be measured using the camera fixed above the working table: at least two pictures must be taken, one before and one after the rotation. When merging the two images using an image editor, the $\Delta e_y$ value in pixels can be precisely determined which can be converted in meters ($\Delta e_{ym}$). If an overestimation occurs the corrected value is $l_{y\_new}=l_y-\Delta e_{ym}$, if an underestimation occurs the corrected value is $l_{y\_new}=l_y+\Delta e_{ym}$.

The $l_z$ translation can be measured similarly performing rotations around the $x^{″}$ axis. In order to correctly estimate the error along the z axis $\Delta e_z$ during the calibration process $x^{″}$ axis must be orthogonal to the camera sensor as shown in Figure 6.

3.2. Painting Surface Calibration

The painting surface calibration allows to compensate errors due to the non-perfect parallelism of the painting surface with the robot base. To solve this problem, it might be useful to derive the equation of the plane approximating its surface, in a way similar to that in Reference [15]. Using this approach, the table height can be expressed as function of the painting knife TCP position. In the calibration program the canvas is used as reference; the end-effector is then manually positioned at each corner of the canvas and its position $P_i=(x_{pi},y_{pi},z_{pi})$ with $i\in [1,4]$ is saved. These points are expressed with respect to the reference frame O - $〈x,y,z〉$ in Figure 4. This procedure provides the position of the canvas corners and its dimensions. Subsequently, the points can be elaborated in order to derive the parameters $a,b,c$ for plane $z_p$, as follows:

$$z_p=a{x}_p+b{y}_p+c.$$

(1)

By introducing the acquired data and Equation (1), it is possible to write the following matrix equation:

$$\left[\begin{array}{c}{z}_{p1}\\ z_{p2}\\ z_{p3}\\ z_{p4}\end{array}\right]=\left[\begin{array}{ccc}{x}_{p1}& y_{p1}& 1\\ x_{p2}& y_{p2}& 1\\ x_{p3}& y_{p3}& 1\\ x_{p4}& y_{p4}& 1\end{array}\right]\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$$

(2)

Equation (2) can be written as $\mathsf{\Phi }=\mathsf{\Psi }\mathsf{\theta }$. Then, it is easy to estimate the vector of surface parameters as:

$$\mathsf{\theta }={\left({\mathsf{\Psi }}^T\mathsf{\Psi }\right)}^{-1}{\mathsf{\Psi }}^T\mathsf{\Phi }.$$

(3)

These parameters are used to create a virtual surface in the software through the minimization of the mean square error; the plane is then used as reference for the planning of painting paths.

3.3. Camera to Robot Calibration

The camera plays an important role in locating the paint on the working surface. Camera and robot work with two different reference frames, which need to be related one to the other. In order to obtain this transformation it is necessary to acquire some 3D real world points and their corresponding 2D image points. For a good accuracy, a prior camera calibration is performed, as in Reference [27].

When the calibration software is run, a window is displayed showing a live camera stream with four virtual red dots superimposed on the image. As already done in the working surface calibration, by manually moving the tip of the knife over the four points, it is possible to acquire the points coordinates $P_1$, $P_2$, $P_3$ and $P_4$ in pixel with respect to the image reference frame $O_i$ - $〈x_i,y_i,z_i〉$ and the points coordinates $P_{1m}$, $P_{2m}$, $P_{3m}$ and $P_{4m}$ in meters with respect to the robot reference frame O - $〈x,y,z〉$. In order to minimize the parallax error during the acquiring process the tool has to be as close as possible to the working surface. This transformation can be computed referring to Figure 7.

The dashed rectangle represents the camera vision field. The red dots are the virtual calibration points, their coordinates with respect to the two frames are available thanks to the performed calibration. Moreover, the camera and the robot frames could not be perfectly aligned, an effect represented by the angle $\beta$. Let now consider a random point P: only its position in pixel with respect to the image reference frame $O_i$ - $〈x_i,y_i,z_i〉$ is available. The aim of the camera to robot calibration is to express this point with respect to the robot reference frame O - $〈x,y,z〉$. ${\mathit{v}}^{\prime }$ is the vector of coordinates of P with respect to $O_i$ - $〈x_i,y_i,z_i〉$. It is possible to calculate $\mathit{v}$, the vector of coordinates of P with respect to the auxiliary reference frame $O_i$ - $〈x_i^{\prime },y_i^{\prime },z_i^{\prime }〉$, as $\mathit{v}={\mathit{v}}^{\prime }-\mathit{s}$. The components of $\mathit{v}$ are still expressed in pixel, therefore it is required to convert its components in meters. Considering the calibration data it is possible to compute the rectangle base and height in meters and in pixel, then a proportion can compute the vector in meters ${\mathit{v}}_{\mathit{m}}$.

Deriving the required rotation matrices ${\mathit{R}}_{\mathit{z}}\left(\mathbf{\beta }\right)$, ${\mathit{R}}_{\mathit{x}}\left(\mathbf{\pi }\right)$ used to align $〈x_i^{\prime },y_i^{\prime },z_i^{\prime }〉$ with $〈x,y,z〉$ and considering ${\mathit{p}}_{\mathbf{1}}$, the vector of coordinates of $P_1$ with respect to O - $〈x,y,z〉$, it is possible to calculate ${\mathit{p}}_{\mathit{m}}$:

$${\mathit{p}}_{\mathit{m}}={\mathit{p}}_{\mathbf{1}}+{\mathit{R}}_{\mathit{z}}\left(\mathbf{\beta }\right){\mathit{R}}_{\mathit{x}}\left(\mathbf{\pi }\right){\mathit{v}}_{\mathit{m}},$$

(4)

which represents the vector of the P coordinates in meters with respect to the robot base reference frame O-$〈x,y,z〉$.

4. Image Processing and Trajectory Planning Algorithms

In this section the algorithms developed to process a digital image and paint it on the canvas are described. The algorithms can be divided into two parts: the first regards the image low frequencies, with the goal of painting and uniformly filling large areas, whereas the second is meant for the image high frequencies. Figure 8a,b show the considered reference images.

4.1. Low Frequencies Algorithm

Several methodologies aimed at processing large areas of images are proposed in the literature. The technique that has been implemented in this work for a uniform filling is similar to hatching, explained in References [15,28]. In the hatching, an image is divided into different layers, based on grey-scale thresholds. Each layer is than filled with closely spaced parallel lines that are then followed by the painting tool. In this paper, this algorithm has been adapted for a palette knife painting application, by considering not only the position, but also the orientation that the palette knife has to follow to paint a stroke along each line. The algorithm is explained in depth in the following and the pseudocode for the low frequency algorithm is reported in Algorithm 1.

The first step of the low frequencies algorithm consists of the definition of the image subject: this operation can be done manually by removing the reference image background and substituting it with a white one. The subject mask can be easily computed, since it consists of a binary image containing the position of all the pixels of interest in the picture. The reference image is converted in gray scale and then divided into layers defining the areas where the image has similar properties. The proposed method is based on the classification of the image tones by means of a threshold. Given a specific layer number $i\in \mathbb{N}$, the threshold intensity $I_i\in \mathbb{N}$∧$I_i\le 255$ and the 8 bit gray scale image $BW$, the binary layer $L_i$ is composed of all the pixels that satisfy the inequality $BW<I_i$. Considering a total number of layers equal to $n\in \mathbb{N}$, the i-th layer intensity can be computed as:

$$I_i=255-\frac{255}{n}(i-1)i\in [1,n].$$

(5)

Lighter layers contain darker layers, ensuring a better surface coverage. Each of them is then multiplied element-wise with the subject mask to keep only the subject information.

Algorithm 1: Pseudocode for the low frequencies algorithm.

Figure 9a show an example of binary layer obtained considering the reference image Marina. In order to fill up the area with its associated paint tonality, each layer is processed to obtain paths to be subsequently sent to the robot. The algorithm proposed here for the uniform filling of an area consists of the definition of closely spaced parallel lines that fully cover a layer of the image. The intrinsic irregularity introduced by the palette knife technique allows the observer not to perceive the regularity of the parallelism of the lines. For a better artistic result, the angular direction of the lines and their distance should be chosen individually for each layer. This operation is performed using an auxiliary binary mask composed of parallel lines, whose orientation and distance are user defined. Multiplying element-wisely each layer with its associated auxiliary mask, layers composed by parallel lines are obtained. Figure 9b show a rough rendering result, in which each line corresponds to a path that the palette knife has to follow. Hence, it is useful to look for the starting and the ending points on each line, which can be determined by computing the maximum and minimum pixel position of each line (Figure 10). The obtained points expressed in pixels with respect to the image reference frame, are then converted in meters with respect to the robot reference frame.

Since the palette knife is not a point-like tool, it must be oriented correctly for each stroke in order to accurately fill the layer. Thus, it is required to compute the starting and ending point orientation for each path. The orientation information is still available in the layer image (Figure 9a). One method to retrieve this information is by using the layer gradient, defined as:

$$\nabla L_i=\left[\begin{array}{c}{g}_x\\ g_y\end{array}\right]=\left[\begin{array}{c}\frac{\partial L_i}{\partial x}\\ \frac{\partial L_i}{\partial y}\end{array}\right]$$

(6)

Therefore, the layer gradient direction can be calculated for each of the computed starting and ending points as $\mathsf{\theta }={tan}^{-1}(g_y/g_x)$. These data give essential information to align the palette knife with the layer edge, in particular it is useful to compute the starting and ending orientation ${\alpha }_{start}$ and ${\alpha }_{end}$ for each knife segment stroke, shown in Figure 11.

The palette knife has to get some color after each stroke, therefore an optimized pick-up method has been studied: the robot aligns the tool with one edge of the paint blob set onto the palette, then the tool slides trough the paint until it reaches the opposite side of the blob. The starting edge changes at every iteration and consequently the direction of the trajectory changes as well. In this manner the color is mixed at every stroke, extending the drying time of the paint. The stroke length can be around 10–25 mm depending on the paint density and dilution; due to this the computed paths have to be segmented in many strokes, as shown in Figure 11.

The total path length is calculated and divided into many segments corresponding to the required number of strokes per line $N_s$, hence the starting and ending coordinates for each stroke are derived. The starting point of each stroke coincides with the ending point for the previous stroke. Similarly, the starting orientation for each stroke coincides with the ending orientation of the previous stroke. Considering the path starting ${\alpha }_{start}$ and ending orientations ${\alpha }_{end}$, the intermediate orientations are calculated as follows:

$${\alpha }_{start}\left(i\right)={\alpha }_{start}+\left(\frac{{\alpha }_{end}-{\alpha }_{start}}{N_s}\right)(i-1)i\in [1,N_s]$$

(7)

$${\alpha }_{end}\left(i\right)={\alpha }_{start}+\left(\frac{{\alpha }_{end}-{\alpha }_{start}}{N_s}\right)ii\in [1,N_s].$$

(8)

Figure 11 shows an example of path segmentation. After all layer paths are correctly computed, the data are sent to the robot. Two methods can be used to define the order in which the paths are painted by the robot—the sequential and the random strokes methods. The first one mixes the order of the complete trajectories, hence before moving on to the next path the robot finishes painting the selected path. In the second method all segmented strokes are mixed randomly and then sent to the robot. If compared with the first one, this method produces a resulting artwork containing less regular strokes, but the layer surface is usually covered unevenly due to the short paint drying time.

In the low frequencies algorithm all trajectories are linear in tool-space. The speed profile for the motion is trapezoidal, it is composed of three phases: acceleration, constant speed and deceleration. The constant speed phase is given by the speed setting of the motion, whereas the steepness of the acceleration and deceleration phases is given by the acceleration parameter. The maximum speed is equal to $0.5$ m/s and the maximum acceleration is 0.5 m/s${}^2$. The influence of speed and acceleration on the swoosh effect is analyzed in Section 5.

4.2. High Frequencies Algorithm

The algorithm for the processing of high frequencies is based on the Difference of Gaussians (DOG) filter [16,29], and on the skeleton algorithm [30]. In a way similar to the low frequencies, this algorithm has been adapted to be suitable for the palette knife painting. In particular, the novelty of the algorithm is the computation of the orientation of the palette knife point by point for each of the strokes that have to be painted. The algorithm for the high frequencies is described in the following and the pseudocode is reported in Algorithm 2.

Algorithm 2: Pseudocode for high frequencies algorithm.

For the processing of high frequencies, the image to be taken into account is the reference image with background. In order to obtain the image details the DOG filter is used. This algorithm establishes a subtraction of one blurred version of an image (tuned with ${\sigma }_1$) from a less blurred one (tuned with ${\sigma }_2$) of the same image. This filter is an approximation of the Laplacian of Gaussians filter [31], and is commonly used for edge detection. By tuning its parameters it is possible to select the frequencies of interest of an input image. The DOG can also be implemented with the standard convolution method: firstly the filter kernel has to be computed defining the parameters ${\sigma }_1$, ${\sigma }_2$ and the window size, then the filter is convoluted with the image. The output image heavily depends on the parameters choice, therefore to obtain the desired result an iterative tuning of the two parameters has to be carried out.

Figure 12a shows the DOG filter applied to the reference image. This result is obtained with the following parameters: ${\sigma }_1=30$, ${\sigma }_2=50$, and a window of 20 pixels. In the image, the edges and details of the subject are highlighted. However, the image contains additional information not useful for the purpose of this work. Considering a specific threshold intensity value $i_t$ and the 8-bit gray-scale DOG image $I{m}_{DOG}$, a binary image containing only detail information can be generated. This image is composed of all the pixels that satisfy the inequality $I{m}_{DOG}>i_t$.

Finally, in order to obtain one pixel wide paths, the binary image has to be skeletonized [30]; the obtained image features many lines and branches. Before computing the paths it is important to isolate these branches in order to calculate the routes more easily. The result is shown in Figure 12b. Unfortunately, some details in the skeletonization are lost due to the algorithm design. This happens for large areas that cannot be easily transformed into lines and require a dedicated layer to be drawn, such as the eyes of the subject.

Each line in the skeleton image (Figure 12b) represents a path that the tip of the palette knife has to follow. These points are expressed with respect to the camera reference frame, therefore they have to be converter in meters with respect to the robot base reference frame. The transformation can be performed using the acquired canvas corner coordinates with respect to the robot reference frame during the calibration process described in Section 3.2.

Figure 13 shows an example of path. In order to draw the details onto the canvas the painting knife has to be aligned with the specific path. If the path is made up of n sampled points, its orientation $\gamma$ can be calculated as:

$$\gamma \left(i\right)=\mathrm{atan}2\left(\frac{\Delta y_i}{\Delta x_i}\right)i\in [1,n-1].$$

(9)

These data give essential information to align the palette knife tip with the considered path. In order to avoid fast accelerations of the robot joints, the orientation data are filtered using a Gaussian-weighted moving average filter with a minimum window of 40 samples. The most important information in a rendered image is usually located close to the image center. Therefore, before sending the data to the robot, the software sorts the trajectories: generally, the paths closer to the center of the image have a higher priority than those farther away. In this manner, the robot first paints the significant traits that are essential to characterize the artwork.

During the high frequencies painting process the robot moves linearly with constant speed with circular blends. This expedient allows to draw the details more accurately. For operating the robot three parameters are required: acceleration, speed and blending radius. The maximum speed is equal to 0.003 m/s and the acceleration is equal to 0.001 m/s${}^2$ with a blending radius of 5.5 mm. These values have been chosen to avoid fast rotations of the palette knife caused by contours and details with high curvature. High wrist rotation can indeed arrest the robot due to violation of the joint limits. The adoption of a blending radius helps to solve this problem. For the paint pickup process the tool can move faster, in fact the speed is equal to 0.1 m/s and the acceleration to 0.1 m/s${}^2$.

5. Experimental Results

This section reports the experimental results obtained by testing the robotic painting system using the palette knife painting technique. Prior to performing the artworks, a preliminary characterization of the palette knife painting has been carried out. In particular, a series of strokes for the swoosh and the lines have been painted and analyzed by changing the painting parameters $\Delta h$ and ${\alpha }_{draw}$. All the experiments have been performed using undiluted black tempera paint.

The swoosh effect has been analyzed with $|\Delta h|=[0,1,2,3,4]$ mm and ${\alpha }_{draw}=[5^{\circ },7^{\circ },9^{\circ },{11}^{\circ }]$, by measuring the maximum length and thickness of the strokes. Each test has been performed 5 times. Figure 14 reports an example of one of the five tests, whereas in Figure 15 the results for all the five tests for length and thickness are shown. The mean values and ranges are plotted. As it can be seen, by decreasing ${\alpha }_{draw}$ there is an increasing of the strokes in terms of contact area, and therefore in length and thickness. The same effect occurs by increasing $|\Delta h|$. Figure 15b shows the data regarding the swoosh stroke thickness. Strokes characterised by a wide contact area produce less detailed layer contours, therefore a painting containing a more dynamic and artistic effect can be obtained. On the contrary, using strokes characterised by a smaller contact area produces detailed layer contours. In the artworks presented in this paper both approaches are adopted.

The lines have been analyzed with $|\Delta h|=[0,1,2,3,4,5]$ mm and ${\alpha }_{draw}=[5^{\circ },{10}^{\circ },{15}^{\circ },{20}^{\circ }]$, by measuring the maximum length and thickness of the strokes. The tests have been performed 5 times. Figure 16 and Figure 17 shows an example of experimental lines and the results obtained with all the tests. The line stroke is used to draw the subject details. In order to obtain good performance the features have to be sharp and thin. Figure 17 shows that for ${\alpha }_{draw}=5^{\circ }$ and ${10}^{\circ }$ both the line length and thickness increase by increasing $|\Delta h|$. This trend is not marked for higher values of ${\alpha }_{draw}$. Therefore, lower values of the painting angle are preferred for the painting of details.

The influence of speed and acceleration has been analyzed on the swoosh effect for fixed values of $|\Delta h|=2$ mm and ${\alpha }_{draw}=5^{\circ }$. Several combinations of speed $v=[0.5,1.0,1.5]$ m/s and acceleration $a=[0.5,1.0,1.5,2]$ m/s${}^2$ have been tested, by painting swoosh strokes. Each test has been performed 5 times. Figure 18 reports the results of the tests, by showing the contour of the acquired swoosh strokes. The swoosh effect mainly depends on the acceleration, since for values higher than 1.5 m/s${}^2$ the strokes are affected by random bleeding effects. Therefore, in order to avoid this undesirable effect, for the low frequencies painting process, maximum values of speed and acceleration equal to $v=0.5$ m/s and $a=0.5$ m/s${}^2$ have been chosen. These values also avoid dripping of the color attached under the palette knife on the canvas during the robot motion.

The two reference images adopted for the artworks are shown in Figure 8a,b, and are processed with the low and high frequencies algorithm proposed in Section 4. Figure 19 shows a frame sequence of the painting of artwork Martina, whereas Figure 20 shows the complete artwork. In Figure 21 an analogue sequence for artwork Stefano is shown, whereas the final result is reported in Figure 22. Two short videos of the robot performing the paintings are available in the supplementary material attached to this paper (Video 1 for Martina, video 2 for Stefano). The artworks are realized in canvas of $40\times 60$ cm. Each artwork takes few hours to be painted by the robot.

The artwork Marina features six layers. The first five layers are processed with the low frequency algorithm so as to paint and uniformly fill the large areas of the subject. The sixth layer accounts for the image details and contours. The artwork is painted on paper with a 220 g/m${}^2$ grammage and tempera paint. The artwork in Figure 20a is obtained applying only the low frequency algorithm to the reference Figure 8a, the parameters used for the image processing are reported in Table 1a. Angle and distance are the parameters required to build the line mask explained in Section 4.1: the first parameter defines the line angulation in the binary mask, the second sets the distance between the lines. To avoid regular patterns onto the canvas, different values for each layer of angle parameter are chosen. On the contrary, the distance parameter is adjusted according to the footprint of the palette knife. For the first layers high distances using a wide footprint are preferred. This results in a lower resolution in the painting, but leads to a faster filling of the layer. For the last layers a smaller footprint is used to get a higher resolution. Therefore the distance parameter is kept smaller to avoid holes between the lines.

The final artwork in Figure 20b is obtained by applying the high frequency algorithm to the same reference image. Layer 6 is processed using a DOG filter characterized by a 20 pixel window, ${\sigma }_1=51$ and ${\sigma }_2=30$. Then, the DOG image is filtered with a threshold equal to 0.552 and only objects with an area larger than 400 pixel are taken into account for the skeletonization.

The artwork Stefano is composed of seven layers. The first five layers are drawn with the image low frequency algorithm used to paint and uniformly fill in large areas of the subject. The sixth layer regards the face and the papillon details, painted using black paint, and the shirt details in light gray. The seventh layer is exclusively dedicated to draw the eyes of the subject. The background of this artwork was pre-painted using a yellowish canvas panel of $40\times 60$ cm and acrylic paint. The artwork in Figure 22a is obtained applying the low frequency algorithm to the reference Figure 8b, the parameters used for the image processing are reported in Table 1b. Regarding the high frequencies, Layer six is processed using a DOG filter characterized by a 35 pixel window, ${\sigma }_1=25$ and ${\sigma }_2=50$. Then, the DOG image is filtered with a threshold equal to 0.568 and only objects with an area larger than 200 pixel are taken into account for the skeletonization. The last layer is obtained applying the high frequency algorithm to an image containing only the subject’s eyes. A DOG filter characterized by a 35 pixel window, ${\sigma }_1=10$ and ${\sigma }_2=20$ is used. Then, the DOG image is filtered with a threshold equal to 0.5 and only objects with an area larger than 2 pixel were taken into account for the skeletonization. The complete artwork is shown in Figure 22b.

As explained in Section 2, the stroke depends on many parameters such as the painting knife height, its inclination, and so forth. The combination of these parameters changes the stroke effect shown in Figure 2. In

Table 2. Palette knife stroke parameters.

Artwork	Layer	Layer type	${\mathit{\alpha }}_{\mathit{draw}}$	$|\Delta \mathit{h}|$	Max. stroke length
Marina	1	low freq.	3	2.0 mm	20 mm
	2	low freq.	7	4.0 mm	20 mm
	3	low freq.	10	5.0 mm	20 mm
	4	low freq.	12	4.0 mm	20 mm
	5	low freq.	10	4.0 mm	20 mm
	6	high freq.	27	2.0 mm	22 mm
Stefano	1	low freq.	14	7.0 mm	20 mm
	2	low freq.	14	7.5 mm	20 mm
	3	low freq.	19	6.0 mm	20 mm
	4	low freq.	20	6.0 mm	20 mm
	5	low freq.	21	6.0 mm	20 mm
	6	high freq.	25	2.0 mm	25 mm
	7	high freq.	25	2.0 mm	20 mm

the parameters adopted for each layer are reported. The drawing angle ${\alpha }_{draw}$ corresponds to the angulation of the palette knife tip with respect to the working surface and the table (Figure 4). The drawing height $\Delta h$ corresponds to the TCP height with respect to minimum mean square error plane computed in Section 3.2. The setting of parameters $\Delta h$ and ${\alpha }_{draw}$ allows to adjust the pressure exerted by the tool against the canvas, even if, in this work, a pressure feedback is unfortunately not available. Finally, the maximum stroke length is the parameter needed to compute the path segmentation explained in Section 4.1.

The proposed robotic painting system has achieved interesting results, shown in Figure 20 and Figure 22. The low frequency algorithm worked well for uniformly filling large areas, whereas the high frequency algorithm for painting the missing details could be further improved. In fact the last algorithm uses skeleton, causing a loss of details during the process (like the subject’s eyes) because of the algorithm design. Due to this a dedicated eye layer was used for the artwork Stefano in Figure 22b.

6. Conclusions

In this paper a novel robotic system that uses the palette knife painting technique to create artworks starting from a digital image has been presented and experimentally evaluated. The implementation of this method with a robotic system is particularly challenging, since the robot needs to precisely manipulate the palette knife to pick up and release the color on the canvas. The painting system comprises a 6-DOF collaborative robot, a camera to acquire the information on the color positioning, and algorithms for image processing and path planning. Two algorithms for the low and high frequencies of an image are considered: the first one concerns the uniform painting and filling of large areas, the second one regards the details and contours of the image.

The main advantages of the proposed algorithms are the simplicity, the easiness of implementation, and the applicability to any kind of digital image. Disadvantages include the processing of series of stroke together and, therefore, a limited control on the placement of a single stroke. For example, in the low frequency algorithm, the orientation of the strokes within an area only depends on the values of the gradient on the borders of that area. Furthermore, the strokes that belong to one layer are placed regardless of the strokes belonging to the other layers.

During the painting process the user can modify multiple parameters, such as software parameters that affect the image processing, as well as palette knife parameters that affect the stroke effect, that is, the drawing angle, the drawing height and the stroke length. Even if some pilot tests have been performed to estimate the behaviour of the palette knife parameters, the relationships between these parameters, the pressure applied to the canvas, and the stroke effect are challenging to be derived.

Future developments of this work will investigate the integration of further non-photorealistic rendering techniques in order to better exploit the artistic potential of the palette knife painting technique. In particular, processing algorithms, in which the orientation of each stroke depends on the local value of the gradient, and in which all strokes depend on the previously painted ones, will be implemented. Furthermore, the camera feedback system, used in this work to locate the paint on the working surface, will be used to monitor and control the painting stroke, thus achieving an optimal stroke positioning onto the canvas.

Future works will also include the introduction of a force feedback to better control the pressure of the palette knife during the picking up and the releasing of the color. In this manner, the pressure applied by the palette knife on the canvas will be regulated and adjusted during the panting process regardless the calibration of the painting surface and the precise choice by the user of the painting parameters. Finally, a model of the painting knife will be developed in order to precisely compute the painting knife footprint as function of ${\alpha }_{draw}$ and $\Delta h$ or the pressure retrieved by the force feedback.