1. Introduction
Art in its multiple forms is practiced by all human cultures; it is the fulfillment of the human desire to express emotions and creativity. The society of the 21st Century has managed to achieve a remarkable technological knowledge. Even though art and technology seem to be very far apart from each other, if combined together, they can create a new concept of art known as robotic art [
1].
Robotic art involves many disciplines [
2] such as dance, music, theater, and painting. This work focuses on robotic painting art: technology, that is, machines, robots, computers and sensors, are used for drawing and painting. One of the first artists to apply this novel concept of art was the Swiss sculptor Jean Tinguely (1925–1991) [
3]. In the 1950s he started the development of a series of generative works called Métamatics, a collection composed of machines generating complex and random patterns. In the 1970s the English professor Harold Cohen (1928–2016) developed AARON [
4], a computer program that draws and paints stylized images from its programmed “imagination”. The algorithm was implemented in Harold Cohen’s painting machine and received a great attention from international exhibitions and art galleries, including the Tate Gallery in London. In recent years many examples of machines and robots for artistic painting can be found in literature, each using different methodologies and techniques to produce artworks.
In 2006 Calinon et al. [
5] developed an interesting humanoid robot capable of drawing portraits. The system consists of a four degree-of-freedom (DOF) robotic arm and an algorithm based on face detection and image reconstruction. In 2008 Aguilar and Lipson [
6] proposed a robotic system that can produce paintings using a 6-DOF arm and an algorithm for the brushstroke positioning. In 2009 Lu et al. [
7] presented a robotic system that performs automated pen-ink drawing based on visual feedback.
In the last decade many artists used manipulators or robots to create artistic graphics and paintings. Some of them implemented advanced algorithms that achieved excellent results, such as the painting robot eDavid by Deussen et al. [
8,
9]. eDavid is one of the most impressive examples of robot artists, capable of reproducing non-photorealistic images, using visual feedback and complex algorithms to simulate the human painting process. Another interesting example is given by Tresset et al. [
10], who developed Paul, a robotic installation that produces observational face drawings guided by visual feedback. Furthermore, in 2016 Luo et al. [
11] proposed a robot capable of painting colorful pictures with a visual control system like human artists. Two other interesting examples of robotic painting are proposed by Scalera et al.: the first uses the spray painting technique [
12], commonly found in the industrial environment for aesthetic and protection [
13,
14]; the second is the first robotic painting system adopting the watercolor technique [
15,
16]. Other recent examples include the works presented by Karimov et al. [
17], who developed a robot capable of creating full-color images aimed at reproducing a human-like style, and by Igno et al. [
18], who proposed a robotic system focused on painting artworks by image regions. Moreover, Song et al. [
19] presented an impedance-controlled pen-drawing system capable of creating art on arbitrary surfaces. Vempati et al. developed Paint Copter [
20], an unmanned aerial vehicle capable of spray painting on complex 3D surfaces. Moreover, Ren and Kry [
21] investigated the trajectory generation for light paintings with a quadrotor robot.
Several examples of robotic systems for artistic painting that use many different tools, that is, pens, pencils and brushes, can be found in the literature. To the best of the author’s knowledge, no examples of robotic systems using the palette knife painting technique have been developed yet. This technique is characterized by tools called palette knives, which are used to transfer the color to the canvas. Using such tools with a robotic painting system is a challenging task, since not only the positions, but also the orientations of the palette knife have to be accurately planned for the painting process. In this context, Okaichi [
22] managed to model and 3D simulate the palette knife technique, but the algorithms have not been experimentally implemented in a robotic application yet.
This paper proposes a new robotic system capable of painting artworks using the palette knife technique, shown in
Figure 1. The system consists of a 6-axis robotic arm equipped for palette knife painting, a camera for the acquisition of the position of the paint, and a series of algorithms for image processing and trajectory planning. The system receives a digital reference image as input, which is then processed by two different algorithms, introducing an artistic contribution. The first one concerns the image low frequencies, the other one is used to emphasize the information on the high frequencies. The image frequencies are related to the rate of change of intensity per pixel: high frequencies return information about the image details and edges, whereas low frequencies about large and uniform areas. The data extracted from the input image is converted into paths that are reproduced by the robot. The main contributions of this work can be summarized as follows: (a) the development of a novel robotic painting system capable of paining artworks using the palette knife technique, (b) the implementation of image processing and path planning algorithms that accounts for the orientation of the palette knife during paining, and (c) the experimental validation of the system.
The paper is organized as follows: in
Section 2 the painting knife technique is briefly illustrated. In
Section 3 the robotic painting system developed in this work is presented.
Section 4 describes the algorithms used for image processing and trajectory planning.
Section 5 reports the experimental results, whereas
Section 6 discusses the conclusions and possible future developments of the paper.
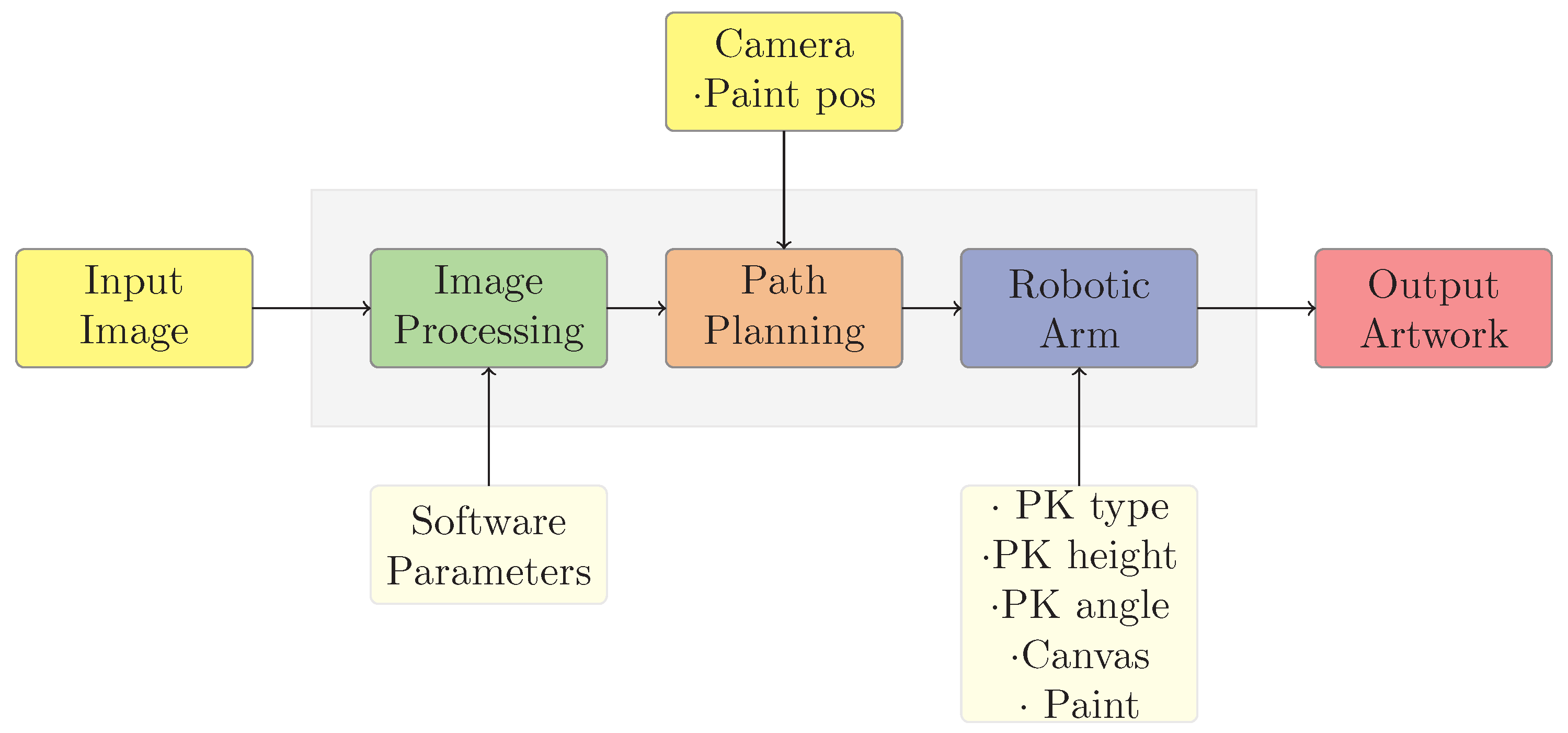
3. Robotic Painting System
This section provides an overview of the architecture of the robotic painting system, which consists of both software, that is, trajectory planning and image processing algorithms, and hardware components, that is, palette knife type (PK type in
Figure 3), canvas, and paint. The robot used in this work is a UR10 collaborative robot by Universal Robots. This type of robot was chosen since its collaborative features allow a human operator to work side by side with the manipulator during the painting process. For the user it is indeed important to have access to the robot proximity to check the correct execution of the artwork, provide color when needed, adjust the dilution of the color, clean the palette knife and eventually change it. The robot is equipped for painting purposes and it is provided with acrylic or tempera colors and painting paper, as shown in
Figure 1a. A custom tool designed in SolidWorks and 3D printed using an Ultimaker 2+ allows the palette knife to be mounted on the robot end-effector (
Figure 1b). Furthermore, a Logitech C310 webcam allows the user to obtain the paint position coordinates on the working surface by clicking on the color image in a live camera stream.
The software for image processing and path planning is implemented in a user friendly graphical interface developed in MATLAB App Designer. The robotic painting system receives a digital image as input; the most common file formats can be loaded (PNG, JPG, BMP). The reference image is processed using different non-photorealistic rendering techniques explained in details in
Section 4. Then, the sequence of paths to be completed by the robot is planned in the operative space. The robot is controlled with the proprietary UR Script Programming Language, which includes built-in functions that monitor and control I/O and robot movements. The motion commands are sent to the robot controller using the TCP/IP protocol. An overview of the system is shown in
Figure 3.
Since the robot interacts with its surroundings, it needs to know exact geometrical information (poses) about the working surface, the canvas position, the tool size, and the color palette position. The following paragraphs provide an overview on the calibrations required by the robotic system to properly operate in the painting environment—tool center point, painting surface and camera. All calibrations are performed in static conditions and, therefore, the compliance of the palette knife does not influence the results. However, small errors due to the compliance of the palette knife during calibration are considered negligible for the aims of this work.
3.1. Tool Center Point Calibration
The tool center point calibration allows to identify the change of coordinates between the center of the robot end-effector and the tool center point (TCP) using translations and rotations. Paining knives can be identified with a tag number, in this work only the painting knife "41 Pastello" (
Figure 1b) is used, therefore this calibration has to be performed only once. If a different tool with a different shape is taken into account, a new TCP calibration is required.
Figure 4 shows a schematic of the tool mounted on the robot flange. Three reference frames are available: the canvas
, the robot flange
and the palette knife
. The TCP is namely the
position and orientation with respect to the robot flange reference frame
, consequently it defines the position and the orientation of
.
Thanks to the design of the palette knife support (
Figure 1b), the blade is kept parallel to the robot flange
axis; moreover the
,
and
,
are co-planar as in
Figure 4. Due to this, the TCP calibration is required to define only two parameters: the translation
and the translation
. During the painting process the tool poses are referred to the frame
, therefore to minimize the position error the TCP has to be determined with high accuracy. In order to handle rotations more easily, the TCP is set on the blade tip. In
Figure 4 is the angle between the palette knife
axis and the canvas plane, whereas
is the distance between the TCP
and the canvas.
, considered with its absolute value, assumes negative values since the palette knife has to press on the canvas flexing itself in order to perform the stroke.
If the procedure is done manually the result may vary depending on the skills of the operator. Luo and Wang [
25] and Hallenberg [
26] proposed two different methodologies to achieve a tool center point calibration by applying computer vision and image processing techniques. The calibration proposed in this paper is a hybrid system halfway between the manual procedure and the methodologies recalled above: thanks to the camera set on the top of the robot working surface a fast and flexible calibration procedure, feasible for many different palette knives with different shapes and dimensions, can be integrated in the software. The procedure to perform the calibration is given below:
Approximately measure and and set the values.
calibration: rotate the tool around the newly defined check if the center of rotation coincides with the tip of the painting knife. If not, correct the value and check again.
calibration: rotate the tool around the newly defined check if the center of rotation coincides with the tip of the painting knife. If not, correct the value and check again.
Steps (2) and (3) are extremely delicate, therefore a more detailed analysis is required. In order to adjust the
translation, it is necessary to perform a rotation around
by
. During this process the
axis must be orthogonal to the camera, hence
.
Figure 5 shows the three possible cases from the camera point of view:
overestimation,
underestimation or
correct estimation. The blue dot is the desired TCP position on the painting knife tip, whereas the red point is the actual TCP position, its location is due to the used
parameter.
and
represent the orientation of the robot flange before and after the rotation.
Figure 5a shows a
overestimation, and
Figure 5b an underestimation. Therefore, it is required to estimate this error and correct the
value in order to obtain the case shown in
Figure 5c.
The error along the y axis can be measured using the camera fixed above the working table: at least two pictures must be taken, one before and one after the rotation. When merging the two images using an image editor, the value in pixels can be precisely determined which can be converted in meters (). If an overestimation occurs the corrected value is , if an underestimation occurs the corrected value is .
The
translation can be measured similarly performing rotations around the
axis. In order to correctly estimate the error along the
z axis
during the calibration process
axis must be orthogonal to the camera sensor as shown in
Figure 6.
3.2. Painting Surface Calibration
The painting surface calibration allows to compensate errors due to the non-perfect parallelism of the painting surface with the robot base. To solve this problem, it might be useful to derive the equation of the plane approximating its surface, in a way similar to that in Reference [
15]. Using this approach, the table height can be expressed as function of the painting knife TCP position. In the calibration program the canvas is used as reference; the end-effector is then manually positioned at each corner of the canvas and its position
with
is saved. These points are expressed with respect to the reference frame
O -
in
Figure 4. This procedure provides the position of the canvas corners and its dimensions. Subsequently, the points can be elaborated in order to derive the parameters
for plane
, as follows:
By introducing the acquired data and Equation (
1), it is possible to write the following matrix equation:
Equation (
2) can be written as
. Then, it is easy to estimate the vector of surface parameters as:
These parameters are used to create a virtual surface in the software through the minimization of the mean square error; the plane is then used as reference for the planning of painting paths.
3.3. Camera to Robot Calibration
The camera plays an important role in locating the paint on the working surface. Camera and robot work with two different reference frames, which need to be related one to the other. In order to obtain this transformation it is necessary to acquire some 3D real world points and their corresponding 2D image points. For a good accuracy, a prior camera calibration is performed, as in Reference [
27].
When the calibration software is run, a window is displayed showing a live camera stream with four virtual red dots superimposed on the image. As already done in the working surface calibration, by manually moving the tip of the knife over the four points, it is possible to acquire the points coordinates
,
,
and
in pixel with respect to the image reference frame
-
and the points coordinates
,
,
and
in meters with respect to the robot reference frame
O -
. In order to minimize the parallax error during the acquiring process the tool has to be as close as possible to the working surface. This transformation can be computed referring to
Figure 7.
The dashed rectangle represents the camera vision field. The red dots are the virtual calibration points, their coordinates with respect to the two frames are available thanks to the performed calibration. Moreover, the camera and the robot frames could not be perfectly aligned, an effect represented by the angle . Let now consider a random point P: only its position in pixel with respect to the image reference frame - is available. The aim of the camera to robot calibration is to express this point with respect to the robot reference frame O - . is the vector of coordinates of P with respect to - . It is possible to calculate , the vector of coordinates of P with respect to the auxiliary reference frame - , as . The components of are still expressed in pixel, therefore it is required to convert its components in meters. Considering the calibration data it is possible to compute the rectangle base and height in meters and in pixel, then a proportion can compute the vector in meters .
Deriving the required rotation matrices
,
used to align
with
and considering
, the vector of coordinates of
with respect to
O -
, it is possible to calculate
:
which represents the vector of the
P coordinates in meters with respect to the robot base reference frame
O-
.
5. Experimental Results
This section reports the experimental results obtained by testing the robotic painting system using the palette knife painting technique. Prior to performing the artworks, a preliminary characterization of the palette knife painting has been carried out. In particular, a series of strokes for the swoosh and the lines have been painted and analyzed by changing the painting parameters and . All the experiments have been performed using undiluted black tempera paint.
The swoosh effect has been analyzed with
mm and
, by measuring the maximum length and thickness of the strokes. Each test has been performed 5 times.
Figure 14 reports an example of one of the five tests, whereas in
Figure 15 the results for all the five tests for length and thickness are shown. The mean values and ranges are plotted. As it can be seen, by decreasing
there is an increasing of the strokes in terms of contact area, and therefore in length and thickness. The same effect occurs by increasing
.
Figure 15b shows the data regarding the swoosh stroke thickness. Strokes characterised by a wide contact area produce less detailed layer contours, therefore a painting containing a more dynamic and artistic effect can be obtained. On the contrary, using strokes characterised by a smaller contact area produces detailed layer contours. In the artworks presented in this paper both approaches are adopted.
The lines have been analyzed with
mm and
, by measuring the maximum length and thickness of the strokes. The tests have been performed 5 times.
Figure 16 and
Figure 17 shows an example of experimental lines and the results obtained with all the tests. The line stroke is used to draw the subject details. In order to obtain good performance the features have to be sharp and thin.
Figure 17 shows that for
and
both the line length and thickness increase by increasing
. This trend is not marked for higher values of
. Therefore, lower values of the painting angle are preferred for the painting of details.
The influence of speed and acceleration has been analyzed on the swoosh effect for fixed values of
mm and
. Several combinations of speed
m/s and acceleration
m/s
have been tested, by painting swoosh strokes. Each test has been performed 5 times.
Figure 18 reports the results of the tests, by showing the contour of the acquired swoosh strokes. The swoosh effect mainly depends on the acceleration, since for values higher than 1.5 m/s
the strokes are affected by random bleeding effects. Therefore, in order to avoid this undesirable effect, for the low frequencies painting process, maximum values of speed and acceleration equal to
m/s and
m/s
have been chosen. These values also avoid dripping of the color attached under the palette knife on the canvas during the robot motion.
The two reference images adopted for the artworks are shown in
Figure 8a,b, and are processed with the low and high frequencies algorithm proposed in
Section 4.
Figure 19 shows a frame sequence of the painting of artwork Martina, whereas
Figure 20 shows the complete artwork. In
Figure 21 an analogue sequence for artwork Stefano is shown, whereas the final result is reported in
Figure 22. Two short videos of the robot performing the paintings are available in the
supplementary material attached to this paper (Video 1 for Martina, video 2 for Stefano). The artworks are realized in canvas of
cm. Each artwork takes few hours to be painted by the robot.
The artwork Marina features six layers. The first five layers are processed with the low frequency algorithm so as to paint and uniformly fill the large areas of the subject. The sixth layer accounts for the image details and contours. The artwork is painted on paper with a 220 g/m
grammage and tempera paint. The artwork in
Figure 20a is obtained applying only the low frequency algorithm to the reference
Figure 8a, the parameters used for the image processing are reported in
Table 1a.
Angle and
distance are the parameters required to build the line mask explained in
Section 4.1: the first parameter defines the line angulation in the binary mask, the second sets the distance between the lines. To avoid regular patterns onto the canvas, different values for each layer of
angle parameter are chosen. On the contrary, the
distance parameter is adjusted according to the footprint of the palette knife. For the first layers high distances using a wide footprint are preferred. This results in a lower resolution in the painting, but leads to a faster filling of the layer. For the last layers a smaller footprint is used to get a higher resolution. Therefore the
distance parameter is kept smaller to avoid holes between the lines.
The final artwork in
Figure 20b is obtained by applying the high frequency algorithm to the same reference image. Layer 6 is processed using a DOG filter characterized by a 20 pixel window,
and
. Then, the DOG image is filtered with a threshold equal to 0.552 and only objects with an area larger than 400 pixel are taken into account for the skeletonization.
The artwork Stefano is composed of seven layers. The first five layers are drawn with the image low frequency algorithm used to paint and uniformly fill in large areas of the subject. The sixth layer regards the face and the papillon details, painted using black paint, and the shirt details in light gray. The seventh layer is exclusively dedicated to draw the eyes of the subject. The background of this artwork was pre-painted using a yellowish canvas panel of
cm and acrylic paint. The artwork in
Figure 22a is obtained applying the low frequency algorithm to the reference
Figure 8b, the parameters used for the image processing are reported in
Table 1b. Regarding the high frequencies,
Layer six is processed using a DOG filter characterized by a 35 pixel window,
and
. Then, the DOG image is filtered with a threshold equal to 0.568 and only objects with an area larger than 200 pixel are taken into account for the skeletonization. The last layer is obtained applying the high frequency algorithm to an image containing only the subject’s eyes. A DOG filter characterized by a 35 pixel window,
and
is used. Then, the DOG image is filtered with a threshold equal to 0.5 and only objects with an area larger than 2 pixel were taken into account for the skeletonization. The complete artwork is shown in
Figure 22b.
As explained in
Section 2, the stroke depends on many parameters such as the painting knife height, its inclination, and so forth. The combination of these parameters changes the stroke effect shown in
Figure 2. In
Table 2 the parameters adopted for each layer are reported. The drawing angle
corresponds to the angulation of the palette knife tip with respect to the working surface and the table (
Figure 4). The drawing height
corresponds to the TCP height with respect to minimum mean square error plane computed in
Section 3.2. The setting of parameters
and
allows to adjust the pressure exerted by the tool against the canvas, even if, in this work, a pressure feedback is unfortunately not available. Finally, the
maximum stroke length is the parameter needed to compute the path segmentation explained in
Section 4.1.
The proposed robotic painting system has achieved interesting results, shown in
Figure 20 and
Figure 22. The low frequency algorithm worked well for uniformly filling large areas, whereas the high frequency algorithm for painting the missing details could be further improved. In fact the last algorithm uses skeleton, causing a loss of details during the process (like the subject’s eyes) because of the algorithm design. Due to this a dedicated eye layer was used for the artwork Stefano in
Figure 22b.
6. Conclusions
In this paper a novel robotic system that uses the palette knife painting technique to create artworks starting from a digital image has been presented and experimentally evaluated. The implementation of this method with a robotic system is particularly challenging, since the robot needs to precisely manipulate the palette knife to pick up and release the color on the canvas. The painting system comprises a 6-DOF collaborative robot, a camera to acquire the information on the color positioning, and algorithms for image processing and path planning. Two algorithms for the low and high frequencies of an image are considered: the first one concerns the uniform painting and filling of large areas, the second one regards the details and contours of the image.
The main advantages of the proposed algorithms are the simplicity, the easiness of implementation, and the applicability to any kind of digital image. Disadvantages include the processing of series of stroke together and, therefore, a limited control on the placement of a single stroke. For example, in the low frequency algorithm, the orientation of the strokes within an area only depends on the values of the gradient on the borders of that area. Furthermore, the strokes that belong to one layer are placed regardless of the strokes belonging to the other layers.
During the painting process the user can modify multiple parameters, such as software parameters that affect the image processing, as well as palette knife parameters that affect the stroke effect, that is, the drawing angle, the drawing height and the stroke length. Even if some pilot tests have been performed to estimate the behaviour of the palette knife parameters, the relationships between these parameters, the pressure applied to the canvas, and the stroke effect are challenging to be derived.
Future developments of this work will investigate the integration of further non-photorealistic rendering techniques in order to better exploit the artistic potential of the palette knife painting technique. In particular, processing algorithms, in which the orientation of each stroke depends on the local value of the gradient, and in which all strokes depend on the previously painted ones, will be implemented. Furthermore, the camera feedback system, used in this work to locate the paint on the working surface, will be used to monitor and control the painting stroke, thus achieving an optimal stroke positioning onto the canvas.
Future works will also include the introduction of a force feedback to better control the pressure of the palette knife during the picking up and the releasing of the color. In this manner, the pressure applied by the palette knife on the canvas will be regulated and adjusted during the panting process regardless the calibration of the painting surface and the precise choice by the user of the painting parameters. Finally, a model of the painting knife will be developed in order to precisely compute the painting knife footprint as function of and or the pressure retrieved by the force feedback.