Abstract
This paper presents a novel inverse kinematics global method for a redundant robot manipulator performing a tracking maneuver. The proposed method, based on the choice of appropriate initial joint trajectories that satisfy the kinematic constraints to be used as inputs for a multi-start optimization algorithm, allows for the optimization of different integral cost functions, such as kinetic energy and joint torques norm, and can provide solutions with a variety of constraints, both linear and nonlinear. Furthermore, it is suitable for multi-objective optimization, and it is able to find multiple optima with minimal input from the user, and to solve cyclic trajectories. Problems with a high number of parameters have been addressed providing a sequential version of the method based on successive stages of interpolation. The results of simulations with a three-Degrees-of-Freedom (DOF) redundant manipulator have been compared with a solution available in the literature based on the calculus of variations, thus leading to the validation of the method. Moreover, the effectiveness of the presented method has been shown when used to solve problems with constraints on joint displacement, velocity, torque, and power.
1. Introduction
Redundant manipulators are extensively used for their ability to perform a prescribed end-effector motion (tracking problem) while taking into account extra goals, such as obstacle avoidance or the minimization of energy consumption, or other cost functions. This is particularly important for manufacturing tasks, which often require robots to perform a repetitive task while keeping energy and time requirements as low as possible. Since this type of application does not require joint motion to be computed in real time, the tracking problem is usually solved globally in this case. That is, the cost function is minimized over the whole trajectory at once rather than one step at a time. The complexity of this problem lies in its nonlinearity and high number of parameters. Furthermore, the physical limits of the manipulator (joint displacement, velocity, torque, power) are difficult to take into account, and the complexity is further increased when the manipulator is required to perform a task cyclically (i.e., reaching the initial joint configuration again at the end of the task).
Several solutions have been proposed in the literature for the global optimal solution of the tracking problem, mostly based on integral cost functions. Early attempts focus on either the Pontryagin Maximum Principle, as proposed by Nakamura et al. [1], or on the calculus of variations, as proposed by Kazerouinian et al. [2]. Both of them use the integral of pseudo-kinetic energy along the trajectory as a cost function, and both their approaches are limited by the fact that they formulate the global tracking problem as a Two-Point Boundary Value Problem (TPBVP). Nedungadi et al. [3] exploited the calculus of variations to provide an analytical solution for the global minimization of kinetic energy, which, however, still required them to solve a TPBVP. In order to overcome issues related to Jacobian inversion, a variational Jacobian-free approach was sought by Hirakawa et al. [4], who proposed an algorithm to find the minimum electrical energy consumption along a trajectory by using a spline approximation of joints trajectory. Martin et al. [5] exploited a B-spline approximation to optimize the joint torques norm while tracking an end-effector trajectory, also limiting joint displacements.
Several solutions have been proposed to compute global inverse kinematics solutions while respecting limits on joint variables or performing cyclic tasks. Zhou and Guyen [6,7] presented an algorithm based on the Pontryagin Maximum Principle and state space augmentation method to either handle joint limits or the periodicity of the trajectory. Nurmi et al. [8] used instead a penalty in the integral cost function to solve the problem of minimizing energy while tracking a trajectory with limits on joint displacements, velocities, and accelerations. Lyu et al. [9] exploited Sequential Quadratic Programming (SQP) to minimize time and energy consumption with constraints on joints displacement, velocity, acceleration, and jerk.
Some researchers also developed dynamic programming approaches to solve the global inverse kinematics problem. In particular, Ferrentino et al. [10] showed the flexibility of dynamic programming for multi-objective optimization and for finding solutions in different homotopy classes and with different type of constraints. The dynamic programming approach, however, has the drawback of the discretization of inputs and the very high dimensionality, although it can be suited for simple planar robots. Dynamic programming approaches were also sought by Guigue et al. [11], who proposed an algorithm to solve multi-objective optimization problems for a seven-Degrees-of-Freedom (DOF) manipulator.
Nonlinear optimization methods have been extensively used for robotic path planning as well, with plenty of attention being focused on evolutionary algorithms, especially Genetic Algorithms (GA), for point-to-point trajectories. This is due to several advantages they have over other methods: they allow for finding a global solution, do not imply the use of derivatives or gradients, and are suitable for a wide range of problems. The first author who extensively described the possibility to use these methods in robotics, to the best of our knowledge, was Davidor [12]. Since then, many different works have been published on the topic, mostly focused on point-to-point trajectories. Shintaku [13] proposed a GA-based solution to find the minimum energy solution for an underwater manipulator, based on solving the optimal control problem as a TPBVP, by searching the solution with a GA. McAvoy et al. [14] proposed to combine B-splines and GAs to obtain an optimal trajectory for a redundant manipulator in a pick-and-place operation. Tian et al. [15] presented a floating point GA-based solution able to avoid obstacles and minimize joint displacements. On the other hand, other research works focused on partially-constrained motion planning or fully-constrained motion planning (as alternatives to point-to-point motion planning). For example, Baba et al. [16] proposed a GA-based path planning algorithm, which included collision avoidance with moving obstacles in the robot workspace thanks to the introduction of the concept of pseudo-potential. Kazem et al. [17] developed a GA to carry out the point-to-point trajectory planning of a three-DOF redundant robot arm minimizing traveling time and space, while not exceeding maximum joint torque, and avoiding singularities and collision with obstacles in the robot workspace. In addition, Ferrentino et al. [18] designed a GA to perform time-optimal control of robotic manipulators along specified paths, subject to torque constraints. Another type of evolutionary algorithm is Particle Swarm Optimization (PSO), which has also been exploited to solve robotics problems. Worth mentioning are Stevo et al. [19], who used it to calculate a point-to-point trajectory optimized with respect to different objectives (minimum time, energy consumption, joint displacement), Hansen et al. [20], who used it to minimize electrical energy consumption with a realistic model of actuators and related losses, and Doan et al. [21], who presented a PSO-based inverse kinematics solution for robotic arc welding. To a small degree, Simulated Annealing (SA) has also received attention by the robotic community, for example by Garg and Kumar [22], who used an adaptive version of the algorithm for non-redundant manipulators, comparing the results with those obtained with a GA. The conclusions were that both reached the same solution, but SA was computationally faster.
Trajectory tracking problems of redundant manipulators—i.e., motion planning problems where the end-effector desired position and velocity of a redundant manipulator are defined along the whole length of the trajectory—are frequent in manufacturing (e.g., robotic machining, laser cutting, paint spraying, arc welding, sand blasting, etc.), and traditional methods that have been mentioned above feature important limitations in tackling these problems. It has already been mentioned that the Pontryagin Maximum Principle and the calculus of variations require the solution of a TPBVP, and that they are not particularly flexible concerning the inclusion of constraints. In addition, some researchers, such as Martin et al. [23], also highlighted that, under certain conditions, optimal control methods may fail to find the global optimum, as two solutions might be in different homotopy classes: this means that the most expensive one cannot be deformed continuously into the less costly one. In such cases, optimization algorithms might fail to find the best optimum if their initial conditions are not in the right homotopy class. On the other hand, Pashkevich et al. proposed multi-objective optimization algorithms [24,25] via a graph representation of the search space and dynamic programming procedures, which allowed for generating smooth manipulator trajectories within acceptable time, simultaneously considering kinematic, collision, and singularities constraints. Moreover, Gao et al. [26] proposed a methodology based on dynamic programming to optimize the robot and positioner motions in redundant robotic systems for the fiber placement process, which allows users to find time-optimal smooth profiles for the joint variables while taking into account maximum joint velocities/accelerations and collision constraints. Nevertheless, none of these works considers quadratic cost functions, which are necessary for the minimization of kinetic energy, joint torques, or reaction forces/torques.
On the other hand, using general nonconvex optimization techniques in trajectory tracking problems can be computationally intensive, as the dimensionality of this problem turns out to be very high. Indeed, the end-effector trajectory has to be divided in several steps, or path points, which need to be as small as possible in order to allow precise tracking and, moreover, each step adds n parameters to the optimization, where n is the number of DOF of the manipulator. Furthermore, only small portions of the search space are relevant to the problem: most of the possible solutions feature excessive errors on trajectory tracking, to the point they are not worth being considered. Even if it was possible to restrict the search space only to solutions with no tracking error, the redundant nature of the manipulator means there is still an infinite amount of them. In this context, Reiter et al. [27] proposed a solution for the time-optimal path tracking problem of kinematically redundant manipulators that takes into account the technological limits of the robot, which is formulated as a nonlinear programming (NLP) problem solved with a multiple shooting method. In [28], the same authors presented a contribution to the solution of the time-optimal trajectory planning problem for kinematically redundant manipulators. In the proposed approach, the problem is divided into the trajectory optimization and an underlying inverse kinematics problem. The former is solved using a numerical computation scheme, augmented to fully exploit redundancy in an optimal way, such that the latter problem yields optimal results.
In this paper, a new optimization method for the solution of the global tracking problem of a redundant manipulator is presented and validated through simulations. The proposed solution overcomes the limitations of optimal control techniques applied to the trajectory tracking problem of redundant manipulators in several ways. First of all, it searches for multiple optima, and thus has an increased chance to find solutions in different homotopy classes, and allows to take into account linear and nonlinear constraints and to tackle cyclic trajectories. Furthermore, the new method is very flexible in optimizing different cost functions, and it is suitable for multi-objective optimization. The presented approach is based on a multi-start optimization method, and it relies on the generation of a population of candidate solutions and choice of the most promising ones as initial conditions for the optimization. All candidate solutions respect the kinematic constraints—i.e., the end-effector trajectory is exactly tracked, although in a non-optimal way. This prevents the proposed method from having initial conditions with high tracking error, and thus allows for lower computational time and increased chance of convergence. In order to extend the method ability to solve problems with very high dimensionality, a sequential procedure is proposed, based on a relaxed problem with a limited number of end-effector path points. The solution of this problem is progressively extended to the full set of path points through interpolation.
Simulation results are presented for the optimization of the integral of kinetic energy and of joint torques norm of a three-DOF planar manipulator, showing that the method hereby presented is able to provide the solution of a linearly and nonlinearly constrained kinematic problem with several different types of constraint (joint displacement, velocity, torque, and power). Even if the presented method is validated by the simulation of a three-DOF planar robot, it is straightforwardly applicable to more complex 3D and multi-DOF robot manipulators and, moreover, is very flexible as to the cost function to be minimized—i.e., a generic cost function can be optimized and multi-objective optimization can be performed.
2. Problem Definition
A kinematically redundant manipulator is a manipulator with more DOF than controlled end-effector variables. The tracking problem of a redundant manipulator is the problem of following a reference end-effector trajectory, expressed as a function of time (t) in the Cartesian space, and finding the related joint variables :
The redundancy implies that the problem expressed by Equation (1) may have an infinite number of solutions in the joint space. Thus, the problem is usually formulated as an optimal control problem, where a solution among all the possible ones is chosen based on the minimization of a cost function. For the global problem, such cost function is an integral cost. In the case hereby analyzed, the expression of the integral cost function is:
where and are the initial and final time of the end-effector trajectory, are the joint positions, are the joint velocities, are the joint accelerations, and are the actual and the reference end-effector trajectories, and is the cost function to be minimized along the trajectory.
In this work, two cost functions are considered: kinetic energy and joint torques norm. In the first case, the cost function is expressed as:
where is the inertia matrix of the manipulator. In the second case, the following expression of joint torques is considered:
where are the joint accelerations, is the term that comprises Coriolis and centrifugal forces, and gravity forces are neglected. Therefore, the following cost function is considered:
In discrete form, the problem becomes:
where is the reference end-effector position at time , the actual end-effector position at time , , , are the joint positions, velocities, and accelerations at time , is the cost function at time , and is the discrete time step.
The problem of minimizing the cost function in the form of Equation (6) can be solved with several different boundary conditions. For the purposes of this work, two possible sets of initial conditions on joint positions and velocities are considered. In the first one, the initial configuration of the robot is left free (i.e., it can be chosen among those that respect the reference end-effector position at time ), while the velocities are set to zero. This represents the case in which the manipulator has to perform a certain task starting from zero initial joint velocities. Another possible set of initial conditions is the one in which the manipulator performs a cyclic task: this is a task in which the initial and final configurations and joint velocities are the same, and it is typical of industrial applications in which robot manipulators perform repetitive operations.
In the first case, initial conditions can be written as:
with infinite possible choices for thanks to robot redundancy.
In the second case the initial conditions can be expressed as:
In the reminder of this work, initial conditions which can be expressed as in Equation (7), will be referred to as free initial configurations, while initial conditions which can be expressed as in Equation (8) will be referred to as cyclic initial conditions.
3. Materials and Methods
3.1. Global Optimization Method
This section presents the method that is proposed to find the joint trajectories which globally optimize the cost function while tracking a desired end-effector trajectory. First, Section 3.1.1 briefly introduces multi-start algorithms. Then, the new method in a simple version featuring its main characteristics (Global Kinematic Planner) is presented in Section 3.1.2. Section 3.1.3 presents a method to compute random initial joint configurations which comply with the end-effector position constraint at . This is a necessary step, since the initial robot configuration that will result in the globally optimal solution is not known a priori, thus a number of trials are necessary. Finally, a more sophisticated implementation of the Global Kinematic Planner, called Interpolation-based Global Kinematic Planner, is introduced in Section 3.1.4. This enhanced version of the method features faster convergence times and thus allows to tackle problems with a higher number of parameters, and ultimately to perform a more complete search over the solution space.
3.1.1. Multi-Start Algorithm
Multi-start optimization algorithms [29] exploit multiple sets of initial conditions to fully explore the search space of the cost function. They belong to the class of Random Search Methods, which have been proven to require mild assumptions to converge to the global optimum as the number of search attempts grows (for a proof, see, for example, [30]). The multi-start algorithm works as follows:
- Generate candidate solution i.
- Apply a local search method to improve i. Let x be the optimal solution obtained.
- If x is the best solution found so far, save it. Otherwise, discard it.
- Repeat steps 1–3 until a stop criterion is fulfilled.
In modern implementations, rather than repeating the steps in a sequential way, steps 1–3 are performed in parallel (starting from different candidate solutions) on different processors, and the best solution is chosen among all outcomes. A huge number of methods to generate initial conditions has been proposed (some references can be found, for example, in [29]), but none of them have been specifically developed for the problem hereby discussed, as most of the existing proposals are aimed at covering as much of the search space as possible. However, this is not ideal for the global optimization of joint trajectories in the tracking problem of redundant manipulators, as most of the values that joint positions can assume do not correspond to positions on the desired end-effector trajectory. Since only the kinematically compliant solutions are relevant (i.e., the solutions in the joint space for which the desired end-effector trajectory is properly tracked), in this paper a method based on the computation of a population of random local solutions of the inverse kinematics problem is proposed. Each member of the population respects the kinematic constraints and is unique, providing the multi-start algorithm with a wide set of feasible initial conditions to draw from.
In the literature, several local search algorithms have been exploited as local search methods for step 2 of the multi-start algorithm. In this case, the analytical gradient is difficult to compute, thus a numerical method is used. In particular, Sequential Quadratic Programming (SQP) is used [30], as implemented in the fmincon function in Matlab. SQP is an iterative optimization technique based on the optimization of a quadratic model of the cost function subject to a linearization of the constraints. Thus, it allows to include both linear and nonlinear constraints, without the need to include them explicitly in the cost function (e.g., using weights), since any output solution of SQP is automatically compliant with them.
3.1.2. Global Kinematic Planner
The method that follows has been called Global Kinematic Planner and exploits a weighted pseudoinverse in order to generate the initial conditions for the multi-start search. The use of the weighted pseudoinverse is a widespread technique in robotics (for local optimal redundancy resolution in differential kinematics), especially in the case , where is the identity matrix, when the weighted pseudoinverse is called Moore Penrose pseudoinverse, and is used to calculate the minimum-norm joint velocities required to obtain a desired end-effector velocity. Its mathematical formulation is:
where is the desired end-effector velocity. The weighted pseudoinverse can be expressed as:
where the weight matrix is a symmetric and positive definite matrix. It computes the local minimum of the quadratic cost function:
The most important feature of Equation (9) for our purposes is that it is possible to generate a different solution by changing the weight matrix , so that the relative importance of each joint in the cost function is modified. In the presented method, a randomly generated weight matrix for the weighted pseudoinverse is exploited to obtain several kinematically compliant candidate solutions (i.e., joint trajectories that respect the desired end-effector trajectory) for the multi-start algorithm. The best candidates are then picked for further optimization. The steps of the proposed method are presented here below. In their description, bold notations, such as , , etc., identify vectors as usual, while a notation with braces, such as , , etc., identifies a set of vectors, each one representing a different time step of the trajectory.
Initialization
- 1.
- Manipulator geometrical and inertial parameters, simulation parameters (see Section 3.2), and desired end-effector trajectory are taken as input.
- 2.
- A set of joint configurations compliant with the desired end-effector initial position is taken as input.
- 3.
- A set of weight matrices is generated, each one symmetric with random eigenvalues comprised between 0 and 1. The number of weight matrices to be generated depends on the available computational power, but it must generally be high enough that a further increase does not improve the best candidate solution anymore (see later in this section for further explanation). A reasonable number is:where is the number of parameters of the problem taken into account, which corresponds to:where is the number of points that define the desired end-effector trajectory, and is the number of DOF of the manipulator.
Population
- 4.
- A set of solutions is computed for each robot initial configuration defined at point 2, using the weight matrices generated at point 3 to weight the pseudoinverse. The joint velocity profiles of each solution are obtained through Equation (9). Each candidate solution is then obtained through numerical integration.
Optimization
- 5.
- All candidate solutions generated during the population phase are ranked according to a criterion. In case of unconstrained optimization, the criterion is the value of the cost function, while, in case of constrained optimization, the criterion is the value of the cost function plus an extra term to penalize the violation of constraints on joint mechanical limits. This term has the same expression as that presented in [31] by Liegeois in a different context:The value is a weight to balance the extra term against the cost function, and the reminder of the expression is a quantity defined as the distance from the joint mechanical limits, computed for each time step and summed over the whole motion time. In Equation (14), () is the maximum (minimum) i-th joint limit, the mean value between the two, and n are the robot DOF. This term is included in the cost function to penalize candidate solutions that exceed joint limits by large amounts, as opposed to excluding all candidate solutions that violate the limits, and for this reason is set to 0.01. In this way, the solver is still able to consider candidate solutions that exceed the limits by a small amount on a limited number of path points. Other constraints are not considered for the ranking of solutions, since in all the simulations carried out joint limits appeared to be by far the most influential constraint for the ranking. The term in Equation (14) is not required to be explicitly part of the cost function used for the optimization (step 6 below), since all constraints, including trajectory tracking, are taken into account as part of the SQP algorithm.
- 6.
- The multi-start algorithm is launched with the best candidate solutions, while all the others are discarded. Joint limits and the other constraints are enforced through the fmincon function, which takes their expression/value as an input. The number depends on the computational power available and on the complexity of the problem. For the examples presented in this work (see Section 4), has been set to 24.
- 7.
- The optimal set of joint position vectors is picked from the results of the multi-start algorithm. This corresponds to the optimal solution.
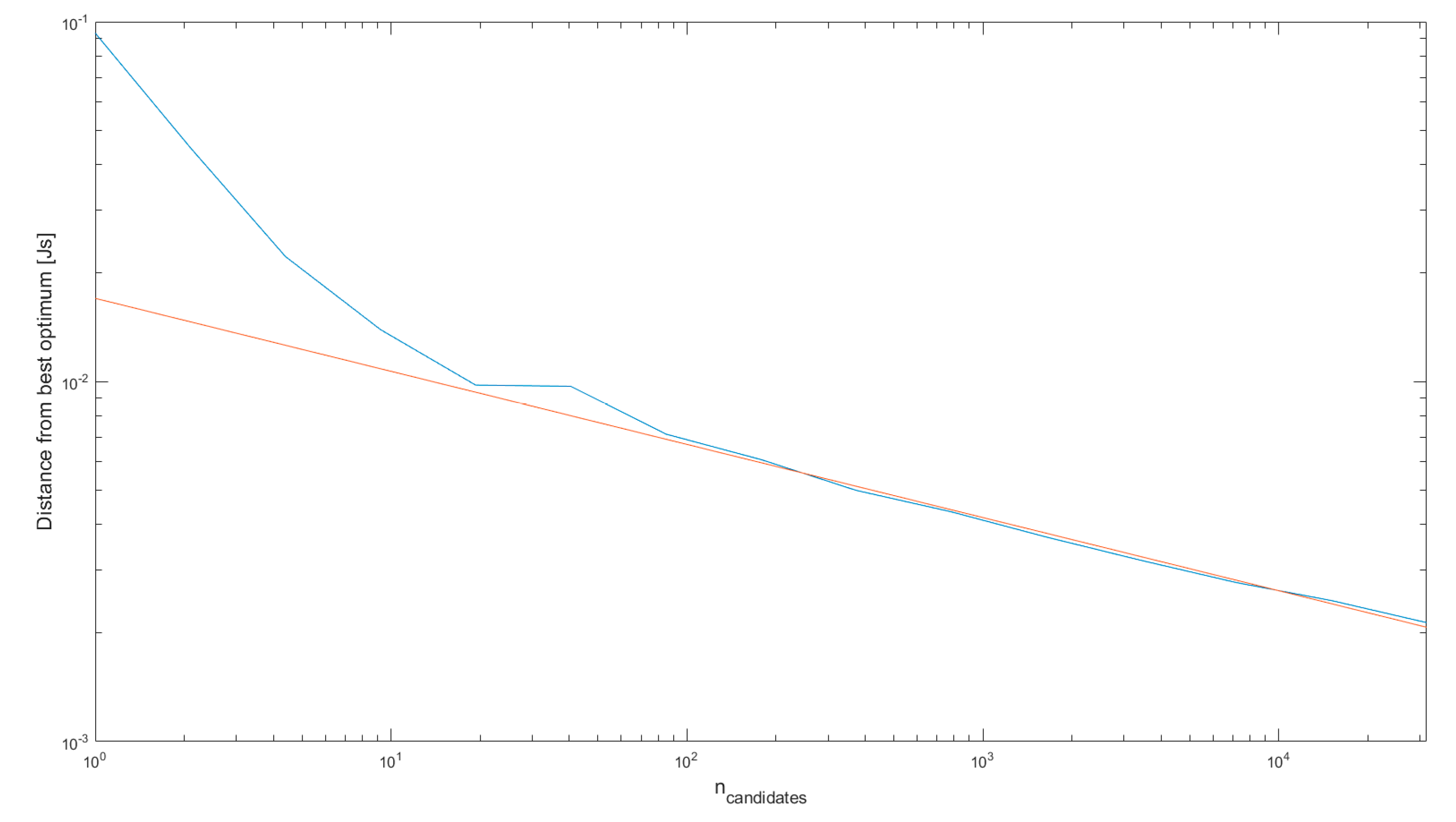
It must be highlighted that the use of a random weight matrix might feature very different results in term of joint displacements over the whole length of the trajectory despite apparently small changes in the weights. This makes it necessary for to be sufficiently high, while on the other hand increasing it above a certain value will require additional computational time but will not sensibly increase the quality of the best candidate solution anymore. In order to investigate the relationship between and the chances to find the best optimum, the value of the kinetic energy cost function for a three-DOF planar robot has been computed for sets with from 1 to 104.5 for a problem with 39 parameters, corresponding to an initial end-effector position and 12 following path points along a line, which for three DOF gives (12 + 1)*3 parameters. In Figure 1, the x-axis shows the number of candidate solutions in the set, and the y-axis shows the difference between the cost function value () for the best member of the set and the best computed value of the cost function obtained in the simulations (see Section 4.2, Simulation 1) for the system under consideration, according to Equation (15).
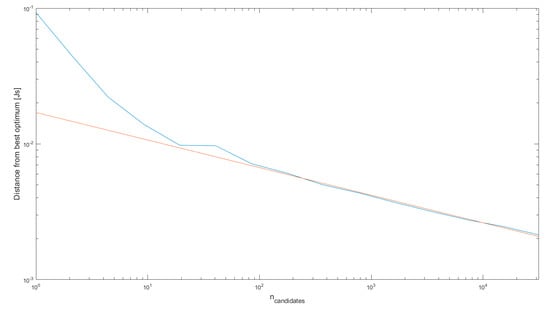
Figure 1.
Difference between cost function value of best candidate solution and best computed value of cost function versus number of candidate solutions.
It can be observed that, for a number of higher than the number of parameters, such difference tends to a linear function in logarithmic scale, which corresponds to a power law in linear scale. The best fit function is:
This suggests that, for the problem under consideration, increasing the number of progressively reduces the distance between the initial guess and the globally optimal solution. It is noted that the value of obtained by Equation (12) is 1521, which falls well within the linear part of the graph.
3.1.3. Generation of Robot Initial Configurations
Step 2 of the Global Kinematic Planner involves the input of a set of initial joint configurations. However, it is most often the case where no known initial configuration is likely to be reasonably close to the one of the global optimum solution. In this case, the following method can compute more initial configurations starting from an existing one ():
- 1.
- A set of joint velocity vectors { is randomly generated. In the examples provided in this paper, a normal distribution has been used, due to its effectiveness and the simplicity of implementation. Other methods are widely used for finding initial conditions for multi-start algorithms, such as Latin hypercube [32]. This was not necessary here, but it could lead to better results when the chosen is thought to be far from the optimal one.
- 2.
- An inverse kinematics problem is solved with end-effector velocity set to zero, robot initial configuration , and secondary task . This leads to a new initial configuration which does not affect the end-effector position:
Equation (17) is obtained by considering the general solution of the inverse kinematics problem with Moore–Penrose pseudoinverse:
where is the desired end-effector velocity and is a secondary task to be executed without modifying the end-effector velocity. This can be achieved by exploiting the null-space operator [33] . If is set to zero in Equation (18), the joint velocities will not be affected by the end-effector velocity and will be equal to . Equation (17) is obtained by integrating Equation (18) from to .
The size of the set of initial configurations is an important parameter to ensure convergence on the best optimum, as the initial configuration of the manipulator influences the whole trajectory. In general terms, this set should be representative of the whole set of configurations that produce the desired end-effector initial position. Inverse kinematics as per Equation (17) is computationally inexpensive, which allows to generate a high number of set members relatively inexpensively. The examples presented in this paper have been produced with a set of 66 initial configurations, which come from a trade-off between the overall computation time required and the probability to discard an initial condition that would give an optimum better than the previous ones found. Some of the 66 initial configurations may violate the manipulator joint limits. On the one hand, the ranking function will penalize initial configurations in which joint limits are violated by large amounts (which will not be processed further) and, on the other hand, the SQP optimization will always provide optimal solutions that are compliant with all the constraints, even if some of the initial configurations violate the joint limit constraints by a small amount.
3.1.4. Interpolation-Based Global Kinematic Planner
While the Global Kinematic Planner can find global optima of the problem expressed by Equation (6), its computational complexity grows with both the number of DOF of the manipulator and the number of path points. Due to this, its use might be computationally expensive for problems featuring multi-DOF manipulators or long trajectories with high precision requirements. In order to overcome this issue, a global optimal solution on a reduced set of parameters can be calculated and extended on a higher number of parameters through interpolation. Such new solution can then be optimized again with the new number of parameters. This two steps approach will reduce computational time, since the second round of optimization starts from an initial guess that is already optimal for a similar problem. The two steps can then be repeated adding more parameters through interpolation, until the desired time step is reached (possibly, the same as the Global Kinematic Planner). This method also allows a more thorough search on the solution space: since the optimization of a single candidate solution is much less time consuming with a low number of parameters, it is possible to first run the multi-start algorithm with a high number of candidate solution , and then focus the following optimization steps on the most promising solutions obtained. This allows to save computational power and may increase the chances to find a global optimum. The method above outlined, called Interpolation-based Global Kinematic Planner, works as follows:
- 1.
- A subset of path points of the end-effector trajectory to track is selected. A sampling interval with integer and discrete time step of the complete problem is used. Sampling can be thicker in parts of the trajectory where the cost function to be minimized is expected to be higher.
- 2.
- The Global Kinematic Planner is used to provide a solution , as explained above.
- 3.
- A new is chosen, according to the formula , where m is an integer submultiple of .
- 4.
- A new set of path points is selected with as a time step.
- 5.
- Cubic splines are used to interpolate the values of on the path points not included in the previous subset , obtaining a complete vectors set on the new set of path points.
- 6.
- A further gradient-based optimization based on SQP is run with initial guess corresponding to the solution obtained at the previous step.
- 7.
- Steps 3–6 are repeated, decreasing until the desired step size is reached. Subject to available computational power, this can be as small as the one of the complete original problem.
The solution obtained at step 5 is likely to be close to the optimal solution of the full global problem since it is an interpolation of a global optimal solution of a simplified version of the problem. For this reason, step 6 can run a much easier optimization (with faster convergence) with respect to step 6 of the Global Kinematic Planner, since the initial guess is already near-optimal.
3.2. Simulation Setup
A three-DOF planar manipulator (with 3 revolute joints) is used for the implementation, validation, and simulation of the presented method. This model corresponds to a real robot prototype that has been used in previous works [34,35,36,37]. The two end-effector Cartesian coordinates are controlled, x and y, thus leaving one degree of kinematic redundancy. Geometrical and inertial characteristics of the manipulator are presented in Table 1.

Table 1.
Manipulator geometrical and inertial parameters.
In order to show the effectiveness of the presented method, five simulations have been performed: one without constraints to validate it with respect to a known global optimum method available in the literature, and the other four with linear and nonlinear constraints to show its ability to handle different cost functions and a set of constraints. Two different end-effector trajectories have been used: a rectilinear one for validation and for testing the effectiveness of the method with joint, velocity, torque, and power constraints, and a circular one to show the effectiveness of the method also with cyclic initial conditions. Both trajectories start from the same end-effector position, , and run for a total time T = 1 s. The rectilinear trajectory has a length of 0.40 m and reaches the end-effector final position , while the final end-effector position is the same as the initial one for the circular trajectory. The radius of the circular trajectory is 0.05 m. The constraints considered in this work are on joint displacement, velocity, torque, and power. It should be noted that torque and power are nonlinear constraints. The numerical values of the limits used are reported in Table 2.

Table 2.
Constraint values.
Using the Global Kinematic Planner method as a reference with , each problem has 303 parameters, since the robot has three DOF and the number of path points is 101 (included the initial point). All simulations were performed using the Interpolation-based Global Kinematic Planner, with an initial , leading to a highly reduced number of parameters (39 parameters). A number of 1521 (= 392) candidate solutions were generated, and the best 48 () selected to be optimized via the multi-start algorithm. The time step has been then progressively halved, doubling the number of parameters at each iteration, until the full solution with 303 parameters and was reached. All the characteristics of the simulated trajectories are summarized in Table 3.

Table 3.
Simulated trajectories.
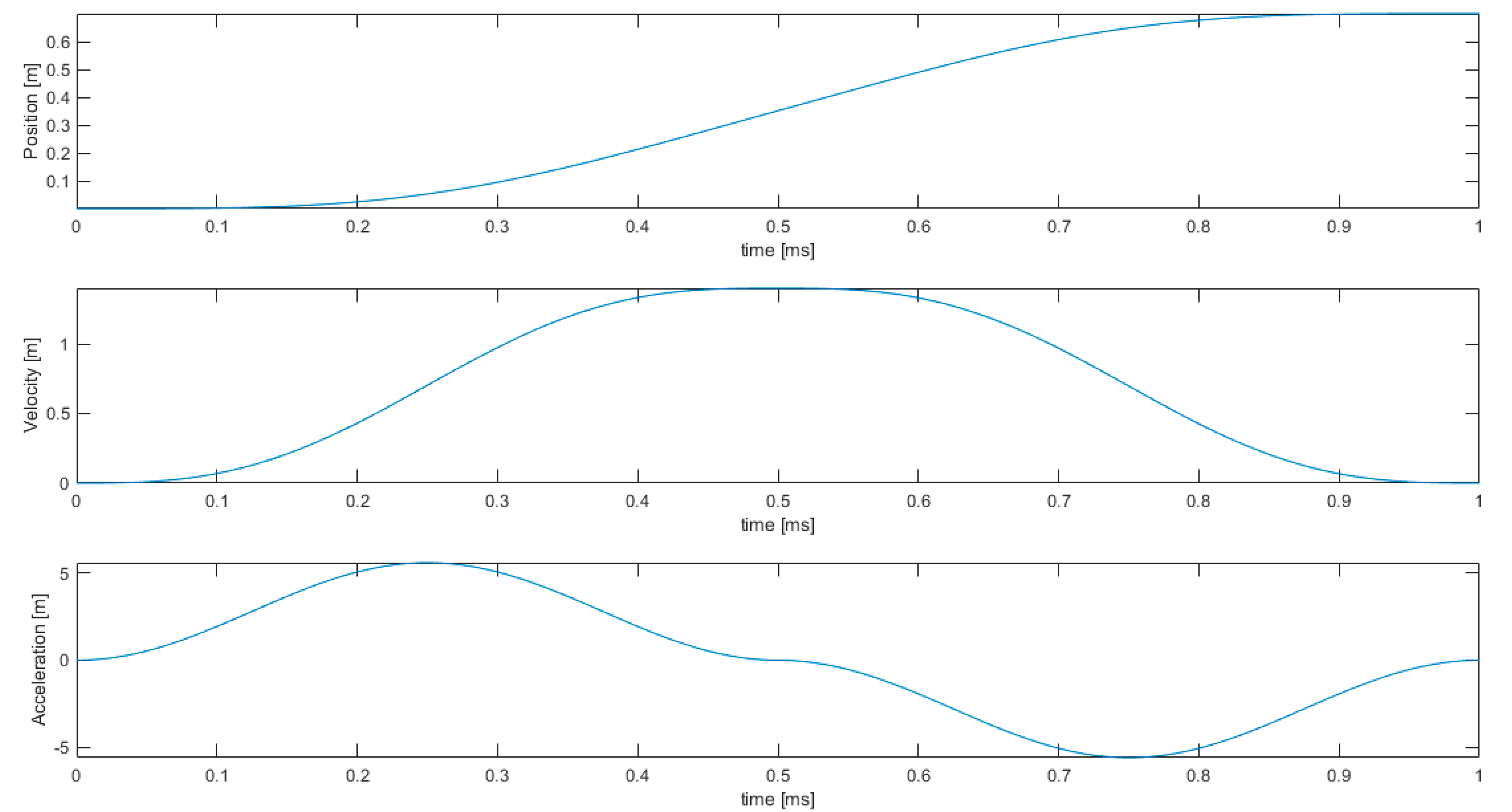
The end-effector velocity profiles have been chosen in order to have sufficiently smooth accelerations (continuous and with continuous derivative), as shown in Figure 2. The equation of the derivative of the curvilinear abscissa of the end-effector used is:
where T is the total motion time, L the overall length of the considered trajectory, and .
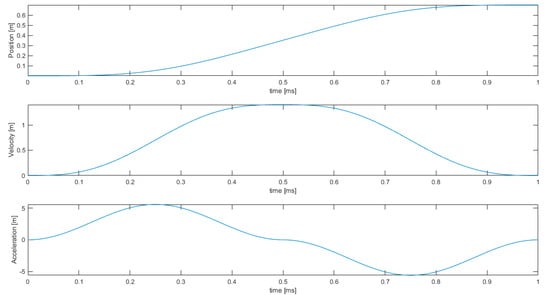
Figure 2.
End-effector curvilinear abscissa and its derivatives.
4. Results
4.1. Validation
In order to validate the proposed method, the solution for the kinetic energy integral cost function (without constraints) is computed and then compared with a solution obtained with a different method available in literature, which is based on the calculus of variations. The method used for the comparison has been proposed by Nedungadi et al. [3] and is based on an acceleration-based inverse kinematics solution:
where is the pseudoinverse weighted with the manipulator inertia matrix (), is the first derivative of the Jacobian matrix, and is the end-effector acceleration. The solution of Equation (20) along an end-effector trajectory gives the joint accelerations which correspond to a minimum of the kinetic energy integral along the trajectory.
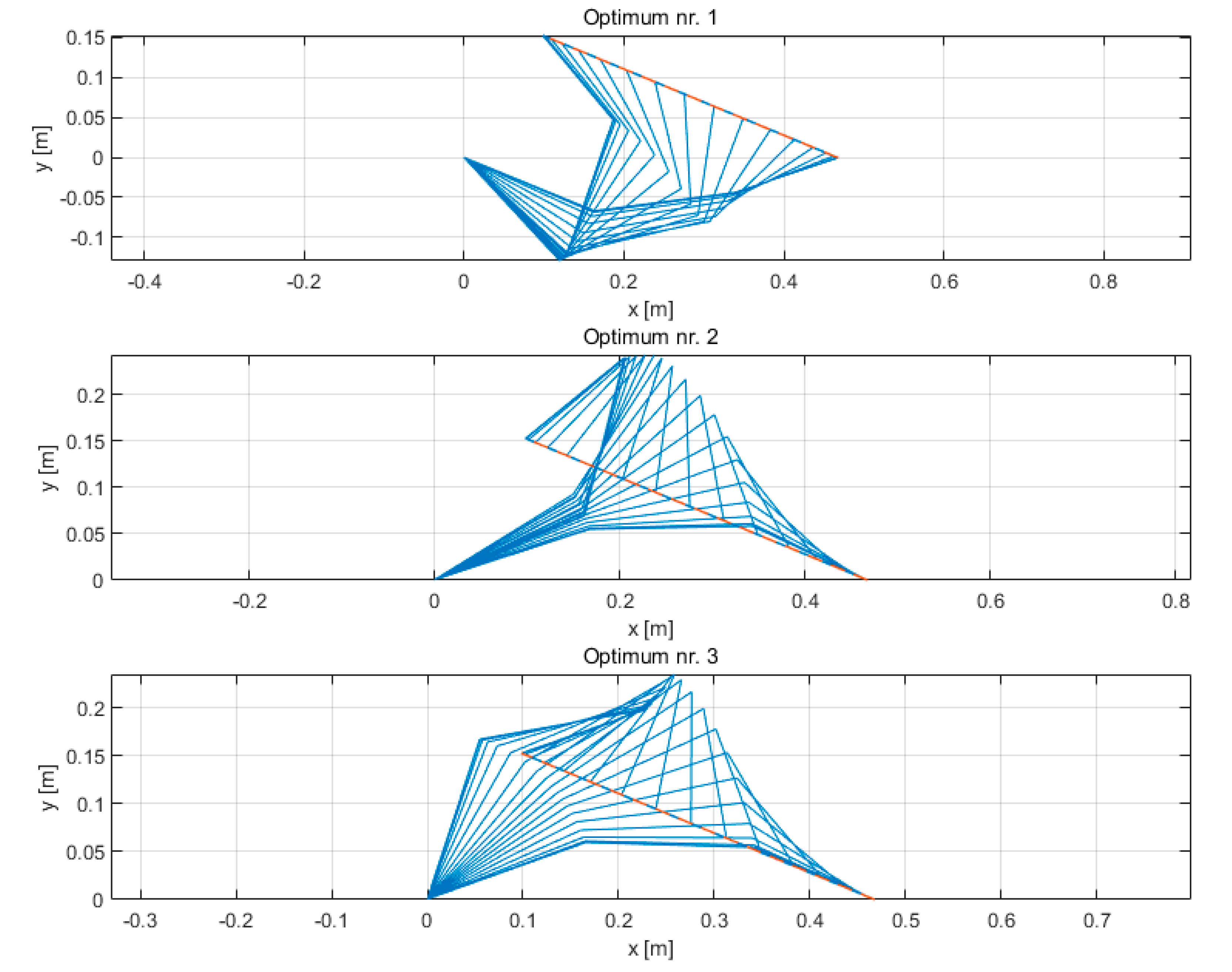
Results for the kinetic energy integral and mean absolute difference of joint displacements between the Interpolation-based Global Kinematic Planner and Nedungadi’s solution, starting from the same joint configuration, are shown in Table 4 for the three optima found, which comply with the boundary conditions of Equation (7). The stroboscopic views of robot motion for the three optimal trajectories are shown in Figure 3.

Table 4.
Comparison between results obtained with the Nedungadi’s method and with the Interpolation-based Global Kinematic Planner.
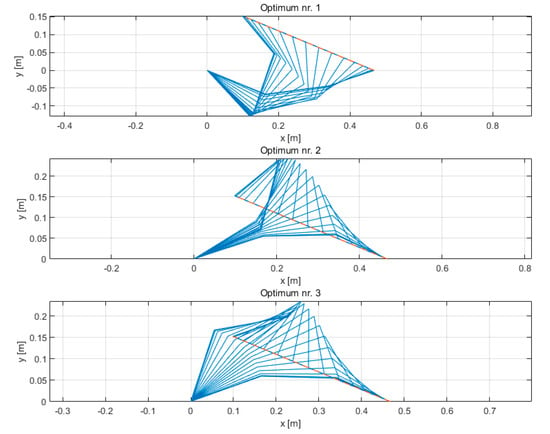
Figure 3.
Stroboscopic views of robot motion for the three optimal trajectories, as computed by the Interpolation-based Global Kinematic Planner.
It can be observed that all three optima results are very similar, with a negligible advantage in terms of kinetic energy integral for the Interpolation-based Global Kinematic Planner, which is probably due to numerical considerations. Moreover, in all three cases the maximum difference in joint motions is considerably small. The similarity of the solutions demonstrates that the proposed method is as effective as a theoretically proven method based on the calculus of variations for unconstrained problems. Therefore, the proposed method is validated and can be used with different cost functions and constraints, as presented in Section 4.2. It should be observed that solutions based on the calculus of variations, such as the one by Nedungadi, require the solution of a TPBVP and the computation of the Jacobian pseudoinverse, which is a source of numerical problems. Moreover, an appropriate choice of the initial guess is necessary to allow for the convergence of the TPBVP. This is, however, difficult, as it requires a trial-and-error process based on specific knowledge of the manipulation problem under examination.
4.2. Simulation Results
Simulations 1–4 feature the same end-effector trajectory optimized according to different cost functions and constraints, as shown in Table 3. The values of kinetic energy integral and joint torques squared norm integral for these simulations are compared in Table 5. Table 6 reports the same results for the circular cyclic trajectory (simulation 5). Computational times have been measured on a machine featuring an Intel i7 ninth generation exa-core processor with 32 GB RAM, SSD mass storage, and using Windows 10 and Matlab version 2019b.

Table 5.
Results for rectilinear trajectories.

Table 6.
Results for circular cyclic trajectory.
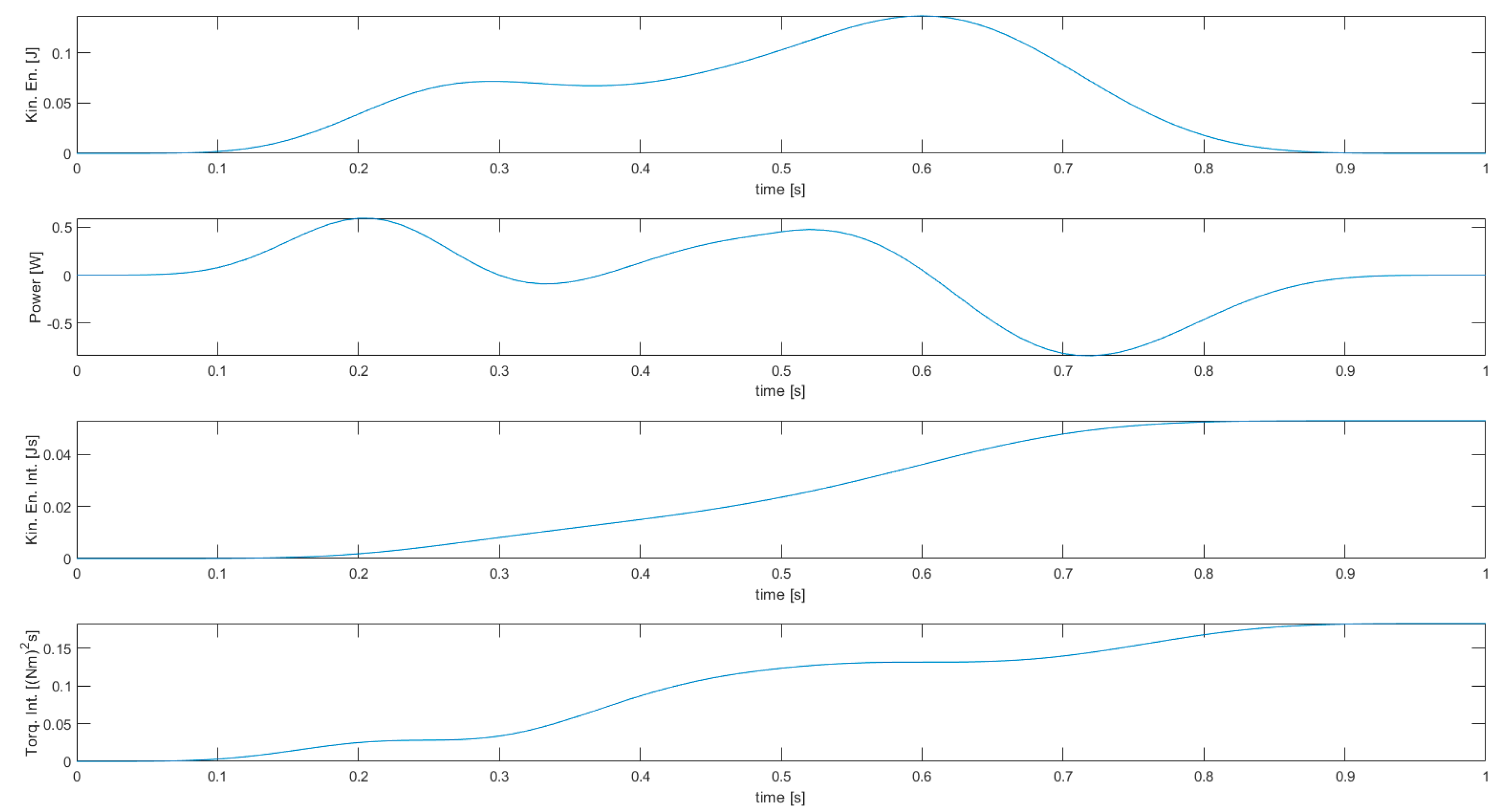
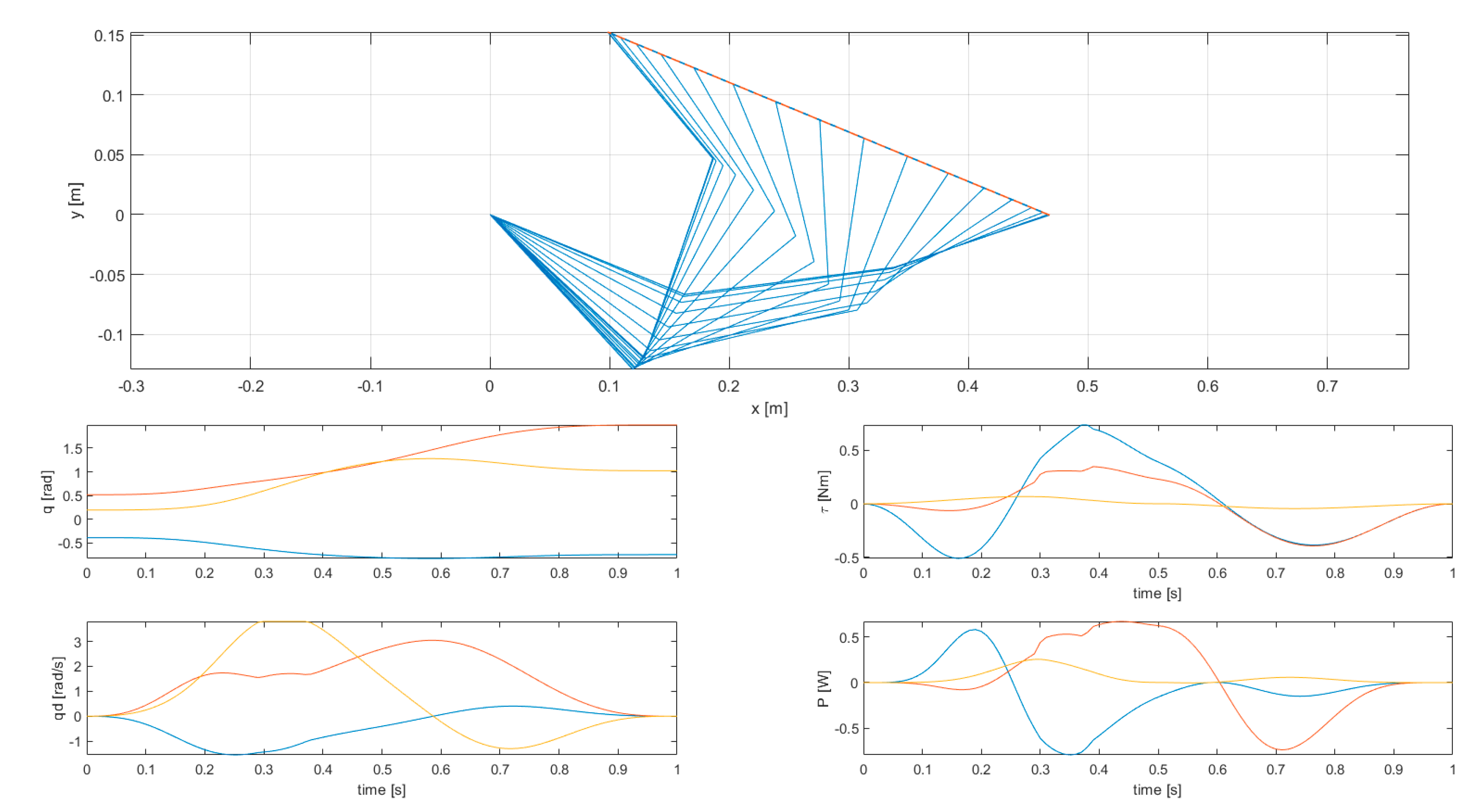
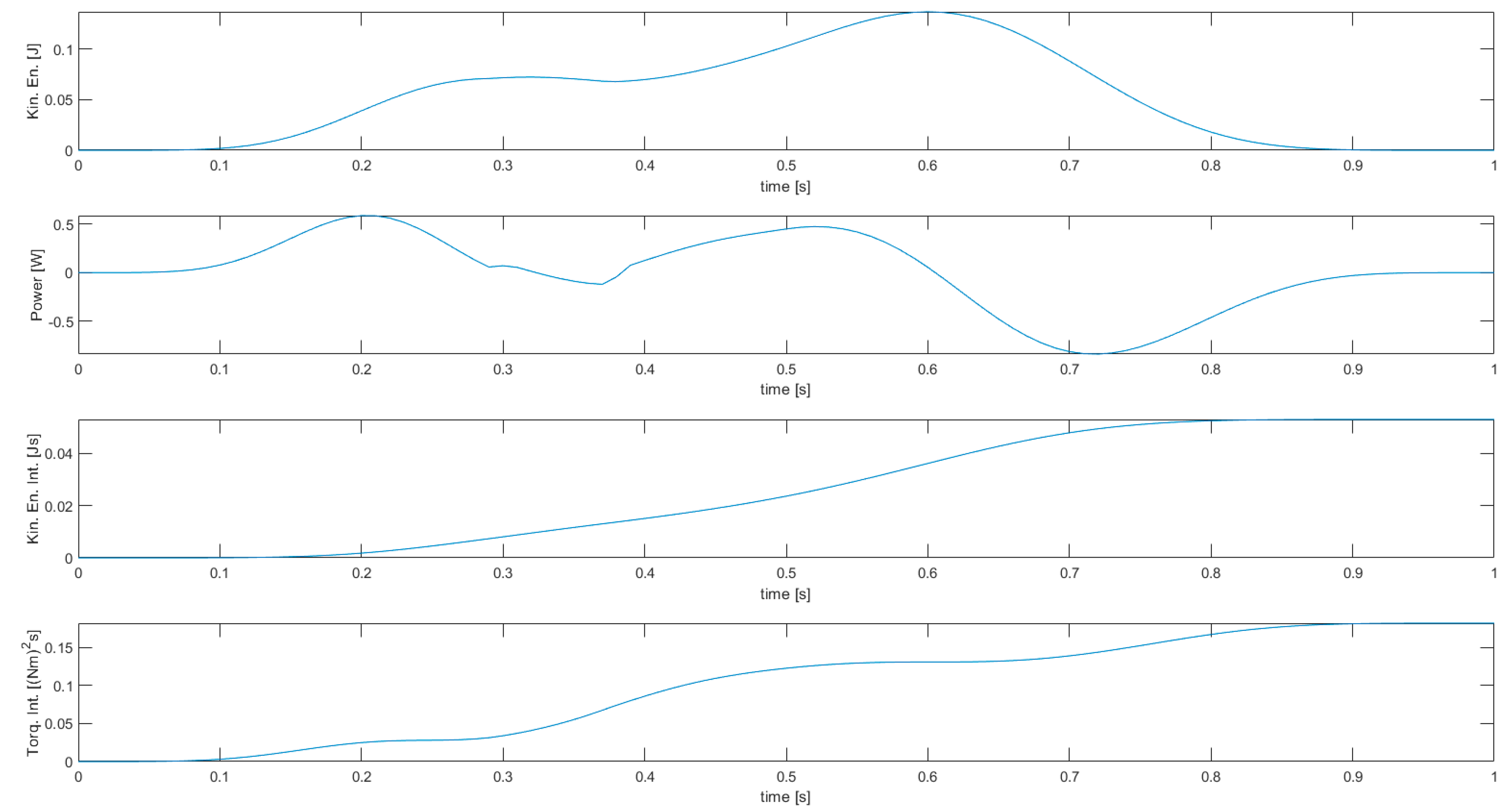
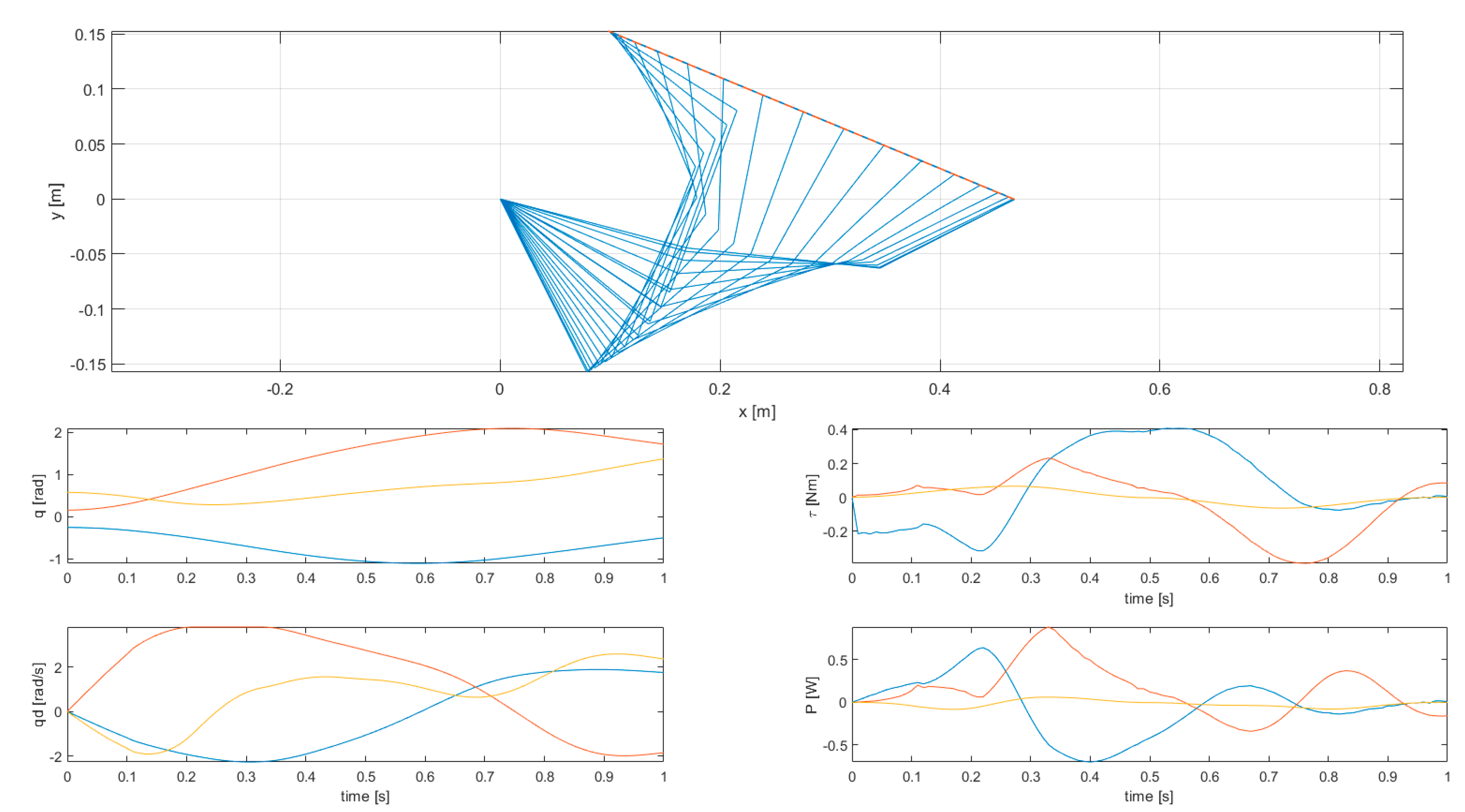
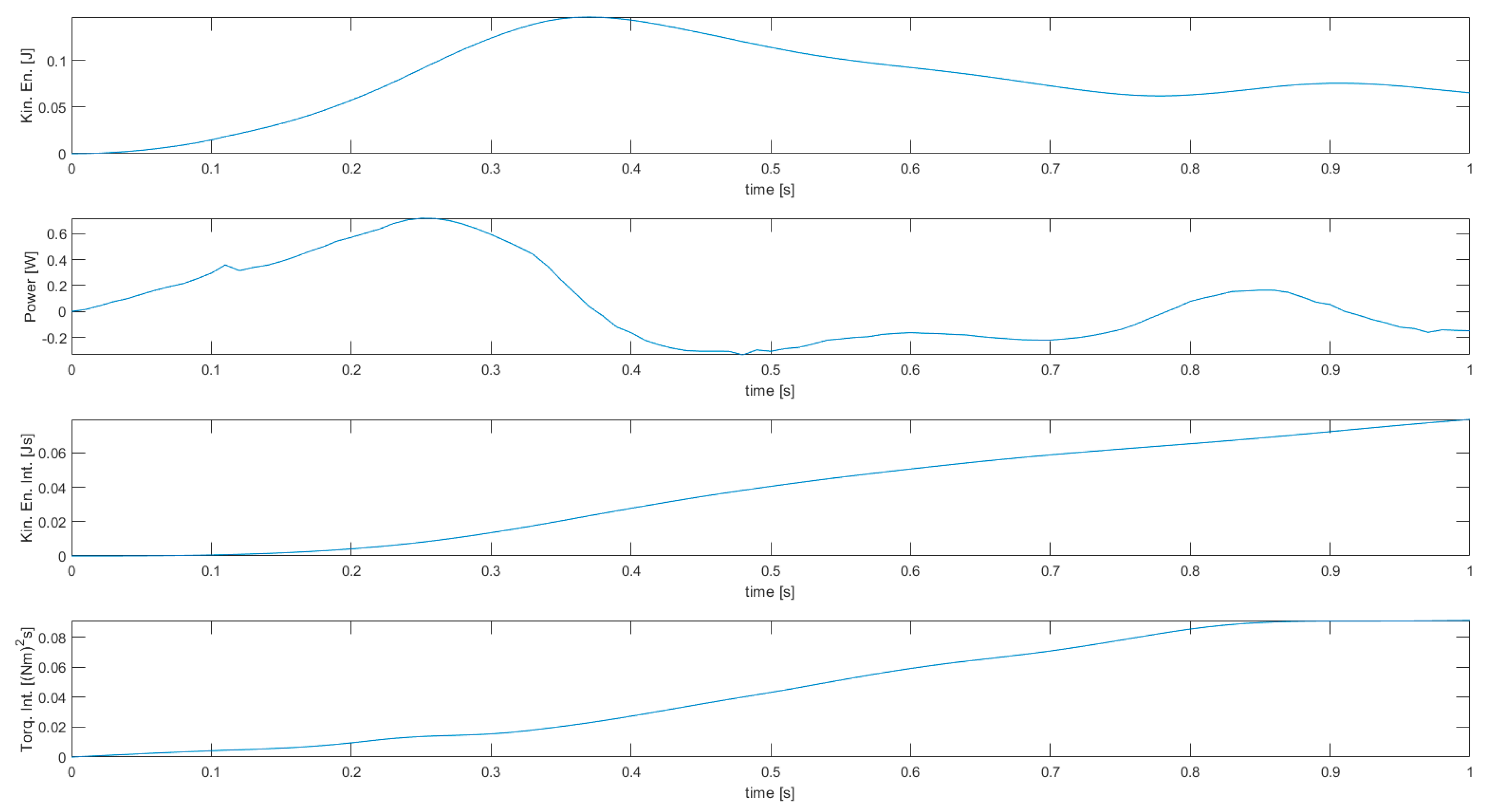
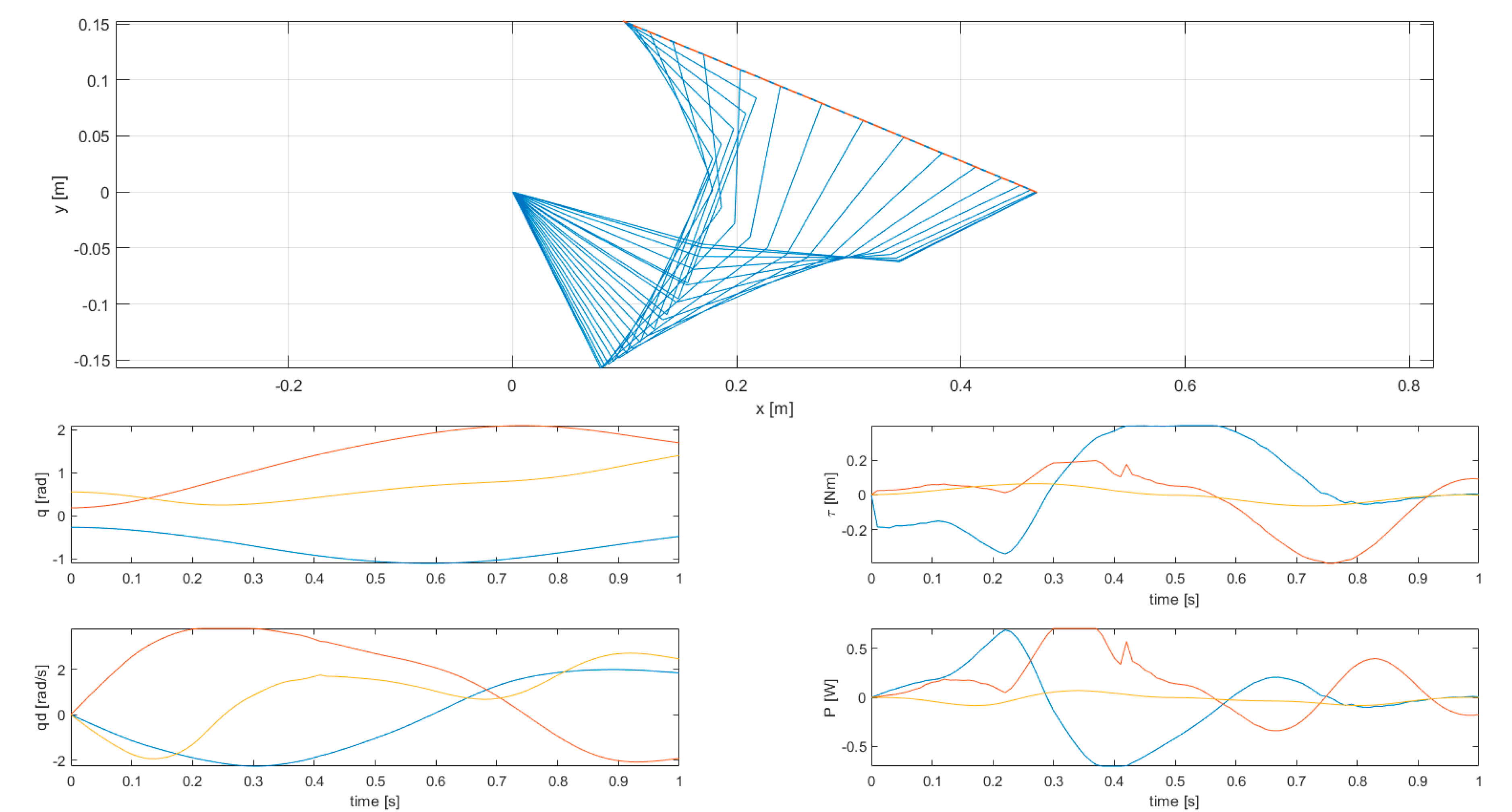
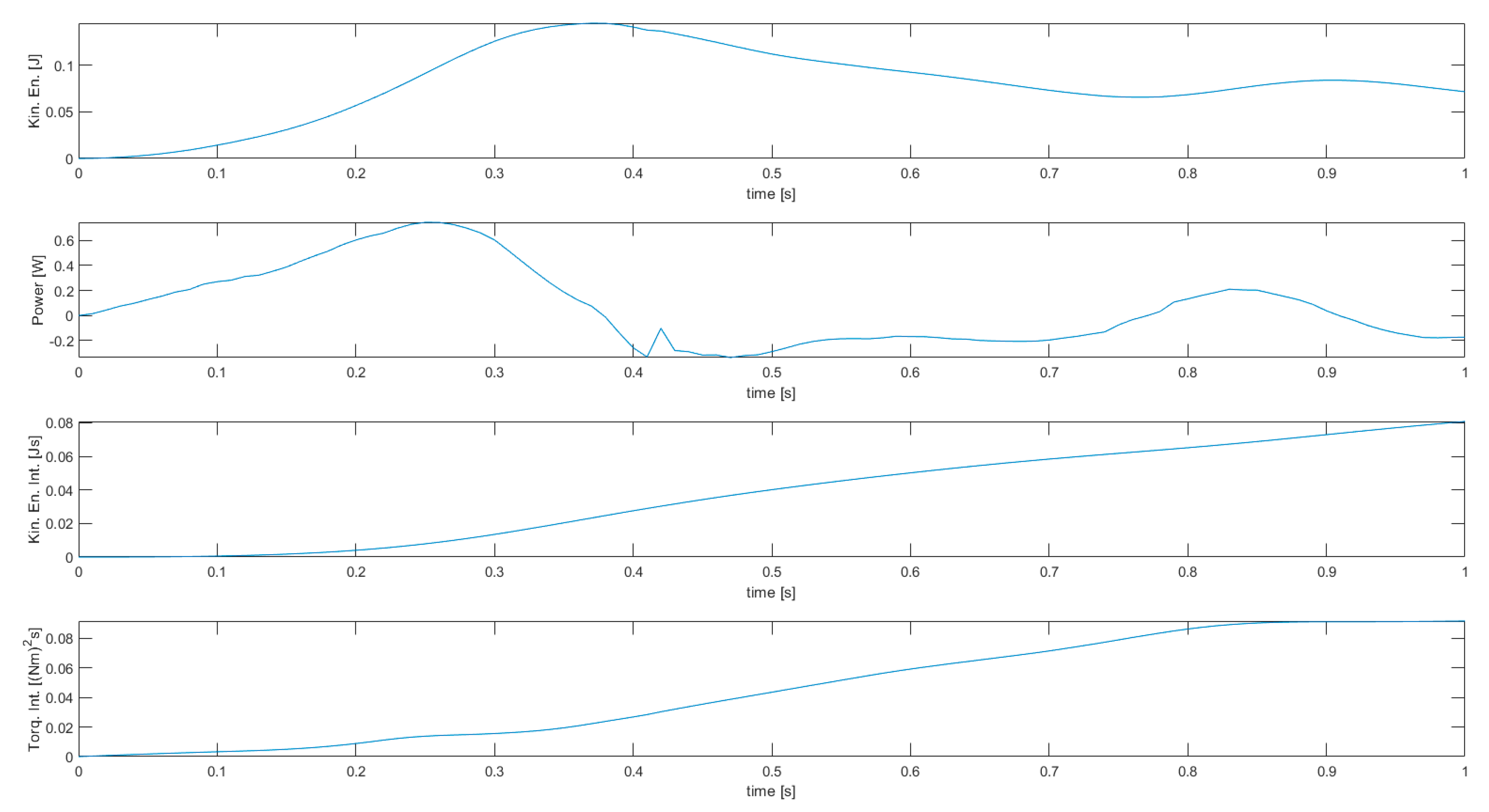
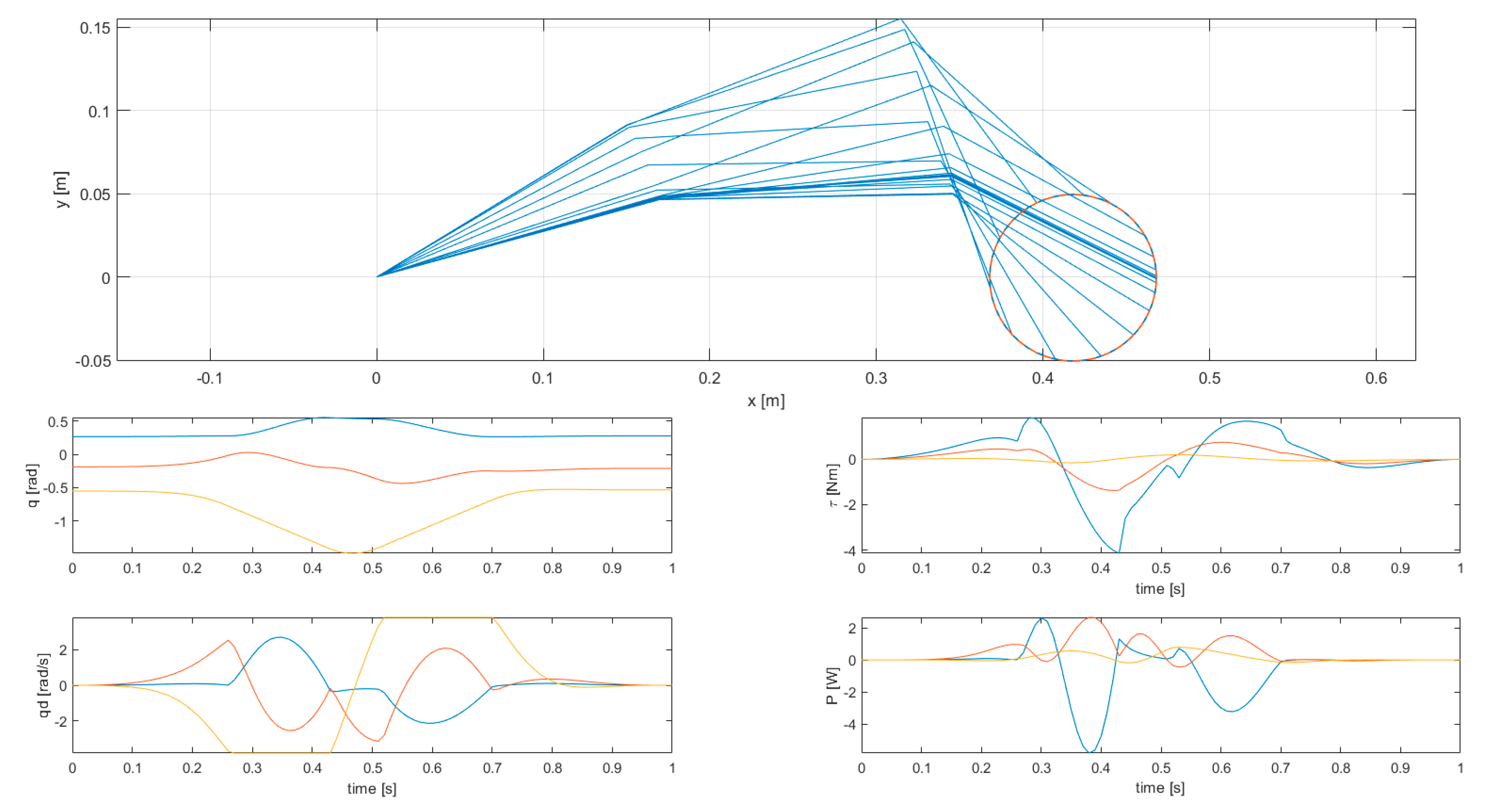
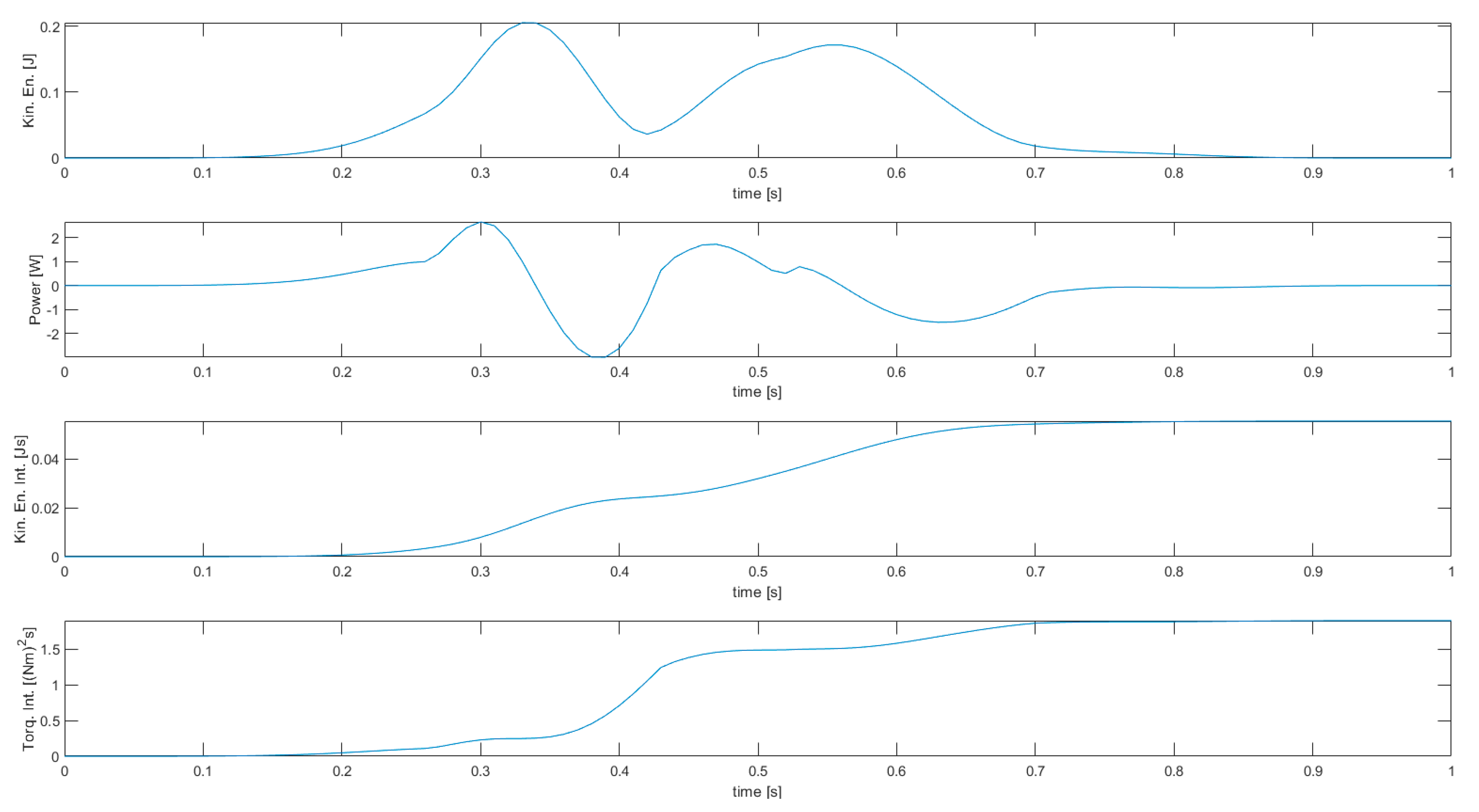
For each simulation two figures are shown, one with manipulator energy-related variables (kinetic energy, power, kinetic energy integral, joint torques squared norm integral), and one with the stroboscopic view of robot motion, joint displacements, velocities, torques, and powers. In the latter case, variables related to the first joint are shown in blue, those related to the second joint are shown in red, and those related to the third joint are shown in yellow.
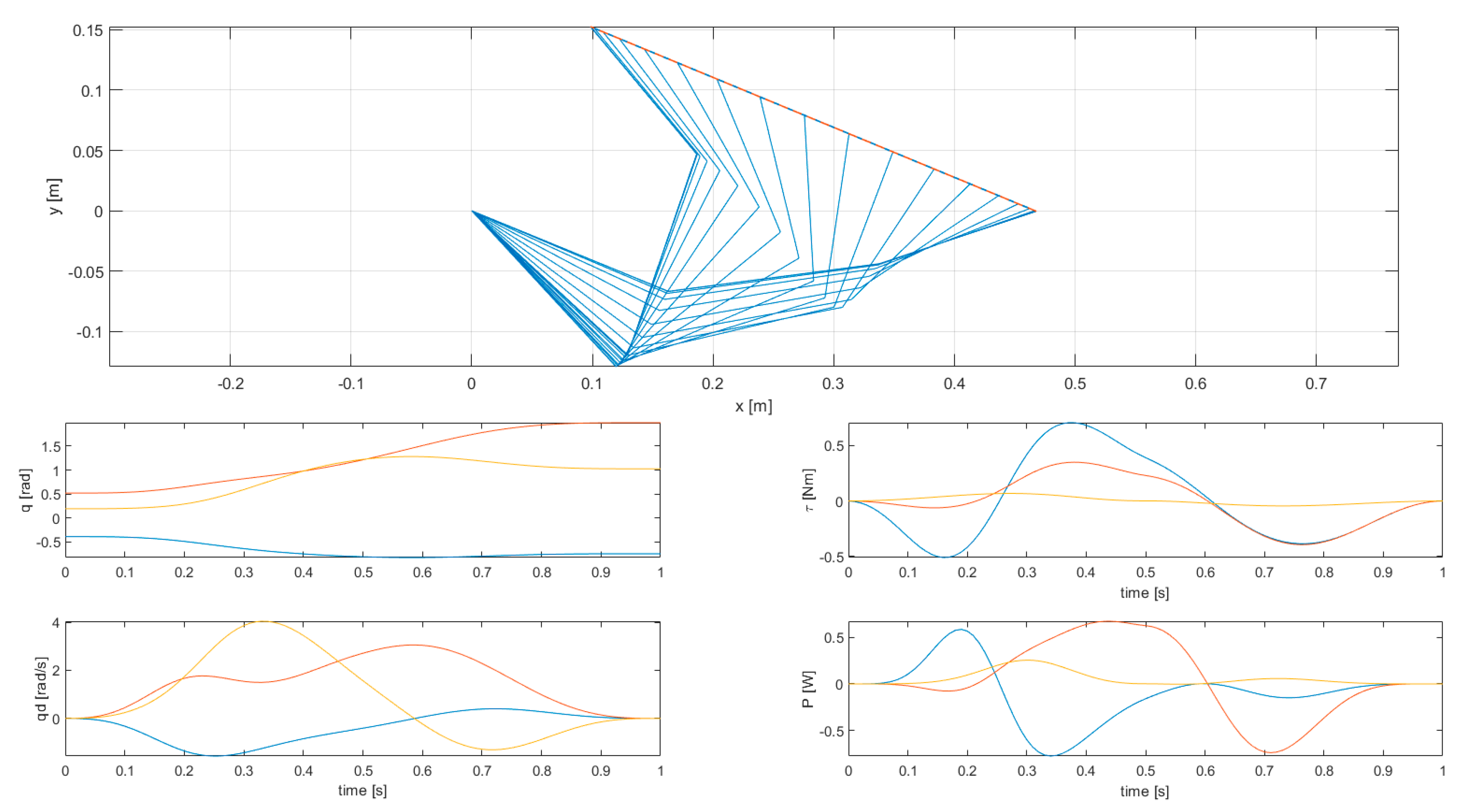
The results of simulation 1 are presented in Figure 4 and Figure 5, while the results of simulations 2, 3, 4, and 5 are presented in Figure 6 and Figure 7, in Figure 8 and Figure 9, in Figure 10 and Figure 11, and in Figure 12 and Figure 13, respectively.
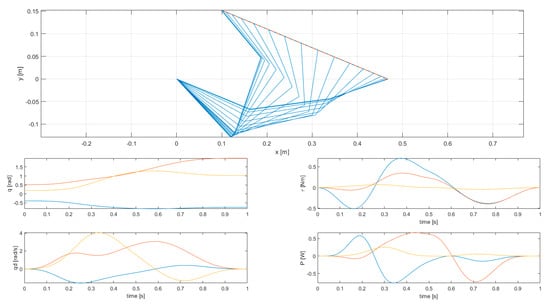
Figure 4.
Results of simulation 1—Stroboscopic view of robot motion (top) and joint variables (bottom).
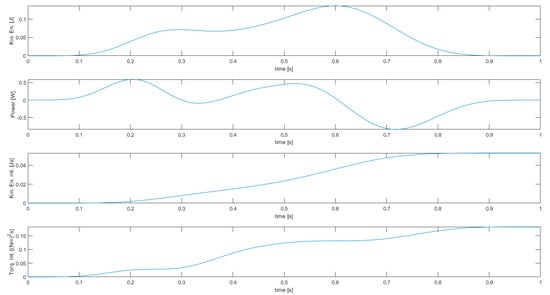
Figure 5.
Results of simulation 1—Energy-related manipulator variables.
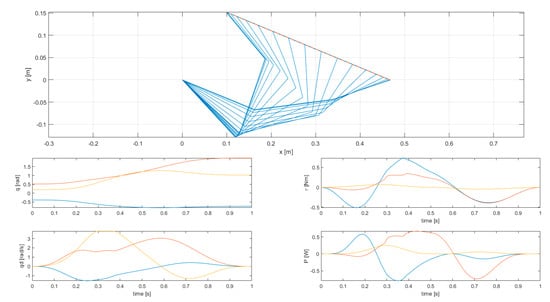
Figure 6.
Results of simulation 2—Stroboscopic view of robot motion (top) and joint variables (bottom).
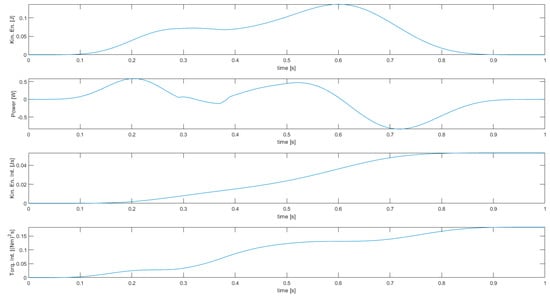
Figure 7.
Results of simulation 2—Energy-related manipulator variables.
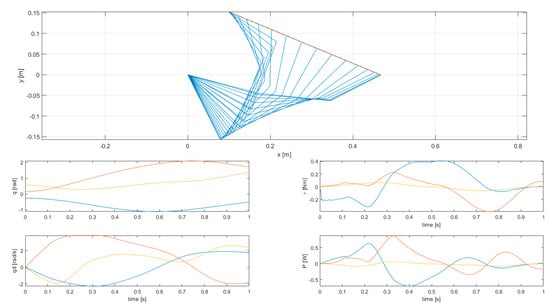
Figure 8.
Results of simulation 3—Stroboscopic view of robot motion (top) and joint variables (bottom).
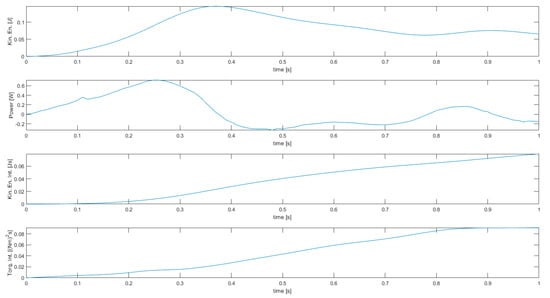
Figure 9.
Results of simulation 3—Energy-related manipulator variables.
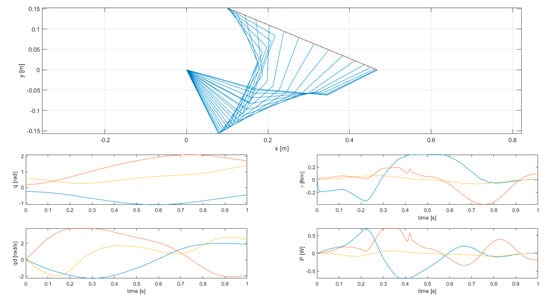
Figure 10.
Results of simulation 4—Stroboscopic view of robot motion (top) and joint variables (bottom).
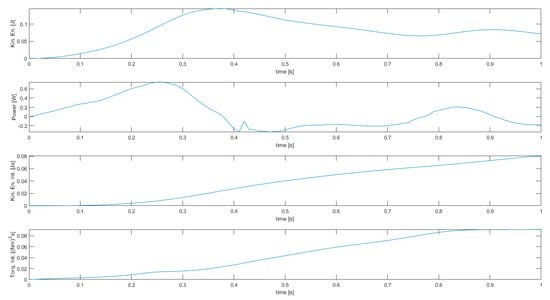
Figure 11.
Results of simulation 4—Energy-related manipulator variables.
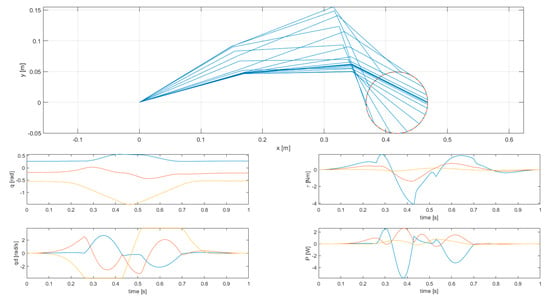
Figure 12.
Results of simulation 5—Stroboscopic view of robot motion (top) and joint variables (bottom).
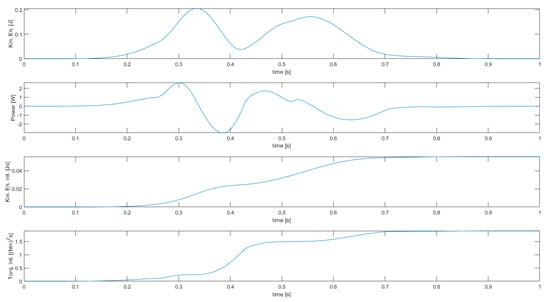
Figure 13.
Results of simulation 5—Energy-related manipulator variables.
Simulation 1, featuring the unconstrained optimization of the kinetic energy integral, is characterized by a considerable motion of the third joint (as can be seen in the stroboscopic view of robot motion), with velocity up to 4.042 rad/s. This is what was expected from a solution with minimum kinetic energy, as the third joint is the one related to the minimum moment of inertia (link 3 only). The second joint also reaches a high speed (3.053 rad/s), while the first one is the slowest one (1.553 rad/s), and this is reasonable since the first joint is related to the highest moment of inertia (all three links). Although this allows for a low kinetic energy integral, the joint torques squared norm integral is very high—this is mostly due to the fact that, despite the limited velocity, the first joint is requiring a high torque (up to 0.7068 Nm) to perform the specified task.
Simulation 2 features kinetic energy integral as a cost function, and joint displacement and velocity limits. The limit on joint velocities does not particularly reduce the joint torques squared norm integral, as it is only active on the third joint between times t = 0.29 s and t = 0.38 s. Although only one active constraint on joint velocities exists, all joint velocities become non-differentiable at these times (generating acceleration peaks)—the activation of the constraint makes the manipulator to lose one DOF, and completely changes the joints motion (since the kinematic redundancy is lost). The change is instantaneous at the times when the constraint is activated or deactivated. In this case, the cost function only depends on joint displacements and velocities, thus there is no advantage in reducing joint acceleration peaks.
Simulation 3 features the same limits (joint displacements and velocities), but the cost function used is the integral of the squared norm of joint torques in this case. The cost function also contains the squared joint accelerations, which would become very high in the case of non-differentiable velocities. Thus, despite a velocity limit is active as in simulation 2, joint velocities are differentiable and continuous over the whole trajectory, with a smooth transition when constraints become active/inactive.
Simulation 4 also features the joint torques squared norm integral as a cost function, but limits are now on joint displacements, velocities, torques, and powers. The trajectory features a small discontinuity in torque and power when torque and power limits are reached at the same time (t = 0.42 s), but the proposed method is still able to find a feasible solution. The results are almost the same as in simulation 3, with only a minor degradation of the solution due to the extra constraints—integrals of both joint torques squared norm and kinetic energy are almost the same, with a difference around 1%.
Simulation 5 features kinetic energy integral minimization on a circular cyclic trajectory with joint displacement and velocity constraints. In this example, both kinetic energy integral and joint torques squared norm integral are higher than in the case of rectilinear trajectories (the latter one is one order of magnitude higher). Looking at the variables of each joint, torques and powers are much higher (up to 4.144 Nm and 5.814 W, respectively), and the joints reach velocity limits more often, causing velocities to be non-differentiable at several points. This fact restricts the mobility of the manipulator: in fact, if the number of active constraints were equal to the number of joints, the manipulator motion would be completely constrained, and tracking would not generally be possible. However, in the solution computed by the proposed method, only one joint reaches the velocity limit at a given time.
Concerning the capability of the presented method to possibly find optimal solutions that cross singularities, a few considerations can be made. First, this work focuses on cost functions that have quadratic terms in joint velocities and accelerations ( and ; see Equations (3) and (5)) and, therefore, the optimal solutions will be likely to have limited joint velocities and accelerations (and thus be far from singularities, near which joint velocities and accelerations usually increase abruptly). Second, it can be noticed from Figure 3 (Optimum nr. 2) that the presented method is also able to find the optimal solution in cases in which two links become aligned (link 1 and link 2 in this case) and the motion of the manipulator is such that it does not cause the abrupt increase in joint velocities. Anyway, it could be useful to better investigate this scenario, considering, for example, a different cost function [38] which optimal solution may cross singularities, and this will be part of future work.
4.3. Multi-Objective Optimization
For some robotic applications, it is required to balance between different cost functions [11]. This kind of problem is tackled by multi-objective optimization.
Considering a set of solutions Χ, and a set of cost functions , a feasible solution is a Pareto optimal solution of a multi-objective optimization problem if, and only if, no exists such that . The set of Pareto optimal solutions of a multi-objective optimization problem form the Pareto optimal set, or Pareto front.
When solving a multi-objective optimization problem, it is usually desired to find a solution that is as close as possible to the Pareto optimal set. In the ideal case, the full Pareto optimal set can be exactly computed, and it is possible to choose the preferred solution among its members. Exhaustive computation of the complete Pareto optimal set is, however, computationally expensive and, in many cases, not possible, thus the problem is usually approached by computing some of the members of the set and using them as a representation of the full set. The most used method to do so in robotics is the weighting method [11], which, however, does not produce evenly distributed solutions, cannot individuate all members of the Pareto optimal set, and, moreover, fails in the case of non-convex Pareto fronts [39]. A complete discussion of all possible algorithms to compute the Pareto front is beyond the scope of this work, but it is noted that methods such as the ε-constraint method can capture the shape of the Pareto front in a more complete and representative way than the weighting method, even when the Pareto front is non-convex [40]. The use of the ε-constraint method requires the imposition of nonlinear constraints on an optimization problem, which is possible through the use of the Interpolation-based Global Kinematic Planner presented in this work. This has been demonstrated by analyzing the bi-objective optimization problem resulting from optimizing both the kinetic energy integral and torques squared norm integral while tracking the rectilinear trajectory used in simulations 1–4. Particularly, its Pareto optimal set has been searched considering joint and velocity limits as per Table 2.
For the equally spaced implementation used here, the ε-constraint method steps are as follows:
- 1.
- The feasible solutions resulting in the minima of the two objective functions, (for the minimum of kinetic energy integral) and (for the minimum of torques squared norm integral), are computed separately.
- 2.
- The intervals and are computed.
- 3.
- Each interval is divided in k equally spaced steps and , so that and .
- 4.
- For each a single-objective kinetic energy integral optimization problem is solved with the formulation:
Likewise, a single-objective torques squared norm integral optimization problem is solved with the formulation:
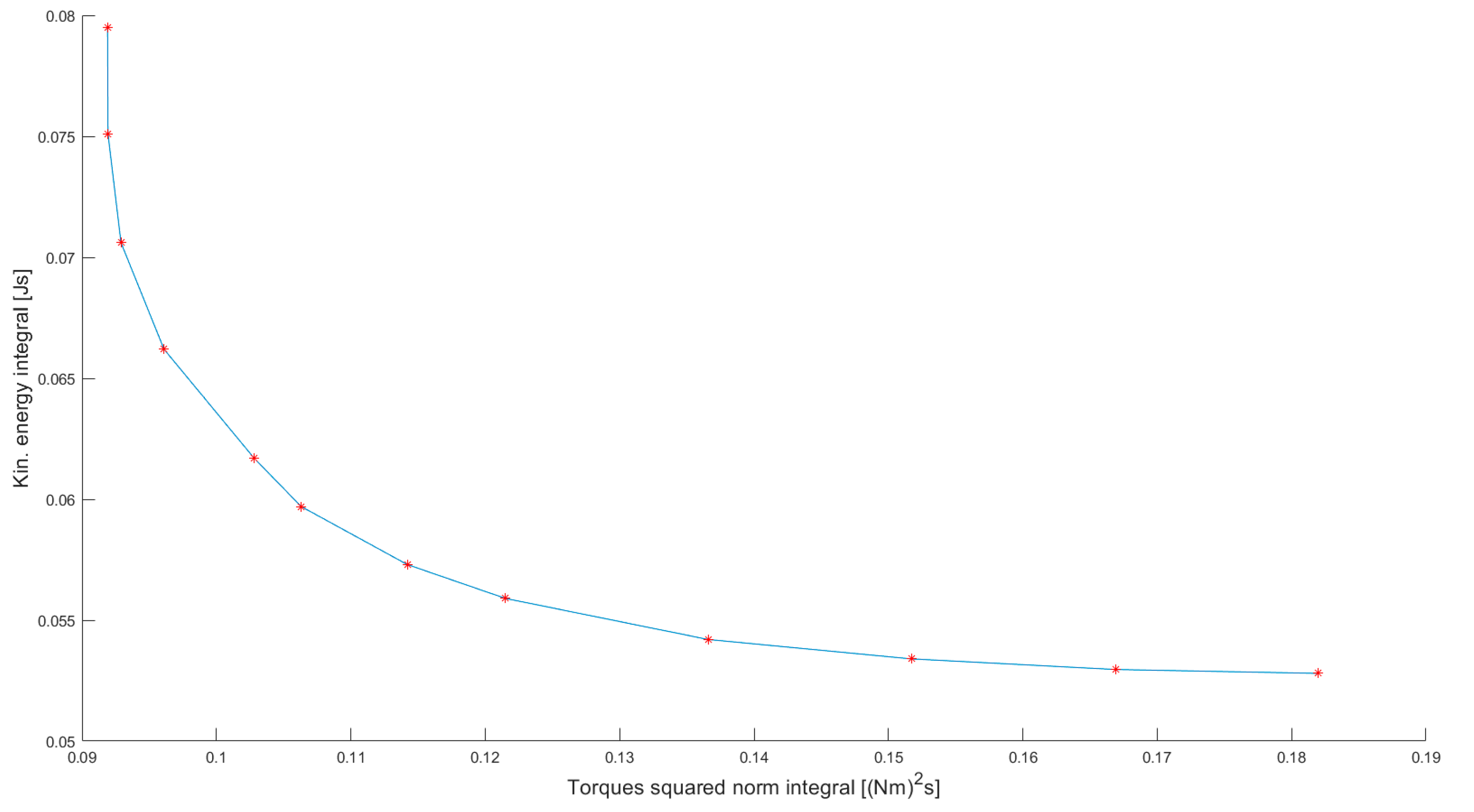
Following these steps, a set of Pareto optimal solutions has been computed, see Figure 14.
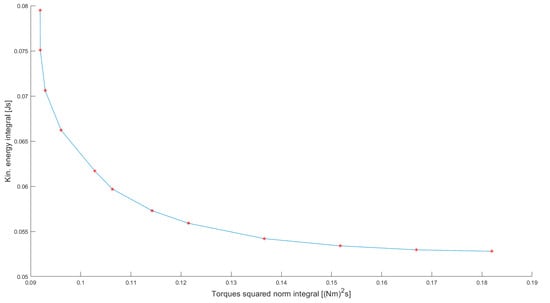
Figure 14.
Pareto front of bi-objective optimization problem under consideration.
This result shows the suitability of the Interpolation-based Global Kinematic Planner for individuating Pareto optimal sets with a more reliable method than the weighting method.
5. Conclusions
A global optimization method has been presented to solve the inverse kinematics problem of a redundant manipulator tracking a specified end-effector trajectory while optimizing a cost function. The proposed method has been validated by comparing its solution for the minimization of kinetic energy integral with that obtained with a different method presented in the literature based on the calculus of variations.
It has been demonstrated that the proposed method is more flexible than existing methods on several aspects: it can compute optimal solutions with different cost functions, such as kinetic energy and joint torques integral, it is suitable for multi-objective optimization, and it is able to find multiple optima, offering a solution for the known issue of optima lying in different homotopy classes. Furthermore, it is able to include a variety of different constraints, such as linear constraints on joint displacement and velocity, and nonlinear constraints on joint torque and power. While doing so, it is also able to tackle cyclic manipulator motions.
In order to reduce the negative effects of the high dimensionality of the global problem, a sequential version of the method has been presented, based on the sequential solution of relaxed problems with a reduced number of path points, with more path points introduced in the problem at every step through cubic spline interpolation.
Future plans include extending and validating the proposed method on multi-DOF and 3D robot manipulators, the introduction of environmental constraints (obstacles), the investigations of cost functions whose optimal solutions may cross singularities, and the implementation and experimental validation on industrial manipulators in the context of real industrial applications.
Author Contributions
Conceptualization, S.C. and A.T.; methodology, S.C. and A.T.; software, A.T.; investigation, S.C. and A.T.; writing—original draft preparation, S.C. and A.T.; writing—review and editing, S.C. and A.T.; supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamura, Y.; Hanafusa, H.; Yoshikawa, T. Task-Priority Based Redundancy Control of Robot Manipulators. Int. J. Rob. Res. 1987, 6, 32–42. [Google Scholar] [CrossRef]
- Kazerouinian, K.; Wang, Z. Global versus Local Optimization in Redundancy Resolution of Robotic Manipulators. Int. J. Rob. Res. 1988, 7, 3–12. [Google Scholar] [CrossRef]
- Nedungadi, A.; Kazerouinian, K. A local solution with global characteristics for the joint torque optimization of a redundant manipulator. J. Robot. Syst. 1989, 6, 631–654. [Google Scholar] [CrossRef]
- Hirakawa, A. Trajectory planning of redundant manipulators for minimum energy consumption without matrix inversion. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; pp. 1–5. [Google Scholar]
- Martin, B.J.; James, E. Minimum-Effort Motions for Open-Chain Manipulators with Task-Dependent End-Effector Constraints. Int. J. Rob. Res. 1999, 18, 213–224. [Google Scholar] [CrossRef]
- Zhou, Z.; Nguyen, C.C. Joint Configuration Conservation and Joint Limit Avoidance of Redundant Manipulators. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; pp. 2421–2426. [Google Scholar]
- Zhou, Z.L.; Nguyen, C.C. Globally Optimal Trajectory Planning for Redundant Manipulators using State Space Augmentation Method. J. Intell. Robot. Syst. Theory Appl. 1997, 19, 105–117. [Google Scholar] [CrossRef]
- Nurmi, J.; Mattila, J. Global energy-optimal redundancy resolution of hydraulic manipulators: Experimental results for a forestry manipulator. Energies 2017, 10, 647. [Google Scholar] [CrossRef]
- Lyu, H.; Song, X.; Dai, D.; Li, J.; Li, Z. Time-optimal and energy-efficient trajectory generation for robot manipulator with kinematic constraints. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 503–508. [Google Scholar]
- Ferrentino, E.; Chiacchio, P. A Topological Approach to Globally-Optimal Redundancy Resolution with Dynamic Programming. In ROMANSY 22, Robot Design, Dynamics and Control; Springer International Publishing: Cham, Switzerland, 2019; pp. 77–85. ISBN 978-3-7091-1378-3. [Google Scholar]
- Guigue, A.; Ahmadi, M.; Langlois, R.; Hayes, M.J. Pareto optimality and multiobjective trajectory planning for a 7-DOF redundant manipulator. IEEE Trans. Robot. 2010, 26, 1094–1099. [Google Scholar] [CrossRef]
- Davidor, Y. Genetic Algorithms and Robotics: A Heuristic Strategy for Optimization; World Scientific Publishing Company: Singapore, 1991. [Google Scholar]
- Shintaku, E. Minimum energy trajectory for an underwater manipulator and its simple planning method by using a genetic algorithm. Adv. Robot. 1998, 13, 115–138. [Google Scholar] [CrossRef]
- McAvoy, B.; Sangolola, B.; Szabad, Z. Optimal trajectory generation for redundant planar manipulators. In Proceedings of the 2000 IEEE International Conference on Systems, Man & Cyberbetics, Nashville, TN, USA, 8–11 October 2000; pp. 3241–3246. [Google Scholar]
- Tian, L.; Collins, C. Motion planning for redundant manipulators using a floating point genetic algorithm. J. Intell. Robot. Syst. Theory Appl. 2003, 38, 297–312. [Google Scholar] [CrossRef]
- Baba, N.; Kubota, N. Collision avoidance planning of a robot manipulator by using genetic algorithm—A consideration for the problem in which moving obstacles and/or several robots are included in the workspace. In Proceedings of the First IEEE Conference on Evolutionary Computation, Orlando, FL, USA, 27–29 June 1994; pp. 714–719. [Google Scholar]
- Kazem, B.I.; Mahdi, A.I.; Oudah, A.T. Motion Planning for a Robot Arm by Using Genetic Algorithm. Jordan J. Mech. Ind. Eng. 2008, 2, 131–136. [Google Scholar]
- Ferrentino, E.; Della Cioppa, A.; Marcelli, A.; Chiacchio, P. An Evolutionary Approach to Time-Optimal Control of Robotic Manipulators. J. Intell. Robot. Syst. Theory Appl. 2019, 245–260. [Google Scholar] [CrossRef]
- Stevo, S.; Sekaj, I.; Dekan, M. Optimization of Energy in Robotic arm using Genetic Algorithm. In Proceedings of the 19th World Congress The International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Hansen, C.; Kotlarski, J.; Ortmaier, T. Experimental validation of advanced minimum energy robot trajectory optimization. In Proceedings of the 2013 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 November 2013. [Google Scholar] [CrossRef]
- Doan, N.C.N.; Tao, P.Y.; Lin, W. Optimal redundancy resolution for robotic arc welding using modified particle swarm optimization. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 554–559. [Google Scholar]
- Garg, D.P.; Kumar, M. Optimization techniques applied to multiple manipulators for path planning and torque minimization. Eng. Appl. Artif. Intell. 2002, 15, 241–252. [Google Scholar] [CrossRef]
- Martin, D.P.; Baillieul, J.; Hollerbach, J.M. Resolution of Kinematic Redundancy Using Optimisation Techniques. IEEE Trans. Robot. Autom. 1989, 5, 529–533. [Google Scholar] [CrossRef]
- Pashkevich, A.P.; Dolgui, A.B.; Chumakov, O.A. Multiobjective optimization of robot motion for laser cutting applications. Int. J. Comput. Integr. Manuf. 2004, 17, 171–183. [Google Scholar] [CrossRef]
- Dolgui, A.; Pashkevich, A. Manipulator motion planning for high-speed robotic laser cutting. Int. J. Prod. Res. 2009, 47, 5691–5715. [Google Scholar] [CrossRef]
- Gao, J.; Pashkevich, A.; Caro, S. Optimization of the robot and positioner motion in a redundant fiber placement workcell. Mech. Mach. Theory 2017, 114, 1339–1351. [Google Scholar] [CrossRef]
- Reiter, A.; Muller, A.; Gattringer, H. On Higher Order Inverse Kinematics Methods in Time-Optimal Trajectory Planning for Kinematically Redundant Manipulators. IEEE Trans. Ind. Informat. 2018, 14, 1681–1690. [Google Scholar] [CrossRef]
- Reiter, A.; Gattringer, H.; Müller, A. Redundancy resolution in minimum-time path tracking of robotic manipulators. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics (ICINCO), Lisbon, Portugal, 29–31 July 2016; Volume 2, pp. 61–68. [Google Scholar] [CrossRef]
- Martì, R. Multi-Start Methods. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2003; Volume 57. [Google Scholar]
- Solis, F.J.; Wets, R.J.-B. Minimization by Random Search Techniques. Math. Oper. Res. 1981, 6, 19–30. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liegeois, A. Automatic Supervisory Control of the Configuration and Behavior of Multibody Mechanisms. IEEE Trans. Syst. Man Cybern. 1977, 7, 868–871. [Google Scholar]
- Beckman, R.J.; Conover, W.J.; McKay, M.D. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Cocuzza, S.; Pretto, I.; Debei, S. Least-Squares-Based Reaction Control of Space Manipulators. J. Guid. Control. Dyn. 2012, 35, 976–986. [Google Scholar] [CrossRef]
- Cocuzza, S.; Pretto, I.; Debei, S. Novel reaction control techniques for redundant space manipulators: Theory and simulated microgravity tests. Acta Astronaut. 2011, 68, 1712–1721. [Google Scholar] [CrossRef]
- Cocuzza, S.; Tringali, A.; Yan, X.-T. Energy-efficient motion of a space manipulator. In Proceedings of the International Astronautical Congress, IAC, Guadalajara, Mexico, 26–30 September 2016. [Google Scholar]
- Tringali, A.; Cocuzza, S. Predictive control of a space manipulator through error and kinetic energy expectation. In Proceedings of the International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Ferrentino, E.; Chiacchio, P. On the Optimal Resolution of Inverse Kinematics for Redundant Manipulators Using a Topological Analysis. J. Mech. Robot. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. A closer look at drawbacks of minimizing weighted sums of objectives for Pareto set generation in multicriteria optimization problems. Struct. Optim. 1997, 14, 63–69. [Google Scholar] [CrossRef]
- Chircop, K.; Zammit-Mangion, D. On Epsilon-Constraint Based Methods for the Generation of Pareto Frontiers. J. Mech. Eng. Autom. 2013, 3, 279–289. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).