FraudMove: Fraud Drivers Discovery Using Real-Time Trajectory Outlier Detection
Abstract
:1. Introduction
- Identifying the popular routes that are guaranteed to be both familiar and safe to decide if a trip is an outlier [16]. Extracting the optimal path is a challenge as the definition of optimal varies in different research works. Some studies focus on finding the shortest/fastest path as an optimal path. While in other work, the popular route is the optimal choice if the passenger is not familiar with the area.
- FraudMove system is proposed for discovering fraud drivers for ongoing trips using a real-time outlier trajectory detection and based on the elapsed trip time.
- An adaptive Viterbi (AV) algorithm is developed to compute the most commonly used route(s) from historical trajectories to be suggested as optimal path(s).
- A novel time-window method is devised to save the computations overhead and minimize the number of needed checks to detect outlier trajectories.
- Intensive experimental evaluations are conducted to ensure the accuracy and efficiency of FraudMove using a real dataset for taxicabs trips in San Francisco, CA, USA. The experimental results confirm that FraudMove outperforms saving in response time by up to 65% compared to the state-of-the-art systems in this direction.
2. Related Work
2.1. Trajectory Outlier Detection
2.1.1. Offline Trajectory Outlier Detection Algorithms
2.1.2. Online Trajectory Outlier Detection Algorithms
2.2. Mining Popular Route
3. Preliminaries and Problem Definition
3.1. Preliminaries
3.2. Problem Statement
- Real-time processing.
- High classification accuracy.
- Scalability with large numbers of trajectories.
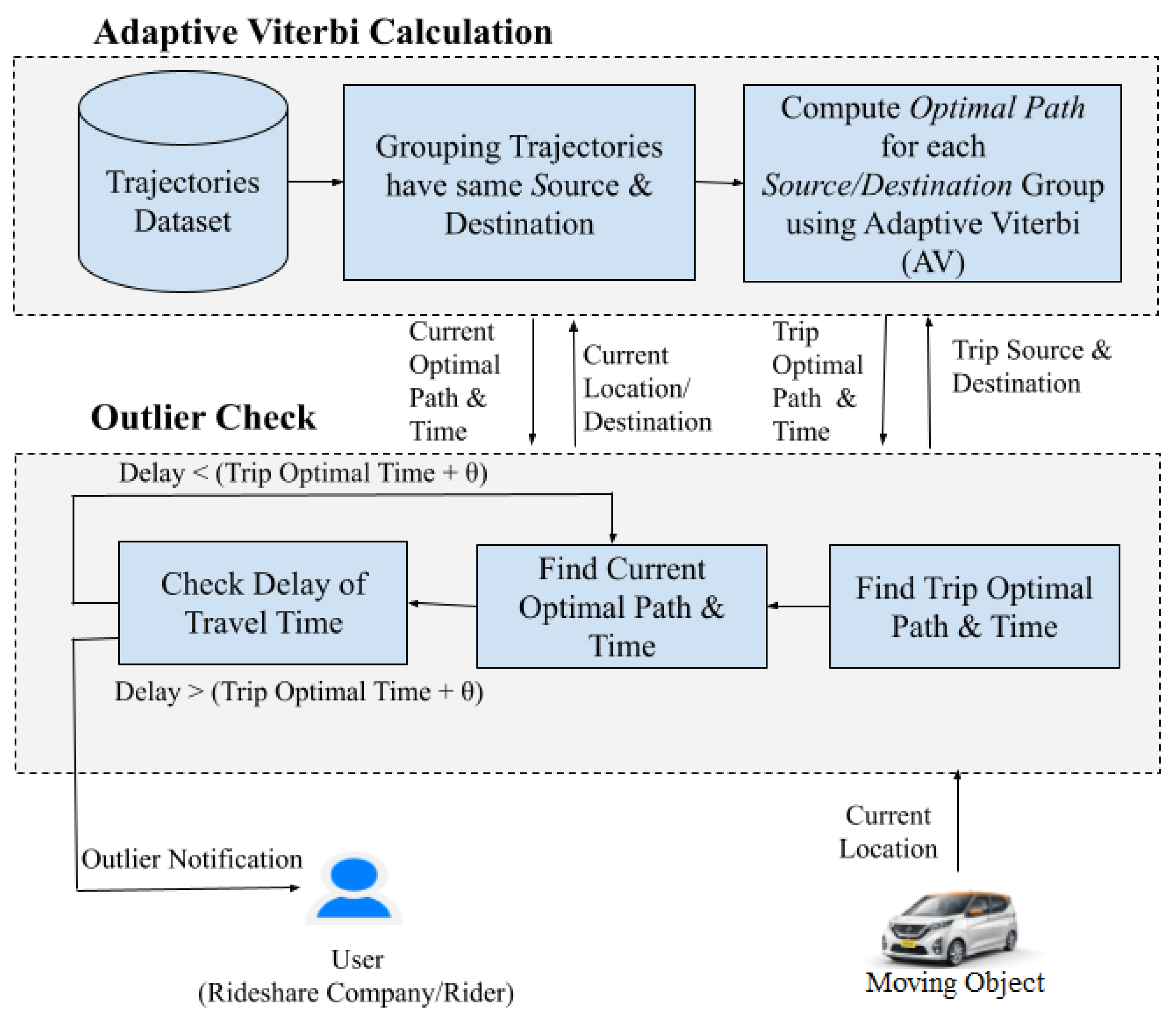
4. FraudMove: Real-Time Trajectory Outlier Detection
4.1. Phase 1: Adaptive Viterbi Calculation
4.1.1. SD Trajectories Grouping
4.1.2. Computing the Optimal Path
- The number of observations M is the length of the longest trip (trip that has the maximum number of nodes) in the .M=Length (longest trip ()).
- The transition matrix (A) contains the probability of move from one node (or vertex) to another. It is computed from the historical trip data of the same source S and destination D (). The size of A is N × N, where N is the number of unique nodes in .
- The emission matrix (B) holds the probability of observing a node in a specific order in the path. It is computed from data and has a size of N × M.
- The Accumulated probability matrix (P). P (n, m) stores the highest probability for a node in a specific order in the route. The matrix P is of size N × M, where and . P is recursively calculated using the column index .
- The Backtrack matrix (E) stores the indices that yield the highest probability in a matrix P. These indices are required in the step of constructing the most likely path using backtracking. The matrix E is of size N × M − 1.
- -
- The probability of start from node N1.P(1, N1) = 1
- -
- The probability of seeing specific nodes in a second order of the trip. In the given data nodes N2, N4, and N5 are found.P(2,N2) = P(1,N1)*[P(2|N2)*P(N1,N2)]=1*[0.1*0.1] = 0.01.P(2,N4) = P(1,N1)*[P(2|N4)*P(N1,N4)]=1*[0.3*0.3] = 0.09.P(2,N5) = P(1,N1)*[P(2|N5)*P(N1,N5)]=1*[0.6*0.6] = 0.36.
- -
- The probability of seeing specific nodes in a third order of the trip. In the given data nodes N3, N6, N7, and N9 are found.P(3,N3) = P(2,N2)*[P(3|N3)*P(N2,N3)] = 0.01*[0.1*1] = 0.001.P(3,N6) = P(2,N5)*[P(3|N6)*P(N5,N6)] = 0.36*[0.2*0.33] = 0.02376.P(3,N7) = P(2,N5)*[P(3|N7)*P(N5,N7)] = 0.36*[0.4*0.67] = 0.09648.P(3,N9) = P(2,N4)*[P(3|N9)*P(N4,N9)] = 0.09*[0.3*1] = 0.027.
- -
- In the third order of a trip, each node N8 and N9 are found. Node N8 reaches this order given it comes from each of N6 and N7 in the third order in the trip. While node N9 reaches this order given it comes from node N7 in the previous order.
- -
- In the fifth order of a trip, node N9 only seen. Node N9 reaches to this order given it comes from node N8 in the previous order of it.P(5,N9) = P(4,N8)*[P(5|N9)*P(N8,N9)] = 0.08297*[1*1] = 0.08297.
| Algorithm 1 Adaptive Viterbi (AV) | |
| 1: | INPUT: Trip source S, Trip destination D, Transition matrix A, Emission matrix B, Observation length M, Hidden states length N. |
| 2: | |
| 3: | |
| 4: | |
| 5: | /* Set probability of staring from S to 1*/ |
| 6: | |
| 7: | /* Complete from the second location in the trip */ |
| 8: | |
| 9: | /* Compute connected nodes to the source S */ |
| 10: | = Get_Connected_Nodes ((NextNodes, S, Order-1) |
| 11: | /* Recursion to fill matrices P and E */ |
| 12: | (ConnectedNodes, Loc, A, B, P, E) |
| 13: | /* Backtracking to get optimal path */ |
| 14: | |
| 15: | /* Using a backtrack matrix E to get OP */ |
| 16: | for n = index−1 to 1 do |
| 17: | OP[n] = E [D, n+1] |
| 18: | D = E [D, n+1] |
| 19: | end for |
| 20: | OUTPUT: Return OP |
4.2. Phase 2: Outlier Check
| Algorithm 2 FraudMove: Real-Time Trajectory Outlier Detection | |
| 1: | INPUT: TTrip source S, Trip destination D, Road network G (V, E, W), Moving object’s current location , Outlier threshold , Time window TW, User preference Pref. |
| 2: | /* Get preference option from the user */ |
| 3: | if Pref = 0 then |
| 4: | OP = Get shortest path based on SD |
| 5: | else if Pref = 1 then |
| 6: | OP = Adaptive Viterbi (SD) |
| 7: | end if |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | |
| 13: | /* Outlier check */ |
| 14: | while CL not equal D do |
| 15: | = − // Update travel time |
| 16: | /* Update Source S by current location CL*/ |
| 17: | for every TW do |
| 18: | S = CL |
| 19: | CP = Updated OP based on current location |
| 20: | = the computed time of |
| 21: | if + ≥ OT+ then |
| 22: | Outlier Notification = True |
| 23: | Break While |
| 24: | Exit |
| 25: | end if |
| 26: | end for |
| 27: | end while |
| 28: | OUTPUT: Return Outlier Notification |
5. Experimental Evaluation
5.1. Experimental Setting
5.2. Data Preprocessing
- First, separation step: the data are separated into occupied or free trips. In this paper, only occupied taxi trips are considered.
- Second, filtering step: the main reason for this step is to remove garbage trips, so a minimum point counter is used as a filter to remove any trips that contain points less than this specified point counter; in the experiments, the counter is set to 5 points. Moreover, a minimum trip distance filter is used to eliminate trips with a distance less than a specified user threshold, which is set to 2 km. Further, trips with points not reachable in the road network are removed.
- Third, grouping step: trips that have the same source S and destinations D are collected into groups; because it is an input to the AV algorithm. After this step, trips that have the same source and destination are stored in one group.
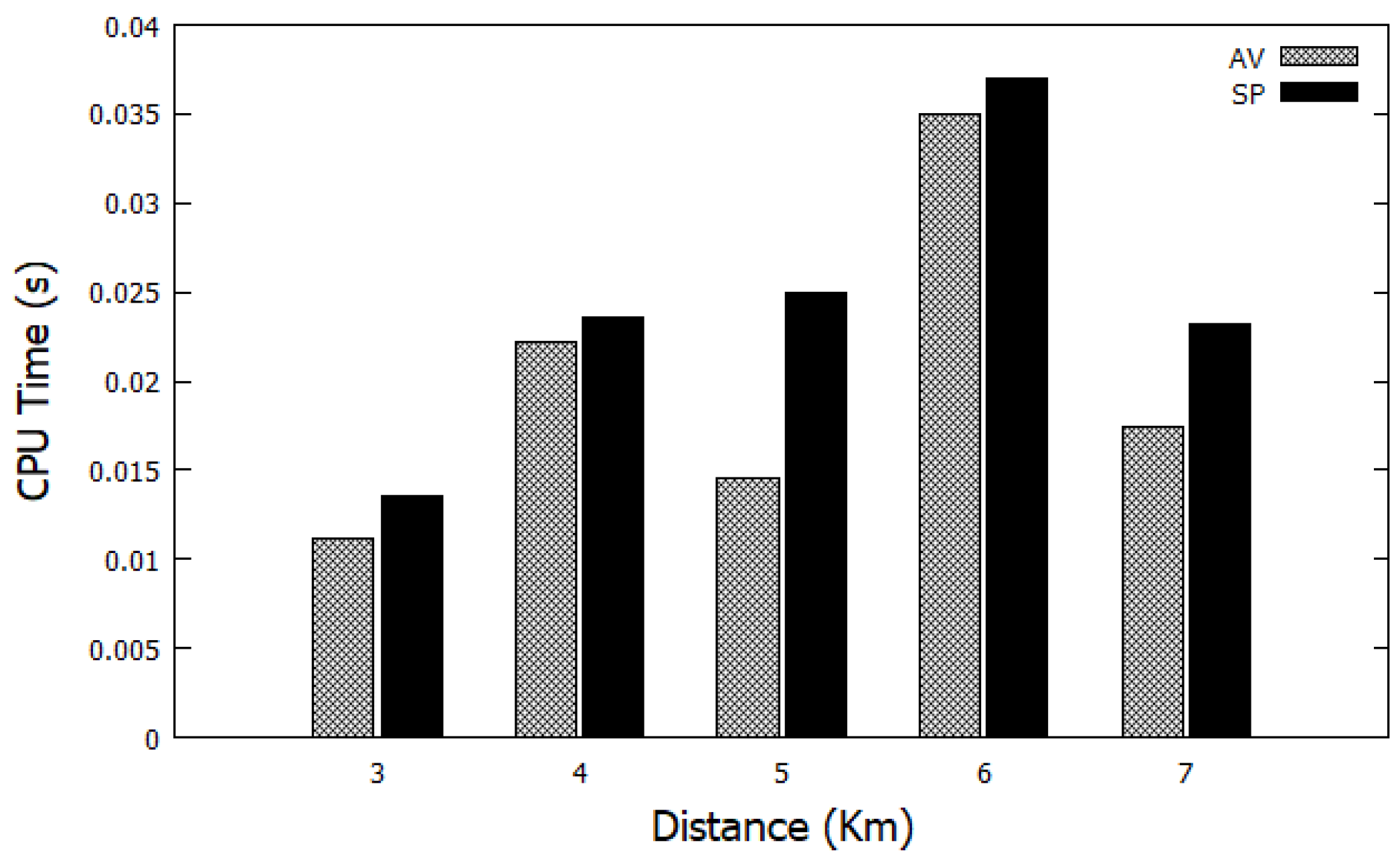
5.3. Adaptive Viterbi (AV) Evaluation
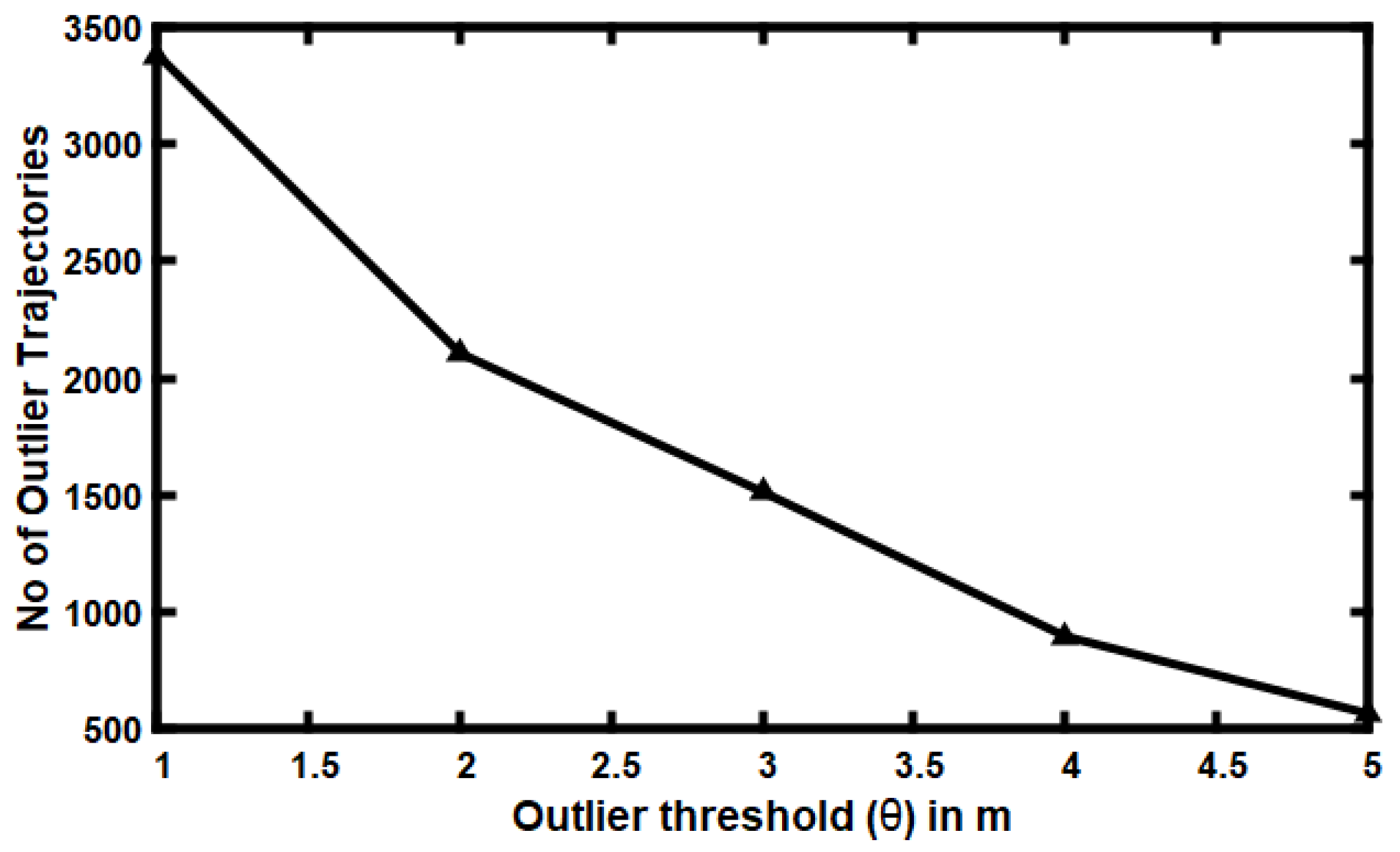
5.4. Impact of Varying Outlier Threshold ()
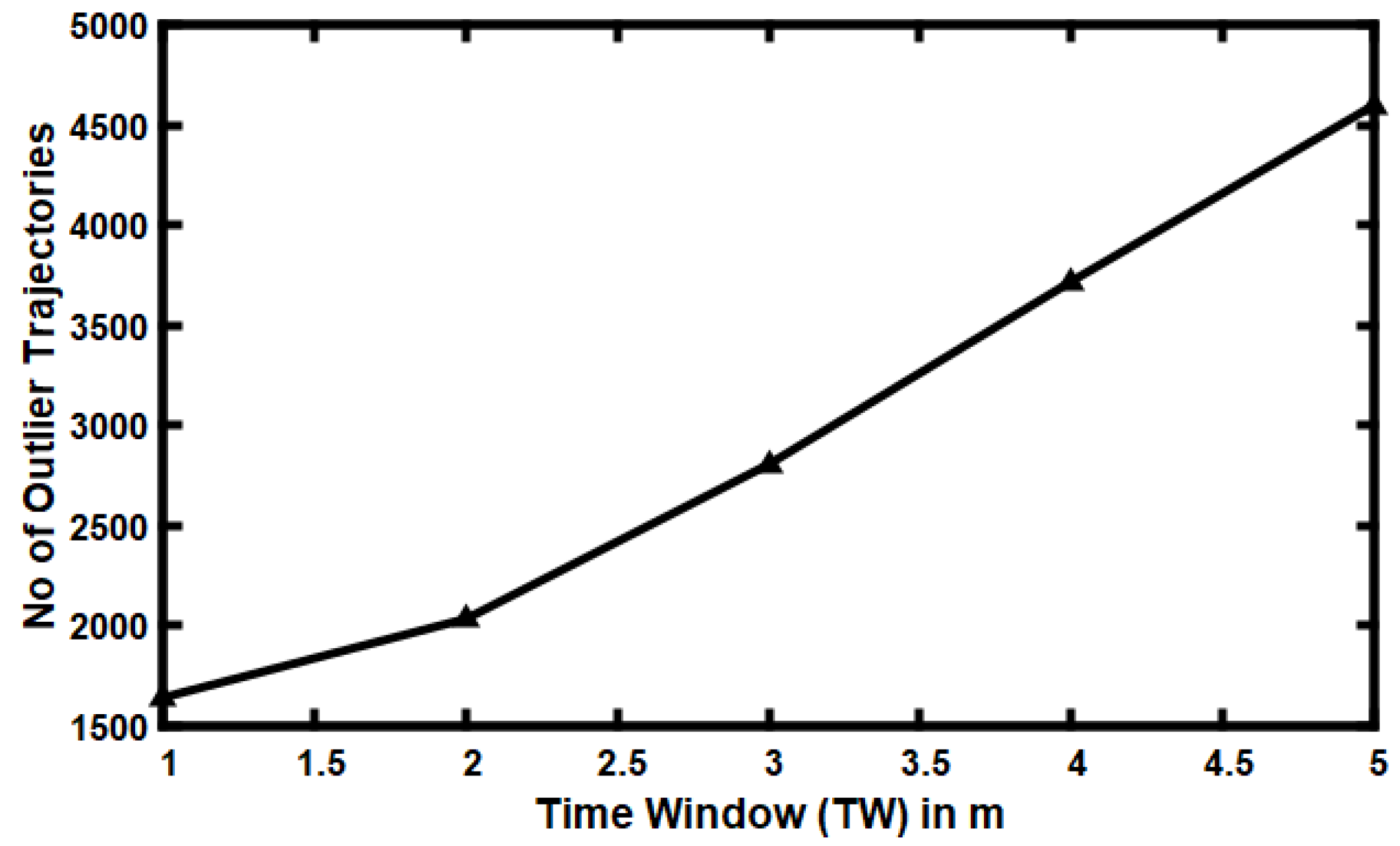
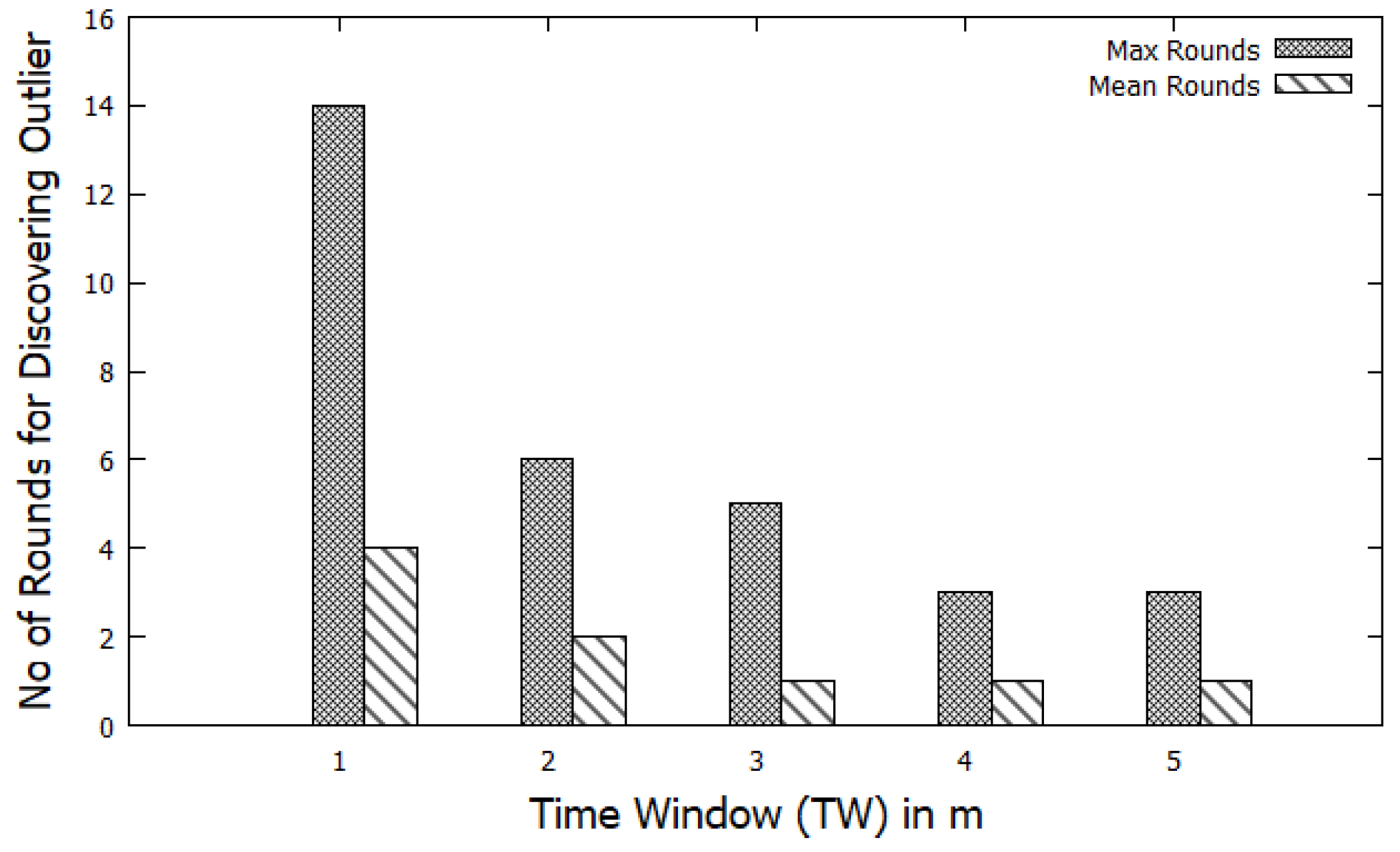
5.5. Impact of Varying Time Window (TW)
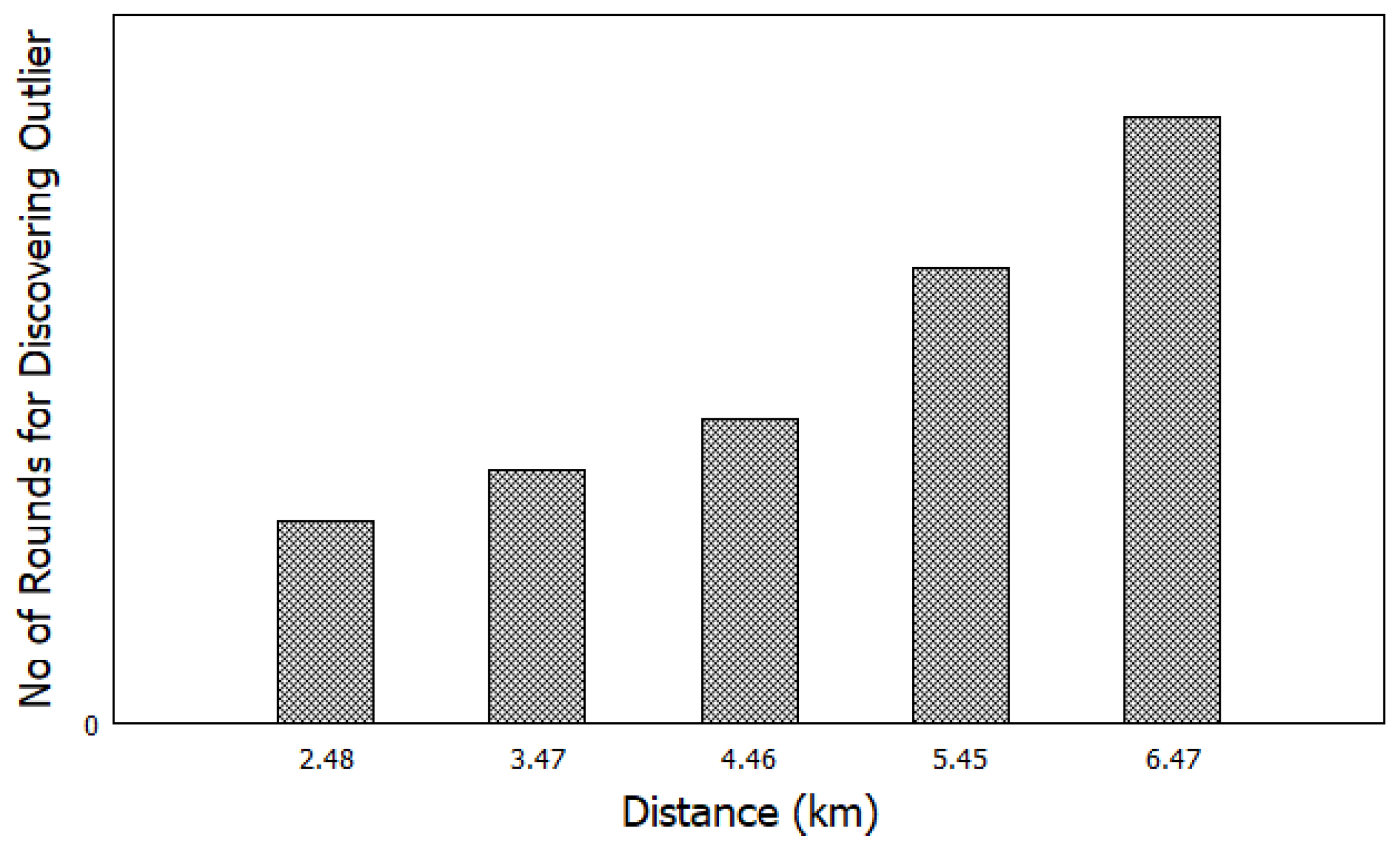
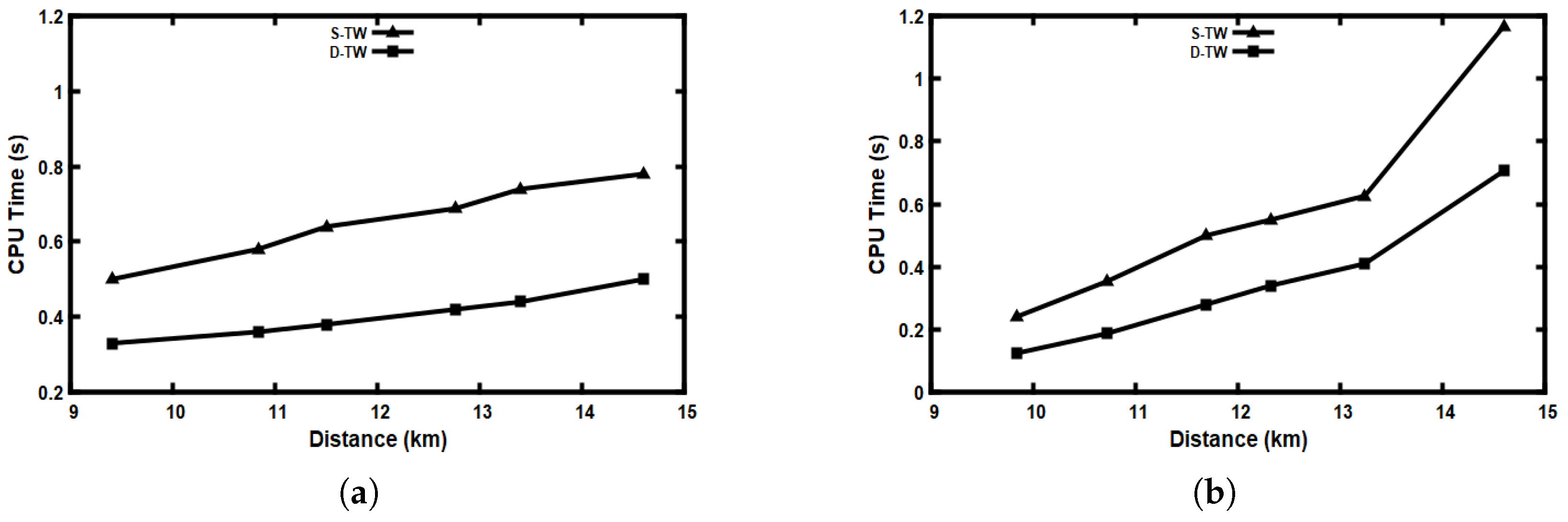
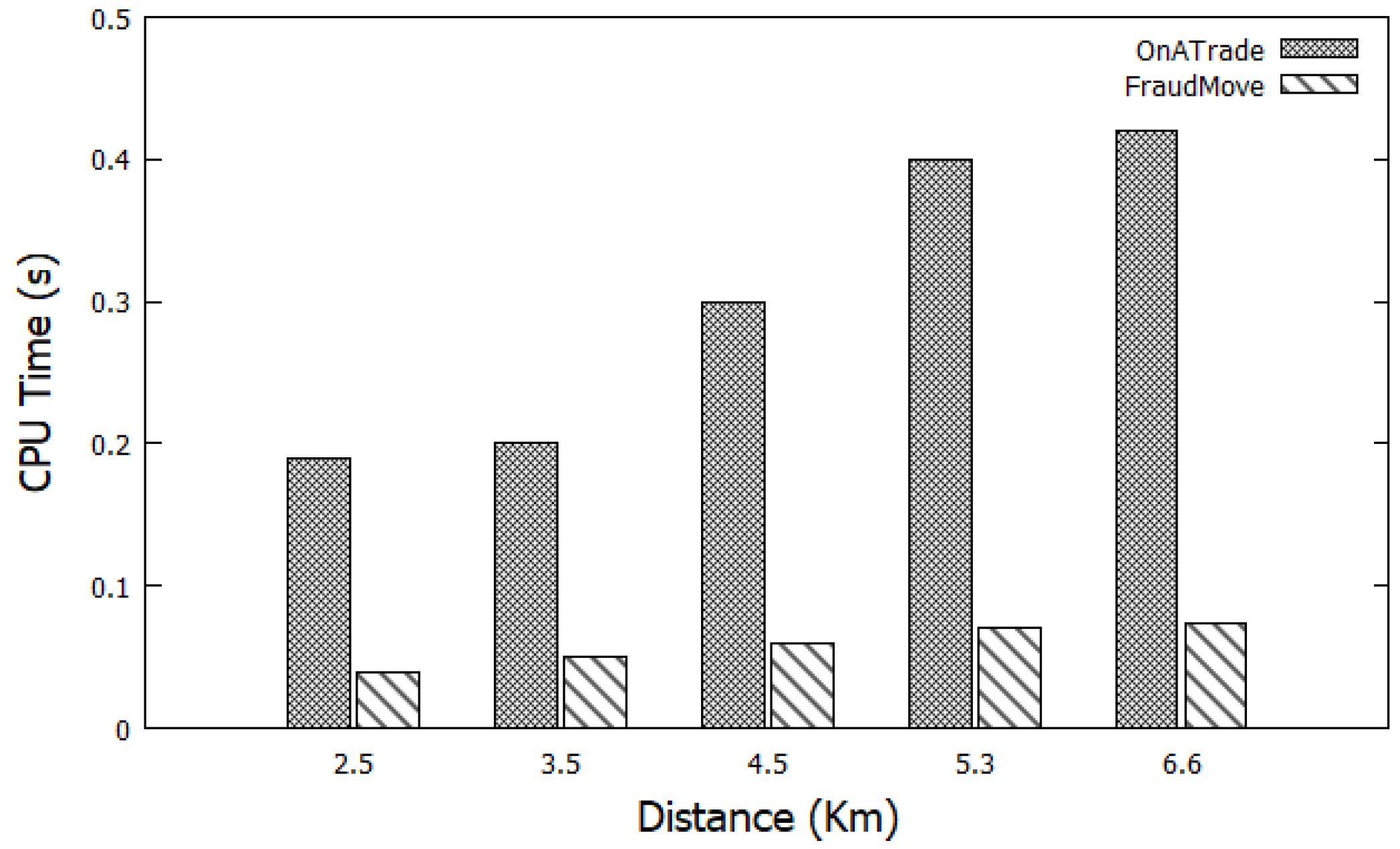
5.6. Performance Evaluation
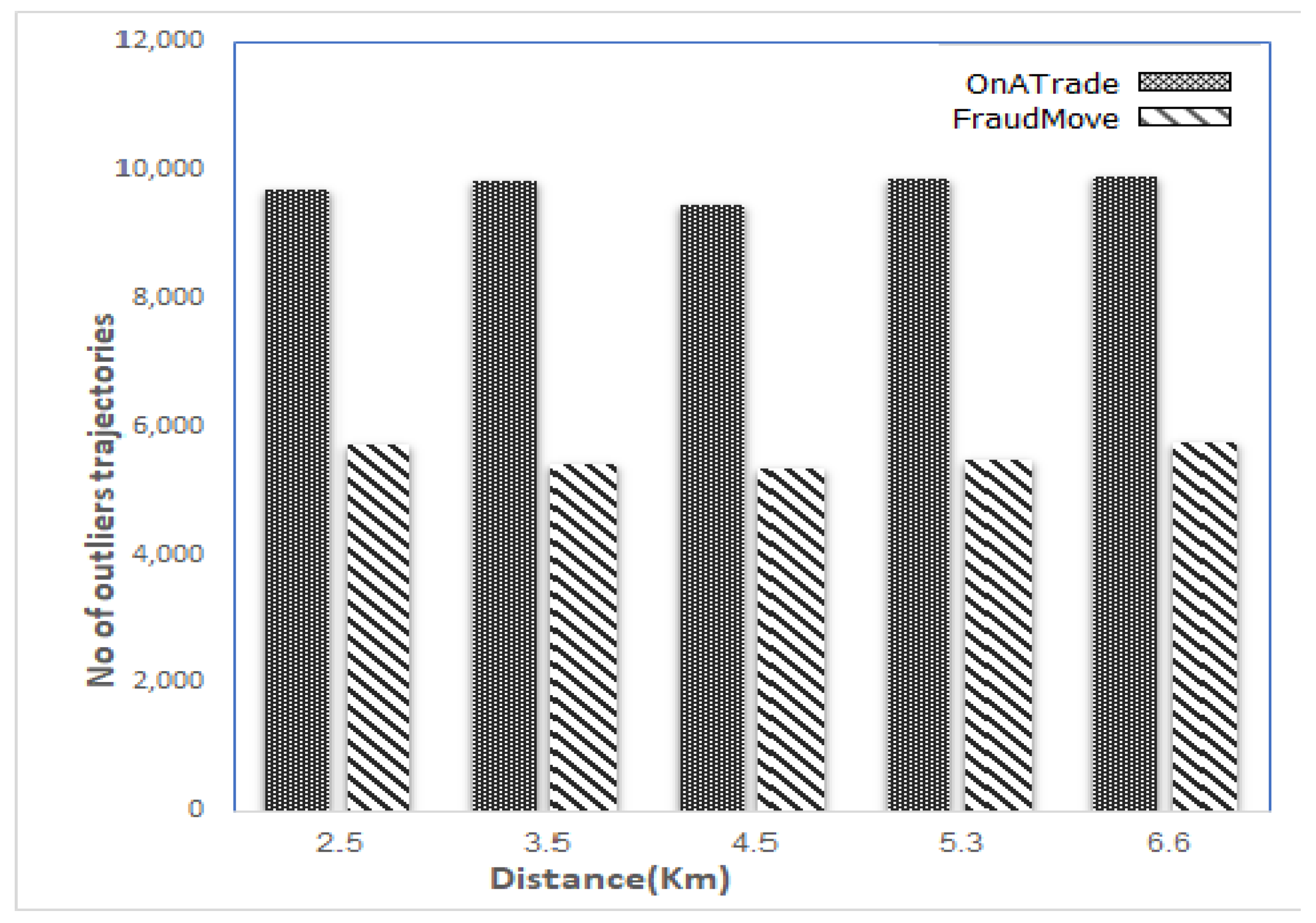
5.7. Accuracy Evaluation
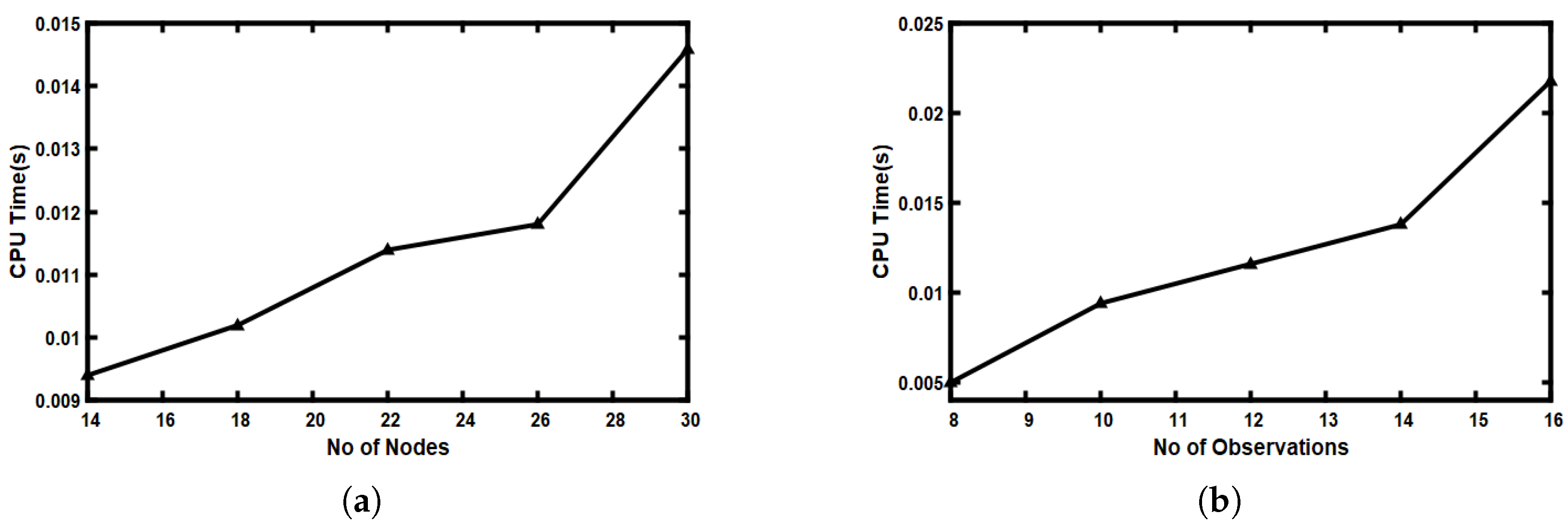
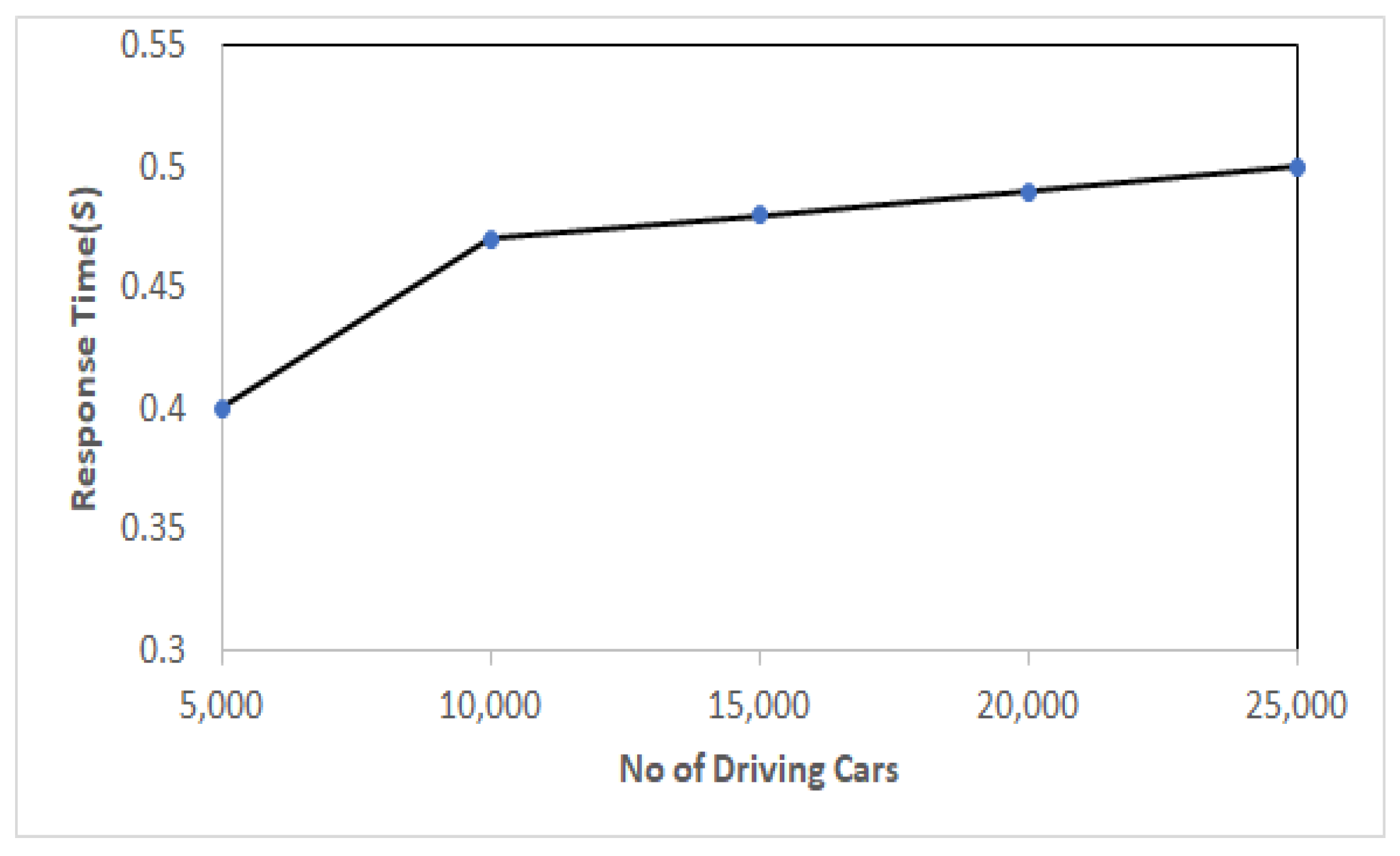
5.8. Scalability
6. Discussion
- Urban traffic detection: discovering outlier trajectories from GPS traces is an attractive topic for finding congested roads. A traffic flow can be recognized by examining moving objects trajectories in urban cities. Traffic flow detection is an essential task in planning smart cities and transportation management.
- Discovering road problems: identifying route problems such as closed roads for emergency conditions (e.g., events, accidents, bad weather, and potholes) is required for finding alternative routes for drivers. Generally, poor driving surfaces are caused by a combination of seasonal and traffic conditions.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Business of Apps. Uber Revenue and Usage Statistics; Business of Apps. 2020. Available online: https://www.businessofapps.com/data/uber-statistics/ (accessed on 1 September 2021).
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, W.; Xie, X.; Sun, G.; Huang, Y. T-drive: Driving directions based on taxi trajectories. In Proceedings of the 18th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010. [Google Scholar]
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W.Y. Mining interesting locations and travel sequences from GPS trajectories. In Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 791–800. [Google Scholar]
- Liu, L.; Andris, C.; Ratti, C. Uncovering cabdrivers’ behavior patterns from their digital traces. Comput. Environ. Urban Syst. 2010, 34, 541–548. [Google Scholar] [CrossRef]
- Calabrese, F.; Colonna, M.; Lovisolo, P.; Parata, D.; Ratti, C. Real-time urban monitoring using cell phones: A case study in Rome. IEEE Trans. Intell. Transp. Syst. 2010, 12, 141–151. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, W.; Liu, A.; Liu, G.; Zhao, L. Effective and efficient trajectory outlier detection based on time-dependent popular route. World Wide Web 2017, 20, 111–134. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, D.; Castro, P.S.; Li, N.; Sun, L.; Li, S.; Wang, Z. iBOAT: Isolation-Based Online Anomalous Trajectory Detection. IEEE Trans. Intell. Transp. Syst. 2013, 14, 806–818. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Y.; Yuan, J.; Xie, X. Urban computing with taxicabs. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011; pp. 89–98. [Google Scholar]
- Zheng, Y.; Liu, L.; Wang, L.; Xie, X. Learning transportation mode from raw gps data for geographic applications on the web. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 21–25 April 2008; pp. 247–256. [Google Scholar]
- Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, D.; Chen, C.; Castro, P.S.; Li, S.; Wang, Z. Real time anomalous trajectory detection and analysis. Mob. Netw. Appl. 2013, 18, 341–356. [Google Scholar] [CrossRef]
- Zhang, D.; Li, N.; Zhou, Z.H.; Chen, C.; Sun, L.; Li, S. iBAT: Detecting anomalous taxi trajectories from GPS traces. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011. [Google Scholar]
- Zhu, J.; Jiang, W.; Liu, A.; Liu, G.; Zhao, L. Time-Dependent Popular Routes Based Trajectory Outlier Detection. In International Conference on Web Information Systems Engineering; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Lee, J.G.; Han, J.; Li, X. Trajectory Outlier Detection: A Partition-and-Detect Framework. In Proceedings of the IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008. [Google Scholar]
- Zhou, Z.; Dou, W.; Jia, G.; Hu, C.; Xu, X.; Wu, X.; Pan, J. A method for real-time trajectory monitoring to improve taxi service using GPS big data. Inf. Manag. 2016, 53, 964–977. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Shen, H.T.; Zhou, X. Discovering popular routes from trajectories. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 900–911. [Google Scholar]
- Li, S.Z.; Jain, A. (Eds.) Viterbi Algorithm. In Encyclopedia of Biometrics; Springer: Boston, MA, USA, 2009; p. 1376. [Google Scholar] [CrossRef]
- Liu, Z.; Pi, D.; Jiang, J. Density-based trajectory outlier detection algorithm. J. Syst. Eng. Electron. 2013, 24, 335–340. [Google Scholar] [CrossRef]
- Ge, Y.; Xiong, H.; Zhou, Z.H.; Ozdemir, H.; Yu, J.; Lee, K.C. Top-Eye: Top-k evolving trajectory outlier detection. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management, Toronto, ON, Canada, 26–30 October 2010. [Google Scholar]
- Ge, Y.; Xiong, H.; Liu, C.; Zhou, Z.H. A Taxi Driving Fraud Detection System. In Proceedings of the IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011. [Google Scholar]
- Kong, X.; Song, X.; Xia, F.; Guo, H.; Wang, J.; Tolba, A. LoTAD: Long-term traffic anomaly detection based on crowdsourced bus trajectory data. World Wide Web 2018, 21, 825–847. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000. [Google Scholar]
- Eldawy, E.O.; Mokhtar, H.M. Clustering-Based Trajectory Outlier Detection. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 133–139. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Kanoulas, E.; Du, Y.; Xia, T.; Zhang, D. Finding fastest paths on a road network with speed patterns. In Proceedings of the IEEE 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 10. [Google Scholar]
- Gonzalez, H.; Han, J.; Li, X.; Myslinska, M.; Sondag, J.P. Adaptive fastest path computation on a road network: A traffic mining approach. In Proceedings of the 33rd International Conference on Very Large Data Bases, VLDB 2007, Vienna, Austria, 23–27 September 2007; Association for Computing Machinery, Inc.: New York, NY, USA, 2007; pp. 794–805. [Google Scholar]
- Sacharidis, D.; Patroumpas, K.; Terrovitis, M.; Kantere, V.; Potamias, M.; Mouratidis, K.; Sellis, T. On-line discovery of hot motion paths. In Proceedings of the 11th International Conference on Extending Database Technology: Advances in Database Technology, Nantes, France, 25–29 March 2008; pp. 392–403. [Google Scholar]
- Luo, W.; Tan, H.; Chen, L.; Ni, L.M. Finding time period-based most frequent path in big trajectory data. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 713–724. [Google Scholar]
- Rabiner, L.; Juang, B. An introduction to hidden Markov models. IEEE Assp Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Castro, P.S.; Zhang, D.; Chen, C.; Li, S.; Pan, G. From taxi GPS traces to social and community dynamics: A survey. ACM Comput. Surv. (CSUR) 2013, 46, 1–34. [Google Scholar] [CrossRef]
- Haklay, M.; Weber, P. Openstreetmap: User-generated street maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.B. A note on Dijkstra’s shortest path algorithm. J. ACM (JACM) 1973, 20, 385–388. [Google Scholar] [CrossRef]
- Piorkowski, M.; Sarafijanovic-Djukic, N.; Grossglauser, M. CRAWDAD Data Set Epfl/Mobility (v. 2009-02-24). 2009. [Google Scholar]
- Meng, F.; Yuan, G.; Lv, S.; Wang, Z.; Xia, S. An overview on trajectory outlier detection. Artif. Intell. Rev. 2018, 52, 2437–2456. [Google Scholar] [CrossRef]





| Symbol | Definition |
|---|---|
| OP | Optimal path from S to D |
| OT | Optimal time of the optimal path |
| Outlier threshold | |
| CL | Current location of a moving object |
| CP | Optimal path from CL to D |
| Travel time from start to current time | |
| Trips that share the same S and D | |
| A | Transition matrix |
| B | Emission matrix |
| P | Accumulated probability matrix |
| E | Backtrack matrix |
| Trip No | Sequence |
|---|---|
| N1 N4 N9 | |
| N1 N5 N6 N8 N9 | |
| N1 N4 N9 | |
| N1 N5 N7 N8 N9 | |
| N1 N5 N6 N8 N9 | |
| N1 N5 N7 N8 N9 | |
| N1 N4 N9 | |
| N1 N2 N3 N9 | |
| N1 N5 N7 N8 N9 | |
| N1 N5 N7 N8 N9 |
| From | To | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| N1 | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | |
| N1 | 0 | 0.1 | 0 | 0.3 | 0.6 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| N4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| N5 | 0 | 0 | 0 | 0 | 0 | 0.33 | 0.67 | 0 | 0 |
| N6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| N7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| N8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| N9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Node | Order | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| N1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0.1 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0.1 | 0 | 0 |
| N4 | 0 | 0.3 | 0 | 0 | 0 |
| N5 | 0 | 0.6 | 0 | 0 | 0 |
| N6 | 0 | 0 | 0.2 | 0 | 0 |
| N7 | 0 | 0 | 0.4 | 0 | 0 |
| N8 | 0 | 0 | 0 | 0.86 | 0 |
| N9 | 0 | 0 | 0.3 | 0.14 | 1 |
| Node | Probability | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| N1 | 1 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0.01 | 0 | 0 | 0 |
| N3 | 0 | 0 | 0.001 | 0 | 0 |
| N4 | 0 | 0.09 | 0 | 0 | 0 |
| N5 | 0 | 0.36 | 0 | 0 | 0 |
| N6 | 0 | 0 | 0.02376 | 0 | 0 |
| N7 | 0 | 0 | 0.09648 | 0 | 0 |
| N8 | 0 | 0 | 0 | 0.08297 | 0 |
| N9 | 0 | 0 | 0.027 | 0.00014 | 0.08297 |
| Node | Order | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| N1 | 0 | 0 | 0 | 0 |
| N2 | N1 | 0 | 0 | 0 |
| N3 | 0 | N2 | 0 | 0 |
| N4 | N1 | 0 | 0 | 0 |
| N5 | N1 | 0 | 0 | 0 |
| N6 | 0 | N5 | 0 | 0 |
| N7 | 0 | N5 | 0 | 0 |
| N8 | 0 | 0 | N7 | 0 |
| N9 | 0 | N4 | N3 | N8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eldawy, E.O.; Hendawi, A.; Abdalla, M.; Mokhtar, H.M.O. FraudMove: Fraud Drivers Discovery Using Real-Time Trajectory Outlier Detection. ISPRS Int. J. Geo-Inf. 2021, 10, 767. https://doi.org/10.3390/ijgi10110767
Eldawy EO, Hendawi A, Abdalla M, Mokhtar HMO. FraudMove: Fraud Drivers Discovery Using Real-Time Trajectory Outlier Detection. ISPRS International Journal of Geo-Information. 2021; 10(11):767. https://doi.org/10.3390/ijgi10110767
Chicago/Turabian StyleEldawy, Eman O., Abdeltawab Hendawi, Mohammed Abdalla, and Hoda M. O. Mokhtar. 2021. "FraudMove: Fraud Drivers Discovery Using Real-Time Trajectory Outlier Detection" ISPRS International Journal of Geo-Information 10, no. 11: 767. https://doi.org/10.3390/ijgi10110767
APA StyleEldawy, E. O., Hendawi, A., Abdalla, M., & Mokhtar, H. M. O. (2021). FraudMove: Fraud Drivers Discovery Using Real-Time Trajectory Outlier Detection. ISPRS International Journal of Geo-Information, 10(11), 767. https://doi.org/10.3390/ijgi10110767






