A Topology-Preserving Simplification Method for 3D Building Models
Abstract
:1. Introduction
2. Related Work
2.1. Simplification of 3D Building Models
2.2. Consistency of Spatial Analysis
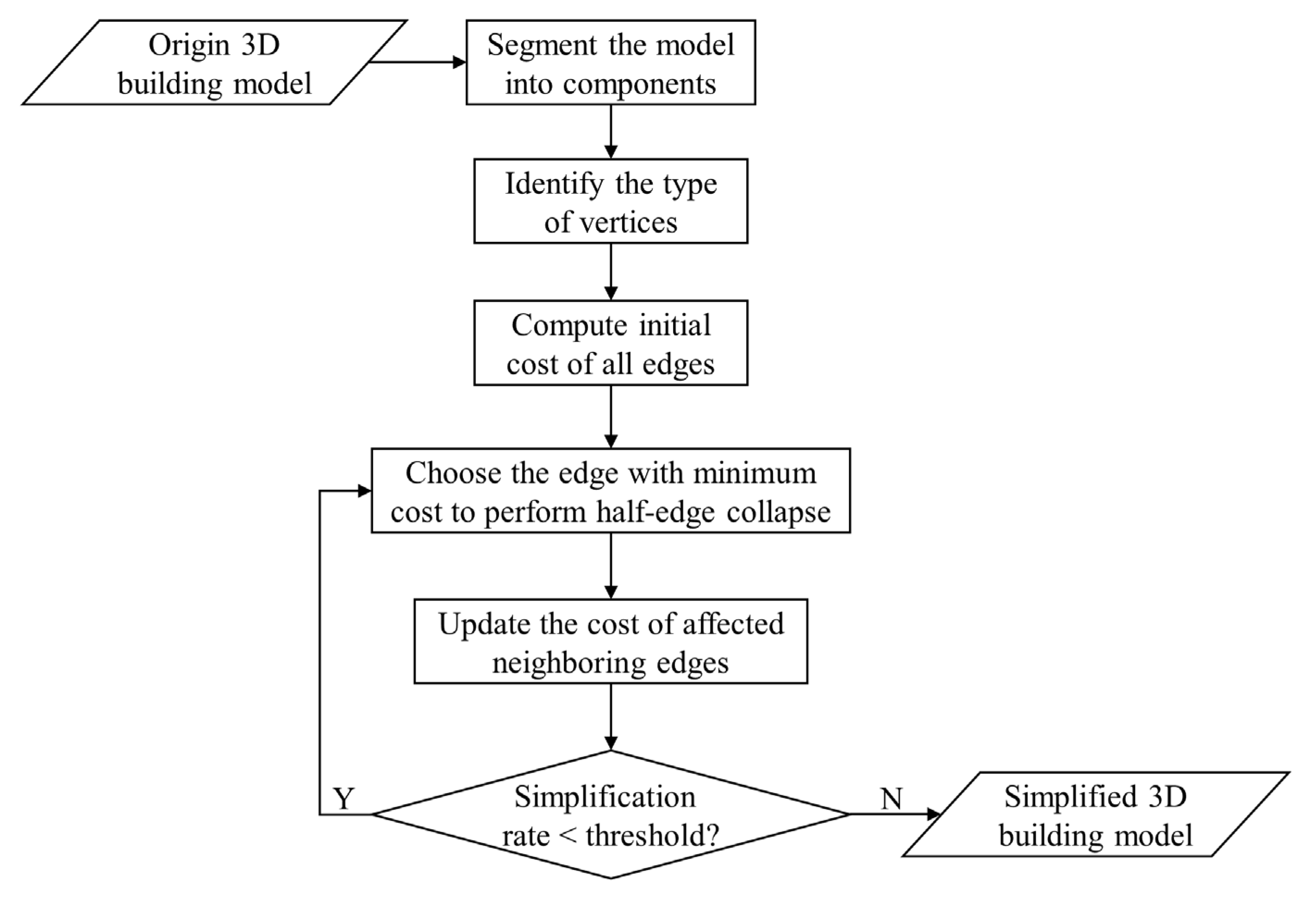
3. Methodology
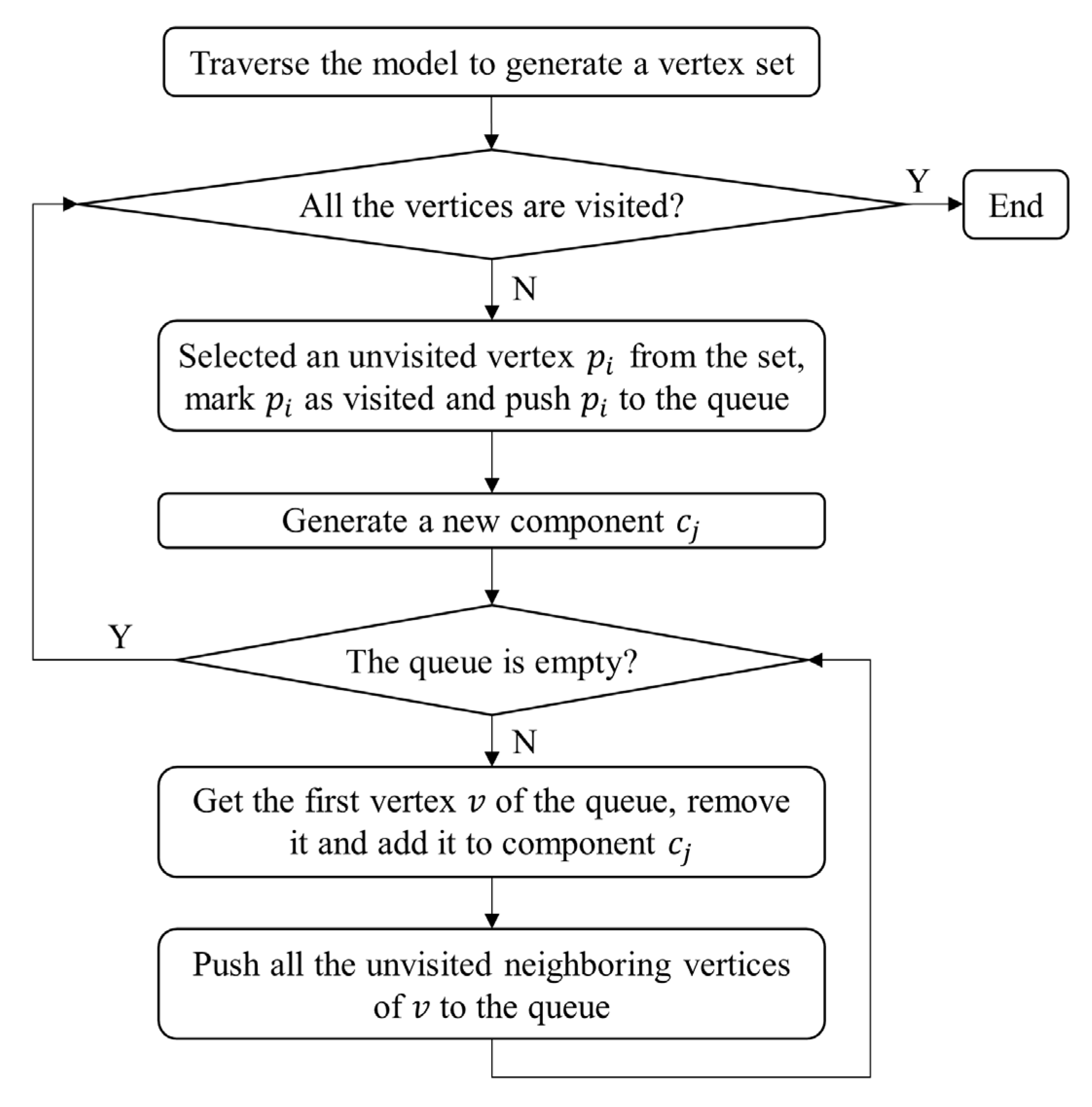
3.1. Component Segmentation of Building Models
3.2. Classification of Vertices
3.2.1. Types of Vertices
3.2.2. Extraction Rules of Boundary Vertices
3.2.3. Supplementary Rules
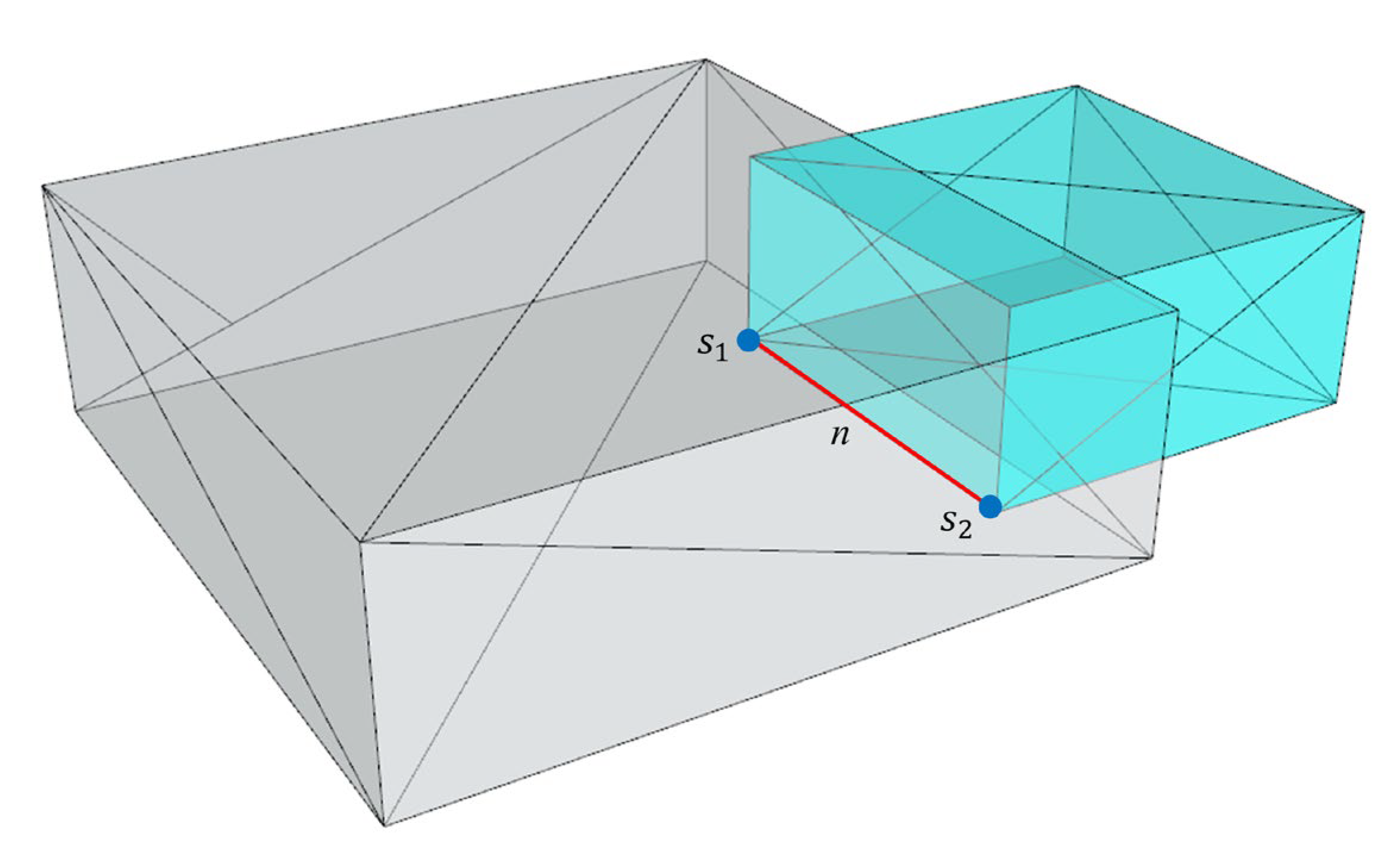
- When a vertex has the characteristics of a boundary vertex and a hole vertex simultaneously, it will be recorded as a boundary vertex. Although the number of adjacent triangles of the edges where these vertices are located is also one (Figure 9), it is caused by modeling errors. These vertices cannot represent the holes of the building models. To prevent these boundary vertices from being simplified first, the holes formed by them will be triangulated to meet the requirements of the proposed method. The retriangulation algorithm used in our method was proposed by Weatherill and Hassan [40]. As shown in Figure 9, edge n has only one adjacent triangle, and the vertical plane where it is located is not closed. However, its vertices s1 and s2 have been recognized as boundary vertices to restrain. Therefore, they are not defined as hole vertices.
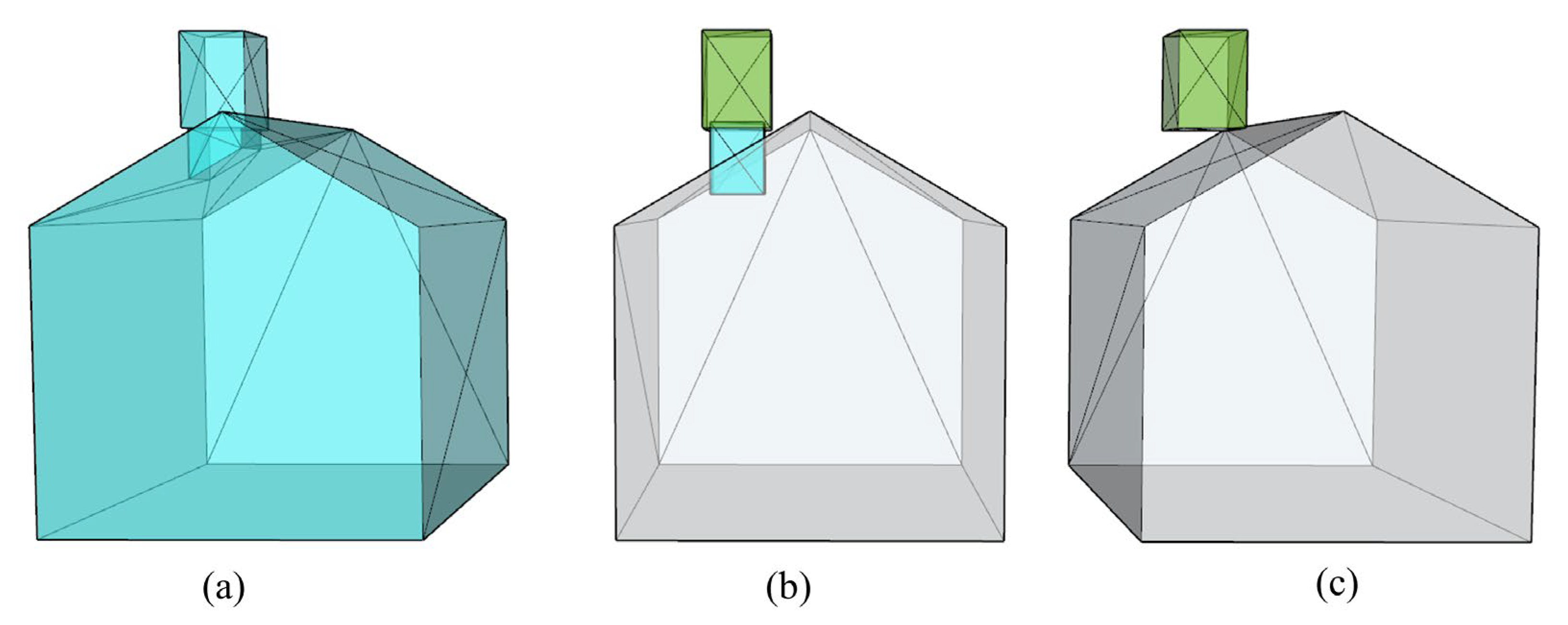
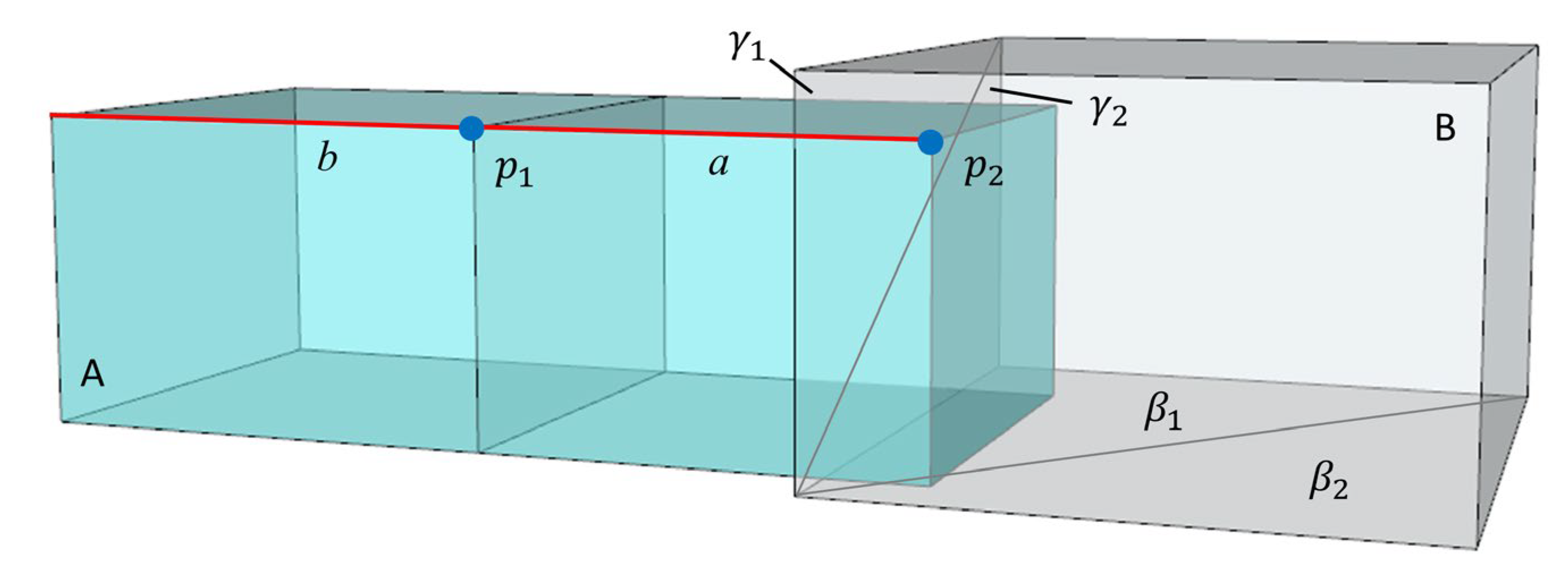
- For multi-component building models, topological dependence is mainly represented by intersecting or attaching among components. However, there are also some special conditions, such as visual attaching. As shown in Figure 10, both components are visually attached. However, there is a small gap between them. In this case, the method based on intersection detection cannot correctly extract the boundary vertices, and the separation of components may still occur during the simplification process. To address this challenge, we temporarily extended the bounding box and the edge to a certain extent during the intersection detection based on the buffering idea, with an amplitude of 1% of the length.
- The supplementary rule (when an edge passes through a component, such as e in Figure 11, both vertices of the edge are regarded as boundary vertices) defined in Section 3.2.2 solves the problem of interleaved components. However, when facing intersection components with an “embedded” relationship, the extraction result may be incomplete. For instance, as shown in Figure 11, the bottom quadrilateral of the roof is composed of two triangles, and its area is larger than the area of the wall, forming an “embedded” relationship. During intersection detection, the hypotenuse e intersects with the wall and passes through it. Both vertices of the edge can be identified as boundary vertices . According to the rule of intersection detection, no edge intersects with the wall for the other two vertices of the bottom quadrilateral—they are recognized as ordinary vertices. However, they also easily collapse during the simplification process, causing separation between the roof and the wall. To solve this kind of problem, we propose a supplementary rule: when an edge passes through a component and the normal vectors of its two adjacent triangles are parallel, the other two vertices of both triangles are also regarded as boundary vertices. The final extraction results are shown in Figure 12.
3.3. Simplification Based on Cost of Edges
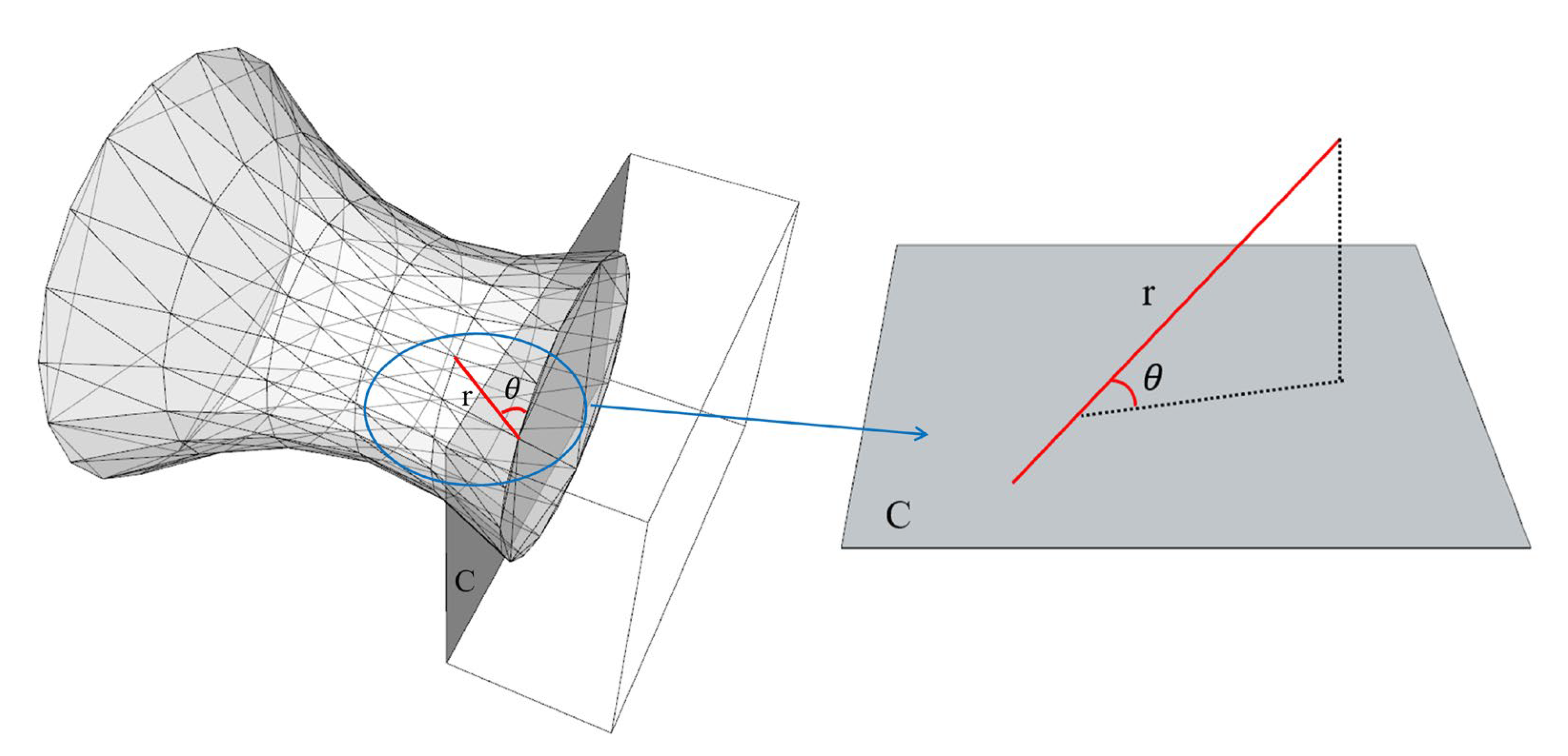
3.3.1. The E–C Angle
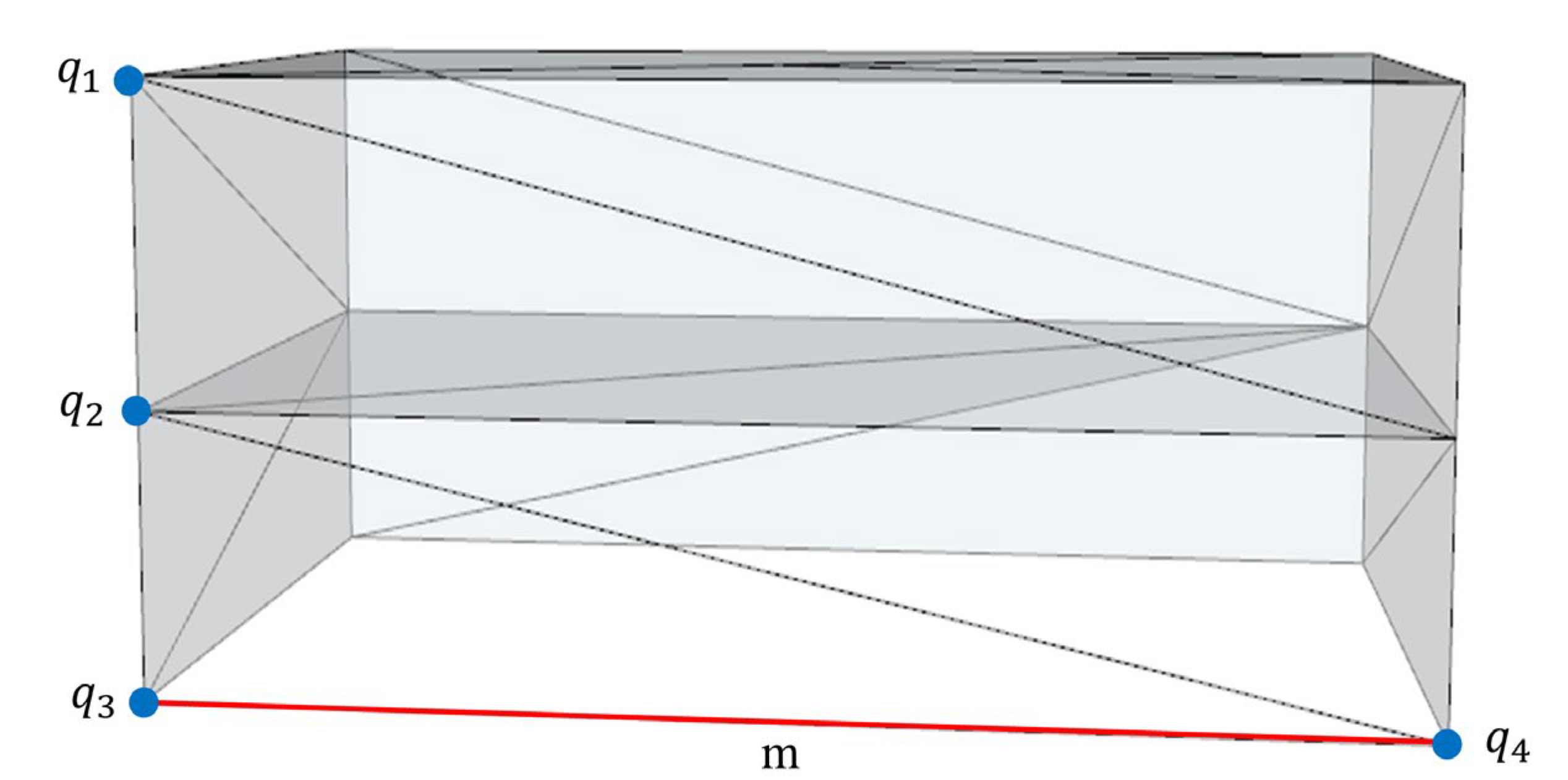
3.3.2. Error metric for Simplification
4. Results and Discussion
4.1. Simplification Effect
4.2. Analysis of Parameter Influence
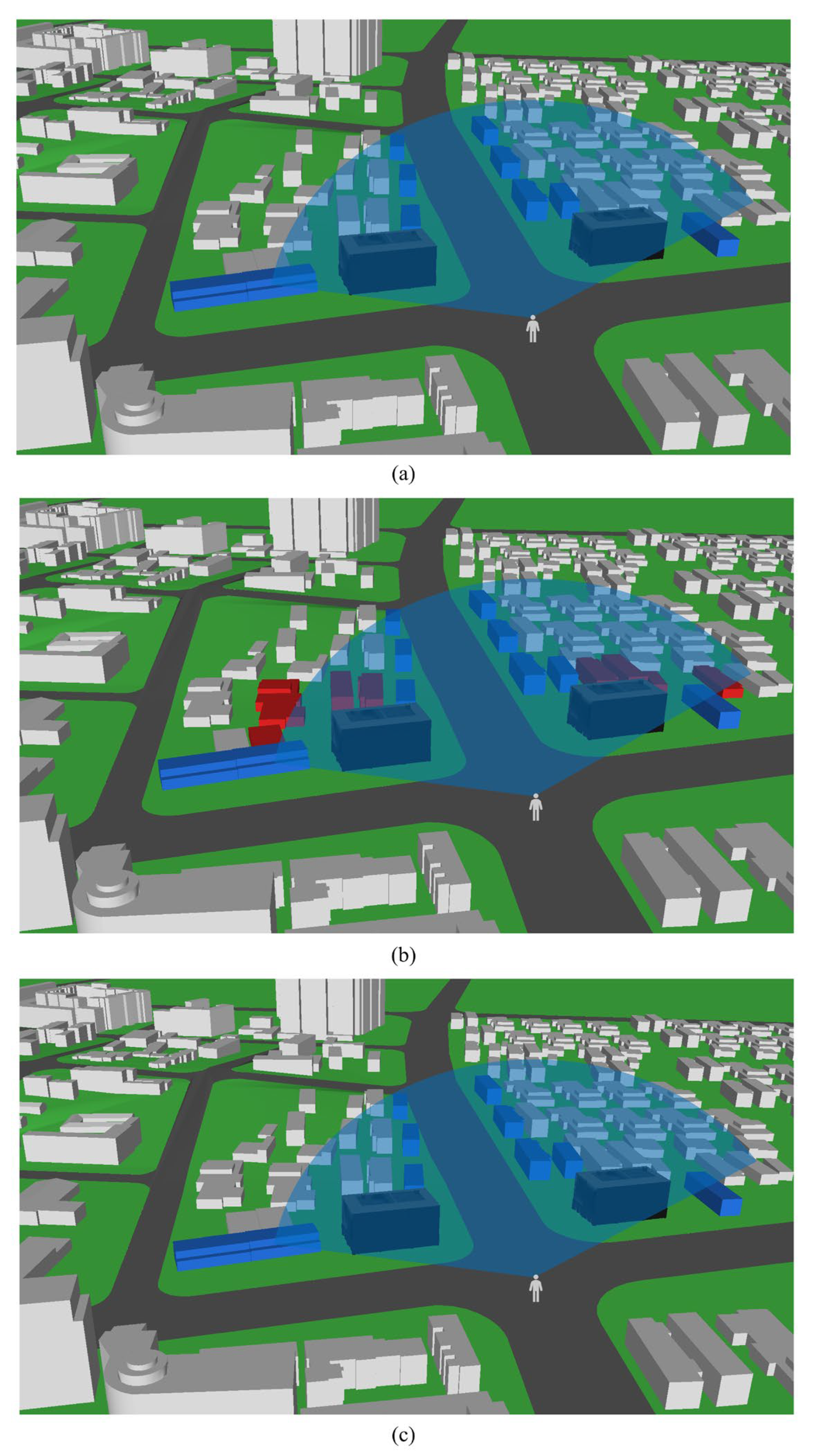
4.3. Consistency of Visibility Analysis among Different LODs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, J.; Feng, C.-C. An Integrated Simplification Approach for 3D Buildings with Sloped and Flat Roofs. ISPRS Int. J. Geo-Inf. 2016, 5, 128. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.H. Hierarchical geometric models for visible surface algorithms. Commun. ACM 1976, 19, 547–554. [Google Scholar] [CrossRef]
- Gröger, G.; Kolbe, T.H.; Nagel, C.; Häfele, K.-H. OGC city geography markup language (CityGML) encoding standard. Open Geospat. Consort. 2012. [Google Scholar]
- Fai, S.; Rafeiro, J. Establishing an appropriate level of detail (LoD) for a building information model (BIM)-West Block, Parliament Hill, Ottawa, Canada. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 123. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, P.; Seppänen, O.; Lappalainen, E.; Peltokorpi, A.; Olivieri, H. Applying level of detail in a BIM-based project: An overall process for lean design management. Buildings 2019, 9, 109. [Google Scholar] [CrossRef] [Green Version]
- Besuievsky, G.; Barroso, S.; Beckers, B.; Patow, G. A Configurable LoD for Procedural Urban Models intended for Daylight Simulation. In Proceedings of UDMV; Eurographics Association: Geneva, Switzerland, 2014; pp. 19–24. [Google Scholar]
- Rossignac, J. 54 Surface Simplification and 3d Geome-Try Compression. Triangle 2004, 2, 4. [Google Scholar]
- Wang, Y.; Zheng, J.; Wang, H. Fast mesh simplification method for three-dimensional geometric models with feature-preserving efficiency. Sci. Program. 2019. [Google Scholar] [CrossRef]
- Ribelles, J.; Heckbert, P.S.; Garland, M.; Stahovich, T.; Srivastava, V. Finding and removing features from polyhedra. In Proceedings of DETC; American Society Of Mechanical Engineers: New York, NY, USA, 2001; pp. 1–10. [Google Scholar]
- Kada, M. Scale-dependent simplification of 3D building models based on cell decomposition and primitive instancing. In Proceedings of the International Conference on Spatial Information Theory, Melbourne, Australia, 19–23 September 2007; Springer: Berlin/Heidelberg, Germany; pp. 222–237. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Q.; Du, Z.; Feng, T.; Zhang, Y. Mathematical morphology-based generalization of complex 3D building models incorporating semantic relationships. ISPRS J. Photogramm. Remote Sens. 2012, 68, 95–111. [Google Scholar] [CrossRef]
- She, J.; Gu, X.; Tan, J.; Tong, M.; Wang, C. An appearance-preserving simplification method for complex 3D building models. Trans. GIS 2019, 23, 275–293. [Google Scholar] [CrossRef]
- Li, Q.; Sun, X.; Yang, B.; Jiang, S. Geometric structure simplification of 3D building models. ISPRS J. Photogramm. Remote Sens. 2013, 84, 100–113. [Google Scholar] [CrossRef]
- Rossignac, J.; Borrel, P. Multi-resolution 3D approximations for rendering complex scenes. In Modeling in Computer Graphics; Springer: Berlin/Heidelberg, Germany, 1993; pp. 455–465. [Google Scholar] [CrossRef]
- Schroeder, W.J.; Zarge, J.A.; Lorensen, W.E. Decimation of triangle meshes. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, Chicago, IL, USA, 26–31 July 1992; pp. 65–70. [Google Scholar]
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Mesh optimization. In Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 2–6 August 1993; pp. 19–26. [Google Scholar]
- Hinker, P.; Hansen, C. Geometric optimization. In Proceedings Visualization’93; IEEE: Piscataway, NJ, USA, 1993; pp. 189–195. [Google Scholar] [CrossRef]
- Garland, M.; Heckbert, P.S. Surface simplification using quadric error metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 3–8 August 1997; pp. 209–216. [Google Scholar] [CrossRef] [Green Version]
- Lindstrom, P.; Turk, G. Image-driven simplification. ACM Trans. Graph. (ToG) 2000, 19, 204–241. [Google Scholar] [CrossRef]
- Luebke, D.; Hallen, B. Perceptually driven simplification for interactive rendering. In Eurographics Workshop on Rendering Techniques; Springer: Berlin/Heidelberg, Germany, 2001; pp. 223–234. [Google Scholar]
- Cohen-Steiner, D.; Alliez, P.; Desbrun, M. Variational shape approximation. In ACM SIGGRAPH 2004 Papers; Association for Computing Machinery: New York, NY, USA, 2004; pp. 905–914. [Google Scholar] [CrossRef] [Green Version]
- Castelló, P.; Sbert, M.; Chover, M.; Feixas, M. driven simplification using mutual information. Comput. Graph. 2008, 32, 451–463. [Google Scholar] [CrossRef]
- González, C.; Castelló, P.; Chover, M.; Sbert, M.; Feixas, M.; Gumbau, J. Simplification method for textured polygonal meshes based on structural appearance. Signal Image Video Process. 2013, 7, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Thiemann, F.; Sester, M. Segmentation of buildings for 3D-generalisation. In Proceedings of the ICA Workshop on Generalisation and Multiple Representation, Leicester, UK, 20–21 August 2004. [Google Scholar]
- Rau, J.-Y.; Chen, L.-C.; Tsai, F.; Hsiao, K.-H.; Hsu, W.-C. Lod generation for 3d polyhedral building model. In Pacific-Rim Symposium on Image and Video Technology; Springer: Berlin/Heidelberg, Germany, 2006; pp. 44–53. [Google Scholar] [CrossRef]
- Jarząbek-Rychard, M.; Borkowski, A. 3D building reconstruction from ALS data using unambiguous decomposition into elementary structures. ISPRS J. Photogramm. Remote Sens. 2016, 118, 1–12. [Google Scholar] [CrossRef]
- Fan, H.; Meng, L.; Jahnke, M. Generalization of 3D buildings modelled by CityGML. In Advances in GIScience; Springer: Berlin/Heidelberg, Germany, 2009; pp. 387–405. [Google Scholar] [CrossRef]
- Ladenhauf, D.; Berndt, R.; Krispel, U.; Eggeling, E.; Ullrich, T.; Battisti, K.; Gratzl-Michlmair, M. Geometry simplification according to semantic constraints. Comput. Sci. Res. Dev. 2016, 31, 119–125. [Google Scholar] [CrossRef]
- Brasebin, M.; Perret, J.; Mustière, S.; Weber, C. Measuring the impact of 3D data geometric modeling on spatial analysis: Illustration with Skyview factor. Usage Usability Util. 3D City Models–Eur. COST Action TU0801 2012, 2012, 02001. [Google Scholar] [CrossRef] [Green Version]
- Fisher-Gewirtzman, D.; Shashkov, A.; Doytsher, Y. Voxel based volumetric visibility analysis of urban environments. Surv. Rev. 2013, 45, 451–461. [Google Scholar] [CrossRef]
- Ahmed, F.C.; Sekar, S. Using three-dimensional volumetric analysis in everyday urban planning processes. Appl. Spat. Anal. Policy 2015, 8, 393–408. [Google Scholar] [CrossRef]
- Gergelova, M.B.; Kuzevicova, Z.; Labant, S.; Kuzevic, S.; Mizak, J. Roof’s Potential and Suitability for PV Systems Based on LiDAR: A Case Study of Komárno, Slovakia. Sustainability 2020, 12, 18. [Google Scholar] [CrossRef]
- Kota, S.; Haberl, J.S.; Clayton, M.J.; Yan, W. Building Information Modeling (BIM)-based daylighting simulation and analysis. Energ Build. 2014, 81, 391–403. [Google Scholar] [CrossRef]
- Salimzadeh, N.; Vahdatikhaki, F.; Hammad, A. Parametric modeling and surface-specific sensitivity analysis of PV module layout on building skin using BIM. Energ Build. 2020, 216, 109953. [Google Scholar] [CrossRef]
- Horna, S.; Meneveaux, D.; Damiand, G.; Bertrand, Y. Consistency constraints and 3D building reconstruction. Comput. Aided Des. 2009, 41, 13–27. [Google Scholar] [CrossRef]
- Ghawana, T.; Zlatanova, S. Data consistency checks for building a 3D model: A case study of Technical University, Delft Campus, The Netherlands. Geospat. World 2010, 2010, 4. [Google Scholar]
- Alam, N.; Wagner, D.; Wewetzer, M.; von Falkenhausen, J.; Coors, V.; Pries, M. Towards automatic validation and healing of CityGML models for geometric and semantic consistency. In Innovations in 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 77–91. [Google Scholar]
- Biljecki, F.; Ledoux, H.; Stoter, J.; Vosselman, G. The variants of an LOD of a 3D building model and their influence on spatial analyses. ISPRS J. Photogramm. Remote Sens. 2016, 116, 42–54. [Google Scholar] [CrossRef] [Green Version]
- Van Oosterom, P. Reactive Data Structures for Geographic Information Systems; Oxford University Press, Inc.: Oxford, UK, 1994. [Google Scholar]
- Weatherill, N.P.; Hassan, O. Efficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints. Int. J. Numer. Methods Eng. 1994, 37, 2005–2039. [Google Scholar] [CrossRef]
- Jing, C.; Mo, L.; Li, J. An improved texture-related vertex clustering algorithm for model simplification. Comput. Geosci. 2015, 83, 37–45. [Google Scholar]








| Model | Number of Triangles | Number of Components | Number of Vertices | Simplification Rate | a | ||||
|---|---|---|---|---|---|---|---|---|---|
| Original | Simplified | Original | Simplified (QEM/ Chen’s/Ours) | Original | Simplified (QEM /Chen’s/Ours) | Boundary | |||
| Pavilion | 5752 | 2300 | 275 | 212/186/170 | 4060 | 2310/2218/2154 | 2510 | 60% | 2.0 |
| Apartment | 2567 | 513 | 103 | 53/47/57 | 1647 | 620/597/644 | 294 | 80% | 1.5 |
| House | 4428 | 2214 | 129 | 71/65/78 | 2317 | 1107/1053/1193 | 853 | 50% | 5.0 |
| Model | Type | Simplification Rate | a |
|---|---|---|---|
 | complex | 60% | 2.0 |
 | complex | 70% | 3.8 |
 | complex | 50% | 5.0 |
 | simple | 80% | 1.5 |
 | simple | 80% | 1.6 |
 | simple | 70% | 2.6 |
 | simple | 70% | 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wu, G.; Zhao, Q.; Li, Y.; Gao, Y.; She, J. A Topology-Preserving Simplification Method for 3D Building Models. ISPRS Int. J. Geo-Inf. 2021, 10, 422. https://doi.org/10.3390/ijgi10060422
Wang B, Wu G, Zhao Q, Li Y, Gao Y, She J. A Topology-Preserving Simplification Method for 3D Building Models. ISPRS International Journal of Geo-Information. 2021; 10(6):422. https://doi.org/10.3390/ijgi10060422
Chicago/Turabian StyleWang, Biao, Guoping Wu, Qiang Zhao, Yaozhu Li, Yiyuan Gao, and Jiangfeng She. 2021. "A Topology-Preserving Simplification Method for 3D Building Models" ISPRS International Journal of Geo-Information 10, no. 6: 422. https://doi.org/10.3390/ijgi10060422
APA StyleWang, B., Wu, G., Zhao, Q., Li, Y., Gao, Y., & She, J. (2021). A Topology-Preserving Simplification Method for 3D Building Models. ISPRS International Journal of Geo-Information, 10(6), 422. https://doi.org/10.3390/ijgi10060422







