Analysis and Evaluation of Non-Pharmaceutical Interventions on Prevention and Control of COVID-19: A Case Study of Wuhan City
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
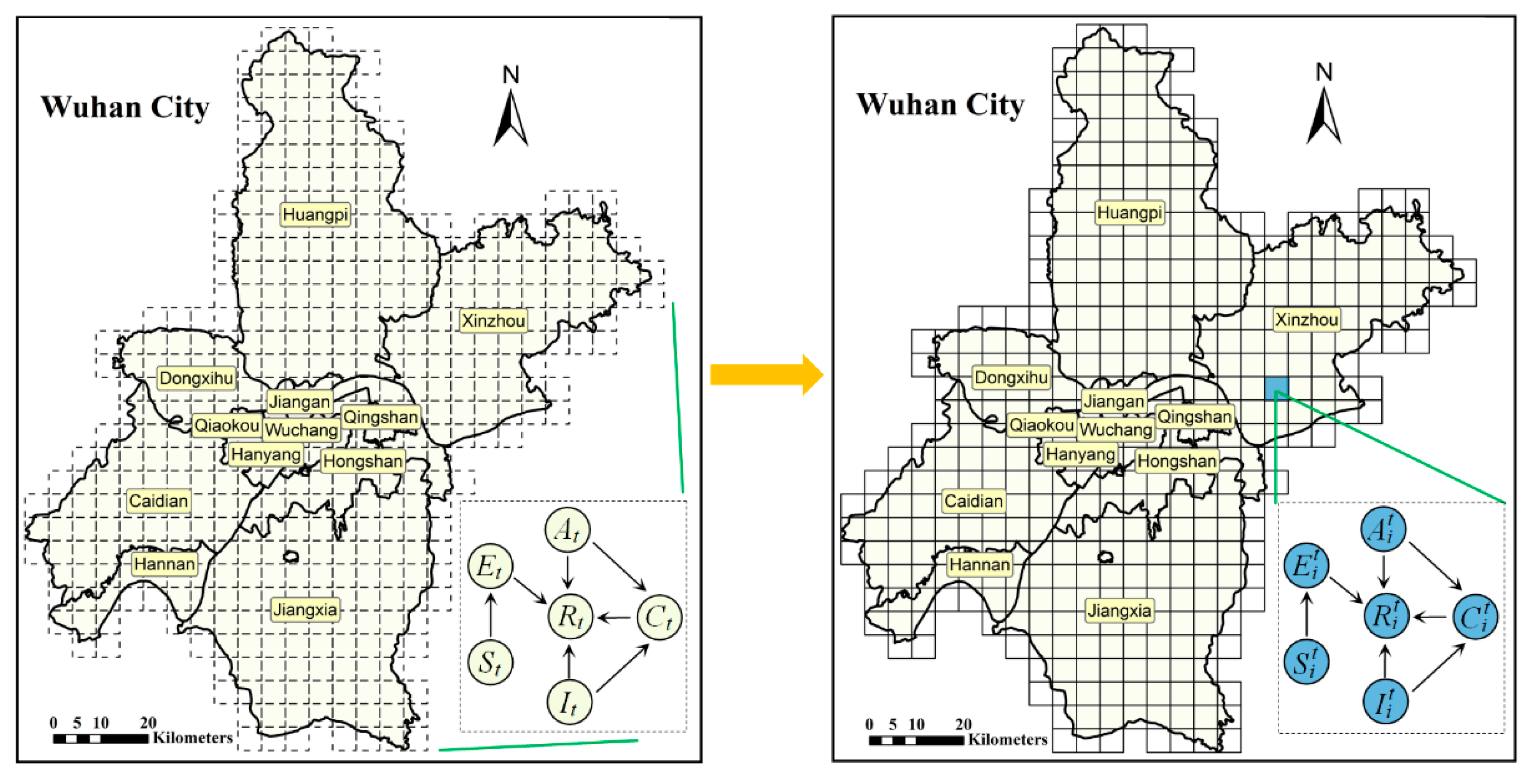
2.2. Medel of Quarantine Measures Based on a Discrete Grid
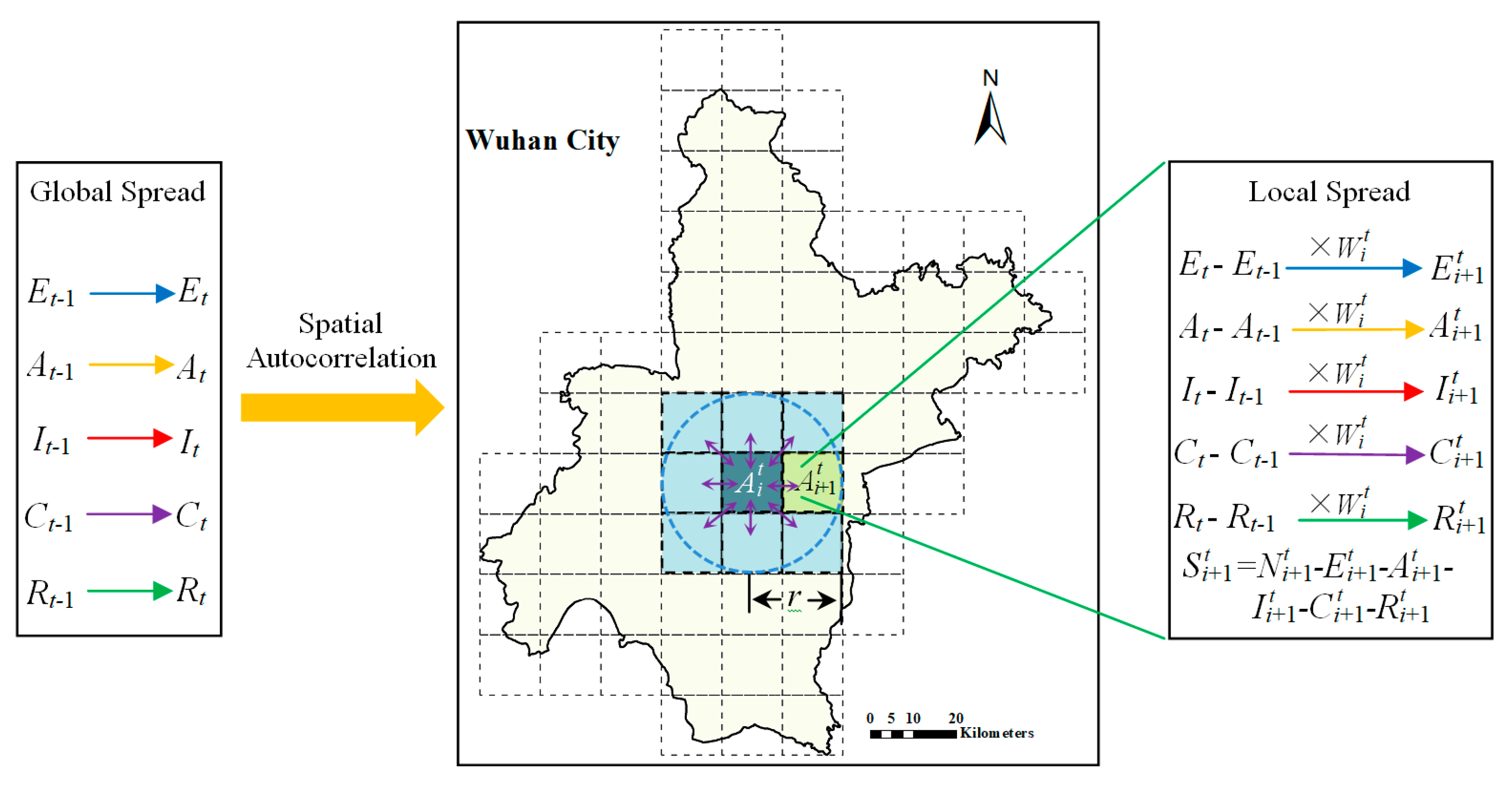
2.3. Spatiotemporal Spread Model of COVID-19 Based on a Discrete Grid
2.4. Model of Self-Protection Measures
2.5. Model of Hospital Isolation Measures
3. Results
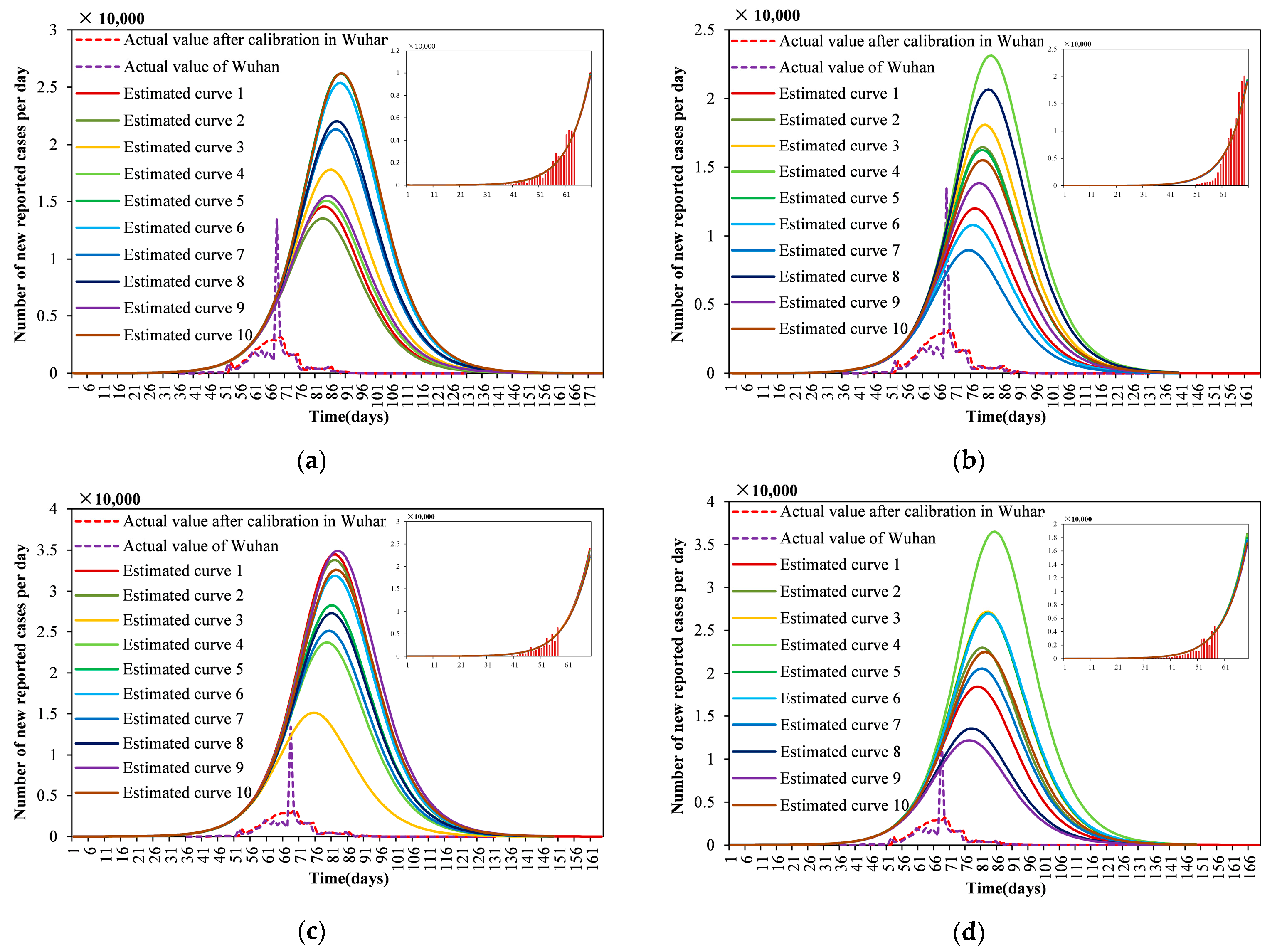
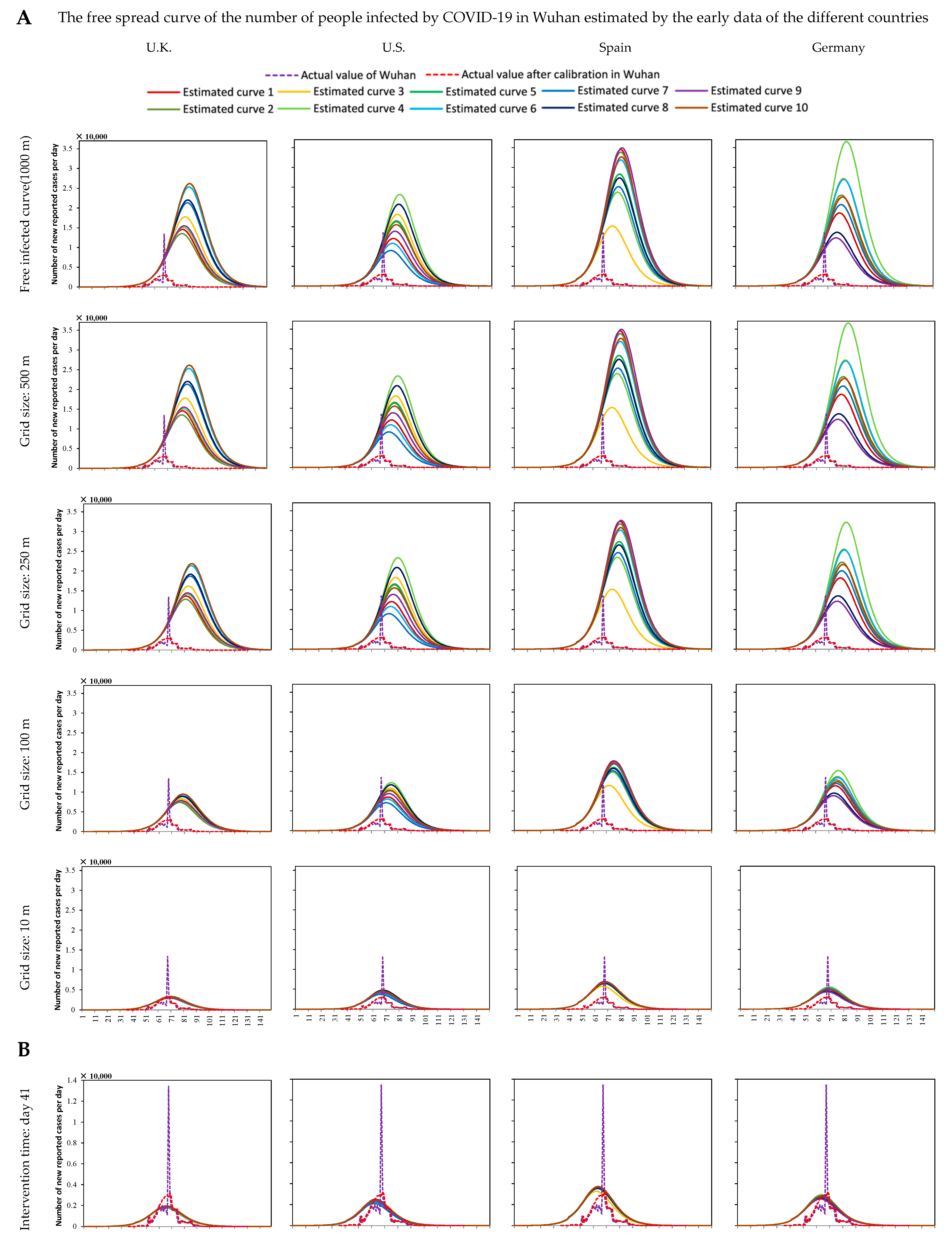
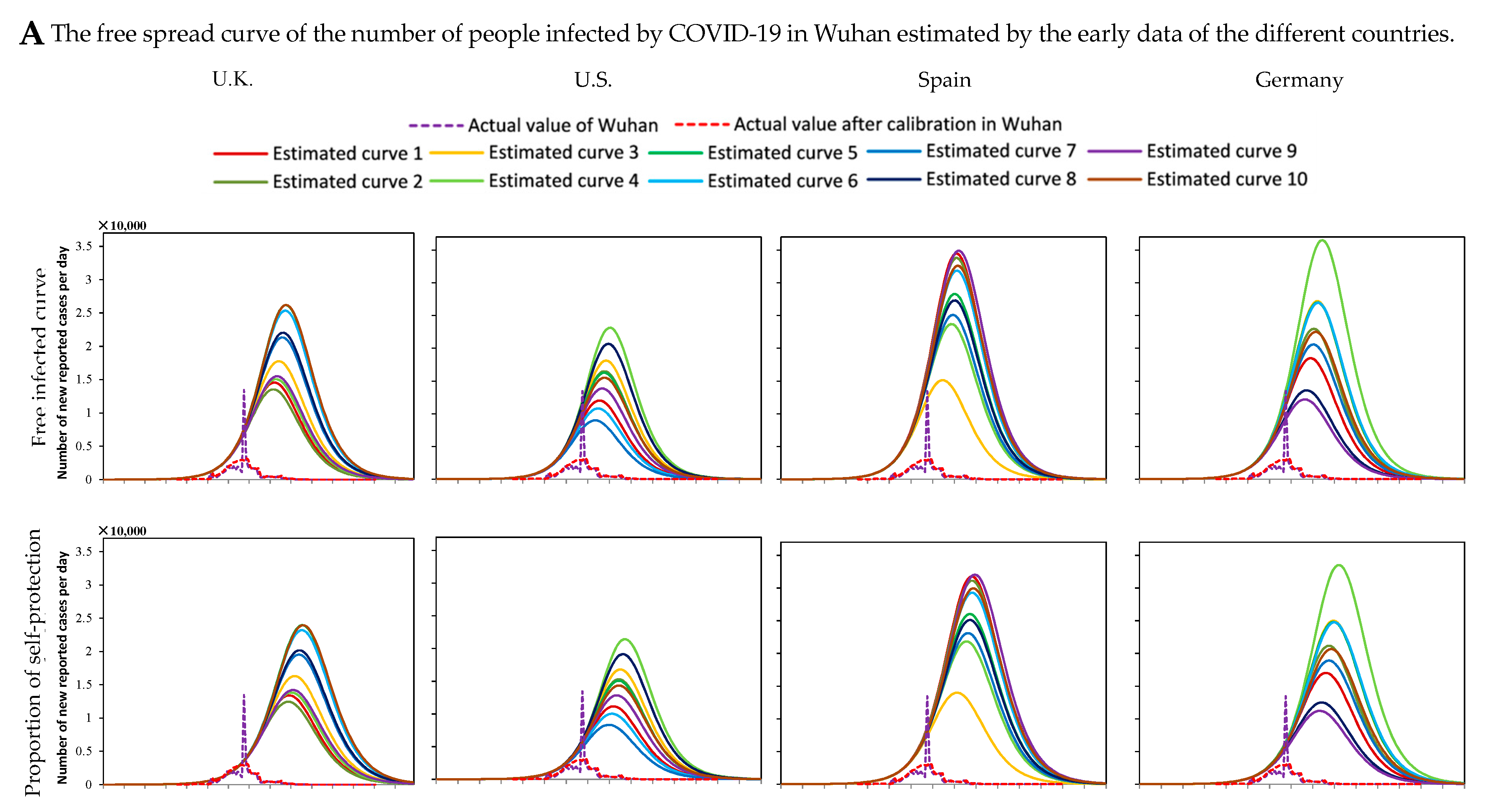
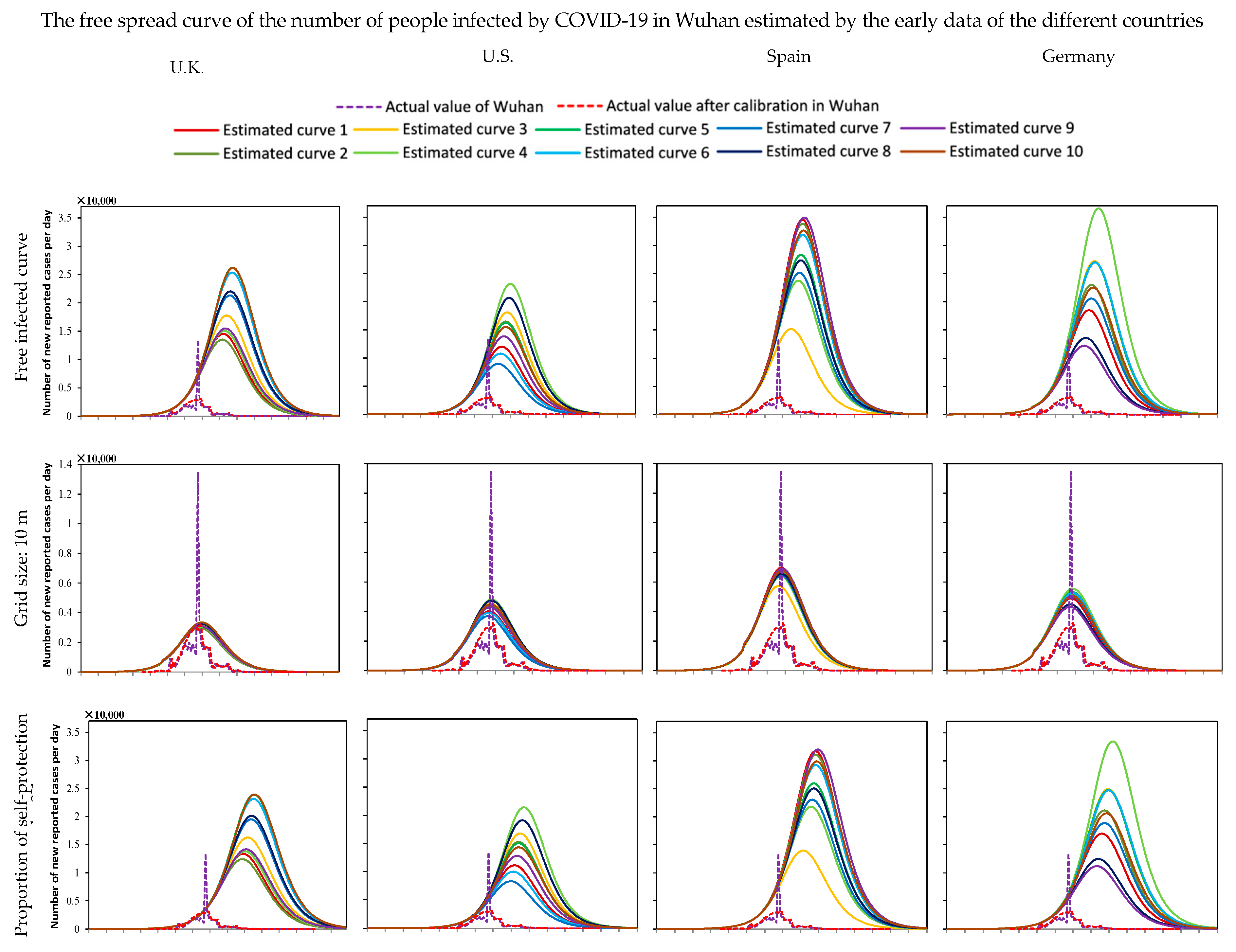
3.1. Numerical Simulation and Analysis of the Number of Infected Humans without Any Interventions
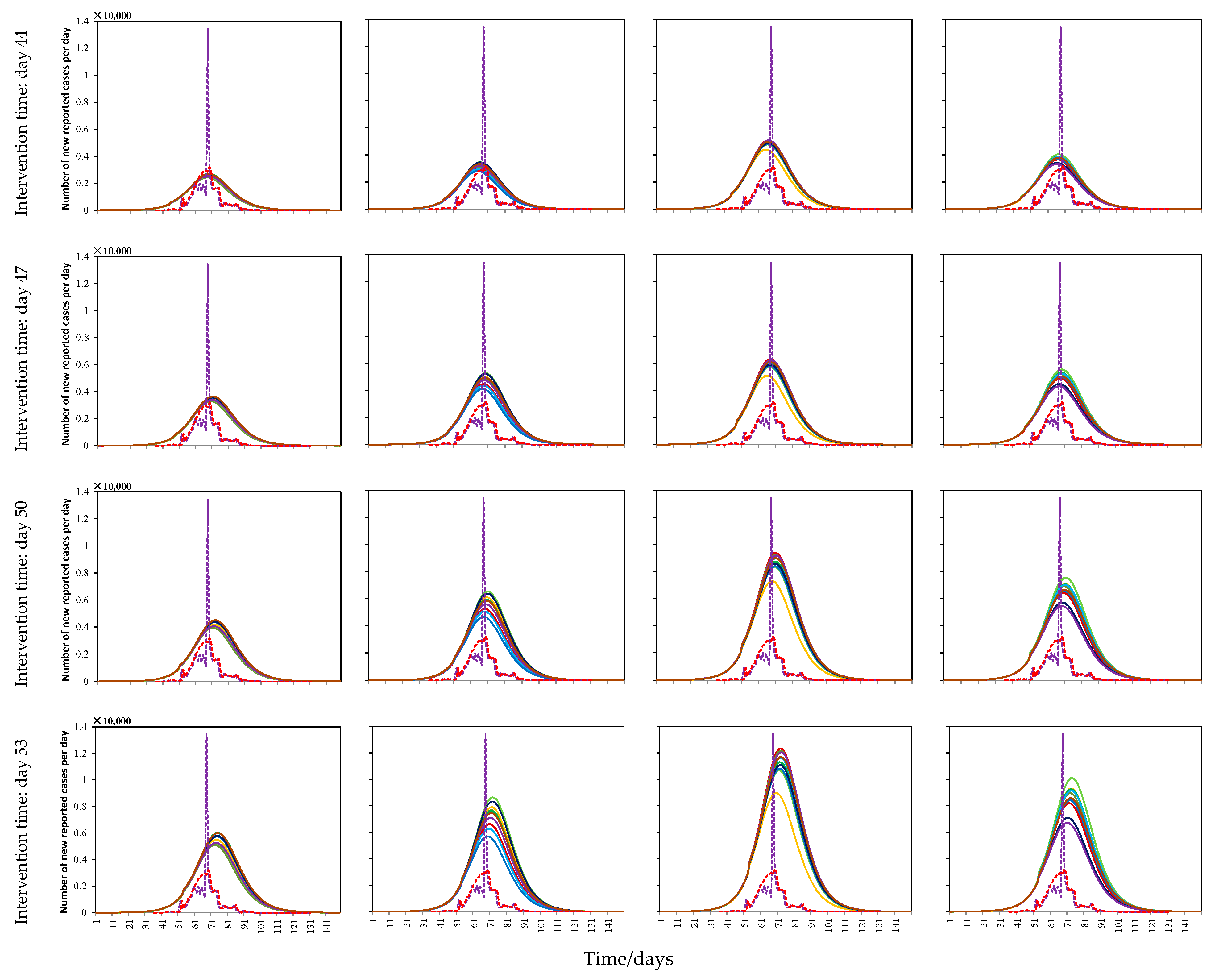
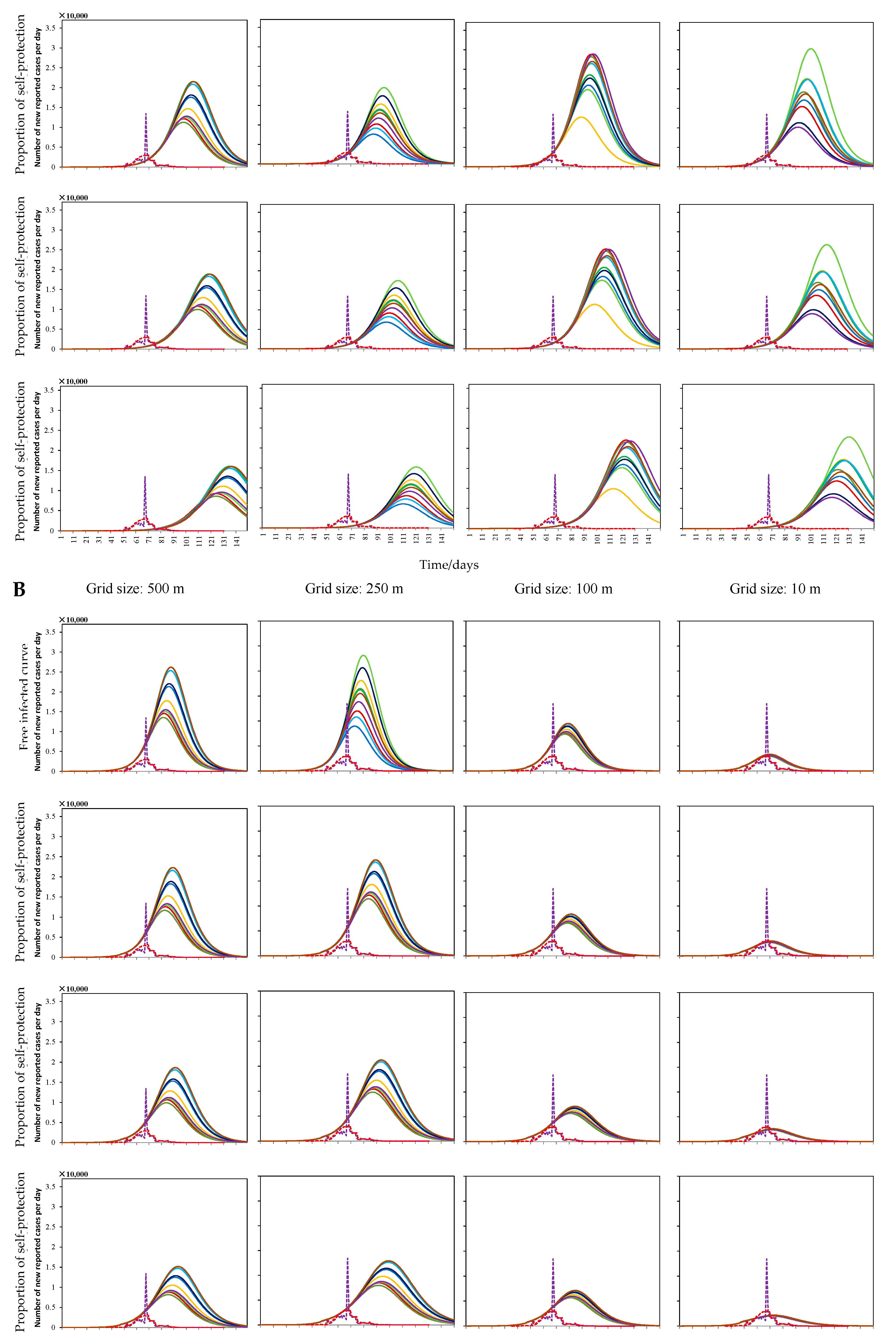
3.2. Experimental Analysis of the Influence of Different Quarantine Measures to Mitigate the Spread of COVID-19
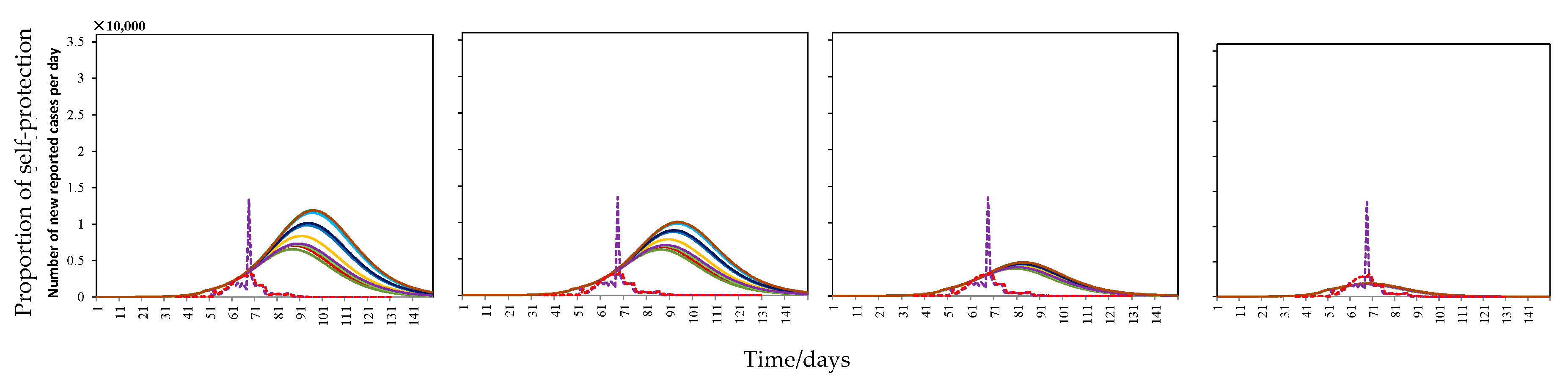
3.3. Experiment Analysis of the Influence of Different Self-Protection Measures to Mitigate the Spread of COVID-19
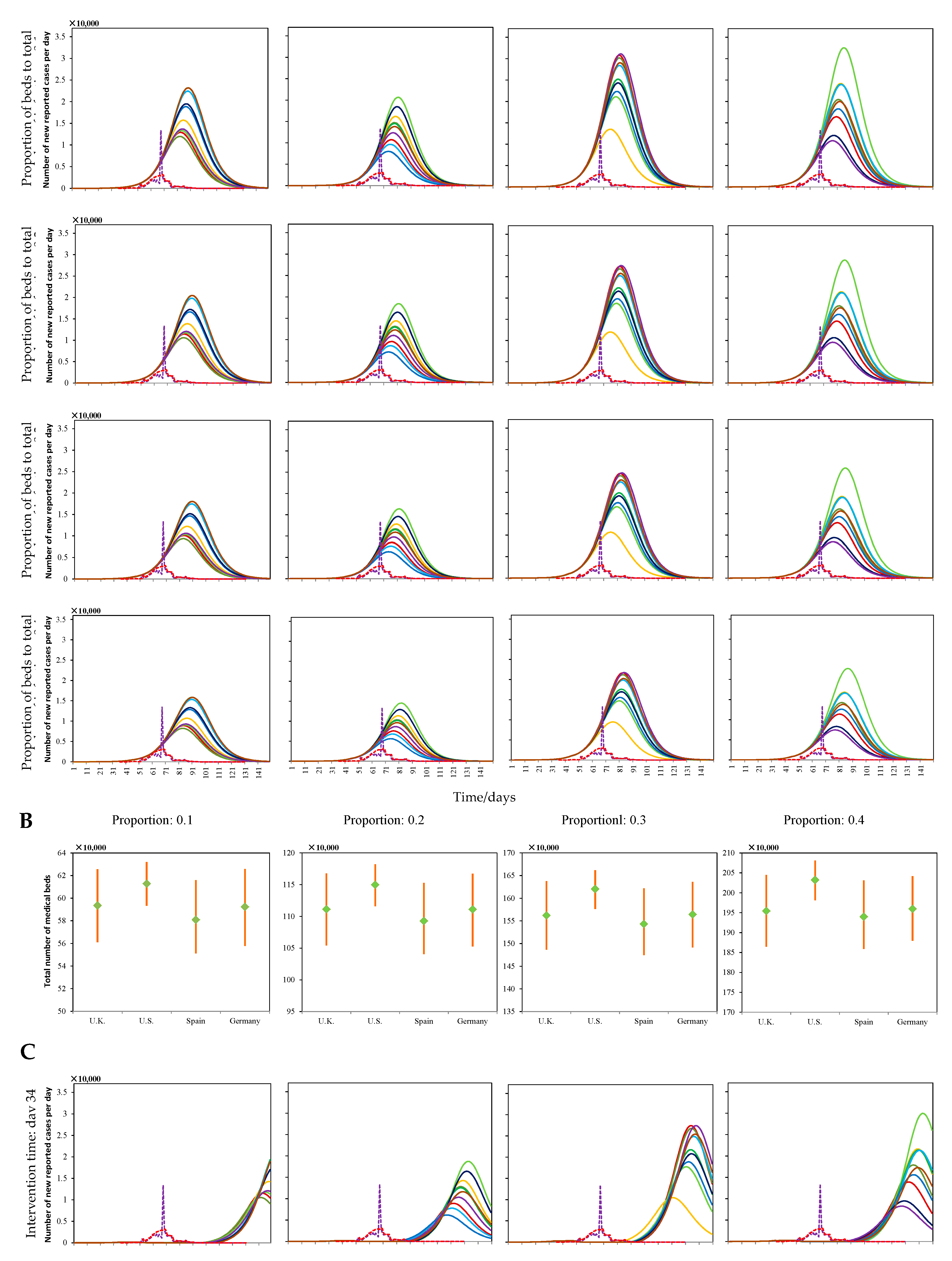
3.4. Experiment Analysis of the Influence of Different Hospital Isolation Measures to Mitigate the Spread of COVID-19
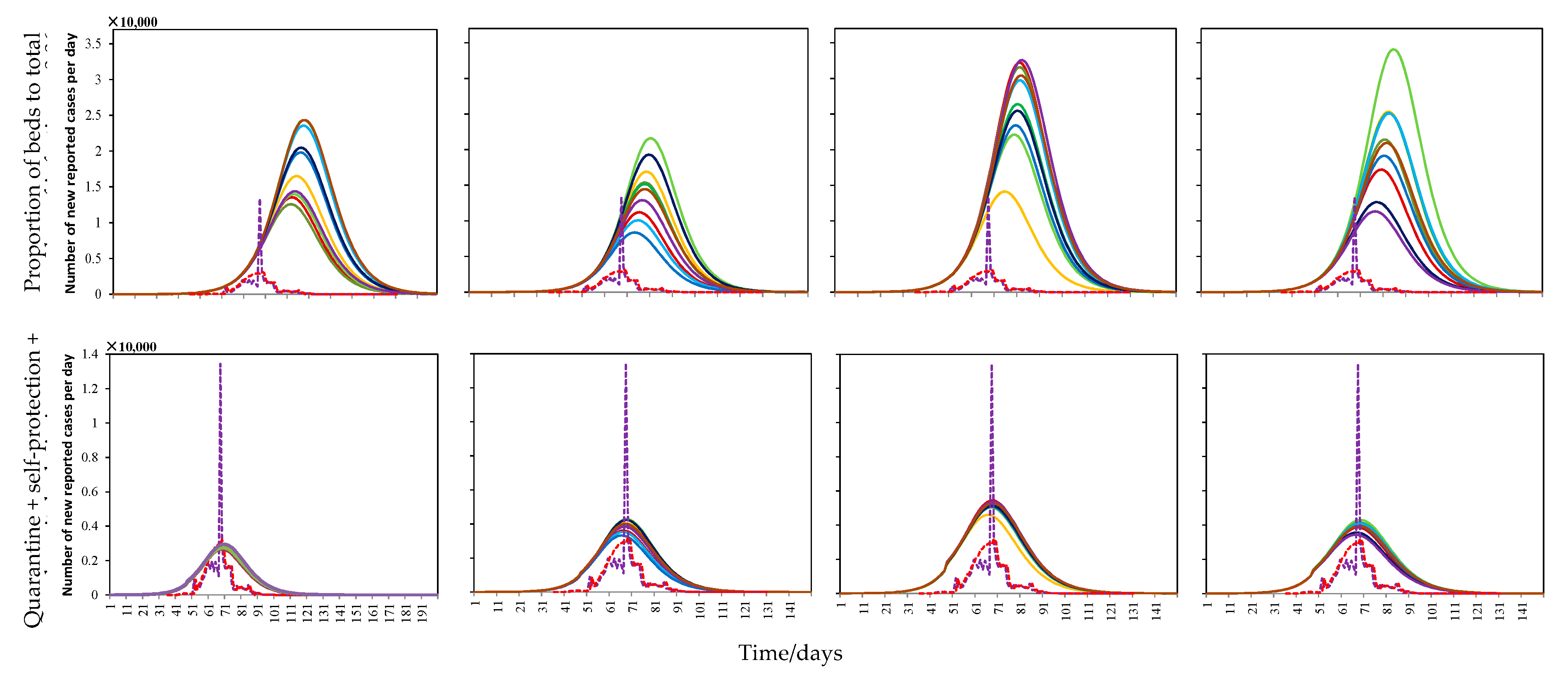
3.5. Model Validation under Actual Interventions of COVID-19 in Wuhan
- There was a certain difference between the free spread trend of COVID-19 estimated by the early data of other countries and the trend in Wuhan city itself;
- There were some errors in the case detection and data recording in Wuhan city because of the large amount of unknown information about the new virus in the early stage;
- There was still an obvious difference between the distribution of the population and the actual situation, such as there was no crowd activity around lakes, fields, and wasteland.
4. Discussion
5. Conclusions
- Quarantine measures were the most effective for prevention and control, especially for infectious diseases with a high infectivity. They were shown to be able to drastically reduce the number of infected humans, advance the arrival of the maximum number of infected humans, and shorten the duration of the COVID-19 outbreak. However, quarantine measures are only effective under a sufficient implementation intensity, and the effect of quarantine measures decreases with the delay of the intervention time. Moreover, strict quarantine measures may be ignored in the early stages of an outbreak because the spread of the epidemic is mild during this period.
- Hospital isolation measures mainly played a role in the early stage of the COVID-19 outbreak. The increase in medical beds effectively reduced the number of infected humans, but had only a small effect on the arrival time of maximum number of infected humans and the duration of the COVID-19 outbreak. Moreover, using an earlier intervention time could effectively delay the arrival of the maximum number of infected humans, but an outbreak would still occur again when the medical beds reach capacity, with a scale similar to that of original infectious state.
- Self-protection measures were able to reduce the number of infected humans and to largely delay the arrival of the peak number of infected humans, providing the government with more time to prepare. However, self-protection measures almost had no effect under stricter quarantine measures. Therefore, medical resources should be concentrated in hospitals and other places in urgent need under the conditions of strict quarantine measures.
- This study qualitatively and quantitatively analyzed the impact of quarantine, self-protection, and hospital isolation measures to slow the spread of COVID-19, which was scientific and reasonable. Meanwhile, the result possess a high interpretability for the practical significance of intervention, and the model parameters can map the model to the actual geographical area, which is helpful for the scientific formulation of specific epidemic prevention and control decisions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, N.; Zhou, M.; Dong, X.; Qu, J.; Gong, F.Y.; Han, Y.; Qiu, Y.; Wang, J.L.; Liu, Y.; Wei, Y.; et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet 2020, 395, 507–513. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Guan, X.H.; Wang, X.Y.; Wu, P.; Wang, X.Y.; Zhou, L.; Tong, Y.Q.; Ren, R.Q.; Leung, K.S.M. Early spread dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. Natl. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Tian, H.Y.; Liu, Y.H.; Li, Y.D.; Wu, C.H.; Chen, B.; Kraemer, M.U.G.; Li, B.Y.; Cai, J.; Yang, Q.Q.; Cui, Y.J. An investigation of spread control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 6491, 638–642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, J.; Yuan, S.F.; Kok, K.; To, K.K.W.; Chu, H.; Yang, J.; Xing, F.F.; Liu, J.L.; Yip, C.C.Y.; Poon, R.W.S. A family cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person spread: A study of a family cluster. Lancet 2020, 395, 514–523. [Google Scholar] [CrossRef] [Green Version]
- Currie, C.S.M.; Fowler, J.W.; Kotiadis, K.; Monks, T.; Onggo, B.S.; Roberston, D.A.; Tako, A.A. How simulation modeling can help reduce the impact of COVID-19. J. Simul. 2020, 2, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 10225, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.W.; Wang, Z.Z.; Dong, Y.Q.; Chang, R.J.; Xu, C.; Yu, X.Y.; Zhang, S.X.; Tsamlag, L.; Shang, M.L.; Wang, Y. Phase-adjusted estimation of the number of Coronavirus Diseases 2019 cases in Wuhan, China. Cell Discov. 2020, 6, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, S.; Lin, Q.Y.; Ran, J.J.; Musa, S.S.; Yang, G.P.; Wang, W.M.; Lou, Y.J.; Gao, D.Z.; Yang, L.; He, D.H. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, fro-m 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, T.; Liu, Q.; Yang, Z.; Liao, J.Y.; Yang, K.X.; Bai, W.; Lü, X.; Zhang, W. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J. Evid. Based Med. 2020, 13, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Read, J.M.; Bridgen, J.R.E.; Cummings, D.A.T.; Ho, A.; Jewell, C.P. Novel coronavirus 2019-nCoV: Early estimation of epidemiological parameters and epidemic size estimates. Phil. Trans. R. Soc. B 2020, 376, 20200265. [Google Scholar] [CrossRef]
- Jumpen, W.; Wiwatanapataphee, B.; Wu, Y.H.; Tang, I.M. A SEIQR model for pandemic influenza and its parameter identification. Int. J. Pure Appl. Math. 2020, 52, 247–265. Available online: http://ijpam.eu/contents/2009-52-2/8/index.html (accessed on 10 January 2020).
- Maier, B.F.; Brockmann, D. Effective containment explains sub-exponential growth in confirmed cases of recent COVID-19 outbreak in Mainland China. Science 2020, 368, 742–746. [Google Scholar] [CrossRef] [Green Version]
- Crokidakis, N. COVID-19 spreading in Rio de Janeiro, Brazil: Do the policies of social isolate-on really work? Chaos Solitons Fractals 2020, 136, 109930. [Google Scholar] [CrossRef]
- Viguerie, A.; Lorenzo, G.; Auricchio, F.; Baroli, D.; Hughes, T.J.R.; Patton, A.; Reali, A.; Yankeelov, T.E.; Veneziani, A. Simulating the spread of COVID-19 via a spatially-resolved susceptible–exposed–infected–recovered–deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2020, 111, 106617. [Google Scholar] [CrossRef] [PubMed]
- Cooke, K.L.; Driessche, P.V.D. Analysis of an SEIRS epidemic model with two delays. J. Math. Biol. 1996, 35, 240–260. [Google Scholar] [CrossRef]
- Okuonghae, D.; Omame, A. Analysis of a mathematical model COVID-19 crowds dynamics in Lagos, Nigeria. Chaos Solitons Fractals 2020, 139, 110032. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Klepac, P.; Liu, Y.; Perm, K.; Jit, M.; Eggo, R.M. Age-dependent effects in the spread and control of COVID-19 epidemics. Nat. Med. 2020, 26, 1205–1211. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.G.; Kucharski, A.J.; Eggo, R.M.; Gimma, A.; Edmunds, W.J. Effects of non-pharmaceutical interventions on COVID-19 cases, deaths, and demand for hospital services in the UK: A modelling study. Lancet 2020, 7, e375–e385. [Google Scholar] [CrossRef]
- Kassa, S.M.; Njagarah, J.B.H.; Terefe, Y.A. Analysis of the mitigation strategies for COVID-19: From mathematical modelling perspective. Chaos Solitons Fractals 2020, 138, 109968. [Google Scholar] [CrossRef]
- Stadnytskyi, V.; Bax, C.E.; Bax, A.; Anfinrud, P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 spread. Proc. Natl. Acad. Sci. USA 2020, 117, 11875–11877. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; Silva, R.G.D.; Mariani, V.C.; Coelho, L.D.S. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar] [CrossRef]
- Chakraborty, T.; Ghosh, I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals 2020, 135, 109850. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Song, K.; Yang, B.R.; Gao, Y.C.; Gao, X.F. Preliminary assessment of the COVID-19 outbreak using 3-staged model e-ISHR. J. Shanghai Jiaotong Univ. Sci. 2020, 25, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.Y.; Li, D.C.; Ren, J.L. Analysis of COVID-19 by Discrete Multi-stage Dynamics System with Time Delay. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 658–666. [Google Scholar] [CrossRef]
- Lymperopoulos, I.N. #stayhome to contain COVID-19: Neuro-SIR-Neurodynamical epidemic modeling of infection patterns in social networks. Expert Syst. Appl. 2021, 165, 113970. [Google Scholar] [CrossRef] [PubMed]
- Bouchnita, A.; Jebrane, A. A hybrid multi-scale model of COVID-19 spread dynamics to assess the potential of non-pharmaceutical interventions. Chaos Solitons Fractals 2020, 138, 109941. [Google Scholar] [CrossRef]
- Lin, Q.Y.; Zhao, S.; Gao, D.Z.; Lou, Y.J.; Yang, S.; Musa, S.; Wang, M.H.; Cai, Y.L.; Wang, W.M.; Yang, L. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef]
- Fang, Y.Q.; Nie, Y.T.; Penny, M. Spread dynamics of the COVID-19 outbreak and effectiveness of government interventions: A data-driven analysis. J. Med. Virol. 2020, 92, 645–659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.Y.; Xiao, Y.N.; Wu, J.H. Estimation of the spread risk of the 2019-nCoV and its impaction for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [Green Version]
- Chu, D.K.; Duda, S.; Solo, K.; Yaacoub, S.; Schunemann, H. Physical distancing, Face masks, and eye protection to prevent person-to-person spread of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 72, 1500. [Google Scholar] [CrossRef]
- Ma, Z.H.; Wang, S.F.; Li, X.H. A generalized infectious model induced by the contacting distance (CTD). Nonlinear Anal. Real World Appl. 2020, 54, 103113. [Google Scholar] [CrossRef]
- Gostic, K.; Gomez, A.C.R.; Mummah, R.O.; Kucharski, A.J.; Lloyd-Smith, J.O. Estimated effectiveness of symptom and risk screening to prevent the spread of COVID-19. eLife 2020, 9, e55570. [Google Scholar] [CrossRef]
- Wells CRSah, P.; Moghadas, S.M.; Pandey, A.; Shoukat, A.; Wang, Y.N.; Wang, Z.; Meyers, L.A.; Singer, B.H.; Galvani, A.P. Impact of international travel and border control measures on the global spread of the novel 2019 coronavirus outbreak. Proc. Natl. Acad. Sci. USA 2020, 117, 7504–7509. [Google Scholar] [CrossRef] [Green Version]
- Hellewell, J.H.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Glob. Health 2020, 4, e488–e496. [Google Scholar] [CrossRef] [Green Version]
- Wölfel, R.; Corman, V.M.; Gugemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.N.; Jones, T.C.; Vollmar, P.; Hoelscher, M. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 281, 465–469. [Google Scholar] [CrossRef] [Green Version]
- Rosa, G.L.; Bonadonna, L.; Luca, L.; Kenmoe, S.; Suffredini, E. Coronavirus in water environments: Occurrence, persistence and concentration methods—A scoping review. Water Res. 2020, 179, 115899. [Google Scholar] [CrossRef]
- Leclerc, Q.J.; Fuller, N.M.; Knight, L.E.; Knight, G.M. What settings have been linked to SARS-CoV-2spread cluster? [version 1; peer review:1 approved with reservations]. Wellcome Open Res. 2020, 5, 83. [Google Scholar] [CrossRef]
- Lu, J.Y.; Gu, J.N.; Xu, C.H.; Su, W.Z.; Lai, Z.S.; Zhou, D.Q.; Yu, C.; Xu, B.; Yang, Z.C. COVID-19 outbreak associated with Air conditioning in restaurant, Guangzhou, China, 2020. Emerg. Infect. Dis. 2020, 26, 1628–1631. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Cao, J.J. Airborne spread of SARS-CoV-2: The world should face the reality. Environ. Int. 2020, 139, 105730. [Google Scholar] [CrossRef] [PubMed]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, W. Inferring change point in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 6500, eabb9789. [Google Scholar] [CrossRef]
- Thu, T.P.B.; Ngoc, P.N.H.; Hai, N.M.; Tuan, L.A. Effect of the social distancing measures on the spread of COVID-19 in 10 highly infected countries. Sci. Total. Environ. 2020, 742, 140430. [Google Scholar] [CrossRef] [PubMed]
- Barmparis, G.D.; Tsironis, G.P. Estimating the infection horizon of COVID-19 in eight counties with a data-driven approach. Chaos Solitons Fractals 2020, 135, 109842. [Google Scholar] [CrossRef]
- Han, W.G. Data-driven and model-driven spatiotemporal data ming-respective case study in traffic flow data and epidemic data. Chin. Acad. Sci. 2006. Available online: http://ir.igsnrr.ac.cn/handle/311030/106 (accessed on 12 January 2020).
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Verges, F.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A Review. Sci. Total. Environ. 2020, 739, 140033. [Google Scholar] [CrossRef]
- Feng, M.X.; Fang, Z.X.; Lu, X.B.; Xie, Z.F.; Xiong, S.W.; Zheng, M.; Huang, S.Q. Traffic Analysis Zone-Based Epidemic Estimation Approach of COVID-19 Based on Mobile Phone Data: An Example of Wuhan. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 651–657, 681. [Google Scholar] [CrossRef]
- Sugg, M.M.; Spaulding, R.J.; Lane, S.J.; Runkle, J.D.; Harden, S.R.; Hege, A.; Lyer, L.S. Mapping community-level determinants of COVID-19 spread in nursing homes: A multi-scale approach. Sci. Total. Environ. 2020, 752, 141946. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.Y.; Zhao, L.; Zhang, A.; Song, L.Y.; Liao, Y.L.; Lu, W.L.; Cui, C. Early forecasting of the potential risk zones of COVID-19 in China’s megacities. Sci. Total. Environ. 2020, 729, 138995. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.X. Thinking and challenges of crow dynamics observation from the perspectives of public health and public security. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 1847–1856. [Google Scholar] [CrossRef]
- Zwęgliński, T.; Radkowski, R. Fire and Rescue Units During COVID-19 Epidemic. Operational Functioning and Tasks in the First Months of SARS-CoV-2 activity. Zesz. Nauk. SGSP 2020, 76, 93–114. [Google Scholar] [CrossRef]
- Cao, Z.D. Mathematical modeling and spatial analysis of spatiotemporal data-case study based on SARS epidemic in Guangzhou. Chin. Acad. Sci. 2008. Available online: http://ir.igsnrr.ac.cn/handle/311030/1774 (accessed on 12 January 2020).
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 422–534. [Google Scholar] [CrossRef]
- Cui, H.J.; Hu, T. Nonlinear regression in COVID-19 forecasting (in Chinese). Sci. Sin. Math. 2020, 50, 1–12. Available online: https://engine.scichina.com/doi/10.1360/SSM-2020-0055 (accessed on 12 January 2020).
- Xia, J.Z.; Zhou, Y.; Li, Z.; Li, F.; Yue, Y.; Cheng, T.; Li, Q.Q. COVID-19 risk assessment driven by urban spatiotemporal big data: Case study of Guangdong-Hong Kong-Macao Greater Bay Area. Acta Geod. Et Cartogr. Sin. 2020, 49, 671–680. Available online: http://xb.sinomaps.com/CN/10.11947/j.AGCS.2020.20200080 (accessed on 12 January 2020).
- Cauchemez, S.; Fraser, C.; Wan, M.D.; Donnelly, C.A.; Riley, S.; Rambaut, A.; Enouf, V.; Werf, S.V.D.; Ferguson, N.M. Middle east respiratory syndrome coronavirus: Quantification of the extent of the epidemic, surveillance biases, and transmissibility. Lancet Infect. Dis. 2020, 1, 50–56. [Google Scholar] [CrossRef] [Green Version]
- Alberti, T.; Faranda, D. On the uncertainty of real-time predictions of epidemic growths: A COVID-19 case study for China and Italy. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105372. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Yang, W.Q.; Bi, Y.F. Research on the Scale of Daily Life Unit Based on Residents’ Travel Characteristics. China Acad. J. Electron. Publ. House 2016, 1004–1015. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CPFD&filename=CSJT201604001098 (accessed on 12 January 2020).
- Wang, C.; Zhu, R.X.; Wu, Y.T. Shanghai 168 Hours: How to Control the Epidemic in a Super City within A Week [EB/OL]. 2021. Available online: https://xw.qq.com/cmsid/20210202A019Z7/20210202A019Z700?ADTAG=hwb&pgv_ref=hwb&appid=hwbrowser&ctype=news (accessed on 11 July 2021).
- Wei, Z. More than 20000 People in Shijiazhuang Have Been Transferred Urgently! This Epidemic Is Not as Simple as You Think [EB/OL]. 2021. Available online: https://new.qq.com/omn/20210113/20210113A02KCY00.html (accessed on 11 July 2021).




| Date | Actual Value | Calibration Data |
|---|---|---|
| 30 January 2020 | 378 | 759 |
| 31 January 2020 | 576 | 1101 |
| 1 February 2020 | 894 | 1182 |
| 2 February 2020 | 1033 | 1574 |
| 3 February 2020 | 1242 | 1683 |
| 4 February 2020 | 1967 | 2082 |
| 5 February 2020 | 1766 | 2195 |
| 6 February 2020 | 1501 | 2542 |
| 7 February 2020 | 1985 | 2618 |
| 8 February 2020 | 1378 | 2856 |
| 9 February 2020 | 1921 | 2857 |
| 10 February 2020 | 1552 | 2949 |
| 11 February 2020 | 1104 | 2852 |
| 12 February 2020 | 13436 | 3212 |
| Parameter | Interpretation |
|---|---|
| Number of susceptible humans per day in grid cell i. | |
| Number of exposed humans per day in grid cell i (infected but not infectious). | |
| Number of asymptomatically infectious humans per day in grid cell i (undetected). | |
| Number of symptomatically infectious humans per day in grid cell i (undetected). | |
| Number of infectious humans detected per day in grid cell i (including asymptomatic and symptomatic, tested but not completely admitted to hospital). | |
| Number of recovered humans per day in grid cell i. | |
| Effective spread rate. | |
| Progression rate from exposed state to the infectious state. | |
| Fraction of new infectious humans that are asymptomatic. | |
| Modification parameter that accounts for the reduced infectiousness of humans in the A class when compared to humans in the I class. | |
| Recovery rate for individuals in the A, I, and C classes, respectively. | |
| Detection rate (via contact tracing and testing) for the I class. | |
| Detection rate (via contact tracing and testing) for the A class. | |
| Disease-induced death rates for individuals in the I and C classes, respectively. |
| Parameter | Baseline Value 1 | Range 1 |
|---|---|---|
| Fitted | Estimated | |
| 0.5/day | [0.1]/day | |
| 0.5/day | [0.1]/day | |
| 1/5.2/day | [1/14,1/3]/day | |
| Fitted/day | Estimated | |
| Fitted/day | Estimated | |
| 1/15/day | [1/30,1/3]/day | |
| 0.13978/day | [1/30,1/3]/day | |
| 0.015/day | [0.001,0.1] |
| Source of Data | Estimated Curve | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| UK | 1 | 994.9963 | 4.9352 × 10−5 | 0.0002 | 0.6820 | 8.0800 × 10−5 | 0.011569 | 0.9683 | 3.2689 |
| 2 | 880.6889 | 1.3909 | 101.8516 | 0.6776 | 3.2035 × 10−5 | 0.010808 | 0.9680 | 3.2576 | |
| 3 | 522.1685 | 1.0038 | 188.0705 | 0.67034 | 4.3437 × 10−6 | 0.014855 | 0.9668 | 3.1747 | |
| 4 | 782.8959 | 10.9702 | 142.8662 | 0.6676 | 9.0100 × 10−7 | 0.01243 | 0.9667 | 3.1905 | |
| 5 | 492.838 | 17.7107 | 68.8706 | 0.6740 | 5.3988 × 10−6 | 0.0231 | 0.9661 | 3.0998 | |
| 6 | 428.4349 | 74.3875 | 77.7457 | 0.6727 | 3.0811 × 10−6 | 0.0223 | 0.9661 | 3.1026 | |
| 7 | 369.0471 | 18.1297 | 199.3840 | 0.6679 | 1.9437 × 10−6 | 0.0184 | 0.9660 | 3.1230 | |
| 8 | 438.4535 | 20.6176 | 156.1451 | 0.6680 | 4.5815 × 10−5 | 0.0190 | 0.9660 | 3.1159 | |
| 9 | 745.7698 | 97.9919 | 137.6607 | 0.6600 | 1.5772 × 10−6 | 0.0130 | 0.9657 | 3.1474 | |
| 10 | 279.9186 | 42.9728 | 161.9717 | 0.6712 | 2.5609 × 10−6 | 0.0233 | 0.9657 | 3.5839 | |
| US | 1 | 556.3781 | 47.2879 | 222.3518 | 0.7393 | 1.4375 × 10−5 | 0.0086 | 0.9528 | 3.5425 |
| 2 | 516.6224 | 3.8532 | 140.3937 | 0.7405 | 9.4490 × 10−6 | 0.0121 | 0.9526 | 3.5190 | |
| 3 | 635.1028 | 43.2186 | 44.0625 | 0.7394 | 5.8214 × 10−6 | 0.0135 | 0.9520 | 3.4706 | |
| 4 | 385.8888 | 66.1527 | 75.3132 | 0.7405 | 4.2351 × 10−6 | 0.0177 | 0.9511 | 3.5168 | |
| 5 | 532.3682 | 24.9516 | 152.9867 | 0.7350 | 2.9878 × 10−6 | 0.0121 | 0.9510 | 3.5569 | |
| 6 | 534.7422 | 2.6723 | 352.6032 | 0.7313 | 2.5243 × 10−5 | 0.0078 | 0.9507 | 3.5575 | |
| 7 | 680.0307 | 103.1939 | 375.1976 | 0.7276 | 1.6587 × 10−6 | 0.0064 | 0.9495 | 3.4564 | |
| 8 | 765.0599 | 0.1725 | 0.2499 | 0.7324 | 5.0923 × 10−6 | 0.0158 | 0.9494 | 3.4904 | |
| 9 | 553.8119 | 31.8721 | 246.6154 | 0.7246 | 6.0201 × 10−6 | 0.0103 | 0.9486 | 3.4200 | |
| 10 | 982.4765 | 25.9922 | 70.1316 | 0.7140 | 3.5647 × 10−5 | 0.0117 | 0.9452 | 3.5839 | |
| Spain | 1 | 545.0229 | 15.8802 | 80.0674 | 0.7335 | 6.4220 × 10−6 | 0.0288 | 0.9110 | 3.3093 |
| 2 | 583.2245 | 12.2590 | 78.7125 | 0.7293 | 8.9861 × 10−7 | 0.0283 | 0.9104 | 3.2957 | |
| 3 | 845.3579 | 139.8717 | 310.5179 | 0.7159 | 3.4132 × 10−5 | 0.0115 | 0.9102 | 3.4336 | |
| 4 | 828.2234 | 36.0338 | 148.3467 | 0.7096 | 1.7847 × 10−6 | 0.0192 | 0.9082 | 3.3084 | |
| 5 | 999.8722 | 0.0271 | 9.5564 | 0.7119 | 4.2396 × 10−5 | 0.0235 | 0.9077 | 3.2692 | |
| 6 | 917.1408 | 0.0022 | 0.0673 | 0.7140 | 8.2659 × 10−5 | 0.0270 | 0.9073 | 3.2400 | |
| 7 | 999.9903 | 27.4579 | 63.5574 | 0.7063 | 1.2845 × 10−6 | 0.0207 | 0.9071 | 3.2763 | |
| 8 | 997.6565 | 0.0477 | 51.1226 | 0.7052 | 9.1473 × 10−5 | 0.0227 | 0.9063 | 3.2467 | |
| 9 | 506.7653 | 61.5072 | 135.7323 | 0.7123 | 4.7674 × 10−5 | 0.0304 | 0.9058 | 3.1964 | |
| 10 | 944.9594 | 0.0097 | 0.0464 | 0.7088 | 4.7779 × 10−5 | 0.0281 | 0.9058 | 3.2053 | |
| Germany | 1 | 508.3597 | 111.0021 | 250.1656 | 0.7009 | 3.8996 × 10−8 | 0.0147 | 0.9305 | 3.3217 |
| 2 | 973.7915 | 0.0002 | 0.0066 | 0.7066 | 7.1014 × 10−5 | 0.0185 | 0.9302 | 3.3017 | |
| 3 | 376.8398 | 4.9588 | 204.2724 | 0.7066 | 2.6810 × 10−5 | 0.0226 | 0.9298 | 3.2550 | |
| 4 | 229.4928 | 28.6409 | 164.7135 | 0.7167 | 7.1487 × 10−6 | 0.0320 | 0.9293 | 3.2004 | |
| 5 | 545.7995 | 21.5850 | 138.4819 | 0.7019 | 3.5717 × 10−6 | 0.0227 | 0.9289 | 3.2329 | |
| 6 | 407.2556 | 1.7347 | 225.0588 | 0.6978 | 2.3474 × 10−5 | 0.0228 | 0.9281 | 3.2129 | |
| 7 | 718.9136 | 109.1937 | 159.6677 | 0.6905 | 2.5158 × 10−5 | 0.0169 | 0.9280 | 3.2464 | |
| 8 | 963.8368 | 0.0508 | 399.6251 | 0.6823 | 3.5494 × 10−5 | 0.0107 | 0.9277 | 3.2809 | |
| 9 | 990.6250 | 0.0013 | 493.6234 | 0.6797 | 2.3706 × 10−5 | 0.0096 | 0.9273 | 3.2826 | |
| 10 | 999.6469 | 19.6512 | 58.0628 | 0.6863 | 7.0825 × 10−5 | 0.0188 | 0.9268 | 3.2038 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Dai, H.; Zhu, J.; Tian, Y.; Peng, F. Analysis and Evaluation of Non-Pharmaceutical Interventions on Prevention and Control of COVID-19: A Case Study of Wuhan City. ISPRS Int. J. Geo-Inf. 2021, 10, 480. https://doi.org/10.3390/ijgi10070480
Cao W, Dai H, Zhu J, Tian Y, Peng F. Analysis and Evaluation of Non-Pharmaceutical Interventions on Prevention and Control of COVID-19: A Case Study of Wuhan City. ISPRS International Journal of Geo-Information. 2021; 10(7):480. https://doi.org/10.3390/ijgi10070480
Chicago/Turabian StyleCao, Wen, Haoran Dai, Jingwen Zhu, Yuzhen Tian, and Feilin Peng. 2021. "Analysis and Evaluation of Non-Pharmaceutical Interventions on Prevention and Control of COVID-19: A Case Study of Wuhan City" ISPRS International Journal of Geo-Information 10, no. 7: 480. https://doi.org/10.3390/ijgi10070480
APA StyleCao, W., Dai, H., Zhu, J., Tian, Y., & Peng, F. (2021). Analysis and Evaluation of Non-Pharmaceutical Interventions on Prevention and Control of COVID-19: A Case Study of Wuhan City. ISPRS International Journal of Geo-Information, 10(7), 480. https://doi.org/10.3390/ijgi10070480






