Modeling the Spatial and Temporal Spread of COVID-19 in Poland Based on a Spatial Interaction Model
Abstract
:1. Introduction
2. Methods
2.1. SIR and SIR-F Models
2.2. Gravity Model
2.3. The Adopted Methodology
3. Data, Experiments and Results
3.1. Data
3.2. SIR-F Model Calibration
3.3. Model Calibration–Spatial Interaction
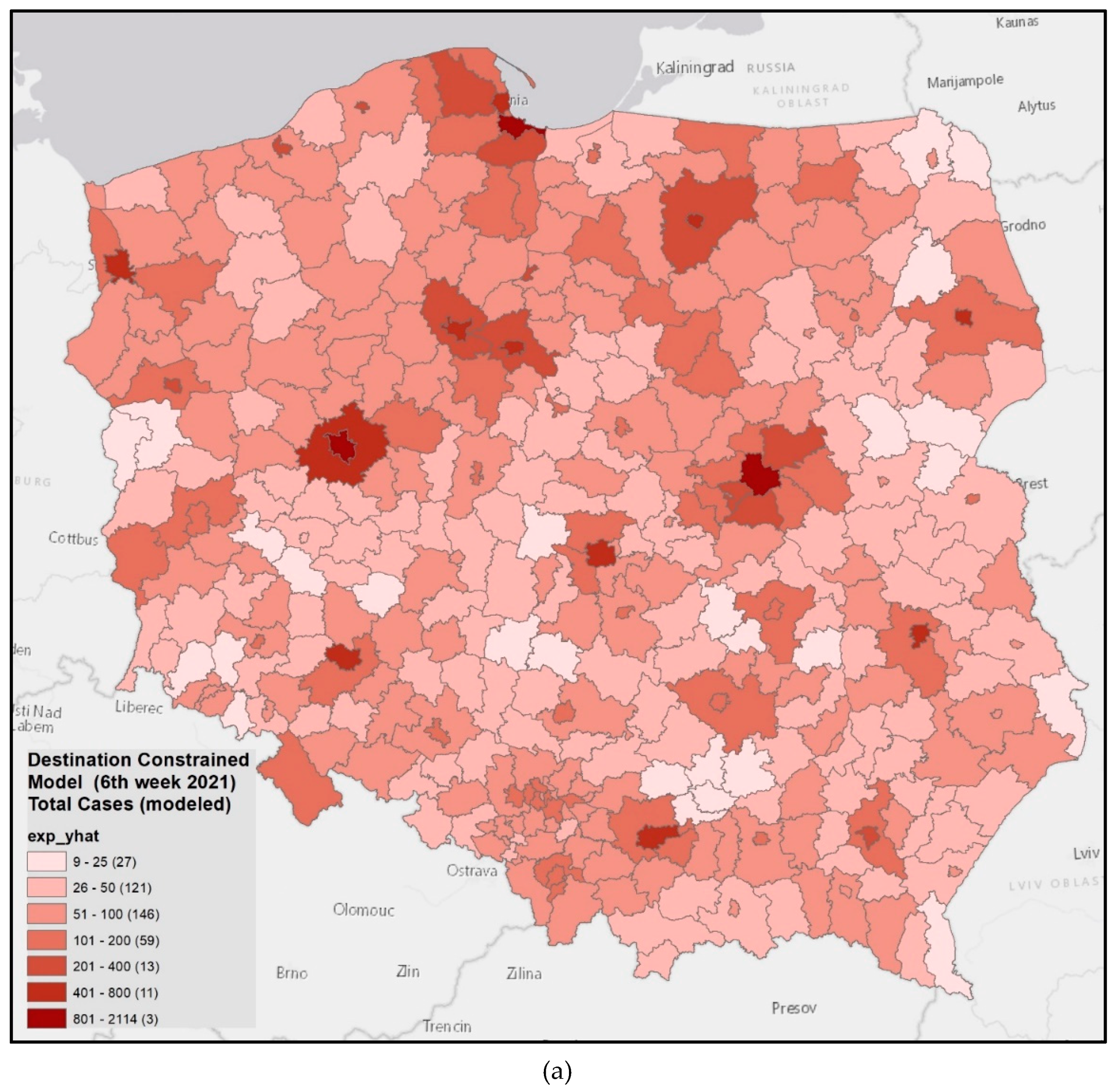
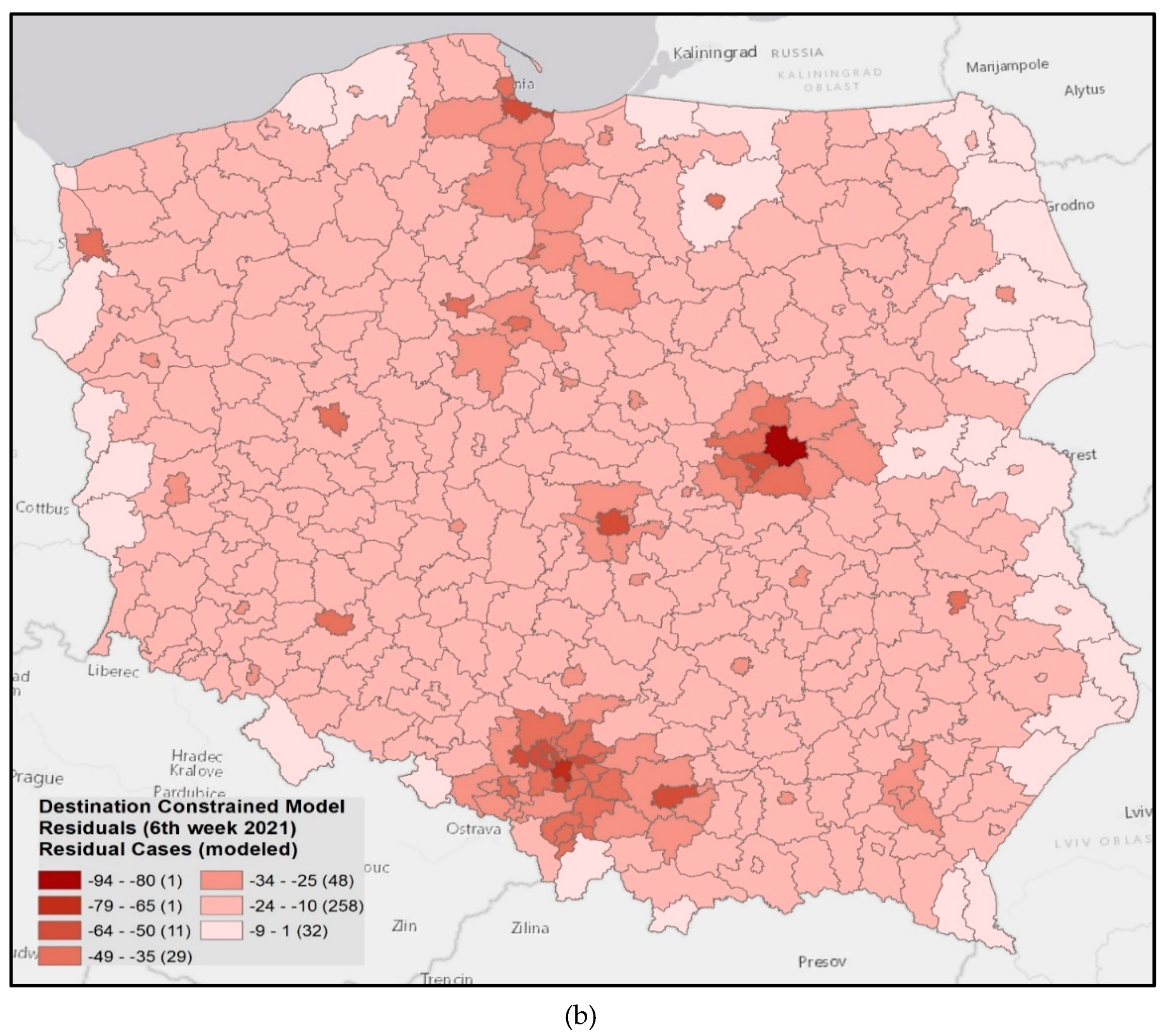
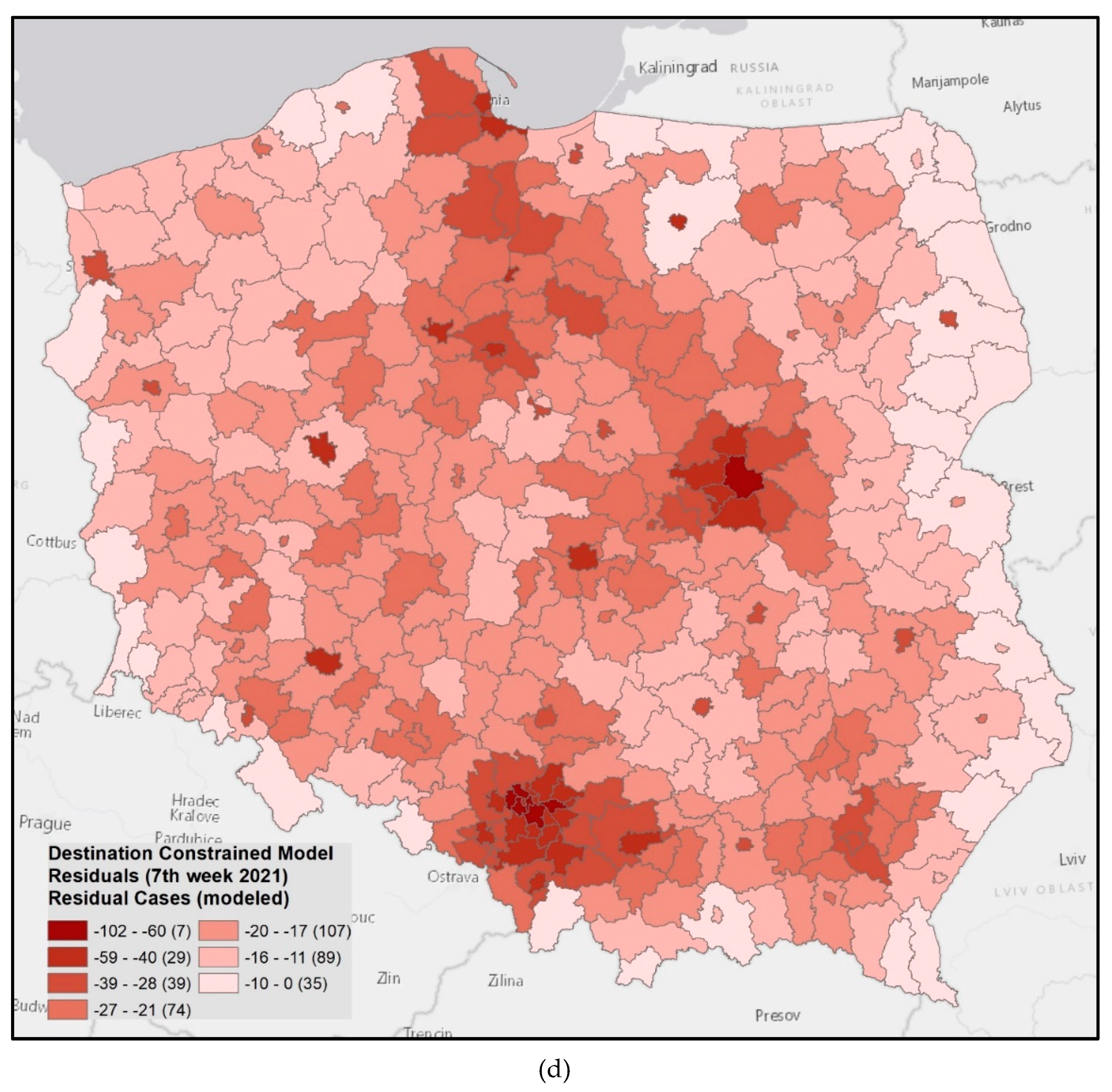
3.4. Model Verification
3.5. Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Werner, P. Tracing and modeling of the COVID-19 pandemic infections in Poland using spatial interactions models. In Computational Science and Its Applications—ICCSA 2021; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Rader, B.; Scarpino, S.V.; Nande, A.; Hill, A.L.; Adlam, B.; Reiner, R.C.; Pigott, D.M.; Gutierrez, B.; Zarebski, A.E.; Shrestha, M.; et al. Crowding and the shape of COVID-19 epidemics. Nat. Med. 2020, 26, 1829–1834. [Google Scholar] [CrossRef] [PubMed]
- Petersen, E.; Koopmans, M.; Go, U.; Hamer, D.H.; Petrosillo, N.; Castelli, F.; Storgaard, M.; Al Khalili, S.; Simonsen, L. Comparing SARS-CoV-2 with SARS-CoV and influenza pandemics. Lancet Infect. Dis. 2020, 20, e238–e244. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Chan, J.F.-W.; Yuan, S.; Kok, K.-H.; To, K.K.W.; Chu, H.; Yang, J.; Xing, F.; BNurs, J.L.; Yip, C.C.-Y.; Poon, R.W.-S.; et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: A study of a family cluster. Lancet 2020, 395, 514–523. [Google Scholar] [CrossRef] [Green Version]
- Grassly, N.C.; Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 2008, 6, 477–487. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.G. Entropy in Urban and Regional Modelling; Wilson, A.G., Ed.; Pion: London, UK, 1970. [Google Scholar]
- Wilson, A. Epidemic models with geography. arXiv 2020, arXiv:2005.07673v1. Available online: https://arxiv.org/abs/2005.07673v1 (accessed on 4 December 2021).
- Marshall, J.M.; Wu, S.L.; Sanchez, S.M.; Kiware, S.S.; Ndhlovu, M.; Ouédraogo, A.L.; Touré, M.B.; Sturrock, H.J.; Ghani, A.C.; Ferguson, N.M. Mathematical models of human mobility of relevance to malaria transmission in Africa. Sci. Rep. 2018, 8, 7713. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Bjornstad, O.N.; Grenfell, B.T. Measles metapopulation dynamics: A gravity model for epidemiological coupling and dynamics. Am. Nat. 2004, 164, 267–281. [Google Scholar] [CrossRef]
- Yan, X.-Y.; Zhou, T. Destination choice game: A spatial interaction theory on human mobility. Sci. Rep. 2019, 9, 9466. [Google Scholar] [CrossRef]
- Stewart, J.Q. Empirical mathematical rules concerning the distribution and equilibrium of population. Geogr. Rev. 1947, 37, 461–485. [Google Scholar] [CrossRef]
- Gregory, D.; Johnston, R.; Pratt, G.; Watts, M.; Whatmore, S. (Eds.) The Dictionary of Human Geography, 5th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2009. [Google Scholar]
- Werner, P. Simulating of accessibility of ICT infrastructure in Poland using geographical potential models. In Proceedings of the 16th International Conference on System Science, Banff, AB, Canada, 8–12 May 2007; pp. 261–269. [Google Scholar]
- Tobler, W.R. Cellular Geography. In Philosophy in Geography; Gale, S., Olsson, G., Eds.; Springer: Dordrecht, The Netherlands, 1979; pp. 379–386. [Google Scholar]
- Riley, S.; Eames, K.; Isham, V.; Mollison, D.; Trapman, P. Five challenges for spatial epidemic models. Epidemics 2015, 10, 68–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossa, F.D.; Salzano, D.; Dimeglio, A.; Bernardo, M.D.; De Lellis, M.; Coraggio, M.; Calabrese, C.; Guarino, A.; Cardona-Rivera, R.; De Lellis, P.; et al. A network model of Italy shows that intermittent regional strategies can alleviate the COVID-19 epidemic. Nat. Commun. 2020, 11, 5106. [Google Scholar] [CrossRef]
- Parino, F.; Zino, L.; Porfiri, M.; Rizzo, A. Modeling and predicting the effect of social distancing and travel restrictions on COVID-19 spreading. JRS Interface 2021, 18, 175. [Google Scholar]
- Gosgens, M.; Hendriks, T.; Boon, M.; Steenbakkers, W.; Heesterbeek, H.; Van der Hofstad, R.; Litvak, N. Trade-offs between mobility restrictions and transmission of SARS-CoV-2. JRS Interface 2021, 18, 175. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Dangermond, J.; De Vito, C.; Pesaresi, C. Using GIS in the Time of the COVID-19 Crisis, casting a glance at the future. A joint discussion. J-READING J. Res. Didat. Geogr. 2020, 1, 195–205. [Google Scholar]
- Boulos, M.N.; Geraghty, E.M. Geographical tracking and mapping of coronavirus disease COVID-19/severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) epidemic and associated events around the world: How 21st century GIS technologies are supporting the global fight against outbreaks and epidemics. Int. J. Health Geogr. 2020, 19, 8. [Google Scholar]
- Esaresi, C.; Pavia, D.; De Vito, C.; Barbara, A.; Cerabona, V.; Di Rosa, E. Dynamic space-time diffusion simulator in a GIS environment to tackle the Covid-19 emergency. Testing a geotechnological application in rome. Geogr. Tech. 2021, 16, 82–99. [Google Scholar]
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Verges, F.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A review. Sci. Total Environ. 2020, 739, 140033. [Google Scholar] [CrossRef] [PubMed]
- Hohl, A.; Delmelle, E.M.; Desjardins, M.R.; Lan, Y. Daily surveillance of COVID-19 using the prospective space-time scan statistic in the United States. Spat. Spatio-Temporal Epidemiol. 2020, 34, 100354. [Google Scholar] [CrossRef] [PubMed]
- Ahasan, R.; Hossain, M.M. Leveraging GIS and spatial analysis for informed decision-making in COVID-19 pandemic. Health Policy Technol. 2021, 10, 7. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; McGoogan, J.M. Characteristics of and Important Lessons from the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72 314 Cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Rao, H.; Wu, Y.; Huang, Y.; Dai, H. Comparison of spatiotemporal characteristics of the COVID-19 and SARS outbreaks in mainland China. BMC Infect Dis. 2020, 20, 805. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2012; Volume 40, ISBN 978-1-4614-1685-2. [Google Scholar]
- Duan, W.; Fan, Z.; Zhang, P.; Guo, G.; Qiu, X. Mathematical and Computational Approaches to Epidemic Modeling: A Comprehensive Review. Front. Comput. Sci. 2015, 9, 806–826. [Google Scholar] [CrossRef] [PubMed]
- Casetti, E. Expansion Method, Dependency, and Multimodeling. In Handbook of Applied Spatial Analysis; Fischer, M.M., Getis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 487–505. ISBN 978-3-642-03646-0. [Google Scholar]
- Kermack, W.O.; McKendric, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Abadie, A.; Bertolotti, P.; Deaner, B.; Shah, D. Epidemic Modeling and Estimation. 2020. Available online: https://idss.mit.edu/wp-content/uploads/2020/04/04.28.2020Epidemic_Modeling_A_Memo.pdf (accessed on 4 December 2021).
- Oshan, T.M. A primer for working with the Spatial Interaction modeling (SpInt) module in the python spatial analysis library (PySAL). Region 2016, 3, R11–R23. [Google Scholar] [CrossRef]
- McFadden, D. Conditional logit analysis of qualitative choice behaviour. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: New York, NY, USA, 1974; pp. 105–142. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Rey, S.J.; Anselin, L. PySAL: A Python library of spatial analytical methods. Rev. Reg. Stud. 2007, 37, 5–27. [Google Scholar] [CrossRef]
- Raport Zakażeń Koronawirusem (SARS-CoV-2). 2021. Available online: https://www.gov.pl/web/koronawirus/wykaz-zarazen-koronawirusem-sars-cov-2 (accessed on 6 December 2021).
- Morrill, R.; Gaile, G.; Thrall, G. Spatial Diffusion. In Web Book of Regional Science; West Virginia University: Morgantown, WV, USA, 2020. [Google Scholar]
- Wilson, A.G. Complex Spatial Systems: The Modelling Foundations of Urban and Regional Analysis; Pearson Education: London, UK, 2000. [Google Scholar]
- O’Kelly, M.E. Spatial Interaction Models. In International Encyclopedia of Human Geography; Kitchin, R., Thrift, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 365–368. [Google Scholar]
- Coronavirus: Information and recommendations. Temporary Limitations. 2021. Available online: https://www.gov.pl/web/coronavirus/temporary-limitations (accessed on 6 December 2021).
- Government Data Shared on Twitter. Available online: https://twitter.com/MZ_GOV_PL (accessed on 8 December 2021).
- Główny Urząd Geodezji i Kartografii. 2021. Available online: http://www.gugik.gov.pl/pzgik/inne-dane-udostepniane-bezplatnie (accessed on 4 December 2021).
- Bank Danych Lokalnych GUS. 2021. Available online: https://bdl.stat.gov.pl/BDL/start (accessed on 4 December 2021).
- CovsirPhy Development Team. CovsirPhy, Python Package for COVID-19 Analysis with SIR-Derived ODE Models. 2020. Available online: https://github.com/lisphilar/covid19-sir (accessed on 4 December 2021).
- Guidotti, E.; Ardia, D. COVID-19 Data Hub. J. Open Source Softw. 2020, 5, 2376. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; O’Kelly, M.E. Spatial Interaction Models: Formulations and Applications; Kluwer Academic Publishers: Alphen aan Den Rijn, The Netherlands, 1989. [Google Scholar]
- ICM UW Model Description—COVID. Available online: https://covid-19.icm.edu.pl/ (accessed on 4 December 2021).
- Zhu, D.; Ye, X.; Manson, S. Revealing the spatial shifting pattern of COVID-19 pandemic in the United States. Sci. Rep. 2021, 11, 8396. [Google Scholar] [CrossRef] [PubMed]
- Mhango, M.; Dzobo, M.; Chitungo, I.; Dzinamarira, T. COVID-19 risk factors among health workers: A rapid review. Saf. Health Work 2020, 11, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Tahmasebi, P.; Shokri-Kuehni, S.M.; Sahimi, M.; Shokri, N. How do environmental, economic and health factors influence regional vulnerability to COVID-19? MedRxiv 2020. Available online: https://www.medrxiv.org/content/10.1101/2020.04.09.20059659v1 (accessed on 23 November 2021).
- Werner, P.A.; Skrynyk, O.; Porczek, M.; Szczepankowska-Bednarek, U.; Olszewski, R.; Kęsik-Brodacka, M. The Effects of Climate and Bioclimate on COVID-19 Cases in Poland. Remote Sens. 2021, 13, 4946. [Google Scholar] [CrossRef]

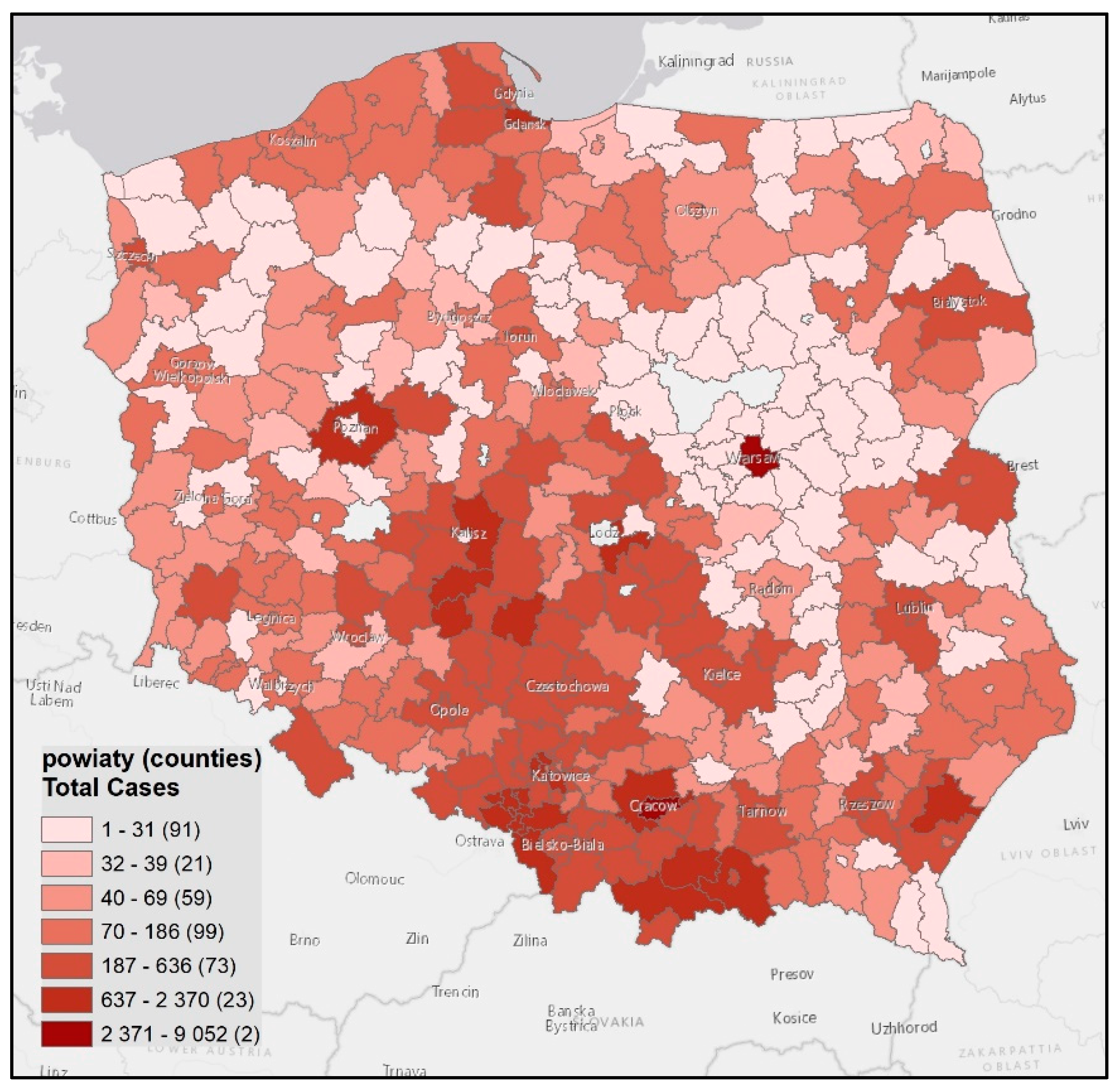
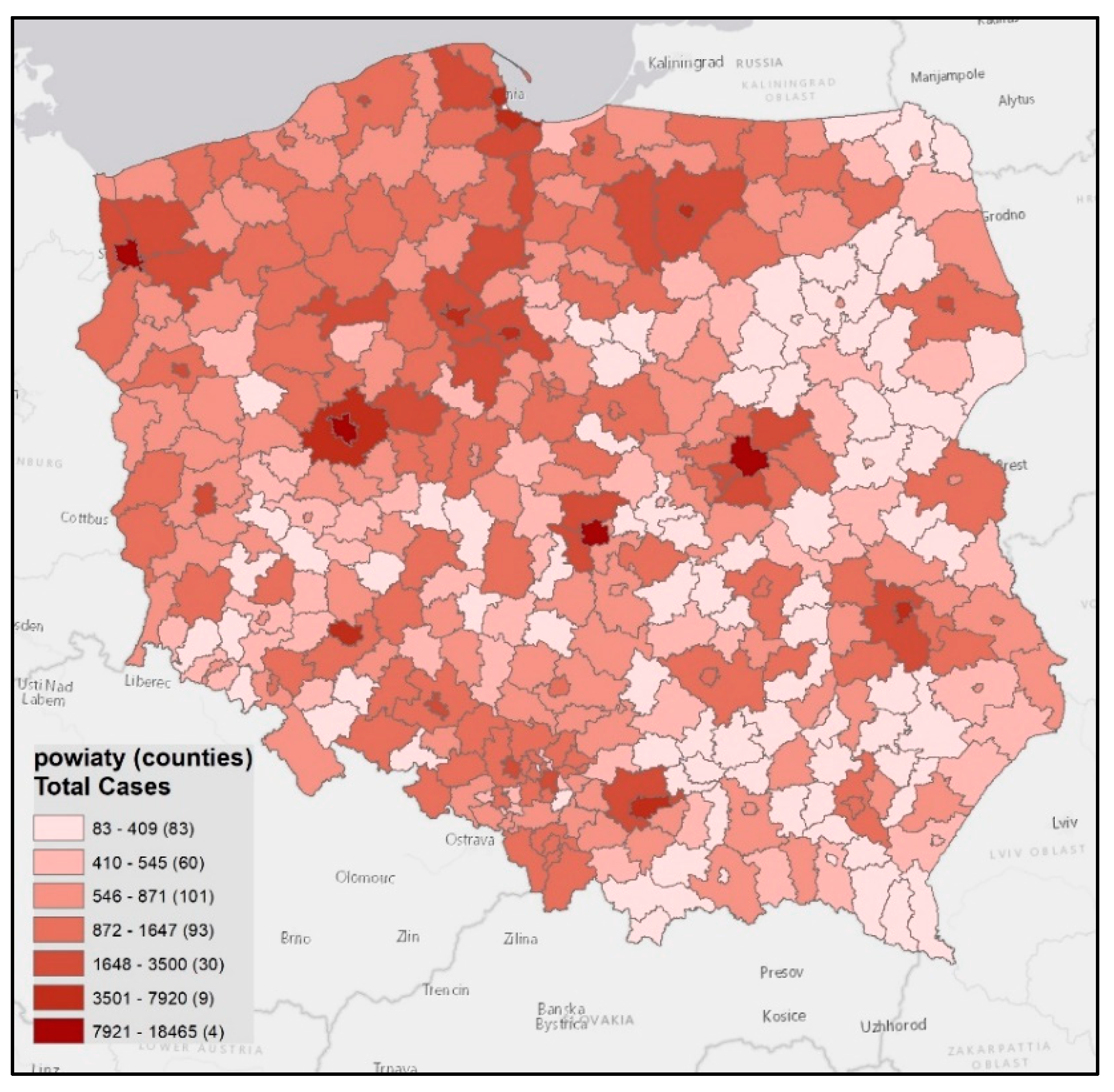

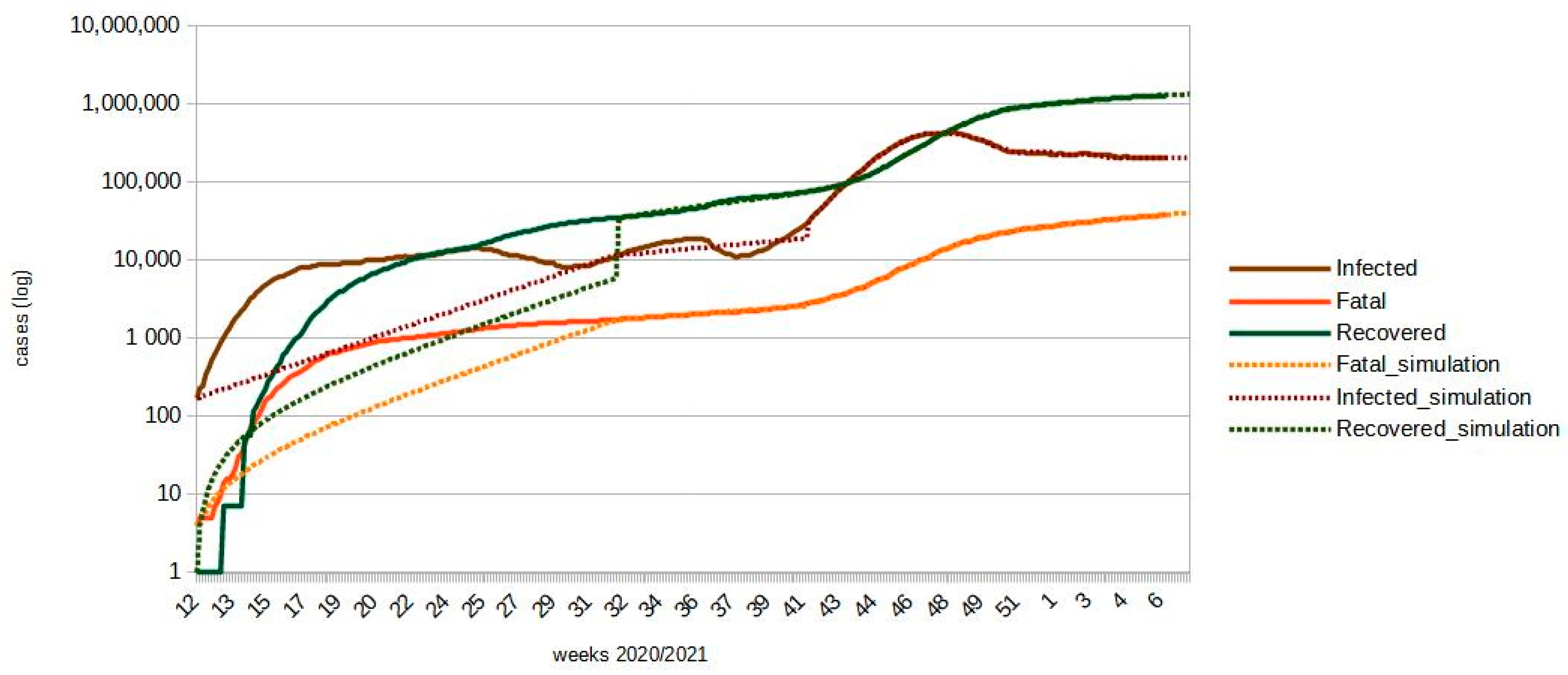
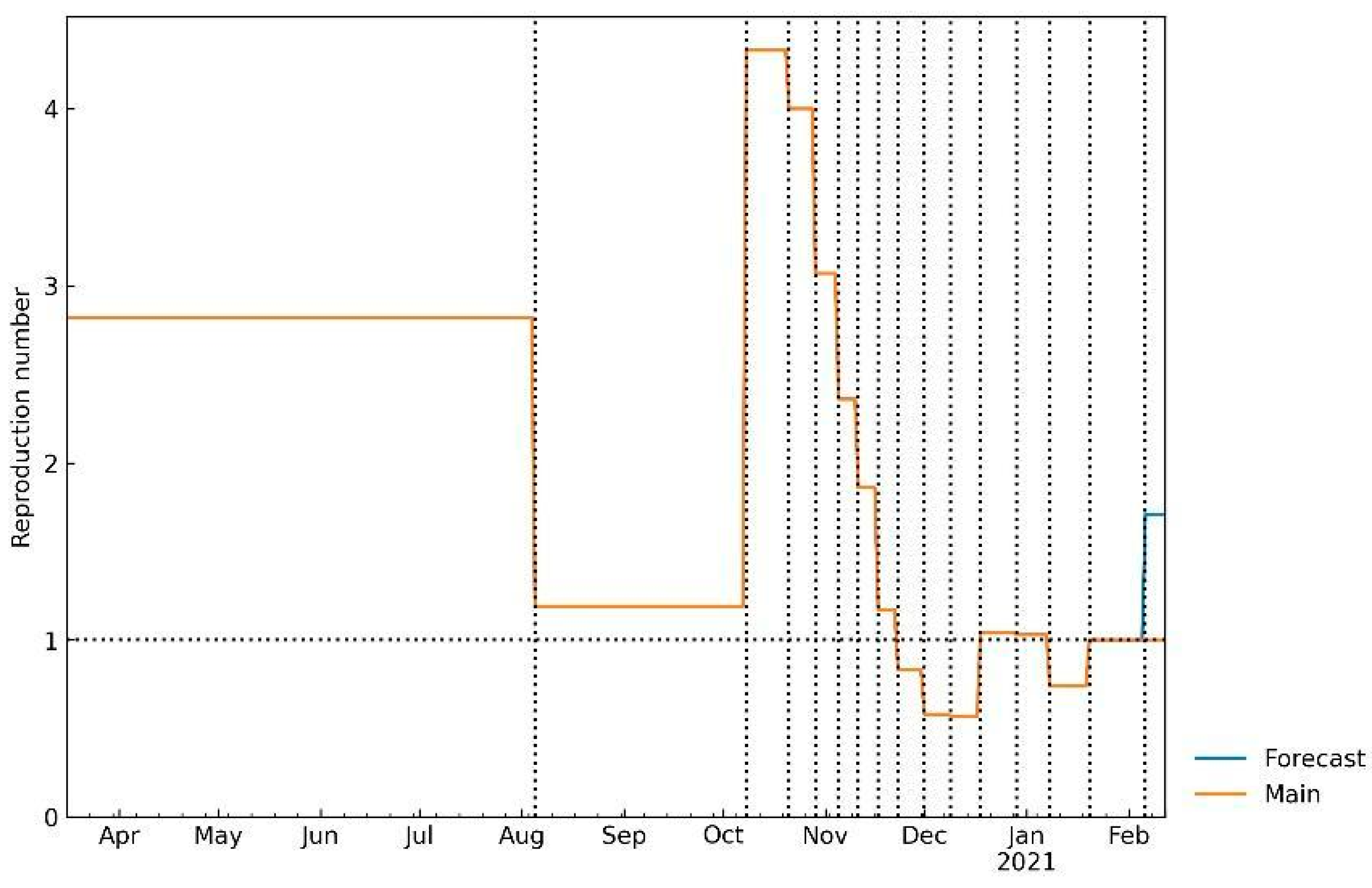

| O\D | Reg. 1 | … | Reg. n | ∑O | O\D | Reg. 1 | … | Reg. n | ∑O | O\D | Reg. 1 | … | Reg. n | ∑O | O\D | Reg. 1 | … | Reg. n | ∑O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reg. 1 | … | … | … | Reg. 1 | … | … | … | ∑O1 | Reg. 1 | … | … | … | Reg. 1 | … | … | … | ∑O1 | ||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| Reg. n | … | … | … | Reg. n | … | … | … | ∑On | Reg. n | … | … | … | Reg. n | … | … | … | ∑On | ||
| ∑D | ∑∑ | ∑D | ∑∑ | ∑D | ∑D1 | … | ∑Dn | ∑∑ | ∑D | ∑D1 | … | ∑Dn | ∑∑ | ||||||
| I. Unconstrained gravity | II. Production (origin) constrained | III. Destination (attraction) constrained | IV. Doubly constrained | ||||||||||||||||
| Model | Unconstrained Gravity Model (I) | Destination (Attraction) Constrained Model (III) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Week No. 2020/2021 | Pseudo R2 | adj. pseudo R2 | AIC | SRMSE | SSI | Pseudo R2 | Adj. Pseudo R2 | AIC | SRMSE | SSI |
| 15 (2020) | 0.208 | 0. 208 | 557,871.6 | 2.69 | 0.25 | 0.74 | 0.74 | 182,944.1 | 1.067 | 0.37 |
| 20 | 0.197 | 0.197 | 1.72 × 106 | 2.14 | 0.31 | 0.82 | 0.82 | 3.89 × 105 | 0.74 | 0.47 |
| 25 | 0.162 | 0.162 | 4.59 × 106 | 4.13 | 0.196 | 0.90 | 0.90 | 5.34 × 105 | 1.38 | 0.34 |
| 28 | 0.162 | 0.162 | 4.795 × 106 | 3.50 | 0.22 | 0.899 | 0.899 | 5.75 × 105 | 1.22 | 0.38 |
| 30 | 0.164 | 0.164 | 3.15 × 106 | 3.66 | 0.25 | 0.88 | 0.88 | 4.44 × 105 | 1.28 | 0.42 |
| 33 | 0.235 | 0.235 | 2.55 × 106 | 2.57 | 0.32 | 0.86 | 0.86 | 4.80 × 105 | 0.99 | 0.51 |
| 35 | 0.34 | 0.34 | 3.13 × 106 | 2.04 | 0.42 | 0.87 | 0.87 | 6.31 × 105 | 0.86 | 0.60 |
| 36 | 0.44 | 0.44 | 5.17 × 106 | 1.63 | 0.44 | 0.89 | 0.89 | 9.72 × 105 | 0.81 | 0.63 |
| 40 | 0.50 | 0.50 | 3.41 × 106 | 2.08 | 0.45 | 0.89 | 0.89 | 7.31 × 105 | 1.28 | 0.62 |
| 48 | 0.78 | 0.78 | 240,549.3 | 23.93 | 0.001 | 0.85 | 0.85 | 167,863 | 19.12 | 0.001 |
| 49 | 0.77 | 0.77 | 2.25 × 105 | 24.69 | 0.001 | 0.845 | 0.844 | 1.55 × 105 | 19.79 | 0.002 |
| 50 | 0.78 | 0.78 | 205,945.5 | 26.42 | 0.001 | 0.849 | 0.848 | 140,473.2 | 20.68 | 0.001 |
| 51 | 0.77 | 0.77 | 193,757.6 | 27.53 | 0.001 | 0.849 | 0.849 | 130,010.9 | 21.87 | 0.001 |
| 52 | 0.77 | 0.77 | 91,125.6 | 29.32 | 0.001 | 0.851 | 0.849 | 59,741.23 | 22.68 | 0.001 |
| 1 (2021) | 0.772 | 0.772 | 178,070.68 | 28.05 | 0.001 | 0.85 | 0.85 | 118,350.50 | 22.97 | 0.002 |
| 2 | 0.77 | 0.77 | 194,127.08 | 27.60 | 0.001 | 0.85 | 0.85 | 129,449.48 | 22.53 | 0.002 |
| 3 | 0.767 | 0.767 | 147,442.42 | 27.19 | 0.001 | 0.849 | 0.848 | 96,156.31 | 21.10 | 0.001 |
| 4 | 0.772 | 0.771 | 115,513.18 | 26.98 | 0.001 | 0.847 | 0.845 | 78,254.32 | 21.39 | 0.001 |
| 5 | 0.776 | 0.776 | 107,080.50 | 26.92 | 0.001 | 0.848 | 0.847 | 73,356.91 | 21.15 | 0.002 |
| 6 * | 0.778 | 0.778 | 103,959.48 | 27.32 | 0.001 | 0.848 | 0.847 | 71,851.31 | 21.05 | 0.001 |
| 7 * | 0.774 | 0.774 | 112,247.09 | 28.04 | 0.001 | 0.847 | 0.846 | 76,803.60 | 21.47 | 0.001 |
| 7 ** | ||||||||||
| Charts/sparkline/for certain weeks | 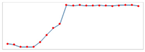 adj. determination coefficient | 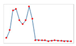 AIC | 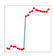 SRMSE |  adj. determination coefficient | 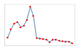 AIC |  SRMSE | ||||
| Model | Unconstrained Gravity Model | Destination (Attraction) Constrained Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Week No. 2020 | Pseudo R2 | Adj. Pseudo R2 | AIC | SRMSE | SSI | Pseudo R2 | Adj. Pseudo R2 | AIC | SRMSE | SSI |
| 10–22/sum/ | 0.122 | 0.122 | 1.75 × 107 | 2.203 | 0.391 | 0.609 | 0.609 | 7.777 × 106 | 2.018 | 0.573 |
| 10–42/sum/ | 0.484 | 0.484 | 3.23 × 107 | 1.607 | 0.576 | 0.947 | 0.947 | 3.33 × 106 | 0.822 | 0.777 |
| 1–7 (2021)/sum/ | 0. 779 | 0. 779 | 925,496.67 | 27.18 | 0.001 | 0.851 | 0.851 | 624,561.11 | 21.49 | 0.002 |
| 1–7 (2021) sum * | 0.781 | 0.781 | 915,074.37 | 25.19 | 0.001 | 0.864 | 0.864 | 569,191.85 | 18.24 | 0.002 |
| Date | Confirmed Cases | Fatal Cases | Infected Cases | Recovered Cases | Diff. Confirmed | Diff. Fatal | Diff. Infected | Diff. Recovered |
|---|---|---|---|---|---|---|---|---|
| 8 February 2021 | 1,553,164 | 39,478 | 203,234 | 1,310,452 | 6060 | 274 | 225 | 6011 |
| 9 February 2021 | 1,558,463 | 39,754 | 202,915 | 1,315,794 | 6051 | 274 | 227 | 6004 |
| 10 February 2021 | 1,563,753 | 40,030 | 202,595 | 1,321,128 | 6044 | 273 | 226 | 5997 |
| 11 February 2021 | 1,569,035 | 40,305 | 202,276 | 1,326,454 | 6036 | 273 | 228 | 5991 |
| 12 February 2021 | 1,574,307 | 40,580 | 201,956 | 1,331,771 | 6029 | 273 | 228 | 5984 |
| 13 February 2021 | 1,579,571 | 40,855 | 201,636 | 1,337,080 | 6020 | 272 | 229 | 5977 |
| 14 February 2021 | 1,603,175 | 41,034 | 203,706 | 1,358,435 | 6013 | 272 | 230 | 5971 |
| Total | 42,206 | 1909 | 1598 | 41,895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Werner, P.A.; Kęsik-Brodacka, M.; Nowak, K.; Olszewski, R.; Kaleta, M.; Liebers, D.T. Modeling the Spatial and Temporal Spread of COVID-19 in Poland Based on a Spatial Interaction Model. ISPRS Int. J. Geo-Inf. 2022, 11, 195. https://doi.org/10.3390/ijgi11030195
Werner PA, Kęsik-Brodacka M, Nowak K, Olszewski R, Kaleta M, Liebers DT. Modeling the Spatial and Temporal Spread of COVID-19 in Poland Based on a Spatial Interaction Model. ISPRS International Journal of Geo-Information. 2022; 11(3):195. https://doi.org/10.3390/ijgi11030195
Chicago/Turabian StyleWerner, Piotr A., Małgorzata Kęsik-Brodacka, Karolina Nowak, Robert Olszewski, Mariusz Kaleta, and David T. Liebers. 2022. "Modeling the Spatial and Temporal Spread of COVID-19 in Poland Based on a Spatial Interaction Model" ISPRS International Journal of Geo-Information 11, no. 3: 195. https://doi.org/10.3390/ijgi11030195
APA StyleWerner, P. A., Kęsik-Brodacka, M., Nowak, K., Olszewski, R., Kaleta, M., & Liebers, D. T. (2022). Modeling the Spatial and Temporal Spread of COVID-19 in Poland Based on a Spatial Interaction Model. ISPRS International Journal of Geo-Information, 11(3), 195. https://doi.org/10.3390/ijgi11030195







