Mapping of Rill Erosion of the Middle Volga (Russia) Region Using Deep Neural Network
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
- Selection and preparation of remote sensing data from space;
- Preparation of training and test sets;
- Training the neural network and evaluating the quality of rill recognition;
- Implementation of the neural network for the entire study area and vectorization of recognition results;
- Calculation of rill erosion length as a measure of rill erosion density index in the basins;
- Analysis of the obtained results.
3.1. Remote Sensing Data
3.2. Preparation of the Training Dataset
3.3. Training a Deep Neural Network
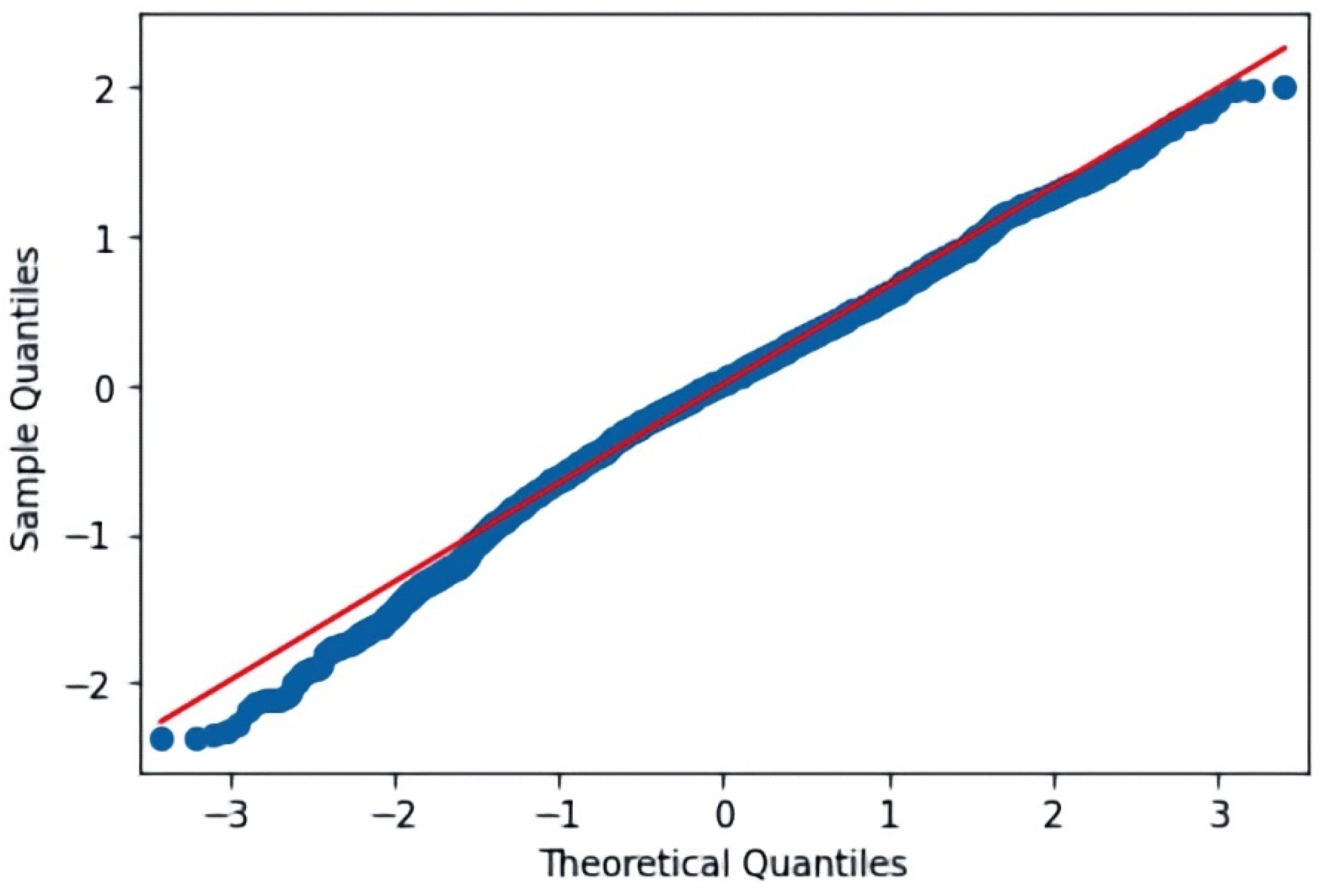
3.4. Statistical Analysis of the Obtained Results
4. Results and Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Shi, Y.; Liang, X.; Huang, T.; Fu, S.; Liu, B. Evaluation of Structure from Motion (SfM) Photogrammetry on the Measurement of Rill and Interrill Erosion in a Typical Loess. Geomorphology 2021, 385, 107734. [Google Scholar] [CrossRef]
- Di Stefano, C.; Ferro, V.; Pampalone, V.; Sanzone, F. Field Investigation of Rill and Ephemeral Gully Erosion in the Sparacia Experimental Area, South Italy. Catena 2013, 101, 226–234. [Google Scholar] [CrossRef]
- Murgatroyd, A.L.; Ternan, J.L. The Impact of Afforestation on Stream Bank Erosion and Channel Form. Earth Surf. Process. Landf. 1983, 8, 357–369. [Google Scholar] [CrossRef]
- Nearing, M.A.; Norton, L.D.; Bulgakov, D.A.; Larionov, G.A.; West, L.T.; Dontsova, K.M. Hydraulics and Erosion in Eroding Rills. Water Resour. Res. 1997, 33, 865–876. [Google Scholar] [CrossRef]
- Yermolaev, O.P.; Gafurov, A.M.; Usmanov, B.M. Evaluation of Erosion Intensity and Dynamics Using Terrestrial Laser Scanning. Eurasian Soil Sci. 2018, 51, 814–826. [Google Scholar] [CrossRef]
- Kociuba, W.; Janicki, G.; Rodzik, J.; Stępniewski, K. Comparison of Volumetric and Remote Sensing Methods (TLS) for Assessing the Development of a Permanent Forested Loess Gully. Nat. Hazards 2015, 79, 139–158. [Google Scholar] [CrossRef]
- Vinci, A.; Brigante, R.; Todisco, F.; Mannocchi, F.; Radicioni, F. Measuring Rill Erosion by Laser Scanning. Catena 2015, 124, 97–108. [Google Scholar] [CrossRef]
- Usmanov, B.; Yermolaev, O.; Gafurov, A. Estimates of Slope Erosion Intensity Utilizing Terrestrial Laser Scanning. Proc. Int. Assoc. Hydrol. Sci. 2015, 367, 59–65. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2021, 13, 77. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D Mapping Applications: A Review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Gafurov, A.M. Possible Use of Unmanned Aerial Vehicle for Soil Erosion Assessment. Uchenye Zap. Kazan. Univ. Ser. Estestv. Nauk. 2017, 159, 654–667. [Google Scholar]
- Gafurov, A. The Methodological Aspects of Constructing a High-Resolution DEM of Large Territories Using Low-Cost UAVs on the Example of the Sarycum Aeolian Complex, Dagestan, Russia. Drones 2021, 5, 7. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.K.; Singh, V.P. Physically Based Soil Erosion and Sediment Yield Models Revisited. Catena 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses-a Guide to Conservation Planning; U.S. Department of Agriculture: Betsville, MD, USA, 1978.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised Universal Soil Loss Equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Sadeghi, S.H.R.; Gholami, L.; Darvishan, A.K.; Saeidi, P. A Review of the Application of the MUSLE Model Worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Knisel, W.G. CREAMS: A Field Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems; Department of Agriculture, Science and Education Administration: Baltimore, MD, USA, 1980. [Google Scholar]
- De Roo, A.P.J.; Wesseling, C.G.; Jetten, V.G.; Ritsema, C. LISEM: A Physically-Based Hydrological and Soil Erosion Model Incorporated in a GIS. In Application of Geographic Information Systems in Hydrology and Water Resources Management; Kovar, K., Nachtnebel, H.P., Eds.; IAHS: Wallingford, UK, 1996; Volume 235, pp. 395–403. [Google Scholar]
- Flanagan, D.C.; Ascough, J.C.; Nearing, M.A.; Laflen, J.M. The Water Erosion Prediction Project (WEPP) Model. In Landscape Erosion and Evolution Modeling; Harmon, R.S., Doe, W.W., Eds.; Springer: Boston, MA, USA, 2001; pp. 145–199. ISBN 978-1-4615-0575-4. [Google Scholar]
- Favis-Mortlock, D.T.; Boardman, J.; Parsons, A.J.; Lascelles, B. Emergence and Erosion: A Model for Rill Initiation and Development. Hydrol. Process. 2000, 14, 2173–2205. [Google Scholar] [CrossRef]
- Misra, R.K.; Rose, C.W. Application and Sensitivity Analysis of Process-Based Erosion Model GUEST. Eur. J. Soil Sci. 1996, 47, 593–604. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.; Ghadiri, H.; Rose, C.; Yu, B.; Rafahi, H.; Rouhipour, H. Evaluation of GUEST and WEPP with a New Approach for the Determination of Sediment Transport Capacity. J. Hydrol. 2014, 513, 413–421. [Google Scholar] [CrossRef]
- Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European Soil Erosion Model (EUROSEM): A Dynamic Approach for Predicting Sediment Transport from Fields and Small Catchments. Earth Surf. Process. Landf. 1998, 23, 527–544. [Google Scholar] [CrossRef]
- Mukharamova, S.; Saveliev, A.; Ivanov, M.; Gafurov, A.; Yermolaev, O. Estimating the Soil Erosion Cover-Management Factor at the European Part of Russia. ISPRS Int. J. Geo-Inf. 2021, 10, 645. [Google Scholar] [CrossRef]
- Maltsev, K.A.; Golosov, V.N.; Gafurov, A.M. Digital Elevation Models and Their Use for Assessing Soil Erosion Rates on Arable Lands. Uchenye Zap. Kazan. Universiteta Seriya Estestv. Nauk. 2018, 160, 514–530. [Google Scholar]
- Pielke, R.A.; Cotton, W.R.; Walko, R.L.; Tremback, C.J.; Lyons, W.A.; Grasso, L.D.; Nicholls, M.E.; Moran, M.D.; Wesley, D.A.; Lee, T.J.; et al. A Comprehensive Meteorological Modeling System—RAMS. Meteorol. Atmos. Phys. 1992, 49, 69–91. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-Year High-Resolution Global Dataset of Meteorological Forcings for Land Surface Modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef] [Green Version]
- Shruthi, R.B.V.; Kerle, N.; Jetten, V. Object-Based Gully Feature Extraction Using High Spatial Resolution Imagery. Geomorphology 2011, 134, 260–268. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully Erosion Susceptibility Assessment by Means of GIS-Based Logistic Regression: A Case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Conoscenti, C.; Agnesi, V.; Cama, M.; Caraballo-Arias, N.A.; Rotigliano, E. Assessment of Gully Erosion Susceptibility Using Multivariate Adaptive Regression Splines and Accounting for Terrain Connectivity. Land Degrad. Dev. 2018, 29, 724–736. [Google Scholar] [CrossRef]
- Golosov, V.; Gusarov, A.; Sharifillin, A.; Ivanova, N.N.; Gafurov, A.; Yermolaev, O.; Rysin, I. Using Bomb-Derived and Chernobyl-Derived 137Cs for the Assessment of Soil Losses Trends in Different Landscape Zones of the European Russia. In Proceedings of the 14th International Symposium on the Interaction between Sediments and Water, Taormina, Italy, 17–22 June 2017; p. 10. [Google Scholar]
- Gusarov, A.V.; Golosov, V.N.; Sharifullin, A.G.; Gafurov, A.M. Contemporary Trend in Erosion of Arable Southern Chernozems (Haplic Chernozems Pachic) in the West of Orenburg Oblast (Russia). Eurasian Soil Sci. 2018, 51, 561–575. [Google Scholar] [CrossRef]
- Golosov, V.; Koiter, A.; Ivanov, M.; Maltsev, K.; Gusarov, A.; Sharifullin, A.; Radchenko, I. Assessment of Soil Erosion Rate Trends in Two Agricultural Regions of European Russia for the Last 60 Years. J. Soils Sediments 2018, 18, 3388–3403. [Google Scholar] [CrossRef]
- Gafurov, A.M. Using Unmanned Aerial Vehicles for Evaluation of Soil Erosion. Belgorod State Univ. Sci. Bull. Nat. Sci. 2019, 43, 182–190. [Google Scholar] [CrossRef]
- Yermolaev, O.P.; Medvedeva, R.A.; Platoncheva, E.V. Methodological Approaches to Monitoring Erosion of Agricultural Lands in the European Part of Russia by Using Satellite Imagery. Uchenye Zap. Kazan. Univ. Ser. Estestv. Nauk. 2017, 159, 668–680. [Google Scholar]
- Yermolayev, O.; Platoncheva, E.; Essuman-Quainoo, B. Spatial-Temporal Dynamics of the Ephemeral Gully Belt on the Plowed Slopes of River Basins in Natural and Anthropogenic Landscapes of the East of the Russian Plain. Geosciences 2020, 10, 167. [Google Scholar] [CrossRef]
- Seutloali, K.E.; Dube, T.; Mutanga, O. Assessing and Mapping the Severity of Soil Erosion Using the 30-m Landsat Multispectral Satellite Data in the Former South African Homelands of Transkei. Phys. Chem. Earth Parts A/B/C 2017, 100, 296–304. [Google Scholar] [CrossRef]
- Saadat, H.; Adamowski, J.; Tayefi, V.; Namdar, M.; Sharifi, F.; Ale-Ebrahim, S. A New Approach for Regional Scale Interrill and Rill Erosion Intensity Mapping Using Brightness Index Assessments from Medium Resolution Satellite Images. Catena 2014, 113, 306–313. [Google Scholar] [CrossRef]
- Desprats, J.F.; Raclot, D.; Rousseau, M.; Cerdan, O.; Garcin, M.; Le Bissonnais, Y.; Ben Slimane, A.; Fouche, J.; Monfort-Climent, D. Mapping Linear Erosion Features Using High and Very High Resolution Satellite Imagery. Land Degrad. Dev. 2013, 24, 22–32. [Google Scholar] [CrossRef]
- Fiorucci, F.; Ardizzone, F.; Rossi, M.; Torri, D. The Use of Stereoscopic Satellite Images to Map Rills and Ephemeral Gullies. Remote Sens. 2015, 7, 14151–14178. [Google Scholar] [CrossRef] [Green Version]
- Kashtanov, A.N.; Vernyuk, Y.I.; Savin, I.Y.; Shchepot’ev, V.V.; Dokukin, P.A.; Sharychev, D.V.; Li, K.A. Mapping of Rill Erosion of Arable Soils Based on Unmanned Aerial Vehicles Survey. Eurasian Soil Sci. 2018, 51, 479–484. [Google Scholar] [CrossRef]
- Karydas, C.; Bouarour, O.; Zdruli, P. Mapping Spatio-Temporal Soil Erosion Patterns in the Candelaro River Basin, Italy, Using the G2 Model with Sentinel2 Imagery. Geosciences 2020, 10, 89. [Google Scholar] [CrossRef] [Green Version]
- Walter, V. Object-Based Classification of Remote Sensing Data for Change Detection. ISPRS J. Photogramm. Remote Sens. 2004, 58, 225–238. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Zhang, B.; Shen, Q.; Ye, H.; Wang, S.; Lu, Z. A Simple Automated Dynamic Threshold Extraction Method for the Classification of Large Water Bodies from Landsat-8 OLI Water Index Images. Int. J. Remote Sens. 2018, 39, 3429–3451. [Google Scholar] [CrossRef]
- Ghosh, A.; Maiti, R. Soil Erosion Susceptibility Assessment Using Logistic Regression, Decision Tree and Random Forest: Study on the Mayurakshi River Basin of Eastern India. Environ. Earth Sci. 2021, 80, 328. [Google Scholar] [CrossRef]
- Dinh, T.V.; Nguyen, H.; Tran, X.-L.; Hoang, N.-D. Predicting Rainfall-Induced Soil Erosion Based on a Hybridization of Adaptive Differential Evolution and Support Vector Machine Classification. Math. Probl. Eng. 2021, 2021, e6647829. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, J.; Qi, W.; Li, X.; Gross, L.; Shao, Q.; Zhao, Z.; Ni, L.; Fan, X.; Li, Z. ARC-Net: An Efficient Network for Building Extraction from High-Resolution Aerial Images. IEEE Access 2020, 8, 154997–155010. [Google Scholar] [CrossRef]
- Cai, J.; Chen, Y. MHA-Net: Multipath Hybrid Attention Network for Building Footprint Extraction from High-Resolution Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5807–5817. [Google Scholar] [CrossRef]
- Luo, L.; Li, P.; Yan, X. Deep Learning-Based Building Extraction from Remote Sensing Images: A Comprehensive Review. Energies 2021, 14, 7982. [Google Scholar] [CrossRef]
- Blais, M.-A.; Akhloufi, M.A. Deep Learning for Low Altitude Coastline Segmentation; Online Only; SPIE: Orlando, FL, USA, 2021; Volume 11752. [Google Scholar]
- Aryal, B.; Escarzaga, S.M.; Vargas Zesati, S.A.; Velez-Reyes, M.; Fuentes, O.; Tweedie, C. Semi-Automated Semantic Segmentation of Arctic Shorelines Using Very High-Resolution Airborne Imagery, Spectral Indices and Weakly Supervised Machine Learning Approaches. Remote Sens. 2021, 13, 4572. [Google Scholar] [CrossRef]
- Garg, R.; Kumar, A.; Bansal, N.; Prateek, M.; Kumar, S. Semantic Segmentation of PolSAR Image Data Using Advanced Deep Learning Model. Sci. Rep. 2021, 11, 15365. [Google Scholar] [CrossRef]
- Dong, Y.; Li, F.; Hong, W.; Zhou, X.; Ren, H. Land Cover Semantic Segmentation of Port Area with High Resolution SAR Images Based on SegNet. In 2021 SAR in Big Data Era (BIGSARDATA); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Wei, H.; Xu, X.; Ou, N.; Zhang, X.; Dai, Y. Deanet: Dual Encoder with Attention Network for Semantic Segmentation of Remote Sensing Imagery. Remote Sens. 2021, 13, 3900. [Google Scholar] [CrossRef]
- Illarionova, S.; Trekin, A.; Ignatiev, V.; Oseledets, I. Tree Species Mapping on Sentinel-2 Satellite Imagery with Weakly Supervised Classification and Object-Wise Sampling. Forests 2021, 12, 1413. [Google Scholar] [CrossRef]
- Song, G.; Wu, S.; Lee, C.K.F.; Serbin, S.P.; Wolfe, B.T.; Ng, M.K.; Ely, K.S.; Bogonovich, M.; Wang, J.; Lin, Z.; et al. Monitoring Leaf Phenology in Moist Tropical Forests by Applying a Superpixel-Based Deep Learning Method to Time-Series Images of Tree Canopies. ISPRS J. Photogramm. Remote Sens. 2022, 183, 19–33. [Google Scholar] [CrossRef]
- Gafurov, A.M.; Yermolayev, O.P. Automatic Gully Detection: Neural Networks and Computer Vision. Remote Sens. 2020, 12, 1743. [Google Scholar] [CrossRef]
- Du, B.; Zhao, Z.; Hu, X.; Wu, G.; Han, L.; Sun, L.; Gao, Q. Landslide Susceptibility Prediction Based on Image Semantic Segmentation. Comput. Geosci. 2021, 155, 104860. [Google Scholar] [CrossRef]
- Yermolaev, O.; Usmanov, B.; Gafurov, A.; Poesen, J.; Vedeneeva, E.; Lisetskii, F.; Nicu, I.C. Assessment of Shoreline Transformation Rates and Landslide Monitoring on the Bank of Kuibyshev Reservoir (Russia) Using Multi-Source Data. Remote Sens. 2021, 13, 4214. [Google Scholar] [CrossRef]
- Yermolaev, O.P.; Mukharamova, S.S.; Maltsev, K.A.; Ivanov, M.A.; Ermolaeva, P.O.; Gayazov, A.I.; Mozzherin, V.V.; Kharchenko, S.V.; Marinina, O.A.; Lisetskii, F.N. Geographic Information System and Geoportal «River Basins of the European Russia». IOP Conf. Ser. Earth Environ. Sci. 2018, 107, 012108. [Google Scholar] [CrossRef]
- Gafurov, A.M.; Rysin, I.I.; Golosov, V.N.; Grigoryev, I.I.; Sharifullin, A.G. Estimation of the recent rate of gully head retreat on the southern megaslope of the East European Plain using a set of instrumental methods. Vestn. Mosk. Univ. Seriya 5 Geogr. 2018, 2018, 61–71. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems 30 (NIPS 2017); Curran Associates, Inc.: Long Beach, CA, USA, 2017; Volume 30. [Google Scholar]
- Chaurasia, A.; Culurciello, E. LinkNet: Exploiting Encoder Representations for Efficient Semantic Segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Iandola, F.; Moskewicz, M.; Karayev, S.; Girshick, R.; Darrell, T.; Keutzer, K. DenseNet: Implementing Efficient ConvNet Descriptor Pyramids. arXiv 2014, arXiv:1404.1869. [Google Scholar]
- Jaccard, P. The Distribution of the Flora in the Alpine Zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Miller, R.G., Jr. Beyond ANOVA: Basics of Applied Statistics; CRC Press: Boca Raton, FL, USA, 1997; ISBN 978-0-412-07011-2. [Google Scholar]
- Huberty, C.J.; Olejnik, S. Applied MANOVA and Discriminant Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0-471-78946-8. [Google Scholar]
- Groisman, P.Y.A.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. In Weather and Climate Extremes; Karl, T.R., Nicholls, N., Ghazi, A., Eds.; Springer: Dordrecht, The Netherlands, 1999; pp. 243–283. ISBN 978-90-481-5223-0. [Google Scholar]
- Dore, M.H.I. Climate Change and Changes in Global Precipitation Patterns: What Do We Know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Gulev, S.K.; Kollet, S. Changing Structure of European Precipitation: Longer Wet Periods Leading to More Abundant Rainfalls: Changing Structure of European Rainfall. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Olchev, A.; Novenko, E.; Popov, V.; Pampura, T.; Meili, M. Evidence of Temperature and Precipitation Change over the Past 100 Years in a High-Resolution Pollen Record from the Boreal Forest of Central European Russia. Holocene 2017, 27, 740–751. [Google Scholar] [CrossRef]
- Zolotokrylin, A.; Cherenkova, E. Seasonal Changes in Precipitation Extremes in Russia for the Last Several Decades and Their Impact on Vital Activities of the Human Population. Geogr. Environ. Sustain. 2017, 10, 69–82. [Google Scholar] [CrossRef] [Green Version]
- Golosov, V.; Gusarov, A.; Litvin, L.; Yermolaev, O.; Chizhikova, N.; Safina, G.; Kiryukhina, Z. Evaluation of Soil Erosion Rates in the Southern Half of the Russian Plain: Methodology and Initial Results. Proc. Int. Assoc. Hydrol. Sci. 2017, 375, 23–27. [Google Scholar] [CrossRef]
- Sharifullin, A.; Gusarov, A.; Gafurov, A.; Essuman-Quainoo, B. Preliminary Estimating the Contemporary Sedimentation Trend in Dry Valley Bottoms of First-Order Catchments of Different Landscape Zones of the Russian Plain Using the 137CS as a Chronomarker. IOP Conf. Ser. Earth Environ. Sci. 2018, 107, 012022. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 1999; ISBN 978-0-412-34390-2. [Google Scholar]
- Yermolaev, O.; Mukharamova, S.; Vedeneeva, E. River Runoff Modeling in the European Territory of Russia. Catena 2021, 203, 105327. [Google Scholar] [CrossRef]
- Servén, D.; Brummitt, C.; Abedi, H. Hlink Dswah/Pygam: V0.8.0; Zenodo: Genève, Switzerland, 2018. [Google Scholar]
- Babayan, L.A.; Protopopov, V.M. The Fertility of Light Chestnut Soils on Different Elements of Watershed Topography. Eurasian Soil Sci. 1997, 30, 1113–1116. [Google Scholar]

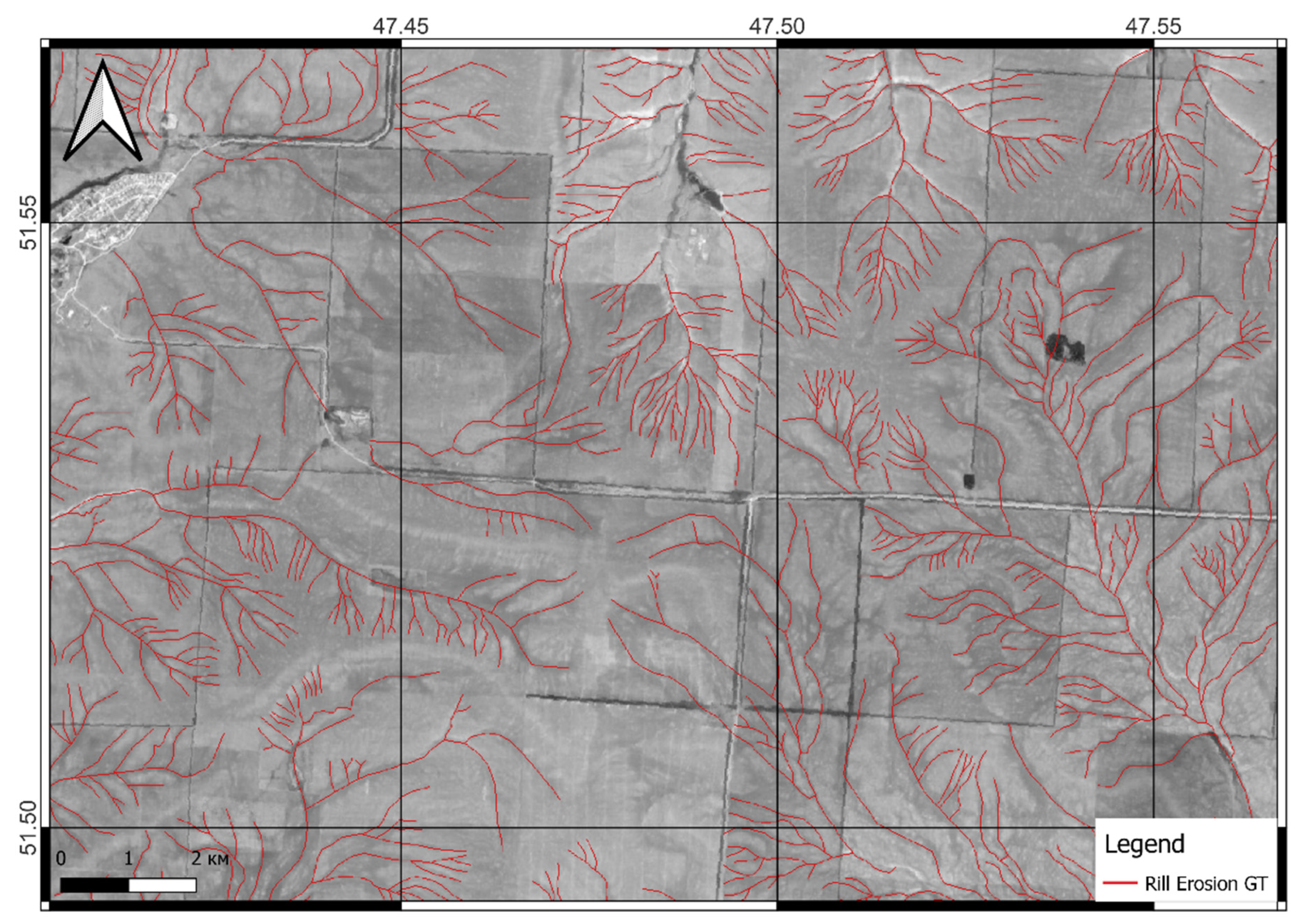

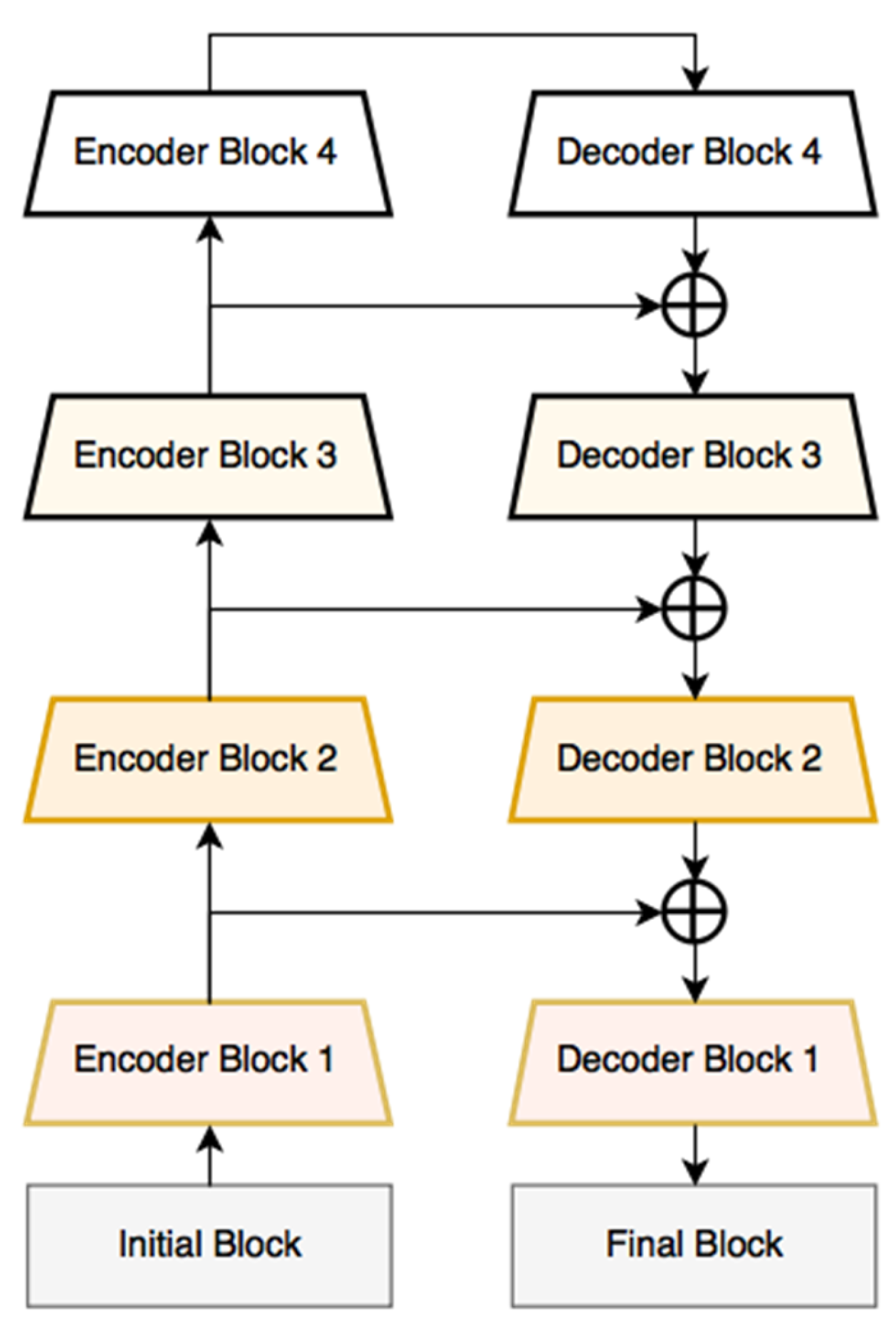



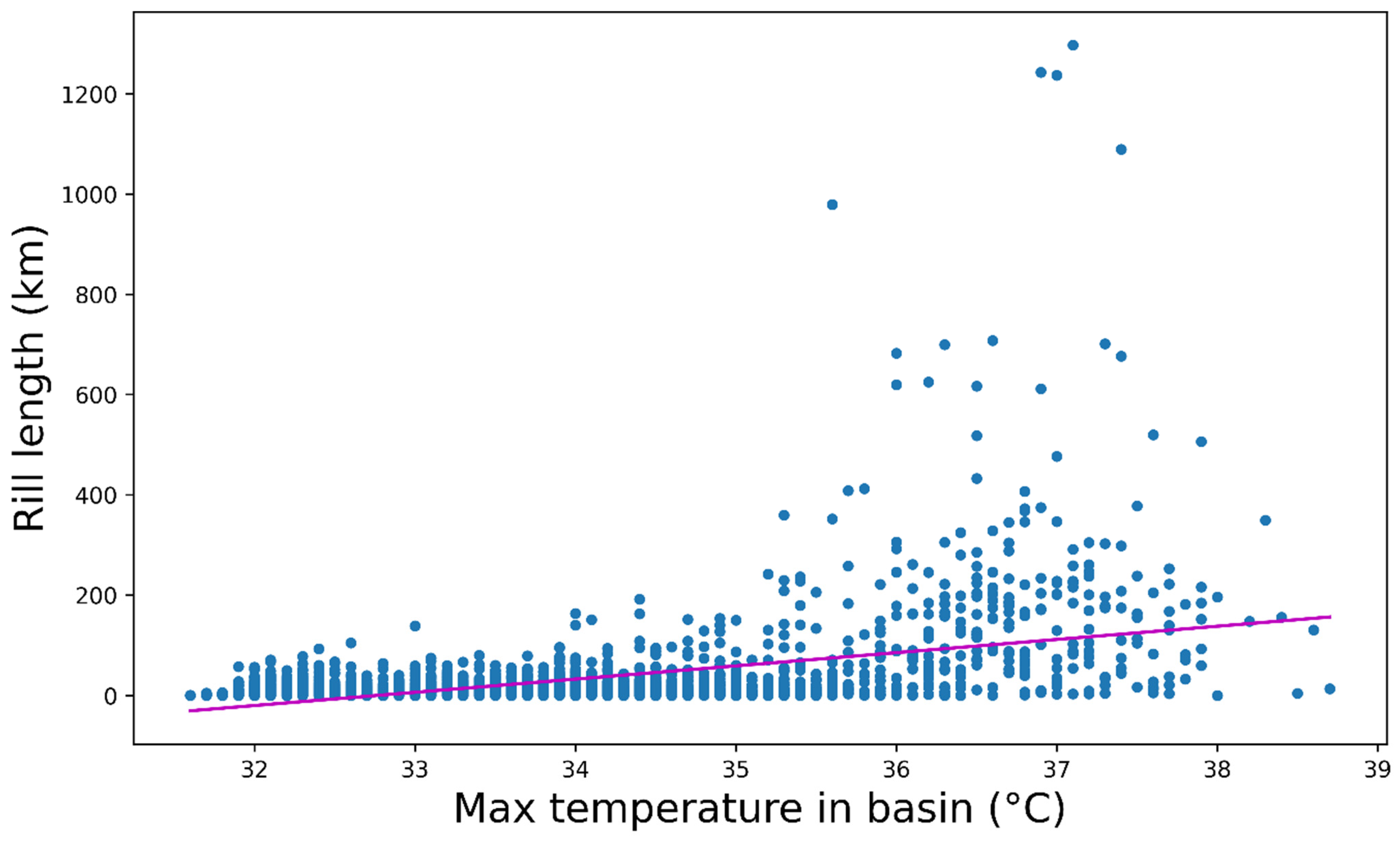
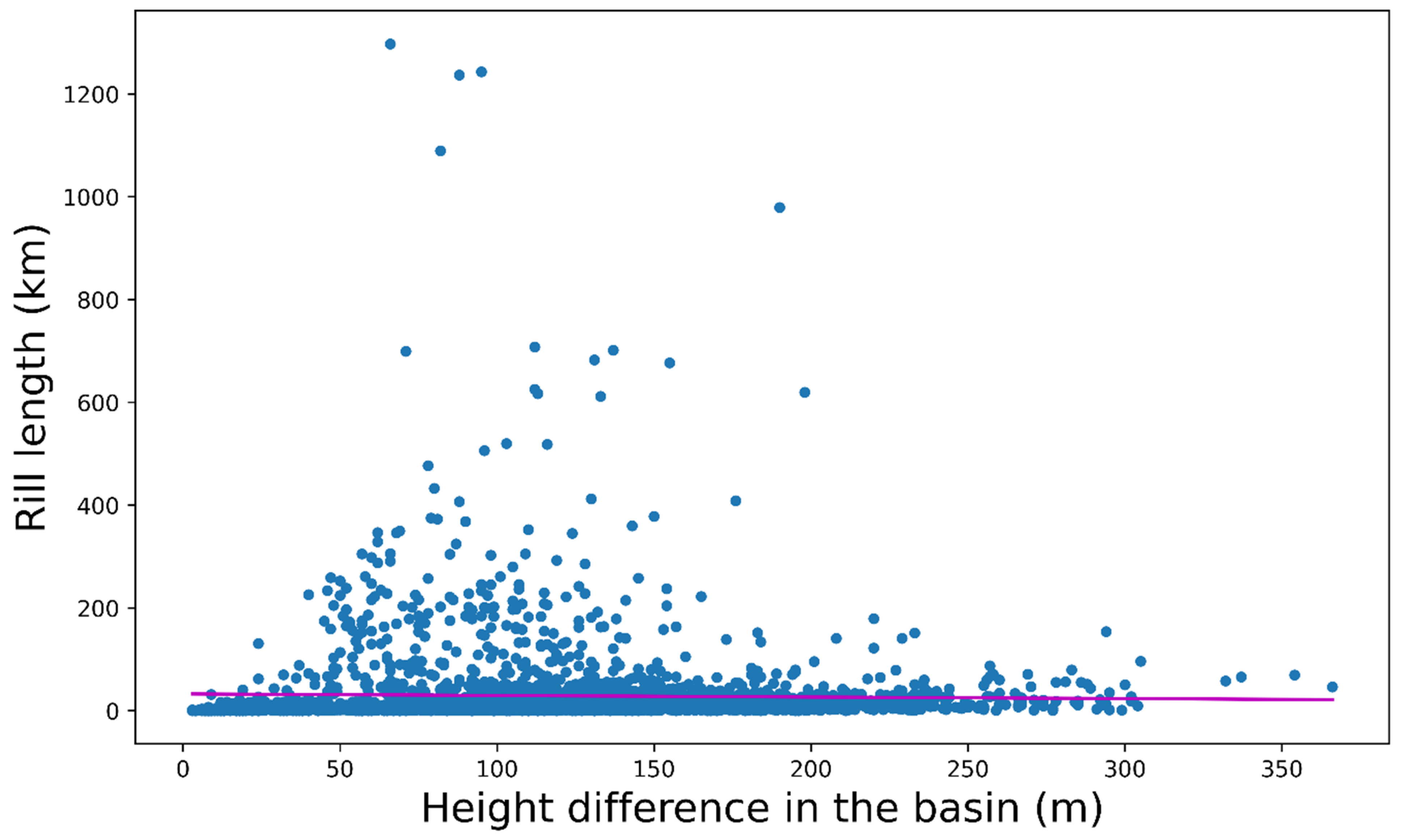
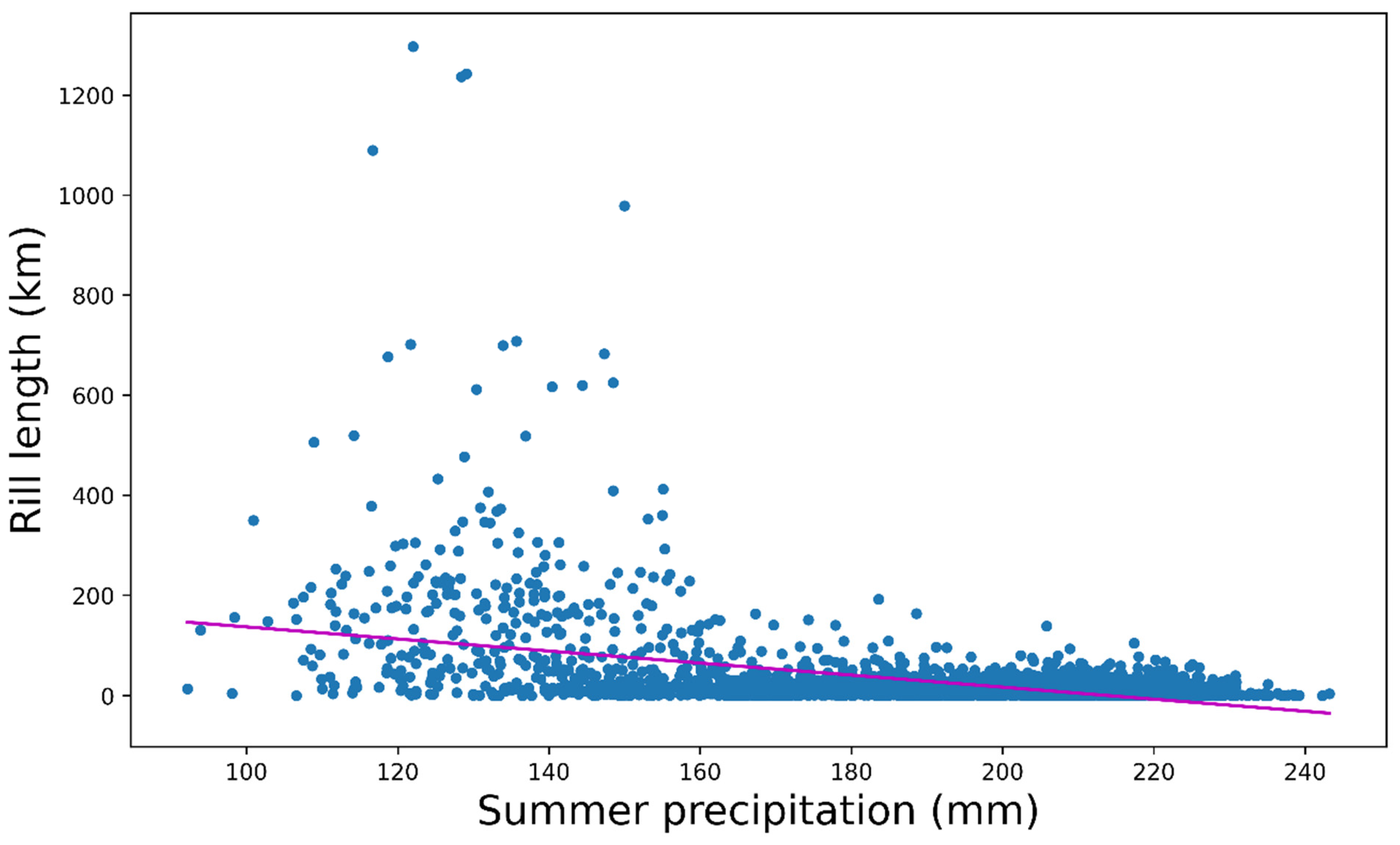
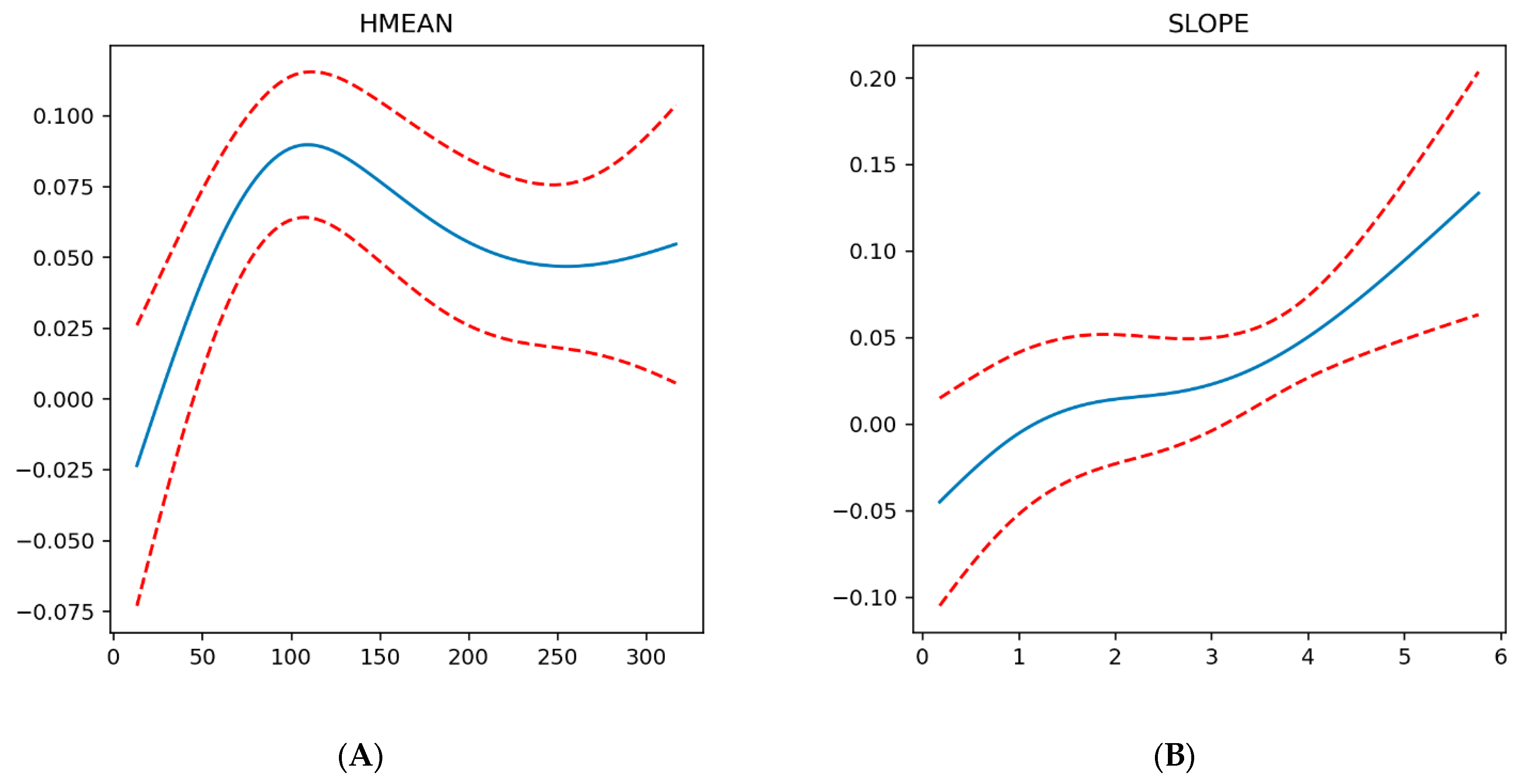
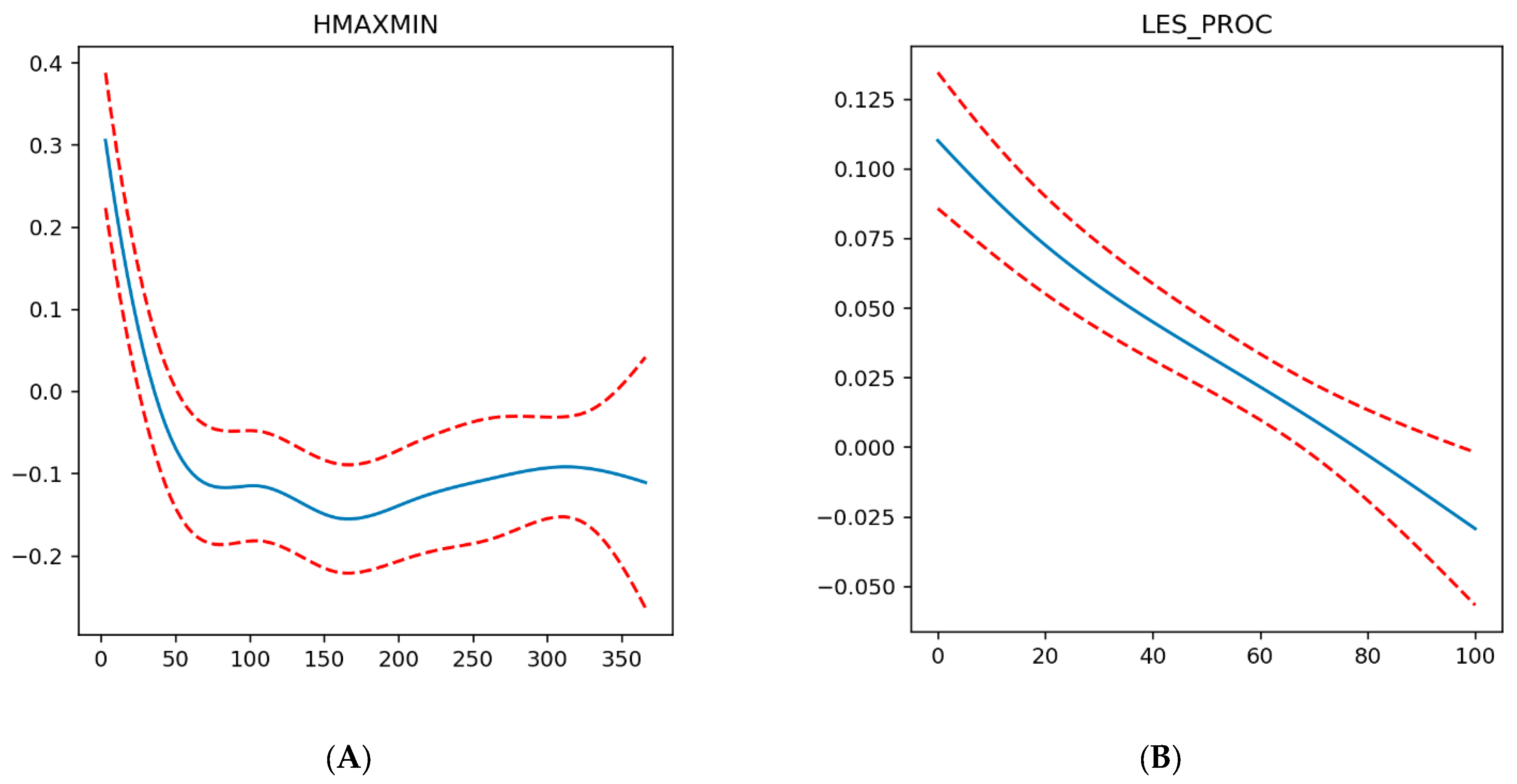


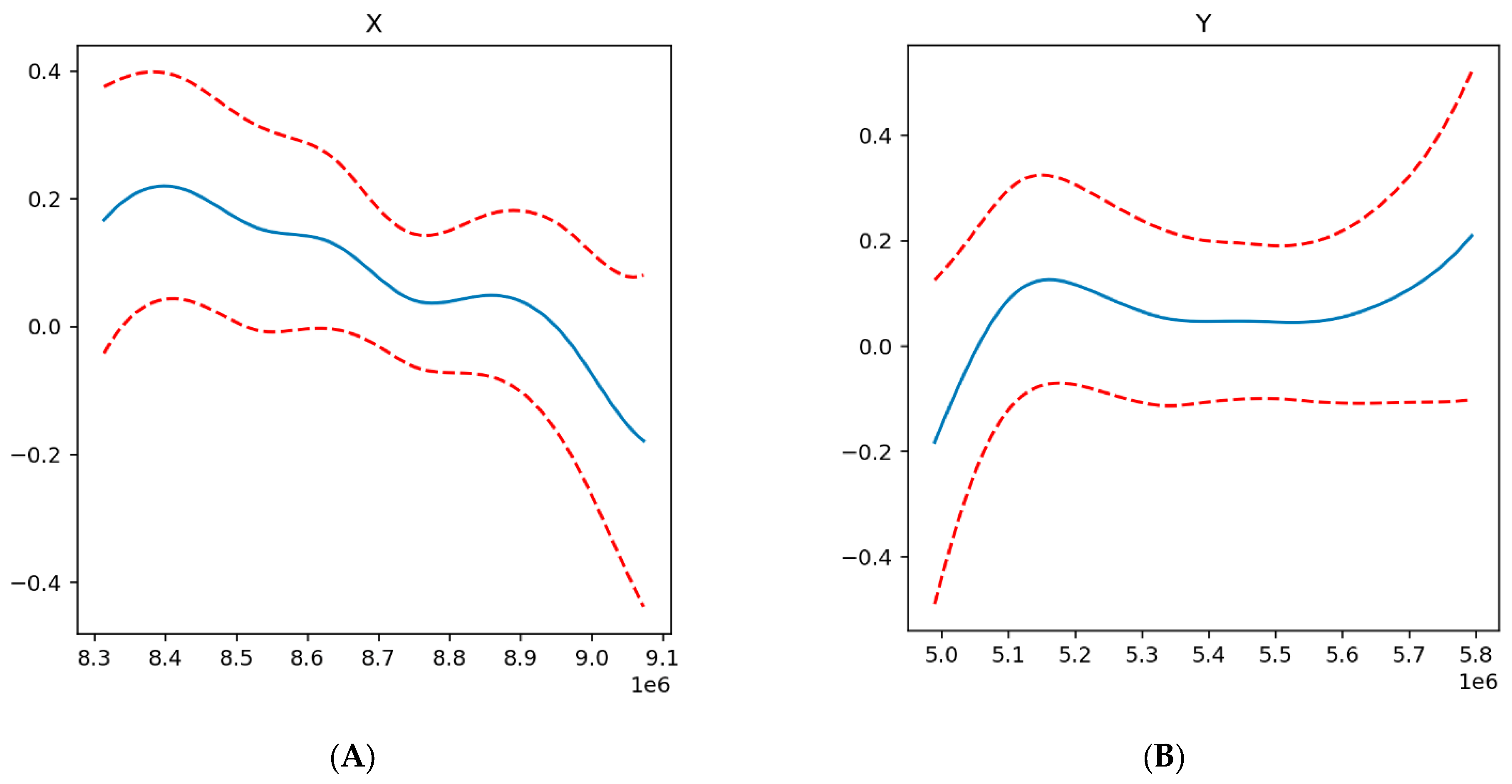
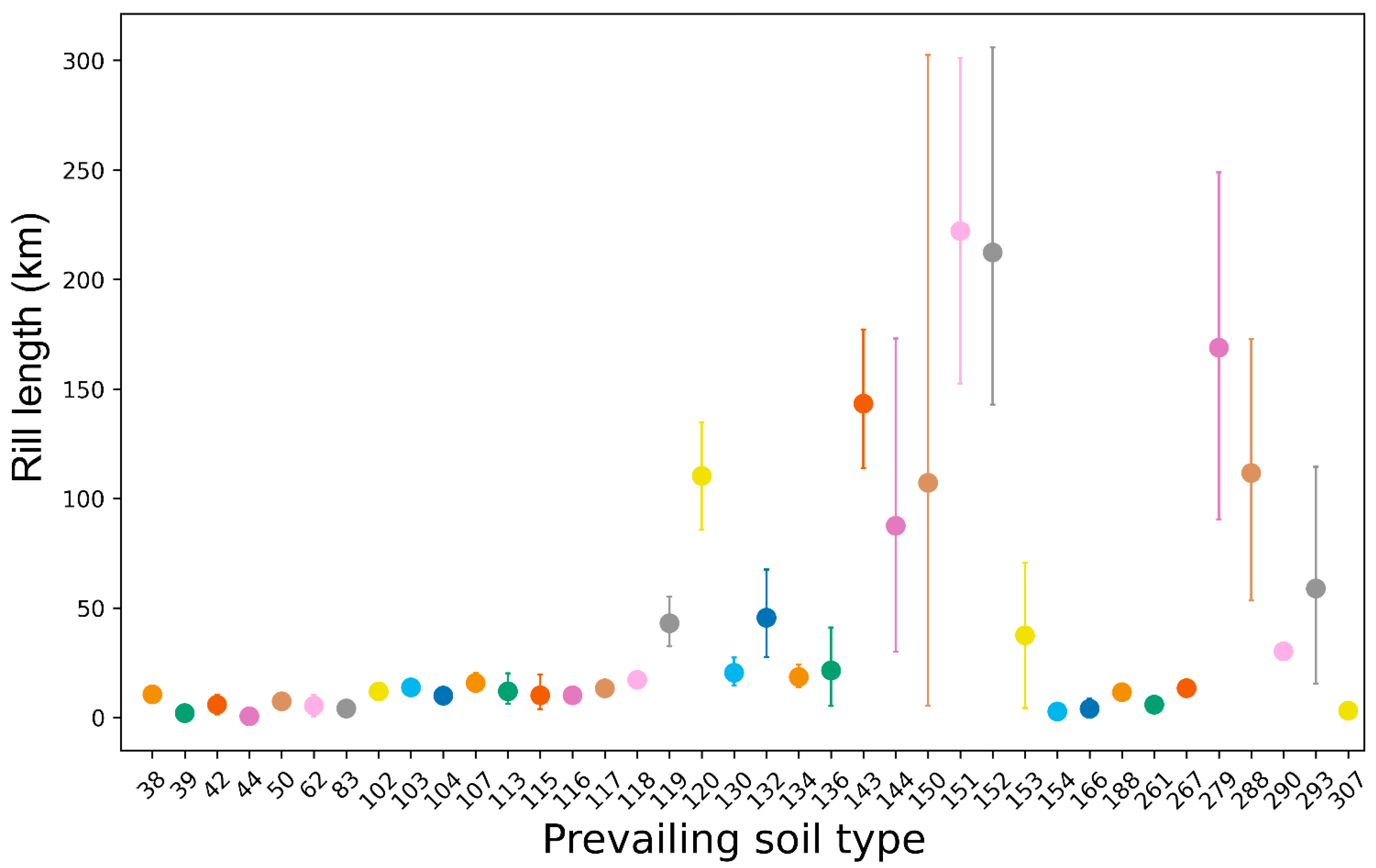
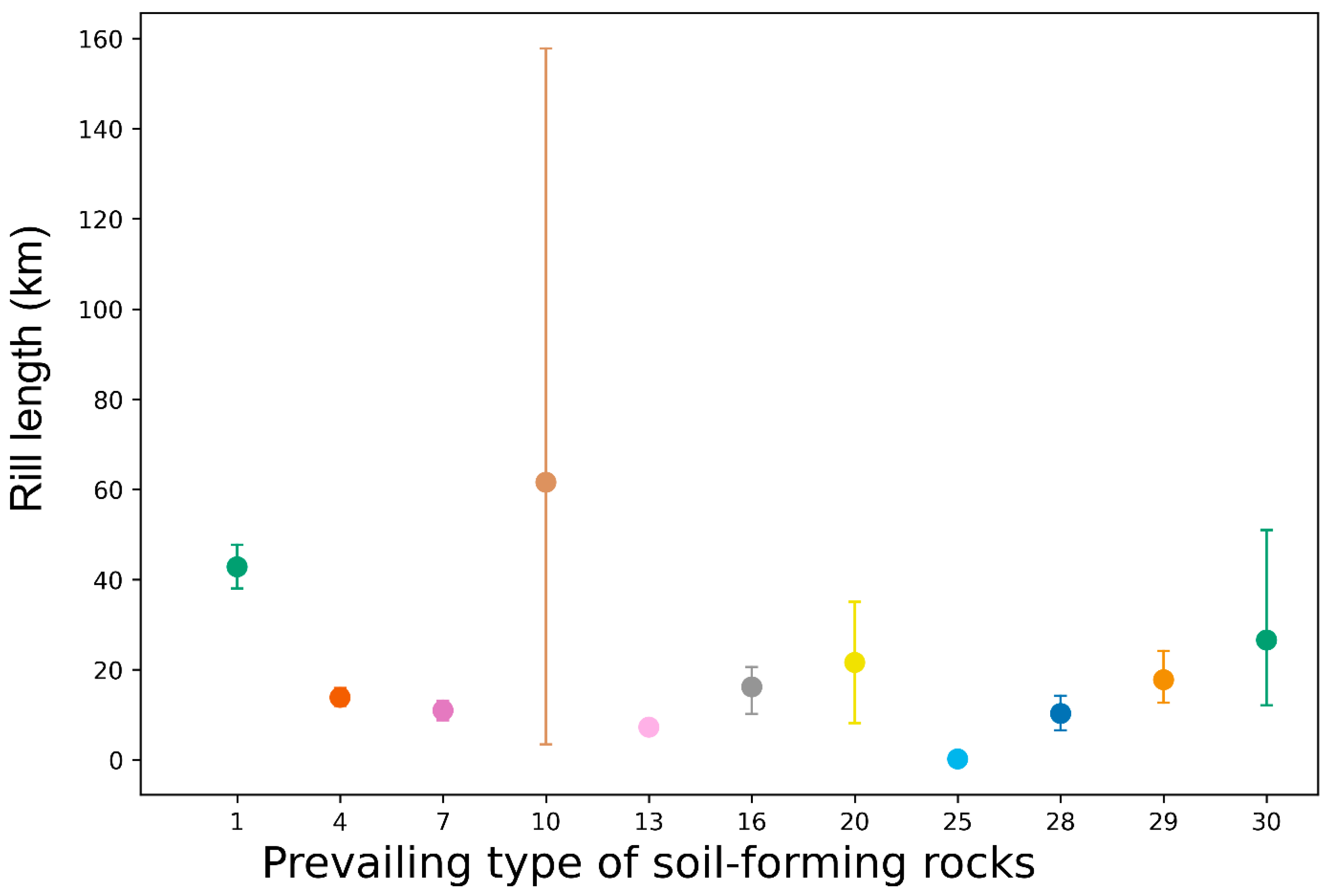

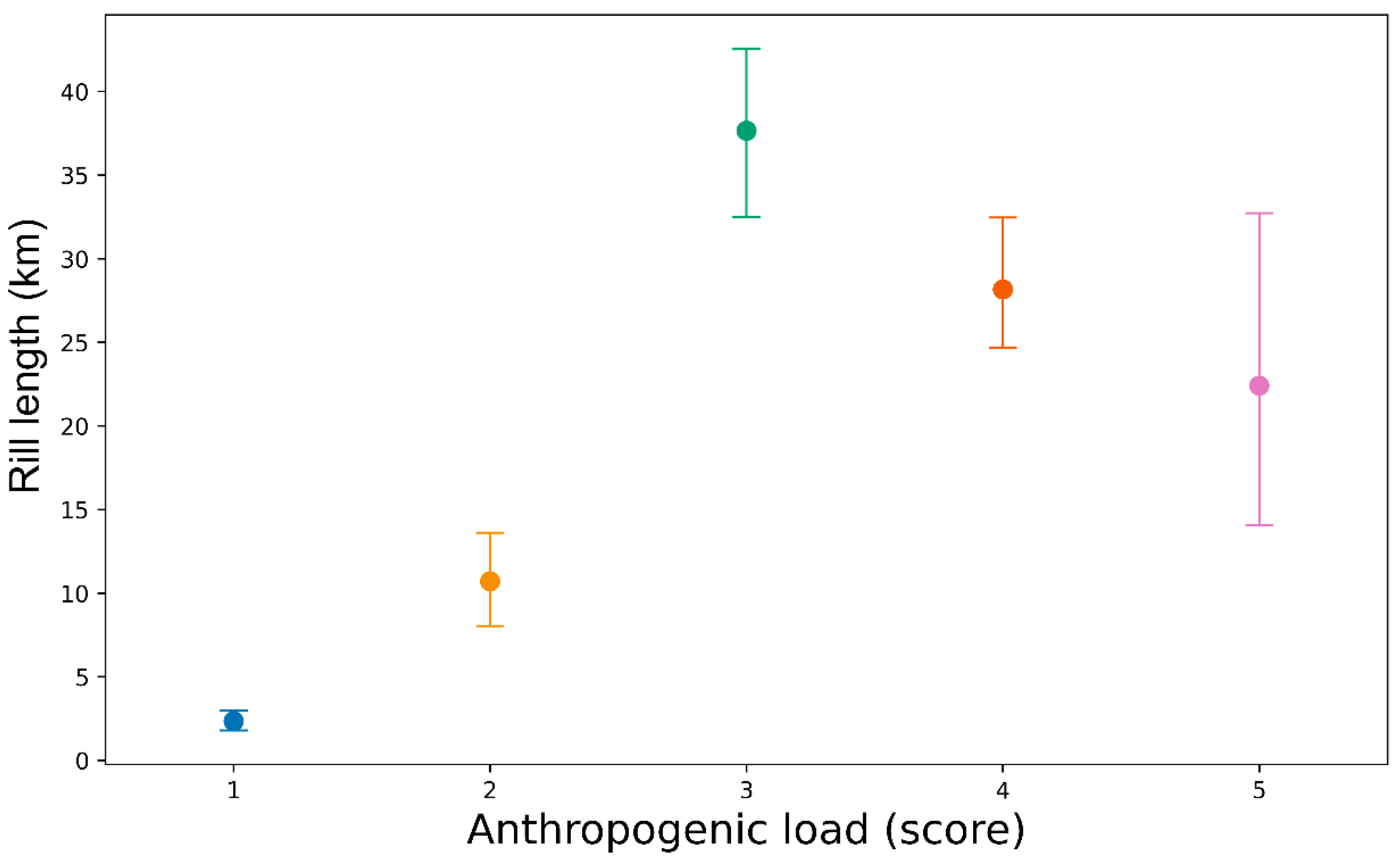
| Name | Description |
|---|---|
| AREA | Basin area (sq. km) |
| SLOPE | Average slope of the basin (degrees) |
| HMEAN | Average elevation in the basin (m) |
| HMAXMIN | Elevation range in the basin (m) |
| TMEAN | Mean annual air temperature (degrees C) in the basin |
| TMAX | Mean annual maximum temperature (degrees C) in the basin |
| TMIN | Mean annual minimums temperature (degrees C) in the basin |
| TAMP | Mean annual variation of air temperature (degrees C) in the basin |
| T1MEAN | Mean air temperature in January (deg. C) in the basin |
| TAKT | Sum of active temperatures (degrees C) in the basin |
| RMEAN | Mean annual precipitation in the basin (mm) |
| R58 | Mean May-August precipitation (mm) in the basin |
| RCOLD | Mean precipitation for the cold period of the year (mm) in the basin |
| RWARM | Mean precipitation for warm period of the year (mm) in the basin |
| RVC | Mean annual precipitation variation coefficient (%) in the basin |
| GTK | Mean value of the hydrothermal coefficient in the basin |
| PARENT1 | Predominant type of soil-forming rocks |
| SOIL0 | Predominant soil type |
| LES_PROC | Forest cover of the basin (%) |
| LAND_COD | Landscape subtype |
| PLT_RANGE | Population density (people/square km) |
| ANTR1 | Anthropogenic load (score) |
| X | Longitude of the basin centroid |
| Y | Latitude of the basin centroid |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gafurov, A. Mapping of Rill Erosion of the Middle Volga (Russia) Region Using Deep Neural Network. ISPRS Int. J. Geo-Inf. 2022, 11, 197. https://doi.org/10.3390/ijgi11030197
Gafurov A. Mapping of Rill Erosion of the Middle Volga (Russia) Region Using Deep Neural Network. ISPRS International Journal of Geo-Information. 2022; 11(3):197. https://doi.org/10.3390/ijgi11030197
Chicago/Turabian StyleGafurov, Artur. 2022. "Mapping of Rill Erosion of the Middle Volga (Russia) Region Using Deep Neural Network" ISPRS International Journal of Geo-Information 11, no. 3: 197. https://doi.org/10.3390/ijgi11030197
APA StyleGafurov, A. (2022). Mapping of Rill Erosion of the Middle Volga (Russia) Region Using Deep Neural Network. ISPRS International Journal of Geo-Information, 11(3), 197. https://doi.org/10.3390/ijgi11030197






