Abstract
In this study, we investigate the urban landscape patterns in Wuhan, China based on the land use data in the vector format. Using the approach of landscape metric analysis, we calculate forty-four vector-based landscape metrics and then reduce redundant ones through a combination of Spearman correlation analysis and factor analysis, in order to extract a core set of characterizing landscape metrics. We find that the urban landscape can be depicted by six factors including the overall shape and diversity, mean proximity, overall area variation, fragmentation variation, elongation variation, and mean shape complexity. After analyzing typical patterns indicated by the core metrics and the spatial distribution of land use patterns, we compare our findings with other studies and discuss how the core metrics coincide and differ.
1. Introduction
Urban ecology systems are predominantly affected by global urbanization. Urbanization dramatically alters urban land use and the spatial patterns of landscapes, directly affecting the ecological safety and sustainable development of cities. Landscape patterns are spatial configurations that combine landscape elements with different sizes and shapes to describe the heterogeneity of landscapes as well as the effects of various ecological processes on different scales [1]. Potentially meaningful orders or rules in disordered landscapes can be identified by analyzing landscape patterns [2].
Land use and its spatial patterns is an element of city spatial patterns and reflects the activities and effects of its inhabitants, which is critical to the regulation of urban ecology systems. Studying current urban land use is significant to the evaluation and improvement of land efficiency, the planning and layout of resource-based cities, and the sustainable development of ecological cities. Therefore, it is important to study the characteristics and patterns of urban spatial landscapes from both theoretical and realistic perspectives, which may lead to the reasonable planning of urban land use, establishment of sustainable urban development modes, and ecological safety of urban landscape patterns.
Landscape metric are used in landscape ecology to describe landscape patterns and measure different aspects of heterogeneity. As quantitative indicators of the structural composition and spatial configuration of landscapes, landscape metrics have been increasingly used for the quantitative expression of sustainable urban land development from meso or macro perspectives. Zhou et al. [3] studied the farmland conversion and urban development patterns by comparing landscape metrics of urban and non-urban planning areas, and found that the farmland patterns were more fragmented in rural areas than in the cities. Jaafari et al. [4] demonstrated the application of landscape metrics to the environmental sustainability assessment of ongoing urbanization processes. Su et al. [5] analyzed the spatiotemporal dynamics of the agricultural landscapes under rapid urbanization using landscape metrics and discovered complexities of relationships between urbanization and agricultural landscape changes.
When analyzing landscape patterns, the characteristics of the landscape and its units, including the type, number, and spatial distribution and configuration of landscape units must be considered. For example, different patches may be distributed in a random, uniform, or aggregated fashion. Many geographic information databases store data in a vector format, such as urban land use maps, administrative diagrams, and cadastral maps. Unlike raster data, every object in vector data is an entity. The topological relationships in spatial data are clear, and the graphic displays are high in quality and precision. In addition, image recovery, updates, and integration can be realized with vector data [6]. Urban land use maps are often stored in a vector data format. These maps serve as a scientific basis [7] for the adjustment and configuration of suitable measures for urban land use patterns and planning in agriculture, mining, urban transportation, urban construction, regional planning, and land consolidation applications.
However, raster data (mostly remote sensing images) have primarily been used to perform landscape metric calculations in previous studies. Although vector data are a commonly used data format, few studies have utilized vector data to directly calculate and analyze landscape metrics [8]. In some studies [9], vector data have been converted into raster data before calculating landscape metrics. Although the technology used to convert vector data into raster data is mature, various problems can occur during the conversion process, such as limitations in the resolution of the raster data. Such problems inevitably reduce the accuracy of the calculation results. The direct calculation of landscape metrics using vector data is a natural solution to this problem.
Meanwhile, many of the existing landscape metrics are correlated. Thus, the use of overlapping metrics to express landscape patterns often leads to redundancy and affects the clarity and accuracy of interpretations. Random subset, expert choice, and exhaustion are the basic methods to extract core landscape metrics in order to describe landscape patterns [10]. Random subset choice and exhaustion methods are less applicable to large volumes of data since they entail the determination of numerous landscape metric combinations [11]. According to Schindler et al. [10], for a set of 52 metrics, it took 7000 random choices to determine the optimal combination; and all of the possible combinations counted to 1.69 million. In addition, expert choice has also low applicability [10], since individuals often have different understandings of mathematical terms and the relationships among landscape metrics and objects of interest. There are also various complex factors influencing expert selections, such as the scape effects of landscape metrics [12,13,14].
Therefore, more objective statistical methods should be used to reduce redundancy in landscape metrics [15], such as decision tree [16], factor analysis or principal component analysis [10,17,18,19], and principal component regression [15]. In decision tree methods, the most significant predictive metrics are selected as the core metrics by predicting the metric randomization process, with the help of statistical tools such as R [10,16]. It is relatively complicated to prevent overfitting caused by outliers [4]. A predefined number of core metrics is needed for principal component regression methods [10,17], but it is not necessary for factor analysis methods, where the core metric set comprise of metrics with the highest factor loadings. Therefore, factor analysis is used in this study, after recommended correlation analyses to exclude highly correlated metrics [10,17,18,19].
In this paper, an exploratory analyzing method based on a combination of correlation analysis and factor analysis is used to extract core landscape metrics from vector land use data obtained from Wuhan, China.
2. Study Area
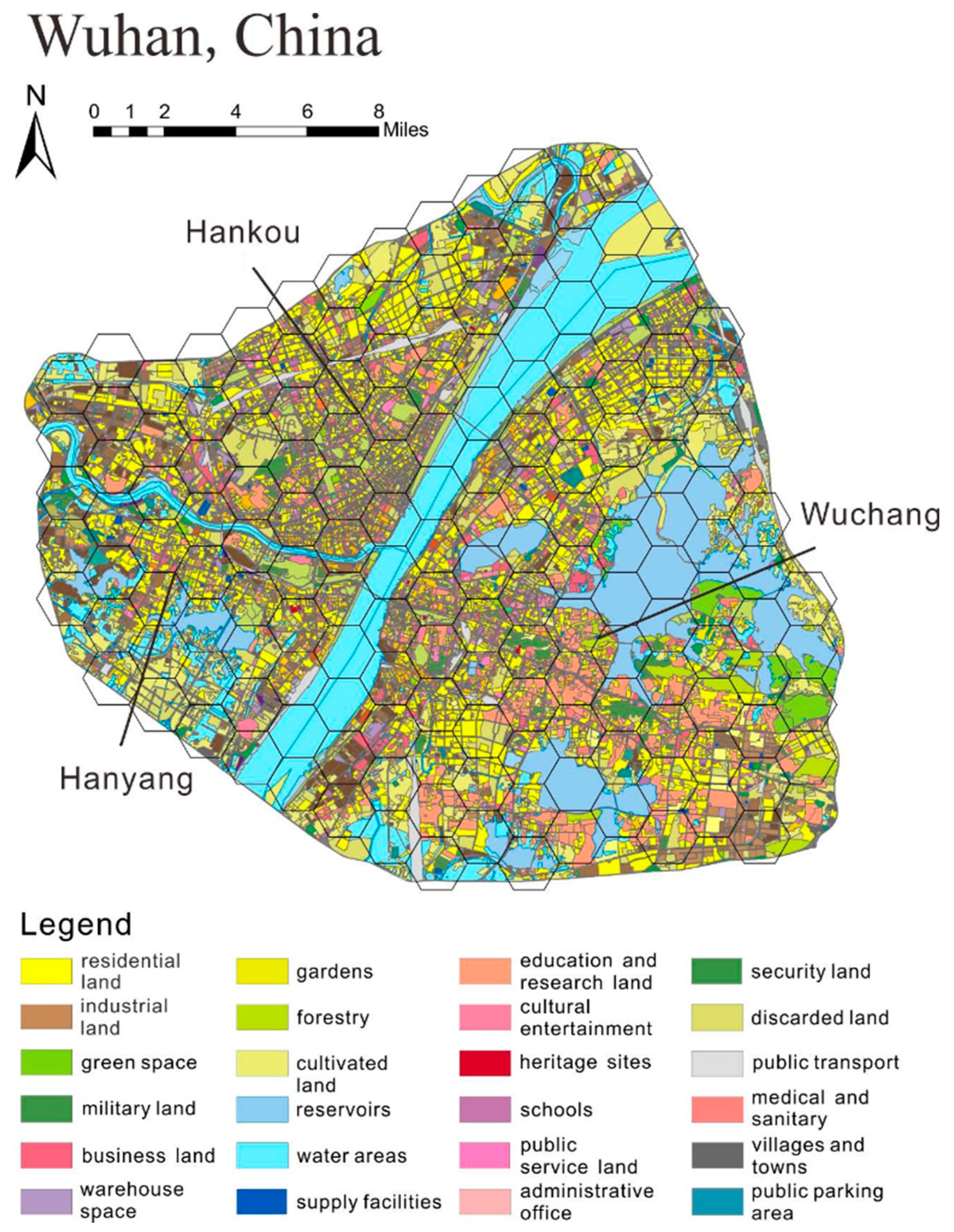
Wuhan, China, is not only a famous historic city, but also serves as an important hub for international trading. The city (Figure 1), which spans from 22°26′ to 23°56′ N and 112°57′ to 114°03′ E, lies at the middle and lower reaches of the Yangtze River in the eastern Jianghan Plain. The Yangtze River, Han River, and many of their branches run through this urban area. The climate of Wuhan is subtropical. The central urban area of Wuhan is comprised of three towns, including Wuchang, Hankou, and Hanyang. These three towns are further divided into seven districts, including Wuchang, Qingshan, Hongshan, Jiang’an, Jianghan, Qiaokou, and Hanyang. The land use classification of Wuhan follows the Code for Classification of Urban Land Use and Planning Standards of Development Land.
Figure 1.
Current urban land use map of Wuhan, China.
Fifty-seven types of land use in Wuhan can be divided into eight broad categories, including residential, commercial, industrial, public service, green, transportation, logistics, and utilities. Residential land consists of four types with varied conditions: R1 (low-rise), R2 (multi-story to high-rise), R3 (mixed with industrial), and R4 land (deteriorated). Industrial land types are based on their environmental effects, ranging from M1 (with rare noise or emission), M2 (moderate level of noise or emission), to M3 (with severe noise or emission). Other categories also consist of multiple types of land for different purposes.
3. Method
3.1. Data Pre-Processing
For a large study area with an area of 79,035 ha, the spatial heterogeneity of the landscape metrics should be investigated. Therefore, in order to achieve homogenous spatial units for proper statistical analysis, we produced equal area hexagons that clipped in different geographic areas from all the study area, and the equal area hexagons were named “sample cells”. The study area was divided into hexagonal cells of equal size, and the landscape metrics of each cell were calculated. The sample cells were designed according to the following principles. (1) An adequate number of sample cells was clipped in order to reduce error in the later exploratory analysis. The number of samples and the area of each sample were carefully selected in order to optimize the metric calculation efficiency and amount of data processing. (2) The sizes and shapes of the sample cells were kept as uniform as possible in order to reduce the effects of the division on the landscape metrics that describe the areas and shapes of features. According to these two principles, the study area was divided into 500-ha hexagons. The hexagons in which less than 80% of the land was in the study area were removed, resulting in a total of 127 sample cells.
3.2. Semantic Similarity
For a hierarchical structure as urban land use type, a semantic similarity matrix can be defined based on the attributes of the hierarchical structure. The semantic similarity matrix represents the similarity between land use types. The larger the value of an element in the matrix is, the more the similarity between two land use types that the element links is. As similarity values range from (completely different) to 1 (completely same) [20]; and contrast weights also range from 0 (no contrast) to 1 (maximum contrast) [2]; therefore, the semantic similarity matrix is used for defining the contrast weights between land use types for Contrast and Aggregation metrics’ calculation in this work.
Based on the set theory and hierarchical structure proposed by Molenaar [7] and Liu et al. [20] and the semantic similarity matrix of urban land use type attributes, the semantic similarity of land use types sij was defined as follows:
where ci and cj are two land use types; l is the shortest distance from the immediate super land use type that subsumes ci and cj at the top of a hierarchy; dci is the shortest distance from the immediate super land use type that subsumes ci and cj to ci; dcj is the shortest distance from the immediate super land use type that subsumes ci and cj to cj; α is a function of the distance from the immediate land use type that subsumes ci and cj to classes ci and cj; and β is used when the immediate super land use type that subsumes ci and cj is located at the top of a hierarchy. All of these distances are expressed in terms of the number of link edges. Experts give a value of 0.5 to the degree of correlation among different sub-trees as well as the degree of correlation among agricultural land, construction land, and unused land [7,20].
3.3. Metric Calculation
When calculating the metrics, it should be noted that the definitions of metrics in vector format might be same as or different from the raster counterpart. There are four cases according to the necessary type of adjustments. The first case is for forty-three landscape metrics suitable for both data formats and yielding the same results regardless of the format. The meanings of such metrics, such as most of the metrics that describe the areas and shapes of patches as well as the diversity metrics, are based on patch properties and are not related to raster units. Therefore, no adjustments were needed to calculate those metrics. The second case is for eighteen landscape metrics which can be properly but differently defined for raster and vector data and thus needing adjustment. The factor 0.25 for squares in shape-related metrics needs to be refactored as 0.282 for round shapes [21], which involves SHAPE (shape index), FRAC (fractal dimension), and LSI (landscape shape index). Inter-patch distances are also affecting aggregation metrics, such as PROX (proximity index) and SIMI (similarity index), when possible zero values of edge-to-edge distances cause arithmetic issues. The third case is when a landscape metric lacks proper meaning though the calculation is valid for vector data formats. Eight such metrics, including the metrics that describe fragmentation and subdivision, such as the Division Index, Splitting Index, and Effective Mesh Size were not considered in this study. The fourth case is when a landscape metric is defined on the basis of raster cells and therefore lacks proper definition in the vector format. This excludes eighteen metrics, such as the Radius of Gyration and Contiguity Index, from this study. After excluding twenty-six metrics in the third and fourth cases, we further selected the most commonly used descriptive statistical metrics, such as the mean (_MN), area-weighted mean (_AM), and coefficient of variance (_CV). Meanwhile, the total area (TA), total edge length (TE), and number of patches (NP) were also excluded from the analysis, since the samples were evenly divided by area.
Given the difference in landscape metrics between the raster format and vector format data presented above, necessary adjustments in metric calculation must be made for the vector data used in this study. A plug-in [22] for ArcMap 10.1 has been developed to implement the adjustments for vector data. Therefore, we used it to calculate landscape metrics for our data in the vector format as the basis of the subsequent exploratory analysis.
Based on the above adjustments, 44 metrics were selected for the vector data calculations in this study (Table A1 in the Appendix). Referencing the grouping in the Fragstats software [2], landscape metrics selected in this study consist of five groups: Group 1—Area and Edge, Group 2—Shape, Group 3—Contrast, Group 4—Aggregation, and Group 5—Diversity.
3.4. Exploratory Analysis
The urban land in Wuhan covers an area of 79,035 ha and contains 20,744 patches. The random subset choice and exhaustion methods were not suitable for the extraction of the landscape metrics herein due to the large volume of data. Principal component regression was also not utilized since an exploratory analysis without predefined factors was adopted. Based on the frequency of use and feasibility of existing methods, a combination of correlation analysis and factor analysis was selected to extract the core landscape metrics of the urban land use of Wuhan. Multivariate statistical analysis methods are easy to operate, practical, and yield relatively accurate results that can be easily analyzed and interpreted compared with other aforementioned methods [10,15,16].
The procedure of the exploratory analysis consists of four steps: First, a Spearman correlation analysis was applied to the landscape metrics of each group. Based on the power to explain variance of possible combination of metrics [23], highly correlated (|r| > 0.9) metrics were then excluded. A factor analysis was performed on the remaining metrics in each group [24]. The metric with the highest factor loading was selected from each group for the overall analysis. The same process was used in the overall analysis, i.e., Spearman correlation analysis followed by metric exclusion and factor analysis. Finally, the metrics with the highest loadings on each factor and meanwhile with high loadings for only that factor were selected as the core set of metrics.
4. Result and Discussion
4.1. Core Set of Metrics
4.1.1. Intra-Group Correlation Analysis
A correlation analysis was performed for each group of metrics. In Group 1 (Area and Edge), the results of the intra-group correlation analysis indicated that correlation coefficients of greater than 0.9 existed between LPI (largest patch index) and AREA_AM (area-weighted mean patch size) as well as ED (edge density) and AREA_MN (mean cell size). The correlation analysis results for the metrics in Group 2 (Shape) and Group 3 (Contrast) indicate no correlation coefficients of greater than 0.9 existed among the metrics. Thus, all of the metrics in these two groups were directly selected for the intra-group factor analysis. For Group 4 (Aggregation), correlation coefficients of greater than 0.9 existed between PD (patch density) and LSI (landscape shape index), PROX_MN (mean proximity index) and PROX_AM (area-weighted mean proximity index). For last Group 5 (Diversity), correlation coefficients of greater than 0.9 existed between the PR (patch richness), PRD (patch richness density), and RPR (relative patch richness). Furthermore, the SHDI (Shannon’s diversity index), SIDI (Simpson’s diversity index), MSIDI (modified Simpson’s diversity index), SHEI (Shannon’s evenness index), SIEI (Simpson’s evenness index), and MSIEI (modified Simpson’s evenness index) metrics all exhibited pair-wise correlation coefficients of greater than 0.9.
4.1.2. Selection among Highly Correlated Metrics
Because the metrics in Group 2 (Shape) and Group 3 (Contrast) had no correlation coefficients over 0.9, these two groups need not make the selection for highly correlated metrics. The metrics from Groups 1, 4, and 5 were selected through the method of Step 2 in Section 3. The results of the metric selection process are shown in Table 1.

Table 1.
Metric selection for Area and Edge, Aggregation, and Diversity.
The results in each group are ranked by the values of last row (i.e., ratio of the explained variance proportion to the sum of the absolute correlation coefficients (∑|r|)) in descending order. In each group, the first line with the largest ratio is highlighted for presenting the results of excluded metrics in this step and selected metrics for overall analysis. In the selection among highly correlated metrics, all possible combinations (4 for Group 1, 4 for Group 4, and 8 for Group 5) where strong correlations could be eliminated with the minimum number of metrics removed and choosing the best subset of all the calculated metrics. Then, the optimum subset of all of the calculated metrics was selected. In addition, since the highest possible richness of all of the samples was 57 and both RPR and PR described richness, only PR was selected. Simpson-based metrics were preferentially selected before Shannon-based metrics due to their efficacy when the richness is greater than 100 [25]. The combinations for each group were ranked by the ratio of cumulative variance to ∑|r|. Through this procedure, LPI, AREA_MN, and AREA_CV (coefficient of variation of cell size) in Group 1; IJI (interspersion and juxtaposition index), LSI, ENN_MN (mean Euclidean nearest-neighbor distance), ENN_AM (area-weighted mean Euclidean nearest-neighbor distance), ENN_CV (coefficient of variation of Euclidean nearest-neighbor distance), PROX_AM, PROX_CV (coefficient of variation of proximity index), SIMI_MN (mean similarity index), SIMI_AM (area-weighted mean similarity index), and SIMI_CV (coefficient of variation of similarity index) in Group 4; and PR and MSIEI in Group 5 were selected for overall analysis.
4.1.3. Selection of the Representative Metrics in Each Group
The highest loading metrics AREA_MN and AREA_CV were chosen from Group 1 (Area and Edge) (Table 1). The five metrics with the highest factor loadings of the 13 metrics in Group 2 (Shape) were selected, namely PARA_CV (coefficient of variance of perimeter-area ratio), SHAPE_MN (mean shape index), FRAC_MN (mean fractal dimension), FRAC_AM (area-weighted mean fractal dimension), and CIRCLE_CV (coefficient of variation of related circumscribing circle). Likewise, five of the metrics in Group 3 (Contrast) were also selected for the factor analysis, namely CWED (contrast-weighted edge density), TECI (total edge contrast index), ECON_MN (mean edge contrast index), ECON_AM (area-weighted mean edge contrast index), and ECON_CV (coefficient of variance of edge contrast index). In Group 4 (Aggregation), the highest loading metrics LSI, PROX_AM, PROX_CV, and ENN_CV were chosen. PR and MSIEI were chosen from Group 5 (Diversity) before. A total of 15 metrics were selected for the overall analysis, namely AREA_MN, AREA_CV, PARA_CV, SHAPE_MN, FRAC_MN, FRAC_AM, CIRCLE_CV, TECI, ECON_CV, LSI, PROX_AM, PROX_CV, ENN_CV, PR, and MSIEI.
4.1.4. Overall Analysis
According to the results of the overall Spearman correlation analysis shown in Table A2 in the Appendix, a correlation coefficient of greater than 0.9 existed between AREA_MN and LSI. As shown by the metric selection results in Table 2, LSI was selected for the overall factor analysis. Six metrics, namely the LSI, PROX_AM, AREA_CV, ECON_CN, CIRCLE_CV, and FRAC_MN, were extracted through the overall analysis.

Table 2.
Metric selection for Overall analysis where strong correlation exists.
As shown in Table 3, a cumulative percent variance contribution of 75.184% was achieved. These six metrics represent six statistical dimensions of landscape patterns:

Table 3.
Overall factor analysis for the 500 ha hexagon grid including 14 metrics retained after Spearman correlation analysis.
- (1)
- Overall shape and diversity, which describes the shape and type diversity of the landscape. It exhibits a high positive loading on the LSI, FRAC_AM and diversity metrics (i.e., PR and MSIEI). LSI measures the ratio of the total edge length to the total area of a landscape and is the overall shape index of the landscape. FRAC_AM measures the mean shape complexity weighted by the patch size, and indicates whether a patch has a regular, simple shape or an irregular, complex shape [2]. The diversity metric measures the richness (PR) and evenness (MSIEI) of the patch types in landscapes.
- (2)
- Mean proximity, which quantifies the spatial context of a patch in relation to its neighbors of the same type [2]. It exhibits a high positive loading on the PROX_AM. The PROX metrics measure the proximity degree of the center patch to other patches of the same type within a certain range. In contrast, the SIMI metrics measure the proximity degree of the center patch to all of the types of patches. The PROX metrics more specifically reflect the background characteristics of the patch in a landscape [2].
- (3)
- Overall area variation, which describes the variance of the patch area and reflects the overall difference in the patch sizes of the landscape. It exhibits a high positive loading on the AREA_CV, coefficient of variation of patch area.
- (4)
- Fragmentation variation, which describes the variance of patch types’ disaggregation. It exhibits a high positive loading on the ECON_CV. The ECON metrics measure the edge contrast of patches. A high degree of variance in the ECON metrics indicate a high edge contrast difference in the corresponding landscape, suggesting that the landscape is highly fragmented.
- (5)
- Elongation variation, which describes the variances of convolution and narrowness. It exhibits a high positive loading on the CIRCLE_CV, which measures the differences in shape among the patches. The CIRCLE metrics use the ratio of the patch area to the circumcircle area to indirectly measure the shape elongation of patches. The CIRCLE metrics reflect the differences among the patch shapes of the landscape.
- (6)
- Mean shape complexity, which describes the mean shape complexity of the landscape based on mean fractal dimension. It exhibits a high positive loading on the FRAC_MN, which is similar to FRAC_AM but without the area-weighted calculation. The fact that the first and the fifth factors both describe the shape characteristics of patches suggests that patch shape is an important spatial attribute of urban land use.
Six landscape metrics with the highest loadings on the six factors (Table 3), including the LSI, PROX_AM, AREA_CV, ECON_CV, CIRCLE_CV, and FRAC_MN, were selected as the core metrics. Thus, each landscape metric representing a factor only exhibits a high loading for that factor, validating the efficacy and practicality of the selected core metrics [9,17].
4.2. Typical Patterns Indicated by Core Metrics
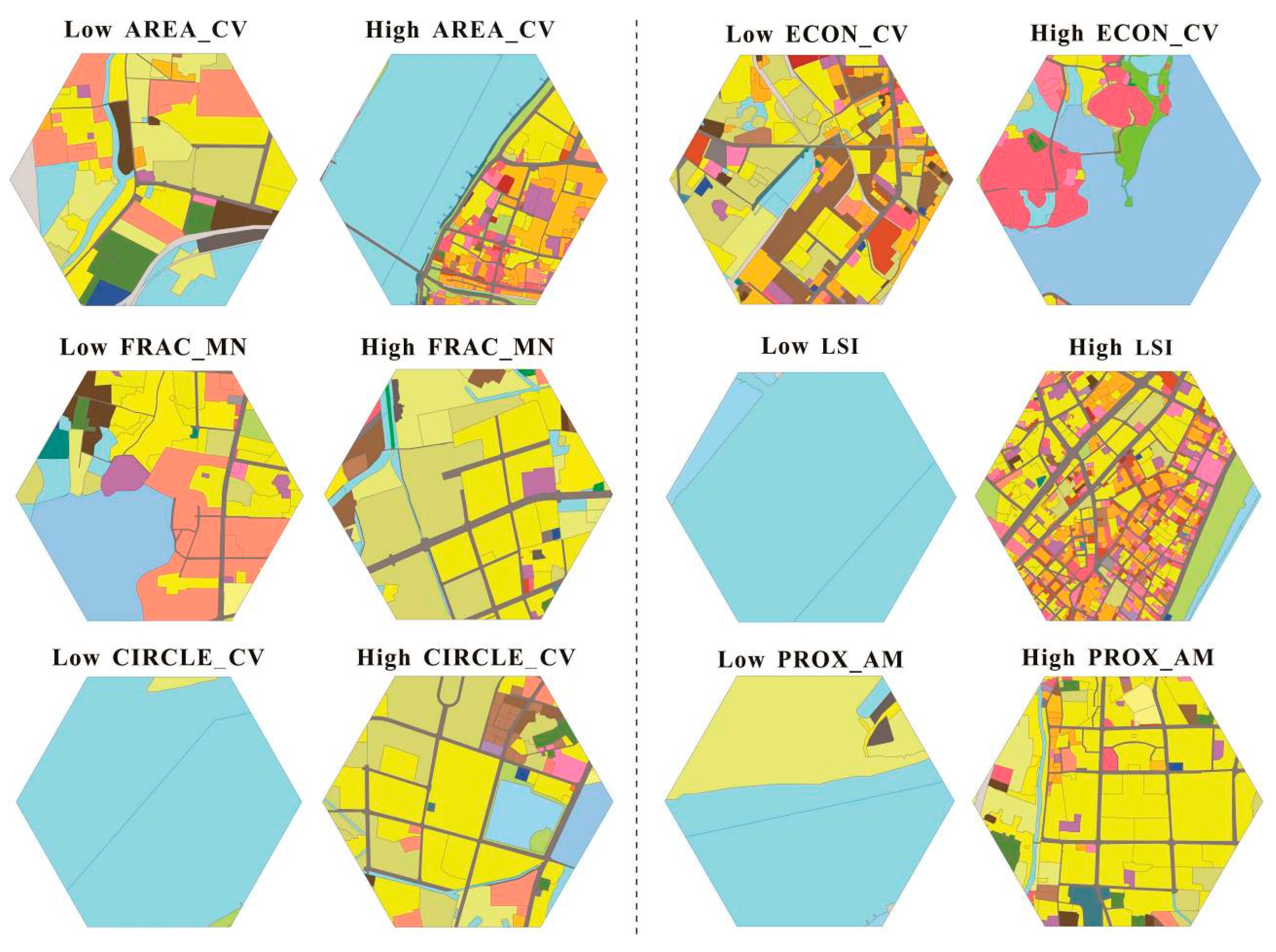
In order to visually illustrate the characteristics of the landscape patterns described by the core metrics, the samples with relatively high values or relatively low values are shown in Figure 2.
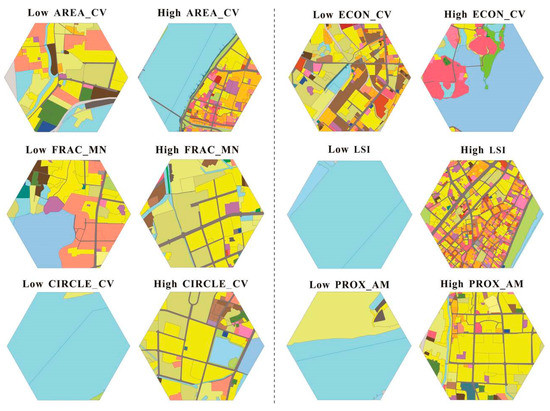
Figure 2.
Resultant gradients of the landscape patterns illustrated with 500-ha hexagons.
The highest LSI value was observed in a hexagon with a large number of high-density patches. The sample with the lowest LSI value contained only a small number of large-area water surface patches.
As shown in Figure 2, the difference in the PROX_AM values was primarily reflected by the spatial proximity of the various types of patches. The sample with the highest PROX_AM value primarily consisted of residential land with scattered commercial land and schools. The lowest PROX_AM value was observed in a sample comprised of natural water surfaces, agricultural land, and a small amount of developed land with a small number of patches.
More than half of the area in the hexagon with the highest AREA_CV value was covered with rivers. However, small-area patches aggregated in the southeast region of the hexagon resulted in a high degree of variance in the patch area. In contrast, the lowest AREA_CV value was observed in a hexagon comprised primarily of patches with similar areas.
The sample with the highest ECON_CV value was comprised of water surfaces, commercial land, and a small amount of residential land and green spaces. The fragmentation variation of this sample was primarily due to the continuity and integrity of the water surfaces as well as the high degree of fragmentation of the other land use types in the northwest region of the sample. The sample with the lowest ECON_CV value was characterized by a mixture of residential land, industrial land, and discarded land, resulting in a high overall edge contrast.
The agricultural land, natural green land, and small number of regular-shaped natural water surface patches in the hexagon with the lowest CIRCLE_CV value resulted in minimal elongation variation. In contrast, the sample with the highest CIRCLE_CV value contained numerous patches with various shape complexities.
The residential and cultivated land patches in the middle of this sample, which were nearly square, and the long, narrow roads segmenting those patches resulted in significant elongation variation. The sample with the highest FRAC_MN value was characterized by numerous long, narrow roads, complex-shaped industrial land, village and town construction land, and irregular natural water surfaces at the edge of the hexagon. In contrast, the sample with the lowest FRAC_MN value was characterized by regular-shaped reservoirs, residential land, and education and research sites.
4.3. Spatial Distribution of Core Metrics
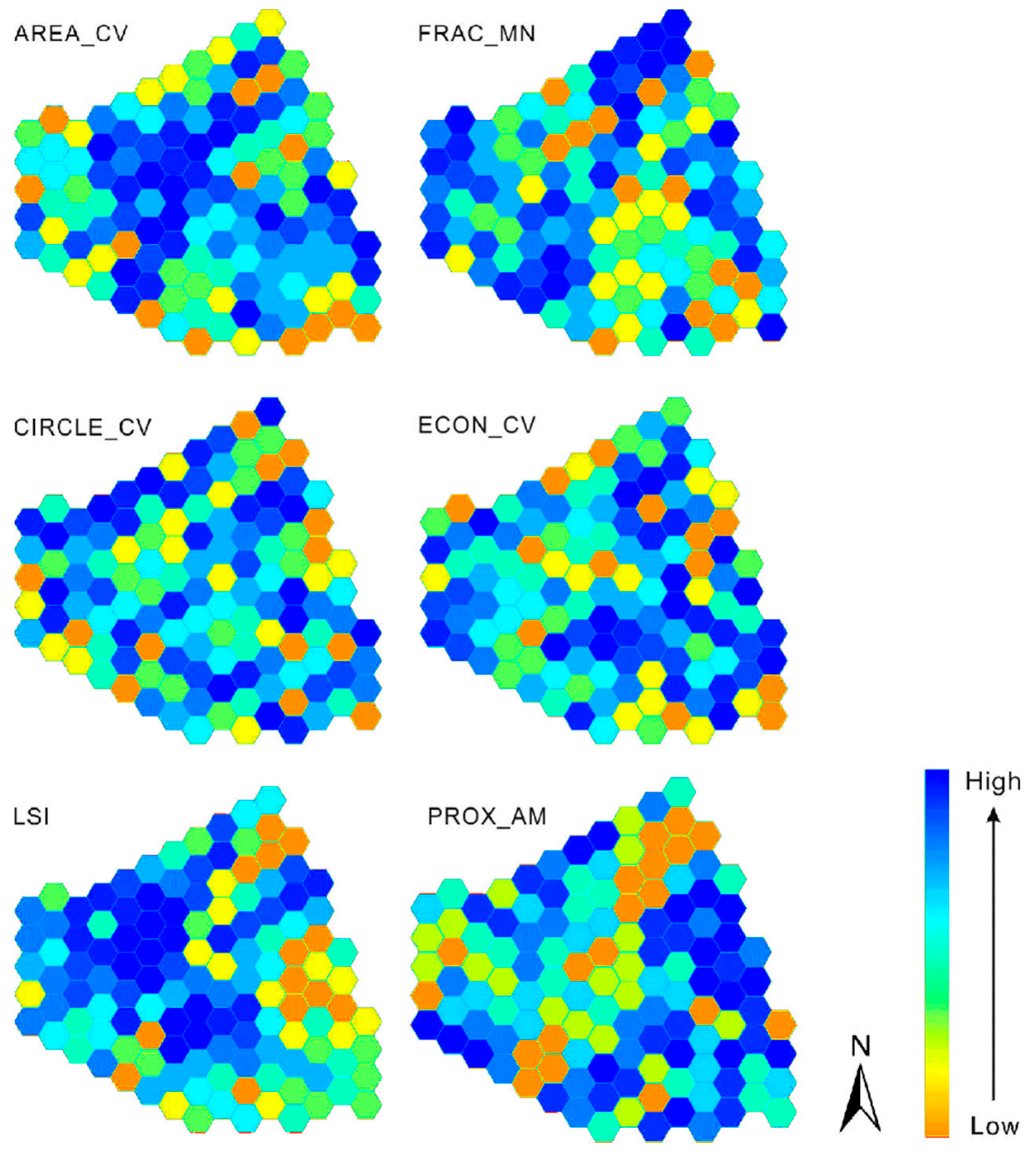
In order to better illustrate the spatial distribution pattern of Wuhan’s urban area, the values of the six core landscape metrics were mapped to all of the hexagons, as shown in Figure 3.
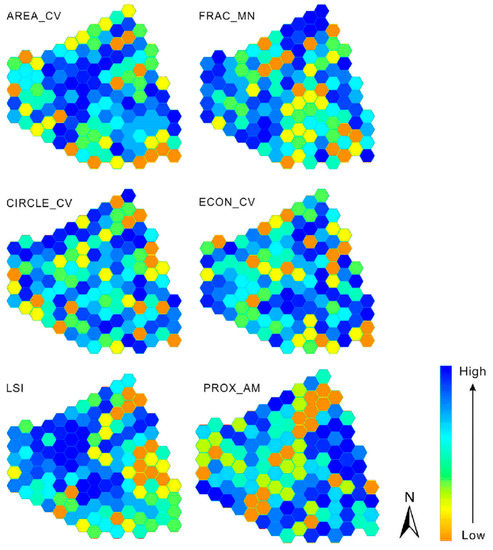
Figure 3.
Value distributions of the six core metrics.
The high values of the LSI metric were clearly clustered on the northwestern area, while the low values were clustered in the southeastern suburbs. The commercial and residential land on the western area was characterized by a high patch density, while the southeastern suburbs primarily consisted of education and research sites, industrial land, and reservoirs with relatively large patch areas and low overall patch density.
A majority of high PROX_AM values were distributed along the eastern edge of the city. In contrast, as shown in Figure 3, relatively low PROX_AM values were apparent in the northeastern region, which was characterized by large areas of natural water surfaces and cultivated land with a high patch proximity. A belt of low PROX_AM values was observed from the northeast to the southwest regions of the city. This region was primarily comprised of the natural water surface patches, which were significantly different from those along the river banks.
The high AREA_CV values were observed in the mid-west region of the city, which was characterized by large areas of unconstructed land, education and research sites, and fragmented residential land and commercial land.
Most of the high ECON_CV values were observed in the western and eastern edges of the city, indicating that higher degrees of fragmentation existed in those regions than in the center of the city. These regions originally consisted of continuous agricultural land, which was later fragmented through human activity in the southern and northern directions. In contrast, a small number of patches with high degrees of fragmentation variation were observed in the central region of the city due to the complex-shaped commercial land and residential land patches near the regular-shaped river and water surface patches.
The CIRCLE_CV metric reflects the degree of variance in the patch shape elongation of a region. As shown in Figure 3, no obvious spatial aggregation or gradient variations in the CIRCLE_CV values were observed, indicating that the degree of elongation variation in the patches was evenly distributed throughout the city. Wuhan is characterized by various types of land use. Moreover, the three towns within Wuhan form multiple business circles with significant human activity. Therefore, the CIRCLE_CV values exhibited a more diffuse pattern.
The high FRAC_MN values were primarily concentrated in the western region of the city, while the low FRAC_MN values were located in the southeastern region of the city. This distribution reflected the effects of human influence on land patch shapes. The southeastern region belongs to the Wuchang District, where urbanization occurred early. Thus, the infrastructure in this region is more complete. In order to intensify the utilization of land, land patches are often reformed into more regular-shaped patches through road construction, patch merging, and other methods.
4.4. Discussion
There are few studies that could be suitable for comparison with this study due to our concern in urban scenario and vector data format. Despite this, we managed to compare our findings with those by Schindler et al. [10], as both studies are at the scale of 500 hectares.
Our depiction of urban landscape needs six core indicators, which is more than four as in the compared study on natural habitats. Both studies find that diversity and shape groups are important source of core indicators, although the relative importance of indicators differs across urban and natural scenarios. Specifically, in our findings, shape complexity (FRAC_AM), variation of patch sizes (AREA_CV), and isolation (PROX_AM) are more useful in characterizing urban landscapes than in natural ones. Interestingly, the variation of fragmentation (ECON_CV) appears more important in urban landscapes while the fragmentation itself (ECON_MN) better captures natural landscapes in the compared study.
Our findings implied difference between urban land use patterns and ecological habitat patterns. For urban landscapes that are usually represented by vector parcels, one might benefit from vector-based analytics, which mitigate potential issues raised during conversion to the raster format.
5. Conclusions
In this study, an exploratory method of landscape metric analysis based on a combination of Spearman correlation analysis and factor analysis is presented. The proposed method reduced metric redundancy and improved the accuracy and clarity of the analysis results. Vector urban land use data obtained from Wuhan, China were used to demonstrate the efficacy of the proposed method. A core set of metrics comprised of six landscape metrics, including LSI, PROX_AM, AREA_CV, ECON_CV, CIRCLE_CV, and FRAC_MN, was extracted from 44 landscape metrics. These six core metrics represent the overall shape and diversity, mean proximity, overall area variation, fragmentation variation, elongation variation, and mean shape complexity of Wuhan’s urban landscape patterns, respectively. This study varied from existing studies in that the landscape metrics were calculated based on vector data with the tool Arc_LIND [22], minimizing potential errors introduced by format conversion.
Future research will focus on the dynamic analysis of urban land use patterns. In addition, the evolution and driving mechanisms of Wuhan’s landscape patterns will be studied using multi-temporal urban land use data and related urbanization data. These studies will provide quantitative standards and assistive means for the sustainable development of cities.
Author Contributions
Conceptualization, Shiwei Shao and Jing Tian; methodology, Jing Tian and Chang Ren; software, Yimin Huang and Yiheng Wang; validation, Shiwei Shao, Mengting Yu and Chang Ren; formal analysis, Shiwei Shao and Mengting Yu; investigation, Mengting Yu and Yimin Huang; resources, Shiwei Shao and Jing Tian; data curation, Shiwei Shao; writing—original draft preparation, Mengting Yu; writing—review and editing, Shiwei Shao and Jing Tian; visualization, Yimin Huang; supervision, Shiwei Shao and Jing Tian; project administration, Jing Tian; funding acquisition, Shiwei Shao All authors have read and agreed to the published version of the manuscript.
Funding
This research was under the project Research on industrial evolution analysis and spatial optimization strategy based on urban residents’ behavioral decision, supported by the Open Fund of Key Laboratory of Urban Land Resources Monitoring and Simulation (grant number KF-2021-06-093) from Chinese Ministry of Natural Resources. It was alsosupported by Natural Science Foundation of China under grant number 41701439.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data in this study have been reported within the article.
Conflicts of Interest
Shao has been working at Zhongzhi Software Technology Company Limited as a technical consultant. There is no potential conflict of interest from this company with regard to this paper. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
Landscape level metrics used in this study (based on FragStats 4.2).
Table A1.
Landscape level metrics used in this study (based on FragStats 4.2).
| Acronym | Metric Name |
|---|---|
| Area and Edge | |
| LPI | Largest Patch index |
| ED | Edge Density |
| AREA_MN | Mean Patch Size |
| AREA_AM | Area-weighted Mean Patch Size |
| AREA_CV | Patch Size Coefficient of Variation |
| Shape | |
| PAFRAC | Perimeter-Area Fractal Dimension |
| PARA_MN | Mean Perimeter-area Ratio |
| PARA_AM | Area-weighted Mean Perimeter-Area Ratio |
| PARA_CV | Perimeter-area Ratio Coefficient of Variation |
| SHAPE_MN | Mean Shape Index |
| SHAPE_AM | Area-weighted Mean Shape Index |
| SHAPE_CV | Shape index Coefficient of Variation |
| FRAC_MN | Mean Fractal Dimension |
| FRAC_AM | Area-weighted Mean Fractal Dimension |
| FRAC_CV | Fractal Dimension Coefficient of Variation |
| CIRCLE_MN | Mean Related Circumscribing Circle |
| CIRCLE_AM | Area-weighted Mean Related Circumscribing Circle |
| CIRCLE_CV | Related Circumscribing Circle Coefficient of Variation |
| Contrast | |
| CWED | Contrast-weighted Edge Density |
| TECI | Total Edge Contrast Index |
| ECON_MN | Mean Edge Contrast Index distribution |
| ECON_AM | Area-weighted Mean Edge Contrast Index distribution |
| ECON_CV | Edge Contrast Index Distribution Coefficient of Variation |
| Aggregation | |
| IJI | Interspersion and Juxtaposition Index |
| LSI | Landscape Shape Index |
| PD | Patch Density |
| ENN_MN | Mean Euclidean Nearest Neighbor Distance |
| ENN_AM | Area-Weighted Mean Euclidean Nearest Neighbor Distance |
| ENN_CV | Euclidean Nearest Neighbor Distance Coefficient of Variation |
| PROX_MN | Mean Proximity Index Distribution |
| PROX_AM | Area-Weighted Mean Proximity Index Distribution |
| PROX_CV | Proximity Index Distribution Coefficient of Variation |
| SIMI_MN | Mean Similarity Index Distribution |
| SIMI_AM | Area-Weighted Mean Similarity Index Distribution |
| SIMI_CV | Similarity Index Distribution Coefficient of Variation |
| Diversity | |
| PR | Patch Richness |
| PRD | Patch Richness Density |
| RPR | Relative Patch Richness |
| SHDI | Shannon’s Diversity Index |
| SHEI | Shannon’s Evenness Index |
| SIDI | Simpson’s Diversity Index |
| SIEI | Simpson’s Evenness Index |
| MSIDI | Modified Simpson’s Diversity Index |
| MSIEI | Modified Simpson’s Evenness Index |

Table A2.
Overall Spearman correlation analysis for the 500 ha hexagon grid, including the 15 metrics, respectively, determined as representatives for the retained factors of the factor analysis per group.
Table A2.
Overall Spearman correlation analysis for the 500 ha hexagon grid, including the 15 metrics, respectively, determined as representatives for the retained factors of the factor analysis per group.
| Metrics | AREA_MN | AREA_CV | PARA_CV | SHAPE_MN | FRAC_MN | FRAC_AM | CIRCLE_CV | TECI | ECON_CV | LSI | ENN_CV | PROX_AM | PROX_CV | PRD | SIDI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AREA_MN | — | ||||||||||||||
| AREA_CV | −0.089 | — | |||||||||||||
| PARA_CV | −0.182 | −0.079 | — | ||||||||||||
| SHAPE_MN | 0.459 | −0.077 | 0.007 | — | |||||||||||
| FRAC_MN | 0.243 | 0.091 | −0.047 | 0.738 | — | ||||||||||
| FRAC_AM | −0.692 | 0.150 | 0.086 | −0.231 | −0.045 | — | |||||||||
| CIRCLE_CV | −0.202 | −0.056 | −0.046 | −0.039 | −0.019 | −0.038 | — | ||||||||
| TECI | −0.076 | −0.177 | −0.037 | 0.084 | 0.060 | 0.265 | 0.153 | — | |||||||
| ECON_CV | 0.038 | 0.132 | −0.238 | −0.224 | −0.096 | 0.174 | 0.004 | 0.111 | — | ||||||
| LSI | −0.963 | −0.051 | 0.167 | −0.372 | −0.196 | 0.751 | 0.174 | 0.155 | −0.003 | — | |||||
| ENN_CV | −0.539 | 0.089 | 0.077 | −0.169 | −0.114 | 0.433 | −0.048 | 0.176 | 0.097 | 0.511 | — | ||||
| PROX_AM | −0.026 | −0.256 | 0.102 | −0.006 | −0.140 | 0.061 | 0.100 | 0.253 | 0.008 | 0.068 | 0.282 | — | |||
| PROX_CV | 0.632 | 0.017 | −0.103 | 0.252 | 0.173 | −0.531 | −0.087 | −0.207 | −0.026 | −0.633 | −0.569 | −0.375 | — | ||
| PRD | −0.799 | 0.064 | 0.129 | −0.303 | −0.100 | 0.544 | 0.300 | 0.047 | −0.126 | 0.778 | 0.233 | −0.215 | −0.392 | — | |
| SIDI | −0.588 | −0.312 | 0.100 | −0.218 | −0.117 | 0.464 | 0.093 | 0.259 | −0.121 | 0.646 | 0.195 | −0.247 | −0.248 | 0.661 | — |
References
- Turner, M.G. The Effect of Pattern on Process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- FRAGSTATS 4.2: Spatial Pattern Analysis Program for Categorical and Continuous Maps; University of Massachusetts: Amherst, MA, USA, 2015.
- Zhou, M.; Tan, S.; Zhang, L. Influences of Different Land Use Spatial Control Schemes on Farmland Conversion and Urban Development. PLoS ONE 2015, 10, e0125008. [Google Scholar] [CrossRef] [PubMed]
- Jaafari, S.; Sakieh, Y.; Shabani, A.A.; Danehkar, A.; Nazarisamani, A. Landscape Change Assessment of Reservation Areas Using Remote Sensing and Landscape Metrics (Case Study: Jajroud Reservation, Iran). Environ. Dev. Sustain. 2016, 18, 1701–1717. [Google Scholar] [CrossRef]
- Su, S.; Jiang, Z.; Zhang, Q.; Zhang, Y. Transformation of Agricultural Landscapes under Rapid Urbanization: A Threat to Sustainability in Hang-Jia-Hu Region, China. Appl. Geogr. 2011, 31, 439–449. [Google Scholar] [CrossRef]
- Fränti, P. Using Hough Transform for Context-Based Image Compression in Hybrid Raster/Vector Applications. J. Electron. Imaging 2002, 11, 236. [Google Scholar] [CrossRef]
- Molenaar, M. (Ed.) The Role of Topological and Hierarchical Spatial Object Models in Database Generalization. In Methods for the Generalization of Geo-Databases; Publications on geodesy; Netherlands Geodetic Commission: Delft, The Netherlands, 1996; pp. 13–36. ISBN 978-90-6132-258-0. [Google Scholar]
- Yang, X.; Liu, Z. Quantifying Landscape Pattern and Its Change in an Estuarine Watershed Using Satellite Imagery and Landscape Metrics. Int. J. Remote Sens. 2005, 26, 5297–5323. [Google Scholar] [CrossRef]
- Schindler, S.; Poirazidis, K.; Wrbka, T. Towards a Core Set of Landscape Metrics for Biodiversity Assessments: A Case Study from Dadia National Park, Greece. Ecol. Indic. 2008, 8, 502–514. [Google Scholar] [CrossRef]
- Schindler, S.; von Wehrden, H.; Poirazidis, K.; Hochachka, W.M.; Wrbka, T.; Kati, V. Performance of Methods to Select Landscape Metrics for Modelling Species Richness. Ecol. Model. 2015, 295, 107–112. [Google Scholar] [CrossRef]
- Williams, J.C.; ReVelle, C.S.; Levin, S.A. Spatial Attributes and Reserve Design Models: A Review. Environ. Model. Assess. 2005, 10, 163–181. [Google Scholar] [CrossRef]
- Wu, J.; Shen, W.; Sun, W.; Tueller, P.T. Empirical Pattern of the Effects of Changing Scale on Landscape Metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Wu, J.G. Effects of Changing Scale on Landscape Pattern Analysis: Scaling Relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Schindler, S.; von Wehrden, H.; Poirazidis, K.; Wrbka, T.; Kati, V. Multiscale Performance of Landscape Metrics as Indicators of Species Richness of Plants, Insects and Vertebrates. Ecol. Indic. 2013, 31, 41–48. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Hochachka, W.M.; Caruana, R.; Fink, D.; Munson, A.; Riedewald, M.; Sorokina, D.; Kelling, S. Data-Mining Discovery of Pattern and Process in Ecological Systems. J. Wildl. Manag. 2007, 71, 2427. [Google Scholar] [CrossRef]
- Riitters, K.H.; O’Neill, R.V.; Hunsaker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A Factor Analysis of Landscape Pattern and Structure Metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Griffith, J.A.; Martinko, E.A.; Price, K.P. Landscape Structure Analysis of Kansas at Three Scales. Landsc. Urban Plan. 2000, 52, 45–61. [Google Scholar] [CrossRef]
- Schindler, S. Dadia National Park, Greece—An Integrated Study on Landscape, Biodiversity, Raptor Populations and Conservation Management. Ph.D. Thesis, University of Vienna, Vienna, Austria, 2010. [Google Scholar]
- Liu, Y.; Molenaar, M.; Kraak, M.J. Semantic Similarity Evaluation Model in Categorical Database Generalisation. In Proceedings of the International Archives of Photogrammetry and Remote Sensing, Ottawa, ON, Canada, 9–12 July 2002; National Resources Canada: Ottawa, ON, Canada, 2002. Part 4 Commission 4. Volume 34, pp. 279–285. [Google Scholar]
- Patch Analyst and Patch Grid; Centre for Northern Forest Ecosystem Research: Thunder Bay, ON, Canada, 2012.
- Yu, M.; Huang, Y.; Cheng, X.; Tian, J. An ArcMap Plug-in for Calculating Landscape Metrics of Vector Data. Ecol. Inform. 2019, 50, 207–219. [Google Scholar] [CrossRef]
- Mishra, S.K. Construction of an Index by Maximization of the Sum of Its Absolute Correlation Coefficients with the Constituent Variables; Social Science Research Network: Rochester, NY, USA, 2007. [Google Scholar]
- Krummel, J.R.; Gardner, R.H.; Sugihara, G.; O’Neill, R.V.; Coleman, P.R. Landscape Patterns in a Disturbed Environment. Oikos 1987, 48, 321–324. [Google Scholar] [CrossRef] [Green Version]
- Yue, T.-X.; Ma, S.-N.; Wu, S.-X.; Zhan, J.-Y. Comparative Analyses of the Scaling Diversity Index and Its Applicability. Int. J. Remote Sens. 2007, 28, 1611–1623. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).