Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Study Area
3.2. Dataset
3.3. Methodology
3.3.1. Evaluation of Land Suitability
3.3.1.1. Calculation of Criteria Value
3.3.1.2. Standardization of Criteria Value
3.3.1.3. Weighting of Criteria
3.3.1.4. Weighted Aggregation of Criteria
3.3.2. Optimized Allocation of Suitable Land
4. Result and Discussion
4.1. Criteria of Residential Land-Use Decision
4.2. Weighted Suitability of Residential Land
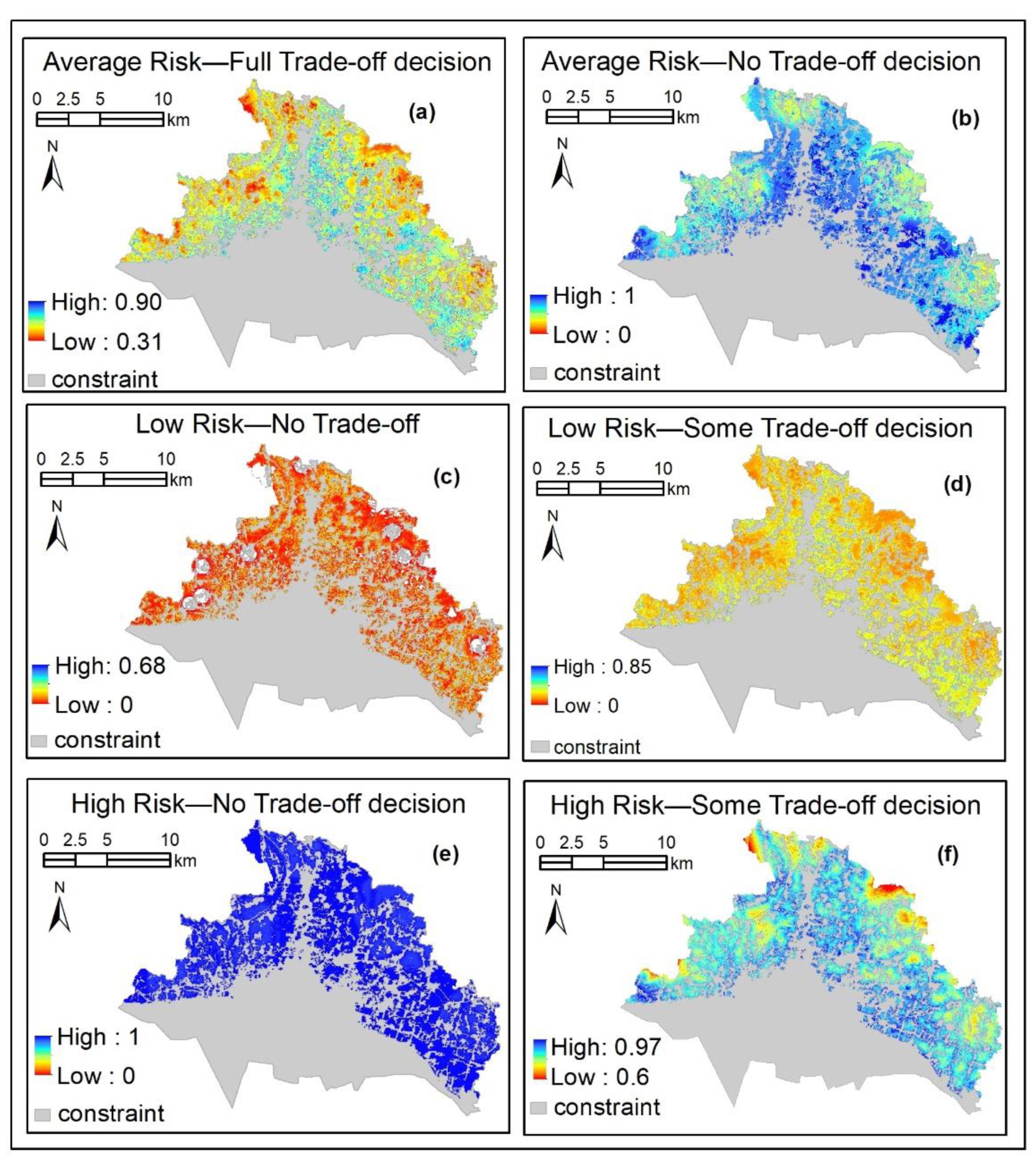
4.3. Optimum Location for Residential Development
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations, Department of Economic and Social Affairs. World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420); United Nations: New York, NY, USA, 2019. [Google Scholar] [CrossRef] [Green Version]
- Knoema. Bangladesh Urban Population, 1960–2021, Jan. 2022. Available online: https://knoema.com/atlas/Bangladesh/Urban-population (accessed on 26 February 2022).
- UN/DESA. World Urbanization Prospect: The 2018 Revision, Key Facts. 2018. Available online: https://population.un.org/wup/Publications/ (accessed on 26 February 2022).
- Jabareen, Y.R. Sustainable Urban Forms: Their typologies, models, and concepts. J. Plan. Educ. Res. 2006, 26, 38–52. [Google Scholar] [CrossRef]
- Persson, C. Deliberation or doctrine? Land use and spatial planning for sustainable development in Sweden. Land Use Policy 2013, 34, 301–313. [Google Scholar] [CrossRef]
- Ward, D.P.; Murray, A.T.; Phinn, S.R. Integrating spatial optimization and cellular automata for evaluating urban change. Ann. Reg. Sci. 2003, 37, 131–148. [Google Scholar] [CrossRef]
- Akash, M.; Akter, J.; Tamanna, T.; Kabir, M.R. The Urbanization and Environmental Challenges in Dhaka City. In Proceedings of the RAIS Conference, Tampa, FL, USA, 19–20 February 2018; pp. 45–57. [Google Scholar] [CrossRef] [Green Version]
- Kudrat-E-Khuda. Causes of Air Pollution in Bangladesh’s Capital City and Its Impacts on Public Health. Nat. Environ. Pollut. Technol. 2020, 19, 1483–1490. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Church, R.L.; Jankowski, P. Spatial optimization as a generative technique for sustainable multiobjective land-use allocation. Int. J. Geogr. Inf. Sci. 2008, 22, 601–622. [Google Scholar] [CrossRef]
- El Din, H.S.; Shalaby, A.; Farouh, H.E.; Elariane, S. Principles of urban quality of life for a neighborhood. HBRC J. 2013, 9, 86–92. [Google Scholar] [CrossRef] [Green Version]
- Dempsey, N.; Bramley, G.; Power, S.; Brown, C. The social dimension of sustainable development: Defining urban social sustainability. Sustain. Dev. 2011, 19, 289–300. [Google Scholar] [CrossRef]
- Badhan, I.M.; Ching, S.W. The Exploration of Effective Spatial Performance of Accessible Neighbourhood Green (Ang), Including its Proportion and Standard Distance from User in Dhanmondi Residential Area, Dhaka. Creat. Space 2021, 8, 57–66. [Google Scholar] [CrossRef]
- Nancy, D.S.J. Urban Densification and Social Sustainability: A Case Study of Dhaka. Glob. J. Hum.-Soc. Sci. 2021, 21, 17–36. [Google Scholar] [CrossRef]
- Roy, S.; Sowgat, T.; Islam, S.M.T.; Anjum, N. Sustainability Challenges for Sprawling Dhaka. Environ. Urban. ASIA 2021, 12, S59–S84. [Google Scholar] [CrossRef]
- Karimi, A.; Hockings, M. A social-ecological approach to land-use conflict to inform regional and conservation planning and management. Landsc. Ecol. 2018, 33, 691–710. [Google Scholar] [CrossRef]
- Wang, S.-D.; Zhang, H.-B.; Wang, X.-C. Simulating Land Use Structure Optimization Based on an Improved Multi-Objective Differential Evolution Algorithm. Pol. J. Environ. Stud. 2019, 28, 887–899. [Google Scholar] [CrossRef]
- Rahman, M.; Szabó, G. Multi-objective urban land use optimization using spatial data: A systematic review. Sustain. Cities Soc. 2021, 74, 103214. [Google Scholar] [CrossRef]
- Song, M.; Chen, D. An improved knowledge-informed NSGA-II for multi-objective land allocation (MOLA). Geo-Spat. Inf. Sci. 2018, 21, 273–287. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Ke, X.; Xiao, B.; Zhou, T. Optimising land use allocation to balance ecosystem services and economic benefits—A case study in Wuhan, China. J. Environ. Manag. 2019, 248, 109306. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, W.; Wang, T. Spatio-temporal land use multi-objective optimization: A case study in Central China. Trans. GIS 2019. [Google Scholar] [CrossRef]
- Cao, K.; Batty, M.; Huang, B.; Liu, Y.; Yu, L.; Chen, J. Spatial multi-objective land use optimization: Extensions to the non-dominated sorting genetic algorithm-II. Int. J. Geogr. Inf. Sci. 2011, 25, 1949–1969. [Google Scholar] [CrossRef]
- Haque, A.; Asami, Y. Optimizing Urban Land-Use Allocation: Case Study of Dhanmondi Residential Area, Dhaka, Bangladesh. Environ. Plan. B Plan. Des. 2011, 38, 388–410. [Google Scholar] [CrossRef]
- Neema, M.; Ohgai, A. Multi-objective location modeling of urban parks and open spaces: Continuous optimization. Comput. Environ. Urban Syst. 2010, 34, 359–376. [Google Scholar] [CrossRef]
- Steele, K.; Carmel, Y.; Cross, J.; Wilcox, C. Uses and Misuses of Multicriteria Decision Analysis (MCDA) in Environmental Decision Making. Risk Anal. 2009, 29, 26–33. [Google Scholar] [CrossRef]
- Romano, G.; Sasso, P.D.; Liuzzi, G.T.; Gentile, F. Multi-criteria decision analysis for land suitability mapping in a rural area of Southern Italy. Land Use Policy 2015, 48, 131–143. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Verdoodt, A.; Van, Y.N.T.; Delbecque, N.; Tran, T.C.; Van Ranst, E. Design of a GIS and multi-criteria based land evaluation procedure for sustainable land-use planning at the regional level. Agric. Ecosyst. Environ. 2015, 200, 1–11. [Google Scholar] [CrossRef]
- Rahman, M.; Szabó, G. A Novel Composite Index to Measure Environmental Benefits in Urban Land Use Optimization Problems. ISPRS Int. J. Geo-Inf. 2022, 11, 220. [Google Scholar] [CrossRef]
- Rahman, M.; Szabó, G. A Geospatial Approach to Measure Social Benefits in Urban Land Use Optimization Problem. Land 2021, 10, 1398. [Google Scholar] [CrossRef]
- Abdullah, A.Y.M.; Masrur, A.; Adnan, M.S.G.; Baky, M.A.A.; Hassan, Q.K.; Dewan, A. Spatio-temporal Patterns of Land Use/Land Cover Change in the Heterogeneous Coastal Region of Bangladesh between 1990 and 2017. Remote Sens. 2019, 11, 790. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Nastaran, M.; Sahebgharani, A. Sustainable Spatial Land Use Optimization through Non-Dominated Sorting Genetic Algorithm-II (NSGA-II): (Case Study: Baboldasht District of Isfahan). Indian J. Sci. Technol. 2015, 8, 118. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, W. Sustainable Land-Use Planning for a Downtown Lake Area in Central China: Multiobjective Optimization Approach Aided by Urban Growth Modeling. J. Urban Plan. Dev. 2014, 140, 04014002. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhang, X.; Skitmore, M. Implications for sustainable land use in high-density cities: Evidence from Hong Kong. Habitat Int. 2015, 50, 23–34. [Google Scholar] [CrossRef]
- Kim, M.; You, S.; Chon, J.; Lee, J. Sustainable Land-Use Planning to Improve the Coastal Resilience of the Social-Ecological Landscape. Sustainability 2017, 9, 1086. [Google Scholar] [CrossRef] [Green Version]
- Handayanto, R.T.; Tripathi, N.K.; Kim, S.M.; Guha, S. Achieving a Sustainable Urban Form through Land Use Optimisation: Insights from Bekasi City’s Land-Use Plan (2010–2030). Sustainability 2017, 9, 221. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Gong, Y.; Cai, L.; Sun, C.; Chen, Y.; Liu, Y.; Jiang, P. Sustainable Land-Use Allocation: A Multiobjective Particle Swarm Optimization Model and Application in Changzhou, China. J. Urban Plan. Dev. 2018, 144, 04018010. [Google Scholar] [CrossRef]
- Cao, K.; Huang, B.; Wang, S.; Lin, H. Sustainable land use optimization using Boundary-based Fast Genetic Algorithm. Comput. Environ. Urban Syst. 2012, 36, 257–269. [Google Scholar] [CrossRef]
- Yuan, M.; Liu, Y.; He, J.; Liu, D. Regional land-use allocation using a coupled MAS and GA model: From local simulation to global optimization, a case study in Caidian District, Wuhan, China. Cartogr. Geogr. Inf. Sci. 2014, 41, 363–378. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, Y.; Jin, X.; Shu, B.; Zhou, Y.; Yang, X. Simulating multi-objective land use optimization allocation using Multi-agent system—A case study in Changsha, China. Ecol. Model. 2016, 320, 334–347. [Google Scholar] [CrossRef]
- Jenks, M.; Jones, C. (Eds.) Issues and Concepts. In Dimensions of the Sustainable City; Springer: London, UK, 2010; p. 9. [Google Scholar]
- Mouratidis, K. Is compact city livable? The impact of compact versus sprawled neighbourhoods on neighbourhood satisfaction. Urban Stud. 2017, 55, 2408–2430. [Google Scholar] [CrossRef]
- Kotulla, T.; Denstadli, J.M.; Oust, A.; Beusker, E. What Does It Take to Make the Compact City Liveable for Wider Groups? Identifying Key Neighbourhood and Dwelling Features. Sustainability 2019, 11, 3480. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, M.; Aziz, A.; Al-Rashid, M.A.; Tesoriere, G.; Asim, M.; Campisi, T. Scaling the Potential of Compact City Development: The Case of Lahore, Pakistan. Sustainability 2021, 13, 5257. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Sremac, S. A New Model for Determining Weight Coefficients of Criteria in MCDM Models: Full Consistency Method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef] [Green Version]
- Hošková-Mayerová, Š.; Talhofer, V.; Otřísal, P.; Rybanský, M. Influence of Weights of Geographical Factors on the Results of Multicriteria Analysis in Solving Spatial Analyses. ISPRS Int. J. Geo-Inf. 2020, 9, 489. [Google Scholar] [CrossRef]
- Köhler, B.; Ruud, A.; Aas, Ø.; Barton, D.N. Decision making for sustainable natural resource management under political constraints—The case of revising hydropower licenses in Norwegian watercourses. Civ. Eng. Environ. Syst. 2019, 36, 17–31. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, A.; Fung, T. Using GIS and Multi-criteria Decision Analysis for Conflict Resolution in Land Use Planning. Procedia Environ. Sci. 2012, 13, 2264–2273. [Google Scholar] [CrossRef] [Green Version]
- Mendas, A.; Delali, A. Integration of MultiCriteria Decision Analysis in GIS to develop land suitability for agriculture: Application to durum wheat cultivation in the region of Mleta in Algeria. Comput. Electron. Agric. 2012, 83, 117–126. [Google Scholar] [CrossRef]
- Luan, C.; Liu, R.; Peng, S. Land-use suitability assessment for urban development using a GIS-based soft computing approach: A case study of Ili Valley, China. Ecol. Indic. 2021, 123, 107333. [Google Scholar] [CrossRef]
- Yager, R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Rahman, M.; Szabó, G. Impact of Land Use and Land Cover Changes on Urban Ecosystem Service Value in Dhaka, Bangladesh. Land 2021, 10, 793. [Google Scholar] [CrossRef]
- Assefa, T.; Jha, M.; Reyes, M.; Srinivasan, R.; Worqlul, A.W. Assessment of Suitable Areas for Home Gardens for Irrigation Potential, Water Availability, and Water-Lifting Technologies. Water 2018, 10, 495. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Liu, Y.; Chen, W. Optimal land use allocation of urban fringe in Guangzhou. J. Geogr. Sci. 2012, 22, 179–191. [Google Scholar] [CrossRef]
- Božanić, D.; Tešić, D.; Milićević, J. A hybrid fuzzy ahp-mabac model: Application in the serbian army—The selection of thelocation for deep wading as a technique of crossing the river by tanks. Decis. Mak. Appl. Manag. Eng. 2018, 1, 143–164. [Google Scholar] [CrossRef]
- Jiang, H.; Eastman, J.R. Application of fuzzy measures in multi-criteria evaluation in GIS. Int. J. Geogr. Inf. Sci. 2000, 14, 173–184. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI Selva Manual—Guide to GIS and Image Processing; Clark University; Worcester, MA, USA, 2012. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Kadoic, N. Characteristics of the Analytic Network Process, a Multi-Criteria Decision-Making Method. Croat. Oper. Res. Rev. 2018, 9, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Olsen, A.A.; Wolcott, M.D.; Haines, S.T.; Janke, K.K.; McLaughlin, J.E. How to use the Delphi method to aid in decision making and build consensus in pharmacy education. Curr. Pharm. Teach. Learn. 2021, 13, 1376–1385. [Google Scholar] [CrossRef] [PubMed]
- Oluleye, I.B.; Ogunleye, M.B.; Oyetunji, A.K. Evaluation of the critical success factors for sustainable housing delivery: Analytic hierarchy process approach. J. Eng. Des. Technol. 2020, 19, 1044–1062. [Google Scholar] [CrossRef]
- Oluleye, I.B.; Oyetunji, A.K.; Olukolajo, M.A.; Chan, D.W. Integrating building information modelling for improving facility management operations: A fuzzy synthetic evaluation of the critical success factors. J. Facil. Manag. 2021. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Nguyen, T.; Bleys, B. Applying Analytic Hierarchy Process to Adaptation to Saltwater Intrusion in Vietnam. Sustainability 2021, 13, 2311. [Google Scholar] [CrossRef]
- Starr, S.; Zeleny, M. MCDM: State and future of the arts. In Multiple Criteria Decision Making; North-Holland: Amsterdam, The Netherlands, 1977; pp. 5–9. [Google Scholar]
- Malczewski, J. Ordered weighted averaging with fuzzy quantifiers: GIS-based multicriteria evaluation for land-use suitability analysis. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 270–277. [Google Scholar] [CrossRef]
- Ustaoglu, E.; Aydınoglu, A. Suitability evaluation of urban construction land in Pendik district of Istanbul, Turkey. Land Use Policy 2020, 99, 104783. [Google Scholar] [CrossRef]
- Masoudi, M.; Centeri, C.; Jakab, G.; Nel, L.; Mojtahedi, M. GIS-Based Multi-Criteria and Multi-Objective Evaluation for Sustainable Land-Use Planning (Case Study: Qaleh Ganj County, Iran) “Landuse Planning Using MCE and Mola”. Int. J. Environ. Res. 2021, 15, 457–474. [Google Scholar] [CrossRef]
- Hajehforooshnia, S.; Soffianian, A.; Mahiny, A.S.; Fakheran, S. Multi objective land allocation (MOLA) for zoning Ghamishloo Wildlife Sanctuary in Iran. J. Nat. Conserv. 2011, 19, 254–262. [Google Scholar] [CrossRef]







| Criteria | Types | Name |
|---|---|---|
| Factors | Physical factors | Distance from the town center |
| Distance from main roads | ||
| Distance from existing residential land | ||
| Distance from brickfield | ||
| Land elevation | ||
| Sustainability factors | Social benefit | |
| Environmental benefit | ||
| Economic benefit | ||
| Constraints | Existing land use | |
| Existing water bodies | ||
| Factors | Fuzzy Membership Function | Control Points | Shape of Function | |||
|---|---|---|---|---|---|---|
| a | b | c | d | |||
| Distance from city center | Linear | 0 | 1531 | Monotonically decreasing | ||
| Distance from main roads | Linear | 30 | 7648 | Monotonically decreasing | ||
| Distance from existing residential land | Linear | 30 | 3222 | Monotonically decreasing | ||
| Distance from brickfield | Sigmoidal | 500 | 3000 | Monotonically increasing | ||
| Land elevation | Linear | 12 | 22 | Monotonically increasing | ||
| Social benefit | Linear | 0.23 | 0.8 | Monotonically decreasing | ||
| Environmental benefit | Linear | 0.05 | 0.84 | Monotonically decreasing | ||
| Economic benefit | Linear | 0.08 | 1 | Monotonically decreasing | ||
| Intensity of Importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two activities contribute equally to the objective |
| 3 | Moderate importance of one over another | Experience and judgment slightly favor one activity over another |
| 5 | Essential or strong importance | Experience and judgment strongly favor one activity over another |
| 7 | Very strong importance | An activity is strongly favored, and its dominance demonstrated in practice |
| 9 | Extreme importance | The evidence favoring one activity over another is of the highest possible order of affirmation |
| 2, 4, 6, 8 | Intermediate values between the two adjacent judgments | When compromise is needed |
| Decision Strategies | Ordered Weights | |||||||
|---|---|---|---|---|---|---|---|---|
| Average Level of Risk—Full Trade-Off | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 |
| Low Risk—No Trade-Off | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| High Risk—No Trade-Off | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Low Level of Risk—Some Trade-Off | 0.4 | 0.3 | 0.12 | 0.07 | 0.05 | 0.03 | 0.02 | 0.01 |
| High Level of Risk—Some Trade-Off | 0.01 | 0.02 | 0.03 | 0.05 | 0.07 | 0.12 | 0.3 | 0.4 |
| Average Level of Risk - No Trade-Off | 0 | 0 | 0 | 0.5 | 0.5 | 0 | 0 | 0 |
| Factors | Weight |
|---|---|
| Distance from brickfield | 0.06 |
| Digital elevation model (DEM) | 0.05 |
| Distance from main roads | 0.16 |
| Distance from the town center | 0.10 |
| Distance from existing residential land | 0.11 |
| Social benefit | 0.27 |
| Economic benefit | 0.04 |
| Environmental benefit | 0.22 |
| Sustainability Dimension | Sustainability Benefit Value (Unitless) | ||
|---|---|---|---|
| Without Considering Sustainability | Considering Sustainability | % Increase of Benefit Considering Sustainability | |
| Social benefit | 95,370.08 | 100,775.70 | 5.67 |
| Environmental benefit | 62,277.21 | 67,616.00 | 8.57 |
| Economic benefit | 20,283.13 | 25,553.56 | 25.98 |
| Total | 177,930.42 | 193,945.26 | 9.00 |
| Sustainability Dimension | Sustainability Values Under Different Decision Strategies (Unitless) | |||||
|---|---|---|---|---|---|---|
| ARFT | ARNT | HRNT | HRST | LRNT | LRST | |
| Social benefit | 64,970.11 | 65,502.01 | 66,184.19 | 63,883.22 | 64,851.03 | 65,333.28 |
| Environmental benefit | 21,122.65 | 21,331.75 | 21,432.61 | 20,814.49 | 21,088.68 | 21,256.21 |
| Economic benefit | 184,282.03 | 185,542.07 | 188,179.53 | 182,448.89 | 184,897.84 | 185,908.95 |
| Total benefit | 64,970.11 | 65,502.01 | 66,184.19 | 63,883.22 | 64,851.03 | 65,333.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Szabó, G. Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach. ISPRS Int. J. Geo-Inf. 2022, 11, 313. https://doi.org/10.3390/ijgi11050313
Rahman MM, Szabó G. Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach. ISPRS International Journal of Geo-Information. 2022; 11(5):313. https://doi.org/10.3390/ijgi11050313
Chicago/Turabian StyleRahman, Md. Mostafizur, and György Szabó. 2022. "Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach" ISPRS International Journal of Geo-Information 11, no. 5: 313. https://doi.org/10.3390/ijgi11050313
APA StyleRahman, M. M., & Szabó, G. (2022). Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach. ISPRS International Journal of Geo-Information, 11(5), 313. https://doi.org/10.3390/ijgi11050313






