Measuring the Spatial Accessibility of Parks in Wuhan, China, Using a Comprehensive Multimodal 2SFCA Method
Abstract
:1. Introduction
2. Related Works
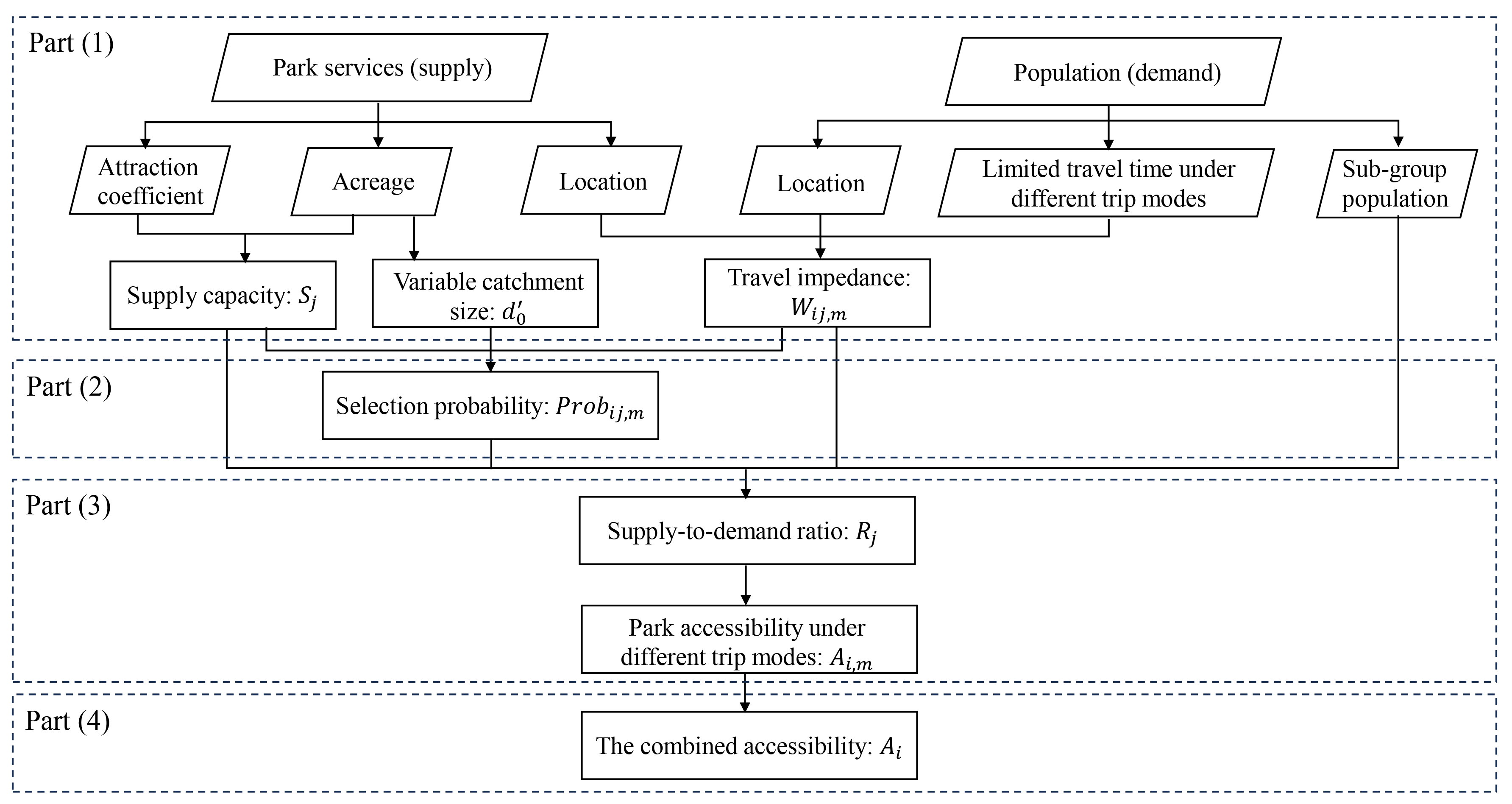
3. Methodology
3.1. Traditional Multimodal 2SFCA Method
3.2. Comprehensive Multimodal 2SFCA Method
3.3. Spatial Pattern Analysis of Park Accessibility
4. Experiment and Analysis
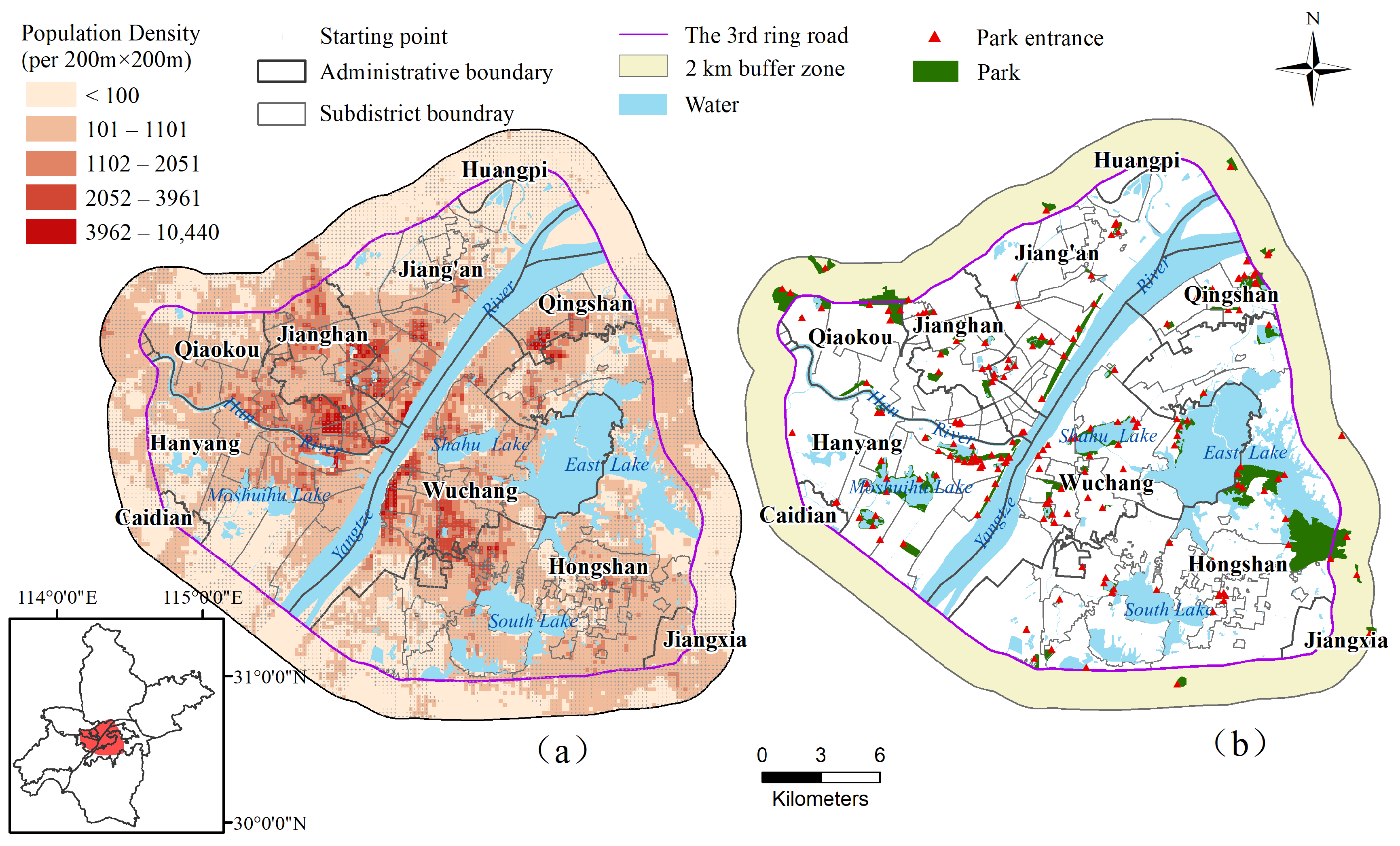
4.1. Study Area and Data
4.1.1. Study Area
4.1.2. Data Sources and Processing
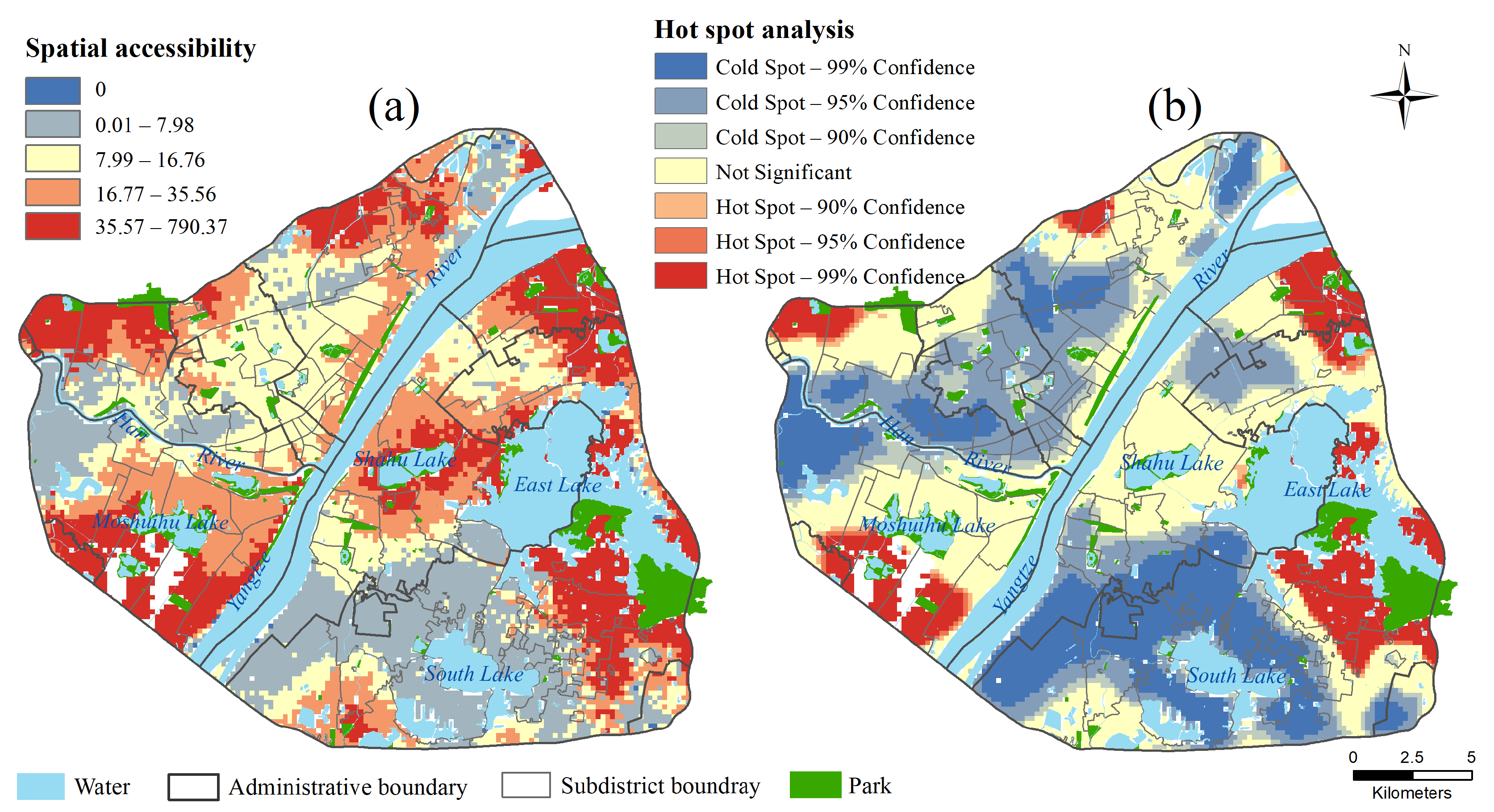
4.2. Multimodel Park Accessibility Analysis
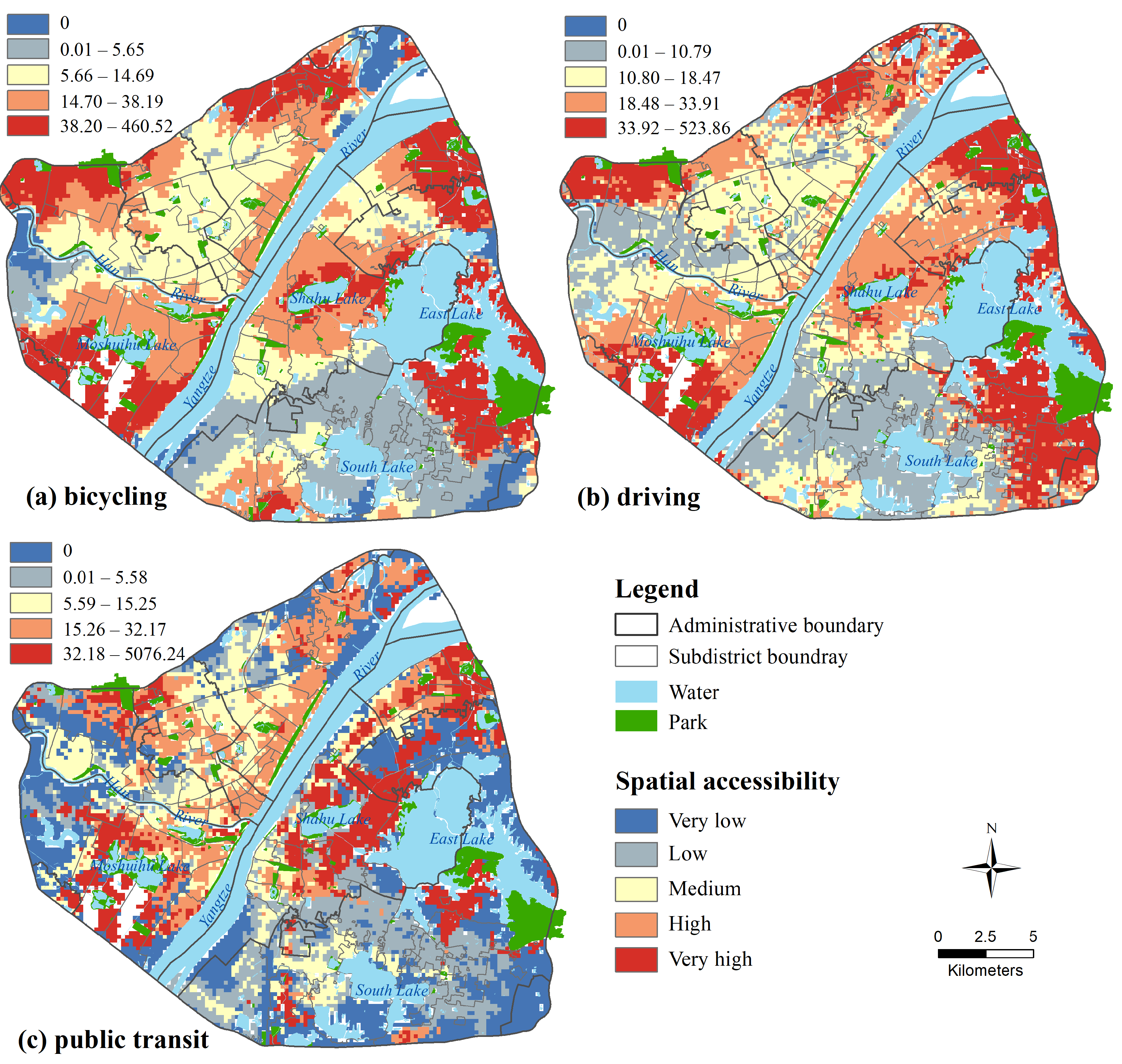
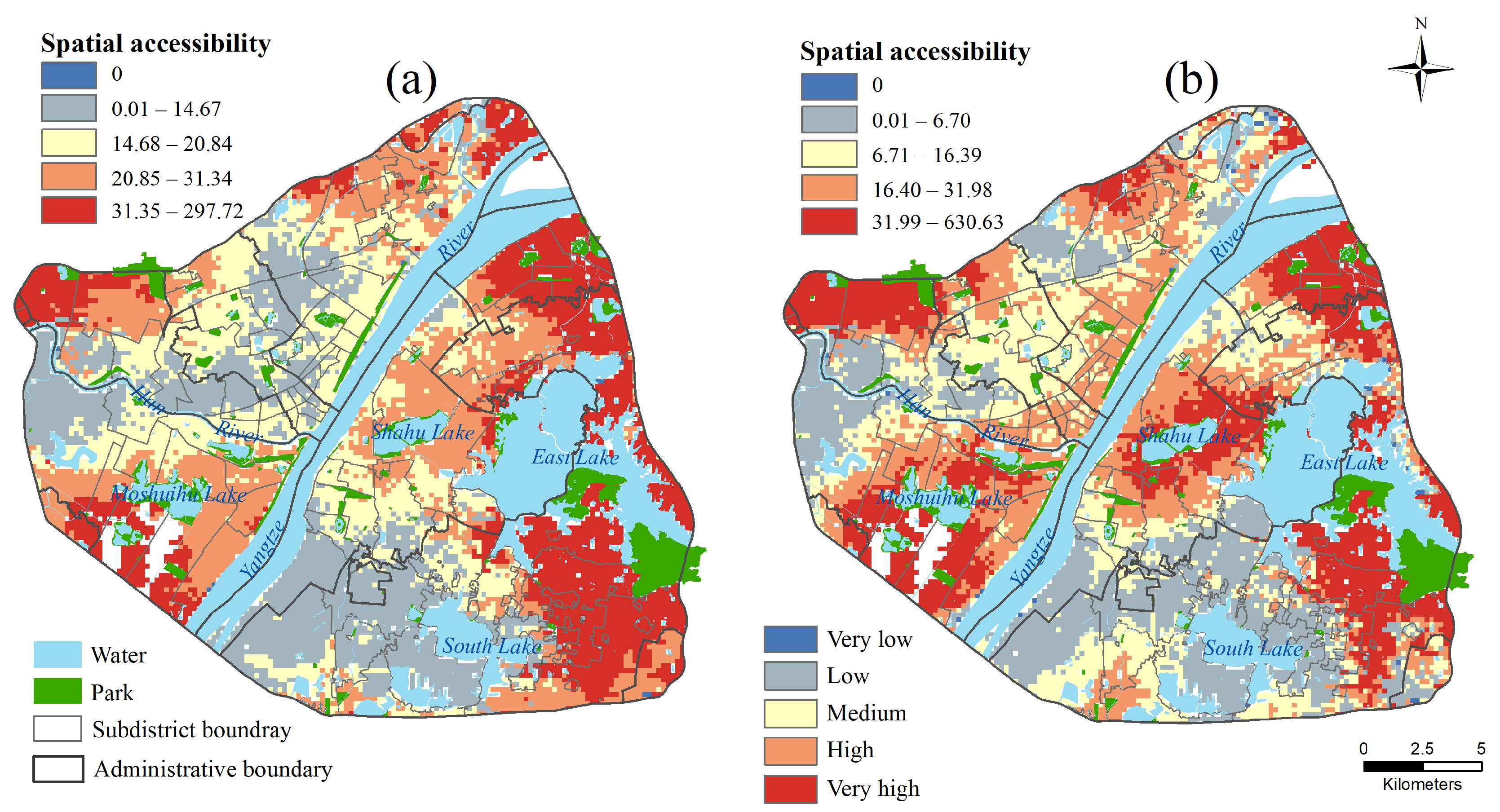
4.3. Comparison with Single-Model Accessibility
4.4. Comparison with Other Methods
4.5. Spatial Relationship between Park Accessibility and Population Density
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertram, C.; Rehdanz, K. The role of urban green space for human well-being. Ecol. Econ. 2015, 120, 139–152. [Google Scholar] [CrossRef]
- Macháč, J.; Brabec, J.; Arnberger, A. Exploring public preferences and preference heterogeneity for green and blue infrastructure in urban green spaces. Urban For. Urban Green. 2022, 75, 127695. [Google Scholar] [CrossRef]
- Onose, D.-A.; Ioja, C.; Niţă, M.-R.; Badiu, D.L.; Hossu, C.-A. Green Struggle—Environmental Conflicts Involving Urban Green Areas in Bucharest City. In Making Green Cities: Concepts, Challenges and Practice; Breuste, J., Artmann, M., Ioja, C., Qureshi, S., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 555–569. [Google Scholar]
- Thompson, C.W.; Roe, J.; Aspinall, P.; Mitchell, R.; Clow, A.; Miller, D. More green space is linked to less stress in deprived communities: Evidence from salivary cortisol patterns. Landsc. Urban Plan. 2012, 105, 221–229. [Google Scholar] [CrossRef]
- Kaźmierczak, A. The contribution of local parks to neighbourhood social ties. Landsc. Urban Plan. 2013, 109, 31–44. [Google Scholar] [CrossRef]
- Beyer, K.M.; Kaltenbach, A.; Szabo, A.; Bogar, S.; Nieto, F.J.; Malecki, K.M. Exposure to neighborhood green space and mental health: Evidence from the survey of the health of Wisconsin. Int. J. Environ. Res. Public Health 2014, 11, 3453–3472. [Google Scholar] [CrossRef] [PubMed]
- Silveira, I.H.D.; Junger, W.L. Green spaces and mortality due to cardiovascular diseases in the city of Rio de Janeiro. Rev. De Saude Publica 2018, 52, 49. [Google Scholar] [CrossRef]
- White, P.C.; Wyatt, J.; Chalfont, G.; Bland, J.M.; Neale, C.; Trepel, D.; Graham, H. Exposure to nature gardens has time-dependent associations with mood improvements for people with mid- and late-stage dementia: Innovative practice. Dementia 2018, 17, 627–634. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Kim, J. Social disparities in tree canopy and park accessibility: A case study of six cities in Illinois using GIS and remote sensing. Urban For. Urban Green. 2013, 12, 88–97. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, D.; Fang, J. Exploring the disparities in park access through mobile phone data: Evidence from Shanghai, China. Landsc. Urban Plan. 2019, 181, 80–91. [Google Scholar] [CrossRef]
- Song, Y.; Chen, B.; Kwan, M.-P. How does urban expansion impact people’s exposure to green environments? A comparative study of 290 Chinese cities. J. Clean. Prod. 2020, 246, 119018. [Google Scholar] [CrossRef]
- Song, Y.; Chen, B.; Ho, H.C.; Kwan, M.-P.; Liu, D.; Wang, F.; Wang, J.; Cai, J.; Li, X.; Xu, Y.; et al. Observed inequality in urban greenspace exposure in China. Environ. Int. 2021, 156, 106778. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; Liu, Y.; Wang, B.; Wang, Y.; Liu, H. An environmental justice study on spatial access to parks for youth by using an improved 2SFCA method in Wuhan, China. Cities 2020, 96, 102405. [Google Scholar] [CrossRef]
- Wei, X.; Zhao, C.; Yan, L.; Fu, J.; Bao, Y.; Liu, X. Spatial accessibility analysis of green space from a health-benefit perspective: Implications for healthy urban development. Front. Ecol. Evol. 2022, 10, 1083563. [Google Scholar] [CrossRef]
- Langford, M.; Higgs, G.; Fry, R. Multi-modal two-step floating catchment area analysis of primary health care accessibility. Health Place 2016, 38, 70–81. [Google Scholar] [CrossRef]
- Lin, Y.; Wan, N.; Sheets, S.; Gong, X.; Davies, A. A multi-modal relative spatial access assessment approach to measure spatial accessibility to primary care providers. Int. J. Health Geogr. 2018, 17, 33. [Google Scholar] [CrossRef]
- Mao, L.; Nekorchuk, D. Measuring spatial accessibility to healthcare for populations with multiple transportation modes. Health Place 2013, 24, 115–122. [Google Scholar] [CrossRef]
- Niu, Q.; Wang, Y.; Xia, Y.; Wu, H.; Tang, X. Detailed Assessment of the Spatial Distribution of Urban Parks According to Day and Travel Mode Based on Web Mapping API: A Case Study of Main Parks in Wuhan. Int. J. Environ. Res. Public Health 2018, 15, 1725. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Zhang, Y.; Li, D. Measuring spatial accessibility and supply-demand deviation of urban green space: A mobile phone signaling data perspective. Front. Public Health 2022, 10, 1029551. [Google Scholar] [CrossRef]
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities ‘just green enough’. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef]
- Rigolon, A. A complex landscape of inequity in access to urban parks: A literature review. Landsc. Urban Plan. 2016, 153, 160–169. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, Y.; Zhao, B. How to accurately identify the underserved areas of peri-urban parks? An integrated accessibility indicator. Ecol. Indic. 2021, 122, 107263. [Google Scholar] [CrossRef]
- Nicholls, S.; Shafer, C.S. Measuring accessibility and equity in a local park system: The utility of geospatial technologies to park and recreation professionals. J. Park Recreat. Adm. 2001, 19, 102–124. [Google Scholar]
- Comber, A.; Brunsdon, C.; Green, E. Using a GIS-based network analysis to determine urban greenspace accessibility for different ethnic and religious groups. Landsc. Urban Plan. 2008, 86, 103–114. [Google Scholar] [CrossRef]
- Moore, L.V.; Diez Roux, A.V.; Evenson, K.R.; McGinn, A.P.; Brines, S.J. Availability of Recreational Resources in Minority and Low Socioeconomic Status Areas. Am. J. Prev. Med. 2008, 34, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Radke, J.; Mu, L. Spatial Decompositions, Modeling and Mapping Service Regions to Predict Access to Social Programs. Ann. GIS 2000, 6, 105–112. [Google Scholar] [CrossRef]
- Ghorbanzadeh, M.; Kim, K.; Ozguven, E.E.; Horner, M.W. Spatial accessibility assessment of COVID-19 patients to healthcare facilities: A case study of Florida. Travel Behav. Soc. 2021, 24, 95–101. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y.; Liu, J. Hierarchical two-step floating catchment area (2SFCA) method: Measuring the spatial accessibility to hierarchical healthcare facilities in Shenzhen, China. Int. J. Equity Health 2020, 19, 164. [Google Scholar] [CrossRef]
- Polzin, P.; Borges, J.; Coelho, A. An extended kernel density two-step floating catchment area method to analyze access to health care. Environ. Plan. B Plan. Des. 2014, 41, 717–735. [Google Scholar] [CrossRef]
- Li, L.; Du, Q.; Ren, F.; Ma, X. Assessing Spatial Accessibility to Hierarchical Urban Parks by Multi-Types of Travel Distance in Shenzhen, China. Int. J. Environ. Res. Public Health 2019, 16, 1038. [Google Scholar] [CrossRef]
- Mao, K.; Chen, Y.; Wu, G.; Huang, J.; Yang, W.; Xia, Z. Measuring Spatial Accessibility of Urban Fire Services Using Historical Fire Incidents in Nanjing, China. ISPRS Int. J. Geo-Inf. 2020, 9, 585. [Google Scholar] [CrossRef]
- Min, S.; Kim, D.; Lee, C.K. Association between spatial accessibility to fire protection services and unintentional residential fire injuries or deaths: A cross-sectional study in Dallas, Texas. BMJ Open 2019, 9, e023780. [Google Scholar] [CrossRef]
- Guo, S.; Song, C.; Pei, T.; Liu, Y.; Ma, T.; Du, Y.; Chen, J.; Fan, Z.; Tang, X.; Peng, Y.; et al. Accessibility to urban parks for elderly residents: Perspectives from mobile phone data. Landsc. Urban Plan. 2019, 191, 103642. [Google Scholar] [CrossRef]
- Dai, D. Racial/ethnic and socioeconomic disparities in urban green space accessibility: Where to intervene? Landsc. Urban Plan. 2011, 102, 234–244. [Google Scholar] [CrossRef]
- Luo, W.; Whippo, T. Variable catchment sizes for the two-step floating catchment area (2SFCA) method. Health Place 2012, 18, 789–795. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Wang, F. Geographic Disparities in Accessibility to Food Stores in Southwest Mississippi. Environ. Plan. B Plan. Des. 2011, 38, 659–677. [Google Scholar] [CrossRef]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [Google Scholar] [CrossRef]
- Dony, C.C.; Delmelle, E.M.; Delmelle, E.C. Re-conceptualizing accessibility to parks in multi-modal cities: A Variable-width Floating Catchment Area (VFCA) method. Landsc. Urban Plan. 2015, 143, 90–99. [Google Scholar] [CrossRef]
- Ekkel, E.D.; de Vries, S. Nearby green space and human health: Evaluating accessibility metrics. Landsc. Urban Plan. 2017, 157, 214–220. [Google Scholar] [CrossRef]
- Wan, N.; Zou, B.; Sternberg, T. A three-step floating catchment area method for analyzing spatial access to health services. Int. J. Geogr. Inf. Sci. 2012, 26, 1073–1089. [Google Scholar] [CrossRef]
- Luo, J. Integrating the Huff Model and Floating Catchment Area Methods to Analyze Spatial Access to Healthcare Services. Trans. GIS 2014, 18, 436–448. [Google Scholar] [CrossRef]
- Tao, Z.; Yao, Z.; Kong, H.; Duan, F.; Li, G. Spatial accessibility to healthcare services in Shenzhen, China: Improving the multi-modal two-step floating catchment area method by estimating travel time via online map APIs. BMC Health Serv. Res. 2018, 18, 345. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y. Modelling the spatial accessibility of the elderly to healthcare services in Beijing, China. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 1132–1147. [Google Scholar] [CrossRef]
- Tao, Z.; Zhou, J.; Lin, X.; Chao, H.; Li, G. Investigating the impacts of public transport on job accessibility in Shenzhen, China: A multi-modal approach. Land Use Policy 2020, 99, 105025. [Google Scholar] [CrossRef]
- Hu, S.; Song, W.; Li, C.; Lu, J. A multi-mode Gaussian-based two-step floating catchment area method for measuring accessibility of urban parks. Cities 2020, 105, 102815. [Google Scholar] [CrossRef]
- Xing, L.; Liu, Y.; Liu, X. Measuring spatial disparity in accessibility with a multi-mode method based on park green spaces classification in Wuhan, China. Appl. Geogr. 2018, 94, 251–261. [Google Scholar] [CrossRef]
- Rigolon, A. Parks and young people: An environmental justice study of park proximity, acreage, and quality in Denver, Colorado. Landsc. Urban Plan. 2017, 165, 73–83. [Google Scholar] [CrossRef]
- Lee, G.; Hong, I. Measuring spatial accessibility in the context of spatial disparity between demand and supply of urban park service. Landsc. Urban Plan. 2013, 119, 85–90. [Google Scholar] [CrossRef]
- Wei, F. Greener urbanization? Changing accessibility to parks in China. Landsc. Urban Plan. 2017, 157, 542–552. [Google Scholar] [CrossRef]
- Amap. Available online: https://ditu.amap.com/ (accessed on 17 March 2023).
- Meituan. Available online: https://www.meituan.com/ (accessed on 17 March 2023).
- Dianping. Available online: https://www.dianping.com/wuhan (accessed on 17 March 2023).
- Liyan, X.; Yin, H.; Fang, J. Evaluating the supply-demand relationship for urban green parks in Beijing from an ecosystem service flow perspective. Urban For. Urban Green. 2023, 85, 127974. [Google Scholar] [CrossRef]
- Tu, X.; Huang, G.; Wu, J.; Guo, X. How do travel distance and park size influence urban park visits? Urban For. Urban Green. 2020, 52, 126689. [Google Scholar] [CrossRef]
- Xu, M.; Xin, J.; Su, S.; Weng, M.; Cai, Z. Social inequalities of park accessibility in Shenzhen, China: The role of park quality, transport modes, and hierarchical socioeconomic characteristics. J. Transp. Geogr. 2017, 62, 38–50. [Google Scholar] [CrossRef]
- The Results of “the Fourth Travel Trial Survey in Wuhan” Are Available. Available online: http://www.wuhan.gov.cn/sy/whyw/202111/t20211104_1826693.shtml (accessed on 5 March 2023).
- Zhang, S.; Yu, P.; Chen, Y.; Jing, Y.; Zeng, F. Accessibility of Park Green Space in Wuhan, China: Implications for Spatial Equity in the Post-COVID-19 Era. Int. J. Environ. Res. Public Health 2022, 19, 5440. [Google Scholar] [CrossRef] [PubMed]
- WorldPop. Available online: https://www.worldpop.org/ (accessed on 7 March 2023).
- Wang, F.; Xu, Y. Estimating O-D travel time matrix by Google Maps API: Implementation, advantages, and implications. Ann. GIS 2011, 17, 199–209. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y.; Dai, T.; Rosenberg, M.W. Spatial optimization of residential care facility locations in Beijing, China: Maximum equity in accessibility. Int. J. Health Geogr. 2014, 13, 33. [Google Scholar] [CrossRef]
- Jin, T.; Cheng, L.; Wang, K.; Cao, J.; Huang, H.; Witlox, F. Examining equity in accessibility to multi-tier healthcare services across different income households using estimated travel time. Transp. Policy 2022, 121, 1–13. [Google Scholar] [CrossRef]
- Path Planning. Available online: https://lbs.amap.com/api/webservice/guide/api/direction (accessed on 1 May 2023).
- Chen, Y.; Li, Y.; Wu, G.; Zhang, F.; Zhu, K.; Xia, Z.; Chen, Y. Exploring Spatiotemporal Accessibility of Urban Fire Services Using Real-Time Travel Time. Int. J. Environ. Res. Public Health 2021, 18, 4200. [Google Scholar] [CrossRef]
- Xia, Z.; Li, H.; Chen, Y.; Yu, W. Integrating Spatial and Non-Spatial Dimensions to Measure Urban Fire Service Access. ISPRS Int. J. Geo-Inf. 2019, 8, 138. [Google Scholar] [CrossRef]

| Size/ha | Number (Proportion/%) | Area/ha (Proportion/%) | Catchment Area/km |
|---|---|---|---|
| 1.0~5.0 | 26 (30.6) | 63.2 (2.0) | 0.5 |
| 5.0~10.0 | 14 (16.5) | 91.2 (2.8) | 1 |
| 10.0~20.0 | 15 (17.6) | 220.9 (6.9) | 2 |
| 20.0~50.0 | 18 (21.2) | 603.7 (18.7) | 3 |
| ≥50.0 | 12 (14.1) | 2240.6 (69.6) | 10 |
| Transportation Mode | Q1 | Q2 | Q3 | Mean | Standard Deviation | Underserved Population | |
|---|---|---|---|---|---|---|---|
| Multimodal | 7.98 | 16.76 | 35.56 | 36.17 | 63.74 | 5553 (0.9%) | |
| Single-modal | Bicycling | 5.65 | 14.69 | 38.19 | 32.23 | 57.60 | 137,188 (2.2%) |
| Driving | 10.79 | 18.48 | 33.91 | 36.13 | 42.28 | 19,671 (0.3%) | |
| Public transit | 0 | 7.24 | 25.92 | 38.14 | 166.60 | 950,379 (15.5%) | |
| Method | Q1 | Q2 | Q3 | Mean | Standard Deviation | Underserved Population |
|---|---|---|---|---|---|---|
| Huff model-based 2SFCA | 14.69 | 20.84 | 31.34 | 29.43 | 28.04 | 2572 (0.04%) |
| V2SFCA | 6.70 | 16.39 | 31.98 | 32.35 | 57.78 | 5523 (0.09%) |
| High Ai-High Pi | High Ai-Low Pi | Low Ai-High Pi | Low Ai-Low Pi | Not Significant | |
|---|---|---|---|---|---|
| Population (Proportion) | 97,813 (1.6%) | 106,187 (1.7%) | 2,890,060 (47.2%) | 233,909 (3.8%) | 2,793,872 (45.6%) |
| Average Accessibility | 67.44 | 102.50 | 14.20 | 13.21 | 35.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, K.; Li, J.; Yan, H. Measuring the Spatial Accessibility of Parks in Wuhan, China, Using a Comprehensive Multimodal 2SFCA Method. ISPRS Int. J. Geo-Inf. 2023, 12, 357. https://doi.org/10.3390/ijgi12090357
Mao K, Li J, Yan H. Measuring the Spatial Accessibility of Parks in Wuhan, China, Using a Comprehensive Multimodal 2SFCA Method. ISPRS International Journal of Geo-Information. 2023; 12(9):357. https://doi.org/10.3390/ijgi12090357
Chicago/Turabian StyleMao, Kainan, Jingzhong Li, and Haowen Yan. 2023. "Measuring the Spatial Accessibility of Parks in Wuhan, China, Using a Comprehensive Multimodal 2SFCA Method" ISPRS International Journal of Geo-Information 12, no. 9: 357. https://doi.org/10.3390/ijgi12090357
APA StyleMao, K., Li, J., & Yan, H. (2023). Measuring the Spatial Accessibility of Parks in Wuhan, China, Using a Comprehensive Multimodal 2SFCA Method. ISPRS International Journal of Geo-Information, 12(9), 357. https://doi.org/10.3390/ijgi12090357





