Effectiveness of Adjacent and Bivariate Maps in Communicating Global Sensitivity Analysis for Geodiversity Assessment

Abstract

This study compares adjacent and bivariate maps in communicating variance-based global sensitivity analysis (GSA) results for a geodiversity assessment spatial multi-criteria model and examines the influence of prior exposure to geodiversity and map reading skills on interpretation. It analyzes the quality of map interpretation, confidence levels, and map communication effectiveness. The findings indicate that there is no significant difference in the quality of map interpretation or confidence levels between the two map types. However, there are nuanced differences in interpretive patterns, suggesting the need for further investigation into factors affecting map interpretation. Adjacent maps are more effective in identifying factors linked to uncertainty in high geodiversity values, while bivariate maps excel in understanding spatial variability. Prior exposure to geodiversity and map reading skills do not significantly impact interpretation quality or confidence levels. Future research could explore other factors influencing map effectiveness and explore the cognitive processes underlying map interpretation. Understanding these processes could lead to more effective strategies for communicating the results of a GSA for spatial models through maps.

1. Introduction

In spatial analysis and modeling, uncertainty often arises from various sources. This uncertainty is especially pronounced in spatial models, which abstract real-world phenomena. It encompasses uncertainties in input data, conceptualization, formalization, and output results. One formal method used to quantify uncertainty is uncertainty analysis (UA) [1]. A UA is a forward-looking approach that assesses how input uncertainties propagate through a model, influencing the output values. However, a UA does not provide information about how much an input influences the variability of the model outputs. This aspect is addressed by a sensitivity analysis (SA), which examines the relationship between output variability and model inputs, determining the contribution of each source of uncertainty to the overall output variability. Therefore, an SA complements a UA by offering a backward-looking perspective.

An SA examines how the outputs of a quantitative model are linked to and impacted by its various inputs. These inputs, known as factors, can encompass model parameters, boundary and initial conditions, structural configurations, assumptions, and constraints. Outputs can encompass any functions of model responses, including those varying across space and time. A contemporary approach to an SA called a global sensitivity analysis (GSA) aims to offer a comprehensive understanding of how various factors operate and interact throughout the entire problem space to impact a specific function of the system’s output [2].

GSA methods are versatile and can be applied regardless of the nature of the input–output relationship. In contrast to the one-at-the-time approach to SA, which evaluates model sensitivity to each factor treated individually, they explore the full range of input possibilities, highlighting non-linearities and interactions among factors. A GSA can serve several key purposes in spatial analysis and modeling, including discovery and hypothesis generation (it helps uncover causal relationships), model dimensionality reduction (it identifies factors that do not significantly affect the model and that, consequently, can be eliminated from further analysis), data cost–benefit analysis (a GSA helps pinpoint the parameters and scales that most strongly influence model’s results, guiding where new data acquisition can reduce uncertainty the most), and model reliability assessment (a GSA quantifies how sensitive model outputs are to assumptions, parameters, and uncertainties). Due to these qualities, a GSA is considered essential for enhancing model comprehension and refinement across various applications [3].

GSA has found applications in spatial analysis and modeling. Lilburne and Tarantola [4] provided an early discussion on alternative methods for conducting an SA in spatial contexts, advocating global approaches that explore the entire input space and assess how simultaneous changes in all inputs impact output variability. Several studies have employed a GSA to test the reliability of models with spatially explicit outputs in such diverse domains as land use change analysis [5,6], land suitability evaluation [7], natural hazard assessment [8], hazardous waste disposal planning [9], hydrologic modeling [10,11,12,13,14], disease transmission modeling [15], habitat restoration analysis [16], pedologic modeling [17], and urban growth simulation [18].

Among many approaches to GSA, the most common is the distribution-based approach, which focuses on the distributional characteristics of the model output. This method aims to measure the contributions of various inputs to shaping the distributional properties. The most widely used distribution-based method involves analyzing the variance of the output. This method breaks down the variance into components attributed to individual or group inputs [19]. The variance components are expressed by synthetic measures called the first-order sensitivity index, which captures the main effects due to individual inputs, and the total order sensitivity index, which represents the total effect due to the individual input and its interactions [20]. Practitioners have widely embraced these indices because they offer a straightforward interpretation. In essence, high values in the first-order indices indicate the factors that, if held constant at their true values, would most significantly reduce uncertainty in the model output, thereby enhancing the reliability of the model’s conclusions. Conversely, low values for total order indices point to factors that have minimal impact on output uncertainty and can thus be set at an arbitrary value within their uncertainty range, simplifying the model [21].

These interpretations, however, are not straightforward in models with spatially or spatiotemporally explicit outputs. To aid in interpreting sensitivity indices, various types of plots and graphs have been employed, including colored scatter plots [22], star graphs [23], parallel coordinate plots [24], Morris plots, regression coefficient plots, principal component analyses [25], stacked bar plots [14], as well as other multivariate data representations in 2D [26]. These visualizations of sensitivity analysis (SA) outputs primarily use non-spatial formats, which do not address the link between locational attributes. The values of sensitivity indices have been communicated via unclassified choropleth and dominance maps [6,8,16]; grid-based maps [13]; classified choropleth and dominance maps [16,21]; pie-chart, snowflake, and multiple choropleth maps [14]; adjacent and coincident thematic maps [27]; and machine learning-based dimensional reduction techniques [28].

However, the effectiveness of the spatial representation of SA outputs, particularly in the context of GSA, is rarely explored in the literature. The predominant focus of current visualization efforts primarily revolves around aspatial data visualization [29,30,31,32]. In most of the papers employing different forms of maps and plots, the interpretations of sensitivity indices came directly from the papers’ authors. Only one study by Şalap-Ayça et al. [27] reported on the interpretations of sensitivity indices made by a diverse group of users involving university students and environmental and engineering professionals. This study tested the efficacy of two types of thematic maps (adjacent and coincident) employed in a controlled experiment, in which two groups of randomly assigned users were given one type of map such that one group received adjacent maps and the other group received coincident maps. Both types of maps depicted the same results of variance-based GSA for a land use change simulation model. The difference was in how the two sensitivity indices (first-order and total order indices) were rendered and presented to participants on adjacent vs. coincident maps. The adjacent maps were arranged side by side, with each map depicting the spatial distribution of only one type of sensitivity index (either first-order or total order index) for each input factor. This type of visualization resulted in k×*2 maps, where k is the number of input factors. In contrast, only two coincident maps (one for the first-order index and the other for the total order index) were needed to display the index values for all k factors. In this type of map, only the index value of the dominant factor was rendered on each mapping unit, resulting in a spatial distribution of the dominant factors [16]. The participants were asked to respond to an online questionnaire to elicit their comprehension of a variance-based GSA informed by the two types of maps. The results did not show a statistically significant difference in map comprehension between the adjacent and bivariate maps. They also indicated difficulty in interpreting the results of the GSA presented on adjacent maps among the users with little or no experience with this type of mapping. Interestingly enough, coincident maps did not lead to better interpretations either. This opens the question of whether a different type of thematic map might be more effective in communicating the results of a GSA in a model with a spatially explicit output.

Adjacent maps [33], also known as small multiples in cartography, are a popular choice for visualizing the distribution of different variables across mapping units comprising a geographical region. They facilitate an easy comparison of variable values among neighboring areas, offering insights into spatial patterns and disparities. This type of map was introduced as a dimension of the uncertainty visualization cube (UVis3) by Kindley et al. [34]. As already mentioned, adjacent maps have been adopted in sensitivity analysis (SA) visualization by Salap-Ayça et al. [27] due to its effectiveness in highlighting regional differences and trends. However, given the complexity of global sensitivity analysis (GSA) outputs and the need to capture multiple dimensions of data simultaneously, a more comprehensive visualization approach is essential. Bivariate maps [35] offer a promising way of exploring the relationship between two distinct variables in spatial terms. These maps enable the simultaneous representation of two variables, aiding in the identification of spatial patterns and correlations between them.

The lack of research on the efficacy of visual techniques aiding the interpretation of GSA results is puzzling, considering the apparent intent of the SA research community to promote the use of GSA methods among practitioners [36]. This paper aims to help fill this void by presenting the results of a study evaluating the efficacy of adjacent and bivariate maps in communicating the results of a GSA for a geodiversity assessment model. This study expands upon the research by Şalap-Ayça et al. [27] by investigating the effectiveness of two distinct thematic map types in conveying GSA results for a model with spatially explicit outcomes. The two research questions driving this study, accompanied by their respective hypothesis, are as follows:

• RQ1: How effective are single-factor, adjacent maps vs. composite, bivariate maps in communicating the input factor sensitivity in a geodiversity assessment?

H1. 

Composite, bivariate maps are more effective than single-factor, adjacent maps in communicating the input factor sensitivity in a geodiversity assessment.

• RQ2: How do differences between adjacent and bivariate maps influence the confidence level in interpreting the results of a variance-based global sensitivity analysis (GSA)?

H2. 

People interpret sensitivity maps with higher confidence when information is represented in the form of bivariate maps rather than single-factor, adjacent maps.

We deal with these questions in the remainder of this paper by first describing the data and methods employed in this study (Section 2), analyzing the study results (Section 3), discussing the implications of our findings (Section 4), and drawing conclusions for this study and similar future studies (Section 5).

2. Data and Methods

This study used data from the geodiversity assessment of Karkonosze National Park (KNP) in Poland, described in detail in [37,38]. The concept of a geodiversity assessment, operationalized by a spatial multi-criteria analysis (S-MCA) model, and the data used for the assessment are described in the following three sub-sections. The essential methods for this study included a spatially explicit variance-based GSA and a map-based questionnaire given to a group of users to compare the effectiveness of adjacent vs. bivariate maps. They are described in Section 2.4 and Section 2.5.

2.1. Geodiversity Assessment

The spatial modeling domain for this study is geodiversity assessment. The concept of geodiversity emerged in the 1990s in the wake of the Convention on Biological Diversity at the Rio Earth Summit [39,40]. Geodiversity encompasses the range of non-living components within an ecosystem, including geology, earth surface relief, soil cover, surface and groundwater, and climate [41,42]. It plays a crucial role in shaping biotic conditions and, consequently, biodiversity [43,44]. The assessment of geodiversity is vital for evaluating protected and conserved areas (such as national parks, reserves, parks, and sites) and for conducting comparative studies of special interest areas. Geodiversity is also integral to geotourism, geoheritage, and geoconservation, underscoring its interdisciplinary nature [45,46]. Assessing geodiversity offers several benefits, including a better understanding of geo-ecosystems’ functioning, the improved management of protected areas, and a more comprehensive grasp of ecosystem services [47,48]. These benefits are particularly significant in the context of global warming and rapid land use and land cover changes.

There is no universally agreed upon direct measurement method of geodiversity. In its absence, indirect methods have been an active area of research [44,45]. These methods can be classified according to the source of data, namely either primary or secondary [49], and, according to the assessment approach, as qualitative, quantitative, or a combination of both (qualitative–quantitative) [47,48]. However, all of these categories introduce uncertainties that depend on expert judgment or data interpretation rather than a direct measurement. To account for these uncertainties, two recent studies [37,38] combined S-MCA models [50,51] with an uncertainty analysis to evaluate the reliability of a geodiversity assessment for the selected national parks in Poland, including KNP. In both studies, an S-MCA model was employed to aggregate expert judgments and interpretations of geodiversity factors to produce a synthetic score for each mapping unit, representing the unit’s assessed geodiversity value. The uncertainty in judgments and interpretations was assessed using Monte Carlo simulation, which yielded the mean score and standard deviation. The following section briefly presents the S-MCA model and its components.

2.2. Spatial Multi-Criteria Analysis Model

In this study, we employed the results of the S-MCA model presented in detail in [37] to assess the geodiversity of Karkonosze National Park (KNP), located in southwestern Poland on the border between Poland and the Czech Republic (Figure 1).

The model calculated a geodiversity value for each spatial assessment unit i using the weighted linear combination (WLC) function from Equation (1).

$${GD}_i={\sum }_{j=1}^N{w}_j{c}_{i,j}$$

(1)

where

i = 1…M is the assessment unit index;

j = 1…N is the geodiversity factor index;

GD_i is the geodiversity index value for the assessment unit I;

c_i,j is the jth factor value for the ith assessment unit;

w_j is the importance weight of jth factor relative to other geodiversity factors, and $\sum _i^M{w}_j=100$.

The following seven factors were used in the model:

1.

Geomorphology: This represents the forms of the Earth’s surface that are present in the park (1—floodplain; 2—hillock moraine; 3—intramontane basin; 4—meadow terraces; 5—planation surface in basin bottom; 6—planation surface on flat-topped hill; 7—planation surface on slope; 8—residual hill—resistance monadnock; 9—rock wall or rock slope; 10—slope; 11—V-shaped valley; 12—valley bottom with moraine cover).

2.

Hydrography: This is represented by the topographic wetness index, TWI, ranging from −3.0 to 6.8.

3.

Lithology: This represents rock types in the park (1—amphibolite; 2—aplite; 3—basaltoids; 4—basanite; 5—cataclasite; 6—mylonite; 7—tectonic breccia; 8—coarse-grained granite; 9—fine-grained granite; 10—hornfels; 11—layered gneiss; 12—liptynite; 13—mica schist; 14—microgranite; 15—porphyritic granite; 16—vein quartz).

4.

Solar Radiation: This is the spatial distribution of climatic conditions in the park represented by the total solar radiation ranging from 172 to 3805 kWh m⁻².

5.

Relief Energy: This is the spatial distribution of relative heights in the park ranging from 0 to 94 m. The calculation of relative heights is based on a local neighborhood of 3 × 3 cells with 10 m/cell ground resolution.

6.

Soils: This refers to the soil types in the park (1—brown soils; 2—leached brown soil; 3—proper river mud; 4—brown forest soils; 5—peat and muck soils; 6—initial soils; 7—anthropogenic soils).

7.

Land Cover/Land Use: This refers to the land cover and land use types present in the park (1—discontinuous development; 2—non-irrigated arable land; 3—pastures; 4—mixed cultivation; 5—agricultural land with areas of natural vegetation; 6—deciduous forest; 7—coniferous forest; 8—mixed forest; 9—natural grasslands; 10—heathlands; 11—transitional forests and shrubs; 12—bare rocks; 13—sparsely vegetated areas; 14—peat bogs).

The values of the four categorical factors (geomorphology, lithology, soils, and land cover/land use) were derived from an expert Likert scale with a 1–5 rating [52], where 1 denotes a given factor’s low contribution and 5 denotes its high contribution to the geodiversity value of the ith spatial assessment unit. The values of three ratio-scale factors (hydrography, solar radiation, and relief energy) were computed using the GIS data for the park. Three factor maps derived from the Digital Elevation Model (DEM) were selected for analysis due to their effectiveness as predictors of geodiversity [53]. These indices represent the spatial diversity of specific components and, as they are continuous data, are more suitable for geodiversity assessments than the more commonly used discrete data [54]. The values for the three ratio-scale factors—hydrography, solar radiation, and relief energy—were calculated using the GIS data for the park.

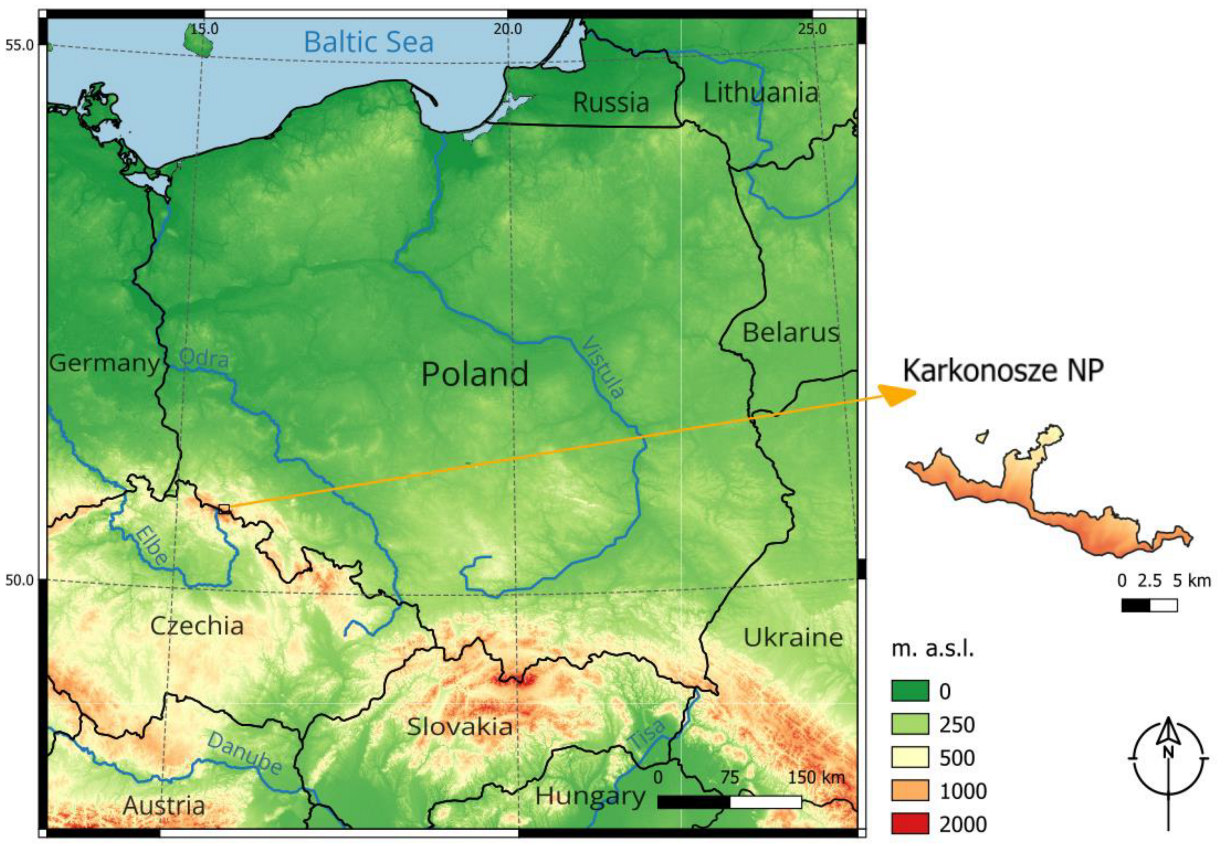
2.3. Assessment Data

The data for the geodiversity assessment of KNP were provided by the park’s GIS laboratory and are subject to agreement; the rest came from publicly available GIS layers and expert interpretations of geodiversity assessment factors. They include the following:

• High-resolution terrain data: A 1 m LiDAR-derived Digital Elevation Model (DEM) from Geoportal [55] provided detailed information about the land surface.
• Thematic map layers: These layers included lithology, geomorphology, hydrology, soil features, and CORINE Land Cover data [56] at the scale of 1:100,000.
• National park GIS data: Most thematic layers were obtained from the KNP GIS lab, typically at the scale of 1:10,000.
• Additional data sources included the following:

  o

  Lithology data layer for parks enhanced with information from the Detailed Geological Map of Poland at the 1:50,000 scale [57].

  o

  Geomorphological data layer compiled using the Digital Geomorphological Map of Poland at the 1:100,000 scale [58].

Water catchment was employed as the primary assessment unit. First-order catchments were delineated within national park boundaries using the r.watershed tool in GRASS GIS v7 [59]. This approach deviates from traditional geodiversity assessments that rely on squares, grid cells, hexagons, or arbitrary polygons. Catchments represent well-defined units with distinct energy and matter cycles, offering a more natural and ecologically relevant framework for analysis. Two hundred twelve polygon catchments were identified within the park, with an average size of 0.27 km².

The datasets were processed with GIS methods to produce a map layer for each of the seven geodiversity factors for KNP. Further details about data processing are given in [37,38]. The resulting seven layers were included in a geo-questionnaire [37] presented online to a group of national and international experts in Earth science and conservation. The experts rated the contribution of each factor to the park’s geodiversity using a five-point [1,2,3,4,5] Likert’s scale [52] and additionally weighted the relative importance of each factor on a 1–100 scale. For the four categorical factors, the respondents rated each category within a factor (e.g., for lithology, they rated 16 lithological categories occurring in the park). For the three ratio scale factors, they rated the subranges of the factor’s value range (e.g., for relief energy, they rated five subranges within the 0–94 m range). The geo-questionnaire resulted in 57 complete responses, which were processed into 57 digital map layers for each of the seven factors. Each map layer included a spatial distribution of factor values and a factor weight. In essence, for each layer j (j = 1…7), each catchment i (i = 1…212) had a factor value ranging between 1 and 5 and a weight ranging between 1 and 100. These data were then used as inputs in the model (1).

2.4. Spatially Explicit Variance-Based Global Sensitivity Analysis

To account for the uncertainty of the geodiversity assessment and to examine how this uncertainty is linked to and impacted by the factor ratings and weights, we carried out a variance-based GSA following the workflow shown in Figure 2. This workflow involves modeling weights and factors as probabilities and sets, respectively. It then calculates a distribution of the spatial outputs and associated statistics like the mean and standard deviation, which are combined into an uncertainty map. Next, it decomposes variance across the study area to identify the independent and interactive contributions of each factor to the variance of geodiversity and the associated assessment uncertainty expressed by standard deviation. The resulting sensitivity maps depict the influence of each factor on the uncertainty of assessment.

The following are the key steps of the procedure (Figure 2):

1.

Represent weights and factors:

• Weights (W₁…_N) are represented as probability distributions.
• Factors (C₁…_N) are represented as sets of k equally probable maps.

2.

Calculate spatial outputs:

• The procedure calculates a geodiversity index value GD_i for each mapping unit i multiple times with different weight and factor values.
• Each calculation uses weight values derived from their probability distributions and factor values from their respective sets.
• This results in a distribution of GD_i values.

3.

Create uncertainty map:

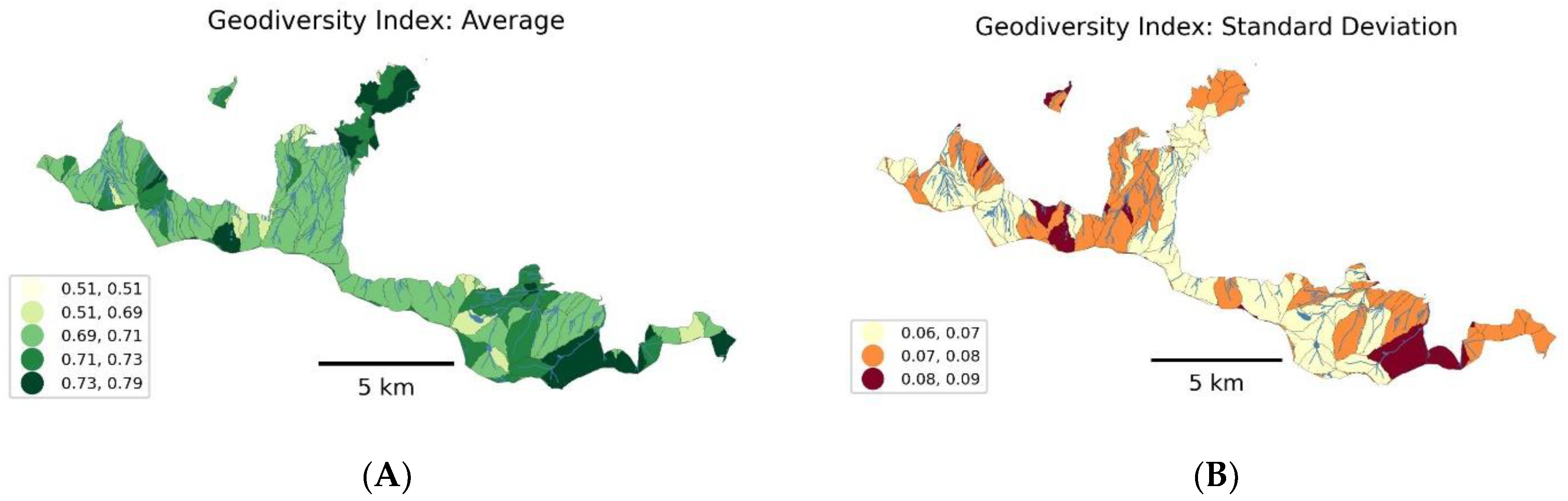
• Statistics like the mean and standard deviation are calculated for the GD_i distribution.
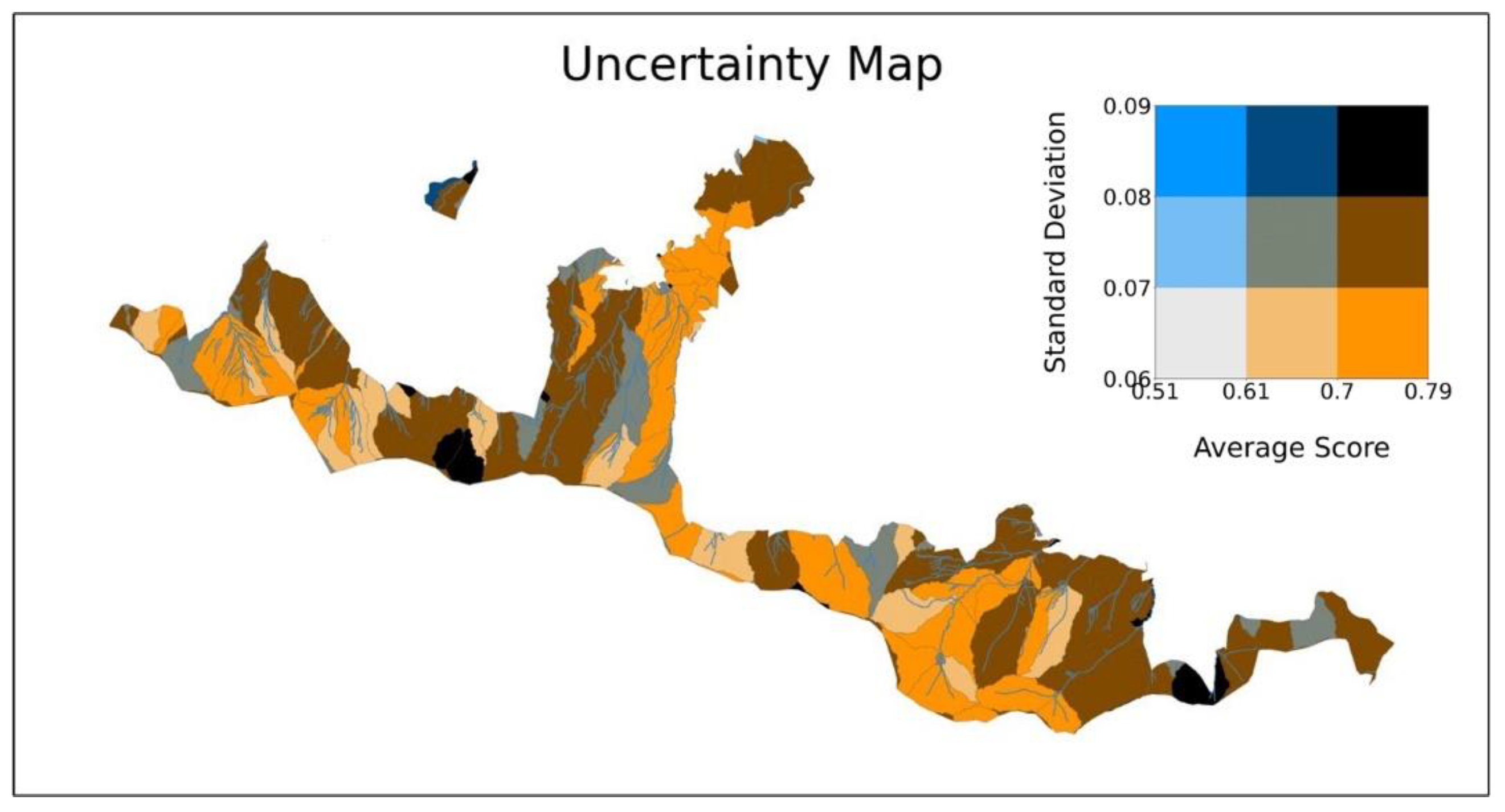
• These statistics are combined to create two adjacent maps: one with the mean GD_i values and the other with the standard deviation values for each i.
• Additionally, a rendering of both statistics is compiled in the form of a bivariate map.

4.

Decompose variance:

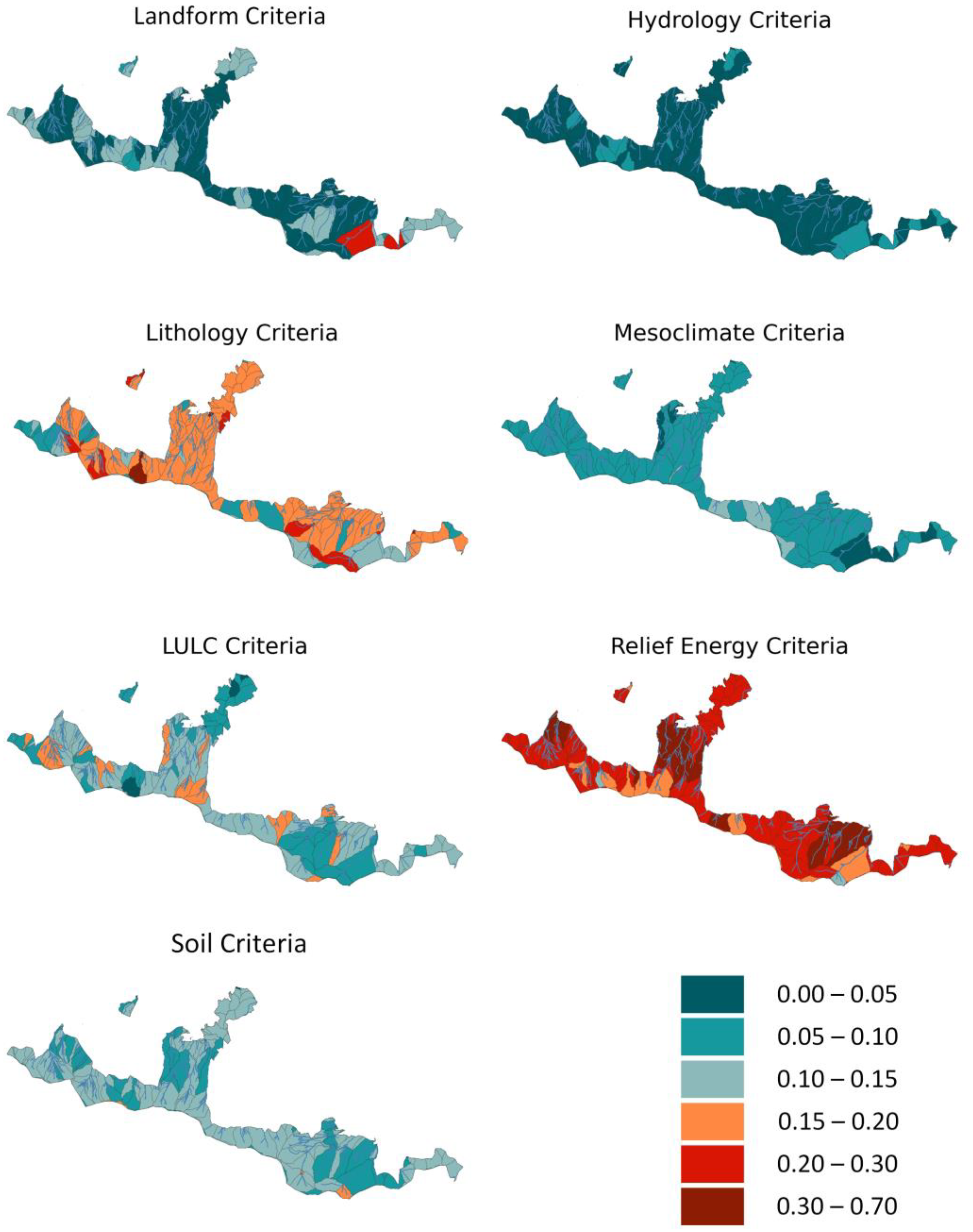
• Variance is decomposed for each mapping unit (i.e., catchment).
• This identifies the contribution of each factor to the total GD_i variance in that catchment.
• Two sensitivity indices are computed per each mapping unit i:

• the first-order effects index (S_j=1…N), which represents the independent contribution of the factor j, and the total effects index (ST_j=1…N), which represents the combined contribution of the factor j, including interactions with other factors.

5.

Generate sensitivity maps:

• Two maps are generated for each factor j: one map depicting the spatial distribution of S_j, and the other with the distribution of ST_j.
• This results in 2N sensitivity maps (one for each index), showing the combined influence of each factor on the output GD_i variance.
• Additionally, a combination of the two spatial distributions (S_j=1…N, ST_j=1…N) is rendered on a bivariate map.

2.5. Questionnaire

To address the two research questions guiding this study, we developed a questionnaire based on thematic maps depicting spatial distributions of geodiversity assessment values and their associated uncertainty (represented by mean geodiversity and standard deviation) and sensitivity. The questionnaire comprised two versions: one for adjacent maps and another for bivariate maps. Each version included the same set of twelve questions corresponding to the maps. The adjacent map version featured sixteen maps: two maps with the distribution of the mean geodiversity and accompanying standard deviation (Figure 3A,B), seven maps illustrating Sj distributions (Figure 4), and seven maps depicting STj distributions (Figure 5).

The bivariate version included eight maps: one depicting the bivariate distribution of the mean geodiversity index and standard deviation—the uncertainty map (Figure 6)—and seven maps displaying the bivariate distributions of Sj and STj (Figure 7).

Questions were formulated to measure the quality of map interpretation (a categorical variable), interpretation confidence (ordinal variable), usage level of factor interaction maps (STj maps) (ordinal variable), ease of map interpretation (ordinal variable), perceptual differences between Sj and STj (ordinal variable), perceived benefit of map visualization for understanding GSA results (ordinal variable), self-assessed thematic map interpretation skills (ordinal variable), and familiarity with the concept of geodiversity (a binary variable) (

Table 1. Questionnaire measures and question wording.

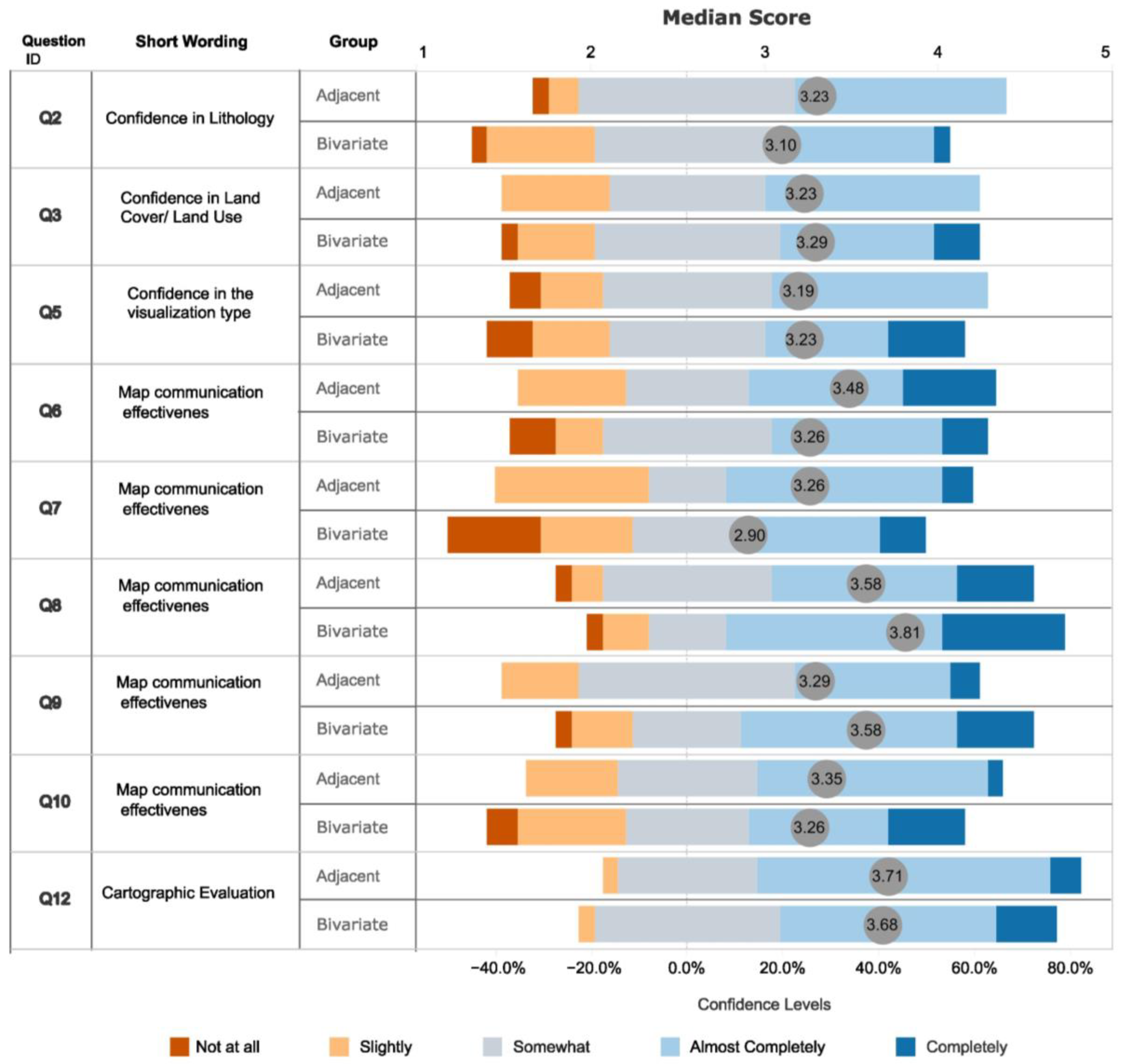
Question ID	What Does the Question Measure?	Question Wording	Answer Options
Q1	Quality of interpretation	According to the presented maps, which geodiversity factor do you consider generally the most influential for the geodiversity of the study area?	Geomorphology (1), hydrography (2), solar radiation (3), relief energy (4), lithology (5), land cover/land use (6), soils (7)
Q2	Confidence in interpretation	On the scale of 1–5 (1—uncertain; 5—certain), how sure are you when creating simple approximations (25%, 50%, 75%, etc.) regarding the assessment of sensitivity of geodiversity to lithology in the KNP area?	1–5 Likert scale 1—uncertain 5—certain
Q3	Confidence in interpretation	On the scale of 1–5 (1—uncertain; 5—certain), how sure are you when creating simple approximations (25%, 50%, 75%, etc.) regarding the assessment of sensitivity of geo-diversity to land cover/land use in the KNP area?	1–5 Likert scale 1—uncertain 5—certain
Q4—Adjacent	Usage of interaction maps	Did you use the total order sensitivity maps (STi) (Figure 5) in response to any of the two questions above?	Yes No
Q4—Bivariate	Usage of bivariate Maps	Did you use information about both sensitivity indices (Si, STi) in the bivariate maps (Figure 7) in response to any of the two questions above?	Yes No
Q5	Confidence in visualization type	If you had to explain the sensitivity in geodiversity assessments to other people, how confident would you feel on a scale of 1–5 (1—uncertain, 5—certain) using this type of visualization as shown in Figure 4 and Figure 5 (adjacent group), Figure 7 (bivariate group)?	1—uncertain 5—certain
Q6	Map effectiveness in communicating GSA results	On the scale of 1–5 (1—not very helpful; 5—very helpful), evaluate how helpful were the maps presented in Figure 4 and Figure 5 (Figure 7 for bivariate) for identifying factors influencing the uncertainty associated with high average geodiversity values in Figure 3A,B (Figure 6 for bivariate).	1–5 Likert scale (1—not very helpful; 5—very helpful)
Q7	Map effectiveness in communicating GSA results	On the scale of 1–5 (1—difficult; 5—easy), assess how easy it was to understand the differences between the sensitivity of main effects (Si) and the sensitivity of total effects (STi)?	1–5 Likert scale (1—difficult; 5—easy)
Q8	Map effectiveness in communicating GSA results	On the scale of 1–5 (1—not very helpful; 5—very helpful), evaluate how much you agree with the following statement: the visualization of maps showing spatial variability of sensitivity indices Si and STi (Figure 4 and Figure 5 adjacent, Figure 7 bivariate) is helpful in understanding the spatial variability of geodiversity assessment (Figure 3A,B adjacent, Figure 6 bivariate).	1–5 Likert scale (1—not very helpful; 5—very helpful)
Q9	Map effectiveness in communicating GSA results	On the scale of 1–5 (1—not at all; 5—fully), assess to what extent the visualization of sensitivity indices Si and STi (Figure 4 and Figure 5 adjacent, Figure 7 bivariate) helps in interpreting the average values of the geo-diversity index (Figure 3A adjacent, Figure 6 bivariate).	1–5 Likert scale (1—not at all; 5—fully)
Q10	Map effectiveness in communicating GSA results	On the scale of 1–5 (1—not at all; 5—fully), assess to what extent the visualization of sensitivity indices Si and STi (Figure 3 and Figure 4 adjacent, Figure 6 bivariate) helps in interpreting the variability of uncertainty associated with the average value of the geodiversity index (Figure 3B adjacent, Figure 6 bivariate).	1–5 Likert scale (1—not at all; 5—fully)
Q11	Familiarity with assessment domain	Before filling out this questionnaire, have you participated in any classes on geo-diversity, and are you familiar with this concept?	Yes/No
Q12	Map reading competence level	On the scale of 1–5 (1—low; 5—high), rate your skills in interpreting thematic maps.	1–5 Likert scale (1—low; 5—high)

).

In the questionnaire, Q1 and Q6–Q10 addressed research question 1, whereas Q2–Q5 pertained to research question 2. Q4 addressed the usage of maps in the responses to Q2–Q3. Questions Q11 and Q12 contextualized the responses to Q1–Q10 by addressing familiarity with the domain and map reading competency.

The questionnaire was implemented using Qualtrics XM, a web-based software for creating surveys and generating reports. It was administered between 24 October and 11 November 2023 to 128 students majoring in geography and geoinformation at the University of Adam Mickiewicz in Poznań, the Jan Kochanowski University of Kielce, and the University of the National Education Commission in Kraków, all in Poland. We received 62 complete questionnaire responses with a 48% response rate. We chose students majoring in geography and geoinformation for three reasons: (1) familiarity with the study area, (2) map reading competency, and (3) familiarity with the concept of geodiversity. It is reasonable to assume that any other group tasked with interpreting maps depicting the results of a GSA would possess similar domain knowledge and basic map reading skills.

The Qualtrics XM application randomly assigned each respondent a version of the questionnaire, maintaining an equal proportion between the two versions. This resulted in 31 complete responses for the adjacent version and the same number for the bivariate version, totaling 62 responses. The responses were exported from the Qualtrics XM application to an Excel spreadsheet file and analyzed with the SPSS statistical software (ver. 28.0.1.0) for differences between the two thematic map types.

3. Results

3.1. Quality of Map Interpretation

Q1 measured the quality of map interpretation by comparing the number of correct responses (relief energy) with incorrect responses (the other six geodiversity factors) between the groups. The crosstabulation of the responses is presented in

Table 2. Crosstabulation of responses to Q1 by groups.

			Group		Total
			Adjacent	Bivariate
Q1	Geomorphology	Count	5	0	5
		% within Q1	100.0	0.0	100.0
		% within group	16.1	0.0	8.1
		% of total	8.1	0.0	8.1
	Hydrography	Count	4	1	5
		% within Q1	80.0	20.0	100.0
		% within group	12.9	3.2	8.1
		% of total	6.5	1.6	8.1
	Land Cover/Land Use	Count	2	9	11
		% within Q1	18.2	81.8	100.0
		% within group	6.5	29.0	17.7
		% of total	3.2	14.5	17.7
	Lithology	Count	2	4	6
		% within Q1	33.3	66.7	100.0
		% within group	6.5	12.9	9.7
		% of total	3.2	6.5	9.7
	Relief Energy	Count	17	16	33
		& within Q1	51.5	48.5	100.0
		% within group	54.8	51.6	53.2
		% of total	27.4	25.8	53.2
	Soil	Count	0	1	1
		% within Q1	0.0	100.0	100.0
		% within group	0.0	3.2	1.6
		% of total	0.0	1.6	1.6
	Solar Radiation	Count	1	0	1
		% within Q1	100.0	0.0	100.0
		% within group	3.2	0.0	1.6
		% of total	1.6	0.0	1.6
Total		Count	31	31	62
		% within Q1	50.0	50.0	100.0
		% within group	100.0	100.0	100.0
		% of total	50.0	50.0	100.0

. It shows that 17 respondents in the adjacent group (54.8%) selected relief energy as the most influential factor. This was compared with 16 respondents in the bivariate group (51.6%). In total, 33 (53.2%) out of 62 respondents (100%) correctly identified the most influential factor driving the variability of geodiversity values in KNP.

The association between the quality of map interpretation and map category is statistically non-significant $(\mathsf{\chi }2$ = 0.065, df = 1, p = 0.799). Hence, based on the questionnaire responses, there is no difference between the quality of map interpretation and the map categories used to depict the GSA results.

3.2. Confidence in Map Interpretation

Questions Q2–Q3 and Q5 measured the respondents’ confidence in their map interpretations using the five-point (1–5) Likert scale. Figure 8 shows the distributions of the responses. The figure also shows the distribution of the responses to Q6–Q10 measuring map communication effectiveness and Q12 measuring map reading competence. For brevity, we refer to the respondents that were given the adjacent maps as the “adjacent group” and those with the bivariate map as the “bivariate group.” The median response scores for the nine questions in Figure 8 range from 2.9 (Q5) for the bivariate group to 3.81 (Q8), also for the bivariate group. The corresponding range for the adjacent group is smaller: 3.19 (Q5)–3.71 (Q12). The comparison of the median response scores (Figure 8) reveals differences between the groups for some but not all questions.

Most respondents in both groups were either “somewhat confident” or “almost confident” in their interpretations of the sensitivity maps. In Q2 and Q3, we asked the respondents to rate their self-confidence levels in assessing the geodiversity’s sensitivity to factors other than energy relief. The adjacent group expressed more confidence in assessing the sensitivity of geodiversity to lithology (Q2) than the bivariate group. Conversely, the bivariate group had slightly more confidence in assessing the sensitivity of geodiversity to land use/land cover (Q3) than the adjacent group. Most respondents in the adjacent group (23 out of 31) used total order sensitivity maps (i.e., factor interaction maps) to answer Q2 and Q3. Similarly, 22 out of 31 respondents in the bivariate group used bivariate maps, combining single-factor influence (Si) with the factor’s interactions (STj–Sj) to answer Q2 and Q3 (Figure 9).

Both groups reported similar confidence levels in their ability to explain the sensitivity analysis results to others (Q5). The differences in the average scores are small (≤2.6) and suggest that there was little, if any, difference between the adjacent and bivariate maps in promoting confidence in the interpretations of the results of the variance-based GSA (research question 1).

3.3. Map Communication Effectiveness

The adjacent sensitivity maps were more helpful in pinpointing the factors linked to the uncertainty of high geodiversity values compared with the bivariate maps (Q6). Similarly, grasping the disparities between the main effects (Si) and the total effects (STi) was more straightforward with the adjacent maps than with the bivariate ones (Q7). Evidently, the respondents found it more convenient to navigate between the sensitivity maps (Figure 4 and Figure 5) than to differentiate between the effects of STi–Si depicted on the bivariate maps (Figure 7).

Interestingly, using the bivariate maps (Figure 7) to comprehend the spatial variability of a geodiversity assessment, such as the geodiversity average and standard deviation (Figure 6), proved more beneficial than using the adjacent maps. This preference could stem from potential visual and cognitive fatigue resulting from the need to switch between the geodiversity mean and standard deviation maps (Figure 3A,B) and the sensitivity maps (Figure 4 and Figure 5). A similar trend is evident in the responses to Q9, where participants found the bivariate maps more effective than the adjacent maps in interpreting the spatial distribution of the geodiversity index’s average values.

However, there is a slight, yet noteworthy, reversal of this pattern in the responses to Q10. Here, the respondents found the adjacent maps slightly more useful than the bivariate maps for understanding the spatial distribution of the standard deviation values (Figure 3B and Figure 6, respectively). These contrasting results for Q9 and Q10 lack an obvious explanation and could hardly be attributed to differences in map reading competence (Q12), as both groups showed similar levels of competence.

We compared the median response scores between the groups by testing for statistically significant differences. The differences between the groups for Q2–Q3 and Q5–Q10 were statistically non-significant (

Table 3. The Mann–Whitney and Wilcoxon test statistics for differences between the medians of the two groups.

Differences in Median Response Scores: Test Statistics
	Q2	Q3	Q5	Q6	Q7	Q8	Q9	Q10	Q12
Mann–Whitney U	430	466.5	476	435.5	405.5	404	381	460	459.5
Wilcoxon W	926.0	962.5	972.0	931.5	901.5	900.0	877.0	956.0	955.5
Z	−0.761	−0.209	−0.066	−0.659	−1.099	−1.136	−1.478	−0.302	−0.329

).

Next, we investigated whether there was an association between the median scores for Q2–Q3, Q5–Q10, and familiarity with the concept of geodiversity (Q11). Similarly, we tested for a statistically significant association between the median scores and map reading skills (Q12).

3.4. The Effect of Prior Exposure to the Geodiversity Concept on Interpreting GSA Results

There was a notable difference between the groups in how they responded to Q11. Despite both groups having been exposed to the concept of geodiversity through various coursework formats (such as lectures, labs, and short introductions), some respondents in each group reported unfamiliarity with the concept. In the bivariate group, 6 out of 31 respondents were unfamiliar with the concept, while 25 were familiar with it. In contrast, in the adjacent group, 13 respondents were unfamiliar, compared to 18 who were familiar. We tested whether prior exposure to the concept of geodiversity affected the quality of map interpretation (Q1). Instead of testing for differences in prior exposure by seven geodiversity factors, we grouped the six less influential factors into one category (no relief energy). We then retained relief energy as the second category (

Table 4. Crosstabulation Q1 × Q11.

		Prior Exposure to Geodiversity		Total
		No	Yes
No Relief Energy (N_RF)	Count	9	20	29
	% within N_RF	31.0	69.0	100.0
	% within Q11	47.4	46.6	46.8
	% of total	14.5	32.32	46.8
Relief Energy (RF)	Count	10	23	33
	% within RF	30.3	69.7	100.0
	% within Q11	52.6	53.5	53.2
	% of total	16.9	37.1	53.2
Total	Count	19	43	62
	% within Q11	100.0	100.0	100.0
	% of total	30.6	69.4	100.0

). We did it because there were many “no relief energy” factors with low counts (<5) for the presence or absence of prior exposure to geodiversity.

Based on Pearson’s Chi-squared test of independence between the groups, there was no statistically significant association between prior exposure to the concept of geodiversity and the correct response (relief energy factor) to Q1 $(\mathsf{\chi }2$ = 0.004, df = 1, p = 0.950).

We also sought to determine whether prior exposure influenced the interpretation of sensitivity indices and confidence levels. According to the Mann–Whitney U test results for group differences, there were no statistically significant variations in the map interpretation or confidence levels across the two categories of prior exposure (

Table 5. Mann–Whitney and Wilcoxon test statistics for differences between geodiversity concept exposure (no or yes) and confidence in interpreting GSA results.

Test Summary
	Null Hypothesis	Test	Significance a,b	Decision
1	The distribution of Q2 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.634	Retain the null hypothesis.
2	The distribution of Q3 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.593	Retain the null hypothesis.
3	The distribution of Q5 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.121	Retain the null hypothesis.
4	The distribution of Q6 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.280	Retain the null hypothesis.
5	The distribution of Q7 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.975	Retain the null hypothesis.
6	The distribution of Q8 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.380	Retain the null hypothesis.
7	The distribution of Q9 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.215	Retain the null hypothesis.
8	The distribution of Q10 is the same across categories of Q11.	Independent-Samples Mann–Whitney U Test	0.410	Retain the null hypothesis.

^a The significance level is 0.050. ^b Asymptotic significance is displayed.

). In essence, whether or not the respondents were familiar with the concept of geodiversity did not impact their interpretations of the maps containing GSA results or their confidence in those interpretations.

Finally, we wanted to determine whether the level of skill in thematic map interpretation, measured on a 5-point scale (1–5), influenced the quality of the interpretation of sensitivity maps. We treated the skill level (Q12) as an independent variable and the quality of map interpretation (Q1) as a dependent variable. We grouped the responses to Q1 into two categories: relief energy (correct response) and Non-Relief Response (incorrect response) (

Table 6. Quality of map interpretation (Q1) based on self-assessed map reading skills (Q12).

	Q12	Number of Responses	Mean Rank
Relief Energy/Non-Relief Response	2	2	15.00
	3	21	31.24
	4	33	32.85
	5	6	30.50

). We employed the Kruskal–Wallis test to determine whether there are statistically significant differences in the quality of map interpretation (measured by the correct response to Q1) across different levels of map reading skills. The test is appropriate for an independent ordinal variable (skill level in this case) with more than two levels (here, five levels) and a dependent variable (here, the map interpretation quality represented by the choice of the most influential factor) that is categorical. There was not a statistically significant difference in the level of thematic map interpretation skill and the quality of map interpretation (H = 2.517; p = 0.472).

4. Discussion

This study aimed to investigate whether adjacent maps differ from bivariate maps in their effectiveness in communicating the results of a variance-based GSA for a spatial multi-criteria model and whether there are differences in promoting confidence in interpreting these results. The analysis focused on the quality of map interpretation, confidence in map interpretation, map communication effectiveness, the effect of prior exposure to the concept of geodiversity on interpreting GSA results, and the effect of map reading skills on map interpretation.

Quality of Map Interpretation: The comparison of correct and incorrect responses between the adjacent and bivariate map groups did not show a statistically significant difference in the quality of map interpretation. Both map types were equally effective in conveying the most influential factor driving the spatial distribution of geodiversity values. That said, the comparison revealed interesting insights into the interpretive differences between the two map types. While both groups showed a similar ability to identify relief energy as the most influential factor, suggesting comparable effectiveness in conveying this specific information, it would be beneficial to explore why certain respondents in each group selected other factors. Understanding these discrepancies could shed light on the nuances of map interpretation and the factors that may influence it. Conducting post-questionnaire interviews with the respondents, which we did not perform in this study, would be a way to facilitate this understanding.

Confidence in Map Interpretation: The study found no significant difference between the adjacent and bivariate map groups in promoting confidence in interpreting the results of a GSA. The respondents in both groups expressed similar levels of confidence in interpreting sensitivity maps and explaining the results to others. Despite the similar levels of confidence reported by the respondents in both map groups, it would be valuable to investigate the underlying reasons behind their confidence levels. Factors such as the complexity of the information conveyed and map interpretation effort could play a role in shaping their confidence. The complexity of the information conveyed by the sensitivity maps could be measured, among others, by the number of polygon features (i.e., catchments) per standard area unit. Additionally, the cognitive complexity of the sensitivity maps could be measured by eye tracking and the amount of time individuals spend looking at different parts of the map and switching between different maps. The map interpretation effort can be approximated by the time spent answering the questionnaire.

In this study, we collected information about the time each respondent spent completing the questionnaire (the completion time). This information was logged for each IP address, as each respondent had a unique IP address. We recorded the start time of opening the questionnaire and the end time of submitting the questionnaire to calculate the completion times. For the adjacent group, the completion times ranged from a minimum of 190 s to a maximum of 6392 s, with a mean of 1103 s and a standard deviation of 1023.47 s. The corresponding completion times for the bivariate group were a minimum of 133 s, a maximum of 2733 s, a mean of 1006 s, and a standard deviation of 608 s. To compare the group means, we used a t-test for independent samples. The results indicated that there was no significant difference between the group means (t = −1.4876, df = 60, p ≤ 0.05, critical t-value = ±2.000).

However, we observed a notable difference between the groups in the association between the completion time (an interval-scale variable) and the quality of map interpretation (a binary variable: 1—correct interpretation; 0—incorrect interpretation). To measure this association, we used the point-biserial correlation coefficient r_pb [60]. This coefficient ranges from −1 to 1, where −1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation. For the adjacent group, the r_pb value of 0.488 suggests a moderate relationship between completion time and the quality of map interpretation. In contrast, for the bivariate group, the r_pb value of 0.775 indicates a strong positive correlation between these two variables. This suggests that spending more time interpreting the results of a GSA rendered on bivariate maps is a better predictor of correctly identifying influential factors than in the case of adjacent maps. Further analysis is needed to determine the nature and strength of this relationship and whether any causal relationship exists between the map type and the interpretation quality.

Map Communication Effectiveness: This study observed that adjacent maps were more helpful in pinpointing factors linked to the uncertainty of high geodiversity values compared to bivariate maps. Respondents also found it easier to navigate between adjacent sensitivity maps than to differentiate between effects on bivariate maps. However, bivariate maps, such as the geodiversity average and standard deviation, were more beneficial in understanding the spatial variability of geodiversity assessment. The differences observed in the effectiveness of adjacent and bivariate maps in pinpointing factors linked to the uncertainty of high geodiversity values highlight the importance of map design in conveying complex spatial information. Further exploration into the specific design elements that contribute to this effectiveness, such as using different color schemes and possibly other visual variables appropriate for mapping quantities (symbol size, color value, and texture), could provide valuable insights for improving the communicative power of sensitivity maps. In this study, we employed a discrete two-color scheme, using blue and red, to emphasize a specific threshold value (0.15) within the distributions of both sensitivity indices. The choice of colors was deliberate, aiming to prompt an interpretation response that categorizes mapping units (i.e., watersheds) as either low sensitivity (below the threshold) or high sensitivity (above the threshold). We hypothesize that a discrete two-color scheme is at least as effective for interpreting sensitivity indices as a single-color scheme, although this assertion warrants further research. Another potential direction for further research, also pointed out by Şalap-Ayça et al. [27], involves thematic maps linked with interactive graphs.

Effects of Prior Exposure to Geodiversity and Map Reading Skills: Prior exposure to the concept of geodiversity did not significantly affect the quality of map interpretation. Familiarity with the concept did not impact respondents’ ability to interpret maps containing GSA results or their confidence in those interpretations. Similarly, thematic map reading skills did not affect the quality of map interpretation. The respondent group was skilled in reading thematic maps (mean = 3.69 on a five-point Likert’s scale (1–5)), and there was a slight variation in the skill level (standard deviation = 0.68), which explains that there was no statistically significant association between the skill and the quality of map interpretation. While prior exposure and map reading skills did not significantly affect the quality of map interpretation or confidence levels, it is worth considering the potential impact of other factors related to prior knowledge and experience relevant to interpreting GSA results, such as experience with spatial analysis and spatial statistics. Understanding how prior knowledge influences map interpretation could help tailor map designs to different user groups.

5. Conclusions

The communication of knowledge and information through maps, and their perception by map users, has an important social dimension and is a challenge for present-day cartographers. Our study suggests that adjacent and bivariate maps are equally effective in communicating GSA results and promoting confidence in interpreting these results. That being said, choosing bivariate maps over adjacent maps would be justified in enhancing the map reader’s understanding of the spatial variability of model output and its uncertainty. Conversely, a preference for using adjacent maps over bivariate maps may be justified when the communication goal is to identify a single factor or a group of factors that contributed the most to the variability in model output. The choice between the two map types may depend on the specific aspects of the results researchers aim to highlight and the cognitive load imposed on map readers. Further research could explore other factors that may influence the effectiveness of different map types in communicating complex spatial information.

The findings of this study have several implications for future research and practice in the area of spatially explicit GSA and map design. Firstly, they underscore the importance of considering the specific objectives of map communication when choosing between adjacent and bivariate maps. Alternative arrangements of adjacent factor maps to the one presented in this study may be considered, in which a single sensitivity index map is paired with a corresponding total sensitivity index map. Different map types may be more suitable depending on the intended audience and the complexity of the information to be conveyed. Secondly, this study highlights the need for further research into the cognitive processes underlying map interpretation, including the role of prior knowledge, experience, and perceptual abilities. Researchers can develop more effective strategies for communicating spatial information through maps by gaining a deeper understanding of these processes.