Interpretable Machine Learning Insights into the Factors Influencing Residents’ Travel Distance Distribution
Abstract
:1. Introduction
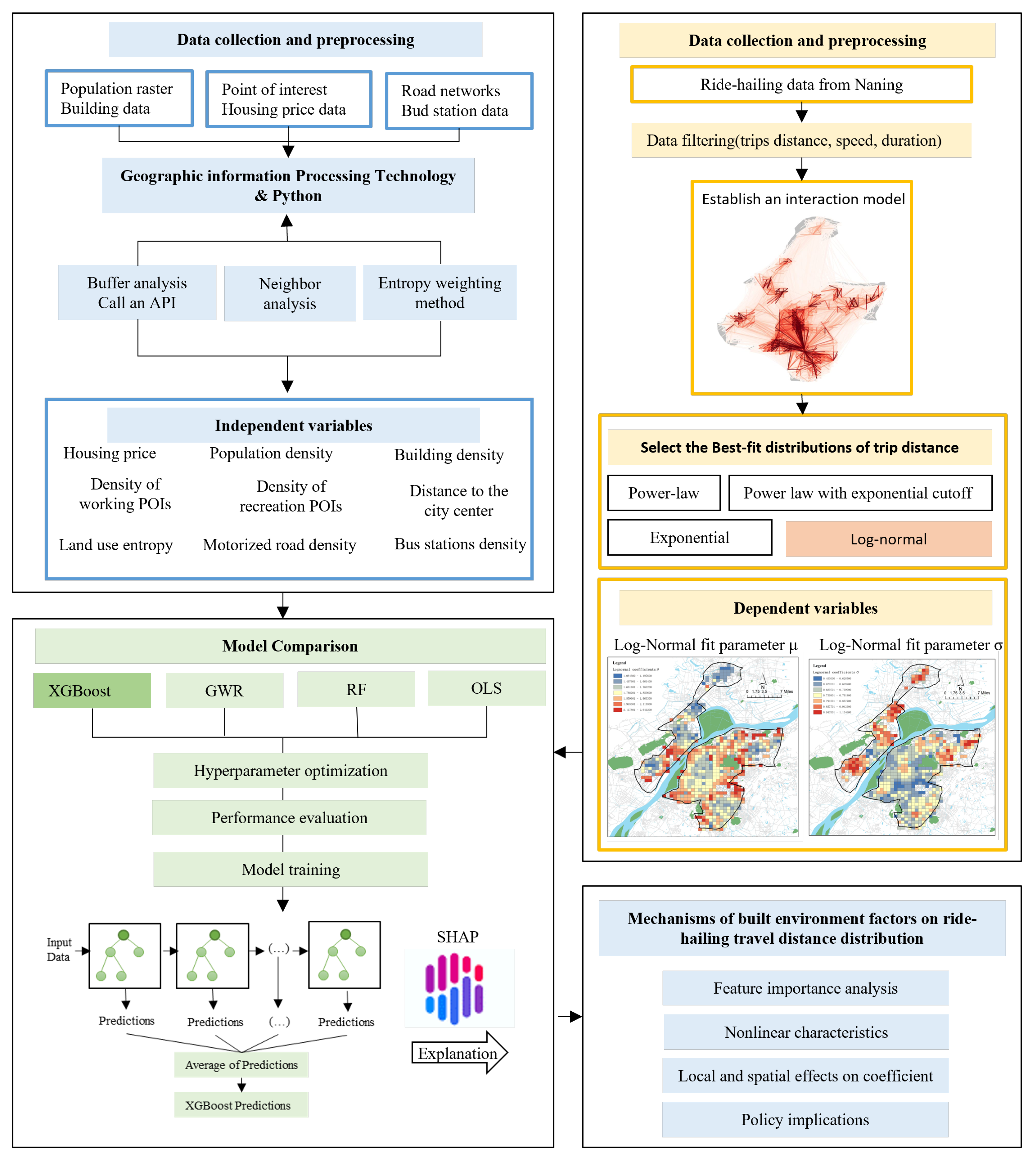
2. Materials and Methods
2.1. Study Area and Data Sources
2.1.1. Study Area
2.1.2. Data Sources
2.2. Variables
2.2.1. Dependent Variables
2.2.2. Independent Variables
2.3. Data Processing and Modeling
2.4. XGBoost Model and SHAP
3. Results
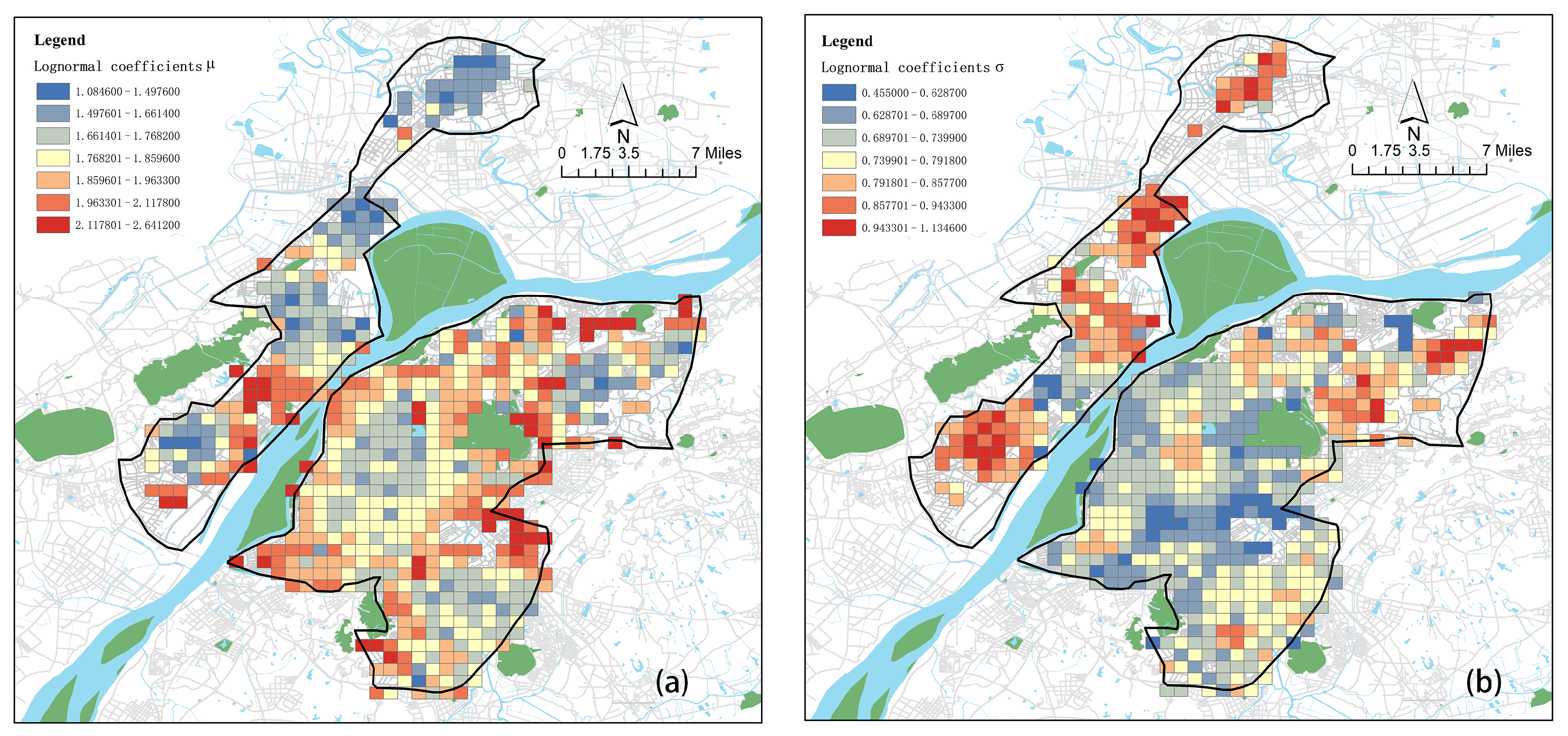
3.1. Spatial Distribution of Coefficients
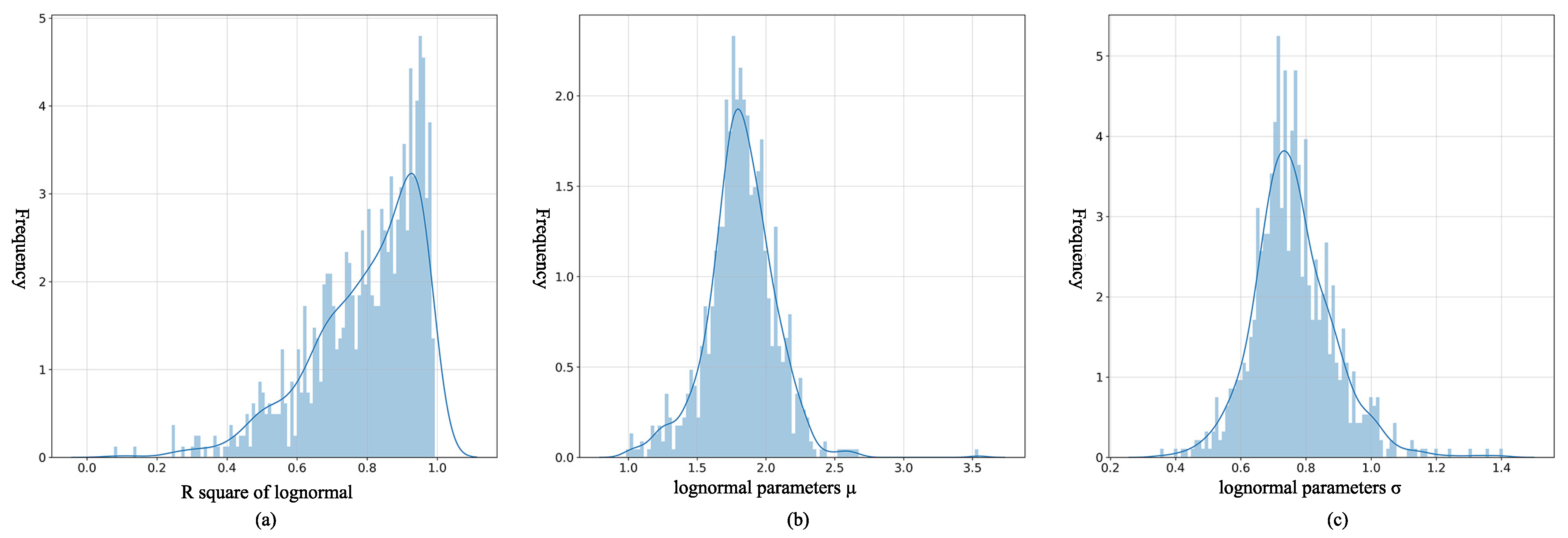
3.1.1. Best-Fit Distributions of Trip Distance
3.1.2. Spatial Distribution of Log-Normal Distribution
3.2. Model Comparison
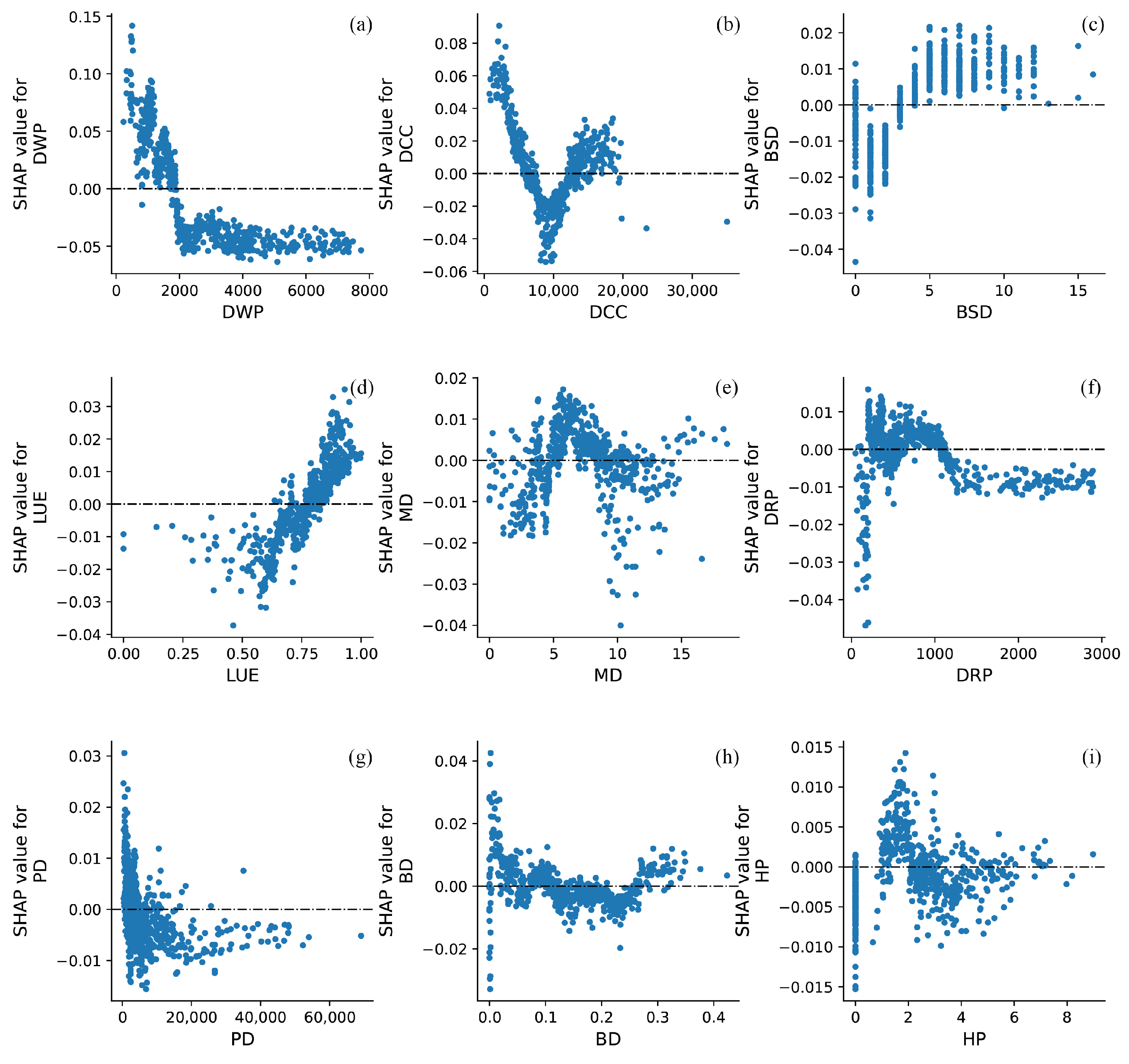
3.3. Nonlinear Relationship Interpretation Using SHAP
3.3.1. Feature Importance Analysis
3.3.2. Nonlinear Relationship Analysis
- (1)
- Driving factors of
- (2)
- Driving factors of
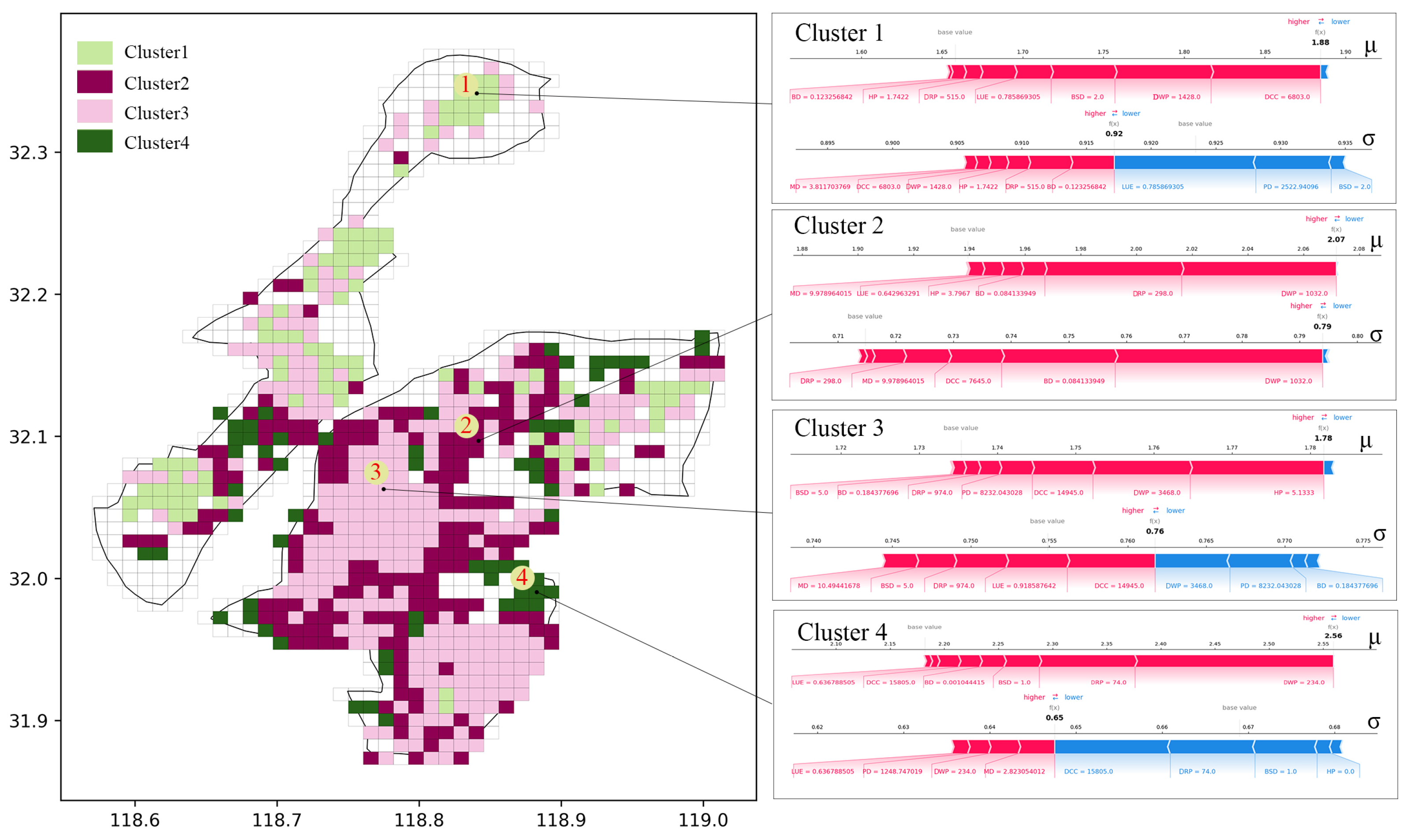
3.3.3. Local and Spatial Effects on Coefficients
4. Discussion
4.1. Comprehensive Interpretation of Nonlinear Relationships
4.2. Policy Implications
4.3. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Land Use Categories | Code | POI Category |
|---|---|---|
| Working POI | 1 | Governmental organizations |
| 2 | Social communities | |
| 3 | Schools and educational institutions | |
| 4 | Company and business | |
| Recreation POI | 5 | Restaurants |
| 6 | Coffee/tea shops | |
| 7 | Sports stadiums | |
| 8 | Tourism spots | |
| 9 | Cultural venues | |
| 10 | Recreation stores and centers | |
| 11 | Supermarkets | |
| 12 | Shopping malls | |
| 13 | Parks/squares | |
| 14 | Hotels |
References
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yin, J.; Zhao, S. Characterizing the human mobility pattern in a large street network. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2009, 80, 021136. [Google Scholar] [CrossRef] [PubMed]
- Ratti, C.; Frenchman, D.; Pulselli, R.M.; Williams, S. Mobile landscapes: Using location data from cell phones for urban analysis. Environ. Plan. B Plan. Des. 2006, 33, 727–748. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Y.H.; Lih, J.S. Crossover from exponential to power-law scaling for human mobility pattern in urban, suburban and rural areas. Eur. Phys. J. B 2015, 88, 1–7. [Google Scholar] [CrossRef]
- Alessandretti, L.; Sapiezynski, P.; Lehmann, S.; Baronchelli, A. Multi-scale spatio-temporal analysis of human mobility. PLoS ONE 2017, 12, e0171686. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhou, S.; Deng, X. Exploring both home-based and work-based jobs-housing balance by distance decay effect. J. Transp. Geogr. 2021, 93, 103043. [Google Scholar] [CrossRef]
- Blondel, V.D.; Decuyper, A.; Krings, G. A survey of results on mobile phone datasets analysis. EPJ Data Sci. 2015, 4, 1–55. [Google Scholar] [CrossRef]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zheng, X.; Lv, W.; Zhu, T.; Xu, K. The scaling of human mobility by taxis is exponential. Phys. A Stat. Mech. Appl. 2012, 391, 2135–2144. [Google Scholar] [CrossRef]
- Bazzani, A.; Giorgini, B.; Rambaldi, S.; Gallotti, R.; Giovannini, L. Statistical laws in urban mobility from microscopic GPS data in the area of Florence. J. Stat. Mech. Theory Exp. 2010, 2010, P05001. [Google Scholar] [CrossRef]
- Riccardo, G.; Armando, B.; Sandro, R. Towards a statistical physics of human mobility. Int. J. Mod. Phys. C 2012, 23, 1250061. [Google Scholar] [CrossRef]
- Jurdak, R.; Zhao, K.; Liu, J.; AbouJaoude, M.; Cameron, M.; Newth, D. Understanding human mobility from Twitter. PLoS ONE 2015, 10, e0131469. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sui, Z.; Kang, C.; Gao, Y. Uncovering patterns of inter-urban trip and spatial interaction from social media check-in data. PLoS ONE 2014, 9, e86026. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhi, Y.; Sui, Z.; Liu, Y. Intra-urban human mobility and activity transition: Evidence from social media check-in data. PLoS ONE 2014, 9, e97010. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Liu, X.; Wu, L.; Liu, Y. Inferring trip purposes and uncovering travel patterns from taxi trajectory data. Cartogr. Geogr. Inf. Sci. 2016, 43, 103–114. [Google Scholar] [CrossRef]
- Wang, W.; Pan, L.; Yuan, N.; Zhang, S.; Liu, D. A comparative analysis of intra-city human mobility by taxi. Phys. A Stat. Mech. Appl. 2015, 420, 134–147. [Google Scholar] [CrossRef]
- Tang, J.; Liu, F.; Wang, Y.; Wang, H. Uncovering urban human mobility from large scale taxi GPS data. Phys. A Stat. Mech. Appl. 2015, 438, 140–153. [Google Scholar] [CrossRef]
- Shi, C.; Li, Q.; Lu, S.; Yang, X. Exploring temporal intra-urban travel patterns: An online car-hailing trajectory data perspective. Remote Sens. 2021, 13, 1825. [Google Scholar] [CrossRef]
- Shi, C.; Li, Q.; Lu, S.; Yang, X. Modeling the Distribution of Human Mobility Metrics with Online Car-Hailing Data—An Empirical Study in Xi’an, China. ISPRS Int. J. Geo-Inf. 2021, 10, 268. [Google Scholar] [CrossRef]
- Chai, Y. Space–time behavior research in China: Recent development and future prospect: Space–time integration in geography and GIScience. Ann. Assoc. Am. Geogr. 2013, 103, 1093–1099. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, X.; Yang, S.; Cao, Z.; De Vos, J.; Witlox, F. Active travel for active ageing in China: The role of built environment. J. Transp. Geogr. 2019, 76, 142–152. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, M. The built environment and travel behavior in urban China: A literature review. Transp. Res. Part D Transp. Environ. 2017, 52, 574–585. [Google Scholar] [CrossRef]
- Dong, W.; Wang, S.; Liu, Y. Mapping relationships between mobile phone call activity and regional function using self-organizing map. Comput. Environ. Urban Syst. 2021, 87, 101624. [Google Scholar] [CrossRef]
- Tu, W.; Zhu, T.; Xia, J.; Zhou, Y.; Lai, Y.; Jiang, J.; Li, Q. Portraying the spatial dynamics of urban vibrancy using multisource urban big data. Comput. Environ. Urban Syst. 2020, 80, 101428. [Google Scholar] [CrossRef]
- Yang, X.; Fang, Z.; Xu, Y.; Yin, L.; Li, J.; Lu, S. Spatial heterogeneity in spatial interaction of human movements—Insights from large-scale mobile positioning data. J. Transp. Geogr. 2019, 78, 29–40. [Google Scholar] [CrossRef]
- Cheng, L.; De Vos, J.; Zhao, P.; Yang, M.; Witlox, F. Examining non-linear built environment effects on elderly’s walking: A random forest approach. Transp. Res. Part D Transp. Environ. 2020, 88, 102552. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.; Fang, Z.; Chen, H.; Li, J.; Zhao, Z. Influence of residential built environment on human mobility in Xining: A mobile phone data perspective. Travel Behav. Soc. 2024, 34, 100665. [Google Scholar] [CrossRef]
- Shaheen, S.; Bell, C.; Cohen, A.; Yelchuru, B. Travel Behavior: Shared Mobility and Transportation Equity; Technical Report; United States Federal Highway Administration, Office of Policy & Governmental Affairs: Washington, DC, USA, 2017.
- Zhang, B.; Chen, S.; Ma, Y.; Li, T.; Tang, K. Analysis on spatiotemporal urban mobility based on online car-hailing data. J. Transp. Geogr. 2020, 82, 102568. [Google Scholar] [CrossRef]
- Šveda, M.; Madajová, M.S. Estimating distance decay of intra-urban trips using mobile phone data: The case of Bratislava, Slovakia. J. Transp. Geogr. 2023, 107, 103552. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Farrell, S. AIC model selection using Akaike weights. Psychon. Bull. Rev. 2004, 11, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Noland, R.B. Variation in ride-hailing trips in Chengdu, China. Transp. Res. Part D Transp. Environ. 2021, 90, 102596. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, J.; Zhang, L.; Li, M.; Rong, P.; Qin, Y. Understanding the impact of the built environment on ride-hailing from a spatio-temporal perspective: A fine-scale empirical study from China. Cities 2022, 126, 103706. [Google Scholar] [CrossRef]
- Ding, C.; Cao, X.J.; Næss, P. Applying gradient boosting decision trees to examine non-linear effects of the built environment on driving distance in Oslo. Transp. Res. Part A Policy Pract. 2018, 110, 107–117. [Google Scholar] [CrossRef]
- Zhao, P.; Xu, Y.; Liu, X.; Kwan, M.P. Space-time dynamics of cab drivers’ stay behaviors and their relationships with built environment characteristics. Cities 2020, 101, 102689. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Li, A.; Qu, X. Spatial heterogeneity in distance decay of using bike sharing: An empirical large-scale analysis in Shanghai. Transp. Res. Part D Transp. Environ. 2021, 94, 102814. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, X.; Liu, X.; Zhao, X. Identifying key factors associated with ridesplitting adoption rate and modeling their nonlinear relationships. Transp. Res. Part A Policy Pract. 2021, 144, 170–188. [Google Scholar] [CrossRef]
- Yi, S.; Li, X.; Wang, R.; Guo, Z.; Dong, X.; Liu, Y.; Xu, Q. Interpretable spatial machine learning insights into urban sanitation challenges: A case study of human feces distribution in San Francisco. Sustain. Cities Soc. 2024, 113, 105695. [Google Scholar] [CrossRef]
- Luo, Y.; Yan, J.; McClure, S. Distribution of the environmental and socioeconomic risk factors on COVID-19 death rate across continental USA: A spatial nonlinear analysis. Environ. Sci. Pollut. Res. 2021, 28, 6587–6599. [Google Scholar] [CrossRef] [PubMed]
- Grekousis, G.; Feng, Z.; Marakakis, I.; Lu, Y.; Wang, R. Ranking the importance of demographic, socioeconomic, and underlying health factors on US COVID-19 deaths: A geographical random forest approach. Health Place 2022, 74, 102744. [Google Scholar] [CrossRef]
- Doan, Q.C.; Ma, J.; Chen, S.; Zhang, X. Nonlinear and threshold effects of the built environment, road vehicles and air pollution on urban vitality. Landsc. Urban Plan. 2025, 253, 105204. [Google Scholar] [CrossRef]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Tu, M.; Li, W.; Orfila, O.; Li, Y.; Gruyer, D. Exploring nonlinear effects of the built environment on ridesplitting: Evidence from Chengdu. Transp. Res. Part D Transp. Environ. 2021, 93, 102776. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Du, M.; Liu, D.; Kwan, M.P. Understanding the spatiotemporal variation of ride-hailing orders under different travel distances. Travel Behav. Soc. 2023, 32, 100581. [Google Scholar] [CrossRef]
- Stead, D.; Marshall, S. The relationships between urban form and travel patterns. An international review and evaluation. Eur. J. Transp. Infrastruct. Res. 2001, 1. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, D.; Wang, S. Optimization for feeder bus route model design with station transfer. Sustainability 2022, 14, 2780. [Google Scholar] [CrossRef]
- Suzuki, T.; Lee, S. Jobs–housing imbalance, spatial correlation, and excess commuting. Transp. Res. Part A Policy Pract. 2012, 46, 322–336. [Google Scholar] [CrossRef]
- Cheng, C.C.; Wu, H.C.; Tsai, M.C.; Chang, Y.Y.; Chen, C.T. Determinants of customers’ choice of dining-related services: The case of Taipei City. Br. Food J. 2020, 122, 1549–1571. [Google Scholar] [CrossRef]
- Kanyepe, J.; Tukuta, M.; Chirisa, I. Urban land-use and traffic congestion: Mapping the interaction. J. Contemp. Urban Aff. 2021, 5, 77–84. [Google Scholar] [CrossRef]
- Xu, Y.; Belyi, A.; Bojic, I.; Ratti, C. Human mobility and socioeconomic status: Analysis of Singapore and Boston. Comput. Environ. Urban Syst. 2018, 72, 51–67. [Google Scholar] [CrossRef]
- Meredith-Karam, P.; Kong, H.; Wang, S.; Zhao, J. The relationship between ridehailing and public transit in Chicago: A comparison before and after COVID-19. J. Transp. Geogr. 2021, 97, 103219. [Google Scholar] [CrossRef]




| Field | Type | Example |
|---|---|---|
| Order ID | Int | 35,295,630,329,820 |
| Pick-up longitude | Float | 119.03238 |
| Pick-up latitude | Float | 31.631422 |
| Drop-off longitude | Float | 119.177723 |
| Drop-off latitude | Float | 31.575701 |
| Pick-up time stamp | Int | 1,676,824,955 |
| Drop-off time stamp | Int | 1,676,826,093 |
| Miles driven | Float | 18.14 |
| Driving time | Float | 19 |
| Distribution | Distribution Function and Normalization Constant * | |
|---|---|---|
| Power law | ||
| Power law with exponential cutoff | ** | |
| Exponential | ||
| Log-normal | *** | |
| Variable | Abbreviation | Description | Mean | Standard Deviation | Source |
|---|---|---|---|---|---|
| Socio-demographic characteristics | |||||
| Housing price (ten thousand CNY/km2) | HP | The average value of second-hand housing prices within each analysis zone. | 2.2713 | 1.7595 | [33,34] |
| Population density (person/km2) | PD | The population divided by the total area within each analysis zone. | 7721.7519 | 9372.4370 | [33,34] |
| Facility Convenience | |||||
| Distance to the city center (m) | DCC | The distance to the nearest city center. | 9444.6175 | 4415.8310 | [35] |
| Density of working POIs (numbers/km2) | DWP | Number of working facilities divided by the total area within each analysis zone. | 1591.4286 | 1739.9334 | [34,36] |
| Density of recreation POIs (numbers/km2) | DRP | The number of recreation facilities divided by total area within each analysis zone. | 817.4651 | 665.3297 | [34,36] |
| Construction intensity | |||||
| Building density | BD | The ratio of the total building base area to the total land area within each analysis zone. | 0.1425 | 0.0876 | [34] |
| Land use entropy | LUE | The mixed status of POIs within the analysis zone. | 0.7673 | 0.1369 | [33,34,36] |
| Traffic accessibility | |||||
| Motorized road density (km) | MD | The length of primary and secondary roads available for ride-hailing in each analysis zone. | 7.2065 | 3.3221 | [37] |
| Bus station density (numbers/km2) | BSD | The number of bus stations in each analysis zone. | 4.4079 | 3.0891 | [38] |
| Olsample Bytree | Gamma | Learning Rate | Max Depth | n Estimators | Reg Alpha | Reg Lambda | Subsample | |
|---|---|---|---|---|---|---|---|---|
| 0.8 | 0 | 0.2 | 5 | 20 | 0 | 1.5 | 0.8 | |
| 1.0 | 0 | 0.2 | 5 | 30 | 0.1 | 1.5 | 0.8 |
| Model | R2 | MAE | RMSE | |
|---|---|---|---|---|
| OLS | 0.13 | 0.14 | 0.18 | |
| 0.27 | 1.07 | 1.09 | ||
| GWR | 0.15 | 1.45 | 0.20 | |
| 0.31 | 1.09 | 0.12 | ||
| RF | 0.16 | 0.13 | 0.17 | |
| 0.40 | 0.05 | 0.07 | ||
| XGBoost | 0.23 | 0.13 | 0.18 | |
| 0.41 | 0.06 | 0.07 |
| Category | Feature Index | Relative Marginal Contribution (%) | Ranking | ||
|---|---|---|---|---|---|
| Socio-demographic characteristic | HP | 7.06 | 3.85 | 7 | 9 |
| PD | 6.85 | 5.12 | 8 | 7 | |
| Facility convenience | DCC | 20.6 | 18.47 | 1 | 2 |
| DWP | 14.25 | 35.25 | 3 | 1 | |
| DRP | 13.41 | 8.34 | 4 | 4 | |
| Construction intensity | BD | 3.76 | 4.33 | 9 | 8 |
| LUE | 8.52 | 8.26 | 5 | 5 | |
| Traffic accessibility | MD | 7.66 | 5.91 | 6 | 6 |
| BSD | 17.9 | 10.45 | 2 | 3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, R.; Lin, Y.; Yang, D.; Guo, Q. Interpretable Machine Learning Insights into the Factors Influencing Residents’ Travel Distance Distribution. ISPRS Int. J. Geo-Inf. 2025, 14, 39. https://doi.org/10.3390/ijgi14010039
Si R, Lin Y, Yang D, Guo Q. Interpretable Machine Learning Insights into the Factors Influencing Residents’ Travel Distance Distribution. ISPRS International Journal of Geo-Information. 2025; 14(1):39. https://doi.org/10.3390/ijgi14010039
Chicago/Turabian StyleSi, Rui, Yaoyu Lin, Dongquan Yang, and Qijin Guo. 2025. "Interpretable Machine Learning Insights into the Factors Influencing Residents’ Travel Distance Distribution" ISPRS International Journal of Geo-Information 14, no. 1: 39. https://doi.org/10.3390/ijgi14010039
APA StyleSi, R., Lin, Y., Yang, D., & Guo, Q. (2025). Interpretable Machine Learning Insights into the Factors Influencing Residents’ Travel Distance Distribution. ISPRS International Journal of Geo-Information, 14(1), 39. https://doi.org/10.3390/ijgi14010039





