Low-Power LoRa Signal-Based Outdoor Positioning Using Fingerprint Algorithm
Abstract
:1. Introduction
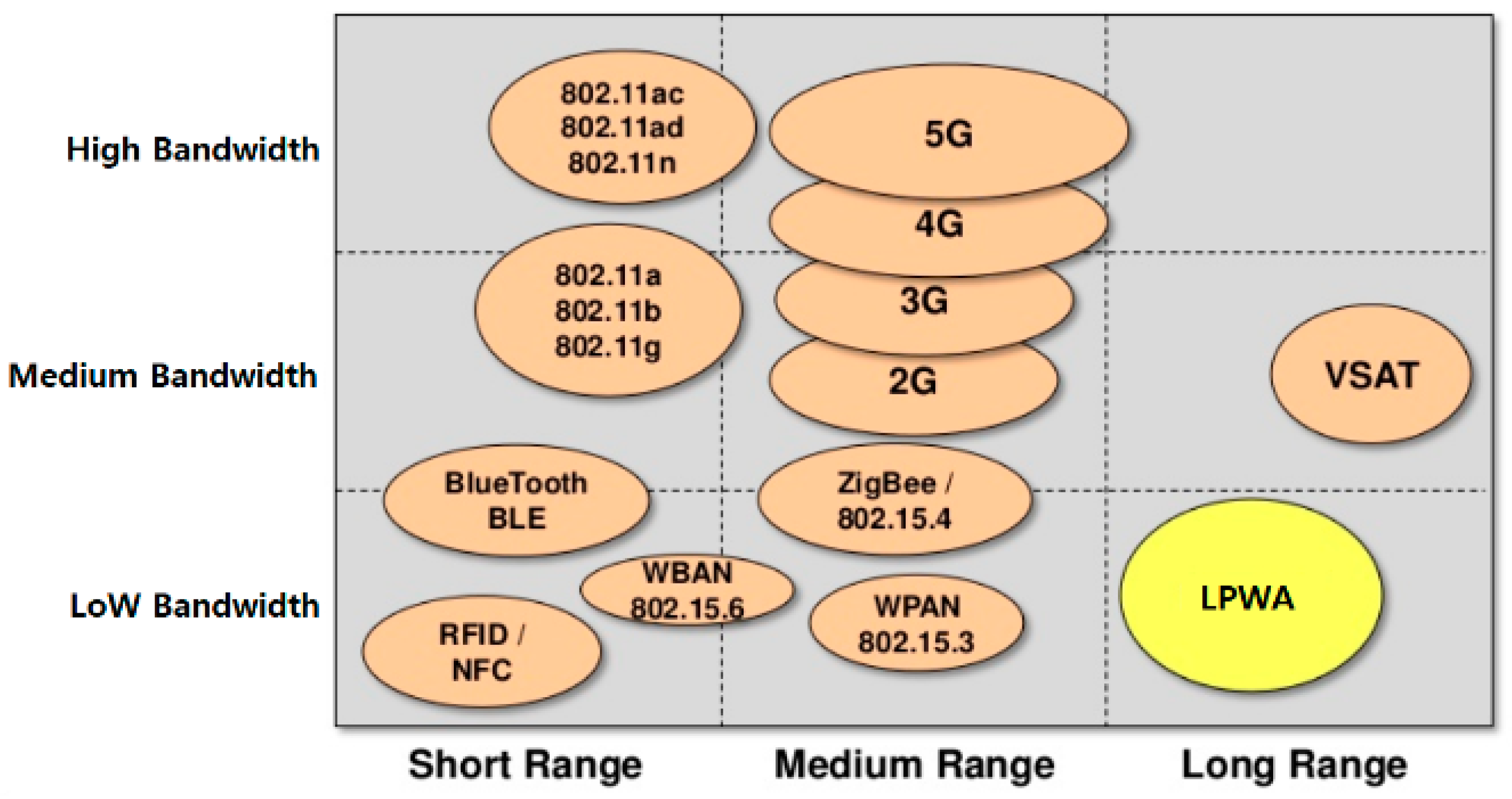
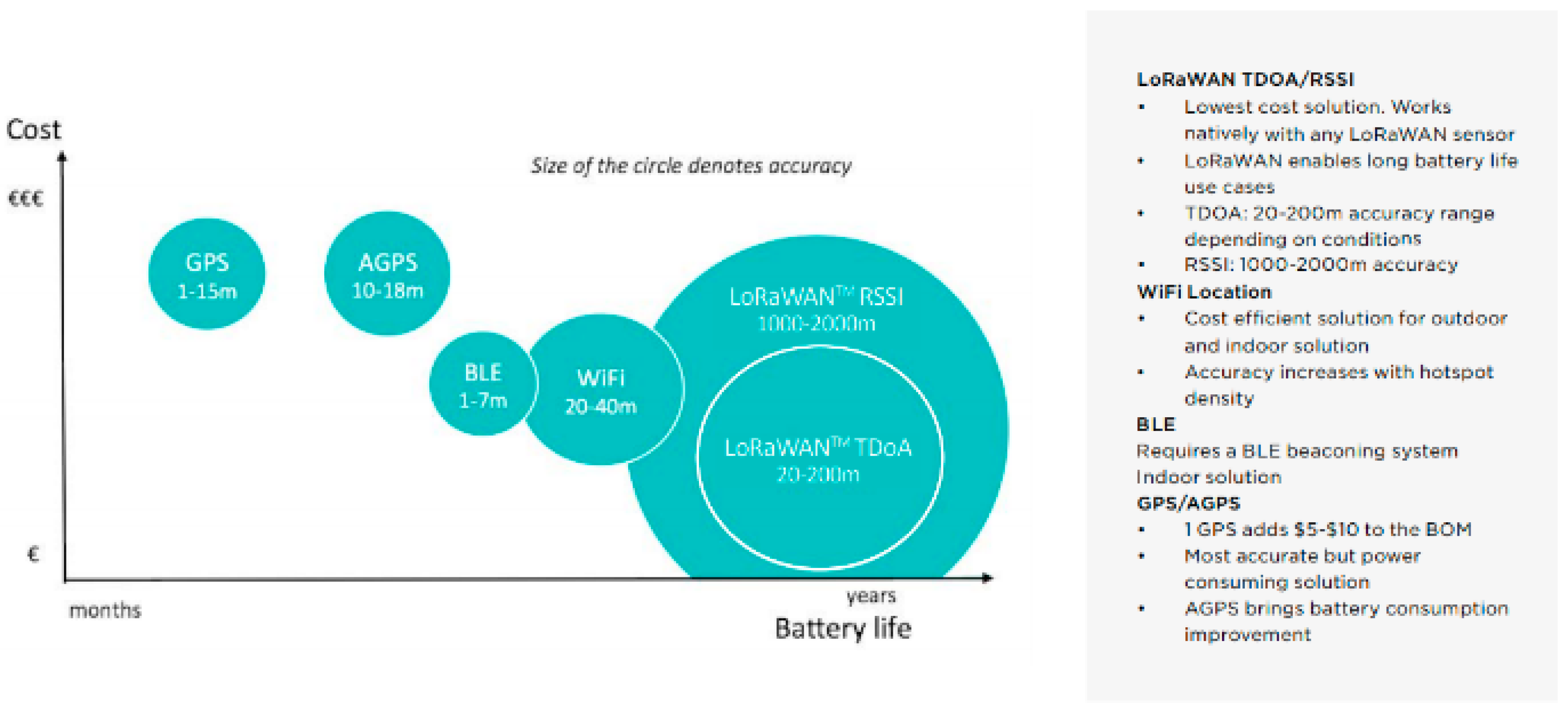
2. Related Work
2.1. RSSI Proximity and Path-Loss-Model-Based Positioning
2.2. TDoA-Based Positioning
2.3. Fingerprint-Algorithm-Based Positioning
3. Proposed Fingerprint Algorithm
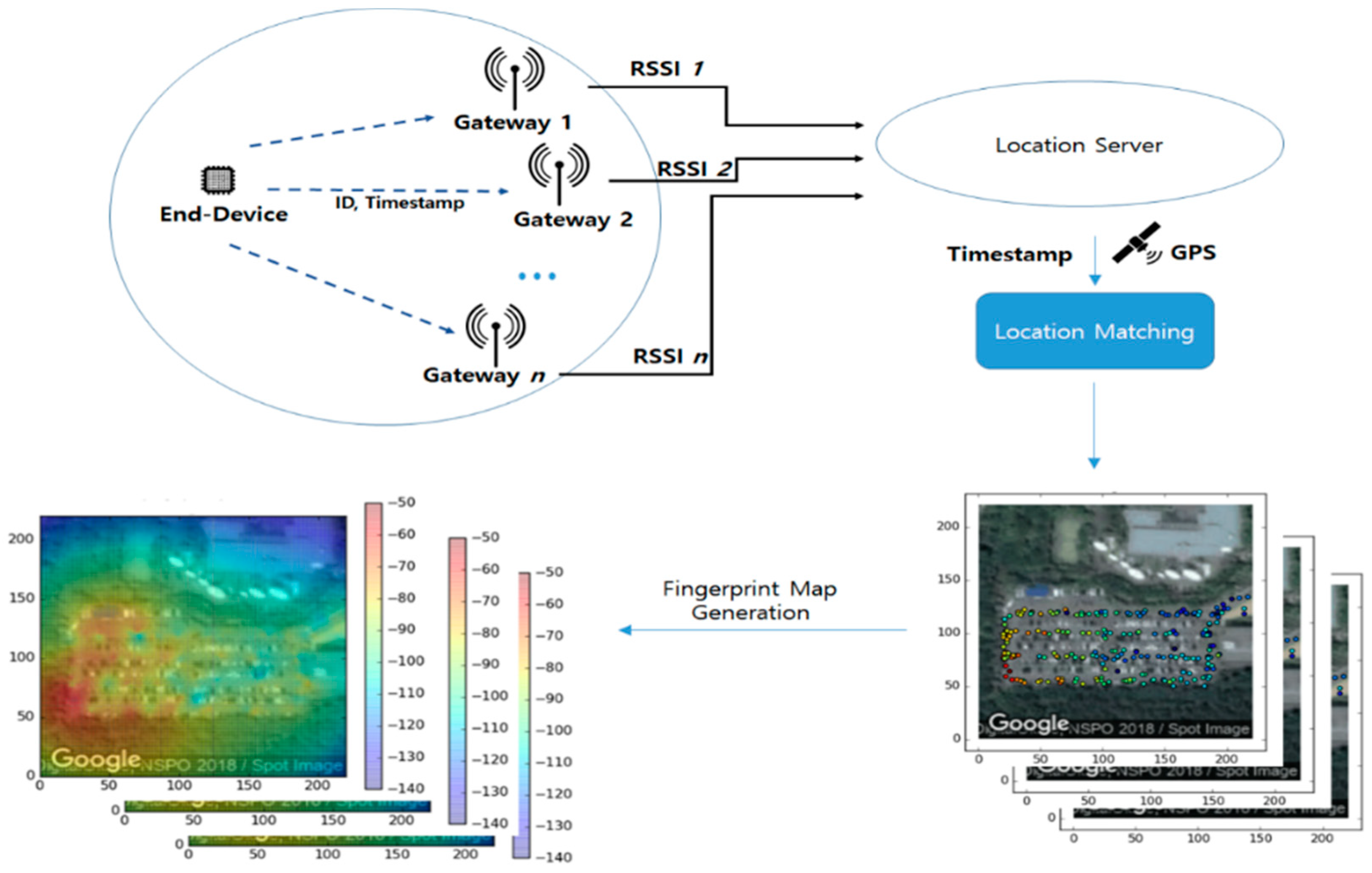
3.1. LoRa-Based Positioning
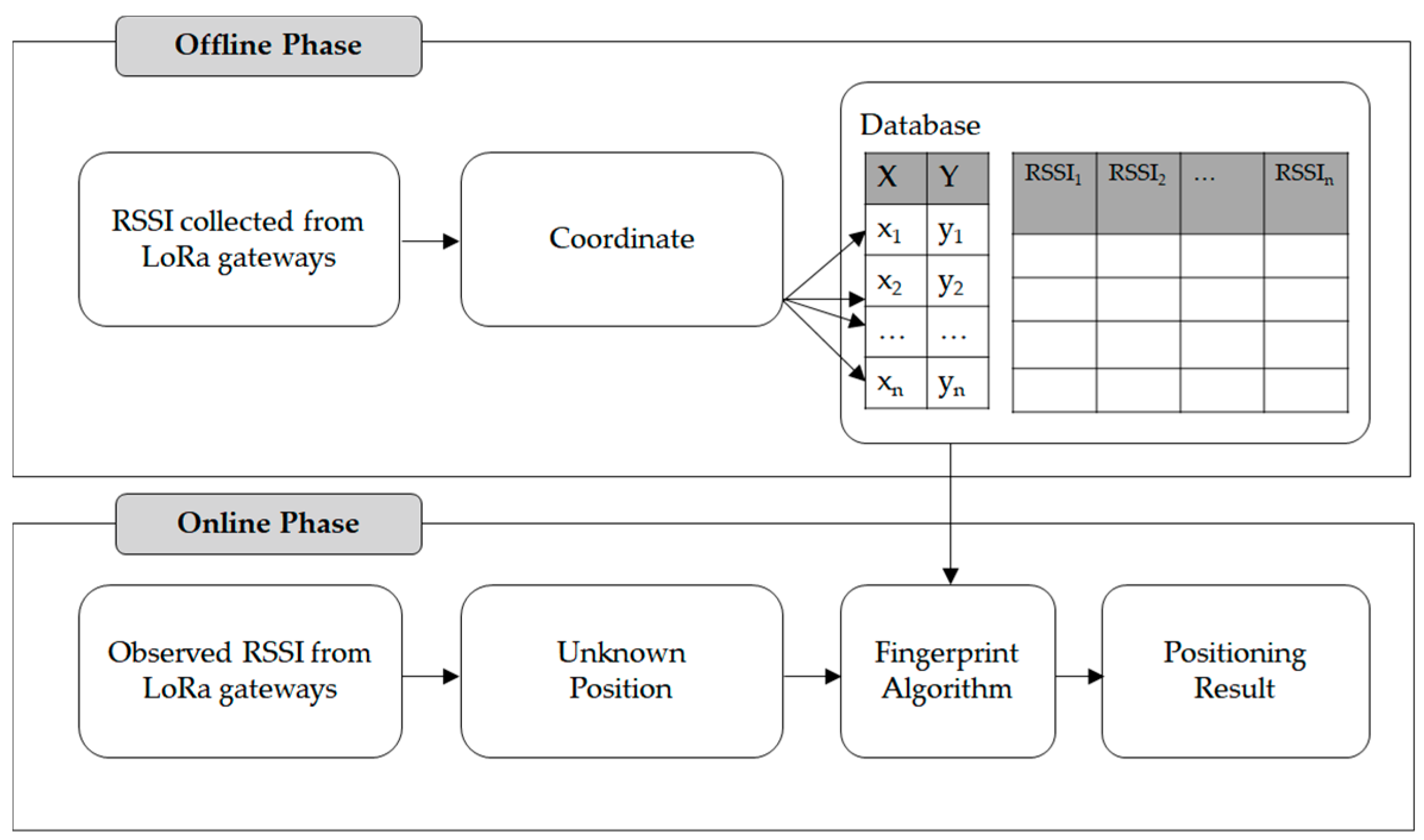
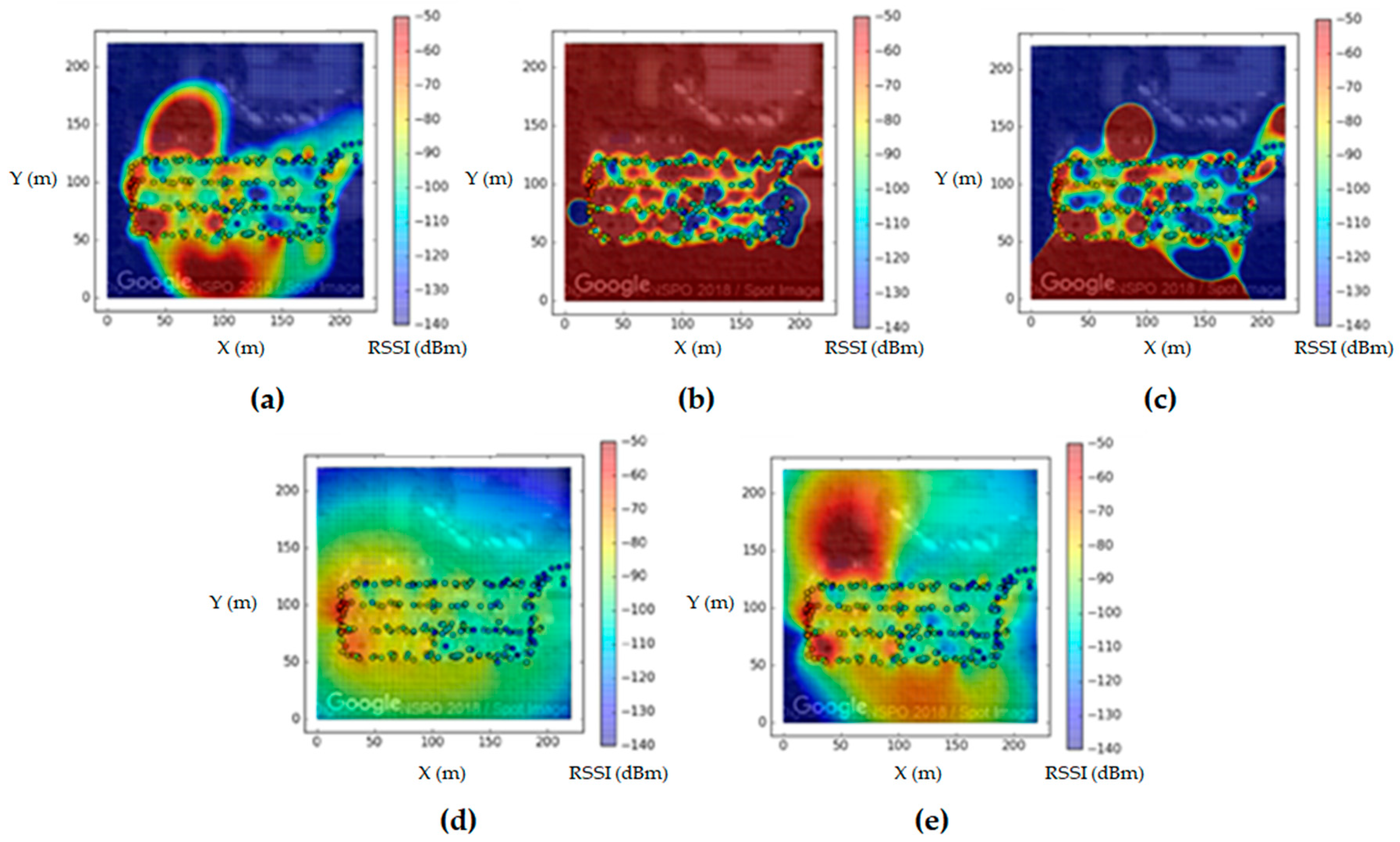
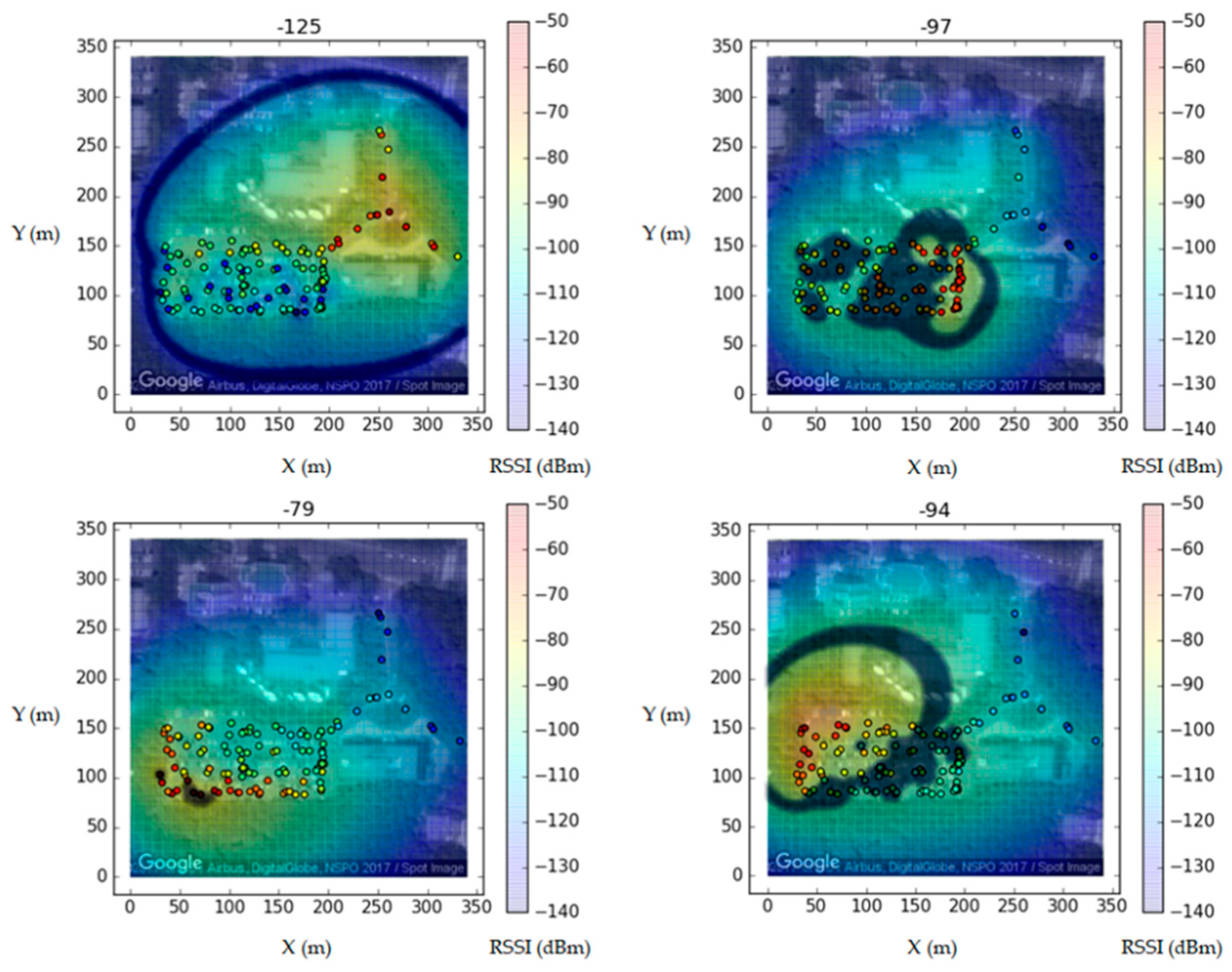
3.2. LoRa Fingerprint Map Generation
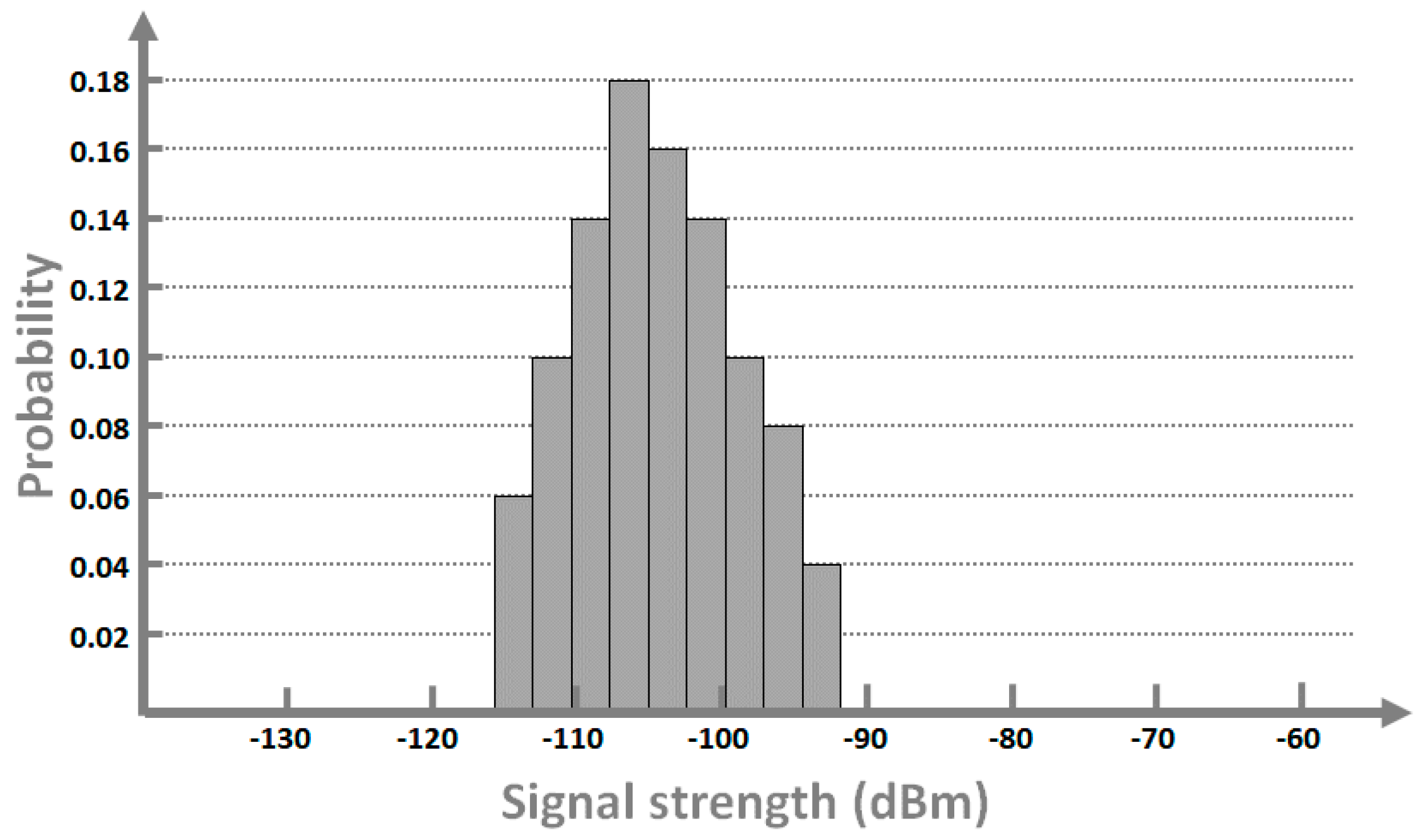
3.3. Probability Map Generation and Positioning
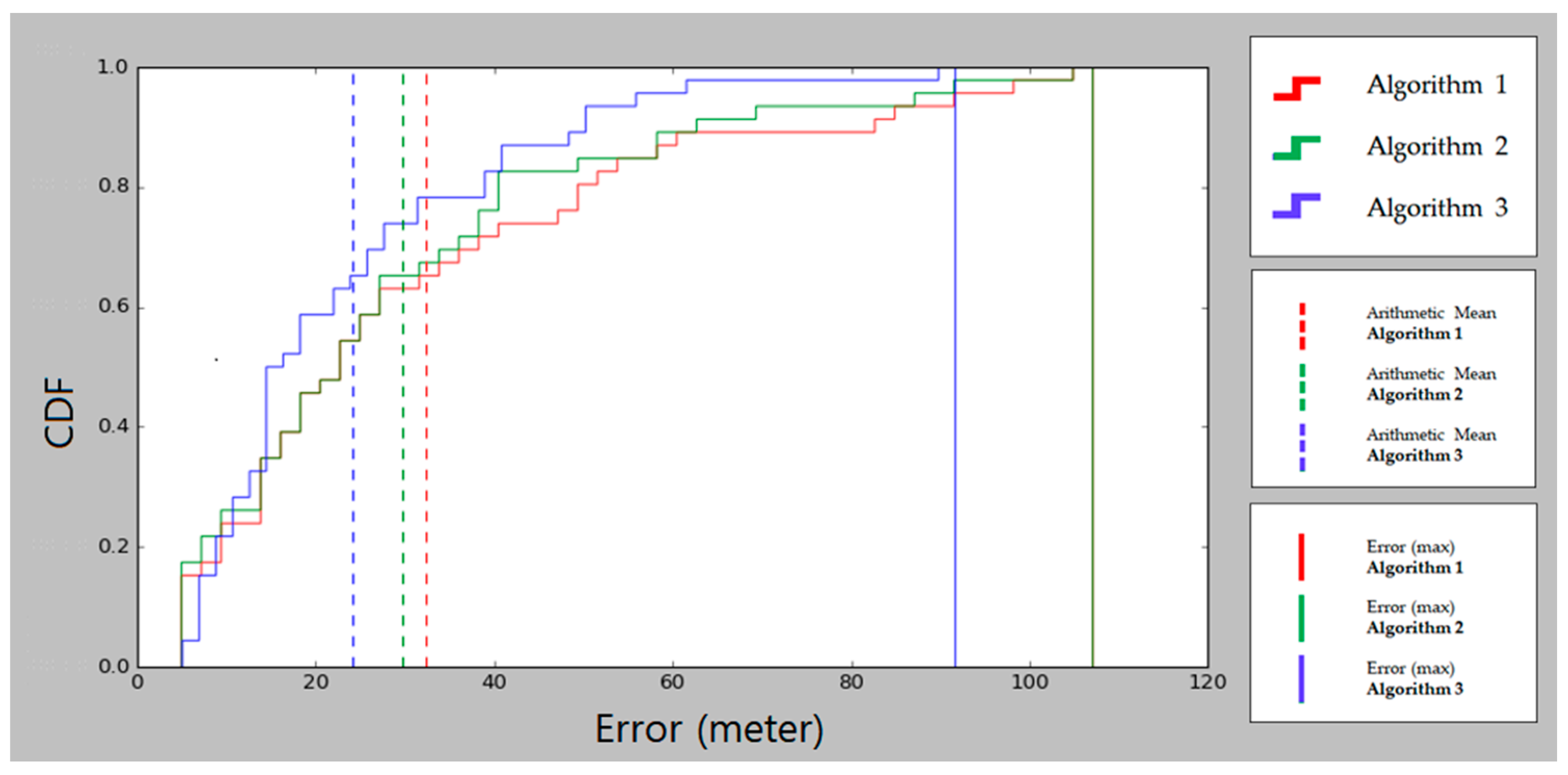
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Evans, D. The Internet of Things: How the Next Evolution of the Internet Is Changing Everything; Cisco Internet Business Solutions Group (IBSG): San Jose, CA, USA, 2011; pp. 3–4. [Google Scholar]
- Egli, P.R. LPWAN Technologies for Internet of Things (IoT) and M2M Scenarios. Available online: https://www.slideshare.net/PeterREgli/lpwan (accessed on 25 May 2018).
- Fargas, B.C.; Petersen, M.N. GPS-free geolocation using LoRa in low-power WANs. In Proceedings of the Global Internet of Things Summit (GIoTS), Geneva, Switzerland, 6–9 June 2017; pp. 1–6. [Google Scholar]
- LoRa Modulation Basics. Available online: https://www.semtech.com/uploads/documents/an1200.22.pdf (accessed on 25 May 2018).
- LoRa Alliance. White Paper: A Technical Overview of LoRa and LoRaWAN; The LoRa Alliance: San Ramon, CA, USA, 2015; pp. 7–11. [Google Scholar]
- LoRa Alliance™ Strategy Committee. LoRa Alliance Geolocation Whitepaper. Available online: https://lora-alliance.org/resource-hub/lora-alliance-geolocation-whitepaper (accessed on 25 May 2018).
- Lam, K.-H.; Cheung, C.-C.; Lee, W.-C. LoRa-based localization systems for noisy outdoor environment. In Proceedings of the 13th IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Rome, Italy, 9–11 October 2017; pp. 278–284. [Google Scholar]
- Islam, B.; Islam, M.T.; Nirjon, S. Feasibility of LoRa for Indoor Localization. Available online: https://pdfs.semanticscholar.org/ab00/c1eacbdd76732b7438ec8e5653f7c875def4.pdf (accessed on 25 May 2018).
- Kim, S.; Ko, J. Low-complexity outdoor localization for long-range, low-power radios. In Proceedings of the 14th Annual International Conference on Mobile Systems, Applications, and Services Companion, Singapore, 26 June 2016; p. 44. [Google Scholar]
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A survey of enabling technologies for network localization, tracking, and navigation. IEEE Commun. Surv. Tutor. 2018, 6, 1. [Google Scholar] [CrossRef]
- Richter, P.; Toledano-Ayala, M. Revisiting Gaussian process regression modeling for localization in wireless sensor networks. Sensors 2015, 15, 22587–22615. [Google Scholar] [CrossRef] [PubMed]
- Bekkali, A.; Masuo, T.; Tominaga, T.; Nakamoto, N.; Ban, H. Gaussian processes for learning-based indoor localization. In Proceedings of the 2011 IEEE International Conference on Signal Processing, Communications and Computing, Xi’an, China, 14–16 September 2011; pp. 1–6. [Google Scholar]
- Li, Z.; Braun, T.; Zhao, X.; Zhao, Z.; Hu, F.; Liang, H. A narrow-band indoor positioning system by fusing time and received signal strength via ensemble learning. IEEE Access 2018, 6, 9936–9950. [Google Scholar] [CrossRef]
- RSSI. Available online: https://en.wikipedia.org/wiki/Received_signal_strength_indication (accessed on 25 May 2018).
- TDoA Algorithm Implementation. Available online: https://forum.loraserver.io/t/tdoa-algorithm-implementation/720/7 (accessed on 25 May 2018).
- Hernández, N.; Alonso, J.M.; Ocaña, M.; Kim, E. WiFi-based indoor localization using a continuous space estimator from topological information. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Calgary, AB, Canada, 13–16 October 2015; pp. 13–16. [Google Scholar]
- Aernouts, M.; Berkvens, R.; Van Vlaenderen, K.; Weyn, M. SigFox and LoRaWAN datasets for fingerprint localization in large urban and rural areas. Data 2018, 3, 13. [Google Scholar] [CrossRef]
- Redondi, A.E.C. Radio map interpolation using graph signal processing. IEEE Commun. Lett. 2018, 22, 153–156. [Google Scholar] [CrossRef]
- Radial Basis Function Interpolation. Available online: https://cs.fit.edu/~dmitra/SciComp/13Spr/KimJessie-rbf3.pdf (accessed on 25 September 2018).
- Reddy, K.B.; Venkatramana, P. Comparison of different spatial interpolation techniques of field measurements to construct radio environment map. Int. J. Future Gener. Commun. Netw. 2018, 11, 21–31. [Google Scholar] [CrossRef]
- A Mesh-free Method for Three-Dimensional Nonlinear Schrödinger Equation. Available online: https://people.maths.ox.ac.uk/siamstudentchapter/webpages/2011_Conference/ThomasY_Talk.ppt (accessed on 15 October 2018).
- Chai, X.; Yang, Q. Reducing the calibration effort for probabilistic indoor location estimation. IEEE Trans. Mob. Comput. 2007, 6, 649–662. [Google Scholar] [CrossRef]









| Gateway | Algorithm | AVG | STD | Gateway | Algorithm | AVG | STD |
|---|---|---|---|---|---|---|---|
| GW1 | cubic | 11.65 | 9.98 | GW3 | cubic | 5.12 | 6.44 |
| Gaussian | 41.70 | 23.82 | Gaussian | 19.71 | 27.90 | ||
| quintic | 14.75 | 5.55 | quintic | 7.27 | 10.49 | ||
| linear | 7.03 | 1.60 | linear | 2.36 | 1.57 | ||
| thin plate | 8.65 | 1.96 | thin plate | 3.32 | 2.95 | ||
| GW2 | cubic | 3.11 | 2.45 | GW4 | cubic | 4.24 | 3.70 |
| Gaussian | 19.61 | 23.82 | Gaussian | 29.69 | 59.20 | ||
| quintic | 5.87 | 5.55 | quintic | 14.43 | 32.36 | ||
| linear | 2.43 | 1.60 | linear | 2.52 | 1.78 | ||
| thin plate | 2.44 | 1.96 | thin plate | 3.00 | 2.10 |
| Point Number | Algorithm | Point Number | Algorithm | Point Number | Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 1 | 49.2 | 18.4 | 14.8 | 17 | 26.1 | 32.6 | 39.3 | 33 | 5.8 | 5.8 | 17.5 |
| 2 | 15 | 15 | 12.2 | 18 | 107.1 | 107.1 | 8 | 34 | 7.2 | 7.2 | 8.1 |
| 3 | 37.4 | 37.4 | 29.4 | 19 | 91.9 | 91.9 | 56.8 | 35 | 53.1 | 42.4 | 13 |
| 4 | 9.4 | 5.8 | 5.1 | 20 | 50.8 | 50.8 | 50.8 | 36 | 100.1 | 24.3 | 19 |
| 5 | 51.2 | 71.3 | 49.2 | 21 | 7.1 | 7.1 | 10.8 | 37 | 9.8 | 9.8 | 13.2 |
| 6 | 19.4 | 19.4 | 15.7 | 22 | 15.3 | 17 | 15 | 38 | 27 | 27 | 25 |
| 7 | 42.4 | 42.4 | 42 | 23 | 21 | 21 | 10.3 | 39 | 16.8 | 9.4 | 15.5 |
| 8 | 85.3 | 39.2 | 15 | 24 | 5 | 5 | 8.5 | 40 | 20.4 | 25.7 | 26.1 |
| 9 | 7.2 | 7.2 | 7.2 | 25 | 40.5 | 40.5 | 40.5 | 41 | 14.6 | 14.6 | 12.4 |
| 10 | 55.7 | 88.1 | 19.7 | 26 | 7.1 | 7.1 | 6.3 | 42 | 15.7 | 13.9 | 28.3 |
| 11 | 32 | 28.1 | 23.5 | 27 | 29.2 | 9.4 | 9.4 | 43 | 11.3 | 15.7 | 15.2 |
| 12 | 22.8 | 22.8 | 22.8 | 28 | 61.2 | 63.1 | 63.1 | 44 | 59.1 | 59.1 | 40.9 |
| 13 | 84 | 34.5 | 32.6 | 29 | 23.4 | 28 | 33 | 45 | 17.5 | 17.5 | 16 |
| 14 | 16 | 6.1 | 7.3 | 30 | 27.5 | 27.5 | 26.1 | 46 | 6.3 | 58.7 | 51 |
| 15 | 24.3 | 24.3 | 91.7 | 31 | 34.2 | 41.1 | 15.3 | AVG | 32.5 | 29.8 | 24.1 |
| 16 | 11.3 | 11.3 | 9.2 | 32 | 18.4 | 18.4 | 18.6 | STD | 26.5 | 24.1 | 17.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, W.; Chang, Y.-S.; Jung, Y.; Song, J. Low-Power LoRa Signal-Based Outdoor Positioning Using Fingerprint Algorithm. ISPRS Int. J. Geo-Inf. 2018, 7, 440. https://doi.org/10.3390/ijgi7110440
Choi W, Chang Y-S, Jung Y, Song J. Low-Power LoRa Signal-Based Outdoor Positioning Using Fingerprint Algorithm. ISPRS International Journal of Geo-Information. 2018; 7(11):440. https://doi.org/10.3390/ijgi7110440
Chicago/Turabian StyleChoi, Wongeun, Yoon-Seop Chang, Yeonuk Jung, and Junkeun Song. 2018. "Low-Power LoRa Signal-Based Outdoor Positioning Using Fingerprint Algorithm" ISPRS International Journal of Geo-Information 7, no. 11: 440. https://doi.org/10.3390/ijgi7110440
APA StyleChoi, W., Chang, Y.-S., Jung, Y., & Song, J. (2018). Low-Power LoRa Signal-Based Outdoor Positioning Using Fingerprint Algorithm. ISPRS International Journal of Geo-Information, 7(11), 440. https://doi.org/10.3390/ijgi7110440




