An Empirical Study Investigating the Relationship between Land Prices and Urban Geometry
Abstract
:1. Introduction
- Is there a relationship between the FD values of urban geometry components and land prices?
- If so, which FD values of building, street network, and block data can be used to determine this relationship?
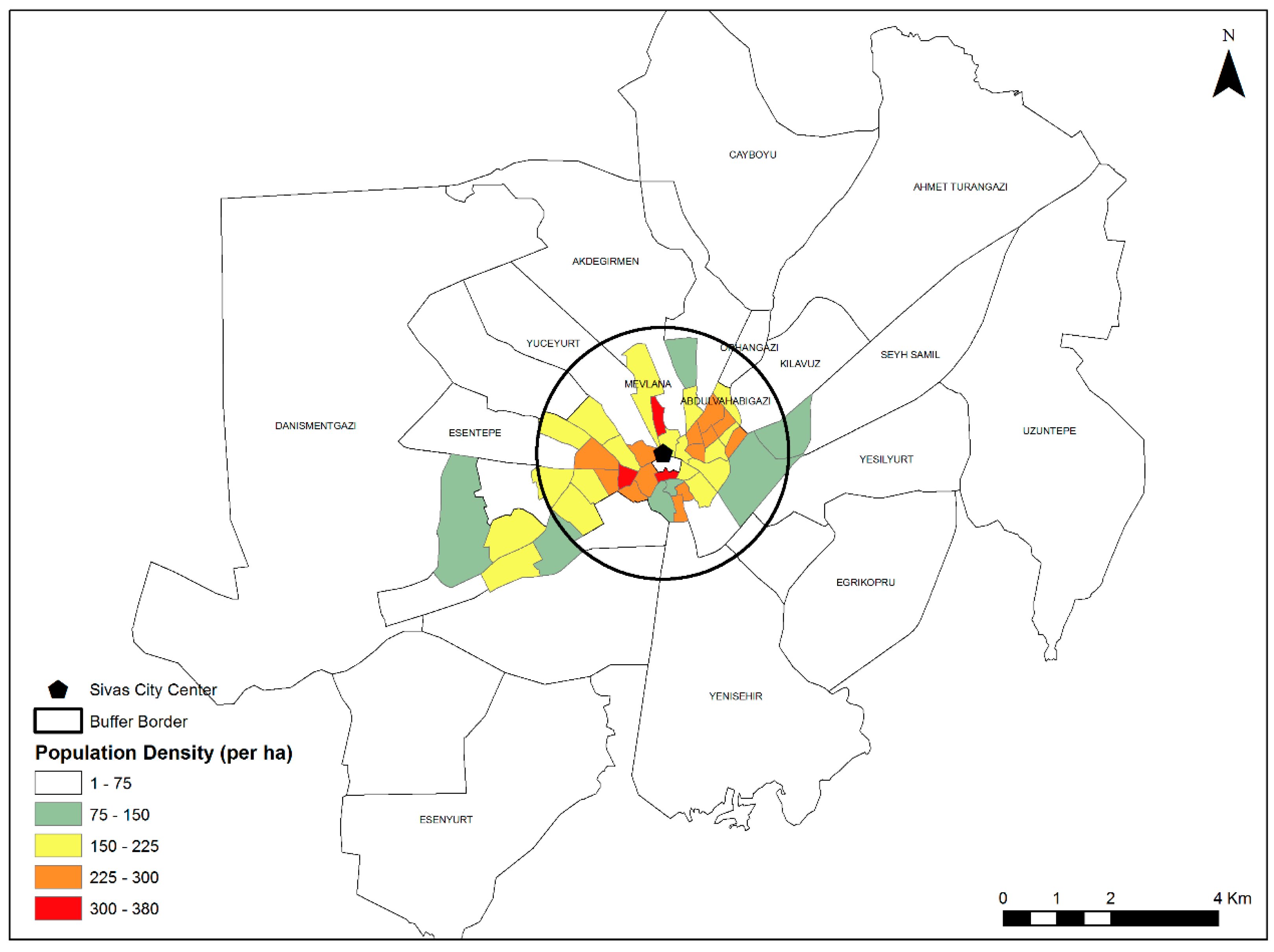
- How are the FD values of urban geometry components geographically distributed?
- Do the factors of population and distance to the city center have any effect on the calculated FD values and the spatial distribution of land prices?
2. Methodology
2.1. Complexity and Fractal Dimension
2.2. Calculation of Fractal Dimension Values in Urban Modeling
2.3. Modeling the Relationship between Urban Geometry and Land Prices
3. Results
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Neighbor ID | Neighbor Name | Fractal Dimension Value | Distance to City Center (m) | Land Prices (TL) | Population | |||||
| Buildings | Blocks | Streets | Min | Max | Mean | Median | ||||
| 1 | Alibaba | 1.425 | 1.725 | 1.424 | 3087.884 | 25 | 500 | 91.537 | 92 | 13833 |
| 2 | Yesilyurt | 1.341 | 1.690 | 1.333 | 4037.070 | 30 | 210 | 86.831 | 84 | 2238 |
| 3 | Yuceyurt | 1.349 | 1.743 | 1.292 | 2844.624 | 30 | 1000 | 155.375 | 134 | 6855 |
| 4 | Cayboyu | 1.056 | 1.526 | 1.199 | 5740.141 | 25 | 30 | 28.571 | 30 | 580 |
| 5 | Emek | 1.606 | 1.777 | 1.390 | 3160.736 | 25 | 300 | 120.019 | 117 | 10816 |
| 6 | Kizilirmak | 1.468 | 1.765 | 1.300 | 1594.873 | 100 | 900 | 271.810 | 250 | 2315 |
| 7 | Gultepe | 1.507 | 1.762 | 1.475 | 3584.100 | 25 | 395 | 117.391 | 142 | 2497 |
| 8 | Esenyurt | 1.194 | 1.810 | 1.301 | 7435.985 | 25 | 109 | 43.992 | 100 | 870 |
| 9 | Danisment Gazi | 1.110 | 1.752 | 1.245 | 6265.904 | 16 | 150 | 29.810 | 50 | 252 |
| 10 | Gokmedrese | 1.630 | 1.783 | 1.314 | 632.241 | 185 | 1100 | 314.074 | 250 | 976 |
| 11 | Mimar Sinan | 1.464 | 1.711 | 1.371 | 5148.313 | 16 | 300 | 127.840 | 142 | 7409 |
| 12 | Altuntabak | 1.695 | 1.774 | 1.364 | 1486.926 | 92 | 450 | 140.375 | 112.5 | 5710 |
| 13 | Akdegirmen | 1.163 | 1.694 | 1.243 | 3750.99 | 16 | 1100 | 224.980 | 200 | 7845 |
| 14 | Gokcebostan | 1.644 | 1.701 | 1.312 | 1020.104 | 100 | 700 | 183.385 | 125 | 3792 |
| 15 | Camii Kebir | 1.704 | 1.781 | 1.275 | 408.04 | 600 | 1750 | 890.208 | 750 | 2087 |
| 16 | Seyh Samil | 1.417 | 1.664 | 1.388 | 4965.116 | 25 | 250 | 67.194 | 67 | 18828 |
| 17 | Carsibasi | 1.696 | 1.723 | 1.275 | 375.615 | 350 | 2300 | 785.185 | 600 | 1616 |
| 18 | Esentepe | 1.366 | 1.789 | 1.344 | 3319.75 | 25 | 350 | 64.613 | 67 | 7391 |
| 19 | Cayyurt | 1.599 | 1.731 | 1.290 | 696.999 | 175 | 1000 | 291.667 | 225 | 3764 |
| 20 | Ortulupinar | 1.668 | 1.734 | 1.331 | 565.509 | 450 | 2300 | 727.056 | 600 | 4632 |
| 21 | Mevlâna | 1.458 | 1.690 | 1.313 | 1339.953 | 16 | 1000 | 257.525 | 225 | 10107 |
| 22 | Yigitler | 1.658 | 1.729 | 1.278 | 916.743 | 117 | 750 | 217.100 | 117 | 1921 |
| 23 | Yenisehir | 1.294 | 1.750 | 1.256 | 4685.355 | 25 | 900 | 238.516 | 300 | 14203 |
| 24 | İnonu | 1.664 | 1.717 | 1.328 | 1159.718 | 92 | 920 | 191.553 | 125.5 | 4529 |
| 25 | Yeni Mahalle | 1.749 | 1.808 | 1.402 | 1261.869 | 92 | 400 | 123.956 | 92 | 7262 |
| 26 | Yenidogan | 1.631 | 1.744 | 1.351 | 1414.015 | 92 | 350 | 121.647 | 117 | 9612 |
| 27 | Halil Rifat Pasa | 1.704 | 1.768 | 1.311 | 914.491 | 275 | 2000 | 533.333 | 400 | 2913 |
| 28 | Aydogan | 1.684 | 1.720 | 1.343 | 755.633 | 125 | 750 | 195.233 | 150 | 4370 |
| 29 | Dirilis | 1.513 | 1.706 | 1.384 | 3956.228 | 25 | 300 | 71.923 | 92 | 14748 |
| 30 | Kaleardi | 1.581 | 1.733 | 1.326 | 900.484 | 168 | 800 | 294.097 | 250 | 3156 |
| 31 | Karsiyaka | 1.442 | 1.772 | 1.446 | 6644.217 | 25 | 67 | 50.148 | 50 | 3811 |
| 32 | Gulyurt | 1.670 | 1.704 | 1.304 | 1362.708 | 150 | 600 | 188.955 | 225 | 2756 |
| 33 | Uçlerbey | 1.631 | 1.735 | 1.309 | 1078.087 | 193 | 900 | 257.148 | 200 | 2385 |
| 34 | Dedebali | 1.628 | 1.696 | 1.278 | 1269.609 | 92 | 344 | 142.938 | 92 | 1288 |
| 35 | Demircilerardi | 1.709 | 1.778 | 1.386 | 986.027 | 252 | 2100 | 458.371 | 378 | 4337 |
| 36 | Kucuk Minare | 1.749 | 1.802 | 1.284 | 635.274 | 300 | 1350 | 451.316 | 300 | 2203 |
| 37 | Ece | 1.655 | 1.744 | 1.309 | 852.491 | 150 | 750 | 233.000 | 160 | 4626 |
| 38 | Cicekli | 1.686 | 1.774 | 1.273 | 1121.098 | 134 | 550 | 177.357 | 142 | 3027 |
| 39 | Ahmet Turan Gazi | 1.323 | 1.625 | 1.277 | 7005.21 | 20 | 67 | 60.787 | 67 | 5516 |
| 40 | Tuzlugol | 1.506 | 1.759 | 1.353 | 2919.538 | 25 | 300 | 57.308 | 67 | 5419 |
| 41 | Pasabey | 1.740 | 1.768 | 1.280 | 553.297 | 350 | 2200 | 697.222 | 600 | 1905 |
| 42 | Kilavuz | 1.385 | 1.751 | 1.358 | 3000.368 | 25 | 500 | 82.847 | 67 | 7869 |
| 43 | Dort Eylul | 1.620 | 1.751 | 1.367 | 1902.519 | 92 | 900 | 171.690 | 125 | 7239 |
| 44 | Istiklal | 1.649 | 1.763 | 1.387 | 2136.043 | 33 | 350 | 90.966 | 92 | 6472 |
| 45 | Yunus Emre | 1.644 | 1.780 | 1.388 | 1906.780 | 67 | 350 | 106.513 | 92 | 6889 |
| 46 | Selcuklu | 1.625 | 1.742 | 1.384 | 3501.248 | 124 | 395 | 154.250 | 150 | 8776 |
| 47 | Fatih | 1.550 | 1.807 | 1.481 | 3647.605 | 16 | 350 | 65.477 | 67 | 16039 |
| 48 | Sularbasi | 1.712 | 1.738 | 1.303 | 238.428 | 275 | 2300 | 630.147 | 450 | 2864 |
| 49 | Kadi Burhanettin | 1.597 | 1.817 | 1.296 | 1517.339 | 225 | 1500 | 532.238 | 500 | 3945 |
| 50 | Abdul Vahab Gazi | 1.571 | 1.665 | 1.330 | 1543.250 | 100 | 454 | 117.741 | 100 | 2984 |
| 51 | Ferhat Bostan | 1.672 | 1.743 | 1.329 | 978.318 | 142 | 800 | 226.607 | 168 | 2732 |
| 52 | Bahtiyar Bostan | 1.674 | 1.746 | 1.272 | 684.528 | 200 | 700 | 288.750 | 225 | 2369 |
| 53 | Mismilirmak | 1.593 | 1.694 | 1.287 | 1263.346 | 100 | 454 | 147.760 | 100 | 2460 |
| 54 | Seyrantepe | 1.563 | 1.738 | 1.344 | 1797.737 | 25 | 500 | 117.021 | 117 | 4127 |
| 55 | Orhan Gazi | 1.419 | 1.663 | 1.253 | 2527.031 | 75 | 237 | 75.353 | 75 | 2412 |
| 56 | Mehmet Pasa | 1.686 | 1.765 | 1.344 | 338.926 | 200 | 1000 | 335.429 | 225 | 4264 |
| 57 | Kumbet | 1.596 | 1.732 | 1.399 | 2608.635 | 84 | 555 | 193.755 | 176 | 7721 |
| 58 | Pulur | 1.634 | 1.751 | 1.322 | 981.009 | 142 | 1750 | 402.629 | 285 | 3531 |
| 59 | Mehmet Akif Ersoy | 1.571 | 1.734 | 1.425 | 1709.665 | 100 | 800 | 160.767 | 126 | 12328 |
| 60 | Yahyabey | 1.643 | 1.749 | 1.253 | 818.471 | 100 | 550 | 228.800 | 250 | 1766 |
| 61 | Huzur | 1.582 | 1.734 | 1.410 | 2370.302 | 84 | 500 | 117.242 | 109 | 11444 |
| 62 | Egrikopru | 1.355 | 1.777 | 1.312 | 4475.886 | 25 | 134 | 90.224 | 134 | 4569 |
| 63 | Uzuntepe | 1.054 | 1.616 | 1.181 | 7283.29 | 25 | 75 | 30.000 | 25 | 849 |
| 64 | Eskikale | 1.702 | 1.838 | 1.351 | 204.043 | 714 | 2300 | 1435.000 | 1250 | 442 |
| 65 | Kardesler | 1.500 | 1.735 | 1.414 | 2811.926 | 33 | 546 | 151.691 | 168 | 5692 |
References
- Wang, X.R.; Hui, E.C.M.; Sun, J.X. Population migration, urbanization and housing prices: Evidence from the cities in China. Habitat Int. 2017, 66, 49–56. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Gyourko, J.; Saks, R.E. Urban growth and housing supply. J. Econ. Geogr. 2005, 6, 71–89. [Google Scholar] [CrossRef] [Green Version]
- Wendt, P.F. Theory of urban land values. Land Econ. 1957, 33, 228–240. [Google Scholar] [CrossRef]
- Ayazli, I.E. Simulation Model of Urban Sprawl Driven by Transportation Networks: 3rd Bosphorus Bridge Example. Ph.D. Thesis, Yildiz Technical University, Istanbul, Turkey, 2011. [Google Scholar]
- Landis, J.; Huang, W. Theoretical foundations and literature review. In Rail Transit Investments, Real Estate Values, and Land Use Change: A Comparative Analysis of Five California Rail Transit Systems; UC Berkeley: Berkeley, CA, USA, 1995; pp. 13–26. [Google Scholar]
- Capozza, D.R.; Helsley, R.W. The fundamentals of land prices and urban growth. J. Urban Econ. 1989, 26, 295–306. [Google Scholar] [CrossRef]
- Baslik, S. Dynamic Urban Growth Model: Logistic Regression and Cellular Automata: The Cases of Istanbul and Lisbon. Ph.D. Thesis, Mimar Sinan Fine Arts University, Istanbul, Turkey, 2008. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press Inc.: San Diego, CA, USA, 1994. [Google Scholar]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Goodchild, M.F. Fractals and the accuracy of geographical measures. J. Int. Assoc. Math. Geol. 1980, 12, 85–98. [Google Scholar] [CrossRef]
- Pentland, A.P. Fractal-based description of natural scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 661–674. [Google Scholar] [CrossRef]
- Clarke, K.C.; Schweizer, D.M. Measuring the fractal dimension of natural surfaces using a robust fractal estimator. Cartogr. Geogr. Inf. Syst. 1991, 18, 37–47. [Google Scholar] [CrossRef]
- Guneroglu, N.; Acar, C.; Dihkan, M.; Karsli, F.; Guneroglu, A. Green corridors and fragmentation in South Eastern Black Sea coastal landscape. Ocean Coast. Manag. 2013, 83, 67–74. [Google Scholar] [CrossRef]
- Jaya, V.; Raghukanth, S.T.G.; Sonika Mohan, S. Estimating fractal dimension of lineaments using box counting method for the Indian landmass. Geocarto Int. 2014, 29, 314–331. [Google Scholar] [CrossRef]
- Jiang, B.; Brandt, S. A fractal perspective on scale in geography. ISPRS Int. J. Geo-Inf. 2016, 5, 95. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P.A. Urban shapes as fractals. Area 1987, 19, 215–221. [Google Scholar]
- Shen, G. Fractal dimension and fractal growth of urbanized areas. Int. J. Geogr. Inf. Sci. 2002, 16, 419–437. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; Biernacki, C. The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices. Landsc. Urban Plan. 2008, 84, 99–115. [Google Scholar] [CrossRef]
- Terzi, F.; KAYA, H.S. Analyzing Urban Sprawl Patterns through Fractal Geometry: The Case of Istanbul Metropolitan Area; University College of London: London, UK, 2008. [Google Scholar]
- Poudyal, N.C.; Hodges, D.G.; Tonn, B.; Cho, S.H. Valuing diversity and spatial pattern of open space plots in urban neighborhoods. For. Policy Econ. 2009, 11, 194–201. [Google Scholar] [CrossRef]
- Ozturk, D. Assessment of urban sprawl using Shannon’s entropy and fractal analysis: A case study of Atakum, Ilkadim and Canik (Samsun, Turkey). J. Environ. Eng. Landsc. Manag. 2017, 25, 264–276. [Google Scholar] [CrossRef]
- Purevtseren, M.; Tsegmid, B.; Indra, M.; Sugar, M. The fractal geometry of urban land use: The case of Ulaanbaatar city, Mongolia. Land 2018, 7, 67. [Google Scholar] [CrossRef]
- Cavailhès, J.; Frankhauser, P.; Peeters, D.; Thomas, I. Residential equilibrium in a multifractal metropolitan area. Ann. Reg. Sci. 2010, 45, 681–704. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Multifractal characterization of urban form and growth: The case of Beijing. Environ. Plan. B Plan. Des. 2013, 40, 884–904. [Google Scholar] [CrossRef]
- Frankhauser, P. Aspects fractals des structures urbaines. L’Espace Géographique 1990, 19, 45–69. [Google Scholar] [CrossRef]
- Frankhauser, P. Fractal properties of settlement structures. In Proceedings of the First International Seminar on Structural Morphology, Montpellier, France, 7–11 September 1992. [Google Scholar]
- Frankhauser, P. The fractal approach. A new tool for the spatial analysis of urban agglomerations. Popul. Engl. Sel. 1998, 10, 205–240. [Google Scholar]
- Frankhauser, P. Comparing the morphology of urban patterns in Europe—A fractal approach. Eur. Cities Insights Outskirts Rep. COST Action 2004, 10, 79–105. [Google Scholar]
- Kaya, H.S.; Bolen, F. Evaluation of Differences in Urban Space Organization with the Fractal Analysis Method. J. Istanb. Kültür Univ. 2006, 4, 153–172. [Google Scholar]
- Turkish Statistical Institute. Available online: http://www.tuik.gov.tr/ (accessed on 10 February 2019).
- Fractalyse. Available online: http://www.fractalyse.org/en-home.html (accessed on 29 February 2016).
- Ma, R.; Gu, C.; Pu, Y.; Ma, X. Mining the urban sprawl pattern: A case study on Sunan, China. Sensors 2008, 8, 6371–6395. [Google Scholar] [CrossRef] [PubMed]
- Thomas, I.; Frankhauser, P.; Frenay, B.; Verleysen, M. Clustering patterns of urban built-up areas with curves of fractal scaling behaviour. Environ. Plan. B Plan. Des. 2010, 37, 942–954. [Google Scholar] [CrossRef]
- Erdogan, G.; Cubukcu, K.M. Explaining fractal dimension in populous cities. In Proceedings of the EURAU 2014-Composite Cities, Istanbul, Turkey, 12–14 November 2014. [Google Scholar]
- Cheng, J. Modelling Spatial & Temporal Urban Growth. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2003. [Google Scholar]
- Batty, M. Cities and Complexity: Understanding Cities with Cellular Automata, Agent-Based Models, and Fractals; MIT Press: London, UK, 2007. [Google Scholar]
- Yetiskul, E. Complex Cities and Complexity in Planning. Planlama 2017, 27, 7–15. [Google Scholar] [CrossRef]
- Frankhauser, P.; Pumain, D. Fractals and Geography. In Models in Spatial Analysis; ISTE Ltd.: London, UK, 2007. [Google Scholar]
- Frankhauser, P.; Tannier, C. A multi-scale morphological approach for delimiting urban areas. In 9th Computers in Urban Planning and Urban Management conference (CUPUM’05); University College London: London, UK, 2005. [Google Scholar]
- Kaya, H.S.; Bölen, F. Examination of change in urban texture with the fractal geometry method. J. ITU Ser. A Archit. Plan. Des. 2011, 10, 39–50. [Google Scholar]
- Ayazli, I.E. Investigation of the Relationship Between Property Geometry and Urbanization by Calculating Fractal Dimension Values: A Case Study of Sivas. Afyon Kocatepe Univ. J. Sci. Eng. 2017, 17, 165–171. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. In ACM Sigmod Record; ACM: New York, NY, USA, 1996; Volume 25, pp. 103–114. [Google Scholar]
- Trpkova, M.; Tevdovski, D. Twostep cluster analysis: Segmentation of largest companies in Macedonia. In Challenges for Analysis of the Economy, the Businesses, and Social Progress; Kovacs, P., Szep, K., Katona, T., Eds.; Universitas Szeged Press: Szeged, Hungary, 2009. [Google Scholar]
- Sarstedt, M.; Mooi, E. A Concise Guide to Market Research: The Process, Data, and Methods Using IBM SPSS Statistics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- SPSS Inc. The SPSS TwoStep Cluster Component. A Scalable Component to Segment Your Customers More Effectively; White paper technical report; SPSS Inc.: Chicago, IL, USA, 2001; pp. 1–9. [Google Scholar]
- Papadimitriou, E.; Athanasios, T.; George, Y. Patterns of pedestrian attitudes, perceptions and behaviour in Europe. Safety Sci. 2013, 53, 114–122. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using SPSS, 4th ed.; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Watson, P.K.; Teelucksingh, S.S. A Practical Introduction to Econometric Methods: Classical and Modern; University of the West Indies Press: Kingston, Jamaica, 2002. [Google Scholar]






| Complexity Level | Building | Block | Street |
|---|---|---|---|
| Low Complexity | 1.303 | 1.700 | 1.289 |
| High Complexity | 1.623 | 1.751 | 1.343 |
| Two-Step Cluster Variables | P |
|---|---|
| Building FD | 0.000 |
| Block FD | 0.018 |
| Street FD | 0.001 |
| Population | 0.550 |
| Land Price (min) | 0.000 |
| Land Price (max) | 0.006 |
| Land Price (mean) | 0.000 |
| Land Price (median) | 0.001 |
| Distance from City Centre | 0.000 |
| Statistics | Mean |
|---|---|
| R2 | 0.609 |
| RMSE | 0.538 |
| MAPE | 8.637 |
| MAE | 0.434 |
| Model Parameters | B | p | VIF |
|---|---|---|---|
| Constant | 5.126 | 0.000 | |
| Factor 1 (Building and Block FD) | 0.621 | 0.000 | 1.000 |
| Factor 2 (Street FD) | −0.228 | 0.000 | 1.000 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayazli, I.E. An Empirical Study Investigating the Relationship between Land Prices and Urban Geometry. ISPRS Int. J. Geo-Inf. 2019, 8, 457. https://doi.org/10.3390/ijgi8100457
Ayazli IE. An Empirical Study Investigating the Relationship between Land Prices and Urban Geometry. ISPRS International Journal of Geo-Information. 2019; 8(10):457. https://doi.org/10.3390/ijgi8100457
Chicago/Turabian StyleAyazli, Ismail Ercument. 2019. "An Empirical Study Investigating the Relationship between Land Prices and Urban Geometry" ISPRS International Journal of Geo-Information 8, no. 10: 457. https://doi.org/10.3390/ijgi8100457
APA StyleAyazli, I. E. (2019). An Empirical Study Investigating the Relationship between Land Prices and Urban Geometry. ISPRS International Journal of Geo-Information, 8(10), 457. https://doi.org/10.3390/ijgi8100457





