Predicting Slope Stability Failure through Machine Learning Paradigms
Abstract
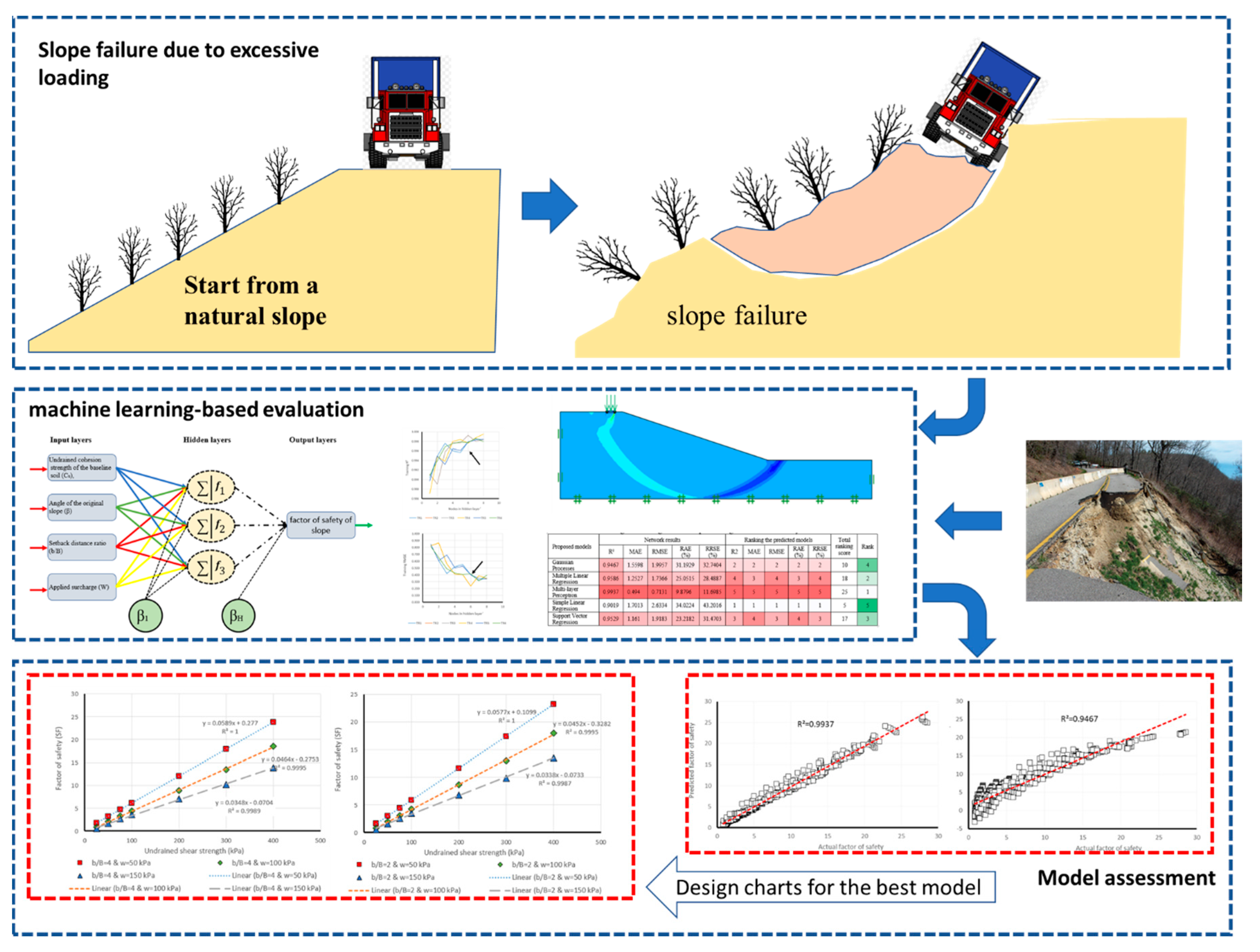
:1. Introduction
2. Machine Learning and Multilinear Regression Algorithms
2.1. Gaussian Processes Regression (GPR)
2.2. Multiple Linear Regression (MLR)
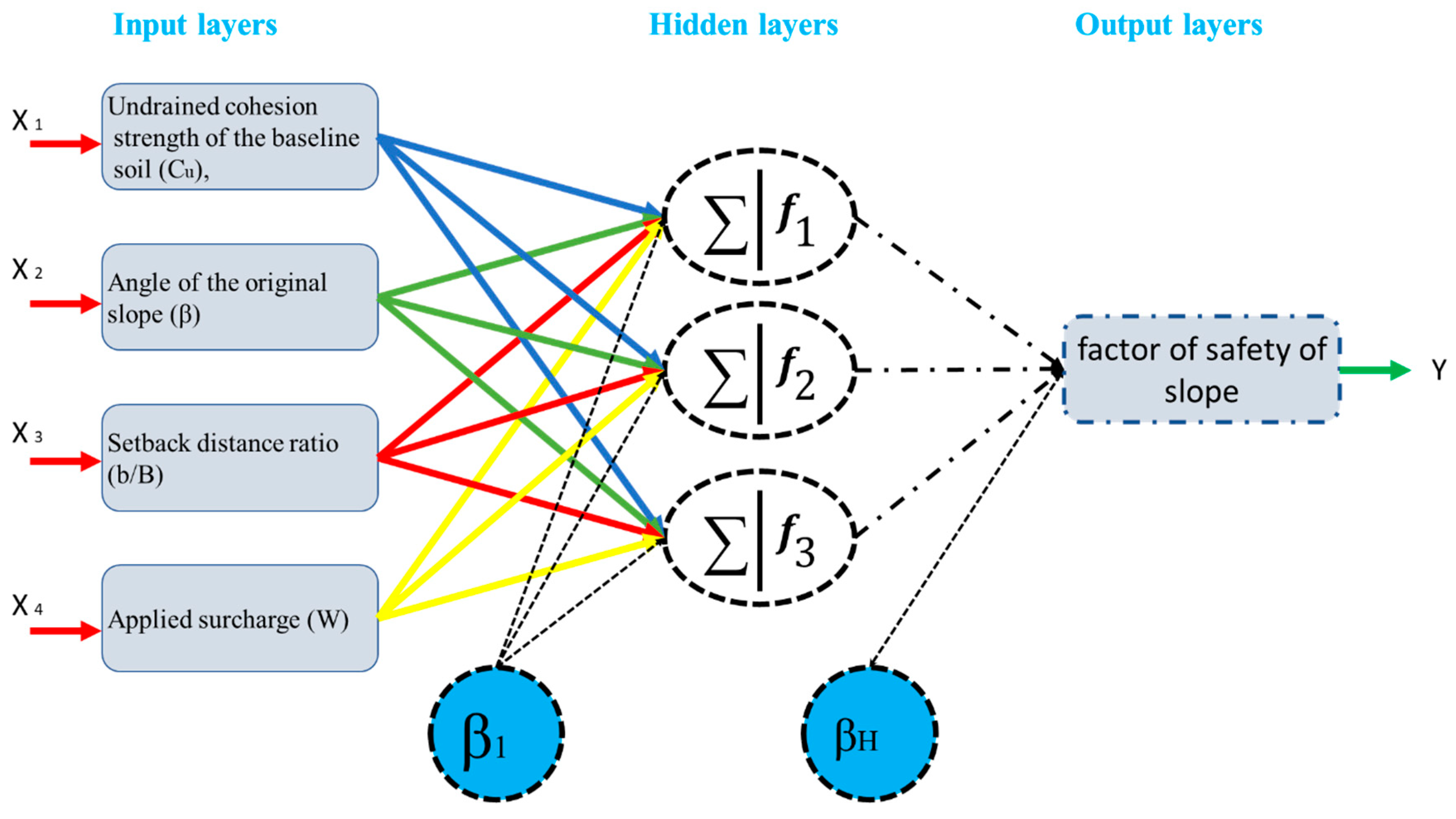
2.3. Multi-Layer Perceptron (MLP)
2.4. Simple Linear Regression (SLR)
2.5. Support Vector Regression (SVR)
3. Data Collection
4. Results and Discussion
5. Design Charts
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Binh Thai, P.; Manh Duc, N.; Kien-Trinh Thi, B.; Prakash, I.; Chapi, K.; Dieu Tien, B. A novel artificial intelligence approach based on Multi-layer Perceptron Neural Network and Biogeography-based Optimization for predicting coefficient of consolidation of soil. Catena 2019, 173, 302–311. [Google Scholar]
- Shao, W.; Bogaard, T.; Bakker, M.; Greco, R. Quantification of the influence of preferential flow on slope stability using a numerical modelling approach. Hydrol. Earth Syst. Sci. 2015, 19, 2197–2212. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.-H.; Chen, H.-K.; Tang, H.-M.; Wang, H. Study on Fracture Stability Analysis of Toppling Perilous Rock. In Proceedings of the 2016 International Conference on Mechanics and Architectural Design, World Scientific, Suzhouo, China, 14–15 May 2016; pp. 422–432. [Google Scholar]
- Kang, F.; Xu, B.; Li, J.; Zhao, S. Slope stability evaluation using Gaussian processes with various covariance functions. Appl. Soft Comput. 2017, 60, 387–396. [Google Scholar] [CrossRef]
- Li, A.; Khoo, S.; Wang, Y.; Lyamin, A. Application of Neural Network to Rock Slope Stability Assessments. In Proceedings of the 8th European Conference on Numerical Methods in Geotechnical Engineering (NUMGE 2014), Delft, The Netherlands, 18–20 June 2014; pp. 473–478. [Google Scholar]
- Jagan, J.; Meghana, G.; Samui, P. Determination of stability number of layered slope using anfis, gpr, rvm and elm. Int. J. Comput. Res. 2016, 23, 371. [Google Scholar]
- Lyu, Z.; Chai, J.; Xu, Z.; Qin, Y. Environmental impact assessment of mining activities on groundwater: Case study of copper mine in Jiangxi Province, China. J. Hydrol. Eng. 2018, 24, 05018027. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Yang, S.; Wang, M.; Shi, X.; Yao, S.; Mitri, H.S. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci. 2019, 118, 505–518. [Google Scholar] [CrossRef]
- Mosallanezhad, M.; Moayedi, H. Comparison Analysis of Bearing Capacity Approaches for the Strip Footing on Layered Soils. Arab. J. Sci. Eng. 2017, 1–12. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.-s.; Li, J.-j. System reliability analysis of slopes using least squares support vector machines with particle swarm optimization. Neurocomputing 2016, 209, 46–56. [Google Scholar] [CrossRef]
- Secci, R.; Foddis, M.L.; Mazzella, A.; Montisci, A.; Uras, G. Artificial Neural Networks and Kriging Method for Slope Geomechanical Characterization; Springer Int. Publishing Ag.: Cham, Switzerland, 2015; pp. 1357–1361. [Google Scholar]
- Sun, H.; Wang, W.; Dimitrov, D.; Wang, Y. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab. J. Chem. 2018, 11, 793–801. [Google Scholar]
- Gao, W.; Dimitrov, D.; Abdo, H. Tight independent set neighborhood union condition for fractional critical deleted graphs and ID deleted graphs. Discret. Contin. Dyn. Syst.-Ser. S 2018, 12, 711–721. [Google Scholar]
- Gao, W.; Guirao, J.L.G.; Abdel-Aty, M.; Xi, W. An independent set degree condition for fractional critical deleted graphs. Discret. Contin. Dyn. Syst.-Ser. S 2019, 12, 877–886. [Google Scholar] [Green Version]
- Sun, H.; Liu, H.; Xiao, H.; He, R.; Ran, B. Use of local linear regression model for short-term traffic forecasting. Transp. Res. Rec. J. Transp. Res. Board 2003, 1836, 143–150. [Google Scholar] [CrossRef]
- Wu, Q.; Law, R.; Xu, X. A sparse Gaussian process regression model for tourism demand forecasting in Hong Kong. Expert Syst. Appl. 2012, 39, 4769–4774. [Google Scholar] [CrossRef]
- Hwang, K.; Choi, S. Blind equalizer for constant-modulus signals based on Gaussian process regression. Signal Process. 2012, 92, 1397–1403. [Google Scholar] [CrossRef]
- Samui, P.; Jagan, J. Determination of effective stress parameter of unsaturated soils: A Gaussian process regression approach. Front. Struct. Civ. Eng. 2013, 7, 133–136. [Google Scholar] [CrossRef]
- Kang, F.; Han, S.; Salgado, R.; Li, J. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling. Comput. Geotech. 2015, 63, 13–25. [Google Scholar] [CrossRef]
- Lyu, Z.; Chai, J.; Xu, Z.; Qin, Y.; Cao, J. A Comprehensive Review on Reasons for Tailings Dam Failures Based on Case History. Adv. Civ. Eng. 2019, 2019, 4159306. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, M.; Ju, Z. Preliminary discussion regarding SVM kernel function selection in the twofold rock slope prediction model. J. Comput. Civ. Eng. 2015, 30, 04015031. [Google Scholar] [CrossRef]
- Chakraborty, A.; Goswami, D. Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 2017, 10, 11. [Google Scholar] [CrossRef]
- Chakraborty, M.; Kumar, J. Bearing capacity of circular footings over rock mass by using axisymmetric quasi lower bound finite element limit analysis. Comput. Geotech. 2015, 70, 138–149. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Yilmaz, I. Comparison of landslide susceptibility mapping methodologies for Koyulhisar, Turkey: Conditional probability, logistic regression, artificial neural networks, and support vector machine. Environ. Earth Sci. 2010, 61, 821–836. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Meng, X.; Pang, Y.; Agca, M. Characterizing forest canopy structure with lidar composite metrics and machine learning. Remote Sens. Environ. 2011, 115, 1978–1996. [Google Scholar] [CrossRef]
- Pasolli, L.; Melgani, F.; Blanzieri, E. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 464–468. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006; Volume 38, pp. 715–719. [Google Scholar]
- Bazi, Y.; Alajlan, N.; Melgani, F.; AlHichri, H.; Yager, R.R. Robust estimation of water chlorophyll concentrations with gaussian process regression and IOWA aggregation operators. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3019–3028. [Google Scholar] [CrossRef]
- Makridakis, S.; Wheelwright, S.C.; Hyndman, R.J. Forecasting Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Artificial intelligence design charts for predicting friction capacity of driven pile in clay. Neural Comput. Appl. 2018, 1–17. [Google Scholar] [CrossRef]
- Yuan, C.; Moayedi, H. Evaluation and comparison of the advanced metaheuristic and conventional machine learning methods for prediction of landslide occurrence. Eng. Comput. 2019, 36. (In press) [Google Scholar] [CrossRef]
- Yuan, C.; Moayedi, H. The performance of six neural-evolutionary classification techniques combined with multi-layer perception in two-layered cohesive slope stability analysis and failure recognition. Eng. Comput. 2019, 36, 1–10. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosallanezhad, M.; Mehrabi, M.; Safuan, A.R.A. A Systematic Review and Meta-Analysis of Artificial Neural Network Application in Geotechnical Engineering: Theory and Applications. Neural Comput. Appl. 2018, 31, 1–24. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Modelling and optimization of ultimate bearing capacity of strip footing near a slope by soft computing methods. Appl. Soft Comput. 2018, 66, 208–219. [Google Scholar] [CrossRef]
- ASCE Task Committee. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Mosallanezhad, M.; Moayedi, H. Developing hybrid artificial neural network model for predicting uplift resistance of screw piles. Arab. J. Geosci. 2017, 10, 10. [Google Scholar] [CrossRef]
- Mena, R.; Rodríguez, F.; Castilla, M.; Arahal, M.R. A prediction model based on neural networks for the energy consumption of a bioclimatic building. Energy Build. 2014, 82, 142–155. [Google Scholar] [CrossRef]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 329. [Google Scholar]
- Carroll, R.; Ruppert, D. Transformation and Weighting in Regression; Chapman and Hall: New York, NY, USA, 1988. [Google Scholar]
- Neter, J.; Wasserman, W.; Kutner, M.H. Regression, analysis of variance, and experimental design. Appl. Stat. Models 1990, 614–619. [Google Scholar]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Cherkassky, V.S.; Mulier, F. Learning from Data: Concepts, Theory, and Methods; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gleason, C.J.; Im, J. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Liu, W.T.; Tang, B. Spacebased estimation of moisture transport in marine atmosphere using support vector regression. Remote Sens. Environ. 2008, 112, 1846–1855. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Krabbenhoft, K.; Lyamin, A.; Krabbenhoft, J. Optum Computational Engineering (Optum G2). 2015. Available online: www.optumce.com (accessed on 1 September 2019).
- Bell, A. Stability Analysis of Shallow Undrained Tunnel Heading Using Finite Element Limit Analysis; University of Southern Queensland: Darling Heights, QLD, Australia, 2016. [Google Scholar]
- Vakili, A.H.; bin Selamat, M.R.; Mohajeri, P.; Moayedi, H. A Critical Review on Filter Design Criteria for Dispersive Base Soils. Geotech. Geol. Eng. 2018, 1–19. [Google Scholar] [CrossRef]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Gao, W.; Guirao, J.L.G.; Basavanagoud, B.; Wu, J. Partial multi-dividing ontology learning algorithm. Inf. Sci. 2018, 467, 35–58. [Google Scholar] [CrossRef]
- Gao, W.; Wu, H.; Siddiqui, M.K.; Baig, A.Q. Study of biological networks using graph theory. Saudi J. Biol. Sci. 2018, 25, 1212–1219. [Google Scholar] [CrossRef] [PubMed]
- Bui, D.T.; Moayedi, H.; Kalantar, B.; Osouli, A.; Pradhan, B.; Nguyen, H.; Rashid, A.S.A. A Novel Swarm Intelligence—Harris Hawks Optimization for Spatial Assessment of Landslide Susceptibility. Sensors 2019, 19, 3590. [Google Scholar] [CrossRef] [PubMed]
- Bui, X.-N.; Moayedi, H.; Rashid, A.S.A. Developing a predictive method based on optimized M5Rules–GA predicting heating load of an energy-efficient building system. Eng. Comput. 2019, 1–10. [Google Scholar] [CrossRef]
- Tien Bui, D.; Moayedi, H.; Abdullahi, M.A.; Rashid, S.A.; Nguyen, H. Prediction of Pullout Behavior of Belled Piles through Various Machine Learning Modelling Techniques. Sensors 2019, 19, 3678. [Google Scholar] [CrossRef]























| Proposed Models | Network Results | Ranking the Predicted Models | Total Ranking Score | Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | RAE (%) | RRSE (%) | R2 | MAE | RMSE | RAE (%) | RRSE (%) | |||
| Gaussian Processes | 0.9467 | 1.5598 | 1.9957 | 31.1929 | 32.7404 | 2 | 2 | 2 | 2 | 2 | 10 | 4 |
| Multiple Linear Regression | 0.9586 | 1.2527 | 1.7366 | 25.0515 | 28.4887 | 4 | 3 | 4 | 3 | 4 | 18 | 2 |
| Multi-layer Perceptron | 0.9937 | 0.494 | 0.7131 | 9.8796 | 11.6985 | 5 | 5 | 5 | 5 | 5 | 25 | 1 |
| Simple Linear Regression | 0.9019 | 1.7013 | 2.6334 | 34.0224 | 43.2016 | 1 | 1 | 1 | 1 | 1 | 5 | 5 |
| Support Vector Regression | 0.9529 | 1.161 | 1.9183 | 23.2182 | 31.4703 | 3 | 4 | 3 | 4 | 3 | 17 | 3 |
| Proposed Models | Network Results | Ranking the Predicted Models | Total Ranking Score | Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | RAE (%) | RRSE (%) | R2 | MAE | RMSE | RAE (%) | RRSE (%) | |||
| Gaussian Processes | 0.9509 | 1.5291 | 1.9447 | 30.9081 | 32.3841 | 2 | 2 | 2 | 2 | 2 | 10 | 4 |
| Multiple Linear Regression | 0.9649 | 1.1949 | 1.5891 | 24.1272 | 26.4613 | 3 | 3 | 4 | 3 | 4 | 17 | 3 |
| Multi-layer Perceptron | 0.9939 | 0.5155 | 0.7039 | 10.4047 | 11.8116 | 5 | 5 | 5 | 5 | 5 | 25 | 1 |
| Simple Linear Regression | 0.9265 | 1.5387 | 2.2618 | 31.0892 | 37.6639 | 1 | 1 | 1 | 1 | 1 | 5 | 5 |
| Support Vector Regression | 0.9653 | 1.0364 | 1.6362 | 20.9366 | 27.247 | 4 | 4 | 3 | 4 | 3 | 18 | 2 |
| Proposed Models | Network Result | Total Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Training Dataset | Testing Dataset | ||||||||||
| R2 | MAE | RMSE | RAE (%) | RRSE (%) | R2 | MAE | RMSE | RAE | RRSE | ||
| Gaussian Processes | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 20 |
| Multiple Linear Regression | 4 | 3 | 4 | 3 | 4 | 3 | 3 | 4 | 3 | 4 | 35 |
| Multi-layer Perceptron | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 50 |
| Simple Linear Regression | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| Support Vector Regression | 3 | 4 | 3 | 4 | 3 | 4 | 4 | 3 | 4 | 3 | 35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien Bui, D.; Moayedi, H.; Gör, M.; Jaafari, A.; Foong, L.K. Predicting Slope Stability Failure through Machine Learning Paradigms. ISPRS Int. J. Geo-Inf. 2019, 8, 395. https://doi.org/10.3390/ijgi8090395
Tien Bui D, Moayedi H, Gör M, Jaafari A, Foong LK. Predicting Slope Stability Failure through Machine Learning Paradigms. ISPRS International Journal of Geo-Information. 2019; 8(9):395. https://doi.org/10.3390/ijgi8090395
Chicago/Turabian StyleTien Bui, Dieu, Hossein Moayedi, Mesut Gör, Abolfazl Jaafari, and Loke Kok Foong. 2019. "Predicting Slope Stability Failure through Machine Learning Paradigms" ISPRS International Journal of Geo-Information 8, no. 9: 395. https://doi.org/10.3390/ijgi8090395
APA StyleTien Bui, D., Moayedi, H., Gör, M., Jaafari, A., & Foong, L. K. (2019). Predicting Slope Stability Failure through Machine Learning Paradigms. ISPRS International Journal of Geo-Information, 8(9), 395. https://doi.org/10.3390/ijgi8090395







