Next Article in Journal
The Correlation between the Jobs–Housing Relationship and the Innovative Development of Sci-Tech Parks in New Urban Districts: A Case Study of the Hangzhou West Hi-Tech Corridor in China
Previous Article in Journal
Structural Elements Detection and Reconstruction (SEDR): A Hybrid Approach for Modeling Complex Indoor Structures
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 9
Issue 12
10.3390/ijgi9120761
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Adjusting the Regular Network of Squares Resolution to the Digital Terrain Model Surface Shape

by
Dariusz Gościewski
1,* and
Małgorzata Gerus-Gościewska
2
1
Department of Geodesy, Institute of Geodesy and Civil Engineering, University of Warmia and Mazury in Olsztyn, Oczapowskiego 1, 10-719 Olsztyn, Poland
2
Department of Geoinformation and Cartography, Institute of Geodesy and Civil Engineering, University of Warmia and Mazury in Olsztyn, Heweliusza 12, 10-720 Olsztyn, Poland
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2020, 9(12), 761; https://doi.org/10.3390/ijgi9120761
Submission received: 28 November 2020 / Revised: 15 December 2020 / Accepted: 17 December 2020 / Published: 20 December 2020
Browse Figures
Review Reports Versions Notes

Abstract

:
A regular network of squares is formed by points uniformly distributed (mostly in the square corners) over the surface that is represented by the network. Each point (node) of the network has specified coordinates (X and Y) with a fixed constant distance between them. The third coordinate in a node (H) is determined by the application of interpolation based on the points distributed (usually dispersed as a point cloud e.g., from LiDAR) over the surface of the area surrounding the node. The regular network of squares formed in this manner allows the representation of a digital terrain model (DTM) to be performed in spatial information systems (SIP, GIS). The main problem that arises during the construction of such a network is the proper determination of its resolution (the base distance between the coordinates X and Y) depending on the topography. This article presents a method of the regular network of squares resolution determination depending on the morphological shape of the terrain surface. Following the application of the procedures being described, a differently shaped terrain is assigned various network densities. This enables the minimisation of inaccuracies of the surface model being formed. Consequently, a regular network of squares is formed with different base square sizes, which is adjusted with its resolution to the morphology of the surface it describes. Such operations allow the terrain model accuracy to be maintained over the entire area while reducing the number of points stored in the DTM database to the minimum.

1. Introduction

A digital terrain model (DTM) is one of the basic information layers in systems that describe spatial phenomena (GIS) [1,2,3,4,5,6,7,8,9,10]. Currently, data for the construction of this model are frequently acquired in the process of automatic recording of measuring points using aerial laser scanning, multi-beam echo sounders, laser measurement stations, etc. [11,12,13,14,15,16,17]. This enables the collection of very large volumes of data in a relatively short time. However, due to their quantity, spatial distribution and specific characteristics, such datasets cannot, as a rule, be used directly in the creation of a DTM [18,19,20,21,22,23,24,25,26,27,28].
Automatically obtained information often requires thorough processing prior to being entered into a spatial information system; this particularly applies to the dynamic processing of large volumes of data collected in various measurement epochs, and to carry out analyses of large surface structures in real-time [29,30,31,32,33,34]. One of the structures that enable a reduction in data volume, data organisation and redundancy reduction is a regular network of squares [35,36,37,38,39]. It is constructed in the value interpolation process in established nodal points based on the measuring points that surround them.
The accuracy and quality of a terrain model created using a regular network of squares is determined by its design parameters which are affected inter alia by the assumed model accuracy, density of nodes, density of measuring points, the radius for the search of points around a node, interpolation algorithms, etc. [40,41,42,43,44,45,46,47,48,49]. One of the most important structural elements of the network, which has a major effect on the quality of a digital terrain model, is the size of the base square. The mesh size is determined inter alia based on an analysis of the topography. For the entire area to be modelled with identical accuracy, the density of network nodes in morphologically diverse areas should be greater than in zones with small height differences.
In addition, the distances between particular nodal points of the network should be selected in such a way that the structure under construction would allow the topography to be characterised as accurately as possible using a minimum number of nodal points. Morphologically diverse areas are usually located during an analysis carried out based on measuring points or photogrammetric images [4,5,6,7]. This is a labour-intensive process as it requires a very large volume of data to be processed. Before the determination of the base network mesh size, it is often necessary for particular areas to analyse a very diverse terrain and then to generalise it. The correct execution of this task is largely determined by a system operator’s intuition and experience.
In practice, it is not possible to take into account all details of the surface under analysis, and the regular network of squares is, as a rule, constructed as a homogeneous network in morphologically diverse areas. Manual determination of the network size also prevents the precise balancing of the entire model’s accuracy. Consequently, a more diverse area is modelled with the greatest error since the interpolation grid on this area is too sparse. At the same time, an area that is not very diverse is characterised by data redundancy because a network with a larger base square is sufficient for its precise representation. The above difficulties found in most spatial information systems induce researchers to analyse and solve the problem. To improve the process of the base network size determination depending on the topography, while taking into account the balancing of the entire model’s accuracy on morphologically diverse areas, a set of original procedure that allow the issue to be analysed and the possible solutions to be shown was developed.
In the presented methodology, the authors propose to use the value indicated in the article as the morphological index to offset the model’s errors in morphologically diverse zones. The innovativeness of the presented method involves a morphological index which can be used to offset the surface model’s errors in zones of different morphological diversity by selecting the appropriate resolution of the square network nodes in these zones. The morphological index is determined based on the degree of morphological diversity. It enables the examination of the extent to which the surface under analysis differs from a flat surface (without morphological diversity). Ultimately, the distances between the square network nodes are determined based on the degree of morphological diversity of the surface. This enables the determination of the square network of a different size on a surface with various morphologies in such a manner to reduce the effect of morphological diversity of the surface on the accuracy of the surface model (which, from that moment, is represented using a network of squares).
The presented methodology can be applied for the data obtained from LiDAR (Light Detection and Ranging) as typical data acquired on a mass scale. It can be applied to analyse the surface recorded as a point cloud using Airborne Laser Scanning (ALS), Terrestrial Laser Scanning (TLS) or Satellite Laser Scanning (SLS). The methodology can also be applied where the elevation data for points are negative values. To demonstrate the universality of the presented method, a practical example was presented (Section 4.2.) based on the measurement data from a Multi-Beam Echo Sounder (MBES). These are data whose characteristics of the spatial location of measuring points are similar to the data obtained from LiDAR.

2. Materials and Methods

2.1. Development of a Test Model

To distinguish the meaning of the words aimed at describing the spatial distribution of points on the surface model, the following terms were used. The term “resolution” was used to describe the distribution of the square network nodes located in the corners of the network base squares. The higher the resolution, the closer the network nodes are located to one another. The term “density” was used to show the distribution of measuring points. The higher the density, the closer the measuring points are located to one another.
The term “diverse” refers to the single model being analysed at a particular moment and allows the zones found within this model to be defined. As three morphological diversity zones are found in the described cases, the following nomenclature was adopted: a surface of low diversity, a surface of medium diversity and a surface of high diversity.
A reliable comparison of the accuracy of various surfaces created using the regular network of squares requires the application of specific procedures which enable the determination of errors on particular network nodes. To this end, a special theoretical test model was developed using a mathematical function. Using the function of two variables (1), the mathematical surface shown in Figure 1 was created within the specified range of x and y values.
f ( x , y )   =   cos ( x ∗ y ∗ e x p ( y ) ) x   ∈   〈 − 3.0   ;   − 0.8 〉         y   ∈   〈 − 5.0   ; + 4.0 〉
The function was selected in such a way to be able to locate zones with various morphological diversities on the surface it creates. A mathematical function has been selected to demonstrate the methodology of proceedings. Based on this function, the study presented the pattern of proceedings during the offsetting of the model’s accuracy in view of the surface morphology when divided into three zones.
The entire model area was then scaled and shifted so that, consequently, it formed a rectangle with dimensions of 220 m × 900 m and contained only positive values of the xy coordinates. Based on this surface, 10,000 pseudo-measuring points (pp) being equivalent to measuring points (e.g., from LiDAR) were generated. This allowed a mean pp density of approx. 5 pp per 100 m2 of the model surface per the expected base square of the network to be achieved.
The point cloud generated based on the mathematical function was generated based on the random procedure (Fortran: RANDOM_NUMBER()), whose argument is dependent on the system clock time (Fortran: TIMER()). This allows pseudo-measuring points with a random distribution to be obtained, where the error of individual points’ location is randomly generated. Based on the pseudo-measuring points, a surface TIN (Triangulated Irregular Network) model shown in Figure 2 was generated.
The model thus created shows areas with various morphological diversities. To analyse the impact of various surface morphologies on the quality of the interpolation model being created, a homogeneous interpolation grid with the base size S of 10 m was generated over the entire area. The interpolation of network nodes was carried out by the method of surface approximation using third-degree 3R polynomials [21,36,43]. These actions enabled the construction of a practical surface model comprising 2093 nodes, as shown in Figure 3a.
In all cases presented in the article, the areas are determined based on the differential diagram shown in Figure 3b, which shows the differences between the theoretical model and the practical model. The initial practical model is generated at the same resolution of the square network over the entire area (Figure 3a). The diagram enables the identification of three zones with different morphologies over the surface under study. The zone edges are separated as rectangles with sides parallel to the edges of the area under study. The rectangle sides coincide with the location of the square network nodes generated in the analysed area. This enables the determination of the contact points between the areas determined for different resolutions of the square network nodes.
To analyse the generated practical regular network of squares model’s accuracy and its fitting to the theoretical surface, a theoretical grid of nodes forming a theoretical structure of the regular network of squares was generated. This was accomplished based on the same function (1) in the nodes which had the same coordinates as previously. The differences between the practical and theoretical network were then determined, which allowed true errors of the determination of height on particular nodes of the structure to be obtained.
The absolute values of the errors, assigned to the square network nodal points, enabled the development of the differential diagram shown in Figure 3b, which shows the accuracy of the interpolation model’s fit to the theoretical surface. The best-fitting is found in the central (not very diverse) area of the analysed surface, where the true error does not exceed 0.001 m. In the more morphologically diverse zones, fitting errors are greater, yet they still do not exceed 0.1 m. The least accurate fitting of the surface was obtained by the regular network of squares model in the most diverse zone where the errors exceed 0.1 m. The above example shows that a homogeneous network applied over the entire area models the surface with different accuracy.
To characterise the accuracy of fitting of the interpolation surface to the theoretical surface, the RMS coefficient can be used, whose value is determined based on the formula (2),
RMS   =   1 n ∑ i   =   1 n ( f ( x i , y i ) − z i ) 2
where: f(x,y)—the value of the function (1) in a nodal point with coordinates x y; z—the value calculated by an interpolation algorithm based on measuring points in nodal points with coordinates x y; n—the number of nodal points.
The RMS coefficient was applied to determine the extent to which the theoretical surface is matched to the practical (interpolation) surface as a single value. The RMS values are provided in several Figures to illustrate the accuracy of matching of surfaces generated at subsequent stages. Depending on the determined morphological index value and the RMS size, decisions are taken which become the basis for determining the size of the base square of the square network generated in this area.
The value of the coefficient along with the distance between nodes (S = 10 m) is provided inside the diagram shown in Figure 3b. An analysis of the diagram shown in Figure 3b indicates that the application of a homogeneous network over the entire area does not enable the balancing of the errors of the model of a regular network of squares. The balancing of the model’s accuracy over the entire surface requires the separation of zones with various surface morphology and, depending on this, the proper selection of the network density. In the diverse zone where the model is poorly fitted, the network density needs to be increased, while in the central zone of the most accurate model fitting, such a great density of nodes is not required, and they can therefore be rarefied.
In the example concerned, this was concluded based on differential diagrams that require a theoretical surface. In practice, no such surface is at the user’s disposal, as one only has a set of measuring points. In addition, the visualisation of the entire measured area to capture its morphology, based on a very large number of measuring points, is often hindered or even impossible. With this in mind, the possibility of the application of numerical analysis and for the determination of a morphological index which characterises the diversity of the terrain directly from the set of measuring points in the previously defined theoretical points needs to be examined.

2.2. Determination of the Morphological Index

To determine the morphological index (MI), an original procedure was developed to enable the automation of density of the regular network of squares normalisation process on any diverse measurement area. In the system, the indicators of the morphological diversity of the analysed surface can be determined in theoretical points located in the nodes of the network, whose base size is assumed to be the initial one. As a rule, the base size of the network is determined depending on the desired accuracy of the study. Measuring points are sought around each node in the analysed area within a specified radius R (Figure 4a). Based on the measuring points found in this way and located on the analysed surface, an approximation plane [50,51] is determined by the least-squares method [52,53,54,55] (Figure 4b). The linear equation system is solved using the Gauss elimination method [56,57]. The number of measuring points taken into consideration during the approximation is determined by their density on a particular area and is regulated in the system by defining the size of the radius R for the search around the node as a value that is a function of the base square side (R = f(S); e.g., R = √2*S). There is also a possibility of determining the minimum number of the pp located nearest to the node and distributed in selected sectors.
Ultimately, the morphological index (MI) value is assigned to the location of each node. The morphological index is the root of the arithmetic mean of the correction squares determined by the least square method during the plane approximation of the part of the area around the node, based on the found measuring points (3),
M I   =   1 n ∑ i   =   1 n d i 2
where: d—the distance of the i-the measuring point from the approximation plane; n—the number of measuring points found around the node.
The index calculated in this way indicates to what extent the area under study, around each node, differs from the plane being approximated in this place, i.e., from the flat area.
The greater the diversity of a particular area in relation to the flat surface, the greater the index. Since the index values increase with an increase in surface diversity differently for different terrains, they need to be normalised for them to be applied universally in various cases. To this end, a progressive determination of class ranges using a geometrical interval or quantiles (4) was carried out for the index values [58,59,60,61,62],
Q i   =   x Q i   +   z k − ∑ j   =   1 k − 1 n j n Q i · I Q i
where: Q i —the quantile i in the structural interval series; x Q i —the lower limit of the class in which the quantile Q i is located; n Q i —the count of the quantile Q i interval; ∑ j = 1 k − 1 n j —the total count from the first class to the one preceding that in which the quantile Q i is located; I Q i —the span of the interval in which the first quantile Q i is located; k—number of class intervals in the structural interval series; z—the count of the surveyed collectivity.
After the determination of class ranges, the normalisation of the central range was carried out, which brought the lower limit of the range to 1, and the upper limit to N, i.e., the value determined during the progressive determination of class ranges, multiplied by the coefficient of lower limit normalisation for a specified data group (5),
N   =   Q i 1 Q m i n
where: Q i —the quantile i in the structural interval series; Q m i n —the quantile of the lower limit in the structural interval series.
The various class ranges determined for the analysed case of the homogeneous network, at S = 10 m, are shown in Figure 5. By assigning normalised values of the index to particular nodes, diagrams can be created in which areas corresponding to the zones of morphological diversity of the analysed surface will be separated (Figure 5). The division into two classes (Figure 5a) can be used to indicate the zones in which the structure of the regular network of squares needs to be densified or rarefied. By using the division into three classes (Figure 5b), zones in which the network can be left unchanged and zones in which the network needs to be densified or rarefied can be distinguished. The division into four classes (Figure 5c) differentiates the morphology of the analysed area even more accurately while enabling a more precise fitting of the base network size in particular zones.
The method for determining the index is so universal that similar results are obtained irrespective of the regular network of squares initial resolution. Figure 5 shows diagrams that illustrate the zones of morphological diversity, created for the network with side sizes of, respectively: S = 40 m (Figure 5d), S = 10 m (Figure 5e) and S = 2 m (Figure 5f). For all cases, the zones of terrain diversity were determined similarly. The described method for determining zones of diverse topography was also tested on morphologically different surfaces created by mathematical models.
To generate mathematical models, a procedure which enables arbitrary modification of the morphology of the surface being created was applied. Figure 6 shows four various surface models in a spatial arrangement. Three-dimensional diagrams of the morphological index values after the determination of three classes and after the normalisation are shown above them. In all cases, three zones of various morphological diversity were determined. The index was correctly determined for both the surface with different levels of diversity (Figure 6a,b) and the relatively flat surface (Figure 6c). Figure 6d shows the case discussed in detail in this paper.
A similar situation occurs for other surfaces generated at various parameters (Figure 7). On the left side of Figure 7, the surface is shown that was created based on the same function (1), with, however, a different diversity index which was determined in the procedure by the multiplier of the height value—mz. Both the relatively flat (Figure 7a; mz = 5), moderately diverse (Figure 7b; mz = 20), and the highly diverse surface (Figure 7c; mz = 80) are characterised by similar diagrams. In all cases, the applied method of index determination enabled the correct separation of diversity zones. On the right side of Figure 7, surfaces are shown which were created at various densities of measuring points per a network base square of 10 m × 10 m (0.5 pp/100 m2—Figure 7d; 5 pp/100 m2—Figure 7e; 50 pp/100 m2—Figure 7f). In this case, the previously described determination of the index value also enabled the construction of diagrams which allow the three zones of diverse surface morphology to be correctly identified.
The assessment criterion for all cases (Figure 5, Figure 6 and Figure 7) is common: the determination of three zones with a different morphological diversity. The method’s universality is demonstrated in the examples of surface models with various morphologies. The subsequent examples show the surfaces determined for various morphological index parameters (Figure 5) and surface models with various morphologies (Figure 6).
The examples presented in Figure 7 show a universal way of determining the zones of the morphological diversity of the surface under study. Figure 7a–c shows a situation in which the determination of morphological diversity zones for the entire surface morphology occurred. Figure 7d–f show surfaces created at various densities of measuring points per a network base square. In all cases, the applied method of index determination enabled the correct separation of the three diversity zones being sought, which enables its universal application.
Having analysed the analysed cases, it can be concluded that the method for determining the morphological index which characterises zones with various surface morphology diversity levels is universal for all the examined cases. It is independent of the topography, terrain diversity and the measuring point density. The method for determining the index generating the zones of diversity in question were subsequently applied to determine the density of the regular network of squares over the analysed surface that enabled the balancing of the model error over the entire area.

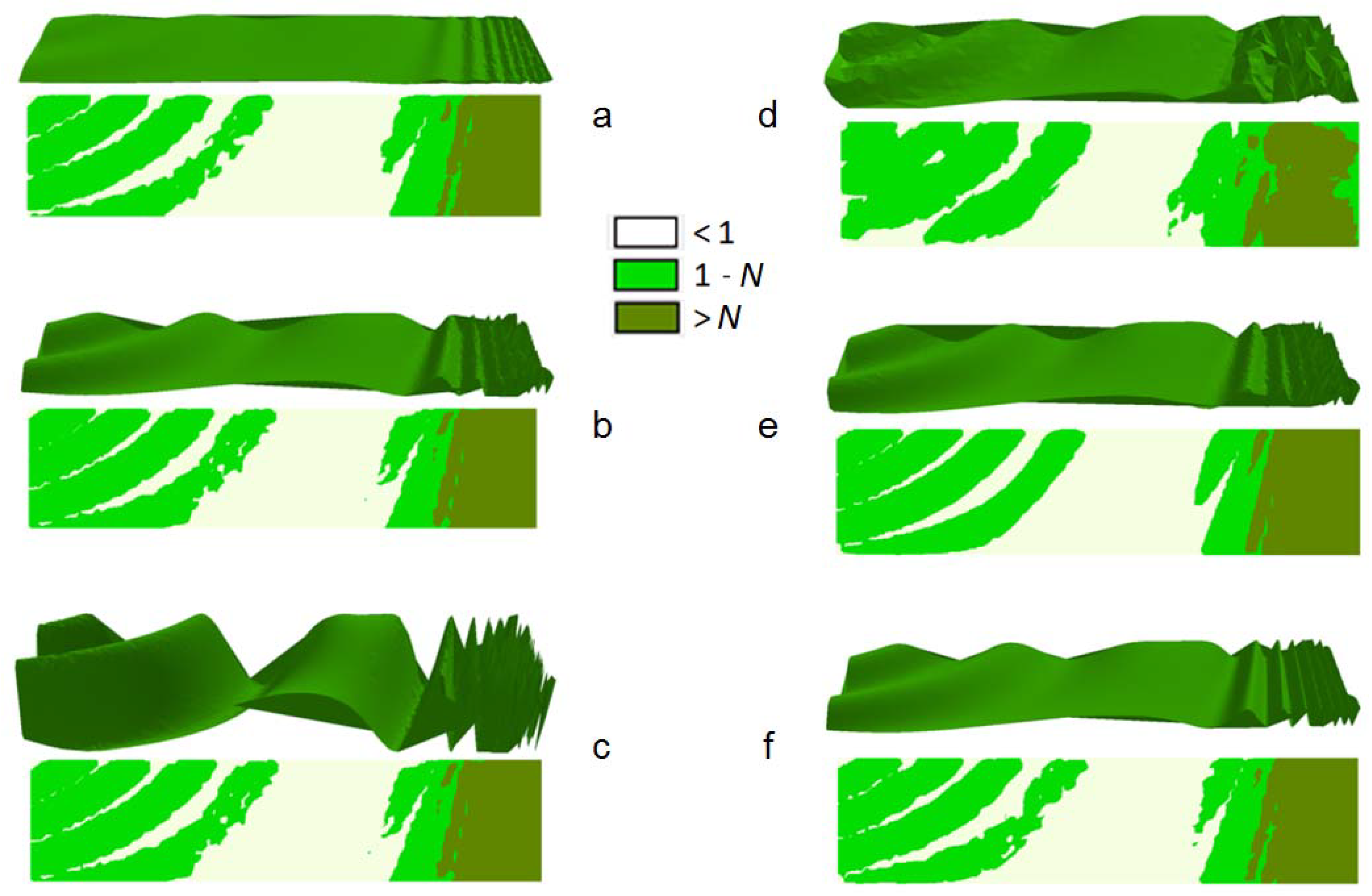
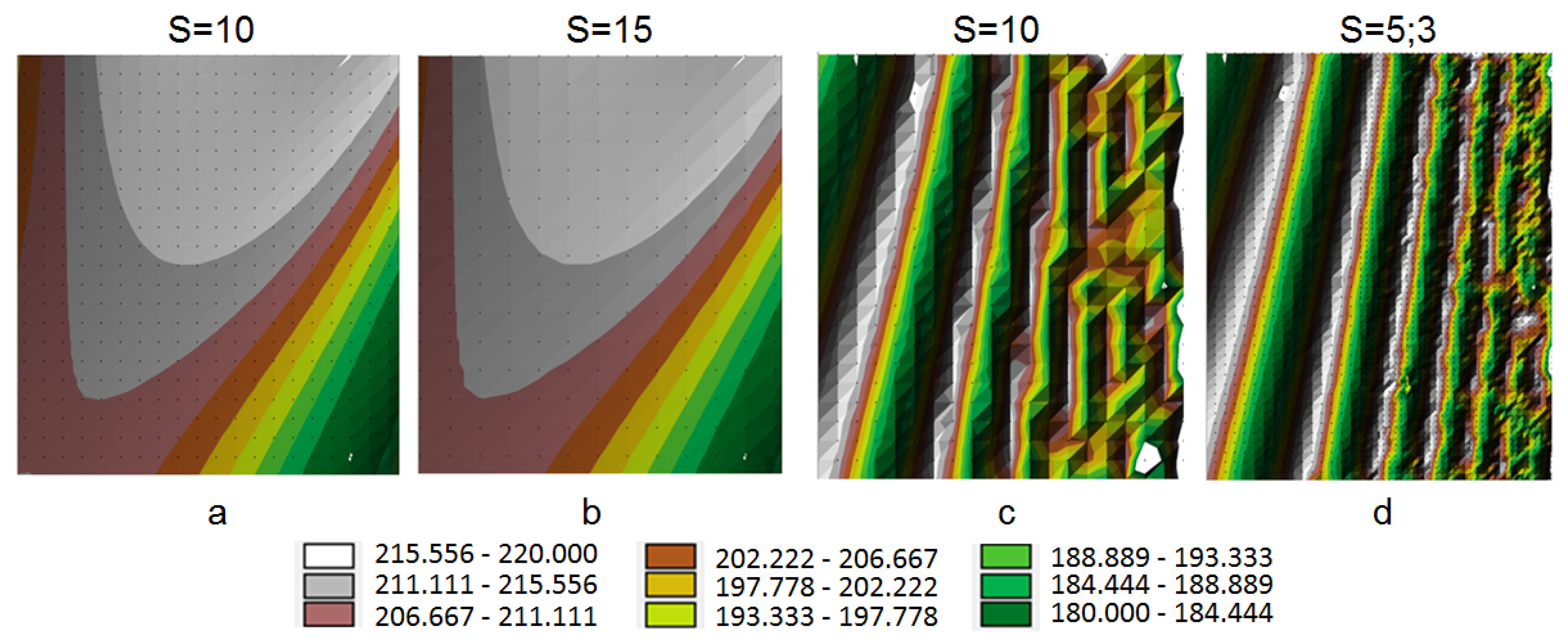
3. Results

The Application of a Morphological Index for the Determination of Density of Regular Network of Squares in Zones of a Different Surface Morphology

The process of size determination of regular network of squares over the entire area can be divided into several stages. The first stage is an analysis of measurement sets in terms of morphological diversity. In the case concerned, the initial set is that of 10,000 pp generated based on function (1) (Figure 8a). Initially, an identical initial base network is determined over the entire area. Its size is determined by the desired accuracy of the study, the density of pp, the interpolation method applied, etc. In the case under consideration, a homogeneous base network with a size S = 10 m was generated. This is followed by the determination of morphological indices in particular nodes of this structure. After the calculation of the values of indices, class ranges are determined using a geometrical interval, and normalisation is carried out. Consequently, the diagram shown in Figure 8b is formed.
Three zones with different levels of surface diversity (Z1, Z2, Z3) can be distinguished in the generated diagram. These correspond to the respective zones of the diversity of the TIN model shown in Figure 8a. The homogeneous regular network of squares that was generated based on the same network (S = 10 m) is shown in Figure 8c. The article presents examples in which the area subject to the study is divided into three rectangular zones (Figure 5, Figure 6 and Figure 7). Each of them covers with its range the area with a predominance of different morphologies divided into three classes (Figure 5), in which the morphological index value is being offset. The zones are shown in Figure 8a overlap with the zones presented in Figure 3a. In the next step, for the selected zones, a change occurs in the resolution of the square network nodes to obtain a similar morphological index value in each zone.
The interpolation of the network in particular nodes was carried out by the method of surface approximation using third-degree 3R polynomials. Having analysed the obtained interpolation surface shown in Figure 8c, it can be noted that the generated homogeneous regular network of squares did not create a uniformly accurate model. Three zones with different levels of diversity can also be located on the interpolation surface. In the centre of each zone, the size of the network base square and the RMS coefficient indicating the accuracy of the regular network model interpolation surface fitting to the theoretical surface in a particular zone were provided (Figure 8b). The first zone includes an area with a medium surface diversity and a medium grid model fitting (Z1—Figure 8b,c). The second zone is the least diverse (Figure 8b), and here the grid model is fitted most accurately (Z2—Figure 8b,c). The third zone in which the network is the worst fitted to the theoretical surface is the most diverse (Z3—Figure 8b,c).
At the second stage of the procedure, a zone needs to be identified where the interpolation model’s accuracy is sufficient and meets the expectations. In the case concerned, it was assumed that the regular network of squares model’s accuracy was sufficient in zone Z1 as the errors of network fitting to the theoretical surface on this area did not exceed 0.1 m, which is illustrated in the differential diagram shown in Figure 3b. To unify the interpolation model’s accuracy over the entire area while minimising the number of grid structure nodes, the base network size needs to be changed in the appropriate zones determined by the morphological index.
To balance the index value over the entire area, the network density needs to be changed correspondingly by decreasing it in the zone of better fitting (Z2) and increasing it in the zone in which the model fitting is worse (Z3). Therefore, in zone Z1 the density of network nodes was left unchanged (S = 10 m), as it was concluded in this zone that the model was correctly fitted. In zone Z2, the network base square was increased to S = 12, and in zone Z3 it was decreased to S = 8. The morphological indices were then calculated in the nodes determined in this way in particular zones, and the diagram shown in Figure 9a was created. Following these operations, the unification of the index was improved (Figure 9a) compared to the previous situation which is illustrated in Figure 8b. To determine the interpolation surface fitting to the theoretical surface, based on the newly established nodes, a non-homogeneous network of squares was generated in particular zones (by the same interpolation method), and the RMS coefficient was calculated. Both in zone Z2 and Z3, the model fitting was improved, which is indicated by the lower values of RMS coefficients (Figure 9a), compared to the situation presented in Figure 8b; however, the morphological index in particular zones has not yet been unified.
The third stage involves the iterative repetition of all operations described in the second stage. This is followed by a decrease in the node density in zone Z2 (S increases) and an increase in zone Z3 (S decreases). New morphological indices are calculated for subsequent network resolutions being changed, and subsequent diagrams are generated to the moment when the indices in particular zones become unified in the most possible way. Such a situation is shown in Figure 9b. The model of a regular network of squares created based on nodes densified in this way is fitted more accurately to the theoretical surface, which is indicated by the RMS coefficients in particular zones (Figure 9b). The subsequent iterations need to be interrupted at the moment when morphological indices create diagrams that are unified worse than those in the previous iteration. Such a situation is shown in Figure 9c, where the base network size in zone Z2 amounts to 30 m, and in zone Z3 to 2 m. The model of a regular network of squares created in zone Z2 at S = 30 m is less accurate (a greater RMS) (Figure 9c) than that in the previous case (Figure 9b).
In zone Z3, the network with a size S = 2 m does indeed create a better fit than that determined at the beginning; this, however, deviates from the initial assumption of the minimum number of nodes over the analysed area and the unification of the morphological index in all zones. Given that zone Z3 shown in Figure 9b still includes the area with indices exceeding the assumed value, it can be additionally divided into two further sub-zones Z31 and Z32 (Figure 10a) to unify the morphological index on this area more accurately. The size of the network in zone Z31 remained at a level of S = 5 m, and in zone Z32 it decreased to S = 3 m. After the calculation of the index, in the nodes determined in this way, the diagram shown in Figure 10a was created. The division into additional zones allowed the unification of the index over the entire area, assumed in the introduction, to be achieved. At the last stage of the procedure, based on the determined, appropriate network resolution that was different in particular zones, a non-homogeneous network of squares was generated over the entire area by the same interpolation as previously.
Ultimately, the entire process of determining the resolution of square network nods in individual zones with different surface morphologies can be divided into 11 stages:
  • Analysis of the measurements sets in terms of the surface morphology.
  • Determination of the initial homogeneous network for the entire area.
  • Calculation of the morphological index values in individual nodes.
  • Division into morphological diversity zones.
  • Determination of the zone with the desired model accuracy.
  • Subsequent iterations changing the network density in individual zones.
  • Determination and verification of the morphological index in individual zones.
  • Offsetting the morphological index values over the entire area.
  • Determination of the final network density in individual zones.
  • Generation of a non-homogeneous network, different in individual zones.
  • Final inspection of the interpolation model in terms of quality and accuracy.

4. Discussion

4.1. The Application of the Morphological Index in the Theoretical Model

An analysis of the interpolation model shown in Figure 10b enables the conclusion that the performed operations allowed a better quality of the surface to be obtained. The improvement in the surface fitting is additionally illustrated by the RMS coefficients assigned to particular zones (Figure 10a). For the regular network of squares generated in this way, true errors in particular nodes were calculated. On their basis, the differential diagram shown in Figure 10c was created. Compared to the diagram generated for the homogeneous network, shown in Figure 3b, the errors of fitting the interpolation surface to the theoretical surface were reduced, which is particularly noticeable on the most morphologically diverse area (zone Z3 = Z31 + Z32; Figure 10c).
At the same time, in zone Z2, despite the rarefaction of the node network and the reduction in their number, the fitting did not deteriorate. The difference in the accuracy of surface matching in graphical form is shown in differential diagrams (Figure 3b and Figure 10c). Improved accuracy of the grid model fitting over the entire area can also be identified based on the RMS coefficient which decreased for the non-homogeneous network of squares (RMS = 0.685; Figure 10c) compared to the RMS coefficient calculated for the homogeneous network of squares (RMS = 2.242; Figure 3b). A comparison of the quality of models of a regular network of squares in the analysed zones is additionally shown in Figure 11. The part of the model from zone Z2, shown in Figure 11b (S = 15), does not differ in terms of quality from the part of the model from Figure 11a (S = 10) despite the increase in distances between nodes and a significant reduction in their number. At the same time, the part of the model from zone Z3, shown in Figure 11d (S = 5, S = 3), is, due to the node density in this area, more accurate than the part of the model shown in Figure 11c (S = 10).
Thanks to the application of the method concerned, the accuracies of the model in different zones are balanced automatically by applying subsequent iterations which enable the proper determination of the resolution of a regular network of squares. The application of a mathematical surface model enabled the verification of the increase in the accuracy of model fitting based on the RMS coefficient and the differential diagrams. However, it is worth testing the method concerned for a real digital terrain model.

4.2. The Application of the Morphological Index in the Digital Terrain Model

A part of the seabed that was measured using a MBES (Multi-Beam Echo Sounder) was selected as a practical model. The discussed case used the data from the measurement of the Szczecin-Świnoujście corridor’s seabed (Poland), conducted using an MBES integrated with the DGPS (Differential Global Positioning System). All measurements covered a section of approx. 68 kilometres and a variable track width ranging from 100 to 250 m. The measurement technology applied (recording of approximately 50 points per second) allowed over 218 million records to be obtained. Each record in the databased had the three following coordinates recorded: B and L determined by DGPS (in the WGS 84 system, which were converted into X, Y in the UTM system) and the normal heights H measured by a probe with an accuracy of up to 0.1 m (referred to the average sea level in Amsterdam). The part subjected to analysis covered an area of 144 m × 114 m (16,416 m2). In the selected part, the measurement was carried out with a resolution of approx. 12 pp per 1 m2. The measurement resolution enabled the use of the TIN model surface as a theoretical surface with which the model constructed using the square network was compared.
The area under analysis contained 195,898 measuring points which enabled the creation of the TIN model shown in Figure 12a. Having considered the high density of measuring points, it was assumed that the method of balancing values with the inverse of the square of the distance for the five nearest measuring points would be applied for the interpolation of height in the nodes, and the resolution of the initial homogeneous grid model over the entire area was established at a level of S = 5 m. An interpolation regular network model comprising 720 nodes, created based on a homogeneous grid (S = 5 m) over the entire area, is shown in Figure 12b. In the morphological diversity zones, on the model of a regular network of squares, a clear deterioration in the quality of the presented surface can be noted. At the same time, in the less diverse zones, the surface represented by the model does not differ from the surface generated by the TIN model.
To enhance the quality of the interpolation model, with the assumption that the minimum number of generating points needs to be maintained while unifying the accuracy of the regular network of squares over the entire area, the stages described previously were applied. Based on the measurement data, a morphological index was determined in particular nodes of the homogeneous network (S = 5 m). The index values were divided into three classes and subjected to normalisation in the manner described previously. This enabled the creation of the diagram shown in Figure 12c.
In each case, it was an area of medium morphological diversity that was assumed to be the Z1 zone. It is characterised by a medium morphological index value. In the methodology being described, this choice enables the offsetting of the morphological index in all zones. To obtain a similar morphological index value in all zones, a different resolution of the square network nodes is set in all zones. In the Z2 zone, the node resolution decreases (the distances between nodes increase). In the Z3 zone, the node resolution increases (the distances between nodes decrease).
In the diagram (Figure 12c), three zones with various morphological diversity were separated, and it was assumed that zone Z1 satisfied the accuracy requirements. At the same time, it was found that zone Z3 included the most diverse area, and both Z2 zones included a similarly shaped area with the smallest diversity of the surface. By applying subsequent iterations described previously, which involved the gradual increase in the network density in zone Z3 while decreasing this density in both zones Z2, the unification of the morphological index over the entire area was then achieved (Figure 12d) while determining various node densities in different zones (Figure 12e). In zone Z1, the initial regular network of squares (S = 5 m) was left, in both zones Z2 the network was rarefied to S = 10 m, and in zone Z3 the network was densified to S = 2 m (Figure 12e). Based on the network resolution determined in this way in particular zones, a non-homogeneous model of a network of squares was then generated over the entire area, which comprised a total of 1600 nodes (Figure 12f). The quality of the surface created based on the non-homogeneous model of a network of squares (Figure 12f) is clearly better than the surface created by a homogeneous grid model (Figure 12b). In the zone with the greatest diversity (Z3; Figure 12f), a characteristic topography was distinguished which was similar in terms of quality to the TIN model (Z3; Figure 12a). At the same time, the grid model’s accuracy in both Z2 zones did not deteriorate despite the reduction in the number of nodes that the model consisted of.
The model’s accuracy was also compared based on the RMS value determined for the TIN model constructed from measuring points and the models constructed based on the (homogeneous and non-homogeneous) square network. RMS determined for the original model (with a constant resolution of the square network nodes, Figure 12b) was 4.521 m. RMS determined for the processed model (with a variable resolution of the square network nodes, Figure 12f) was 1.016 m. This allows one to conclude that a model with a variable resolution of the square network nodes, constructed using the described methodology, is more accurate. Moreover, the offsetting of the morphological index allows a better-quality surface model to be obtained. The model has a resolution of the square network nodes that is better matched to the surface morphology.
It can be concluded that the interpolation surface model accurately reflects the topography despite the reduction in the number of points that form the model from 195,898 pp for the TIN model to 1600 nodes for the model of a regular network of squares. Consequently, the objective of reducing the number of points forming the model while balancing the accuracy of surface representation over the entire diverse area was accomplished.

5. Conclusions

One of the ways of representing a digital terrain model in spatial information systems is a regular network of squares. The basic problem that arises during the construction of such a network is the proper determination of its density depending on the topography. The network size is crucial for the accuracy of the digital terrain model being generated. For the entire area to be modelled with identical accuracy, the density of network nodes in morphologically diverse areas should be greater than in zones with small height differences. In addition, the distances between particular nodal points of the grid structure should be selected in such a way that the structure under construction allows the topography to be characterised as accurately as possible using a minimum number of nodal points.
In most cases, the selection of an elementary design parameter, i.e., the base square size, is performed by a system operator. The proposed solution enables the unification of the process of determining the base interpolation network size depending on the topography. Thanks to the application of the morphological index, zones of the analysed area in which the surface is shaped differently can be distinguished. After the identification of zones determined by the index values, a change in the resolution of a regular network of squares can be made in them.
In not very diverse zones, the distances between nodes can be increased, which results in the rarefication of the network and a reduction in the number of points forming the model. On the other hand, in the zones of great morphological diversity, these distances can decrease, which leads to a gradual densification of the network, thus enhancing the quality of the surface being generated. By applying subsequent iterations, the index can be unified over the entire analysed terrain. The unification of the morphological index simultaneously results in the balancing, in terms of accuracy, of the size of the interpolation network over the entire area. This also enables a selection of node density to ensure that the interpolation model’s accuracy is similar in particular morphologically diverse zones.
The entire process exempts the system operator from procedures associated with an analysis of terrain morphology based on measuring points prior to the selection of the network density in particular areas. By applying the methods presented in the article, the system operator has the opportunity to analyse the morphology of the surface under study before determining the size of the network base square. Apart from taking into account the accuracy requirements of the study, the determination of the network node resolution can be dependent on the determined morphological index in individual zones. By applying the presented methodology, one can additionally offset the morphological index in the determined zones of the study by changing the resolution of the square network nodes. This allows a similar accuracy of the study to be obtained in morphologically diverse zones.
The theoretical analysis (conducted based on theoretical models) is described in Section 2. It enables a demonstration of the method’s universality for the models determined for various parameters of the morphological index (Figure 5), for various surface models (Figure 6) or various surface diversities and various densities of measuring points (Figure 7). In all cases, the applied method of index determination allowed the three diversity zones being sought to be separated. The methodology, explained using a theoretical example, was then applied to analyse the real model. The practical analysis based on the real seabed model measured by an MBES is presented in Section 4.2.
In each case, the non-homogeneous interpolation network of squares being created enables the optimum selection of the number of points that form the model while balancing its accuracy. The procedures in question were tested using a variety of regular network of squares interpolation methods, with various topographies and different measuring point densities. In each case, an improvement in the accuracy and quality of the interpolation model was achieved. The method, when applied in practice, increases the accuracy of digital terrain models created when using the regular network of squares.

Author Contributions

Conceptualization, Dariusz Gościewski and Małgorzata Gerus-Gościewska; methodology, Dariusz Gościewski; software, Dariusz Gościewski; validation, Dariusz Gościewski and Małgorzata Gerus-Gościewska; formal analysis, Małgorzata Gerus-Gościewska; investigation, Dariusz Gościewski and Małgorzata Gerus-Gościewska; resources, Dariusz Gościewski and Małgorzata Gerus-Gościewska; data curation, Dariusz Gościewski; writing original draft preparation, Dariusz Gościewski; writing review and editing, Małgorzata Gerus-Gościewska; visualization, Dariusz Gościewski; supervision, Dariusz Gościewski and Małgorzata Gerus-Gościewska; project administration, Dariusz Gościewski and Małgorzata Gerus-Gościewska. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Goodchild, M.F. Geographic information systems and science: Today and tomorrow. Ann. GIS 2009, 15, 3–9. [Google Scholar] [CrossRef] [Green Version]
  2. Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D.W. Geographical Information Systems and Science, 3rd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
  3. Yue, T.X.; Du, Z.P.; Song, D.J. A new method of surface modelling and its application to DEM construction. Geomorphology 2007, 91, 161–172. [Google Scholar] [CrossRef]
  4. Choi, J.; Usery, E. System integration of GIS and a rule-based expert system for urban mapping. Photogramm. Eng. Remote Sens. 2004, 70, 2017–2024. [Google Scholar] [CrossRef]
  5. Zhou, Q.; Chen, Y. Generalization of DEM for terrain analysis using a compound method. ISPRS J. Photogramm. Remote Sens. 2011, 66, 38–45. [Google Scholar] [CrossRef]
  6. Kraus, K.; Briese, C.; Attwenger, M.; Pfeifer, N. Quality measures for digital terrain models. Int. Arch. Photogramm. Remote Sens. and Spat. Inf. Sci. 2004, 35, 1682–1750. [Google Scholar]
  7. Shan, J.; Sampath, A. Urban DEM generation from raw LiDAR data: A labeling algorithm and its performance. Photogramm. Eng. Remote Sens. 2005, 71, 217–222. [Google Scholar] [CrossRef] [Green Version]
  8. Lee, H.S.; Younan, N. DTM extraction of LiDAR returns via adaptive processing. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2063–2069. [Google Scholar] [CrossRef]
  9. Isenburg, M.; Liu, Y.; Shewchuk, J.; Snoeyink, J.; Thirion, T. Generating raster DEM from mass points via TIN streaming. Geogr. Inf. Sci. Lect. Notes Comput. Sci. 2006, 4197, 186–198. [Google Scholar]
  10. Brovelli, M.A.; Cannata, M.; Longoni, U.M. LiDAR data filtering and DTM interpolation within GRASS. Trans. GIS 2004, 8, 155–174. [Google Scholar] [CrossRef]
  11. Aruga, K.; Sessions, J.; Akay, A.E. Application of an airborne laser scanner to forest road design with accurate earthwork volumes. J. For. Res. 2005, 10, 113–123. [Google Scholar] [CrossRef]
  12. Tovari, D.; Vogtle, T. Classification methods for 3D objects in laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 408–413. [Google Scholar]
  13. Zandbergen, P.A. Accuracy Considerations in the Analysis of Depressions in Medium Resolution LiDAR DEMs. Giscience Remote Sens. 2010, 47, 187–207. [Google Scholar] [CrossRef]
  14. Lihong, W.; Wenhai, X.; Wenbo, W. Survey of Seafloor Targets with Varied Sizes by Multi Beam Sonar in Different Depth Water. Trans. Tech. Publ. Appl. Mech. Mater. 2013, 263–266, 909–914. [Google Scholar]
  15. Wang, C.; Tseng, Y. DEM generation from airborne LiDAR data by an adaptive dualdirectional slope filter. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 628–632. [Google Scholar]
  16. Calder, B.; Mayer, L. Automatic processing of high-rate, highdensity multibeam echosounder data. Geochem. Geophys. Geosyst. 2003, 4, 1048–1069. [Google Scholar] [CrossRef]
  17. Rivas, M.; Maslanik, J.; Sonntag, J.; Axelrad, P. Sea ice roughness from airborne LiDAR profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3032–3037. [Google Scholar] [CrossRef]
  18. Shi, W.; Fisher, P.F.; Goodchild, M.F. Recent developments in modeling uncertainties in geo-spatial data and analysis. Photogramm. Eng. Remote Sens. 2004, 70, 919–930. [Google Scholar]
  19. Harmon, J.E.; Anderson, S.J. The Design and Implementation of Geographic Information Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
  20. Pigozzi, B.W. A hierarchy of spatial marginality through spatial filtering. Prof. Geogr. 2004, 56, 460–470. [Google Scholar]
  21. Gościewski, D. Reduction of deformations of the digital terrain model by merging interpolation algorithms. Comput. Geosci. 2014, 64, 61–71. [Google Scholar] [CrossRef]
  22. Szczepańska, A.; Gościewski, D.; Gerus-Gościewska, M. A GRID-Based Spatial Interpolation Method as a Tool Supporting Real Estate Market Analyses. ISPRS Int. J. Geo. Inf. 2020, 9, 39. [Google Scholar] [CrossRef] [Green Version]
  23. Mongus, D.; Zalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012, 66, 1–12. [Google Scholar] [CrossRef]
  24. Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
  25. Gaboardi, C.; Mitishita, E.; Firkowski, H. Digital terrain modeling generalization with base in Wavelet Transform. Boletim de Ciências Geodésicasl. 2011, 17, 115–129. [Google Scholar] [CrossRef] [Green Version]
  26. Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
  27. Sithole, G. Filtering of laser altimetry data using a slope adaptive filter. Int. Arch. Photogramm. Remote Sens. 2001, 34, 203–210. [Google Scholar]
  28. Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering airborne laser scanning data with morphological methods. Photogramm. Eng. Remote Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef] [Green Version]
  29. Arctur, D.; Zeiler, M. Designing Geodatabases: Case Studies in GIS Data Modeling; ESRI Press: Redlands, CA, USA, 2004. [Google Scholar]
  30. Gerus-Gościewska, M.; Gościewski, D.; Szczepańska, A. The Use of a Grid Structure for Reconstructing and Forecasting the Value of Real Estate in Selected Measurement Epochs. Geosciences 2019, 9, 485. [Google Scholar] [CrossRef] [Green Version]
  31. Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef] [Green Version]
  32. Zhang, K.Q.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
  33. Finley, A.; Sang, H.; Banerjee, S.; Gelfand, A. Improving the performance of predictive process modeling for large datasets. Comput. Stat. Data Anal. 2009, 53, 2873–2884. [Google Scholar] [CrossRef] [Green Version]
  34. Furrer, R.; Genton, M.; Nychka, D. Covariance tapering for interpolation of large spatial datasets. J. Comput. Graph. Stat. 2006, 15, 502–523. [Google Scholar] [CrossRef] [Green Version]
  35. Raaflaub, L.D.; Collins, M.J. The effect of error in gridded digital elevation models on the estimation of topographic parameters. Environ. Model. Softw. 2006, 21, 710–732. [Google Scholar] [CrossRef]
  36. Chen, C.F.; Li, Y.Y.; Dai, H.L. An application of Coons patch to generate grid- based digital elevation models. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 830–837. [Google Scholar] [CrossRef]
  37. Gao, J. Resolution and accuracy of terrain representation by grid DEMs at a micro-scale. Int. J. Geogr. Inf. Sci. 2001, 11, 199–212. [Google Scholar] [CrossRef]
  38. Wu, J.; Amaratunga, K. Wavelet triangulated irregular networks. Int. J. Geogr. Inf. Sci. 2003, 17, 273–289. [Google Scholar] [CrossRef]
  39. Yanalak, M. Effect of gridding method on digital terrain model profile data based on scattered data. J. Comput. Civ. Eng. 2003, 17, 58–67. [Google Scholar] [CrossRef]
  40. Zhang, X.; Drake, N.A.; Wainwright, J.; Mulligan, M. Comparison of slope estimates from low resolution DEMs: Scaling issues and a fractal method for their solution. Earth Surf. Process. Landf. 1999, 24, 763–779. [Google Scholar] [CrossRef]
  41. Deng, Y. New trends in digital terrain analysis: Landform definition, representation, and classification. Prog. Phys. Geogr. 2007, 31, 405–419. [Google Scholar] [CrossRef]
  42. Hjort, J.; Luoto, M. Modelling patterned ground distribution in Finnish Lapland: An integration of topographical, ground and remote sensing information. Phys. Geogr. 2006, 88, 19–29. [Google Scholar] [CrossRef]
  43. Pitas, I. Digital Image Processing Algorithms and Applications; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
  44. Haugerud, R.A.; Harding, D.J. Some algorithms for virtual deforestation (VDF) of LiDAR topographic survey data. Int. Arch. Photogramm. Remote Sens. 2001, 34, 211–217. [Google Scholar]
  45. Chaplot, V.; Darboux, F.; Bourennane, H.; Leguédois, S.; Silvera, N.; Phachomphon, K. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
  46. Arefi, H.; Hahn, M. A morphological reconstruction algorithm for separating off-terrain points from terrain points in laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, 120–125. [Google Scholar]
  47. Zhang, K.; Whitman, D. Comparison of three algorithms for filtering airborne LiDAR data. Photogramm. Eng. Remote Sens. 2005, 71, 313–324. [Google Scholar] [CrossRef] [Green Version]
  48. Cressie, N.; Pavlicová, M. Calibrated spatial moving average simulations. Stat. Model. Int. J. 2002, 4, 267–279. [Google Scholar] [CrossRef]
  49. Sirmacek, B.; Taubenbock, H.; Reinartz, P.; Ehlers, M. Performance evaluation for 3-D city model generation of six different DSMs from air- and spaceborne sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 59–70. [Google Scholar] [CrossRef]
  50. Bickel, P.; Doksum, K. Mathematical Statistics: Basic Ideas and Selected Topics; Holden-Day: San Francisco, CA, USA, 1977. [Google Scholar]
  51. Najman, L.; Talbot, H. (Eds.) Mathematical Morphology: From Theory to Applications; Wiley-ISTE: London, UK, 2010. [Google Scholar]
  52. Harper, H.L. The method of least squares and some alternatives. Part I, II, II, IV, V, VI. Int. Satistical Rev. 1974, 42, 147–174. [Google Scholar]
  53. Deakin, R.E. A review of Least Squares theory applied to traverse adjustment. Aust. Surv. 1991, 36, 245–253. [Google Scholar] [CrossRef]
  54. Abdi, H. The Method of Least Squares; Encyclopedia of Measurement and Statistics: Thousand Oaks, CA, USA, 2007. [Google Scholar]
  55. Menke, W. Review of the generalized least squares method. Surv. Geophys. 2015, 36, 1–25. [Google Scholar] [CrossRef]
  56. Larson, R.; Farber, E. Elementary Statistics: Picturing the World; Prentice-Hall: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
  57. Chen, T.; Ohlsson, H.; Ljung, L. On the estimation of transfer functions, regularizations and Gaussian processes revisited. Automatica 2012, 48, 1525–1535. [Google Scholar] [CrossRef] [Green Version]
  58. Pasławski, J. Jak Opracować Kartogram; Wydawnictwa Uniwersytetu Warszawskiego: Warszawa, Poland, 2003. [Google Scholar]
  59. Robinson, A.; Sale, R.; Morrison, J. Elements of Cartography. Podstawy Kartografii; PWN: Warszawa, Poland, 1998. [Google Scholar]
  60. Van Overschee, P.; de Moor, B. Subspace Identification for Linear Systems: Theory, Implementation, Applications; Kluwer Academic Publishers: Boston, MA, USA, 1996. [Google Scholar]
  61. Casella, G.; Berger, R. Statistical Inference, 2nd ed.; Duxbury Advanced Series: Pacific Grove, CA, USA, 2002. [Google Scholar]
  62. Moore, D.; McCabe, G. Introduction to the Practice of Statistics; W.H. Freeman and Co.: London, UK, 2003. [Google Scholar]
Ijgi 09 00761 g001 550
Figure 1. A mathematical surface model. Source: own elaboration.
Figure 1. A mathematical surface model. Source: own elaboration.
Ijgi 09 00761 g001
Ijgi 09 00761 g002 550
Figure 2. A surface model generated by the Triangulated Irregular Network (TIN) structure (model units in meters). Source: own elaboration.
Figure 2. A surface model generated by the Triangulated Irregular Network (TIN) structure (model units in meters). Source: own elaboration.
Ijgi 09 00761 g002
Ijgi 09 00761 g003 550
Figure 3. An interpolation surface model created by the regular network of squares being homogeneous over the entire area (RMS, S and model units in meters). (a) practical surface model; (b) differential diagram. Source: own elaboration.
Figure 3. An interpolation surface model created by the regular network of squares being homogeneous over the entire area (RMS, S and model units in meters). (a) practical surface model; (b) differential diagram. Source: own elaboration.
Ijgi 09 00761 g003
Ijgi 09 00761 g004 550
Figure 4. Approximation plane of the morphological index. R—the radius of the searches for measuring points around the node. (a) orthogonal projection; (b) isometric projection. The approximation plane is presented as a network of squares. Hpp—the height of measuring points; Hap—the height of the approximation plane. Source: own elaboration.
Figure 4. Approximation plane of the morphological index. R—the radius of the searches for measuring points around the node. (a) orthogonal projection; (b) isometric projection. The approximation plane is presented as a network of squares. Hpp—the height of measuring points; Hap—the height of the approximation plane. Source: own elaboration.
Ijgi 09 00761 g004
Ijgi 09 00761 g005 550
Figure 5. Areas of morphological diversity determined for various parameters of the morphological index. k—the number of class intervals in the structural interval series. (a) two classes; (b) three classes; (c) four classes; (d) side of the square S = 40 m; (e) side of the square S = 10 m; (f) side of the square S = 2 m. Source: own elaboration.
Figure 5. Areas of morphological diversity determined for various parameters of the morphological index. k—the number of class intervals in the structural interval series. (a) two classes; (b) three classes; (c) four classes; (d) side of the square S = 40 m; (e) side of the square S = 10 m; (f) side of the square S = 2 m. Source: own elaboration.
Ijgi 09 00761 g005
Ijgi 09 00761 g006 550
Figure 6. The areas determined by the morphological index for various surface models. (a,b) varied surface; (c) flat surface; (d) case discussed in detail in this paper. Source: own elaboration.
Figure 6. The areas determined by the morphological index for various surface models. (a,b) varied surface; (c) flat surface; (d) case discussed in detail in this paper. Source: own elaboration.
Ijgi 09 00761 g006
Ijgi 09 00761 g007 550
Figure 7. The areas determined by the morphological index for different diversities of surface and different densities of measuring points. (a) flat surface (mz = 5); (b) varied surface (mz = 20); (c) highly diverse surface (mz = 80); (d) 0.5 pp/100 m2; (e) 5 pp/100 m2; (f) 50 pp/100 m2. Source: own elaboration.
Figure 7. The areas determined by the morphological index for different diversities of surface and different densities of measuring points. (a) flat surface (mz = 5); (b) varied surface (mz = 20); (c) highly diverse surface (mz = 80); (d) 0.5 pp/100 m2; (e) 5 pp/100 m2; (f) 50 pp/100 m2. Source: own elaboration.
Ijgi 09 00761 g007
Ijgi 09 00761 g008 550
Figure 8. The areas determined by the morphological index, corresponding to the model surface diversity zones (RMS, S and model units in meters). (a) TIN model; (b) differential diagram; (c) model of a regular network of squares. Source: own elaboration.
Figure 8. The areas determined by the morphological index, corresponding to the model surface diversity zones (RMS, S and model units in meters). (a) TIN model; (b) differential diagram; (c) model of a regular network of squares. Source: own elaboration.
Ijgi 09 00761 g008
Ijgi 09 00761 g009 550
Figure 9. Balancing the size of the morphological index in the model surface diversity zones (RMS and S units in meters). (a–c) subsequent phases of model accuracy analyses. Source: own elaboration.
Figure 9. Balancing the size of the morphological index in the model surface diversity zones (RMS and S units in meters). (a–c) subsequent phases of model accuracy analyses. Source: own elaboration.
Ijgi 09 00761 g009
Ijgi 09 00761 g010 550
Figure 10. An interpolation surface model created in four diversity zones by the network of squares being non-homogeneous over the entire area (RMS, S and model units in meters). (a) RMS coefficients assigned to particular zones; (b) interpolation surface model; (c) differential diagram. Source: own elaboration.
Figure 10. An interpolation surface model created in four diversity zones by the network of squares being non-homogeneous over the entire area (RMS, S and model units in meters). (a) RMS coefficients assigned to particular zones; (b) interpolation surface model; (c) differential diagram. Source: own elaboration.
Ijgi 09 00761 g010
Ijgi 09 00761 g011 550
Figure 11. A comparison of the accuracy of the models for a homogeneous and non-homogeneous network of squares (S and model units in meters). (a,b) flat surface; (c,d) varied surface. Source: own elaboration.
Figure 11. A comparison of the accuracy of the models for a homogeneous and non-homogeneous network of squares (S and model units in meters). (a,b) flat surface; (c,d) varied surface. Source: own elaboration.
Ijgi 09 00761 g011
Ijgi 09 00761 g012 550
Figure 12. Balancing the morphological index values and the determination of node density in the digital terrain model. The upper scale of colours refers to the surface model, while the lower scale of colours refers to the morphological index (RMS and model units in meters). (a) TIN model; (b) homogeneous grid model; (c) three zones with various morphological diversity; (d) unification of the morphological index over the entire area; (e) zoning (Z1: S = 5 m, Z2: S = 10 m, Z3: S = 2 m); (f) non-homogeneous model grid. Source: own elaboration.
Figure 12. Balancing the morphological index values and the determination of node density in the digital terrain model. The upper scale of colours refers to the surface model, while the lower scale of colours refers to the morphological index (RMS and model units in meters). (a) TIN model; (b) homogeneous grid model; (c) three zones with various morphological diversity; (d) unification of the morphological index over the entire area; (e) zoning (Z1: S = 5 m, Z2: S = 10 m, Z3: S = 2 m); (f) non-homogeneous model grid. Source: own elaboration.
Ijgi 09 00761 g012
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gościewski, D.; Gerus-Gościewska, M. Adjusting the Regular Network of Squares Resolution to the Digital Terrain Model Surface Shape. ISPRS Int. J. Geo-Inf. 2020, 9, 761. https://doi.org/10.3390/ijgi9120761

AMA Style

Gościewski D, Gerus-Gościewska M. Adjusting the Regular Network of Squares Resolution to the Digital Terrain Model Surface Shape. ISPRS International Journal of Geo-Information. 2020; 9(12):761. https://doi.org/10.3390/ijgi9120761

Chicago/Turabian Style

Gościewski, Dariusz, and Małgorzata Gerus-Gościewska. 2020. "Adjusting the Regular Network of Squares Resolution to the Digital Terrain Model Surface Shape" ISPRS International Journal of Geo-Information 9, no. 12: 761. https://doi.org/10.3390/ijgi9120761

APA Style

Gościewski, D., & Gerus-Gościewska, M. (2020). Adjusting the Regular Network of Squares Resolution to the Digital Terrain Model Surface Shape. ISPRS International Journal of Geo-Information, 9(12), 761. https://doi.org/10.3390/ijgi9120761

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop