A Multi-Objective Permanent Basic Farmland Delineation Model Based on Hybrid Particle Swarm Optimization
Abstract
:1. Introduction
2. Data
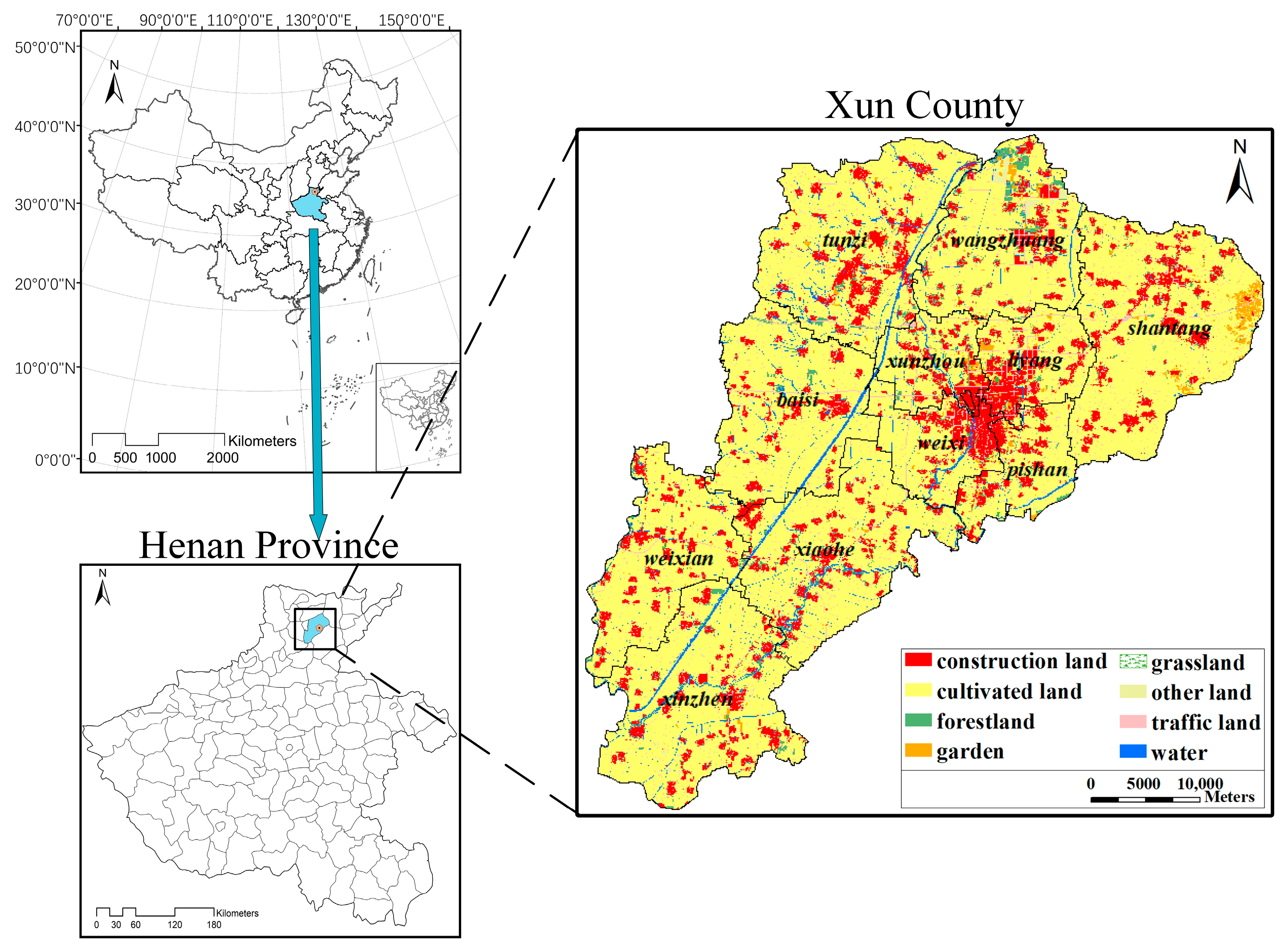
2.1. Overview of The Study Area
2.2. Data Processing
3. Methodology
3.1. Multi-objective Optimization Model of Permanent Basic Farmland Delimitation
3.1.1. Objective Functions
3.1.2. Constraint Conditions
3.2. Design of AIA-PSO Model
3.2.1. Particle Encoding and Initialization
3.2.2. Particle Position and Velocity Update
3.2.3. Improvement of PSO with the Artificial Immune Algorithm
3.2.4. Fitness Function Design
3.2.5. Flow of AIA-PSO Model
4. Analysis of the Permanent Basic Farmland Demarcation Results
4.1. Setting PSO Model Parameters
4.2. Comparison of the Different Schemes
4.3. Analysis of the Impact of Improvement on the Model
4.4. Analysis of the Pattern of Permanent Basic Farmland in Xun County
5. Conclusions
- The results of the experimental comparative analysis showed that there were conflicts between land suitability, land continuity, and land stability. The improvement in the value of any one subobjective function was at the expense of the other two subobjective values. The corresponding weights , , and were allocated according to the specific decision objectives to obtain a more satisfactory delineation scheme.
- With the increase in the weights and corresponding to the continuity and stability in the experiment, the consistency target guided the particles to find the area where the spatial concentration was formed and gradually produced a more obvious concentration effect. The stability objective caused the selected area to gradually move away from towns and roads from the periphery of the town, reducing the possibility of land occupation due to the renewed expansion of the town.
- The PSO algorithm has a strong spatial search ability and global optimization ability to solve multi-objective problems. Combined with the spatial processing capabilities of GIS, which reduced manual intervention and improves work efficiency, it has strong operability and provides a favorable guarantee of permanent basic farmland demarcation results and quality.
- The global search capability of the artificial immune algorithm was used to compensate for the shortcomings of particle swarm optimization, which easily falls into a local optimal solution. A hybrid particle swarm optimization algorithm was constructed to improve the efficiency of the model. Compared with the original model, the number of iterations was reduced by 34.2%, and the optimization ability of the three subobjective functions was increased by 3.36%, 5.04%, and 4.68%. However, the improved AIA-PSO had 2.4 times the running time of PSO and had large fluctuations.
Author Contributions
Funding
Conflicts of Interest
References
- Shan, L.; Ann, T.; Yu, W.; Wu, W. Strategies for risk management in urban–rural conflict: Two case studies of land acquisition in urbanising China. Habitat Int. 2017, 59, 90–100. [Google Scholar] [CrossRef]
- Piana, P.; Faccini, F.; Luino, F.; Piliaga, G. Geomorphological landscape research and flood management in a heavily modified Tyrrhenian catchment. Sustainability 2019, 11, 4594. [Google Scholar] [CrossRef] [Green Version]
- Paliaga, G.; Luino, F.; Turconi, L.; Marincioni, F. Exposure to Geo-Hydrological Hazards of the Metropolitan Area of Genoa, Italy: A Multi-Temporal Analysis of the Bisagno Stream. Sustainability 2020, 12, 1114. [Google Scholar] [CrossRef] [Green Version]
- Viciani, D.; Dell’Olmo, L.; Gabellini, A.; Gigante, D.; Lastrucci, L. Landscape dynamics of Mediterranean montane grasslands over 60 years and implications for habitats conservation. A case study in the northern Apennines (Italy). Landsc. Res. 2018, 43, 952–964. [Google Scholar] [CrossRef]
- Antrop, M. Landscape change and the urbanization process in Europe. Landsc. Urban Plan 2004, 67, 9–26. [Google Scholar] [CrossRef]
- Rulli, M.C.; Odorico, P.D. Food appropriation through large scale land acquisitions. Environ. Res. Lett. 2014, 9, 064030. [Google Scholar] [CrossRef]
- Niu, S.; Fang, B. Cultivated Land Protection System in China from 1949 to 2019: Historical Evolution, Realistic Origin Exploration and Path Optimization. China Land Sci. 2019, 33, 1–12. (In Chinese) [Google Scholar]
- Ministry of Natural Resources of the People’s Republic of China. Notice on Fully Implementing Special Protection for Permanent Basic Farmland; 2018. Available online: http://f.mnr.gov.cn/201803/t20180323_1766137.html (accessed on 23 March 2018).
- Mazzocchi, C.; Sali, G.; Corsi, S. Land use conversion in metropolitan areas and the permanence of agriculture: Sensitivity Index of Agricultural Land (SIAL), a tool for territorial analysis. Land Use Policy 2013, 35, 155–162. [Google Scholar] [CrossRef]
- Terres, J.M.; Scacchiafichi, L.N.; Wania, A.; Ambar, M.; Anguiano, E.; Buckwell, A.; Coppola, A.; Gocht, A.; Källström, H.N.; Pointereau, P.; et al. Farmland abandonment in Europe: Identification of drivers and indicators, and development of a composite indicator of risk. Land Use Policy 2015, 49, 20–34. [Google Scholar] [CrossRef]
- Kim, D.-S.; Mizuno, K.; Kobayashi, S. Analysis of urbanization characteristics causing farmland loss in a rapid growth area using GIS and RS. Paddy Water Environ. 2003, 1, 189–199. [Google Scholar] [CrossRef]
- Zubair, O.A.; Ji, W.; Festus, O. Urban Expansion and the Loss of Prairie and Agricultural Lands: A Satellite Remote-Sensing-Based Analysis at a Sub-Watershed Scale. Sustainability 2019, 4673. [Google Scholar] [CrossRef] [Green Version]
- Fazal, S. Urban expansion and loss of agricultural land—a GIS based study of Saharanpur City, India. Environ. Urban. 2000, 12, 133–149. [Google Scholar] [CrossRef]
- Song, W.; Pijanowski, B.C.; Tayyebi, A. Urban expansion and its consumption of high-quality farmland in Beijing, China. Ecol. Indic. 2015, 54, 60–70. [Google Scholar] [CrossRef]
- Antrop, M. Changing patterns in the urbanized countryside of Western Europe. Landsc. Ecol. 2000, 15, 257–270. [Google Scholar] [CrossRef]
- Acquaotta, F.; Faccini, F.; Simona, F.; Paliaga, G. Increased flash flooding in Genoa Metropolitan Area: a combination of climate changes and soil consumption? Meteorol. Atmos. Phys. 2019, 131, 1099–1110. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A. Zoning land for agricultural protection by the integration of remote sensing, GIS, and cellular automata. Photogramm. Eng. Remote Sens. 2001, 67, 471–477. [Google Scholar]
- Yang, X.; Jin, X.; Jia, P.; Ren, J. Designation method and demonstration of permanent basic farmland in county level on view of multi-planning integration. Trans. Chin. Soc. Agric. Eng. 2019, 35, 250–259. (In Chinese) [Google Scholar]
- Liu, Y.; Liu, C.; He, Z. Delineation of Basic Farmland Based on Local Spatial Autocorrelation Analysis of Cultivated Land Quality in Pixel Scale. Trans. Chin. Soc. Agric. Mach. 2019, 50, 260–268, 319. (In Chinese) [Google Scholar]
- Zhang, Y.; Yan, H.; Zhao, X.; Sun, S. Permanent prime farmland demarcation in city periphery inpeninsula hill areas: A case of Haiyang City in Shandong Province. Chin. J. Eco-Agric. 2018, 26, 1080–1088. (In Chinese) [Google Scholar]
- Cheng, Q.; Jiang, P.; Cai, L.; Shan, J.; Zhang, Y.; Waang, L.; Li, M.; Li, F.; Axing, Z.; Dong, C. Delineation of a permanent basic farmland protection area around a city centre: Case study of Changzhou City, China. Land Use Policy 2017, 60, 73–89. [Google Scholar]
- Bian, Z.; Liu, L.; Wang, Q.; Qian, F.; Kang, M.; Yang, Z.; Zhu, R. Permanent prime farmland demarcation in urban fringes based on the LESA system. Resour. Sci. 2015, 37, 2172–2178. (In Chinese) [Google Scholar]
- Ren, Y.; Sun, J.; Liu, Y.; Pan, Y. Delineation Method of Permanent Basic Farmland on County Scale. Trans. Chin. Soc. Agric. Mach. 2017, 48, 135–141. (In Chinese) [Google Scholar]
- Hu, F.; Ke, X.; Chai, M.; Yu, Y.; Xie, X.; Ma, Y. Determining the Urban Growth Boundary by Balancing Urban Expansion and Permanent Basic Farmland Protection: A Case Study of Wuhan. Geogr. Geo-Inf. Sci. 2019, 35, 72–77. (In Chinese) [Google Scholar]
- Liu, X.; Li, X.; Tan, Z.; Chen, Y. Zoning farmland protection under spatial constraints by integrating remote sensing, GIS and artificial immune systems. Int. J. Geogr. Inf. Sci. 2011, 25, 1829–1848. [Google Scholar] [CrossRef]
- Zeng, J.; Shao, J.; Wei, C.; Xie, D. Delimitation of permanent basic farmland in mountain and hill areas in southwest China based on multiple-objective decision model. Trans. Chin. Soc. Agric. Eng. 2014, 30, 263–274. (In Chinese) [Google Scholar]
- Ma, S.; Wu, K.; Lao, C.; Zhong, W. Establishment and application of iZone system for intelligently identifying preserved zones of permanent prime farmland. Trans. Chin. Soc. Agric. Eng. 2017, 33, 276–282. (In Chinese) [Google Scholar]
- Eldrandaly, K. A GEP-based spatial decision support system for multisite land use allocation. Appl. Soft Comput. J. 2010, 10, 694–702. [Google Scholar] [CrossRef]
- Wang, D.; Li, F.; Chen, D. Research on Optimal Land Use Allocation Based on Pareto Optimal and Multi-particle Swarm Algorithm. Resour. Environ. Yangtze Basin 2019, 28, 2019–2029. (In Chinese) [Google Scholar]
- Mao, Y.; Liu, Y.; Wang, H.; Tang, W. A Spatial-Territorial Reorganization Model of Rural Settlements Based on Graph Theory and Genetic Optimization. Sustainability 2017, 9, 1370. [Google Scholar] [CrossRef] [Green Version]
- Hao, L.; Su, X.; Singh, V.P.; Ayantobo, O.O. Spatial Optimization of Agricultural Land Use Based on Cross-Entropy Method. Entropy 2017, 19, 592. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Ming, D.; Lv, X.; Zhou, K.; Bao, H.; Hong, Z. SO-CNN based urban functional zone fine division with VHR remote sensing image. Remote. Sens. Environ. 2020, 236, 111458. [Google Scholar] [CrossRef]
- Bahram, S.; Saadi, M.M.; Biswajeet, P.; Alamri, A.M. Irrigation Water Allocation at Farm Level Based on Temporal Cultivation-Related Data Using Meta-Heuristic Optimisation Algorithms. J. Hydrol. Eng. 2019, 11, 2611. [Google Scholar]
- Wu, T.; Song, L.; Liang, K. Study on Optimization of Emergency Public Service Facilities Layout Based on SA Algorithm——Shanghai Changning district emergency shelter as an example. Math. Pract. Theory 2018, 48, 32–40. (In Chinese) [Google Scholar]
- Wei, Y.; Chen, Y.; Tong, X.; Ou, X. Research on Optimizing the Spatial Pattern of Rural Residential Points Based on Improved Particle Swarm Optimization Algorithm. Geogr. Geo-Inf. Sci. 2014, 30, 72–76. (In Chinese) [Google Scholar]
- Liu, Y.; Tang, W.; He, J.; Liu, Y.; Ai, T.; Liu, D. A land-use spatial optimization model based on genetic optimization and game theory. Comput. Environ. Urban Syst. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Parth, P.; Bhaben, K.; Deepak, S. A game theory based land layout optimization of cities using genetic algorithm. Int. J. Manag. Sci. Eng. Manag. 2019, 14, 155–168. [Google Scholar]
- Ma, S.; Liu, F.; Ma, C.; Ouyang, X. Integrating logistic regression with ant colony optimization for smart urban growth modelling. Front. Earth Sci. 2020, 14, 77–89. [Google Scholar] [CrossRef]
- Ma, S.; Li, X.; Cai, Y. Delimiting the urban growth boundaries with a modified ant colony optimization model. Comput. Environ. Urban Syst. 2017, 62, 146–155. [Google Scholar] [CrossRef]
- Hou, J.; Ho, B.; Sun, S. Spatial Optimization of Low-Impact Development Facilities Based on a p-Median Model and an Ant Colony Optimization. J. Hydrol. Eng. 2019, 24, 04019055. [Google Scholar] [CrossRef]
- Tao, Z.; Cheng, Y.; Dai, T. Rosenberg, M. W. Spatial optimization of residential care facility locations in Beijing, China: maximum equity in accessibility. Prog. Geogr. 2015, 13, 33. [Google Scholar]
- Wang, H.; Zhu, F. Site selection model of land consolidation projects based on multi-objective optimization PSO. Trans. Chin. Soc. Agric. Eng. 2015, 31, 255–263. (In Chinese) [Google Scholar]
- Zhao, Y.; Zhang, X.; Kang, T. An Ant Colony Algorithm Based on Multi-way Tree for Optimal Site Location. Acta. Geogr. Sinica 2011, 66, 279–286. [Google Scholar]
- Li, F.; Gong, Y.; Cai, L.; Sun, C. Sustainable Land-Use Allocation: A Multi-objective Particle Swarm Optimization Model and Application in Changzhou, China. J. Urban Plan. Dev. 2018, 144, 2074–2081. [Google Scholar] [CrossRef]
- Zohreh, M.; Sadi, M.M.; Majid, H. Allocation of urban land uses by Multi-Objective Particle Swarm Optimization algorithm. Int. J. Geogr. Inf. Sci. 2013, 27, 542–566. [Google Scholar]
- Theodor, S.J.; Ron, G. A multi-objective GIS-based land use planning algorithm. Comput. Environ. Urban Syst. 2014, 46, 25–34. [Google Scholar]
- Jonas, S.; Kalyanmoy, D.; Erik, G.; Sander, K. Using multi-objective optimization to secure fertile soils across municipalities. Appl. Geogr. 2018, 97, 75–84. [Google Scholar]
- Liu, Y.; Wang, H.; Ji, Y.; Ji, Y.L.; Liu, Z.Q.; Zhao, X. Land Use Zoning at the County Level Based on a Multi-Objective Particle Swarm Optimization Algorithm: A Case Study from Yicheng, China. Int. J.Environ. Res. Public Health 2012, 9, 2801–2826. [Google Scholar] [CrossRef] [Green Version]
- Su, R.; Cao, Y. Methods Analysis on Cultivated Land Use Changes in China——Based on Driving and Simulation. Chin. J. Agric. Resour. Reg. Plan. 2019, 40, 96–105. (In Chinese) [Google Scholar]
- Xiao, R.; Chen, T. Relationships of swarm intelligence and artificial immune system. Int. J. Bio-Inspired Comput. 2013, 5, 35–51. [Google Scholar] [CrossRef]
- Carlisle, A.; Dozier, G. An off-the-shelf PSO. In Proceedings of the Workshop on Particle Swarm Optimization, Purdue School of Engineering and Technology, Indianapolis, IN, USA, 1 January 2001; pp. 1–6. [Google Scholar]









| No. | Data | Description of Data Source | Department of Data Source |
|---|---|---|---|
| 1 | Soil fertility, topography and landforms, irrigation facilities, field shape, field size | The latest results of the cultivated land quality grades, cultivated land quality update evaluation results, and agricultural land classification results | Agriculture Bureau |
| 2 | Land use type | The land use change survey results, the results of the third national land survey, three-line delineation results and data | Natural Resources Bureau |
| 3 | The forest net and shelter forest | The forestry resource survey results | Forestry Bureau |
| 4 | Annual average temperature, annual average precipitation | Meteorological monitoring results | Meteorological Bureau |
| 5 | Road accessibility | Road distribution maps, traffic planning, and layout information | Traffic and Transportation Bureau |
| 6 | Ecological red line constraint | The "13th Five-Year Plan" for environmental protection | Environmental Protection Bureau |
| 7 | Town bound boundaries | Industrial and tourism development planning | Development and Reform Commission |
| Land Use Grade | 5 | 6 | 7 | 8 |
| Mapped value | 1.0 | 0.7 | 0.4 | 0.1 |
| N | ||||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 100 | 0.9 | 0.4 | 2.8 | 1.3 | [0,1] | [0,1] | 6 |
| Scheme | Weight of Land Suitability | Weight of Land Continuity | Weight of Land Stability |
|---|---|---|---|
| D | 1.00 | 0.00 | 0.00 |
| A | 0.80 | 0.10 | 0.10 |
| E | 0.50 | 0.25 | 0.25 |
| H | 0.34 | 0.33 | 0.33 |
| Scheme | Land Suitability | Land Continuity | Land Stability |
|---|---|---|---|
| D (1.0:0.0:0.0) | 39,353.9 | 0.7923 | 41,763.87 |
| A (0.8:0.1:0.1) | 39,027.4 | 0.8481 | 41,879.81 |
| E (0.5:0.25:0.25) | 36,891.8 | 0.8864 | 43,312.71 |
| H (0.34:0.33:0.33) | 34,988.9 | 0.9102 | 44,836.75 |
| Scheme | Weight of Land Suitability | Weight of Land Continuity | Weight of Land Stability |
|---|---|---|---|
| B | 0.10 | 0.80 | 0.10 |
| F | 0.25 | 0.50 | 0.25 |
| H | 0.34 | 0.33 | 0.33 |
| D | 1.00 | 0.00 | 0.00 |
| Scheme | Land Suitability | Land Continuity | Land Stability |
|---|---|---|---|
| B(0.1:0.8:0.1) | 33,828.2 | 0.9646 | 42,174.14 |
| F(0.25:0.5:0.25) | 34,314.2 | 0.9293 | 43,617.10 |
| H(0.34:0.33:0.33) | 34,988.9 | 0.9102 | 44,836.75 |
| D(1.0:0.0:0.0) | 39,353.9 | 0.7923 | 41,763.87 |
| Scheme | Weight of Land Suitability | Weight of Land Continuity | Weight of Land Stability |
|---|---|---|---|
| C | 0.10 | 0.10 | 0.80 |
| G | 0.25 | 0.25 | 0.50 |
| H | 0.34 | 0.33 | 0.33 |
| D | 1.00 | 0.00 | 0.00 |
| Scheme | Land Suitability | Land Continuity | Land Stability |
|---|---|---|---|
| C (0.1:0.1:0.8) | 33,414.2 | 0.8273 | 49,230.57 |
| G (0.25:0.25:0.5) | 34,014.2 | 0.8775 | 47,161.21 |
| H (0.34:0.33:0.33) | 34,988.9 | 0.9102 | 44,836.75 |
| D (1.0:0.0:0.0) | 39,353.9 | 0.7923 | 41,763.87 |
| Model | Average Convergence Iterations | Mean Convergence Time (h) |
|---|---|---|
| PSO | 79 | 1.7 |
| AIA | 86 | 2.3 |
| AIA-PSO | 52 | 4.1 |
| Model | |||
|---|---|---|---|
| PSO | 34,988.8 | 0.9102 | 44,836.75 |
| AIA | 38,268.3 | 0.9273 | 45,397.92 |
| AIA-PSO | 36,163.4 | 0.9561 | 46,934.68 |
| Model | Mean Value | Standard Deviation | ||||
|---|---|---|---|---|---|---|
| PSO | 34,984.81 | 0.91006 | 44,836.769 | 174.56 | 0.00406 | 86.948 |
| AIA | 38,255.35 | 0.92736 | 45,703.902 | 277.52 | 0.00682 | 153.377 |
| AIA-PSO | 36,127.13 | 0.95574 | 46,923.043 | 179.63 | 0.00604 | 103.046 |
| No. | Administrative Regions | Type of Cultivated Land | Average Grade | |||
|---|---|---|---|---|---|---|
| Code | Name of Town | Irrigated | Dry | Subtotal | ||
| 1 | 410621100 | Chengguan | 0 | 0 | 0 | |
| 2 | 410621101 | Shantang | 10,827.39 | 0 | 10,827.39 | 7.03 |
| 3 | 410621102 | Tunzi | 9071.26 | 313.53 | 9384.79 | 6.42 |
| 4 | 410621104 | Xinzhen | 8847.94 | 2.69 | 8850.63 | 6.18 |
| 5 | 410621105 | Xiaohe | 7687.47 | 0 | 7687.47 | 6.05 |
| 6 | 410621106 | Liyang | 3190.08 | 0 | 3190.08 | 6.48 |
| 7 | 410621107 | Weixian | 6073.82 | 7.71 | 6081.53 | 5.73 |
| 8 | 410621200 | Wangzhuang | 5858.45 | 4.62 | 5863.07 | 6.15 |
| 9 | 410621201 | Baisi | 8249.82 | 67.27 | 8317.09 | 6.2 |
| 10 | 410621203 | Liyang | 0 | 0 | 0 | |
| 11 | 410621204 | Xun County woodland | 0 | 0 | 0 | |
| 12 | 410621205 | Shantang township woodland | 0 | 0 | 0 | |
| 13 | 410621206 | Xun County farm | 13.81 | 0 | 13.81 | 8 |
| 14 | 410621208 | Original forest farm six team | 11.93 | 0 | 11.93 | 8 |
| 15 | 410621209 | Original forest farm six team | 37.48 | 0 | 37.48 | 6 |
| 16 | 410621210 | Disputed areas of Dongzhu, Zhongzhu and Xizhu | 0 | 0 | 0 | |
| Total | 59,869.45 | 395.82 | 60,265.27 | 6.32 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Li, W.; Huang, W.; Nie, K. A Multi-Objective Permanent Basic Farmland Delineation Model Based on Hybrid Particle Swarm Optimization. ISPRS Int. J. Geo-Inf. 2020, 9, 243. https://doi.org/10.3390/ijgi9040243
Wang H, Li W, Huang W, Nie K. A Multi-Objective Permanent Basic Farmland Delineation Model Based on Hybrid Particle Swarm Optimization. ISPRS International Journal of Geo-Information. 2020; 9(4):243. https://doi.org/10.3390/ijgi9040243
Chicago/Turabian StyleWang, Hua, Wenwen Li, Wei Huang, and Ke Nie. 2020. "A Multi-Objective Permanent Basic Farmland Delineation Model Based on Hybrid Particle Swarm Optimization" ISPRS International Journal of Geo-Information 9, no. 4: 243. https://doi.org/10.3390/ijgi9040243
APA StyleWang, H., Li, W., Huang, W., & Nie, K. (2020). A Multi-Objective Permanent Basic Farmland Delineation Model Based on Hybrid Particle Swarm Optimization. ISPRS International Journal of Geo-Information, 9(4), 243. https://doi.org/10.3390/ijgi9040243





